Abstract
Nucleus pulposus (NP) cells of the intervertebral disk (IVD) have unique morphological characteristics and biologic responses to mechanical stimuli that may regulate maintenance and health of the IVD. NP cells reside as single cell, paired or multiple cells in a contiguous pericellular matrix (PCM), whose structure and properties may significantly influence cell and extracellular matrix mechanics. In this study, a computational model was developed to predict the stress–strain, fluid pressure and flow fields for cells and their surrounding PCM in the NP using three-dimensional (3D) finite element models based on the in situ morphology of cell–PCM regions of the mature rat NP, measured using confocal microscopy. Three-dimensional geometries of the extracellular matrix and representative cell–matrix units were used to construct 3D finite element models of the structures as isotropic and biphasic materials. In response to compressive strain of the extracellular matrix, NP cells and PCM regions were predicted to experience volumetric strains that were 1.9–3.7 and 1.4–2.1 times greater than the extracellular matrix, respectively. Volumetric and deviatoric strain concentrations were generally found at the cell/PCM interface, while von Mises stress concentrations were associated with the PCM/extracellular matrix interface. Cell–matrix units containing greater cell numbers were associated with higher peak cell strains and lower rates of fluid pressurization upon loading. These studies provide new model predictions for micromechanics of NP cells that can contribute to an understanding of mechanotransduction in the IVD and its changes with aging and degeneration.
Keywords: Nucleus pulposus, Intervertebral disk, Cell, Pericellular matrix, In situ morphology, Mechanics
1 Introduction
The nucleus pulposus (NP) is a highly hydrated and gel-like tissue located in the center of the intervertebral disk (IVD), providing for compressive load support and load transfer to adjacent structures in the spine. The NP tissue is maintained by NP cells, which have been demonstrated to respond to different types of mechanical stimuli, such as compressive, tensile or shear stresses and strains, fluid flow, hydrostatic or osmotic pressures, and electrokinetic effects in many mechanobiology studies (Lotz et al. 2002; Setton and Chen 2004; Iatridis et al. 2006; Setton and Chen 2006). Although the effects of mechanical loading have been well studied at the organ and tissue level using finite element modeling, little is known about the associated micromechanical stimuli at the cell level due to the lack of data on complex cell and pericellular matrix geometries or mechanical properties, which together may influence cell–matrix interactions. Studies that advance an understanding of micromechanical stimuli in the NP cell have potential to reveal the magnitudes of mechanical stimuli that regulate mechanobiologic responses and their changes with disk degeneration and aging.
Cells of the immature NP may be rounded and exist in “clusters” with significant changes in morphology observed with maturity and aging of the IVD (Trout et al. 1982a,b; Ishii et al. 1991; Hastreiter et al. 2001; Cao et al. 2007). NP cells are surrounded by a pericellular matrix (PCM) that is rich in type VI collagen (Wu et al. 1987; Roberts et al. 1991) and reside as single cell, paired or multiple cells in a contiguous PCM in the NP tissue (Hastreiter et al. 2001; Cao et al. 2007). More than half of NP cells have been found to reside in a common PCM shared by multiple cells in the immature (>80%) or mature (∼60%) rat lumbar IVD, representing both chondrocyte-like cells and notochordal cells (Cao et al. 2007). It is likely that the PCM region in the NP influences the mechanical environment at the cell level upon loading of the extracellular matrix (ECM), as seen for chondrocytes in articular cartilage (Alexopoulos et al. 2005a,b; Guilak et al. 2006; Michalek and Iatridis 2007) and fibrochondrocytes in the anulus fibrosus (Cao et al. 2009). However, the presence of the PCM containing multiple cells and the associated mechanical role of the PCM in the NP has not been previously studied.
Finite element modeling (FEM) is particularly useful in the study of cell mechanics in cases where loading conditions or mechanical responses cannot be easily quantified experimentally. Various theoretical models have been developed to predict single cell mechanics in the extracellular matrices of articular cartilage (Wu et al. 1999; Guilak 2000; Wu and Herzog 2000; Haider 2004; Alexopoulos et al. 2005a,b; Guilak et al. 2006; Korhonen et al. 2006; Wu and Herzog 2006; Haider and Guilak 2007; Michalek and Iatridis 2007; Kim et al. 2008), the anisotropic meniscus (Upton et al. 2006) and the anisotropic anulus fibrosus and isotropic NP (Baer and Setton 2000; Baer et al. 2003; Cao et al. 2009), showing complex dependence of model predictions on geometric and regional inhomogeneity and material properties. As an example, a previous study reporting FEM predictions of isolated NP cell mechanics in an extracellular matrix subjected to compression predicted lower strain values in cells when compared to extracellular matrix due to assumed properties for both cell and matrix (Baer et al. 2003). These previous models for NP cells (Baer and Setton 2000; Baer et al. 2003) assumed 2D axi-symmetric cell geometry (spheroidal or ellipsoidal) and thus could not represent the “cell cluster” features observed in the NP (Trout et al. 1982a,b; Ishii et al. 1991; Hastreiter et al. 2001; Cao et al. 2007) nor include a PCM region that has since been demonstrated to significantly affect predicted cell stress and strain, and fluid pressure and flow profiles for other cell types (Guilak 2000; Alexopoulos et al. 2005a,b; Haider et al. 2006; Kim et al. 2008; Cao et al. 2009). In this respect, a fully 3D FEM constructed from geometrically accurate 3D in situ morphology of the PCM and enclosed cell(s) has potential to advance an understanding of how these features contribute to the micromechanics of NP cells.
The objective of this study was to describe the micromechanical environment of NP cells from theoretical FEM predictions based on 3D in situ morphology of the PCM and enclosed cell(s) in the NP. The 3D solid geometries of the PCM and cell regions were segmented and registered from serial confocal images of cell–matrix units (CMU—cell and associated PCM) from mature rat NP tissues and used to generate 3D meshed volumes for 3D FEM of interacting extracellular matrix, PCM and cell sub-domains. FEM predictions of the cell–PCM units as linearly elastic, biphasic and isotropic domains based on custom code (COMSOL Multiphysics) were used to investigate the local stress, strain, fluid pressure and flow fields in the cell and PCM domains that may be experienced by NP cells residing as single cell units, paired or multiple cell units.
2 Methods
2.1 3D biphasic finite element method
A weak form of 3D mixed u–p formulation (Wayne et al. 1991; Meng et al. 2002) of linear biphasic theory (Mow et al. 1980) was implemented and validated in COMSOL Multiphysics using “custom weak form” application mode with structural mechanics module, as described previously (Cao et al. 2009). As is standard for this model, the solid phase for each domain was modeled as a linearly elastic solid with strain-independent permeability values, while the fluid phase was modeled as an incompressible and inviscid fluid.
2.2 3D geometry registration and meshing
Three-dimensional reconstructions and morphometric measurements of the PCM and cell regions were obtained in situ using fluorescence confocal microscopy of en bloc sections of the NP from the mature rat lumbar disk immunolabeled for type VI collagen (Cao et al. 2007). A total of six distinct cell–matrix units (CMU) were chosen for FEM presented here as representative of a majority of CMU observed for the NP region. These CMU models were chosen with aspect ratios around the mean values in each CMU subgroup (1 cell, 2 cells, and 3 or 4 cells, 2 representative models for each CMU group, Fig. 1). The reconstructed surfaces of the PCM and enclosed cell(s) in the CMU were separately registered as 3D solid geometry objects in COMSOL by custom programs written in MATLAB (The Mathworks, Inc., Natick, MA) and COMSOL Script (COMSOL, Inc., Burlington, MA), as described previously (Cao et al. 2009). A cube representing the ECM with dimensions (a × a × h) of at least three times the PCM dimensions was then added to the geometry, in which a is the width of the transverse plane of the ECM and h is the height of the ECM along the longitudinal direction (the principal axis of the CMU). A preliminary study confirmed that the choice of this ECM size was sufficient to accurately predict viscoelastic responses in all sub-domains that were independent of dimension and associated with acceptable computational cost. Thus, a 3D solid geometry model with three sub-domains including the extracellular matrix, PCM and enclosed cell(s) was built based on their in situ 3D morphologies. These three sub-domains were exclusive to each other but physically connected via enforcement of continuity of displacement and pressure boundary conditions.
Fig. 1.
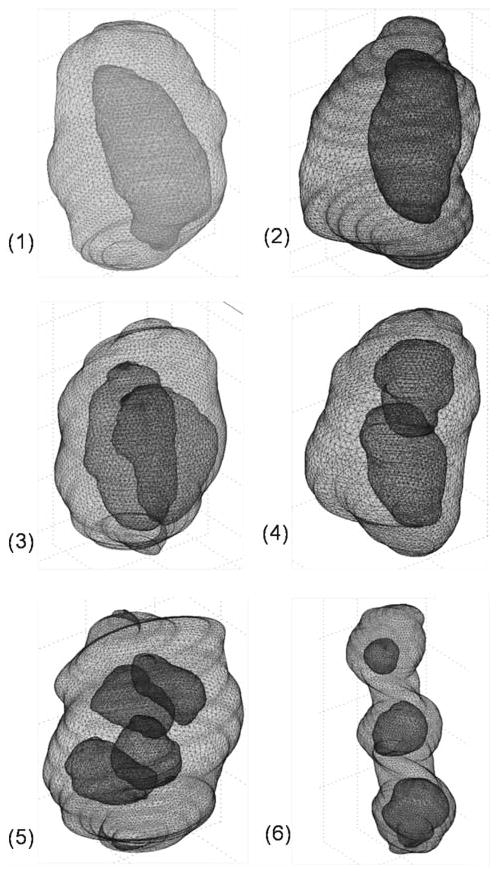
Registered 3D solid geometries in tetrahedron meshes in the nucleus pulposus. Models include different cell–matrix unit (CMU) subgroups: 1 cell CMUs 1 and 2; 2 cell CMUs 3 and 4; and 3 or 4 cell CMUs 5 and 6. For clarity, only meshes on the surfaces of the pericellular matrix and cells are shown above (not shown on equivalent scales)
The combined 3D solid objects were meshed using tetrahedron elements in COMSOL Multiphysics (Fig. 1). The registered 3D geometries required a large number of tetrahedron elements to generate good quality meshes due to the curvature and roughness on the surfaces of the PCM and cells, as seen in examples of meshed CMUs in the NP region. The meshes generally consisted of 28,000–35,000 tetrahedron elements and approximately 120,000–150,000 degrees of freedom, dependent on the CMU size and shape. The average minimum element quality index across all models was ∼0.15, satisfying the requirement for tetrahedral elements in COMSOL (>0.1). In the elemental interpolation, the shape function for pressure (linear) was set to be one order lower than displacements (quadratic) to obtain convergence in COMSOL.
2.3 Material properties
FEM definitions closely follow those developed previously for anulus fibrosus and PCM domains in the IVD (Cao et al. 2009) with the exception of the isotropic material assumption that is invoked for all material domains in the NP here. In brief, the extracellular matrix, PCM and cell sub-domains were assumed to be isotropic, linearly elastic biphasic materials with a constant permeability (Mow et al. 1980). The material constants were chosen from the literature for the extracellular matrix (Iatridis et al. 1997; Johannessen et al. 2004; Johannessen and Elliott 2005; Perie et al. 2005; Cloyd et al. 2007), PCM (Alexopoulos et al. 2003, 2005a,b) and cells (Guilak et al. 1999) (Table 1).
Table 1.
Material properties chosen for the extracellular matrix, pericellular matrix and cells in the nucleus pulposus
| Young's Modulus E (kPa) | Poisson's ratio v | Permeability k (m4/N-s) | |
|---|---|---|---|
| ECM | 5 | 0.45 | 2 × 10−15 |
| PCM | 30 | 0.2 | 7 × 10−17 |
| Cell | 0.9 | 0.4 | 4 × 10−15 |
The extracellular matrix (Umehara et al. 1996; Iatridis et al. 1997; Johannessen et al. 2004; Johannessen and Elliott 2005; Perie et al. 2005; Cloyd et al. 2007), pericellular matrix (Alexopoulos et al. 2003, 2005a,b) and cell (Guilak et al. 1999) of the nucleus pulposus are assumed to be biphasic, linearly elastic and isotropic materials
2.4 Boundary conditions
The 3D solid models were used to simulate a stress relaxation response under application of a compressive deformation in a laterally unconfined configuration, a simplified loading condition that may be experienced by the NP tissue under physiological loading (Tsantrizos et al. 2005). Compressive displacements were applied instantaneously to the top surface (z = h/2) of the NP volume to correspond to a constant compressive strain (5%) generated in the z-direction across all models. Free draining was assumed on all exterior faces of the NP volume, or cube.
The associated boundary conditions on six surfaces of the cubic NP matrix were as follows for all time (t ≥ 0):
| (1) |
| (2) |
| (3) |
| (4) |
Here, t is time and H(t) is the Heaviside step function (modeled as a smoothed Heaviside step function), u, v, w are three displacement components, p is the fluid pressure, w0 is the applied displacement along the z-axis and S is the applied surface traction on the boundary. The interfaces between the cell and PCM or the PCM and extracellular matrix were assumed to be fully bonded.
2.5 Solution procedure and post-processing
The models were solved for a simulation time of 0–500 s after load application using a generalized minimal residual method (GMRES) as an iterative linear system solver and a backward Euler difference approximation for time-dependent analysis (computational times of 30,000–50,000 s across all models; Dell Inspiron, 3.2GHz 32-bit computer with 2GB RAM). The convergence was examined by refining the mesh and tightening the tolerance. Post-processing results to calculate stress, strain, fluid pressure and fluid pressure gradients were obtained using COMSOL post-processing features. Additional measurements such as the average volumetric strain, ε̄v, and average fluid pressure, p̄, were calculated from the integrals of pressure and strain in each sub-domain, Ω, according to the following equations, respectively.
| (5) |
| (6) |
where V represented the volume of the sub-domain. Note that these averaging measurements provide valuable information of the overall response for each sub-domain with complex 3D geometry; however, their values in the extracellular matrix domain may be underestimated due to a boundary effect caused by averaging over all elements in the extracellular matrix that included large domains near the boundaries on which the pressure or displacement was set to zero.
An effective von Mises stress, σe, was defined as
| (7) |
and a deviatoric strain invariant, εdev, was defined to describe the shear strain as,
| (8) |
where εm = (εxx + εyy + εzz) /3. All predicted values were compared across models to examine for differences among extracellular, PCM or cellular levels, and to examine for differences among the three CMU subgroups.
3 Results
Mechanics in the extracellular matrix domain were generally insensitive to the presence of subdomains of the PCM and enclosed cell(s). Upon loading in compression, fluid pressure in the extracellular matrix domain first rose to a peak value followed by decay to zero pressure at equilibrium, representative of the behavior of a biphasic material under free-draining boundary conditions. The rate of fluid pressurization and decay was similar at extracellular matrix and PCM levels (Fig. 2a, extracellular matrix values not shown). The decay of fluid pressurization in the cell domain occurred more slowly than for the PCM domain and decreased with an increasing number of cells enclosed in one PCM, as determined by comparing the 1 cell, 2 cell, and 3 or 4 cell CMU subgroups (Fig. 2b).
Fig. 2.
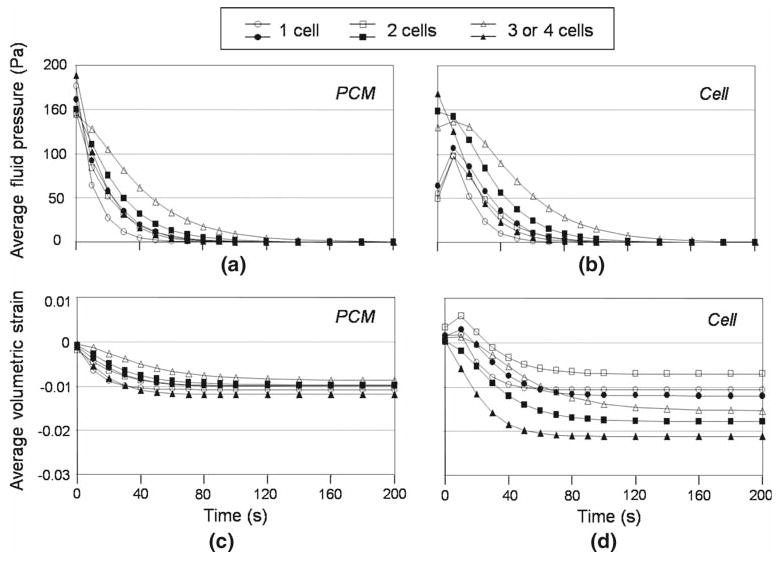
Average fluid pressure and volumetric strain at multiple material domains in the nucleus pulposus. The average fluid pressures in the PCM domain a in the 1 cell, 2 cell, and 3 or 4 cell cell–matrix unit subgroups showed similar temporal responses with negative pressures throughout time, while the overall fluid pressures in the cell domain b showed a period of positive fluid pressure characteristic of flow reversal after some time of loading. The pressurization rate was lower in the cell domain and decreased with increasing cell numbers in one PCM. Comparisons of average volumetric strain among the PCM c and cell d domains in the 1 cell, 2 cell, and 3 or 4 cell cell–matrix unit subgroups showed that the average volumetric strain in the extracellular matrix (−0.006) was amplified in the PCM domain (∼ −0.01) and furthermore in the cell domain (−0.007–0.021) with a value depending on the cell number and relative position within the PCM. Open and closed signs represent two different models in the same cell–matrix unit subgroup
The average volumetric strain in the extracellular matrix exhibited rapid onset of an equilibrium value (−0.006), as expected for the assumed short path for fluid exudation in the extracellular matrix (data not shown). The average volumetric strain in the PCM decayed more rapidly than cell domains to an equilibrium value, with fewer variations when comparing different CMU subgroups (Fig. 2c, d). In general, the volumetric strains were spatially non-uniform in the PCM but not cell domains (Fig. 3). The predicted average volumetric strain in the PCM of NP tissues at equilibrium was significantly higher than that in the extracellular matrix with a strain amplification ratio ranging from 1.4 to 2.1, giving evidence of a strain amplification effect in the PCM noted previously for modeling of chondrons and anulus fibrosus cells (Guilak and Mow 2000; Cao et al. 2009). Large variations in equilibrium volumetric strains in the cell domain were observed depending on cell number and relative position within the PCM (Figs. 2, 3), with the highest value of strain amplification ratio in 3 or 4 cell CMUs (up to 3.7) and lowest in 1 cell CMUs (∼1.9). Of interest was a trend observed for the cell domain, which was predicted to experience a volume gain for short periods after loading followed by a large volume loss (Figs. 2, 3); this behavior was not noted for the PCM nor extracellular matrix domains. The strain concentration was highest at the cell/PCM interface and decreased over time (Fig. 3). No consistent nor significant differences were noted in average PCM nor cell volumetric strain among the different CMU subgroups, likely due to averaging over values for strain within one PCM, or among cells within one CMU, that were shown to be highly variable.
Fig. 3.
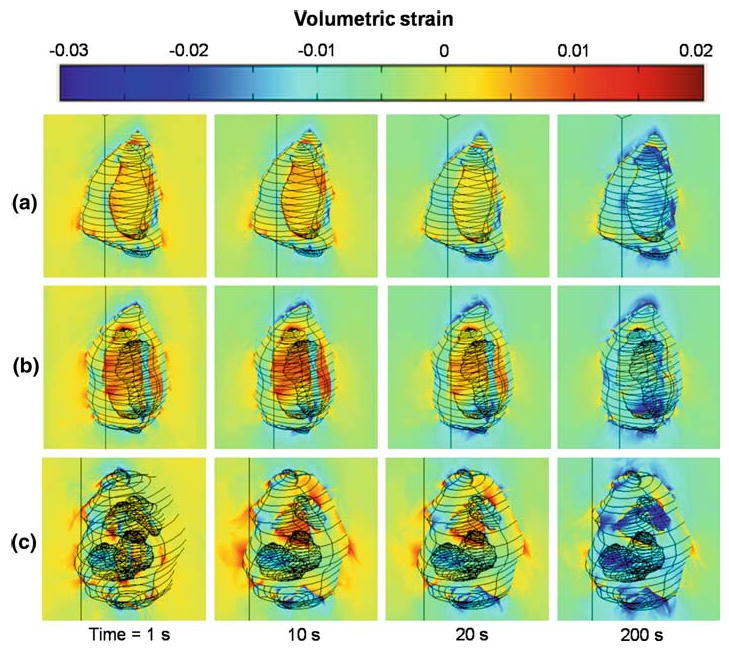
Temporal responses of volumetric strain at multiple material domains in the nucleus pulposus. High strain concentration (generally with positive values) was seen near the cell/PCM interface and decreased over time. Similar trends were seen among 1 cell a, 2 cell b, and 3 or 4 cell c cell–matrix unit subgroups
The deviatoric strains were higher in the extracellular matrix than in the cell and PCM domains, with virtually zero magnitude of deviatoric strain in the PCM domains (Fig. 4). Deviatoric strain concentrations were seen at the PCM/extracellular matrix interface rather than at the cell/PCM interface and were largest along the long axis of the PCM in all models. No consistent or significant differences were noted in PCM or cell deviatoric strain among the different CMU subgroups.
Fig. 4.

Deviatoric strain at multiple material domains in the nucleus pulposus at equilibrium. The deviatoric strain in the cell domain was 25% lower than that of the extracellular matrix. The strain concentrations were seen at the PCM/extracellular matrix interface, mainly along the long axis of the PCM
The stress was uniform in the far-field of the NP extracellular matrix and inside the cell, but highly non-uniform in the PCM, with nearly zero magnitude of stress in the cell domain. The effective von Mises stress was highest in the PCM with the largest magnitudes frequently coincident with the region of smallest width of the CMU (Fig. 5). A stress concentration was seen at the cell/PCM interface in this smallest dimension, in accordance with the location of the highest stress gradient. Peak values for the von Mises stress were predicted to be ∼2,000 Pa, although the average value in the PCM domain was ∼800 Pa.
Fig. 5.
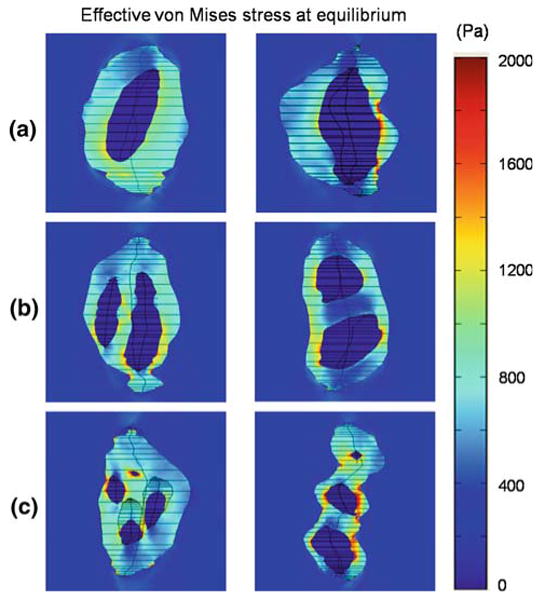
Effective von Mises stress at multiple material domains in the nucleus pulposus. The stress was highly heterogeneous in the PCM, when compared to the extracellular matrix and cells (viewed in YZ plane at x = 0). The stress concentration (up to ∼2,000 Pa) was mainly at the cell/PCM interface and significantly higher than the average value in the PCM (∼800 Pa)
Individual cells in multi-cell-containing CMUs were predicted to experience very similar trends for transient change in pressure, strain and stress upon loading of the NP matrix, although the magnitudes of these parameters were observed to differ among cells within one CMU (Fig. 6). It was difficult to identify a repeatable relationship between cell position or cell geometry and magnitude of average stress, strain or pressure, illustrating the very complex interaction among these variables and mechanical behaviors. Strain or stress concentrations were consistently observed, however, at interfaces with high curvatures.
Fig. 6.
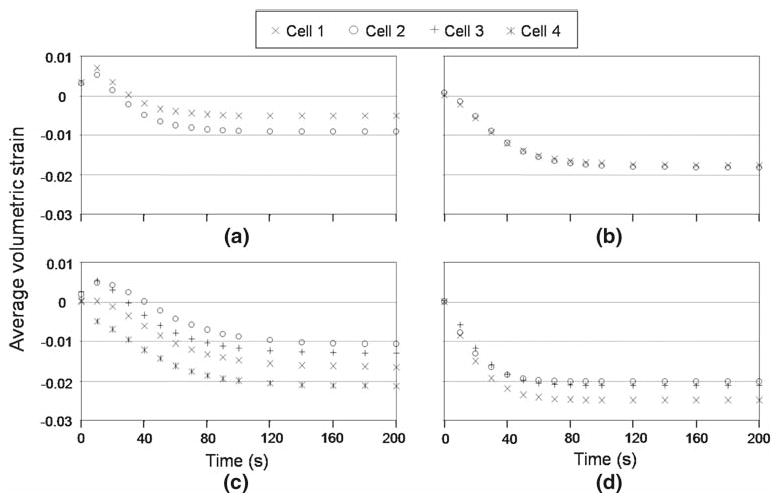
Average volumetric strain of individual cells enclosed in one PCM containing multiple cells in the nucleus pulposus. Similar responses were seen for all cells, but the magnitude of strain can be different for individual cells in both the 2 cell a and b and 3 or 4 cell c and d cell–matrix unit subgroups
4 Discussion
The micromechanical environment of cells and their PCM were predicted for NP cells embedded within the NP extracellular matrix, using a biphasic finite element model and geometrically accurate 3D morphologies. This is the first study to make use of physically realistic 3D cell–PCM geometries that represent the unique feature of NP cells as existing in multi-cell clusters, or in the stacked multi-cell “arrays” more commonly seen in the anulus fibrosus (Bruehlmann et al. 2002; Cao et al. 2007). The results of model predictions suggest that significant differences exist in the strain, stress and pressure fields at extracellular, PCM and cellular levels in the NP, with a dependence on in situ geometry and assumed relative mechanical properties of the three subdomains (Guilak and Mow 2000; Breuls et al. 2002; Michalek and Iatridis 2007). In general, NP cells and PCM domains were predicted to experience volumetric strains that were significantly larger than those in the far-field extracellular matrix, with strain amplification ratios that varied from 1.9 to 3.7 and 1.4 to 2.1, respectively. This trend is consistent with that reported previously for FEM of anulus fibrosus cells, along with observations of peak strain concentrations at the cell/PCM interface and stress concentrations observed at the PCM/extracellular matrix interface. As for modeling of anulus fibrosus cells, the prediction of higher volumetric strain in the NP cell and PCM depends on the assumed properties that were stiffer for the extracellular matrix when compared to cell or PCM domains. An interesting observation was that the mechanical environment in the PCM domains was predicted to be highly non-uniform, in contrast to rather uniform mechanics inside the cell. This observation is related to the narrow dimensions of the PCM (e.g., width) that contained large or multiple cells, as steep pressure and strain gradients, as well as high von Mises stresses, were associated with these smallest dimensions. FEM models not incorporating this unique PCM geometry for the NP cells enabled by labeling of type VI collagen would thus not predict many of the features reported here. Thus, the complex interactions among geometric and mechanical factors gave rise to unique predictions for micromechanics in the NP matrix.
The presence of the PCM greatly alters the local micromechanical environment of NP cells, when compared to previous models of NP cell mechanics (Baer et al. 2003). The volumetric strain amplification at the cellular level depended on the number of cells and relative positions within one PCM, with the highest values at the cell–PCM interface and occurring for cells residing in 3 or 4 cell CMUs (up to 3.7× greater that of the extracellular matrix) when compared to 1 cell CMUs (∼1.9× greater than extracellular matrix). In addition, the NP cell was predicted to experience a complex pattern of transient strain change with an early volume gain followed by a volume loss, due to a net inward fluid flux to the cell domain at short times after loading. These predictions for transient and equilibrium volumetric strains in the NP cells differ from predictions of an earlier model of cells in matrix alone, which reported that NP cells would experience little deformation upon loading (Baer et al. 2003). This difference may arise from the presence of the PCM domain in the current model and the assumed relative material properties among the cell, PCM and ECM domains. These findings suggest that the PCM may be an important component for cell–matrix interactions and that it may regulate mechanotransduction from extracellular to cellular level in the NP tissue, as similarly predicted for chondrocyte mechanics (Guilak 2000; Alexopoulos et al. 2005a,b).
Interstitial fluid flow in the NP is driven by compressive loading and is necessary for nutrient transport and cell–cell communication (Urban et al. 2004). Fluid pressure and flow in the PCM can impart forces on the cells, including fluid shear stress and normal stress at the cell membrane, and they can also have non-mechanical effects on the cells, through transport of solutes and modulation of the pericellular distribution of key signaling proteins or matrix-binding proteins. The peak fluid pressure was generally higher in the PCM of the NP than in the cell and was higher in both cell and PCM domains for CMUs containing multiple cells. CMUs containing multiple cells were associated with smaller characteristic geometric dimensions for the PCM domains, both smaller dimensions separating cells and smaller overall dimensions from cell to extracellular matrix margins. Thus, this higher peak fluid pressure and pressurization rate can be explained by the smaller dimensions existing among mechanical interfaces of the cell, PCM and extracellular matrix. The fluid pressurization rate at the cellular level was always lower than that in the PCM and extracellular matrix, however, suggesting the PCM may provide a shielding layer for acute fluid pressurization and promote fluid pressure homeostasis in the cell. The assumed permeability values for the NP matrix, PCM and cell gave rise to predictions of maximum fluid-flow velocities of 0.0001–0.01 μm/s in the PCM domains, two orders lower than that of the NP tissue. These predicted values may assist an understanding of mechanical force effects on the biologic responses of NP cells.
Significant regional differences of cell–matrix interactions were predicted by region-specific finite element models in the NP, when compared to those in the AF regions (Cao et al. 2009), despite some similar features observed, such as strain amplification, low stress, low fluid pressurization rate and complex fluid pressurization pattern at the cellular level. The magnitudes of micromechanical stimuli that NP cells perceive are quite different from those that AF cells perceive, as shown by predicted values of stress, strain, fluid pressure and flow in the vicinity of cells. For example, AF cells were predicted to experience large amplified volumetric strain and deviatoric strain compared to the ECM values, while NP cells had amplified volumetric strain but attenuated deviatoric strains. In addition, fluid pressurization was significantly longer in the NP (in hundreds of seconds) than that in the AF tissue (in tens of seconds) at multiple material domains. While these differences partly reflect different ECM mechanical environments due to the region-specific material properties assumed for AF and NP problems, these differences were presumed to reflect physiological conditions. As a result, it appears that AF cells may experience large deformations in general, while NP cells may experience more shape change (higher deviatoric strain) but little volume change (lower volumetric strain) under loading. Thus, fluid pressurization may be one of the major mechanisms for NP cells to maintain normal tissue function, which was in agreement with previous models of intervertebral disk cell mechanics (Baer et al. 2003).
An interesting model prediction was that individual cells residing in a shared PCM exhibit similar transient mechanical responses to loading of the NP matrix, but possibly at different magnitudes of strain, stress and pressure, depending on the cell size, shape and relative position within the PCM. Such differences may have some role in regulating cell–cell communication in these CMU subgroups, particularly if inter-cellular processes or paracrine signaling mechanisms are important for NP cells (Errington et al. 1998; Bruehlmann et al. 2002; Baer et al. 2003; Johnson and Roberts 2003). It is of some interest that the largest cell strain and PCM stresses were observed within the middle regions of the CMUs, consistent with the smaller dimensions from cell to extracellular matrix margins for those cells. Given findings of a shift toward fewer cells in each cell–matrix unit with aging in the NP region of the rat (Cao et al. 2007) and lower cell densities in the NP matrix of the human (Maroudas et al. 1975), these mechanical stimuli in the PCM can be expected to change with aging and degeneration. Nevertheless, the prediction based on the morphometric features of the NP cells and PCM in the rat model may be limited when extrapolated to the human IVD. These rodents exhibit a prolonged period of growth in body mass that extends beyond 12 months, with an NP that contains notochordal cells even in the 12-month-old animal. Both of these features are markedly different from what has been shown for the human IVD; thus, future studies of the human IVD using these techniques will be of great interest.
While FEM predictions have utility in suggesting cell-level physical stimuli and the impact of geometry and mechanical loading on cell biology, such theoretical models rely on many assumptions, thus requiring physical confirmation of model predictions. Although heterogeneous tissue mechanics exist in the local regions of the IVD (Weidenbaum et al. 1996), spatially uniform properties and NP loading conditions were used here for model simplicity. A main goal of the current study was to illustrate complexities introduced by the geometrically distinct PCM in the NP alone, due to the presence of different numbers and unique geometries of NP cells. The use of uniform physical properties with no presumed variation in material parameters may limit interpretation of the current study conclusions but was felt necessary to accommodate introduction of the geometric complexity of the physically realistic 3D cell–matrix units here. Prior studies of geometrically simplified, axisymmetric models of cell–matrix interactions in chondrocytes and other cell systems have yielded predictions of material property effects on stress–strain, fluid pressure and fluid-flow fields in cells and vicinity that may shed light on trends expected for these more complex cell–matrix units here (Guilak 2000; Breuls et al. 2002; Michalek and Iatridis 2007). More accurate boundary conditions, such as displacement and fluid pressure in the near cell region, and physical assumptions representing loading and material properties appropriate to non-degenerate or pathological disk tissues, as well as the presence of cell processes or other cell–matrix interfaces could be implemented and subsequently transferred to the microscale. This would greatly increase our understanding of IVD cell mechanics in diseased and injured states.
While chemical and electrical effects have been shown to be important in understanding physical signaling and solute transport in the NP tissue (Gu et al. 1999; Yao and Gu 2006, 2007), the presence of charged biochemical species can be expected to significantly impact mechanotransduction of IVD cells through the formation of chemical or electrical potentials across the cell membrane (Lai et al. 1991; Gu et al. 1998). Future modeling advances could incorporate some of these features in order to construct more realistic predictions of cell-level stimuli expected to impact cell mechanobiology. Another potential limitation of the current model includes the assumption of linearity and elasticity for the solid phase of the NP as a biphasic material, although intrinsic viscoelasticity and nonlinear effects have been well documented for the NP extracellular matrix (Iatridis et al. 1997; Johannessen and Elliott 2005). Therefore, a multi-phasic FEM incorporating features of non-linearity and viscoelasticity may be useful in future studies for revealing a more complete understanding of the cell–matrix interaction in the IVD.
In summary, the micromechanics of NP cells in their unique PCM domains were predicted using 3D, isotropic, linearly elastic and biphasic finite element models based on in situ morphology of the PCM and cells. Model predictions of region-specific micromechanics of the PCM and NP cells were highly heterogeneous but revealed that NP cells experience higher volumetric strains, lower deviatoric strains and longer periods of fluid pressurization than the adjacent extracellular matrix. The PCM was shown to influence cell mechanics and to generate micromechanical fields that varied among cells sharing one PCM and depended on the spatial arrangement of multiple cells within the PCM. The predicted temporal and spatial responses of mechanical stimuli in the vicinity of NP cells provide useful information in understanding mechanotransduction in the intervertebral disk.
Acknowledgments
This study was supported by NIH grants AR04 7442, AR050245, AR048182, AR048852, and AG015768.
References
- Alexopoulos LG, Haider MA, Vail TP, Guilak F. Alterations in the mechanical properties of the human chondrocyte pericellular matrix with osteoarthritis. J Biomech Eng. 2003;125(3):323–333. doi: 10.1115/1.1579047. [DOI] [PubMed] [Google Scholar]
- Alexopoulos LG, Setton LA, Guilak F. The biomechanical role of the chondrocyte pericellular matrix in articular cartilage. Acta Biomater. 2005a;1(3):317–325. doi: 10.1016/j.actbio.2005.02.001. [DOI] [PubMed] [Google Scholar]
- Alexopoulos LG, Williams GM, Upton ML, Setton LA, Guilak F. Osteoarthritic changes in the biphasic mechanical properties of the chondrocyte pericellular matrix in articular cartilage. J Biomech. 2005b;38(3):509–517. doi: 10.1016/j.jbiomech.2004.04.012. [DOI] [PubMed] [Google Scholar]
- Baer AE, Laursen TA, Guilak F, Setton LA. The micromechanical environment of intervertebral disc cells determined by a finite deformation, anisotropic, and biphasic finite element model. J Biomech Eng. 2003;125(1):1–11. doi: 10.1115/1.1532790. [DOI] [PubMed] [Google Scholar]
- Baer AE, Setton LA. The micromechanical environment of intervertebral disc cells: effect of matrix anisotropy and cell geometry predicted by a linear model. J Biomech Eng. 2000;122(3):245–251. doi: 10.1115/1.429655. [DOI] [PubMed] [Google Scholar]
- Bruehlmann SB, Rattner JB, Matyas JR, Duncan NA. Regional variations in the cellular matrix of the annulus fibrosus of the intervertebral disc. J Anat. 2002;201(2):159–171. doi: 10.1046/j.1469-7580.2002.00080.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breuls RG, Sengers BG, Oomens CW, Bouten CV, Baaijens FP. Predicting local cell deformations in engineered tissue constructs: a multilevel finite element approach. J Biomech Eng. 2002;124(2):198–207. doi: 10.1115/1.1449492. [DOI] [PubMed] [Google Scholar]
- Cao L, Guilak F, Setton LA. Three-dimensional morphology of the pericellular matrix of intervertebral disc cells in the rat. J Anat. 2007;211(4):444–452. doi: 10.1111/j.1469-7580.2007.00784.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao L, Guilak F, Setton LA. Pericellular matrix mechanics in the anulus fibrosus predicted by a three-dimensional finite element modeling and in situ morphology. Cell Mol Bioeng. 2009;2(3):306–319. doi: 10.1007/s12195-009-0081-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cloyd JM, Malhotra NR, Weng L, Chen W, Mauck RL, Elliott DM. Material properties in unconfined compression of human nucleus pulposus, injectable hyaluronic acid-based hydrogels and tissue engineering scaffolds. Eur Spine J. 2007;16(11):1892–1898. doi: 10.1007/s00586-007-0443-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Errington RJ, Puustjarvi K, White IR, Roberts S, Urban JP. Characterisation of cytoplasm-filled processes in cells of the intervertebral disc. J Anat. 1998;192(Pt 3):369–378. doi: 10.1046/j.1469-7580.1998.19230369.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu WY, Lai WM, Mow VC. A mixture theory for charged-hydrated soft tissues containing multi-electrolytes: passive transport and swelling behaviors. J Biomech Eng. 1998;120(2):169–180. doi: 10.1115/1.2798299. [DOI] [PubMed] [Google Scholar]
- Gu WY, Mao XG, Rawlins BA, Iatridis JC, Foster RJ, Sun DN, Weidenbaum M, Mow VC. Streaming potential of human lumbar anulus fibrosus is anisotropic and affected by disc degeneration. J Biomech. 1999;32(11):1177–1182. doi: 10.1016/s0021-9290(99)00118-9. [DOI] [PubMed] [Google Scholar]
- Guilak F. The deformation behavior and viscoelastic properties of chondrocytes in articular cartilage. Biorheology. 2000;37(1–2):27–44. [PubMed] [Google Scholar]
- Guilak F, Alexopoulos LG, Upton ML, Youn I, Choi JB, Cao L, Setton LA, Haider MA. The pericellular matrix as a transducer of biomechanical and biochemical signals in articular cartilage. Ann NY Acad Sci. 2006;1068:498–512. doi: 10.1196/annals.1346.011. [DOI] [PubMed] [Google Scholar]
- Guilak F, Mow VC. The mechanical environment of the chondrocyte: a biphasic finite element model of cell-matrix interactions in articular cartilage. J Biomech. 2000;33(12):1663–1673. [PubMed] [Google Scholar]
- Guilak F, Ting-Beall HP, Baer AE, Trickey WR, Erickson GR, Setton LA. Viscoelastic properties of intervertebral disc cells. Identification of two biomechanically distinct cell populations. Spine. 1999;24(23):2475–2483. doi: 10.1097/00007632-199912010-00009. [DOI] [PubMed] [Google Scholar]
- Haider MA. A radial biphasic model for local cell-matrix mechanics in articular cartilage. SIAM J Appl Math. 2004;64(5):1588–1608. [Google Scholar]
- Haider MA, Guilak F. Application of a three-dimensional poroelastic bem to modeling the biphasic mechanics of cell-matix interactions in articular cartilage. Comput Methods Appl Mech Eng. 2007;196:2999–3010. doi: 10.1016/j.cma.2006.08.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haider MA, Schugart RC, Setton LA, Guilak F. A mechano-chemical model for the passive swelling response of an isolated chondron under osmotic loading. Biomech Model Mechanobiol. 2006;5(2–3):160–171. doi: 10.1007/s10237-006-0026-1. [DOI] [PubMed] [Google Scholar]
- Hastreiter D, Ozuna RM, Spector M. Regional variations in certain cellular characteristics in human lumbar intervertebral discs, including the presence of alpha-smooth muscle actin. J Orthop Res. 2001;19(4):597–604. doi: 10.1016/S0736-0266(00)00069-3. [DOI] [PubMed] [Google Scholar]
- Iatridis JC, MacLean JJ, Roughley PJ, Alini M. Effects of mechanical loading on intervertebral disc metabolism in vivo. J Bone Joint Surg Am. 2006;88(2):41–46. doi: 10.2106/JBJS.E.01407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iatridis JC, Setton LA, Weidenbaum M, Mow VC. Alterations in the mechanical behavior of the human lumbar nucleus pulposus with degeneration and aging. J Orthop Res. 1997a;15(2):318–322. doi: 10.1002/jor.1100150224. [DOI] [PubMed] [Google Scholar]
- Iatridis JC, Setton LA, Weidenbaum M, Mow VC. The viscoelastic behavior of the non-degenerate human lumbar nucleus pulposus in shear. J Biomech. 1997b;30(10):1005–1013. doi: 10.1016/s0021-9290(97)00069-9. [DOI] [PubMed] [Google Scholar]
- Ishii T, Tsuji H, Sano A, Katoh Y, Matsui H, Terahata N. Histochemical and ultrastructural observations on brown degeneration of human intervertebral disc. J Orthop Res. 1991;9(1):78–90. doi: 10.1002/jor.1100090111. [DOI] [PubMed] [Google Scholar]
- Johannessen W, Elliott DM. Effects of degeneration on the biphasic material properties of human nucleus pulposus in confined compression. Spine. 2005;30(24):E724–E729. doi: 10.1097/01.brs.0000192236.92867.15. [DOI] [PubMed] [Google Scholar]
- Johannessen W, Vresilovic EJ, Wright AC, Elliott DM. Intervertebral disc mechanics are restored following cyclic loading and unloaded recovery. Ann Biomed Eng. 2004;32(1):70–76. doi: 10.1023/b:abme.0000007792.19071.8c. [DOI] [PubMed] [Google Scholar]
- Johnson WE, Roberts S. Human intervertebral disc cell morphology and cytoskeletal composition: a preliminary study of regional variations in health and disease. J Anat. 2003;203(6):605–612. doi: 10.1046/j.1469-7580.2003.00249.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim E, Guilak F, Haider MA. The dynamic mechanical environment of the chondrocyte: A biphasic finite element model of cell-matrix interactions under cyclic compressive loading. J Biomech Eng. 2008;130(6):061009. doi: 10.1115/1.2978991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korhonen RK, Julkunen P, Rieppo J, Lappalainen R, Konttinen YT, Jurvelin JS. Collagen network of articular cartilage modulates fluid flow and mechanical stresses in chondrocyte. Biomech Model Mechanobiol. 2006;5(2–3):150–159. doi: 10.1007/s10237-006-0021-6. [DOI] [PubMed] [Google Scholar]
- Lai WM, Hou JS, Mow VC. A triphasic theory for the swelling and deformation behaviors of articular cartilage. J Biomech Eng. 1991;113(3):245–258. doi: 10.1115/1.2894880. [DOI] [PubMed] [Google Scholar]
- Lotz JC, Hsieh AH, Walsh AL, Palmer EI, Chin JR. Mechanobiology of the intervertebral disc. Biochem Soc Trans. 2002;30(Pt 6):853–858. doi: 10.1042/BST0300853. [DOI] [PubMed] [Google Scholar]
- Maroudas A, Stockwell RA, Nachemson A, Urban J. Factors involved in the nutrition of the human lumbar intervertebral disc: cellularity and diffusion of glucose in vitro. J Anat. 1975;120(Pt 1):113–130. [PMC free article] [PubMed] [Google Scholar]
- Meng XN, LeRoux MA, Laursen TA, Setton LA. A nonlinear finite element formulation for axisymmetric torsion of biphasic materials. Int J Solids Struct. 2002;39(4):879–895. [Google Scholar]
- Michalek AJ, Iatridis JC. A numerical study to determine pericellular matrix modulus and evaluate its effects on the micromechanical environment of chondrocytes. J Biomech. 2007;40(6):1405–1409. doi: 10.1016/j.jbiomech.2006.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress-relaxation of articular-cartilage in compression–theory and experiments. J Biomech Eng-Trans Asme. 1980;102(1):73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
- Perie D, Korda D, Iatridis JC. Confined compression experiments on bovine nucleus pulposus and annulus fibrosus: sensitivity of the experiment in the determination of compressive modulus and hydraulic permeability. J Biomech. 2005;38(11):2164–2171. doi: 10.1016/j.jbiomech.2004.10.002. [DOI] [PubMed] [Google Scholar]
- Roberts S, Ayad S, Menage PJ. Immunolocalisation of type vi collagen in the intervertebral disc. Ann Rheum Dis. 1991;50(11):787–791. doi: 10.1136/ard.50.11.787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts S, Menage J, Duance V, Wotton S, Ayad S. 1991 volvo award in basic sciences. Collagen types around the cells of the intervertebral disc and cartilage end plate: An immunolocalization study. Spine. 1991;16(9):1030–1038. [PubMed] [Google Scholar]
- Setton LA, Chen J. Cell mechanics and mechanobiology in the intervertebral disc. Spine. 2004;29(23):2710–2723. doi: 10.1097/01.brs.0000146050.57722.2a. [DOI] [PubMed] [Google Scholar]
- Setton LA, Chen J. Mechanobiology of the intervertebral disc and relevance to disc degeneration. J Bone Joint Surg Am. 2006;88(2):52–57. doi: 10.2106/JBJS.F.00001. [DOI] [PubMed] [Google Scholar]
- Trout JJ, Buckwalter JA, Moore KC. Ultrastructure of the human intervertebral disc: Ii. Cells of the nucleus pulposus. Anat Rec. 1982a;204(4):307–314. doi: 10.1002/ar.1092040403. [DOI] [PubMed] [Google Scholar]
- Trout JJ, Buckwalter JA, Moore KC, Landas SK. Ultrastructure of the human intervertebral disc. I. Changes in notochordal cells with age. Tissue Cell. 1982b;14(2):359–369. doi: 10.1016/0040-8166(82)90033-7. [DOI] [PubMed] [Google Scholar]
- Tsantrizos A, Ito K, Aebi M, Steffen T. Internal strains in healthy and degenerated lumbar intervertebral discs. Spine. 2005;30(19):2129–2137. doi: 10.1097/01.brs.0000181052.56604.30. [DOI] [PubMed] [Google Scholar]
- Umehara S, Tadano S, Abumi K, Katagiri K, Kaneda K, Ukai T. Effects of degeneration on the elastic modulus distribution in the lumbar intervertebral disc. Spine. 1996;21(7):811–819. doi: 10.1097/00007632-199604010-00007. discussion 820. [DOI] [PubMed] [Google Scholar]
- Upton ML, Guilak F, Laursen TA, Setton LA. Finite element modeling predictions of region-specific cell-matrix mechanics in the meniscus. Biomech Model Mechanobiol. 2006;5(2–3):140–149. doi: 10.1007/s10237-006-0031-4. [DOI] [PubMed] [Google Scholar]
- Urban JP, Smith S, Fairbank JC. Nutrition of the intervertebral disc. Spine. 2004;29(23):2700–2709. doi: 10.1097/01.brs.0000146499.97948.52. [DOI] [PubMed] [Google Scholar]
- Wayne JS, Woo SLY, Kwan MK. Application of the u-p finite-element method to the study of articular-cartilage. J Biomech Eng-Trans Asme. 1991;113(4):397–403. doi: 10.1115/1.2895418. [DOI] [PubMed] [Google Scholar]
- Weidenbaum N, Iatridis J, Setton LA, Foster RJ, Mow VC. Mechanical behavior of the intervertebral disc and the effects of degeneration. In: Weinstein JN, Gordon SL, editors. Low back pain: a scientific and clinical overview. AAOS; Rosemont: 1996. pp. 557–582. [Google Scholar]
- Wu JJ, Eyre DR, Slayter HS. Type vi collagen of the intervertebral disc. Biochemical and electron-microscopic characterization of the native protein. Biochem J. 1987;248(2):373–381. doi: 10.1042/bj2480373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu JZ, Herzog W. Finite element simulation of location- and time-dependent mechanical behavior of chondrocytes in unconfined compression tests. Ann Biomed Eng. 2000;28(3):318–330. doi: 10.1114/1.271. [DOI] [PubMed] [Google Scholar]
- Wu JZ, Herzog W. Analysis of the mechanical behavior of chondrocytes in unconfined compression tests for cyclic loading. J Biomech. 2006;39(4):603–616. doi: 10.1016/j.jbiomech.2005.01.007. [DOI] [PubMed] [Google Scholar]
- Wu JZ, Herzog W, Epstein M. Modelling of location- and time-dependent deformation of chondrocytes during cartilage loading. J Biomech. 1999;32(6):563–572. doi: 10.1016/s0021-9290(99)00034-2. [DOI] [PubMed] [Google Scholar]
- Yao H, Gu WY. Physical signals and solute transport in human intervertebral disc during compressive stress relaxation: 3d finite element analysis. Biorheology. 2006;43(3–4):323–335. [PubMed] [Google Scholar]
- Yao H, Gu WY. Three-dimensional inhomogeneous triphasic finite-element analysis of physical signals and solute transport in human intervertebral disc under axial compression. J Biomech. 2007;40(9):2071–2077. doi: 10.1016/j.jbiomech.2006.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]


