Loss of Visual Working Memory within Seconds: The Combined Use of Refreshable and Non-Refreshable Features

Abstract

We re-examine the role of time in the loss of information from working memory, the limited information accessible for cognitive tasks. The controversial issue of whether working memory deteriorates over time was investigated using arrays of unconventional visual characters. Each array was followed by a post-perceptual mask, a variable retention interval (RI), and a recognition probe character. Dramatic forgetting across an unfilled RI of up to 6 s was observed. Adding a distracting task during the RI (repetition, subtraction, or parity judgment using spoken digits) lowered the level of recall, but not increasingly so across RIs. Also, arrays of English letters were not forgotten during the RI unless distracting stimuli were included, in contrast to the finding for unconventional characters. The results suggest that unconventional visual items include some features inevitably lost over time. Attention-related processing, however, assists in the retention of other features, and of English letters. We identify important constraints for working memory theories and propose that an equilibrium between forgetting and reactivation holds, but only for elements that are not inevitably lost over time.

The primary memory of James (1890) and the active neural cell assemblies of Hebb (1949) long ago reflected a special status of a small amount of information that is currently in mind or is temporarily very accessible for the completion of cognitive tasks, which was later termed working memory (Baddeley & Hitch, 1974; Miller, Galanter, & Pribram, 1960). Cognitive psychologists long have disagreed profoundly, though, on the nature of the processes that eliminate information from working memory. One especially persistent debate has been about whether information is lost as a function of time (e.g., Brown, 1958; Keppel & Underwood, 1962). The present work shows that time is indeed an important factor in forgetting from working memory, at least for unconventional visual stimuli. It shows, moreover, that some but not all of the time-based forgetting can be counteracted by maintenance activities such as covert verbal rehearsal of the material (Baddeley, 1986) or the brief direction of attention to items in order to reactivate their memory traces held in working memory, i.e., attentional refreshing (Raye, Johnson, Mitchell, Greene, & Johnson, 2007).

The issue of time-based forgetting has been debated primarily in the verbal domain (except for studies of sensory information, e.g., Cowan, Saults, & Nugent, 1997). Long ago, researchers (e.g., Brown, 1958; Glanzer & Cunitz, 1966; Peterson & Peterson, 1959) showed that verbal information can be lost over short periods of time filled with a distracting task. The loss of this information in the absence of rehearsal has long been a mainstay of the theory of working memory, primarily under the assumption that when words are not repeated they are forgotten (Baddeley, 1986; Baddeley & Hitch, 1974). Other researchers (e.g., Bjork & Whitten, 1974; Keppel & Underwood, 1962), however, suggested that verbal forgetting occurs not because memory representations rapidly fade away or decay if they are unrehearsed, as was originally assumed by Brown and others, but because of proactive interference between stimuli presented for recall that depends on the temporal proximity of these stimuli to one another. This is relative to the retention interval (RI); with increasing RIs, it presumably becomes more difficult to discriminate adjacent items, which are often confused because they have lost their temporal distinctiveness (e.g., Crowder, 1976; Glenberg & Swanson, 1986), a time-related form of proactive interference.

Recently, some researchers have found simple situations in which there is very little loss of information over time at all (Cowan et al., 2006; Lewandowsky, Duncan, & Brown, 2004; Oberauer & Lewandowsky, 2008). In these studies, verbal lists are presented and must be recalled at varying speeds in the correct serial order. This speed manipulation is accomplished either through training participants to recall list items at different paces or by asking participants to articulate a single word once or multiple times before each item is recalled. When either method is used there is little effect of these manipulations on the accuracy of recall. Based on this evidence, Lewandowsky et al. (2004) and Oberauer & Lewandowsky (2008) propose that interference, and not time, is the determinant of forgetting.

The investigators who believe there is no forgetting as a function of time per se disagree on the reason for forgetting. Some propose that forgetting occurs because irrelevant events interfere with relevant memory representations (Farrell & Lewandowsky, 2002; Lewandowsky, Oberauer, & Brown, 2009). According to this event-related interference approach to forgetting, the novelty of an event determines its encoding strength, with stronger representations having more weight in short-term memory. When novel distracters are encoded this causes weaker memory items to be relatively impoverished in their representation and unavailable for memory. Others claim that memory representations of distracting items overwrite features they share with the memory items (Oberauer & Kliegl, 2006; Nairne, 1990). In this feature-based approach new distracting items disrupt memory items because they compete for the neural correlates of a common feature, such as being purple (for visual objects) or high-pitched (for sounds), when being represented in the brain. It is assumed that each feature can only be bound to one item, inevitably leading to some level of forgetting when memory or distracting items share features.

Despite this work, though, others have held to the premise that information is indeed lost as a function of time. For example, Cowan (1988) proposed that long-term memory traces which achieved an activated state through means such as perception or internal thought were available to working memory. These activated memories according to Cowan (1988), lost activation, or decayed, until the traces returned to their dormant status as a long-term memory trace. Theories, such as Cowan (1988)’s, claiming that information is lost as a function of time necessarily require some sort of maintenance process to explain the persistence of information in working memory. These maintenance processes generally fall into two methods for reactivating memories: covert verbal rehearsal and attentional refreshing. There are several differences between the two processes. First, covert verbal rehearsal consists of silently repeatedly speaking a word to yourself, whereas attention based refreshing consists of briefly directing attention to a concept or memory, bringing it into conscious awareness. Some evidence suggests that covert verbal rehearsal uses very little general attentional resources after the first few repetitions of the cycle (Guttentag, 1984, 1997; Naveh-Benjamin & Jonides, 1984). Attentional refreshing may act on visual images or abstract ideas in addition to verbal materials, and possibly any neural trace, but they appear to require more attention (Raye et al., 2007). Although it presumably is possible for both processes to apply to materials that can easily be labeled, covert verbal rehearsal would appear impractical for materials that cannot be labeled.

As proponents of attentional refreshing, Barrouillet and colleagues (Barrouillet, Bernardin, & Camos, 2004; Barrouillet, Bernardin, Portrat, Vergauwe, & Camos, 2007; Portrat, Barrouillet, & Camos, 2008) have shown a strong linear relationship between the number of items recalled from a verbal list and the proportion of time between items that is available for maintenance activities, as opposed to being taken up by a distracting cognitive task. The proportion of time during which attention is occupied by distraction is called the cognitive load. They explain their results on the grounds that information is lost from working memory during the time that it cannot be refreshed through the use of attention because of the cognitive load. According to this theoretical view, recall stays constant across RIs because the number of items kept active in memory is just the amount that can be refreshed repeatedly using attention in the periods not used up by the cognitive load. In order to reconcile these results with studies in which no time-related loss was observed, such as Lewandowsky et al. (2004), they must be explained on the grounds that, in those studies, attentional refreshing somehow takes place between distractions. This view is related to the earlier view of Baddeley (1986) but attention-based refreshing is proposed instead of the less attention-demanding process of covert verbal rehearsal. It should be noted that attentional refreshing as theorized by Barrouillet and colleagues is a necessary byproduct of any conscious cognitive operation that is conducted upon a memory trace. This is because the item must be retrieved into awareness, which refreshes the item, for any controlled processing to occur. For this reason attentional refreshing of a particular item is deemed probable in many circumstances as a byproduct of other processing.

It may be necessary to consider nonverbal materials to understand working memory fully. It can be argued that the visual domain may be a better basis on which to look for the time-related loss of working memory information. Although participants can attentionally refresh at least some visual information (Vergauwe, Barrouillet, & Camos, 2009), it is not clear that participants have a means either to verbally rehearse or attentionally refresh all such information. It is possible that information that is difficult to label or rehearse verbally often is also difficult to attentionally refresh (Johnson, Raye, Mitchell, Greene, & Anderson, 2003) because each item does not form a single, identifiable chunk in long-term memory. This information may, depending on one’s theoretical orientation, be said to be held in a visuospatial buffer (Baddeley & Logie, 1999; Logie, 2003) or represented as temporarily-activated visual features from long-term memory (Cowan, 1988).

Recently, in fact, Zhang and Luck (2009) found memory loss for arrays of visual objects over a 10-s period. Each array was followed by a variable period and then a single probed location, and the array item previously in that same location was to be judged on a continuum (e.g., for arrays of colored spots, the participant was to select the location on a color wheel that best matched that array object). This allowed an estimation of the precision of each response. It was determined that the representations of items did not decrease in precision across delays; instead, some items dropped out of working memory entirely by the 10-s delay.

We do not address this issue raised by Zhang and Luck (2009) of whether time-based memory loss is sudden or gradual here, but we do replicate and extend the evidence for time-based loss and investigate how it is combined with working-memory maintenance processes. To this end, we examined memory for items in arrays differently, with a procedure illustrated in Figure 1. We used unconventional printed characters in order to discourage the covert verbal rehearsal of the items. We also followed each target array with a blank period long enough to allow encoding of the array, and then we presented a masking array (Vogel, Woodman, & Luck, 2006) in order to ensure that we were not studying sensory memory features (cf. Saults & Cowan, 2007). After a variable RI, a single probe item was presented and was to be judged same or different from the item in the corresponding location of the target array. Given the finding of Zhang and Luck, we expected memory loss over time.

Figure 1.

An example of a single trial in Experiment 1. During the RI a blank screen was displayed for a variable duration of 1400, 2900, or 5900 ms. Throughout this retention interval participants heard digits spoken over computer speakers at a rate of one digit every 1500 ms beginning at mask offset. In different conditions, participants did not hear the digits, were to repeat each digit immediately, or were to subtract one from each digit and pronounce the result.

A key additional question of our study was whether there would be more forgetting over time on trials in which a cognitive load was introduced during the RI between the mask and the probe. If there is more forgetting over time on such trials, it implies the presence of interference or distraction processes, as will be more fully explained shortly. In Experiment 1 we included a no-load condition and also a low load, repeating spoken digits, and a high load, subtracting 1 from each spoken digit and pronouncing the answer aloud. The digits were spoken instead of being presented visually, in order to reduce the number of features shared between stimuli in the two tasks (Nairne, 1990) so that the effects of this task on array memory could be attributed primarily to general distraction (cf. Vergauwe et al., 2009) rather than domain-specific interference (cf. Klauer & Zhao, 2009).

Previous research with the same set of unconventional characters as in the present study helps to shape our expectations. Ricker, Cowan, and Morey (in press, Experiment 2) showed participants did not rely on covert verbal rehearsal to retain these characters. Although there was a small effect of articulatory suppression (counting) on memory for the array characters, the same size effect was obtained when simple tapping at a constant pace was used instead. For the same characters, there was evidence that verbal memory retrieval interfered with retention. Specifically, participants were to examine a set of words for the inclusion of a word from one of two memorized lists, and performance on the visual arrays was lower when a word from the memorized lists was in fact found. For words from one of the memorized lists, no overt response was required, yet retrieval of such words lowered array performance. The interpretation was that articulatory suppression, tapping, and retrieval from memory all require a small but non-trivial amount of attention that otherwise would have been used to refresh the unconventional characters in the array. This study shows no indication of verbal-modality-specific interference with memory for the unconventional characters.

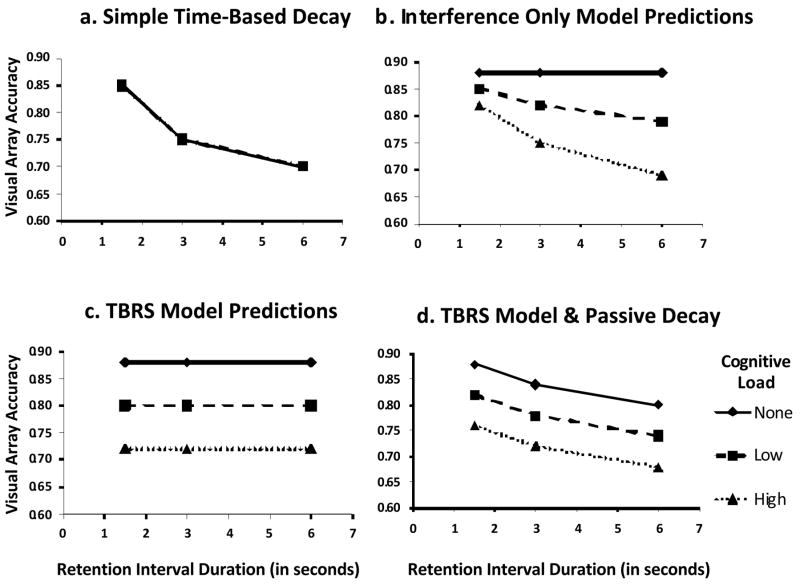
Several very different sets of predictions for the procedure shown in Figure 1 are suggested by the research literature, as shown in Figure 2. It is important to note, however, that the reason to consider these predictions is not to determine which extant model is correct, which is beyond the scope of this article. Indeed, we believe that the results are not closely predicted by any extant model. Instead, the predictions help to establish certain principles that any successful model of working memory must incorporate.

Figure 2.

Predictions from several models. See text for a detailed description of these predictions.

First, a pure effect of time would lead to a drop in visual array memory performance as RIs increase, as illustrated in Figure 2a. This would be a possibility according to any theoretical view in which memory loss over time is proposed, but only if the unconventional characters do not lend themselves to memory maintenance processes such as covert verbal rehearsal or attentional refreshing.

Second, models that emphasize interference instead of time-based loss of memory, such as the serial order in a box (SOB) model (Farrell & Lewandowsky, 2002; Oberauer & Lewandowsky, 2008), would lead to the expectation of memory loss over time in the presence of retroactive interference, but not without such interference, as illustrated in Figure 2b. There are multiple reasons why interference can take place (for a review see Lewandowsky et al., 2009). What they seem to have in common is that forgetting only occurs when new interfering items are presented.

In Figure 2b, more forgetting over time is shown for the subtract condition than for the repeat condition inasmuch as there are a greater number of different digits in the subtract condition if one includes the participants’ response digits as well as the stimulus digits. Event-based interference positing each non-repeated digit representation as a novel event should predict that more interfering representations are the sole cause of forgetting, leading to the predicted pattern of results shown in Figure 2b. Feature-based forgetting (e.g., Nairne, 1990) generally predicts this type of result as well, and increasing interference over time has been found in previous work (e.g., Lewandowsky & Farrell, 2008). However, there were few shared features between the memory and secondary task stimuli for the unconventional characters in the present study, so feature overwriting should have been be largely avoided.

The same sort of pattern would be predicted by models in which working memory includes only specific buffers that hold verbal and visuospatial materials, respectively (e.g., Baddeley & Logie, 1999), provided that there is some specific interference between the array characters and the interference task. If one accepts that Ricker et al. (in press) correctly ruled out the use of a verbal representation for these unconventional characters, the pattern still could be predicted if there were a visual component to the distraction tasks used in the experiment (repetition and subtraction). Then the longer the distraction task is carried out, the more time there is for forgetting from the relevant visuospatial memory buffer.

Third, as illustrated in Figure 2c, the time-based resource sharing (TBRS) model (Barrouillet et al., 2004) somewhat paradoxically predicts no loss of information over time in any of the cognitive load conditions. That is because attentional refreshing is thought to occur on the scale of hundreds of milliseconds (Hudjetz & Oberauer, 2007; Portrat et al., 2009). The participant presumably reaches a load-dependent level of equilibrium between distraction allowing decay and refreshing of memory items extremely quickly. As a consequence, according to this view, imposing a cognitive load lowers the overall level of recall, but accuracy does not change as a function of the RI.

Fourth, using these models, there is a way we can predict a decline of information over the RI without an interaction between the RI and the cognitive load, as illustrated in Figure 2d. This pattern would be expected if some of the information in visual working memory can be attentionally refreshed over time, as in the TBRS model, whereas other information that is concurrently present cannot be refreshed using attention or any other means but is lost inevitably over time. To anticipate, that hybrid account essentially matches the pattern we obtained for unconventional visual stimuli.

It might also be possible to anticipate these results on the basis of a version of the multiple-store model that includes decay over time and mnemonic activities to counteract that decay (Baddeley & Logie, 1999). Given that Ricker et al. (in press) found no evidence that verbal rehearsal was used for our unconventional characters, we assume it would have to be a process that can be used to maintain visual features, such as attentional refreshing. There are two assumptions that would have to be added to make this account work. First, it would have to be postulated that there are parts of the representation that can be lost over time during the RI in the absence of any distraction or retroactive interference. This is counter to the usual assumption that there are specific processes that can reactivate either verbal or visuospatial representations in working memory. Second, the principle of equilibrium between the mnemonic process such as attentional refreshing and memory loss over time might have to be added, as in the TBRS model, in order to explain why the difference between distraction versus no distraction in the RI would not grow as a function of the duration of the RI. The main result of the study is to establish these two principles, regardless of the other aspects of the underlying account.

Experiment 1

Method

Design

We used a dual-task design consisting of a visual array memory task and an auditory secondary task that was performed during the visual array RI. Total RI Duration (1500, 3000, or 6000 ms) and Cognitive Load (No Load, Low/Repeat, or High/Subtract) were manipulated within participants, in 9 separate trial blocks in a counterbalanced order (see Procedure). In the no-load trial block, participants were told they did not have a secondary task during the RI, and no stimuli were presented. In the low-cognitive-load trial block, participants were instructed to repeat spoken digits and, in the high-cognitive-load trial block, they were instructed to subtract 1 from each digit and then speak the result.

The cognitive load was held fixed within a trial block to avoid confusion. Total RI time was held fixed within a trial block to prevent any differential preparation effects for each RI. With mixed presentations, there would have been uncertainty about the time of test for the early or middle retention interval, and the uncertainty would have been eliminated after the time exceeded that middle retention interval. With blocked presentation, the time of test is certain for each retention interval and differential preparation for the delay intervals is prevented

Participants

36 students from the University of Missouri participated in exchange for course credit. Data from 2 participants were not analyzed because they demonstrated less than 90% accuracy on the secondary task in one or more blocks. Data from 4 additional participants were also excluded due to below-chance performance in the primary task for one or more blocks, leaving a total n of 30 (18 female, 12 male).

Apparatus and materials

Participants were seated in a sound-attenuated booth at a comfortable distance from the computer screen. All visual stimuli were displayed within an area 72 mm wide and 54 mm tall, viewed at a distance of about 50 cm. Visual array task stimuli were 113 characters from the extended character sets in Microsoft Word 2002, selected because they were not easily namable by the authors (e.g., Greek, Cyrillic, and Arabic letters; unusual symbols). Characters appeared in black on a grey background and each was enclosed within an invisible 8-mm × 8-mm square. For each trial, the reference array consisted of 3 random stimuli selected from the 113 character list without any repetitions of the same stimuli within a trial. Blocks consisted of 30 trials in Experiment 1 and 24 trials in Experiment 2. This means that on average each stimulus was included in the reference array once per block, and 7 times across the experiment. Auditory task stimuli were the numbers 1–9 spoken in a male voice, digitally recorded and played at a comfortable listening volume, with the digits’ sound levels adjusted to be subjectively equal. Their intensities were within 3 dB(A) of each other at their peaks.

Procedure

As shown in Figure 1, each trial started with a fixation cross displayed in the center of the screen for 1000ms. Next, an array of 3 unconventional characters (the reference array) appeared on the screen for 750 ms¹, followed by a blank screen for 250 ms, and then a visual mask which remained for 100ms. Item locations in the reference array varied randomly on each trial and could be anywhere within the display area. After the mask offset, a blank screen was displayed for a variable duration of 1400, 2900, or 5900 ms. When calculating total time of memory retention both the mask display duration and the blank interval should be considered leading to RIs of 1500, 3000, and 6000 ms. During the blank portion of the RI, participants heard digits spoken over computer speakers at a rate of one digit every 1500 ms in the low- and high-load conditions. Digit presentation began immediately following mask offset. During the no-load condition participants did not hear any digits. Repetition or subtraction were to be performed as quickly as possible after hearing each digit. The participants spoke each response out loud as soon as possible at a volume loud enough to be heard by an experimenter who sat in the booth and monitored compliance. After the RI, a single character was presented on the screen in the same position as one of the characters in the reference array. Concurrently, two circles appeared to mark the positions of undisplayed characters from the reference array, eliminating any confusion over which item was cued. Participants entered a response by pressing the “s” key if they thought the single character was the same one that had been displayed in its position in the reference array (which was true on half the trials), or the “d” key if they thought there was a difference. When a different item was presented it was always an entirely new item that was not part of the reference array. The order of the same/different trials was random.

Experiment 1 started with 10 array practice trials with no secondary task. All stimuli used in practice trials throughout both experiments were common symbols such as punctuation marks. There were then 9 experimental blocks of trials, one for each combination of cognitive load and RI duration. Participants completed all three blocks of trials at each cognitive load consecutively and then moved on to the next cognitive load condition. Each cognitive load condition began with a set of 10 practice trials, including both the array task with a 3000-ms delay and the secondary task. Each of the 9 blocks included 30 experimental trials. The order of the cognitive load conditions was determined by a Latin square, whereas the order of interval durations was randomly assigned for each participant, separately in each load condition.

Results

Analysis of block order

There was no main effect of block order F(5,24)<1, p=.55, and no interaction between block order and any of the experimental effects.

Analysis of character array accuracy

Mean visual array accuracies for all conditions are shown in Figure 3. A 3×3 within-participants ANOVA of Cognitive Load and RI Duration produced a main effect of Cognitive Load, F(2,58)=30.59, MSE=0.005, η_p²=.51, p<.0001. Newman-Keuls follow-up tests indicated that performance in the no-load condition was better than in the low/repeat condition, p=.0009; or the high/subtract condition, p=.0001; and that performance was better in the low/repeat condition than in the high/subtract condition, p=.0002 (No Load, M=.83; Low/Repeat, M=.79; High/Subtract, M=.74). There was also a main effect of RI Duration, F(2,58)=23.43, MSE=0.005, η_p²=.45, p<.0001. Newman-Keuls follow-up tests indicated that performance in the 1500-ms delay condition was better than in the 3000-ms delay condition, p=.0009; or the 6000-ms delay condition, p=.0001; and that performance was better in the 3000-ms delay condition than in the 6000-ms delay condition, p=.002 (1500 ms, M=.82; 3000 ms, M=.79; 6000 ms, M=.75). Critically, there was no interaction between the two factors, F(4,116)<1, p=.57, η_p²=.02.

Figure 3.

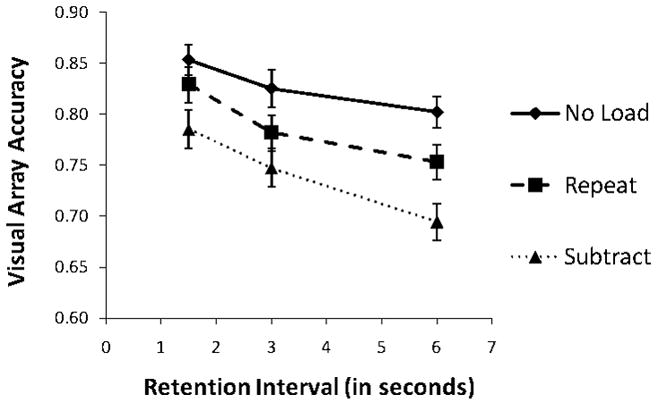
Mean proportion correct on the visual array task accuracy task as a function of retention interval duration for each load condition (graph parameter) in Experiment 1. Error bars are standard errors.

The data were also log transformed and analyzed in the same manner in order to confirm the independence of the two main effects suggested by the lack of an interaction in the untransformed data. This analysis yielded similar results to the previous analysis, with both main effects still significant and the interaction still not approaching significance, F(4,116)<1, p=.44, η_p²=.03.

Analysis of hits and correct rejections

Hits (correct change-detection responses) and correct rejections (correct no-change responses) were separately analyzed in order to find out more about the nature of performance. Mean proportions of hits and correct rejections are shown in Table 1. An ANOVA of hits with the same factors as overall accuracy produced a main effect of Cognitive Load, F(2,58)=21.07, MSE=0.01, η_p²=.42, p<.0001 but no effect of RI Duration, F(2,58)<1, p=.62, η_p²=.02; or any interaction between the two factors, F(4,116)=1.97, p=.10, η_p²=.06. In contrast, a comparable ANOVA of correct rejections produced both a main effect of Cognitive Load, F(2,58)=8.45, MSE=0.016, η_p²=.23, p=.0006 and a main effect of RI Duration, F(2,58)=26.94, MSE=0.015, η_p²=.48, p<.0001. There was no interaction between the two factors, F(4,116)<1, p=.90, η_p²=.01.

Table 1.

Mean Visual Array Task Accuracy by Condition for Hits and Correct Rejections in Experiment 1

Retention Interval (ms)	Cognitive Load
	No Load	Repeat	Subtract
Hits (Correct Change-Detection Responses)
1500	.89(.02)	.90(.02)	.83(.02)
3000	.92(.01)	.86(.02)	.82(.02)
6000	.91(.02)	.89(.02)	.79(.03)
Correct Rejections (Correct No-Change Responses)
1500	.82(.03)	.76(.03)	.74(.03)
3000	.73(.03)	.70(.03)	.68(.04)
6000	.69(.03)	.62(.03)	.60(.04)

Note: Standard errors of the mean in parentheses.

Item analysis

It is possible that our data is composed of two subsets of items. Some characters could be maintained in working memory (through covert verbal rehearsal or attentional refreshing) whereas others could not be so maintained (e.g., because they could not be easily labeled). If this were true, and if it is assumed that any amount of working memory maintenance creates an equilibrium state across retention intervals, then our results could be interpreted as follows. Information would inevitably decay over time for the characters that could not be maintained, with no effect of a cognitive load whereas, for characters that could be maintained in some equilibrium state, there would be no decay but there would be susceptibility to a cognitive load. According to this account, there would be a negative correlation between a character’s susceptibility to RI effects and its susceptibility to cognitive load effects. To examine this possibility, we collapsed the data across individuals and separated trials instead in terms of the probed character within the reference array. For each character we estimated the effect of RI as the difference between the 1.5-s and 6.0-s conditions, averaged across load conditions; and we estimated the effect of cognitive load as the difference between the no-load and high-load conditions, averaged across the three RIs. There was no correlation across characters between the RI and load effects, r(112)=.09, n.s., demonstrating that the decay effect and cognitive load effect are not driven by different subsets of characters.

Discussion

The results from Experiment 1 show a clear effect of RI duration on visual array task accuracy, with longer delays resulting in lower performance regardless of the cognitive load. This effect is purely time-based as it is observed to the same degree across all load conditions, including the no-load condition. There was no fanning out of proportions correct across conditions, a form of interaction between RI duration and cognitive load that might have been expected on the basis of event-related interference (i.e. Lewandowsky et al., 2009; see Figure 2).

Experiment 1 also produced a clear effect of cognitive load with greater cognitive loads resulting in greater impairment to memory performance. There was an equal impairment in visual array performance across all delays for both the repetition and subtraction tasks, demonstrated by the lack of an interaction between cognitive load and RI duration. This is consistent with predictions from the TBRS model.²

Separate analyses of hits and correct rejections revealed a significant effect of load condition similar to that in the overall proportion correct. The effect of RI, however, was not present in the hits but was large in the correct rejections (correct responses in no-change trials), as Table 1 shows. This makes sense if the ability to recognize that a probe matched the corresponding array item declined over time as the template against which the probe had to be compared disintegrated. This finding, and the absence of an effect of RI on change detection, suggests that the tendency was to indicate that a change had occurred if a match with the reference array was not observed.

When both the time-based and load-based effects are considered together, the results of Experiment 1 are not compatible with a straight decay model, an interference-based model, or the TBRS model (Figures 2a, 2b, and 2c). Instead, the results seem compatible with a hybrid: a combination of the decay and TBRS models (Figure 2d). This suggests that there is time-based memory loss but that part of the fading information can be attentionally refreshed but disrupted by secondary tasks, producing the load effect, whereas another part cannot be attentionally refreshed, producing the effect of RIs.

As mentioned above, it might also be possible to explain these data on the basis of a multi-store model of working memory in which each store is domain specific (e.g., Baddeley & Logie, 1999) on the grounds that the type of coding carried out for the unconventional characters partly overlaps with the distraction tasks. To do so, however, at least two assumptions would have to be added. The first is the loss of some information over time in the absence of interference or distraction. Another assumption that is needed is equilibrium between forgetting over time and whatever process is reactivating information in this study (as in the TBRS model), to account for the absence of an interaction of the distraction condition and RI. Even with those assumptions, the theory would either have to allow that the distraction effect is on general attention, or would have to postulate that we have overlooked a form of coding in common between the arrays and the distraction task. Results of Experiment 2, and findings of the recent study we have described (Ricker et al., in press), make the latter interpretation improbable.

The effect of time in our data is discrepant from the findings of several other researchers (Lewandowsky et al., 2004; Oberauer & Lewandowsky, 2008). We have suggested that these other researchers may not have observed an effect of RI because they used verbal materials, whereas the use of nonverbal visual materials may be a more fruitful for discovering time-based forgetting.

Experiment 2

The second experiment is intended to clear up several uncertainties remaining from the first experiment. First, we would like to know more about the nature of the interference between the visual arrays and the distracting task. According to the TBRS theory of Barrouillet et al. (2004, 2007), the interference could come from general attentional distraction that does not require any specific overlap in content between the arrays and the distracting task. According to all theories, there might also be content-specific interference between the two. Given that Ricker et al. (in press) determined that articulatory suppression and tapping have equal effects on these array stimuli, by default it would have to be visuospatial information that is shared between the two sets of stimuli. In the subtraction condition of our secondary task in Experiment 1, participants could have used a spatial frame of reference, such as a number line representation, to subtract 1 from each number (cf. Dehaene, Piazza, Pinel, & Cohen, 2003). In this case the load effect of subtraction could be based on interference from visuospatial-code-specific information despite the acoustic presentation of numbers. Although this would not effect the repeat condition, to avoid this potential problem in Experiment 2 the load task was a parity (odd or even) judgment of each spoken number (Barrouillet et al., 2007). In that task, there is no basis for a visual representation so there should be little feature overlap between memory for unconventional characters and the secondary load task. Replication of the result from Experiment 1 should indicate that the nature of the interference is in the diversion of attention, rather than in code-specific interference.

Second, we would like to verify that the pattern we have observed is specific to unconventional characters. According to the previous literature using series of known verbal stimuli, information is not lost very much as a function of time alone in the absence of distraction (e.g., Oberauer & Lewandowsky, 2008). Similarly, other theories assert that known verbal stimuli can be kept active over time through covert verbal rehearsal (Baddeley & Logie, 1999), attentional refreshing (Barrouillet et al., 2004, 2007), or both (e.g., Cowan, 1999). That has not been examined for simultaneous arrays of known verbal stimuli. Therefore, we added a condition in which the arrays contained English letters. We used six letters per array, as pilot work indicated that performance levels for such arrays were comparable to what we obtained with three unconventional characters.

Third, the nature of distraction effects with English characters could help to strengthen the notion that the effect of distraction for unconventional characters may not be content-specific. The latter produced no interaction of distraction condition and RI. For English letters, though, the odd-even task, which is of course verbally based, should produce verbal-code-specific interference (e.g., Nairne, 1990) in addition to attentional distraction. Given the presence of these two effects instead of just attentional distraction, an equilibrium between attentional refreshing and memory loss over time may not be possible, and the aforementioned interaction may be observed.

Method

Design

The design was the same as the first experiment except that (1) half of the trial blocks involved arrays of 6 English letters instead of the 3 unconventional characters, (2) the cognitive load conditions included a no-load condition and a parity judgment condition, and (3) there were 24 trials per block instead of 30.

Participants

36 students from the University of Missouri participated in exchange for course credit. Data from 4 participants were not analyzed because they demonstrated less than 90% accuracy on the secondary task in one or more blocks, placing the total n at 32 (22 female).

Apparatus and materials

Apparatus and materials were the same as in Experiment 1 except that the visual array stimuli used in half of the trials were 6 English letters drawn from a set consisting of all 26 letters displayed in upper case. Pilot data showed that performance levels were roughly comparable for sets of 3 unconventional characters and 6 English letters.

Procedure

Experiment 2 had a within-participant design in which Memory Array Stimulus Type (Characters or Letters), Total RI Duration (1500, 3000, or 6000 ms), and Cognitive Load (No Load or High/Parity) were manipulated. The procedure was as in Experiment 1 except for a few modifications. The repeat condition of the cognitive load manipulation was dropped and the subtract condition was replaced with a parity task in which participants responded to the same spoken digits as in Experiment 1, this time with an odd or even judgment (e.g., if 3 was heard, the correct response was “odd”).

At the start of the experiment, participants completed a set of 10 practice trials of the basic array task. Participants then performed all 12 blocks of 24 experimental trials, one for each combination of conditions. The block order was determined by a Latin square for the cognitive load and stimuli type, whereas the order of interval durations was randomly assigned for each participant. Within each stimuli/load condition combination, the order of the blocks differing in retention interval was randomized individually for each stimuli/load condition. Before the experimental trials for each load condition a set of 10 practice trials was administered to teach participants the secondary task using the visual array practice stimuli paired with a 3000-ms retention interval during which the secondary task was performed.

Results

Analysis of block order

There was no main effect of block order F(3,28)<1, p=.46, and no interaction between block order and any of the experimental effects.

Overall analysis of array task accuracy

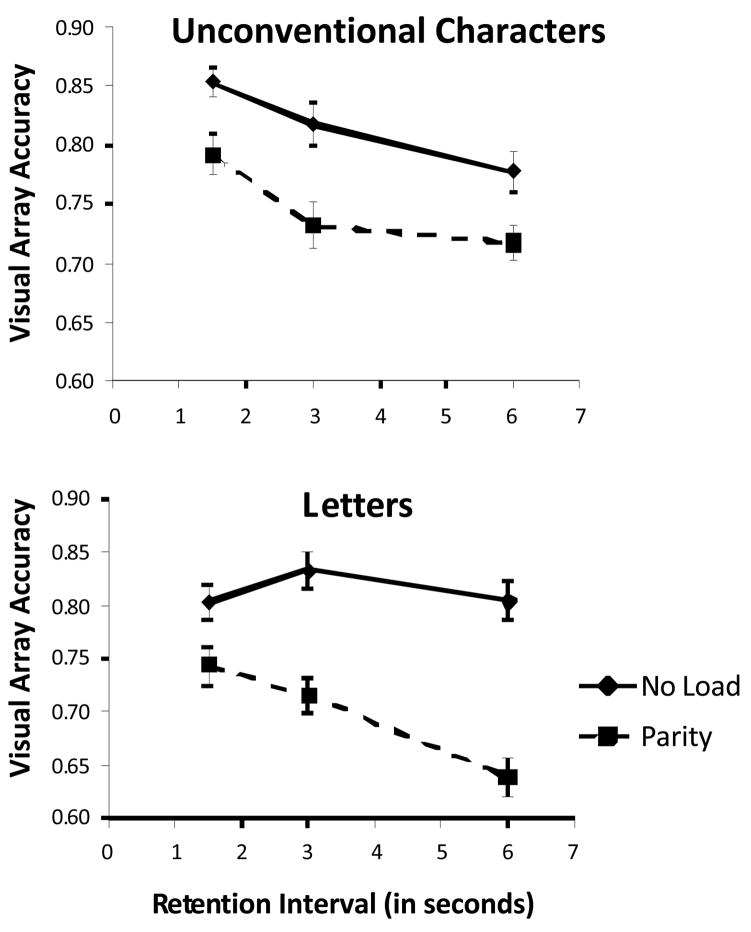
Mean visual array accuracies for all conditions are shown in Figure 4. A 2×2×3 within-participants ANOVA of Stimulus Type, Cognitive Load, and RI Duration was conducted to assess whether a different pattern of results was observed in the unconventional character versus letter array data. This produced a main effect of Stimulus Type, F(1,31)=4.64, MSE=0.013, η_p²=.13, p=.04. A main effect of Cognitive Load was also present, F(1,31)=100.02, MSE=0.008, η_p²=.76, p<.0001. There was also a main effect of RI Duration, F(2,62)=20.70, MSE=0.006, η_p²=.40, p<.0001. Significant 2-way interactions existed for Stimulus Type × Cognitive Load, F(1,31)=6.77, MSE=0.007, η_p²=.18, p=.01; and Stimulus Type × RI Duration, F(2,62)=3.82, MSE=0.005, η_p²=.11, p=.03. The interaction of Cognitive Load × RI Duration was not significant, F(2,62)=2.58, p=.08, η_p²=.08. Importantly, the 3-way interaction between all variables, Stimulus Type × Cognitive Load × RI Duration, was also significant, F(2,62)=3.45, MSE=0.007, η_p²=.10, p=.04. Separate 2-factor ANOVAs of Cognitive Load and RI Duration were conducted on accuracy for the character and letter stimuli in order to help interpret the data in the presence of multiple interactions.

Figure 4.

Mean proportion correct on the visual array task accuracy task using unconventional characters (top panel) and English letters (bottom panel) as a function of retention interval duration for each load condition (graph parameter) in Experiment 2. Error bars are standard errors.

Unconventional character stimuli analysis

A 2×3 within-participants ANOVA of Cognitive Load × RI Duration conducted with the character data produced a main effect of Cognitive Load, F(1,31)=29.62, MSE=0.008, η_p²=.49, p<.0001 (No Load, M=.82; Parity Load, M=.75). There was also a main effect of RI Duration, F(2,62)=17.25, MSE=0.005, η_p²=.36, p<.0001. Newman-Keuls follow-up tests indicated that performance in the 1500-ms delay condition was better than in the 3000-ms delay condition, p=.0006; or the 6000-ms delay condition, p=.0001; and that performance was better in the 3000-ms delay condition than in the 6000-ms delay condition, p=.04 (1500 ms, M=.82; 3000 ms, M=.77; 6000 ms, M=.75). Critically, there was no interaction between the two factors, F(2,62)<1, p=.62, η_p²=.02.

The unconventional character data was also log transformed and analyzed in the same manner in order to confirm the independence of the two main effects suggested by the lack of an interaction in the untransformed data. This analysis yielded similar results to the previous analysis, with both main effects continuing to be significant, while the interaction still did not approach significance, F(2,62)<1, p=.60, η_p²=.02.

Letter stimuli analysis

A 2×3 within-participants ANOVA of Cognitive Load × RI Duration conducted with the letter data produced a main effect of Cognitive Load, F(1,31)=82.78, MSE=0.008, η_p²=.73, p<.0001 (No Load, M=.81; Parity Load, M=.70). There was also a main effect of RI Duration, F(2,62)=9.68, MSE=0.006, η_p²=.24, p=.0002 (1500 ms, M=.77; 3000 ms, M=.77; 6000 ms, M=.72). Critically, there was a significant interaction between the two factors, F(2,62)=4.90, MSE=0.009, η_p²=.14, p=.01. Newman-Keuls follow-up tests indicated that performance was not different across retention intervals when there was no cognitive load, all p’s>.1, but was different across retention intervals when under cognitive load from the parity task. When under cognitive load performance in the 1500-ms delay condition was not significantly better than in the 3000-ms delay condition, p=.26; but was significantly better than performance in the 6000-ms delay condition, p=.0002. Performance was also better in the 3000-ms delay condition than in the 6000-ms delay condition, p=.0002 (see Figure 4 for all condition means).

Hits and correct rejections

The separate analysis of hits and correct rejections (shown in Table 2) underscores the difference in the processes involved in carrying out the array comparison task with the two types of stimuli. For arrays of unconventional characters, the results of the first experiment were replicated. A 2×3 within-participants ANOVA of Cognitive Load and RI within the hits produced a main effect of Cognitive Load, F(1,31)=28.88, MSE=0.012, η_p²=.48, p<.0001 (No Load, M=.89; Parity Load, M=.80) but no effect of RI Duration, F(2,62)<1, p=.93, η_p²=.00, and no interaction between the two factors, F(2,62)<1, p=.53, η_p²=.02. The comparable analysis for correct rejections (for no-change trials) produced not only a main effect of Cognitive Load, F(1,31)=8.69, MSE=0.015, η_p²=.22, p=.006 (No Load, M=.75; Parity Load, M=.69), but also a main effect of RI Duration, F(2,62)=20.94, MSE=0.017, η_p²=.40, p<.0001, with no interaction between the two factors, F(2,62)<1, p=.58, η_p²=.02.

Table 2.

Mean Visual Array Task Accuracy by Condition for Hits and Correct Rejections in Experiment 2

Retention Interval (ms)	Cognitive Load by Stimuli
	Characters		Letters
	No Load	Parity Load	No Load	Parity Load
Hits (Correct Change-Detection Responses)
1500	.86(.02)	.82(.02)	.88(.02)	.82(.02)
3000	.89(.02)	.79(.03)	.91(.02)	.79(.02)
6000	.89(.02)	.79(.02)	.87(.02)	.68(.04)
Correct Rejections (Correct No-Change Responses)
1500	.83(.02)	.77(.02)	.73(.03)	.67(.03)
3000	.75(.03)	.67(.03)	.76(.03)	.64(.03)
6000	.66(.03)	.64(.03)	.74(.03)	.59(.03)

Note: Standard errors of the mean in parentheses.

For the English letters, the analysis of hits produced both a main effect of Cognitive Load, F(1,31)=40.67, MSE=0.018, η_p²=.57, p<.0001 (No Load, M=.89; Parity Load, M=.76) and a main effect of RI Duration, F(2,62)=8.08, MSE=0.013, η_p²=.21, p=.0008. Similar to that in the overall proportion correct data, there was a significant interaction between the two factors, F(2,62)=5.92, MSE=0.010, η_p²=.16, p=.004. For the correct rejections, there was a main effect of Cognitive Load, F(1,31)=34.53, MSE=0.015, η_p²=.53, p<.0001 (No Load, M=.74; Parity Load, M=.64) but no effect of RI Duration, F(2,62)= 1.32, p<.28, η_p²=.04, and no interaction between the two factors, F(2,62)=1.47, p=.24, η_p²=.05.

Item analysis

As in the first experiment, we examined RI and cognitive load effects on an item-by-item basis for the unconventional characters. The RI effect was defined as the difference between 1.5-s and 6-s conditions (averaged across cognitive loads) and the load effect was defined as the difference between no-load and parity conditions (averaged across RIs). The correlation between the two effects was again non-significant, r(112)=.05. There was no reason to carry out the calculation for English letters, given the absence of an RI effect for the no-load condition.

Discussion

The results for unconventional characters in Experiment 2 replicated the findings of Experiment 1 with a different secondary task, the parity-judgment task of Barrouillet et al. (2007), which was presented in spoken form and would not appear to have a visual component. These findings are meaningful when taken together with the finding that memory for the unconventional character arrays sustains no more interference from articulatory suppression than from tapping, but sustains more interference from long-term memory retrieval than from long-term memory search without retrieval (Ricker et al., in press). Together, these findings seem to indicate that the nature of the interference is through attentional distraction rather than the overlap in specific codes.

The pattern of cognitive load and RI effects when participants were to remember unconventional characters was in stark contrast to the same relationship when they were to remember familiar English letters, in two ways. First, memory for English letters did not diminish as time passed when no cognitive load was present. A plethora of previous research findings points to a reason for this discrepancy between the unconventional character data and the English letter data: participants rehearse items they can verbalize during unfilled RIs (Baddeley, 1986). Moreover, for such easily labeled stimuli, the work of Lewandowsky and colleagues (e.g., Lewandowsky & Oberauer, 2009; Oberauer & Lewandowsky, 2008) suggests little forgetting across time even when verbal rehearsal and attentional refreshing are prevented.

Second, the effect of a cognitive load increased across RIs for the English letters, but not for the unconventional characters. If we were to try to account for the English letter condition by itself, we would note that it yields a pattern of data closest to Figure 2, Panel b, which depicts an effect of interference and no other effect. That finding alone is also compatible with a model in which the parity task prevents verbal rehearsal of the English letters (e.g., Baddeley & Logie, 1999).

However one accounts for the English letter condition, though, the main point is that it contrasts with the findings for unconventional characters, which therefore require a different explanation. Reinforcing the results of Ricker et al. (in press), the results do not appear to indicate that unconventional characters can be labeled and treated like English letters.

As in Experiment 1, separate analyses of hits and correct rejections revealed a significant effect of load condition in the unconventional character data similar to that in the overall proportion correct data for unconventional character arrays. The effect of time was, again, not present in the hits (correct detection of a change) but was large in the correct rejections (correct indication of no change). This makes sense if the ability to recognize that a probe matched the corresponding array item declined over time as the template against which the probe had to be compared disintegrated. Hit and false alarm data for the English letter arrays in Experiment 2, however, demonstrated a different pattern of results. In these data, there was only a non-significant trend toward an effect of time in the correct rejection data, whereas there was a significant effect of time in the hits (i.e., on change detection). This suggests that participants may have performed for trials with unconventional characters as if they comprised a recognition task, and may have performed for trials with English letters as if they comprised a change-detection task. For English letters, old item recognition is a less salient cue because, in one sense, all of the letters are recognized as old and item familiarity cannot serve as a good indication that the letter was in the present array. Instead, the participant must notice that a particular item cannot be found within the memory set and therefore must be new. As the RI progresses, familiarity of all letters remains high and assists performance on no-change trials, but performance on the change trials deteriorates because the participant cannot tell whether the familiarity comes from the presence of the item in the present reference array or a previous encounter with the letter.

General Discussion

In the present study of memory for unconventional characters and English letters, we examined how the passage of time affects short-term retention and how cognitive load and interference events interact with the passage of time. In both Experiments 1 and 2 (shown in Figure 3 and 4, respectively), memory for an array of unconventional characters was seen to decrease with retention time, irrespective of the amount of interference present during the delay between encoding and recall. There was also an effect of cognitive load that did not change with the RI. In Experiment 2, a condition with arrays of English letters showed a pattern that differed markedly from unconventional characters, in two ways. First, for English letters there was no effect of RI in the absence of a distracting task. Second, in the presence of a parity judgment task, there was a large effect of RI, resulting in an interaction of distraction condition with RI.

This pattern of results establishes that performance is quite different for unconventional characters than for English letters. Most importantly, it shows that there is a form of nonverbal information that cannot be attentionally refreshed or otherwise kept active, even in the absence of distraction. It is not sensory memory, given that a mask was always used.

It is a considerable challenge to find a single theory that can account for all of these results, and at this point we cannot propose any one theory with much confidence. The English letter condition is not different from what would be expected according to a number of theories in that there could be no memory loss over time in the absence of distraction, whereas there would be loss of memory over time in the presence of verbal distraction or interference, either because of the ability to engage in verbal rehearsal (Baddeley & Logie, 1999) or attentional refreshing (Barrouillet et al., 2007; Raye et al., 2007) or because of the absence of time-based forgetting (Oberauer & Lewandowsky, 2008; Lewandowsky & Oberauer, 2009). The pattern of results we found using English letters does, however, point out the uniquely nonverbal nature of memory for unconventional characters.

To understand performance for unconventional characters, we reiterate two new phenomena that any theory must accommodate, and discuss possible bases for these phenomena.

Forgetting of Unconventional Characters Across RIs In the Absence of Distraction

There are two ways to understand this effect. First, there could be decay of some features of the stimuli as a function of the absolute amount of time elapsed. Although every theory seems to include some means to retain stimuli in memory so they cannot be lost over time (for these stimuli including, but perhaps not limited to, verbal rehearsal and attentional refreshing), it is possible that something about the stimuli prevents these mnemonic processes from being completely effective. It may well be that many or most of the unconventional characters are perceived as multiple chunks. There appears to be a limit in working memory of about 3 or 4 chunks in adults (Cowan, 2001) and even 3 unconventional characters could overwhelm that capacity. For example, if each character in a 3-character array contained, say, 2.5 chunks on average, then the array would include 7.5 chunks and it might be impossible to use any method to retain or reactivate all of them before they decay. Losing some features of an unconventional character across RIs could reduce the tendency for the character to be distinguishable from the probe, even if other features still remain.

Losing features from unconventional characters and retaining imperfect copies of those characters is consistent with how such characters are retained in working memory. Awh, Barton, and Vogel (2007) used an array item recognition procedure (like ours) in which the array items varied in complexity: they included simple colored spots but also irregular polygons, Chinese characters, and cubes of different orientations within the same arrays. It was found that change detection was equally good for all of these types of objects, provided that the change was between categories. Thus, performance was equivalent across stimulus types when the probe changed to an object in a different category than the array item it replaced; on average about 4 items could be retained in memory. When a within-category change took place, though, performance was much lower for complex objects than for colored spots. This pattern of results suggested that capacity is distributed among a small number of items but that some features of a complex item couild be omitted or lost from the representation.

An alternative method of explaining memory loss over time in the absence of distraction is one based on temporal distinctiveness. of representations in memory, a kind of proactive interference (e.g., Brown, Neath, & Chater, 2007; Unsworth, Heitz, & Parks, 2008; Winkler, Schröger, & Cowan, 2001). To paraphrase a much cited analogy from Crowder (1976), as the RI following an array lengthens, the distinctness of the items in the array of the current trial may diminish, similar to the manner in which telephone poles appear closer together as they recede into the distance. It becomes more difficult to point to one telephone pole in particular and not the one next to it on accident as they become farther away. If memory representations are distinguished according to the temporal locations of events, a longer RI may mean more difficulty in retrieving the target reference array from long-term memory, which must be recalled in a manner distinct from other recent reference arrays. The loss of temporal distinctiveness is a type of proactive interference that can mimic decay. One might even imagine a modified version of the TBRS model in which the attentional refreshing process serves to increase the distinctiveness of items in the current list or array from those in previous trials by reminding the participant of the items closer toward the time of test (cf. Tan & Ward, 2000). At any rate, the present data show that the role of time in forgetting cannot be dismissed.

Zhang and Luck (2009) also found memory loss after 10 s in a visual array procedure with no intervening stimuli but the time course of memory loss appears faster in the present study. Important differences are that their stimuli were not as complex, in that our characters may have been composed of multiple features (cf. Sakai & Inui, 2002) and that they did not use a mask, whereas we did. These differences are critical because less complexity in the stimuli likely results in easier or more accurate application of preexisting visual templates that could be accessed to attentionally refresh materials, resulting in less extreme forgetting. The absence of a mask may also have resulted in continued encoding for a short period into the RI as well as more remaining visual features in memory that could be used to select a response. The present study shows that there is a boundary condition to forgetting across time, inasmuch as it appeared absent from arrays of English letters.

Main Effect of Distraction on Memory for Unconventional Characters with No Increase in Distraction Effects Across RIs

Most theoretical treatments of working memory have suggested that interference or distraction effects, when they occur at all, should increase across RIs (e.g., Lewandowsky et al., 2004). In the present study, however, the interference changed from each presentation to the next and yet the effect of this interference, or distraction, did not cause increasing loss of memory across RIs.

One type of theoretical treatment leads to the prediction of no increase in distraction effects across RIs, despite changing distracting stimuli. Cowan (1992) suggested that the process of searching for the next item in a list to be recalled, between words pronounced during the recall period, reactivates those words. Barrouillet et al. (2004, 2007) developed this idea into a model in which an equilibrium is reached between reactivation of items using attentional refreshing and forgetting of the same items between reactivations. Presumably because of that equilibrium, it is found that the time between items does not matter, whereas the ratio of time that is free for attentional refreshing does matter. The principle of attentional refreshing seems apt in that the distraction task in Experiment 2 (a verbally-presented parity task) appeared to contain no features in common with the retention of unconventional characters, which were not hurt by articulatory suppression more than by steady tapping (Ricker et al., in press).

In the model of Barrouillet et al. (2004, 2007) it is supposed that the focus of attention can refresh or reactivate at most one item at a time (cf. Oberauer & Bialkova, 2009). This is in conflict with the hypothesis of Cowan (1999, 2001) and others that the focus of attention can accommodate several items at once. A careful consideration of the notion of reactivation, though, indicates that a multi-item focus of attention could operate in the same way. Provided that the rate of reactivation of items is in balance with the rate of forgetting, it is the ratio of free time to occupied time that should matter for recall, not the total amount of free time or total amount of occupied time.

To explain the absence of an interaction of distraction condition with RI for unconventional characters in both experiments, an equilibrium between mnemonic processing (such as attentional refreshing) and forgetting over time is necessary unless there is some type of interference that only has an effect early on in the RI period. However, it is difficult to understand what such a process could be; it is not consolidation of the items into working memory (Vogel et al., 2006), given that a mask precedes the RI, and we have found that the load effect depends on continuation of the distraction throughout the RI (Footnote 2). Therefore, it seems inescapable that an equilibrium process must apply.

Finally, it is worth emphasizing that this distraction effect occurred between sets of stimuli with no known features in common. Ricker et al. (in press) ruled out the use of specific verbal codes for memory of these unconventional characters by showing the same magnitude of effects of articulatory suppression and tapping on memory. The parity judgment task used in the present Experiment 2 involves spoken stimuli and no clear visual coding. The parity judgment task therefore appears to have interfered with memory for unconventional characters not through a shared code, but by capturing attention needed for refreshing of the visual code. If these suppositions are correct, then general attentional distraction would have to be included as a means of interference between stimuli, a mechanism that was disavowed in some previous work from the standpoint of the multiple-stores model of working memory (e.g., Cocchini, Logie, Della Sala, MacPherson, & Baddeley, 2002).

Concluding Remarks

In working memory for arrays of unconventional characters, two new effects have been established: time-based loss, and an effect of distraction on the level of performance but not the rate of loss across RIs. The distraction occurs in Experiment 2 using a parity judgment task presented via spoken stimuli, which seems to share few features with arrays of unconventional characters given that they are not specifically susceptible to articulatory suppression effects (Ricker et al., in press). Any future theory of working memory will have to account for these new findings; we have proposed multiple hypotheses about how they can occur, but have not yet resolved them.

Despite the unresolved question of the nature of time-based loss, the present work is important for theories of working memory. First, it shows that the previous theories of forgetting from working memory, which have been developed primarily with respect to verbal stimuli, cannot be applied wholesale to the understanding of visual stimuli that are difficult to label. Second, it shows that more than one factor influencing forgetting may be present at the same time. The results we obtained can be understood as a combination of time-based forgetting of visually-coded information and attentional refreshing of some, but not all, of the information in the portion of the RI that is not taken up by a distracting task.

The finding of two memory components may also help to resolve a discrepancy between past studies of visual working memory. The studies of Morey and Cowan (2004) and Cocchini et al. (2002) have previously been assumed to each support structural descriptions of working memory which are in conflict with one another. Morey and Cowan found significant interference between a verbal digit load and a visual array memory task composed of colored squares, supporting a domain general approach to memory storage mediated by general attention. Cocchini et al., on the other hand, found little interference between tasks occupying different modalities, such as digit recall and visual pattern recall. This was used as evidence to support a structural split in which there are two independent working memory systems, one for verbal information and one for visuo-spatial information. The present study provides evidence that both interpretations may be right to some extent. In our data we found that there is an attention-demanding component of memories for visual objects that can be interrupted by a verbal distracting task, in agreement with the findings of Morey and Cowan (2004); but there is also an attention-free component that is unstable over time, agreeing with the suggestion of Cocchini et al. (2002) that visual stimuli can survive verbal distraction.

The healthiness of several theories may hinge in part on extensive further exploration of the phenomena we have uncovered. For example, manipulation of the time between trials could indicate whether the inevitable forgetting of unconventional characters across the RI can be better explained by decay in a fixed period of time (e.g., Baddeley, 1986; Baddeley & Logie, 1999; Cowan, 1988) or by loss of temporal distinctiveness (Brown et al., 2007). Manipulation of the ratio of distraction to free time across the RI could help to confirm or disconfirm whether the effect of distraction depends on the ratio, as in the list studies of Barrouillet et al. (2004, 2007). It will be important also to understand whether attentional refreshing of an unconventional item in an array is neutral to other array items or causes increased competition with them (Higgins & Johnson, 2009).

In future work, it might also be possible to examine a transition from unconventional to conventional characters as a function of learning. Using Japanese kanji characters with literate Japanese participants, Saito, Logie, Morito, and Law (2008) showed that working memory for a character can rely upon both verbal and visuospatial information at the same time. With learning, unconventional characters could begin to take on a verbalizable code as they become unified, or that verbalizable code might have to be explicitly taught.

A final issue is whether the working memory representation that is lost as a function of time comprises temporarily activated portions of long-term memory (Cowan, 1988, 1999) or whether it comprises a separate copy of that information in a dedicated short-term buffer (Baddeley, 1986; van der Meulen, Logie, & Della Sala, 2009). Although recent brain research has implied that the intraparietal sulcus is associated with the retention of visual information (e.g., Todd & Marois, 2004; Xu & Chun, 2006), this brain area more recently has been shown to track both visual and verbal stimuli (Majerus et al., 2010) held in working memory and may serve as a locus of a more general, amodal working memory area such as the focus of attention (Cowan, 1988, 1999, 2001) or episodic buffer (Baddeley, 2000). The present procedure is one that could be brought to bear upon this recent brain research to determine whether the forgetting of visual information over time in the absence of distraction involves this region or, as we would expect, takes place independent of it. In sum, the disparate theories of working memory have relied on experimental procedures that highlight different phenomena. Integration across procedures, such as that used here, is needed in order to examine the underlying processes affecting short-term retention of information.