Abstract
It is well established that the memory strength of studied items is more variable than the strength of new items on tests of recognition memory, but the reason why this occurs is poorly understood. One account for this old item variance effect is based on single-process theory, which proposes that this effect is due to variability in how well items are initially encoded into memory (i.e., the encoding variability account). In contrast, dual-process theory argues that old items are more variable because they are influenced by both recollection and familiarity, whereas recognition of new items relies primarily on familiarity. The current study shows that increasing encoding variability did not increase old item variance, and that old item variance is directly related to the contribution of recollection. These results indicate that old item memory variability is due to the relative contribution of recollection and familiarity.
Keywords: Recognition Memory, Dual-Process Theory, Single-Process Theory, Recollection, Encoding Variability
A longstanding debate in the memory literature has been to determine if recognition memory is best explained by single- or dual-process theories of memory. Single-process theories propose that recognition judgments are based on assessments of a single underlying memory strength signal (e.g., Donaldson, 1996; Mickes, Wais, & Wixted, 2009; Wiesmann & Ishai, 2009; Wixted, 2007), whereas dual-process theories argue that recognition is based on either assessments familiarity or on the products of a recollection process whereby qualitative information about the study event is retrieved (e.g., Atkinson & Juola, 1974; Mandler, 1980; Jacoby, 1991; Yonelinas, 1994). Discriminating between single- and dual-process theories has been difficult because they often provide equally good accounts of the data even when they lead to entirely different theoretical interpretations of the results (e.g., Rotello, MacMillan, Reeder & Wong, 2005; Yonelinas & Parks, 2007). However, one fundamental way in which these models differ is with respect to how they account for memory variability.
The extant literature indicates that studied items are not only stronger than non-studied items, but that they are also associated with greater variability in memory strength (i.e., old item variance is greater than new item variance). This old item variance effect was first documented by Egan (1958) and has since been replicated numerous times using a variety of different experimental methods (Mickes, Wixted, & Wais, 2007; Ratcliff Sheu, & Gronlund, 1992; Yonelinas 1994). Furthermore, this effect is quite substantial in tests of item recognition memory, with old items showing 25–67% more variability in strength than the new items (for reviews see Ratcliff et al., 1992; Yonelinas & Parks, 2007; Wixted, 2007). Despite the ubiquity of the old item variance effect, the reason this phenomenon occurs remains unclear. The purpose of the present experiment is to test the single- and dual-process accounts of this effect.
One way of accounting for the old item variance effect is to adopt a single-process, unequal-variance signal detection model. This model assumes that old items are stronger than new items, and that old items can also have greater variance than new items. The memory strength signal could reflect the combination of many different underlying memory processes (Wixted, 2007), but the model is considered a single-process model because recognition responses are based exclusively on a single aggregate strength signal. Proponents of such a model conjecture that increases in the variability of studied item memory strengths arise because of encoding variability1 (Hintzman, 1986; Ratcliff et al., 1992; Ratcliff, McKoon, & Tindall, 1994; Wixted, 2007). Specifically, the old item strength distribution will be more variable than the new item distribution because some items are encoded very well whereas others are encoded less well. As Wixted (2007) argued, “…if the amount of strength added differs across items, which surely must be the case, then both strength and variability would be added, and an unequal-variance model would apply (p. 154).” Although it seems reasonable that encoding variability may account for the old item variance effect, this hypothesis has never been tested.
An alternative account of the old item variance effect is based on dual-process theory (Yonelinas, 1994, 1999, 2001), which argues that studied items are associated with more variable memory strengths than new items because both recollection and familiarity contribute to the recognition of old items, whereas only familiarity typically contributes to new item recognition. According to this account, the variance of studied and non-studied items recognized on the basis of familiarity is approximately equal. However, because recollection is assumed to support relatively high confidence recognition responses of old items compared to familiarity, recollection will effectively cause the old items to be more variable than the new items.
The purpose of the present experiment was to test novel predictions of the encoding variability and dual-process accounts of the old item variance effect. Participants studied two lists of words. In the pure study list, every word was presented for 2.5 s. In the mixed study list, which was designed to increase encoding variability relative to the pure study list, half of the words at study were presented for 1 s and half were presented for 4 s. These presentation rates were selected because they were expected to lead to significant differences in encoding, but avoid floor and ceiling effects that can bias recognition memory variance measures (Yonelinas & Parks, 2007). The expectation was that the average strength of items in the pure and mixed lists would be approximately equal, but the variability in memory strength should be greater in the mixed list because some items are encoded very well (4 s items) whereas others are encode less well (1 s items). This can be verified by looking to see if memory is better for the 4 s items compared to the 1 s items. After each study list, participants completed a recognition memory test where they made two judgments. Participants first made an old or new judgment on a 6-point confidence scale (e.g., 1 = sure new; 6 = sure old), which was used to assess variability in memory strength, followed by a remember, know, or new judgment (Gardiner, 1988; Tulving, 1985), which was used to assess recollection and familiarity. The confidence judgment was always made first because the primary aim was to examine old item variance.
If the old item variance effect is due to encoding variability, then estimates of old item variance should be larger in the mixed list compared to the pure list. However, if old item variance is due to the relative contribution of recollection and familiarity, old item variance should be directly related to the inclusion of recollection-based responses as measured by remember/know judgments (Yonelinas, 2001; Yonelinas & Jacoby, 1995), and not encoding variability per se. It is important to note that when using standard remember/know instructions, participants often make remember responses even when they don’t recollect any specific details about the study event (Rotello et al., 2005; Yonelinas 2001; Yonelinas & Parks, 2007). To ensure that the remember/know responses were indicative of recollection and familiarity, participants in the current study were given more conservative remember/know instructions, which have been shown to produce process estimates that converge with estimates from other measures (see Rotello, et al., 2005; Yonelinas, 2001).
Method
Participants and Materials
Thirty-two undergraduates (22 females) from the University of California, Davis with an average age of 19.16 (SD = 1.25) consented to participate in this experiment for partial fulfillment of a course requirement. One participant’s data was excluded from the remember/know analysis because they failed use the new response.
The materials consisted of 640 seven letter low-frequency nouns (i.e., frequencies between 1 and 30, M = 5.73; SD = 6.45; Kučera & Francis, 1967) taken from the MRC psycholinguistic database (Coltheart, 1981). Low-frequency words were chosen to facilitate comparison to other studies examining similar issues (e.g., Yonelinas, 1999). Participants viewed the materials on a Dell computer using E-Prime software (version 1.1.4.1; www.pstnet.com).
Design and Procedure
After informed consent was obtained, each participant completed a study-test phase for both the pure and mixed study conditions. In the pure study condition, 160 words were each presented for 2.5 s at study. In the mixed study condition, 80 of the 160 words in the study list were presented for 1 s, and these were mixed with the remaining 80 words, which were presented for 4 s. A 500 ms blank screen followed the presentation of each word in both study conditions. The order of the mixed and pure study conditions was counterbalanced across participants2. After each study phase, participants completed a series of arithmetic problems for 30 s, which served as a distracter task.
After each study list, participants were given a self-paced recognition memory test that contained the 160 words from the study phase intermixed with 160 new words. First, participants judged each word as old or new using a 6-point confidence scale (e.g., 1 = sure new, 6 = sure old) and were instructed to use the entire range of confidence responses to make their memory judgments. Following the confidence response, participants were required to give a remember, know, or new judgment. The instructions for this task were similar to previous studies (see Yonelinas, 2001). Specifically, participants were instructed to respond remember only if they could remember something specific about the study environment, such as what they were thinking when they studied the word or what the word looked like. They were further instructed that they may have to communicate the information they recollected to the experimenter, although they were never asked to do so. Participants were instructed to respond know if they believed that the word had appeared on the study list but were unable to remember anything specific about previously seeing the word. Finally, participants were instructed to respond new if the word was new and had not been previously studied. The materials were counterbalanced such that each word appeared in each condition an equal number of times across participants. A brief practice study-test phase was completed before both the pure and mixed study conditions.
Results
Figure 1 presents the proportion of responses in each confidence bin given to old and new items in both the pure and mixed study lists, as well as the proportion of items that were given a remember response (hatched area). An examination of this figure reveals that the old items (top panels) were associated with higher levels of confidence than new items (lower panels), indicating that old items achieved higher memory strengths than new items. More importantly, the distributions in the pure list conditions (left panels) were almost identical to those in the mixed list conditions (right panels), showing that increasing encoding variability did not influence old item variability, which contradicts the prediction made by the encoding variability account. Moreover, the old item distributions appear to be more variable than the new item distributions because the old items had a disproportionately large number of the highest confidence responses. Critically, this difference was driven primarily by items receiving a remember response. Thus, it is apparent from the strength distributions that the increased variability of the old item distributions was not related to encoding variability, but rather was due largely to the inclusion of the recollected items. More formal analyses confirming these initial observations are described below.
Figure 1.
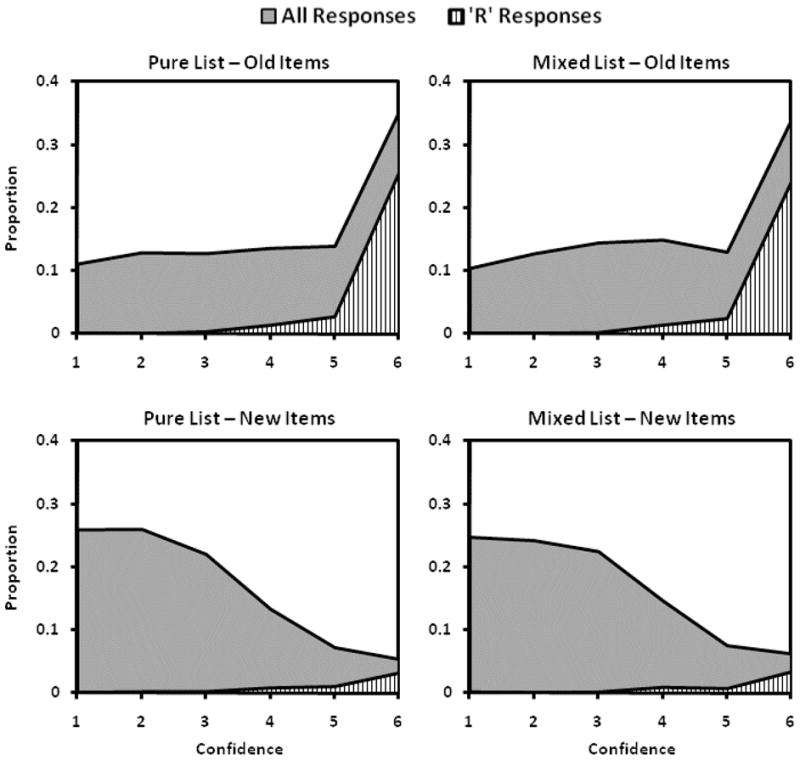
Proportion of responses in each confidence bin and the proportion of ‘remember’ (R) responses given in each confidence bin to old (top panels) and new (bottom panels) items in the pure (left panels) and mixed (right panels) study conditions.
Assessing the effects of encoding variability on old item variance
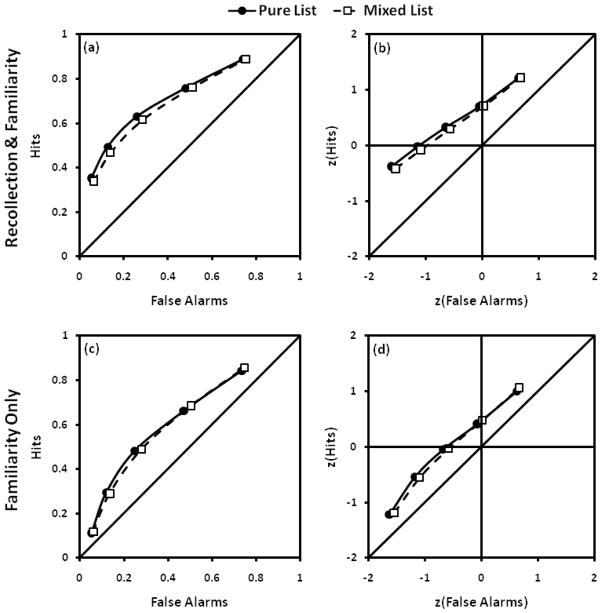
Memory strength and variance was assessed by plotting the hit rate against the false alarm rate as a function of response confidence and analyzing the resulting receiver operating characteristics (ROCs) using signal detection theory (for review see MacMillan & Creelman, 2005). When the ROC is plotted on z-coordinates, the intercept of the z-ROC provides a rough index of recognition memory strength or sensitivity, such that a higher intercept reflects better sensitivity. Moreover, the slope of the z-ROC provides a measure of the relative variance of the old and new items (i.e., snew/sold). A z-slope of one indicates that the old and new item variances are the same, whereas z-slopes less than one indicate that old items are associated with greater variance than new items. Thus, if encoding variability increases old item variance, the z-slope should be lower in the mixed list than in the pure list.
The aggregate ROCs and z-ROCs for the pure and mixed list conditions are plotted in Figure 2a and 2b, respectively. As can be seen in Figure 2b, the z-ROCs for the mixed and pure conditions were quite similar, and there was no evidence that the z-ROC in the mixed condition had a lower slope than that of the pure condition. An examination of each individual’s z-ROCs demonstrated that the z-slope for the mixed study condition was not lower than the z-slope in the pure study condition (see Table 1), which is inconsistent with the encoding variability account, and in fact there was a numerical trend in the opposite direction, t(31) = 1.38, SE = .04, p = .18. The same pattern of results was obtained when the data was fit to the unequal-variance signal detection model using maximum likelihood estimation.
Figure 2.
The aggregate ROC (a) and z-ROC (b) for the pure and mixed study conditions. The aggregate familiarity-only ROC (c) and z-ROC (d) for the pure and mixed study conditions after recollection was removed from each cumulative hit rate.
Table 1.
Mean intercept and slope measures for the overall and familiarity-only z-ROCs in the pure and mixed study conditions.
| Study Condition | z-Intercept | z-Slope |
|---|---|---|
| Overall z-ROC | ||
| Pure | .81 (.07) | .68 (.03) |
| Mixed | .83 (.07) | .74 (.04) |
| Familiarity z-ROC† | ||
| Pure | .52 (.06) | .95 (.04) |
| Mixed | .52 (.06) | .98 (.05) |
Note. Standard errors of the mean are provided in parentheses. Lower z-slopes reflect increased old item variance.
These values are based on the 31 participants included in the remember/know analysis.
Next, we directly contrasted performance (i.e., z-intercept) on the weak (1 s) and strong (4 s) items in the mixed list to verify that the strength manipulation in the mixed list had a significant impact on memory encoding. As would be expected, the z-intercept was significantly larger for words presented for four seconds than for words presented for one second, t(31) = 4.31, SE = .04, d = .39, p < .01, indicating that the strong items were better encoded than the weak items. However, the difference in performance between the 1 s and 4 s items was associated with a small effect size (Cohen, 1988). Thus, we were concerned that it may not have been large enough to bring about a variance difference between the pure and mixed lists. To address this possibility, we conducted a median split analysis in which we examined only the participants who had the largest difference in intercept between the strong and weak items in the mixed list (i.e., those showing the largest 4 s > 1 s encoding difference). For this subset of participants, the z-intercept was greater for the words presented for four seconds (M = 1.09, SE = .10) than for words present for one second (M = .77, SE = .08), and this difference was accompanied by a large effect size, t(15) = 16.62, SE = .02, d = .89, p < .01. Furthermore, these participants showed no difference in z-slope between words in the mixed study condition presented for four seconds (M = .71, SE = .03) and words presented for one second (M = .72, SE = .04), t(15) < 1, and no difference between the z-intercept in the pure (M = .87, SE = .09) and mixed (M = .92, SE = .09) study conditions, t(15) < 1. Most importantly, as with the initial analysis, there was no evidence in this subset of participants that the z-slopes in the mixed list (M = .71, SE = .03) were lower than in the pure list (M = .66, SE = .04), t(15) = 1.33, SE = .03, p = .20. In conclusion, the present data does not support the encoding variability account of the old item variance effect.
However, one might still argue that increasing the encoding duration by a factor of four was simply not sufficient to produce an increase in old item variability in the mixed item condition above and beyond the old item variance generated by the encoding variability already present within the weak and strong items. To address this, the strength distributions of the weak and strong items in the mixed condition were separately measured. Next, we estimated what the overall z-ROC would look like given that half the items were from the strong condition and half were from the weak condition by combining the two distributions into a single distribution. If encoding variability can accurately account for the old item variance effect, then old item variability estimated from combining the weak and strong distributions into a single distribution should converge with the old item variability as measured by the z-ROC analysis of the overall mixed list. However, the z-slope estimated from the weak and strong item distributions (M = .70, SE = .03) was significantly lower than the observed z-slope, t(31) = 2.72, SE = .01, d = .21. These results provide further evidence that encoding variability does not explain the old item variance effect because the variability of old item memory strengths estimated from the weak and strong item distributions did not converge with the observed old item variance in the mixed list condition.
Assessing the effects of recollection and familiarity on old item variance
The remember/know responses were used to provide estimates of recollection and familiarity to determine if the increased variability of old items was related to the contribution of recollection. This was examined by (1) assessing the old item variance after removing the contribution of recollection from recognition performance, and (2) using the estimates of recollection and familiarity to predict the amount of old item variability that was observed. If the old item variance effect is due to recollection, then the old and new item variance measures should be equal (i.e., the slope of the z-ROC should not differ from one) after recollected items are removed from the analysis. The contribution of recollection was removed from each individual’s z-ROC by subtracting the recollection estimate from the cumulative hit rate at each confidence point (cf. Yonelinas, 2001). The resulting familiarity-only ROCs and z-ROCs are presented in Figure 2c and 2d, respectively. An examination of Figure 2d shows that the z-slope no longer differed from one in either the pure or mixed study conditions once recollection was removed. The analysis of each individual’s familiarity-only z-ROC confirmed this observation as the average z-slope did not differ from one in either the pure or mixed study conditions after recollection was removed, t’s(30) < 1.12 (Table 1). This demonstrates that it was the contribution of recollection to recognition of studied items that produced the old item variance effect.
Next, we investigated whether the estimates of recollection and familiarity derived from remember/know responses could be used to accurately predict the old item variance observed in the confidence z-ROCs on a participant-by-participant basis. Specifically, each participants recollection and familiarity estimates from the remember/know reports were inserted in the dual-process signal detection model using the observed false-alarm rates from each participant’s confidence data to examine the implied z-slope (for further discussion, see Yonelinas, 1994, 1999). Finally, the relationship between the predicted z-slopes and the z-slopes obtained from the confidence data was examined. There was a significant positive correlation between the observed z-slope and the dual-process predicted z-slope in both study conditions, rpure(29) = .50; rmixed(29) = .56, both p’s < .05, indicating that the old item variance was directly related to the relative contributions of recollection and familiarity to the recognition of studied items. This result suggests that one can accurately predict the size of the old item variance effect if one estimates the contribution of recollection and familiarity using remember/know reports.
However, the confidence and remember/know procedures are quite similar, and it may be possible to capture the same relationship using a single-process model such as the unequal-variance signal detection model (e.g., Starns & Ratcliff, 2008; Wixted & Stretch, 2004). To examine this, remember and know judgments were plotted in z-space as different confidence levels and the slope and intercept of the best fitting line was measured. One participant was excluded from this analysis because their estimated z-slope was greater than five standard deviations from the group mean. Unlike the results obtained with the dual-process signal detection model, the correlation between the observed z-ROC slope and the slope predicted by the unequal-variance signal detection model was not significant in either study condition, rpure(28) = .09; rmixed(28) = .17; both p’s >.36. Thus, the success of the dual-process approach in accounting for old item variance does not generalize to just any model of recognition memory, such as the unequal-variance signal detection model (for related arguments, see Rotello, MacMillan, & Reeder, 2004).
Discussion
The present experiment investigated the encoding variability (e.g., Wixted, 2007) and dual-process (e.g., Yonelinas, 1994) accounts of the common finding that the memory strengths of studied items are more variable than the memory strengths of new items (i.e., the old item variance effect). We directly manipulated encoding variability by varying presentation rate at study (e.g., 2.5 s in the pure lists compared to 1 s and 4 s in the mixed list), and found no evidence that encoding variability led to an increase in old item variance. In fact, the old item variance in the mixed study condition was numerically smaller than in the pure study condition, which is the opposite of what the encoding variability account predicts. In addition, an examination of performance on the weak and strong items in the mixed study condition showed that the observed old item variance in the mixed list was not consistent with the encoding variability hypothesis. In contrast, the results revealed that the increased old item variability was directly related to the contribution of recollection and familiarity. Specifically, we found that the old item variance effect was due entirely to the inclusion of recollected items, and the magnitude of the old item variance effect observed in the confidence responses was accurately predicted on the basis of recollection and familiarity estimates derived from remember/know reports.
The results from the present experiment are relevant in resolving the debate between single- and dual-process models of recognition memory. Most importantly, the results supported the a priori prediction of the dual-process model, which states that the old item variance effect arises because both recollection and familiarity contribute to old item recognition. The current results join several previous examples of empirical regularities that were discovered by directly testing the novel predictions of the dual-process model, such as finding U-shaped z-ROCs in associative and source memory recognition tests, and z-ROCs with unit slopes (i.e., equal variances between old and new item memory strengths) in patients with hippocampal damage (see Yonelinas & Parks, 2007). Additionally, the lawful relationship that was observed between subjective reports of remembering and old item variability was revealed when the results were interpreted from the viewpoint of the dual-process model. However, this relationship was not observed if one attempted to understand recognition memory in terms of a single-process model like the unequal-variance signal detection model. Although the single-process approach provides a parsimonious account of remember/know judgments, the current results indicate that this account is insufficient because remember judgments do not simply reflect high confidence responses; they provide important information about the variability present in the distribution of old item memory strengths.
However, a number of recent reports have suggested that results from remember/know studies can be well explained by a single-process model whereby remember responses simply reflect stronger memories than familiarity-based responses (e.g., Dunn, 2004, 2008; Malmberg, 2008; Wixted & Stretch, 2004). These results, however, do not show that the remember/know reports do not reflect recollection and familiarity, just that a single-process model can also account for the data. As Dunn (2004) noted about the results from his meta-analysis, “…it should not be inferred that the alternative dual-process interpretation has been shown to be incorrect (p. 539).” Moreover, a review of the literature indicates that when appropriate instructions are used, remember/know judgments provide process measures that converge quite well with other measures of recollection, such as source discrimination or ROC estimates (Rotello et al., 2005; Yonelinas, 2001; for review see Yonelinas, 2002). When more constraining data sets are considered, like the one in the current experiment, it becomes clear that a single-process account of recognition memory is insufficient, and that a dual-process model should be adopted.
Although the results argue against an encoding variability account of the old item variance effect, one may ask, “doesn’t encoding variability have to account for at least some of the old item variance?” Intuitively it seems like this should be the case, but a careful consideration of current computational work suggests otherwise. For example, computational models such as the complementary learning systems model (Norman & O’Reilly, 2003) and TODAM2 (Murdock, 1993) assume that familiarity reflects how well a test item matches what is stored in a distributed memory network, and models such as these can produce old and new item distributions with equal variance. This occurs because both old and new items are assessed in exactly the same way; the test item is matched to all items stored in memory. The amount of encoding variability will influence what is stored in memory, but this in turn influences how well both old and new items match what is stored there. In this way, encoding variability can have similar impacts the familiarity of both old and new items. It remains to be determined, however, whether more extreme manipulations of encoding strength (e.g., a study time ratio of greater than 4 to 1) might begin to impact old item variability (see Norman & O’Reilly, 2003).
In summary, the present results help to clarify why the strength of studied items is more variable than the strength of new items. Specifically, our results support a dual-process model of recognition memory by suggesting that the reason studied items are more variable in memory strength than new items is because recollection and familiarity contribute to old item recognition whereas recognition of new items is primarily influenced by only the familiarity process. In addition, there was no evidence that encoding variability increased the old item variance, and the unequal-variance signal detection model did not capture the relationship between remember/know reports and the amount of old item variability seen in recognition responses. Importantly, the results from this experiment add to the extant literature indicating that at least two processes are required to adequately explain recognition memory, and that understanding recognition memory performance can be obscured if the unequal-variance signal detection model is adopted.
Acknowledgments
Preparation of this article was supported by National Institute of Mental Health grants MH07019 and MH59352. This research was presented at the 2009 Meeting of the Psychonomic Society in Boston, MA. We would like to thank Arne Ekstrom, Charan Ranganath, Elizabeth Chua, members of the Human Memory Lab and three reviewers for their thoughtful comments on a previous version of this manuscript, and Saira Shariff for help with data collection.
Footnotes
In the spacing effect literature, the term encoding variability refers to encountering an item in different contexts, usually across multiple presentations (e.g., Gartman & Johnson, 1972). In contrast, here, the term encoding variability refers to the case where some items are encoded more strongly than others.
The order of the pure and mixed phases had no appreciable effect and is not discussed further.
Publisher's Disclaimer: The following manuscript is the final accepted manuscript. It has not been subjected to the final copyediting, fact-checking, and proofreading required for formal publication. It is not the definitive, publisher-authenticated version. The American Psychological Association and its Council of Editors disclaim any responsibility or liabilities for errors or omissions of this manuscript version, any version derived from this manuscript by NIH, or other third parties. The published version is available at www.apa.org/pubs/journals/xlm.
Contributor Information
Joshua D. Koen, University of California, Davis
Andrew P. Yonelinas, University of California, Davis
References
- Atkinson RC, Juola JF. Search and decision processes in recognition memory. In: Krantz DH, Atkinson RC, Luce RD, Suppes P, editors. Contemporary developments in mathematical psychology: Vol. 1. Learning, memory, and thinking. San Francisco: Freeman; 1974. [Google Scholar]
- Cohen J. Statistical power analysis for the social sciences. 2. Hillsdale, NJ: Lawrence Earlbaum Associates; 1988. [Google Scholar]
- Coltheart M. The MRC psycholinguistic database. Quarterly Journal of Experimental Psychology. 1981;33A:497–505. [Google Scholar]
- Donaldson W. The role of decision processes in remembering and knowing. Memory and Cognition. 1996;24:523–533. doi: 10.3758/bf03200940. [DOI] [PubMed] [Google Scholar]
- Dunn JC. Remember-Know: A matter of confidence. Psychological Review. 2004;111:524–542. doi: 10.1037/0033-295X.111.2.524. [DOI] [PubMed] [Google Scholar]
- Dunn JC. The dimensionality of a remember-know task: A state-trace analysis. Psychological Review. 2008;115:426–446. doi: 10.1037/0033-295X.115.2.426. [DOI] [PubMed] [Google Scholar]
- Egan JP. Tech Note AFCRC-TN-58–51. Bloomington: Indiana University, Hearing and Communication Laboratory; 1958. Recognition memory and the operating characteristic. [Google Scholar]
- Elfman KW, Parks CM, Yonelinas AP. Testing a neurocompuutational model of recollection, familiarity, and source recognition. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2008;34:752–768. doi: 10.1037/0278-7393.34.4.752. [DOI] [PubMed] [Google Scholar]
- Gardiner JM. Functional aspects of recollective experience. Memory & Cognition. 1988;16:309–313. doi: 10.3758/bf03197041. [DOI] [PubMed] [Google Scholar]
- Gartman LM, Johnson NF. Massed versus distributed repetition of homographs: A test of the differential-encoding hypothesis. Journal of Verbal Learning & Verbal Behavior. 1972;11:810–808. [Google Scholar]
- Hintzman D. “Schema abstraction” in a multiple-trace memory model. Psychological Review. 1986;93:411–428. [Google Scholar]
- Jacoby LL. A process dissociation framework: Separating automatic from intentional uses of memory. Journal of Memory and Language. 1991;30:213–541. [Google Scholar]
- Kučera H, Francis W. Computational analysis of present-day American English. Providence, RI: Brown University Press; 1967. [Google Scholar]
- MacMillan NA, Creelman CD. Detection theory: A user’s guide. 2. New York: Cambridge University Press; 2005. [Google Scholar]
- Malmberg KJ. Recognition memory: A review of critical findings and an integrated theory for relating them. Cognitive Psychology. 2008;57:335–384. doi: 10.1016/j.cogpsych.2008.02.004. [DOI] [PubMed] [Google Scholar]
- Mandler G. Recognizing: The judgment of previous occurrence. Psychological Review. 1980;87:252–271. [Google Scholar]
- Mickes L, Wais PE, Wixted JT. Recollection is a continuous process: Implications for dual-process theories of recognition memory. Psychological Science. 2009;20:509–515. doi: 10.1111/j.1467-9280.2009.02324.x. [DOI] [PubMed] [Google Scholar]
- Mickes L, Wixted JT, Wais PE. A direct test of the unequal-variance signal detection model of recognition memory. Psychonomic Bulletin & Review. 2007;14:2007. doi: 10.3758/bf03194112. [DOI] [PubMed] [Google Scholar]
- Murdock BB. TODAM2: A model for the storage and retrieval of item, associative, and serial-order information. Psychological Review. 1993;100:183–203. doi: 10.1037/0033-295x.100.2.183. [DOI] [PubMed] [Google Scholar]
- Norman KA, O’Reilly RC. Modeling hippocampal and neocortical contributions to recognition memory: A complementary-systems-learning approach. Psychological Review. 2003;110:611–646. doi: 10.1037/0033-295X.110.4.611. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, McKoon G, Tindall M. Empirical generality of data form recognition memory receiver-operating characteristic functions and implications for the global memory models. Journal of Experimental Psychology: Learning, Memory,& Cognition. 1994;20:763–785. doi: 10.1037//0278-7393.20.4.763. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, Sheu C, Gronlund SD. Testing global memory models using ROC curves. Psychological Review. 1992;99:518–535. doi: 10.1037/0033-295x.99.3.518. [DOI] [PubMed] [Google Scholar]
- Rotello CM, MacMillan NA, Reeder JA. Sum-difference theory in remembering and knowing: A two-dimensional signal-detection model. Psychological Review. 2004;111:588–616. doi: 10.1037/0033-295X.111.3.588. [DOI] [PubMed] [Google Scholar]
- Rotello CM, MacMillan NA, Reeder JA, Wong M. The remember response: Subject to bias, graded, and not a process-pure indicator of recollection. Psychonomic Bullentin & Review. 2005;12:865–873. doi: 10.3758/bf03196778. [DOI] [PubMed] [Google Scholar]
- Starns JJ, Ratcliff R. Two dimensions are not better than one: STREAK and the univariate signal detection model of remember/know performance. Journal of Memory and Language. 2008;59:169–182. doi: 10.1016/j.jml.2008.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tulving E. Memory and consciousness. Canadian Psychologist. 1985;26:1–12. [Google Scholar]
- Wiesmann M, Ishai A. Recollection- and familiarity-based decisions reflect memory strength. Frontiers in Systems Neuroscience. 2009;2:1–9. doi: 10.3389/neuro.06.001.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wixted JT. Dual-process and signal detection theory of recognition memory. Psychological Review. 2007;114:152–176. doi: 10.1037/0033-295X.114.1.152. [DOI] [PubMed] [Google Scholar]
- Wixted JT, Stretch V. In defense of the signal-detection interpretation of Remember/know judgments. Psychonomic Bulletin & Review. 2004;11:616–641. doi: 10.3758/bf03196616. [DOI] [PubMed] [Google Scholar]
- Yonelinas AP. Receiver operating characteristics in recognition memory: Evidence for a dual process model. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1994;20:1341–1354. doi: 10.1037//0278-7393.20.6.1341. [DOI] [PubMed] [Google Scholar]
- Yonelinas AP. The contribution of recollection and familiarity to recognition and source memory: An analysis of receiver operating characteristics and a formal model. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1999;25:1415–1434. doi: 10.1037//0278-7393.25.6.1415. [DOI] [PubMed] [Google Scholar]
- Yonelinas AP. Consciousness, control and confidence: The three Cs of recognition memory. Journal of Experimental Psychology: General. 2001;130:361–379. doi: 10.1037//0096-3445.130.3.361. [DOI] [PubMed] [Google Scholar]
- Yonelinas AP. The nature of recollection and familiarity: A review of 30 years of research. Journal of Memory and Language. 2002;646:441–517. [Google Scholar]
- Yonelinas AP, Jacoby LL. The relation between remembering and knowing as bases for recognition: Effects of size congruency. Journal of Memory and Language. 1995;34:622–643. [Google Scholar]
- Yonelinas AP, Parks CM. Receiver operating characteristics (ROCs) in recognition memory: A review. Psychological Bulletin. 2007;133:800–832. doi: 10.1037/0033-2909.133.5.800. [DOI] [PubMed] [Google Scholar]