SeqEM: an adaptive genotype-calling approach for next-generation sequencing studies

Abstract

Motivation: Next-generation sequencing presents several statistical challenges, with one of the most fundamental being determining an individual's genotype from multiple aligned short read sequences at a position. Some simple approaches for genotype calling apply fixed filters, such as calling a heterozygote if more than a specified percentage of the reads have variant nucleotide calls. Other genotype-calling methods, such as MAQ and SOAPsnp, are implementations of Bayes classifiers in that they classify genotypes using posterior genotype probabilities.

Results: Here, we propose a novel genotype-calling algorithm that, in contrast to the other methods, estimates parameters underlying the posterior probabilities in an adaptive way rather than arbitrarily specifying them a priori. The algorithm, which we call SeqEM, applies the well-known Expectation-Maximization algorithm to an appropriate likelihood for a sample of unrelated individuals with next-generation sequence data, leveraging information from the sample to estimate genotype probabilities and the nucleotide-read error rate. We demonstrate using analytic calculations and simulations that SeqEM results in genotype-call error rates as small as or smaller than filtering approaches and MAQ. We also apply SeqEM to exome sequence data in eight related individuals and compare the results to genotypes from an Illumina SNP array, showing that SeqEM behaves well in real data that deviates from idealized assumptions.

Conclusion: SeqEM offers an improved, robust and flexible genotype-calling approach that can be widely applied in the next-generation sequencing studies.

Availability and implementation: Software for SeqEM is freely available from our website: www.hihg.org under Software Download.

Contact: emartin1@med.miami.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Recent technological advances in massively parallel, high-throughput DNA sequencing, commonly called next-generation sequencing, are producing an unprecedented volume of sequence data. The next few years are likely to see public databases, such as the Short Read Archive at the National Center for Biotechnology Information, filled with hundreds of thousands of terabases of human sequence data. Next-generation sequencing promises to be a powerful tool for discovery of genetic variation contributing to risk of complex diseases by providing rapid and complete sequencing of a set of candidate genes, the entire exome or even the whole genome (Ng et al., 2010; Tucker et al., 2009).

Current next-generation sequencing technologies are shotgun approaches that produce base sequences for multiple, individual DNA molecules which, depending upon the sequencing technology, range from 30 to 350 bp in average length. Once aligned to a reference genome, the number of reference nucleotides and the number of variant (non-reference) nucleotides among multiple sequences overlapping a given DNA site can be counted. Apart from sequencing error, an individual homozygous at the site would yield either all reference or all variant nucleotides. However, because of random sampling of homologous base pairs in heterozygotes and sequencing or alignment errors, the raw counts do not directly identify the genotype at that site. This uncertainty requires a genotype-calling algorithm to determine the latent genotype of an individual from multiple aligned sequence reads.

Two primary methods are currently implemented for genotype calling: (i) a filtering method based on a fixed number of observed variant nucleotides and (ii) a probabilistic method based on posterior genotype probabilities. Commercial software (e.g. Roche GSMapper, CLC and Lasergene) employs simple filters to distinguish heterozygotes from reference homozygotes by calling an individual heterozygous if more than a prespecified number or proportion of variant reads are seen at a position. The difficulty with an arbitrary threshold for determining genotypes is that it does not explicitly take into account the number of aligned sequences (read depth) or information about allele frequency or nucleotide-read error. It also does not quantify the uncertainty of the call. A related approach determines filter thresholds for genotype calls empirically using results from known genotypes (Hedges et al., 2009). Probabilistic approaches, which assign genotype calls based on the maximum posterior genotype probability given the read data, have been implemented in programs such as MAQ and SOAPsnp (Li et al., 2008; Li,J.B. et al., 2009; Li,R. et al., 2009). These use fixed prior values for heterozygote probabilities and nucleotide-read error probabilities, which may not be representative for a given sample, in calculating posterior probabilities.

These approaches make genotype calls for a single individual at a time, and thus do not utilize information from additional individuals in the sample. Anticipating that most resequencing studies will produce data for multiple individuals, we recognized that there is information about sample allele frequency and nucleotide-read error in the data. Consequently, genotype-calling algorithms could be improved by incorporating this information. Accordingly, we propose a novel approach for genotype calling using next-generation sequencing data from multiple unrelated individuals. Our approach (SeqEM) seeks to provide a principled statistical framework that is adaptive in that it does not rely on prespecified or known allele frequency information. Our approach leverages information from next-generation sequence data for multiple individuals by using the Expectation-Maximization (EM) algorithm to numerically maximize the observed data likelihood with respect to genotype frequencies and the nucleotide-read error rate. Using maximum likelihood point estimates of these parameters, we compute the posterior probabilities of each genotype given the read data and classify an individual's genotype as the one with the largest posterior probability. This is a Bayes classification procedure that can be expected to minimize the overall genotype misclassification rate (i.e. genotype-call error). Here, we describe our approach and compare its genotype misclassification rate to different filtering algorithms and the MAQ algorithm, both theoretically and with simulated data. Finally, we compare the performance of alternative methods using validated SNP genotypes in a real dataset of eight related individuals with exome capture data.

2 METHODS

2.1 Statistical model for genotype-calling in next-generation sequence data

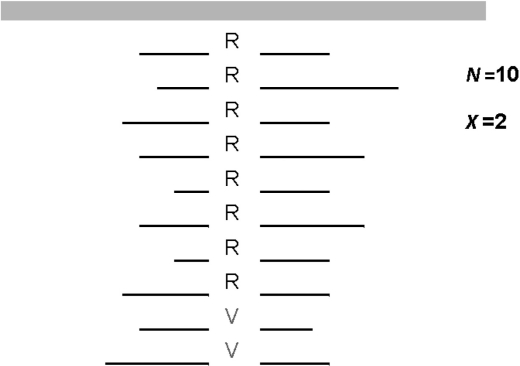
There are many levels of data in next-generation sequencing, from image data to aligned sequences. Genotype calling is concerned with the endpoint following base calling and sequence alignment. For a given reference base position, we have a variable number of short-read sequences that overlap the reference position (Fig. 1). We refer to that number as read depth (N). At each reference position, a nucleotide is called from each aligned short read. In practice, this nucleotide read is observed with error, which is a combination of base-call error and alignment error. Consequently, the number of variant reads observed (X) at a position depends on the true genotype, read depth and nucleotide-read error.

Fig. 1.

Schematic of 10 aligned next-generation sequencing reads (R = reference nucleotide, V = variant nucleotide) for a single base position. N is read depth. X is variant count.

A probability model for next-generation sequence data can be described as follows. For a diploid individual (i), a specific biallelic base position is sampled at random N_i times (i.e. N_i reads) from a large pool of sequences. We observe X_i copies of nucleotide V (a variant nucleotide) and N_i − X_i copies of nucleotide R (the reference nucleotide; Fig. 1). For simplicity, we assume that the probabilities that V is falsely called R and R is falsely called V are equal, and denote the probability of this error α. Given the true genotype (G_i) and independent observations, the nucleotide V count (X_i) follows a binomial distribution:

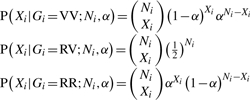Under a symmetric error assumption, if an individual is heterozygous and homologous sites are represented with equal probability, then the conditional probability that we observe an allele V is 1/2, regardless of the error rate, in which case X_i ∼ Binomial (N_i, 1/2). Thus, for a heterozygote, the binomial distribution of the variant count is symmetric and depends only on the observed read depth. On the other hand, if an individual is homozygous VV then X_i ∼ Binomial (N_i, 1 − α) or if an individual is homozygous RR then X_i ∼ Binomial (N_i, α). Thus, for homozygotes the binomial distribution depends on the nucleotide-read error rate as well as on read depth.

2.2 Genotype-calling algorithms

The problem of genotype calling is to identify the latent true genotype from the observed next-generation sequence data {N_i, X_i}. Intuitively, if an individual has all variant reads (i.e. X_i = N_i) then the genotype is likely to be a VV homozygote. On the other hand, if half of the reads are variant and half of the reads are reference, then the genotype is likely to be a heterozygote. However, the randomness associated with sampling multiple reads in heterozygotes and the inherent error in base calling and alignment makes calling genotype based on less extreme observations ambiguous. A decision procedure based on fixed cutoffs {c_l, c_u} for the number of variant reads observed (X_i) with a total read depth N_i can be defined as follows:

If X_i ≤ c_l, the assignment is RR.

If c_l < X_i < c_u, the assignment is RV.

If X_i ≥ c_u, the assignment is VV.

The problem is to choose c_l and c_u to minimize genotype misclassification.

One approach used in commercial software (e.g. GS Analyzer from Nimblegen/Roche Genome Sequencer FLX System) is to apply a simple filter for the number or proportion of variant reads at a site to determine genotype. For example, GS Analyzer specifies that if >30% of the reads are variant calls, then the genotype is called a heterozygote, otherwise it is called a reference homozygote. Implicitly, this assumes that the variant allele is rare so that variant homozygotes are unlikely, but an upper bound can be specified to allow for the presence of individuals homozygous for the variant allele.

Alternative approaches are based on the Bayes classifier (Mitchell, 1997). This approach assigns the genotype with maximum posterior probability to an individual, given sequence data {N_i, X_i}, prior genotype frequencies and the nucleotide-read error rate (α). For the model described above, the joint probability of the V nucleotide count and the latent genotype for an individual is as follows:

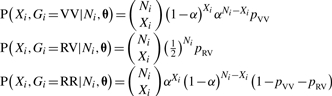(1)

where θ = {α, p_VV, p_RV} is a vector of parameters in which {p_VV, p_RV} are prior genotype frequencies for VV and RV. The posterior probabilities given the observed data are proportional to these joint probabilities; hence, for an individual with data X_i and N_i and a vector of known parameters θ, the Bayes classifier assigns the genotype with the greatest joint (and therefore posterior) probability. With true parameter values for prior genotype frequencies and nucleotide-read error, genotype assignment using the maximum posterior probability gives an optimum classifier, defined by the minimum total genotype-call error (Mitchell, 1997). In most studies, however, we will not know the true prior genotype frequencies or error rates and may not have good estimates for many variants. MAQ (Li et al., 2008), which bases its calls on the Bayes classifier, requires the user to specify the heterozygous genotype frequency and then sets the two homozygote genotype frequencies equal (p_VV = p_RR = (1 − p_RV)/2). The author's recommendation for the heterozygous genotype frequency is either p_RV = 0.001 or 0.2 depending on whether the user is searching for novel or known variants, respectively. Estimation of nucleotide-read error is based on base-quality and mapping-quality scores from image analysis and alignment.

2.3 An EM approach to parameter estimation: SeqEM

Our proposed algorithm takes advantage of sample information to obtain estimates of prior genotype frequencies and the nucleotide-read error rate. Suppose that we have a sample of reads from S unrelated (i.e. independent) individuals. The observed data log-likelihood has the following form:

(2)

The parameter estimates that maximize this likelihood are consistent and asymptotically efficient estimates of the parameters θ = {α, p_VV, p_RV} (Casella and Berger, 2002). However, direct maximization of (2) is difficult because a sum over unobserved individual genotypes is required to obtain the marginal likelihood of the observed data. Therefore, we employ the EM algorithm (Dempster et al., 1977) to maximize (2) with respect to θ by successive maximizations of the expected value of the more tractable complete-data log-likelihood:

(3)

Starting with initial guesses of the parameter values and iterating through the algorithm (detailed in Supplementary Methods) until successive EM parameter estimates differ by no more than some small absolute amount (e.g. 10⁻⁸) provides maximum likelihood estimates of the parameters θ = {α, p_VV, p_RV}. These estimates can then be substituted into the probabilities in (1), and, using the Bayes classifier, genotype calls can be made for each individual in the sample as the genotype with highest estimated posterior probability.

The model above is expressed in terms of genotype parameters (two prior genotype frequencies). Instead, we could assume Hardy–Weinberg equilibrium (HWE), allowing genotypes to be expressed in terms of a single allele frequency parameter p, such that p_VV = p², p_RV = 2p(1 − p) and p_RR = (1 − p)². The effect of reducing the number of genotype parameters from two to one on genotype misclassification is discussed below.

We note that it is necessary to restrict the parameter space to α < 0.5, otherwise we may encounter datasets in which the likelihood does not have a unique global maximum. For example, suppose that we have a sample of four individuals with data {N_i, X_i}: {10, 1}, {10, 5}, {10, 5} and {10, 9}. For this sample, there are two sets of parameter values that yield the same maximum likelihood value: {α, p_VV, p_RV} = {0.10, 0.25, 0.50} and {0.90, 0.25, 0.50}. For the first set, individual 1 would be called RR, individuals 2 and 3 would be called RV and individual 4 would be called VV. For the second set of parameter values, the genotypes of individuals 1 and 4 would be reversed. Restricting the error rate to a reasonable range, α < 0.5, removes this ambiguity. This restriction can be justified based on our prior knowledge; α of 0.5 or more is an unreasonable value for a nucleotide read error rate on any platform, so we would eliminate solutions in this region of the parameter space a priori. Sites with true errors in this range are expected to be detected as experimental failures by quality control metrics before genotype calling. Note that the algorithm is allowed to reach absorbing parameter values on the boundaries (p = 0 or 1, α = 0) because these could be legitimate maximum likelihood estimates.

3 RESULTS

3.1 The Bayes classifier versus the filtering approach

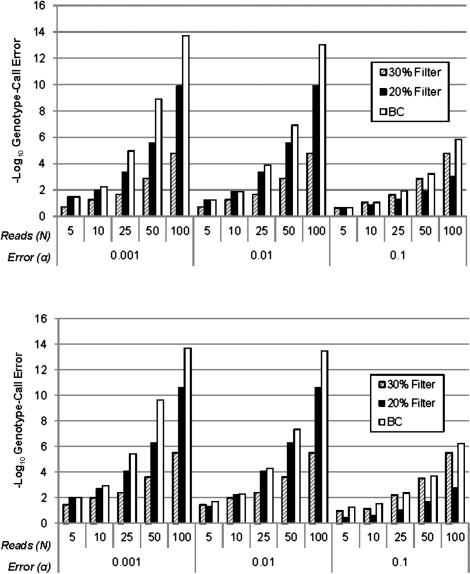
We begin by comparing the performance of the simple filtering approaches to what would be expected if we used the Bayes classifier based on the probabilities in (1) with the true parameter values. We derived expected values for genotype-call error from the filtering approach and the approach using the Bayes classifier (see Supplementary Methods), given values for the nucleotide-read error and allele frequency, {α, p}, for model (1) assuming HWE. The expectation was taken with respect to all possible values of the number of variant reads in an individual, X_i, given the read depth (N_i) and parameters. We defined genotype-call error as the proportion of genotypes that were assigned an incorrect genotype by the calling algorithm. Figure 2 shows a comparison of the expected genotype call errors for nucleotide-read error rates α = 0.1, 0.01 and 0.001 and allele frequencies p = 0.05 and 0.5, assuming HWE and various read depths. For the filtering approach, we considered symmetric 30% and 20% filters, such that if X_i ≤ 0.3^*N_i (0.2 for 20% filter) the genotype is called RR, if X_i ≥ 0.7^*N_i (0.8 for 20% filter) the genotype is called VV, otherwise the genotype is called RV. Figure 2 and the following figures show −log₁₀ (genotype-call error rate), with higher values indicating lower error rates.

Fig. 2.

Expected values for genotype-call error rates (− log 10-scaled) under HWE for the Bayes classifier (BC) using true parameter values compared with the filtering approach with 20 and 30% thresholds. Higher values on the − log 10 scale correspond to lower error rates. We considered nucleotide-read error rates of α = 0.001, 0.01 and 0.1, read depths of N = 5, 10, 25, 50 and 100 and allele frequencies of p = 0.5 (a; top) and 0.05 (b; bottom).

The results in Figure 2 show that, as predicted by theory, the Bayes classifier always has an expected genotype-call error rate as small as or smaller than that of the filtering approach. For both approaches, genotype-call error decreases as read depth (N) increases and nucleotide-read error (α) decreases. If nucleotide read error is not too large, even loci with low read depth can provide reliable genotype calls. For example, with α < 0.01 we obtained genotype-call errors of <6% with a read depth of 5 and <1.5% for read depth of 10 for the Bayes classifier and 20% filter. In general, the 30% threshold is preferable to 20% when nucleotide-read error is high and the 20% threshold preferable to the 30% when nucleotide-read error is low. Importantly, however, for read depths of 10 or greater and low nucleotide-read error, the Bayes classifier is capable of genotype-call error rates that are orders of magnitude lower than a filtering approach.

3.2 The effect of parameter specification in the Bayes classifier: MAQ and SeqEM

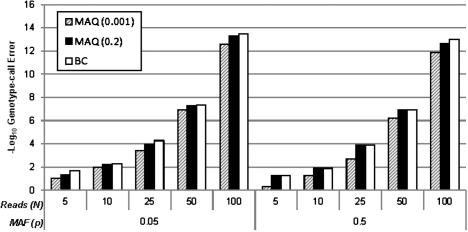
While the Bayes classifier is optimal when the true parameter values are given, in practice genotype frequencies and nucleotide-read error are unknown. As described above, MAQ (Li et al., 2008) uses fixed values for heterozygous genotype frequency (p_RV) and bases its estimate of nucleotide-read error on mapping quality score. Figure 3 shows the expected error probabilities for MAQ using the true error (α = 0.01) and either p_RV = 0.2 or 0.001, as recommended for common and rare variant analyses, respectively, compared to the Bayes classifier based on the probabilities in (1) using the true parameter values. As expected, we find for all cases that the Bayes classifier with true values had genotype-call error equal to or smaller than MAQ. These results show that for common alleles, MAQ specifying a heterozygote frequency of 0.2 results in genotype call errors close to the Bayes classifier with true parameter values, but for lower frequency variants using true parameter values in the Bayes classifier dominates.

Fig. 3.

Expected values for genotype-call error rates (−log 10-scaled) under HWE for the Bayes classifier (BC) using true parameter values compared with MAQ using the true nucleotide-read error rate and MAQ's assumed heterozygote proportions of 0.2 and 0.001. Higher values on the -log10 scale correspond to lower error rates. We considered a nucleotide-read error rate of α = 0.01, read depths of N = 5, 10, 25, 50 and 100 and allele frequencies of p = 0.5 and 0.05.

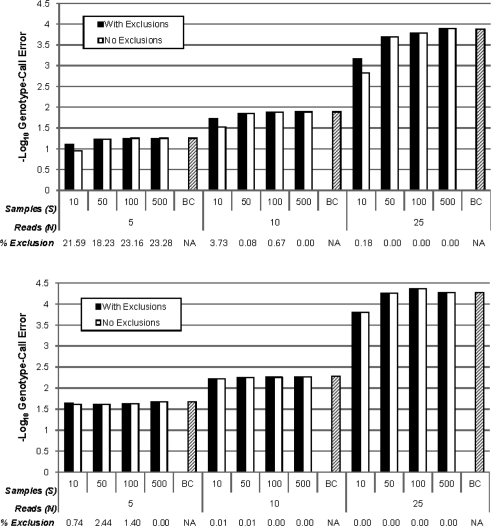
Unlike MAQ, SeqEM estimates genotype/allele frequencies and nucleotide-read error rates from a sample of S > 1 unrelated individuals, each with next-generation sequence data. For large samples, we expect SeqEM to perform close to the Bayes classifier using true parameter values as studied above. However, for small samples, there is additional variability in genotype calls due to the estimation of parameters from the sample. To study the effect of sample size on error, we conducted simulations with various sample sizes (S = 10, 50, 100 and 500), and applied the SeqEM algorithm to call genotypes. Figure 4 shows the estimated genotype call error rates from these simulations (with α = 0.01 and p = 0.5 and 0.05, assuming HWE). The error of SeqEM rapidly approaches the expected value of the Bayes classifier for fixed read depth as sample size increases. Sample sizes of 50 or greater provide nearly optimal genotype-call error for all read depths, and smaller samples can be tolerated without large increases in error provided read depth is not too small. Importantly, even for small samples and low read depth, SeqEM has lower genotype-call error than the expected values calculated for MAQ (Fig. 3) for low-frequency variants (p = 0.05).

Fig. 4.

Simulated genotype-call error rates (− log 10-scaled) for SeqEM assuming HWE in populations in HWE. Higher values on the − log 10 scale correspond to lower error rates. We considered a nucleotide-read error rate of α = 0.01, sample sizes of S = 10, 50, 100 and 500, read depths of N = 5, 10 and 25 and allele frequencies of p = 0.5 (top) and 0.05 (bottom). Results are presented for all variants as well as excluding variants flagged as potentially poorly modeled by our heuristic (no EM convergence within 100 iterations or nucleotide-read error rate estimate exceeding 0.1). Percentage exclusion indicates the percentage of flagged variants. Expected genotype-call error rates for the Bayes classifier (BC) using true parameter values (Fig. 3) are also included as a sample size of BC.

In small samples, we observed that for some variant sites the EM algorithm converged very slowly or converged to unrealistic parameter values because of lack of identifiability (i.e. more than one set of parameter values maximize the observed data likelihood). This happens when there is not enough information in the data to provide unique estimates of all parameters. Assuming HWE and constraining the nucleotide-read error α < 0.5, as discussed above, reduces the dimension of and eliminates unrealistic regions of the parameter space, improving identifiability in some situations. Yet, we still encountered some variant sites for which EM convergence was slow, suggesting lack of indentifiability of the model with the observed data (Meng and Rubin, 1991). Failure of the EM algorithm to meet the convergence criterion of 10⁻⁸ within 100 iterations or convergence to a nucleotide-read error estimate > 0.1 within 100 iterations was therefore taken as indicative of variants for which the data provided insufficient information for accurate parameter estimation or the model was misspecified.

We found that excluding these variants reduced the genotype-call error rate by as much as 55%, while reducing the number of loci called substantially only for very low read depths (N = 5) and high minor allele frequencies (p = 0.50) (Fig. 4). Therefore, we propose flagging potentially poorly modeled variants using this heuristic as an important step in quality control. Variants flagged by this procedure could then be reviewed and called by an alternate method.

We also examined the parameter estimates from SeqEM for the examples in Figure 4. In variants not flagged as potentially poorly modeled, the mean parameter estimates of nucleotide error were close to the true parameter values, even in small samples, and the variance of the estimates decreased with increasing S and N resulting in narrower confidence intervals for larger sample sizes and read depth (Supplementary Fig. 1). The only exception was for conditions combining a very low read depth (N = 5) with a minor allele frequency of p = 0.50, in which case the observed data contain sparse information about the latent genotypes. Under these conditions, the mean nucleotide-read error rate estimate was inflated in small samples and converged slowly to the true value of 0.01 with increasing sample size. Estimates of allele frequency are also close to true values and have decreasing variance with increasing sample size S, but unlike estimates of nucleotide-read error, allele frequency estimates are largely unaffected by read depth for the examples considered.

3.3 Deviations from HWE

We evaluated the robustness of SeqEM to deviations from HWE when HWE was assumed in the model. We first investigated the performance of the Bayes classifier with true parameter values under systematic departure from HWE in simulated data (Supplementary Material). Estimates of genotype-call error rates are shown in Supplementary Figure 2. We found that when HWE held (i.e. f = 0), genotype-call error rate estimates based on classification assuming HWE were equivalent to those not assuming HWE. As the true genotype distribution diverged from HWE, classification based on the true genotype distribution had smaller genotype-call error than classification based on HWE. For large positive f values (excess homozygosity) or for large negative f values (excess heterozygosity), the decrease in genotype-call error when the true genotype distribution is used rather than assuming HWE was sometimes substantial, decreasing by as much as ∼75% in this example. The effect of deviation from HWE on genotype-call error was especially pronounced with low allele frequencies. However, such a scenario may be somewhat pathological because departure from HWE requires that rare alleles be present mostly in homozygotes rather in heterozygotes. Also, it is important to note that, although better performance could be obtained using the true genotype distribution, the genotype-call error rate assuming HWE was largely invariant to deviations from HWE; that is, the errors differ largely because assuming the correct model when there are deviations from HWE tends to decrease the error, not because assuming the wrong model increases the error.

Because SeqEM uses sample-based maximum likelihood estimates of the parameters rather than true parameter values in its Bayes classifier, a misspecified model for the sample genotype frequencies means that these parameters may not be consistently estimated. Consequently, we also examined the percentage of flagged variants and the genotype-call error rate when HWE was assumed but the true genotype frequencies deviated substantially from HWE (Supplementary Fig. 3). In the case of substantial excess homozygosity (f = 0.5), both the percentage of flagged variants and genotype-call error rates were comparable to or better than those when the population genotype frequencies conformed to HWE for both p = 0.05 and p = 0.50. However, in the case of substantial excess heterozygosity (f = −0.50) for p = 0.50, more variants were flagged and genotype-call error rates were worse than when the population genotype frequencies conformed to HWE, especially for low read depths. For p = 0.05, though, excess heterozygosity had negligible effect on the variant flagging and genotype-call error rates.

One important question is whether using the genotype calls from SeqEM assuming HWE when the population deviates from HWE yields biased genotype frequency estimates. We therefore examined the mean and SD of the genotype frequencies estimated from SeqEM's calls under the HWE model when there was deviation from HWE (Supplementary Fig. 4A). For p = 0.05, we found that there was minimal bias in estimated genotype frequencies for excess heterozygosity and more bias for excess homozygosity at N = 5. For p = 0.50, there was little bias for excess homozygosity and but notable bias in the case of excess heterozygosity at N = 5. For all examples, the bias largely disappeared for N ≥ 10. Using the model not assuming HWE also reduced the bias in all examples but still showed some modest bias for N = 5 due to the discreteness of the data at low read depths (Supplementary Fig. 4B).

We compared the performance in terms of percentage of flagged variants and genotype-call error between SeqEM assuming HWE and not assuming HWE (Supplementary Fig. 5). With p = 0.05, the model not assuming HWE performed similarly to the model assuming HWE under all scenarios except for excess homozygosity, in which case it often performed better. With p = 0.50, the information content of the data is lower, and not assuming HWE yielded similar performance for N ≥ 5 with the genotype frequencies in HWE, slightly worse performance in the presence of excess homozygosity and better performance in the presence of excess heterozygosity.

3.4 Analysis of exome data

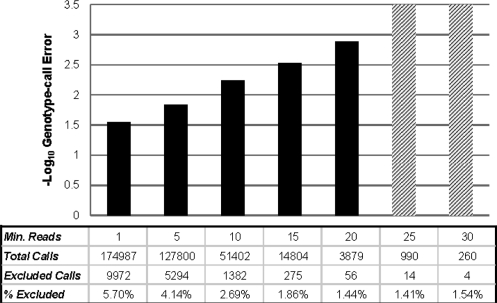
We analyzed a total of 23 500 variants in eight related individuals from an extended pedigree. The average read depth over the 23 500 positions was 7.5. Details of exome sequence coverage are discussed by Hedges et al. (2009). We compared genotypes called by SeqEM with genotypes obtained from an Illumina GWAS in the same individuals. Approximately 6% of calls were excluded because they were at variants that exceeded the iteration threshold (100) or nucleotide-read error threshold (0.1) and so were dropped from further analysis. Figure 5 shows the estimated genotype-call error for SeqEM for various minimum bounds on read depth (e.g. N ≥ 5; N ≥ 10; …). In general the estimates of genotype misclassification rates of SeqEM agree well with expected values of the Bayes classifier and results from simulations shown above (Fig. 4). They tend to be closer to the expected values and simulated error rates for low frequency variants (e.g. p = 0.05), which seems appropriate since the average allele frequency for the Illumina genotypes is 0.11. We expect that the genotype-call error rate estimates will overestimate the true error rate due to the additional errors in the Illumina data. In fact, six of the erroneous calls involved one homozygote being called as the other homozygote; closer inspection of these errors revealed that these likely resulted from incorrect Illumina genotype calls rather than incorrect sequencing calls.

Fig. 5.

Estimated genotype-call error rates (− log 10-scaled) for SeqEM assuming HWE based on Illumina genotype calls in exome sequence data for an extended pedigree of eight individuals. Higher values on the − log 10 scale correspond to lower error rates. Errors are shown for variants with minimum read depth of N = 1, 5, 10, 15, 20, 25 and 30. Results exclude variants flagged as potentially poorly modeled by our heuristic (no EM convergence within 100 iterations or nucleotide-read error rate estimate exceeding 0.1). The number of calls made, the number excluded and the percent excluded at each minimum read depth are shown below the graph. The cross-hatched bars indicate genotype-call error rates of 0%, which are infinite on the − log 10 scale, for read depths of 25 and 30.

Unfortunately, neither MAQ (version 0.7.1) nor SOAPsnp (version 1.0.3) could be run on these data because the short-read lengths from the 454 GS FLX Titanium (Roche, Inc.) (mean of 340 bp in our data) exceeded the maximum allowable read lengths of 63 bp for MAQ (MAQ version 0.7.1 documentation) and 45 bp for SOAPsnp (http://soap.genomics.org.cn/soapsnp.html). However, we did compare the results from SeqEM to the empirical method that we used previously (Hedges et al., 2009). We found that SeqEM had lower genotype-call error estimates than the empirical method. For example, for minimum read depths of N ≥ 5, 10 and 15 the genotype-call error rates were 0.016, 0, 0.008 and 0.005 for the empirical method and 0.015, 0.006 and 0.003 for SeqEM. Moreover, SeqEM has the advantage of not requiring prior genome-wide genotyping.

The program took only 2.11 s and 7.5 MB of RAM to conduct the analysis of the exome dataset consisting of eight individuals and 23 500 variants on a single thread of an Intel Xeon E5430 processor running at 2.66 GHz. Program I/O and EM complexity are approximately O(mS), where m is the number of variants and S the number of individuals, assuming that all EM iterations run to the user-specified iteration limit. Further benchmarking of our program on this platform confirmed that the time and memory usage scale approximately linearly with m when S is constant and vice versa. Scaling factors were approximately 1 for time and memory with m and 1 for memory and 1.1 for time with S. Extrapolating to whole genome sequencing studies being run on a similar platform, for a sample of 500 individuals with 3 000 000 variants (allowing for only 1% of sites in the genome to be polymorphic) the program would require ∼60 GB of RAM and take ∼5.25 h on one thread. Multithreading could reduce this time but only by about 10% with each additional thread.

4 DISCUSSION

For disease studies, we expect that researchers will want to genotype a sample of individuals and make inferences about the population of genotypes, often conditional on disease status. For example, investigators often sequence samples of unrelated affected and unaffected individuals for comparison. The availability of next-generation sequence data from a sample of unrelated individuals provides information to estimate nucleotide-read error rate and genotype frequency parameters; our approach capitalizes on such sample information to provide an improved genotype-calling method. By accurately estimating these parameters based on the likelihood of the sample data, we ensure consistent and asymptotically efficient estimates of genotype frequencies and the nucleotide-read error rate that should minimize genotype misclassification. Because we maximize the observed data likelihood using the EM algorithm to estimate parameters, we call this approach SeqEM.

We stress that SeqEM should be run separately for cases and controls or distinct racial and ethnic groups because the true model parameters may differ among these groups. Running SeqEM on the pooled sample will result in biased parameter estimates reflecting mixtures of the true parameters in the distinct subgroups. For example, in a case–control study, running SeqEM on a pooled sample of cases and controls will assume a common prior genotype frequency, which will then bias estimated posterior genotype probabilities toward the null.

We also recommend that SeqEM be applied without assuming HWE as a default. The average performance of this more complex model was generally comparable to that of the model assuming HWE, although it was better in cases of excess heterozygosity and worse in cases of excess homozygosity with p = 0.50. Moreover, this should reduce potential biases in genotype frequency estimates for low read depths. For variants for which our heuristic indicates a lack of model identifiability or misspecification, a second pass of SeqEM could easily be made using the model assuming HWE.

Applying the model assuming HWE as a second pass should not cause substantial problems even if the true genotype frequencies do not conform to HWE. Our simulation results suggest that assuming HWE in the Bayes classifier and the observed data likelihood does not appreciably affect genotype-call error rates when there is excess homozygosity. Although the same appears to hold in the case of excess heterozygosity for the Bayes classifier using true parameter values, it does not necessarily hold for SeqEM. SeqEM's performance in our simulations depended to a large extent on the availability of homozygotes because, as noted earlier, heterozygotes carry no information about nucleotide-read error rates. Thus, the tendency of deviations from HWE in the direction of excess homozygosity to improve EM convergence and genotype-call error rates can be explained by the information on the nucleotide-read error rate provided by additional homozygotes outweighing the effect of misspecifying the genotype frequency model. Likewise, the worse EM convergence and genotype-call error rates when deviations from HWE were in the direction of excess heterozygosity reflects the dual negative effects on parameter estimation of model misspecification and fewer homozygotes providing nucleotide-read error rate information. That said, the percentage of flagged variants and genotype-call error rates were still quite tolerable with read depths of 10 or more and moderate sample sizes, even in the presence of substantial excess heterozygosity. Furthermore, with sufficient read depth, the sample genotype frequencies estimated using the calls from SeqEM converged rapidly to the true values with increasing sample size.

Not only does SeqEM provide a tool for improved genotype calling, but employing a likelihood framework suggests how to incorporate genotype classification uncertainty into disease-association tests. Although one could simply use genotype calls based on the above algorithm as observed genotypes in case–control and/or family-based tests, this approach does not account for uncertainty in genotype calls nor does it exploit the quantitative nature of next-generation sequencing observations. Failing to account for uncertainty in genotype calls can result in an association test that is invalid (i.e. uncontrolled Type I error) and may reduce power. The likelihood approach provides a natural framework for incorporating the uncertainty in genotype calls into statistical tests relating common and rare variants to phenotype. The same situation is faced in haplotype-based analyses (Schaid et al., 2002) and association tests in imputed data (Lin et al., 2008; Marchini et al., 2007), in which we do not know the underlying data of interest with certainty but do know the how to model the probability distribution of these data. One possible solution, which has worked well in these applications, is to incorporate the posterior genotype probabilities into the association test. Such an approach would follow naturally using the calculations from SeqEM.

Two practical issues that we faced using SeqEM were convergence to local maxima on the boundaries of the parameter space (p = 0 or 1, α = 0) and slow convergence. Parameter estimates on the boundaries above cannot be discarded, as α > 0.5 can, because they are legitimate possible values for the parameters. However, the EM algorithm may arrive at these absorbing points even when they are not global maxima simply due to a poor choice of starting values. Therefore, we suggest re-examining variants with final estimates on these boundaries using multiple starting values for the EM algorithm to increase the chance of finding the global maximum and possibly further improve estimates and genotype-call error rates. We have implemented this capability in our software.

Slow convergence generally indicates that the data provide insufficient information for estimating all parameters in the model. Under regularity conditions, each successive step of the EM algorithm is guaranteed to increase the observed-data likelihood, but the size of successive steps depends on the structure of the observed-data likelihood as embodied in the observed-data observed information matrix. EM steps leading to small increments in this likelihood and thus requiring many iterations to traverse the parameter space are indicative of a nearly singular observed-data observed information matrix (Meng and Rubin, 1991), which implies limited independent information about model parameters. Consequently, we classify a variant that exhibits extremely slow EM convergence, as evidenced by failure to achieve a standard convergence criterion of 10⁻⁸ in 100 iterations, as uninformative with respect to the model and thus likely to produce poor estimates of the posterior genotype distribution. In our implementation, the user may specify an alternate convergence tolerance and maximum number of iterations to adjust the stringency of our proposed heuristic.

Data for a variant may be uninformative for several reasons, including low read depth, small sample size or, perhaps, a misspecified model. Our experience calling genotypes using SeqEM suggests that low read depth can play an important role in failure to meet our convergence criterion. It is important to note that although introducing multiple starting values for the EM algorithm (which is recommended for markers converging to estimates on the boundaries p = 0 or 1 or α = 0) is likely to improve the overall chance of locating a global optimum, such a strategy still does not guarantee proper estimates in uninformative data. An alternative to using our heuristic that may recapture some lost variants that were slow to converge in informative samples would be to use diagnostics for information loss based on the observed-data observed information matrix such as condition number or the spectral decomposition approach suggested by Meng and Rubin (1991). However, estimation of this matrix is very computationally intensive relative to EM optimization and is therefore unlikely to be tractable in high-throughput genotype calling.

SeqEM makes some simplifying assumptions. First, some capture/enrichment methods for next-generation sequencing may show allele bias; that is, one nucleotide may be observed preferentially in reads from a heterozygous individual. Our method assumes there is no allele bias at heterozygous sites so that the two nucleotides are sampled with equal probability. Previous analysis of the exome data analyzed herein shows no evidence of bias in these data (Hedges et al., 2009); however, some capture methods could show more substantial allele bias (Porreca et al., 2007). For biased data examples, the model assumed by SeqEM is not appropriate. A model with more parameters would be required to handle these more complex situations, but such a model would require larger samples or possibly a fully Bayesian approach with informative priors to achieve identification.

Second, SeqEM assumes that the sample comprises independent, unrelated individuals, which means that equations (2) and (3) are appropriate log-likelihoods. In situations where individuals are related, (2) and (3) are no longer appropriate log-likelihoods, so standard results for the EM algorithm no longer apply. The good performance of SeqEM in our data example, which uses a single pedigree of eight individuals, provides some indication that SeqEM does not break down when applied to related individuals, although care should be taken in generalizing based on a single dataset. Further work will be required to characterize fully the performance of SeqEM in samples containing related individuals.

Finally, like other genotype-calling algorithms based on posterior probabilities (e.g. MAQ), the model in SeqEM assumes that there are at most two distinct nucleotides within an individual at any position and in the sample as a whole. The exomes analyzed in our example were preprocessed to include only the two most frequent nucleotides aligned at a specific position within an individual (less frequent nucleotides are assumed to be errors). So, within an individual, only two distinct alleles can be inferred. This assumption is reasonable unless the variant is, for example, part of a variable duplicated site, in which case an individual may actually carry three alleles. Furthermore, our model assumes that there are at most two alleles present at the position in the sample of individuals (i.e. the variant is biallelic). It is possible with sufficient sample size that the likelihood model could be extended to include additional genotype or allele frequencies. However, the majority of variation in the human genome will typically will be biallelic within a population based on empirical observation and the infinite sites model of mutation (Hartl and Clark, 2007).

It is important to point out that we attack the problem following successful alignment of the sequence. SeqEM provides only one step in the sequencing pipeline. We recognize that accurate sequence alignment plays an important role in site-specific error rates, but we anticipate that as technology moves toward larger numbers of concurrently sequenced base pairs, sequence alignment should be a decreasing source of site-specific errors. An advantage of our approach is that it is not necessary to distinguish errors due to misalignment and those due to erroneous base calls; an error rate subsuming both sources of error is estimated from the sample information in the single nucleotide-read error parameter.

In conclusion, our results demonstrate that approaches using the Bayes classifier based on maximum posterior probabilities outperform arbitrary filters and that the SeqEM approach we propose provides a principled way to estimate the required parameters in unrelated individuals. SeqEM is an adaptive approach that does not require prior estimates of genotype frequencies or nucleotide-read error but rather is driven by the data. We found that SeqEM is comparable to MAQ for common variants when the parameters are fixed close to their true values, but for rarer variants, SeqEM results in improved genotype-call error rates. We believe that the improved genotype-call error rate and tractable computability of SeqEM make it a key genotype-calling step in the next-generation sequencing pipeline.