Abstract
Motivation: Membrane proteins (MPs) are important drug targets but knowledge of their exact structure is limited to relatively few examples. Existing homology-based structure prediction methods are designed for globular, water-soluble proteins. However, we are now beginning to have enough MP structures to justify the development of a homology-based approach specifically for them.
Results: We present a MP-specific homology-based coordinate generation method, MEDELLER, which is optimized to build highly reliable core models. The method outperforms the popular structure prediction programme Modeller on MPs. The comparison of the two methods was performed on 616 target–template pairs of MPs, which were classified into four test sets by their sequence identity. Across all targets, MEDELLER gave an average backbone root mean square deviation (RMSD) of 2.62 Å versus 3.16 Å for Modeller. On our ‘easy’ test set, MEDELLER achieves an average accuracy of 0.93 Å backbone RMSD versus 1.56 Å for Modeller.
Availability and Implementation: http://medeller.info; Implemented in Python, Bash and Perl CGI for use on Linux systems; Supplementary data are available at http://www.stats.ox.ac.uk/proteins/resources.
Contact: kelm@stats.ox.ac.uk
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Membrane proteins (MP) constitute about 30% of all known proteins and are one of the largest classes of drug targets. They have roles in a multitude of biological processes such as cell recognition and neurotransmitter transport (Müller et al., 2008; Wallin and von Heijne, 1998).
Currently, the Universal Protein Resource (UniProt; Wu et al., 2006) contains more than 11 million protein sequences. In comparison, the Protein Data Bank (PDB; Berman et al., 2000) contains only about 65 thousand known protein structures. Both numbers have been following an exponential growth trend. For MPs, the sequence-structure gap is even larger. Over 1.7 million UniProt entries contain the word ‘membrane’, whereas only 4700 PDB entries match this criterion and only 616 structures are specifically annotated as belonging to the SCOP (Murzin et al., 1995) class ‘membrane and cell surface proteins and peptides’ (the stated numbers were obtained from the respective databases on May 19, 2010).
Physically, MPs differ significantly from water-soluble proteins (Schulz, 2002; Stevens and Arkin, 1999; Ulmschneider and Sansom, 2001). These differences have been used in various computational methods (Punta et al., 2007), e.g. to identify MPs from sequence alone (Gromiha et al., 2005; Wallin and von Heijne, 1998). Soluble proteins often adopt a globular conformation, with their hydrophobic residues mainly in the protein core and their polar and charged residues predominantly on the water-exposed surface. Membrane proteins sit in a lipid bilayer and thus contain stretches of residues that are exposed to the hydrophobic environment at the core of the membrane (Eyre et al., 2004). These transmembrane (TM) segments usually have one of two structure types: α-helices or β-strands.
Many protein structure prediction algorithms have been developed in order to close the gap between the number of known sequences and the number of known structures. Current structure prediction methods can be classified into two main types: template-based and ab initio modelling. So far, ab initio methods have only been truly successful for small globular proteins. Template-based modelling methods, however, have succeeded in producing high accuracy models, if a good template exists, for proteins of almost any type or size (CASP; Moult et al., 2009).
Template-based protein structure prediction for any type of protein can be divided into several steps. For globular, water-soluble proteins a multitude of programmes are available to perform each of these separate steps (Eswar et al., 2007; Wallner and Elofsson, 2005). The input to the entire modelling procedure is a single target sequence, whose structure is to be predicted. The steps of a typical template-based modelling protocol are briefly described below.
The first step is the identification of a template protein of known structure. Structural databases are scanned for proteins homologous to the target protein.
One or more templates are then selected from the homologues. By choosing one or more template structures, a 3D-fold is implicitly assigned to the target sequence.
A target–template alignment is then generated. The alignment between target and template is one of the major contributors to the accuracy of the final model. An incorrect alignment will almost always result in an inaccurate model (Sánchez and Sali, 1997).
The final step in modelling is coordinate generation based on the alignment between template protein structures and the target sequence. The three main approaches to this problem are (i) assembly of rigid bodies (Bates et al., 2001; Deane et al., 2001; Koehl and Delarue, 1995; Petrey et al., 2003; Schwede et al., 2003), (ii) segment matching (Levitt, 1992) and (iii) satisfaction of spatial restraints (Sali and Blundell, 1993).
In order to improve the final model, this entire procedure may be iterated. This has been shown to produce superior results as well as being able to correct errors in the initial alignment between target sequence and template structures (Burke et al., 1999).
The current computational structure prediction methods may not be ideal for TM proteins, designed as they are for water-soluble proteins (Elofsson and von Heijne, 2007). The physical differences between water-soluble and MPs may mean that many of the steps in structure prediction should be approached differently.
The successful ab initio fragment assembly method ROSETTA has been adapted to specifically predict MP structure (ROSETTA Membrane; Yarov-Yarovoy et al., 2006). The adapted method included an energy function that modelled a multi-layer artificial membrane environment. The performance of ROSETTA Membrane was tested on 12 MPs of known structure, producing complete models with backbone root mean square deviations (RMSDs) between 6 Å and 10 Å. Sub-sets of each model (between 51 and 145 residues long) achieved RMSDs of 3–4 Å. More recently, the method was modified to include experimentally derived constraints, such as known helix–helix contacts (Barth et al., 2009). The best models selected by the method had RMSDs of ∼4 Å, with all test proteins being single chains of at most 230 amino acids. The authors ventured that for larger proteins, multiple constraints were likely to be required in order to obtain accurate results. It should also be noted that, being a combinatorial ab initio method, ROSETTA requires large amounts of computing time and is typically run across large (possibly distributed) computing clusters. Homology modelling methods on the other hand, while relying on the availability of a template, can be run on a single desktop computer.
In this article, we consider the coordinate generation step in a homology modelling framework and show how it can be significantly improved, without the use of experimental information, by considering the different physical environment of MPs.
Wallner and Elofsson (2005) demonstrated that existing co-ordinate generators, on soluble proteins, showed little difference in terms of overall accuracy and none of the methods consistently produced models that were much closer to the native target structure than the template. In general, the models were also worse than simply copying the backbone co-ordinates of the template.
They identified Modeller (Sali and Blundell, 1993) as one of the best methods, due to its reliability and consistent model quality. Modeller attempts to satisfy spatial restraints in order to build a target protein structure. Its probability density function uses data obtained from the input target–template alignment, as well as prior knowledge obtained from a database of structural alignments (Sali and Overington, 1994). This original database contained 105 families of soluble proteins and no MPs. In this article, we use the most up-to-date version of Modeller (9v7, at the time of the experiment) as a representative of existing modelling methods and compare it to our own method.
Modeller's accuracy for modelling MPs has been tested previously (Forrest et al., 2006). It was noted that it was possible to build models whose TM region had <2 Å C-α RMSD to the native structure, given a template with >30% sequence identity. The accuracy for the whole protein was much lower than that of the TM region. This reflected important local differences in the regions connecting TM segments in MPs with similar topology. This result indicated that template-based approaches can be successfully applied to MPs.
However, this result also showed that Modeller (as a representative of the current standard in homology modelling software), in its current state, is not ideal for creating complete, accurate models of MPs. A 2 Å RMSD in the TM region is surprisingly high, given that the problem of TM protein prediction should theoretically be simplified by the additional physical constraints imposed by the presence of the lipid bilayer. Modelling errors in the TM region can then propagate to the loops that connect TM segments, thus resulting in even lower accuracy outside the TM region. Nevertheless, scientists commonly use Modeller, and comparable methods, to predict MP structure (software reviews: Reddy et al., 2006; Saxena et al., 2008; example case studies: Fenosa et al., 2009; Yang et al., 2008).
We present MEDELLER, a new method for coordinate generation specialized for MPs. The input is a template protein structure and a sequence alignment between the target and template proteins. This alignment is not altered by MEDELLER. The most important part of the method is the identification of the reliable ‘core’ structure shared by the template and target proteins. First, the template protein's membrane insertion is calculated using iMembrane (Kelm et al., 2009). The ‘core’ is initially restricted to the template residues buried in the middle layer of the membrane. It is then gradually extended using a specialized membrane-specific substitution score. The model is then completed, as far as possible, using the loop modelling protocols FREAD (Choi and Deane, 2009) and Modeller.
We test the modelling accuracy of our method on four large test sets, containing a total of 616 target–template pairs of TM proteins.
Our method, MEDELLER, builds highly reliable core models (which usually correspond to a protein's TM region). Averaged over all test sets, MEDELLER produces more accurate core models and achieves a core model accuracy of 1.97 Å RMSD versus 2.57 Å for Modeller.
With added high-accuracy loops, MEDELLER remains the more accurate method in 65% of test cases and at least as good as Modeller in 77% of test cases, with an average accuracy of 2.62 Å RMSD versus 3.16 Å for Modeller.
2 METHODS
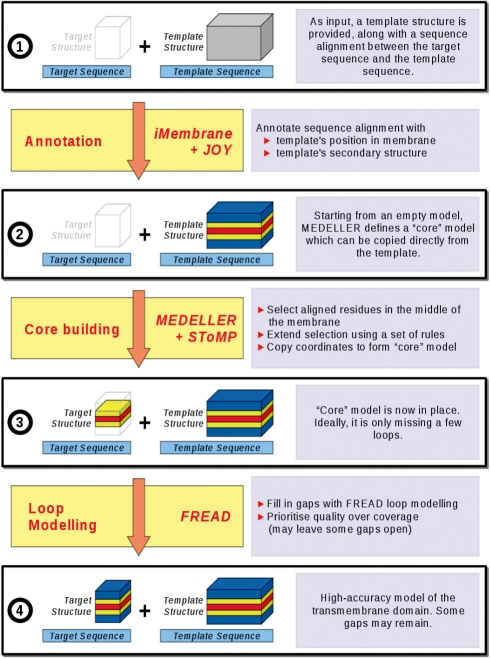
We have created a homology-based protocol for coordinate generation. The method is specific to MPs. The algorithm is outlined below, with detailed explanations of the more complex steps following in separate sub-sections. Figure 1 gives a flowchart of the algorithm. All algorithm steps are identical, irrespective of the input protein's structure type (α-helical or β-barrel), although the substitution score itself is secondary structure dependent and will thus differ for residues in helices or β sheets.
Fig. 1.
Algorithm for modelling from a single template. Progression from the initial user input to the high-accuracy model. When modelling from multiple templates, steps up to stage 3 are performed for each template separately. The data are then combined into a single core model (stage 3) and the algorithm proceeds as for a single template.
2.1 Algorithm overview
2.1.1 User input
The input to our coordinate generation method is the target protein's sequence, aligned to one or more homologous template protein sequences, as well as the 3D co-ordinates of those template structures.
2.1.2 Annotation of the sequence alignment
iMembrane (Section 2.2; Kelm et al., 2009) and JOY (Mizuguchi et al., 1998) are run on the template structure in order to annotate its membrane insertion and secondary structure.
2.1.3 Building the ‘core’ model
The core is built over four phases (for full details, see Supplementary Section 1.1). In each of these, a specific set of masking rules is in place (Section 2.3), alongside our smoothed fragment-based environment-specific substitution score (section 2.4). Once the four core modelling stages are considered ‘complete’ the remaining gaps, where the target and template are not aligned or where the substitution score is low, are modelled using FREAD (Choi and Deane, 2009). FREAD is a database search loop prediction method, which selects fragments based on an environment-specific substitution score and anchor RMSD. FREAD prioritizes accuracy over coverage and thus may not make predictions for all the missing segments.
2.1.4 Prioritizing accuracy or coverage
Our core building algorithm and our conservative use of FREAD are designed to give high accuracy coordinates. However, the model produced may still contain gaps. For the case where high coverage is required, MEDELLER also produces a ‘high-coverage’ model, in addition to the default ‘high-accuracy’ model. In this case, FREAD is used on a less conservative setting, resulting in a larger number of possibly less accurate loop predictions. Loops longer than 26 residues or terminal gaps cannot be modelled using FREAD. MEDELLER thus builds a set of backbone coordinates for the majority of the structure. For convenience, we include an option to fill any remaining gaps using Modeller, allowing the user to always output a complete all-atom model, including side chains.
2.2 Insertion of proteins into the membrane
iMembrane is a method to ascertain a protein's position within the lipid bilayer (Kelm et al., 2009). It relies on a database of known TM protein structures, which have been simulated in an artificial lipid bilayer using molecular dynamics (Scott et al., 2008). iMembrane is used here to annotate the template protein structure with regards to its membrane insertion.
Since its original publication, iMembrane has been re-implemented and the output format consolidated. TM align (Zhang and Skolnick, 2005) now performs the structure superposition and, as a result, all Z-scores have been replaced by TM scores in the programme's output. The new version of iMembrane is included in the MEDELLER distribution and is available as a web server at http://imembrane.info.
2.3 Alignment column masking
During each phase of the core building procedure, masks are used to prevent certain alignment columns from being selected. Masked columns may be those containing a gap in target or template, those annotated as ‘loop’ (where masking may be dependent on loop length) or those outside the middle layer of the membrane (where the lipid tails reside). All rules are active at the beginning of the core building procedure and are then consecutively deactivated during the following phases of the algorithm (Supplementary Section 1.2).
2.4 Substitution score
During core building, a smoothed fragment-based environment-specific substitution score Scand is used to determine the order, by which alignment columns are added to the model's core. During the later phases of core extension, a score cut-off is used at each alignment column selection step, in order to decide whether the core building process should be halted.
2.4.1 Environment-specific substitution tables (ESSTs)
Using the membrane layer annotation provided by iMembrane (Section 2.2) and the secondary structure annotation provided by JOY, we have created 12 ESSTs specific to various structural environments in MPs (e.g. ‘helix residues in the membrane tail region’). The procedure of creating these ESSTs is similar to SUBST by Kenji Mizuguchi (Shi et al., 2001) and newer methods based on it (Lee and Blundell, 2009). In our procedure, we count the substitutions between one protein of known structure and many sequence homologues. This drastically increases the number of observed substitutions in MPs, where few resolved 3D structures are available. Our programme (JSUBST, written in Java) is available upon request. For further detail see Supplementary Sections 1.3–1.4.
2.4.2 Calculating the smoothed fragment-based environment-specific substitution score Scand
Our ESSTs are used to assign a raw score Sraw (Supplementary Section 1.4) to every column in the sequence alignment. Sraw is smoothed over a window (of three residues, by default) to form Ssmoothed (Equation 1). Scand is the score given to a candidate alignment column. It is the sum of the smoothed scores Ssmoothed of all alignment columns already in the selected fragment, plus the candidate's own smoothed score.
| (1) |
| (2) |
where i, j, Ffirst and Flast are alignment column indices; i is the index of the alignment column, whose score is to be determined; W is a constant dependent on the window size (V), which is 3, by default; W = (V − 1)/2; L is the actual number of scores inside the window (L = W in the normal case, but can be smaller if the window contains alignment gaps or extends past an end of the sequence); Ffirst and Flast are the indices of the first and last columns of the fragment to be extended, respectively.
2.4.3 Calculating the substitution score cut-off
The substitution score cut-off Scutoff for each core extension phase is dependent on the previous phase and is calculated as follows:
| (3) |
where Smean,prev is the mean score of the previous phase and Slast,prev is the score of the last-added residue in the previous phase.
2.4.4 Using Scand to determine selection order
Assume an alignment with several fragments (consecutive stretches of alignment columns) already selected. During a core extension iteration, one of the many fragments is extended by a single residue. In order to decide which fragment is extended by which residue, the following steps are taken: (i) identify all possible candidates (unselected alignment columns adjacent to an already selected column); (ii) discard any masked candidates; (iii) calculate the substitution score of each remaining candidate (Equation 2); and (iv) discard all but the best-scoring candidate—this alignment column is now selected. In the later phases of the core extension procedure, if the candidate score Scand is below a defined score cut-off (Equation 3), the candidate is rejected and core extension halted (Section 2.4.5).
2.4.5 Halting core extension
When core extension is halted, it regresses (i.e. columns are removed in the reverse order they were added) until a local Scand score maximum is reached.
2.5 Multiple templates
MEDELLER allows the user to provide more than one template protein. In this case, the same algorithm (Section 2.1.3) is run for each template separately, in order to identify the fragments that constitute the common core between the target protein and each template. Then, the fragments from all templates are pooled and the top-scoring subset of fragments is chosen to build the core model. Two fragments are allowed to overlap only if (i) the overlapping region is shorter than half the length of the smaller fragment, (ii) there are no alignment gaps in the overlapping region and (iii) the backbone RMSD of the overlap is lower than 1 Å. Overlapping coordinates are melded (Choi and Deane, 2009). After assembling the single best-scoring core model, the algorithm proceeds as for a single template (Section 2.1.4).
2.6 Testing the modelling accuracy
Modelling accuracy was tested using the all-backbone-atom (C-α, N, C, O) RMSD between a model and the ‘native’ target X-ray structure, as found in the PDB. In addition, we report GDT_TS (Zemla et al., 1999) scores in the Supplementary Material. We also analysed the models' TM region in terms of tilt angle and rotation angle and shift (as number of residues) relative to the native structure. The accuracy of the models generated by our method was compared to the ‘top’ model out of 10 equivalent models generated using Modeller with default settings. In every case, both methods started from an identical ‘ideal’ sequence alignment, generated from a structure alignment between the template and the native target structure. The ‘top’ Modeller model was selected using Modeller's own DOPE energy score (Eswar et al., 2007). To make the comparison fair, we calculated Modeller's RMSD using only that sub-set of residues present in the MEDELLER model. Two models with RMSDs to the native structure that differ by no more than 0.05 Å were deemed to be equally accurate. We also conducted identical tests using the ‘best’ Modeller model, which was selected from the set of 10 as the one with the lowest RMSD to the native target X-ray structure.
2.7 Sequence identity and coverage measures
Sequence identity (ID) is calculated as the number of identical residues divided by the total number of alignment columns. On this scale, a value of ∼20% identity corresponds to the ‘twilight zone’ of sequence identity (Rost, 1999). Target coverage (Cov) is the number of residues, for which the model provides 3D coordinates, divided by the total length of the target sequence. Target ‘core coverage’ (CoreCov) is calculated as above, except that the sequence is shortened to exclude any N- or C-terminal stretches of unmodelled residues.
2.8 Creation of the test sets
A list of MP structures was compiled by combining data from several publicly available databases: all PDB entries annotated with the SCOP class ‘membrane proteins’, the OPM database (Lomize et al., 2006), the PDB TM database (Tusnády et al., 2005) and the CGDB database (Scott et al., 2008). A list of unique PDB entries was compiled and filtered to include only X-ray structures with a resolution ≤3 Å. These structures were split into single protein chains. The protein sequences were extracted and made non-redundant at a level of 80% sequence identity using CD-HIT (Li and Godzik, 2006). Thus, none of the target proteins in any of our test sets share >80% sequence identity. The remaining protein chains were run through iMembrane, in order to identify possible template structures in the CGDB database. The ‘structure search’ option was used; this method searches iMembrane's database for homologous structures using pairwise structure alignment. All iMembrane search hits with a TM score (TM align; Zhang and Skolnick, 2005) above 0.50 were kept. Some target proteins did not receive any iMembrane hits and were thus removed from the dataset. Pairs where target and template were of the same protein chain were also removed. The remaining protein pairs were then classified into four test sets of varying sequence identity ranges. The test set for modelling multiple templates is a subset of the above set and contains targets associated with at least two templates.
3 RESULTS
3.1 Test sets
Our complete test set contains 616 pairs of protein chains (target–template pairs). Proteins of both the α-helical (413) and the β-barrel (203) type are included. The target–template pairs were classified, by their sequence identity, into four test sets representing four different levels of modelling difficulty:
‘easy’ set: 128 protein pairs, 40–100% sequence identity.
‘medium’ set: 115 protein pairs, 20–40% sequence identity.
‘hard’ set: 102 protein pairs, 10–20% sequence identity.
‘hardest’ set: 271 protein pairs, 0–10% sequence identity.
A target may be paired with more than one template. Conversely, a template may also be paired with more than one target. The full list of target–template pairs is given in Supplementary Section 2.1.
Our test set is roughly two-thirds of the size of that used by Wallner and Elofsson (2005; 1036 representative protein pairs from different protein families) for testing co-ordinate generation in soluble proteins, and ∼17 times larger than the HOMEP set by Forrest et al. (2006; 36 pairs of MPs).
3.2 Modelling from a single template
We ran our new coordinate generator, MEDELLER, as well as Modeller on all target–template pairs in our test set. Modelling accuracy and target coverage were compared. The average accuracy of both methods as well as MEDELLER's coverage are summarized in Table 1. The distribution of both methods' accuracy over all target–template pairs in the ‘easy’ test set is shown in Figure 2.
Table 1.
Accuracy of MEDELLER's high-accuracy model versus Modeller
| Test | More | Less | MED | MOD | Diff | CoreCov | Cov |
|---|---|---|---|---|---|---|---|
| set | acc (%) | acc (%) | RMSD (Å) | RMSD (Å) | RMSD (Å) | (%) | (%) |
| All | 65 | 23 | 2.62 | 3.16 | −0.54 | 92 | 71 |
| Easy | 68 | 13 | 0.93 | 1.56 | −0.63 | 99 | 88 |
| Med. | 59 | 23 | 1.92 | 2.40 | −0.48 | 92 | 80 |
| Hard | 49 | 39 | 2.82 | 2.97 | 0.15 | 90 | 70 |
| Hardest | 72 | 21 | 3.64 | 4.32 | −0.68 | 88 | 58 |
Rows correspond to test sets. The ‘all’ test set is the union of all the test sets. ‘More acc’ and ‘Less acc’ are the percentages of test cases where MEDELLER (MED) is more or less accurate, respectively, than Modeller (MOD). If the two methods' accuracies are within 0.05 Å RMSD of each other, they are deemed equal. ‘MED rmsd’ and ‘MOD rmsd ‘are accuracy values measured using the RMSD between the native structure and the MEDELLER or Modeller model, respectively. ‘Diff rmsd’ is the difference in accuracy between the two methods. Cov is the percentage coverage of the target sequence by the MEDELLER model. CoreCov is equivalent to Cov, but disregards uncovered terminal regions. All values are averaged over an entire test set.
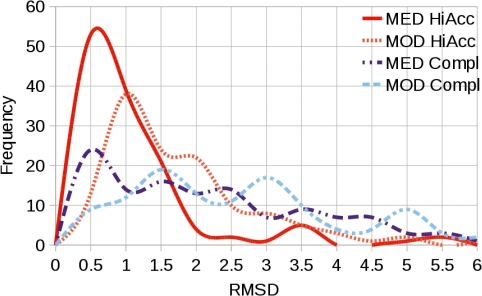
Fig. 2.
Distribution of modelling accuracy for the ‘easy’ dataset, when modelling from structure-based sequence alignments. Backbone RMSD to the native structure achieved by MEDELLER's high-accuracy (MED HiAcc) and complete (MED Compl) models and the corresponding coordinates in the Modeller model (MOD HiAcc, MOD Compl). MEDELLER's accuracy distribution peaks at ∼0.6 Å for both high-accuracy and complete models, compared with a 1.0 Å and a 1.5 Å peak for Modeller's equivalent coordinates to the two model types.
On average, our method outperforms Modeller on the entire test set, in terms of accuracy, by 0.60 Å RMSD for the core model and by 0.54 Å RMSD for the high-accuracy model. On our ‘easy’ dataset, the difference in average modelling accuracy between the methods is the most visible, with 0.71 Å versus 1.46 Å RMSD for the core model and 0.93 Å versus 1.56 Å RMSD for the high-accuracy model. This can also be seen in terms of GDT_TS with MEDELLER achieving a GDT_TS of 0.94 for high-accuracy models in the easy test set, whereas Modeller achieves 0.85. GDT_TS scores for all the sets that are given in Supplementary Section 2.2.
The major advantage of MEDELLER lies in its highly reliable core models. Compared with Modeller, our core models are at least 0.05 Å more accurate in 66% of test cases and at least as good (±0.05 Å) in 88% of test cases. With added high-accuracy loops, MEDELLER remains the more accurate method in 65% of test cases and at least as good as Modeller in 77% of test cases.
The worst core models made by the two methods have respective RMSDs of 5.40 Å (MEDELLER) and 10.47 Å (Modeller). Mostly, these inaccurate models are where target and template have different beta barrel diameters or considerable local changes in helix bundle geometry. With added ‘high accuracy’ loops, the worst accuracy values are 13.72 and 13.33 Å, respectively. Any errors in the core models are propagated and result in a worse loop accuracy overall. In terms of loop accuracy, both globally and locally, MEDELLER's high-accuracy models outperform Modeller, with average RMSDs of 5.9 Å (global) and 1.32 Å (local). This relatively high global RMSD is mainly due to a number of loops whose general shape is correct, but which are at a wrong angle to the rest of the model, resulting in a very high RMSD. Both MEDELLER and Modeller show relatively poor performance if all loops are built (complete model) with global RMSDs of over 11 Å.
In terms of coverage, Modeller always provides a complete model. However, its loop regions tend to be unreliable. MEDELLER, on the other hand, provides four models: a core model with only highly conserved regions, a high-accuracy model containing high-confidence loops, a high-coverage model that includes low-confidence regions and a complete model. MEDELLER's modelling confidence is shown in the output using an atom's B-factor (Figure 3B). All our tests were repeated when selecting the ‘best’ out of the 10 Modeller decoys using the RMSD to the native structure, instead of Modeller's DOPE energy score. This did not change the overall trend of the results.
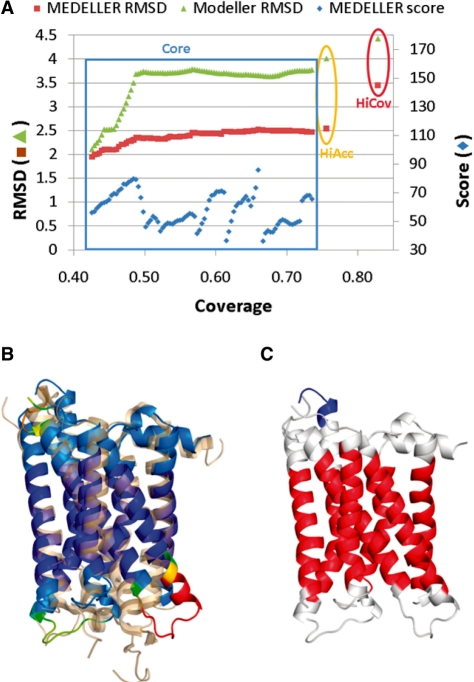
Fig. 3.
Example model of human adenosine A2A receptor (PDB 3EML, chain A). (A) Progression of model accuracy through the modelling process. The modelling phases corresponding to the different MEDELLER models [Core, High Accuracy (HiAcc) and High Coverage (HiCov)] are labelled. (B) MEDELLER's high-coverage model, coloured by modelling confidence in a blue-to-red spectrum, aligned to the native X-ray structure (transparent orange). (C) MEDELLER's high-coverage model, coloured by membrane insertion using iMembrane [red, middle hydrophobic (tail group) layer; white, peripheral polar (head group) layers; blue, aqueous (non-membrane) layers].
For further details, see Supplementary Section 2.2.
3.3 Modelling from pure sequence alignments
All accuracy values reported in Section 3.2 are achieved when modelling from an ‘ideal’ alignment, based on a structure superposition between target and template. Whether such values can be achieved in a real modelling case always depends on the quality of the input alignment. As a practical ‘worst case’ scenario, we report accuracy values achieved when modelling from a simple pairwise sequence alignment, generated using MUSCLE (Edgar, 2004). As expected, the resulting model accuracy was reduced for both MEDELLER and Modeller. On average MEDELLER's high-accuracy model achieved a backbone accuracy of 0.96 Å compared with 1.78 Å for the equivalent Modeller coordinates, on the ‘easy’ test set. For further details, see Supplementary Section 2.3. In practice, users will most likely use a more sophisticated alignment method, such as FUGUE (Shi et al., 2001), yielding somewhat better accuracies.
It should, of course, be understood that, even when using MUSCLE alignments as input, we still base our results on the prior knowledge that the chosen template is adequate for homology modelling (target template TM score >0.50; see Section 2.8). In the regular modelling case, this knowledge is not available and one has to rely on the accuracy of homology detection methods.
3.4 Comparison to the naïve model
When modelling from an ‘ideal’ alignment, the core selected by MEDELLER is on an average smaller but has a far lower RMSD (1.97 Å for MEDELLER versus 2.77 Å for the naïve model). The high-accuracy MEDELLER model covers on average a very similar fraction of the model (excluding terminal gaps) to the naïve model and the average RMSD (2.62 Å) is still lower than the naïve model. The same trend is observed when modelling from a pure sequence alignment (0.93 and 0.96 Å for MODELLER's core and high-accuracy models versus 1.15 Å for the naïve model, on the ‘easy’ test set). For further details, see Supplementary Section 2.4.
3.5 Main chain bumps and transmembrane geometry
The model quality assessment software WHATCHECK (Hooft et al., 1996) was run on the complete MEDELLER and Modeller models. On average, both methods had a significantly higher amount of bumps between main chain atoms than the template and target structures. Modeller produces slightly fewer bumps, thanks to its model refinement function. For details, see Supplementary Section 2.5.
Using iMembrane, we also compared the accuracy of TM helix/β sheet geometry, relative to the native X-ray structure. While both methods behaved very similarly, on average MEDELLER produced slightly better geometries. MEDELLER and Modeller, respectively, had average TM shifts of 1.9 versus 2.3 residues, tilt angle deviations of 2.4○ versus 3.4○ and rotation angle deviations of 31.2○ versus 36.0○. For further details, see Supplementary Section 2.6.
3.6 Modelling from multiple templates
We tested both MEDELLER and Modeller on a set of 35 target proteins with at least two templates per target. On average, MEDELLER's core model achieves an accuracy of 3.24 Å RMSD, compared with 3.32 Å for the corresponding Modeller coordinates. This average is heavily biased by two outliers, where both methods each produced one ‘less bad’ model but both methods' accuracy was worse than 9 Å. After discarding these two test cases, the two methods' average accuracies are 2.20 Å for MEDELLER and 2.44 Å for Modeller. In almost every test case, both MEDELLER and Modeller could create a better core model when given only a single template structure (e.g. the one with the highest sequence identity to the target). For further details, see Supplementary Section 2.7.
3.7 Example model: human adenosine A2A receptor
The human adenosine A2A receptor (PDB 3EML, chain A) is a G-protein coupled receptor (GPCR). The structure was resolved at a resolution of 2.6 Å and contains only a single gap in a loop connecting two TM helices. In 2008, this protein was the subject of a CASP-style blind prediction competition (Michino et al., 2009) in order to assess the current state in GPCR MP structure prediction. The most direct comparison possible is between values for TM helix accuracy from Michino et al. (2009) and our MEDELLER ‘core’ models, which are roughly equivalent.
Our test set contains three models of 3EML (all from the ‘hard’ set), with core accuracies (C-α RMSD) of 2.1, 2.3 and 2.5 Å. The model in Michino et al. (2009) to best predict the TM helices had a C-α accuracy of 2.1 Å (the model submitted by Davis, Barth and Baker). The average TM helix (C-α) accuracy for all submitted models was 2.8 ± 0.5 Å. This places MEDELLER's models at the top end of the scale. Of course, this comparison is not entirely fair, as our models are based on a structure alignment to the native structure. However, Michino et al. (2009) reported that alignment did not seem to be a problem due to the conserved TM sequence patterns.
The high-coverage MEDELLER model with a core (C-α) accuracy of 2.5 Å is shown in Figure 3. The template structure is Opsin (PDB 3CAP, chain A), another GPCR. The MEDELLER model is more accurate than the corresponding co-ordinates of the top Modeller model. MEDELLER's backbone RMSD was 2.64, 2.65 and 3.57 Å for its core, high-accuracy and high-coverage models, respectively. Modeller achieved an RMSD of 4.70, 4.83 and 5.11 Å for the corresponding coordinates.
Loops modelled using FREAD had the right general shape, even in the high-coverage model, whereas Modeller's loops tended to be at the wrong angle relative to the core of the protein. Only one very long loop was not modelled by FREAD. Modeller produced coordinates for this loop but these were far from the loop's position in the X-ray structure.
One particular mistake was made by both methods: failure to predict a helix kink that was present in the native structure but not in the template. For further details, see Supplementary Section 2.8.
4 DISCUSSION
We present MEDELLER, a new template-based coordinate generation protocol for MPs. First, a common core between target and template proteins is defined, using membrane insertion and secondary structure information. Then, any gaps in this core model are completed, as far as possible, using FREAD, a database search loop modelling algorithm. Finally, any remaining gaps are filled using Modeller. This results in four models with increasing target coverage: the ‘core’, ‘high-accuracy’, ‘high-coverage’ and ‘complete’ models. In the output, coordinate reliability is indicated using B-factors. MEDELLER's algorithm speed is comparable to that of Modeller (Supplementary Section 2.9).
MEDELLER's core and high-accuracy models are potentially incomplete. However, the level of certainty in these coordinates is high. We have shown that MEDELLER's core models (1.97 Å RMSD) are consistently more accurate than their corresponding coordinates in the Modeller models (2.57 Å RMSD). Even adding high-accuracy loops, MEDELLER still outperforms Modeller in most cases. MEDELLER's high-coverage model represents a trade-off between accuracy and coverage. At this coverage level, the two methods are, on average, approximately equal, with MEDELLER better in the ‘easy’ set and Modeller better in the ‘hard’ set. Where complete coverage is required, we also produce a complete model by filling any remaining gaps using Modeller. However, the accuracy of such coordinates is unreliable. Here both methods have average RMSDs of over 10 Å, mainly due to large regions of the targets not aligned to a template in the ‘hard’ and ‘hardest’ test sets. Only on the easy set, where unaligned regions are short, MEDELLER's complete models have a clear advantage with 2.80 Å RMSD versus 3.39 Å for Modeller. In the ‘medium’ set, Modeller's complete models lead with 5.33 Å versus 5.84 Å for MEDELLER.
The fact that MEDELLER's core models are consistently better than Modeller's, even though MEDELLER employs no structure optimization methods, suggests that Modeller's probability density function, which was created to model soluble proteins, may distort the template structure of a MP.
The high quality of MEDELLER's core models is achieved by reliably selecting parts of the template structure that are similar to the correct target coordinates. This is made possible by using membrane insertion annotation and an environment-specific substitution score along with the rule-based MEDELLER algorithm (Sections 2.1–2.4).
In terms of loop modelling, MEDELLER is the first software to use the recently revised FREAD algorithm (Choi and Deane, 2009). For soluble proteins, FREAD guarantees consistent loop quality independent of loop length as long as the anchor structures are correctly modelled. The high accuracy of our core models allows FREAD, in many cases, to produce accurate loop structures (‘high-accuracy’ models). In our test set, FREAD sometimes does not correctly filter out loops which are similar in shape to the native structure but are attached at a wrong angle to the model core. We have not observed this phenomenon when modelling loops in soluble proteins. Future versions of MEDELLER will introduce MP-specific loop selection procedures to deal with such errors.
MEDELLER's loss in accuracy in the higher coverage models, especially at low target-template sequence identity, is due to small local structure differences in the MP ‘core’ region. These errors are amplified when adding loops to the model, based on such erroneous anchor structures. Modeller lessens this dependency using its model refinement method. This has two opposing effects, however: smaller errors at low target-template identity (which is desirable) and also worse core models overall (which is not).
The obvious way to improve model accuracy would be to either greatly reduce the size of the model core or to create a refinement method that corrects local structural differences such as helix kinks. Helix kink prediction will allow better core accuracy, even with templates that are locally different from the correct target structure. Future versions of MEDELLER will include such refinement methods, as well as a more accurate ab initio loop modelling protocol that should allow for better ‘high-coverage’ and ‘complete’ models.
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank the Oxford Protein Informatics Group for useful discussion and feedback.
Funding: Biotechnology and Biological Sciences Research Council (to S.K.); University of Oxford Doctoral Training Centres (to C.M.D.).
Conflict of Interest: none declared.
REFERENCES
- Barth P, et al. Prediction of membrane protein structures with complex topologies using limited constraints. Proc. Natl Acad. Sci. USA. 2009;106:1409–1414. doi: 10.1073/pnas.0808323106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bates PA, et al. Enhancement of protein modeling by human intervention in applying the automatic programs 3d-jigsaw and 3d-pssm. Proteins. 2001;45:39–46. doi: 10.1002/prot.1168. [DOI] [PubMed] [Google Scholar]
- Berman HM, et al. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burke DF, et al. An iterative structure-assisted approach to sequence alignment and comparative modeling. Proteins. 1999;37:55–60. doi: 10.1002/(sici)1097-0134(1999)37:3+<55::aid-prot8>3.3.co;2-2. [DOI] [PubMed] [Google Scholar]
- Choi Y, Deane CM. Fread revisited: accurate loop structure prediction using a database search algorithm. Proteins. 2009;78:1431–1440. doi: 10.1002/prot.22658. [DOI] [PubMed] [Google Scholar]
- Deane CM, et al. Score: predicting the core of protein models. Bioinformatics. 2001;17:541–550. doi: 10.1093/bioinformatics/17.6.541. [DOI] [PubMed] [Google Scholar]
- Edgar RC. Muscle: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Res. 2004;32:1792–1797. doi: 10.1093/nar/gkh340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elofsson A, von Heijne G. Membrane protein structure: prediction versus reality. Annu. Rev. Biochem. 2007;76:125–140. doi: 10.1146/annurev.biochem.76.052705.163539. [DOI] [PubMed] [Google Scholar]
- Eswar N, et al. Comparative protein structure modeling using modeller. Curr. Protoc. Protein Sci. 2007;50:2.9.1–2.9.31. doi: 10.1002/0471140864.ps0209s50. [DOI] [PubMed] [Google Scholar]
- Eyre TA, et al. Computational analysis of alpha-helical membrane protein structure: implications for the prediction of 3d structural models. Protein Eng. Des. Sel. 2004;17:613–624. doi: 10.1093/protein/gzh072. [DOI] [PubMed] [Google Scholar]
- Fenosa A, et al. Role of tolc in klebsiella oxytoca resistance to antibiotics. J. Antimicrob. Chemother. 2009;63:668–674. doi: 10.1093/jac/dkp027. [DOI] [PubMed] [Google Scholar]
- Forrest LR, et al. On the accuracy of homology modeling and sequence alignment methods applied to membrane proteins. Biophys. J. 2006;91:508–517. doi: 10.1529/biophysj.106.082313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gromiha MM, et al. Application of residue distribution along the sequence for discriminating outer membrane proteins. Comput. Biol. Chem. 2005;29:135–142. doi: 10.1016/j.compbiolchem.2005.02.006. [DOI] [PubMed] [Google Scholar]
- Hooft RW, et al. Errors in protein structures. Nature. 1996;381:272. doi: 10.1038/381272a0. [DOI] [PubMed] [Google Scholar]
- Kelm S, et al. iMembrane: homology-based membrane-insertion of proteins. Bioinformatics. 2009;25:1086–1088. doi: 10.1093/bioinformatics/btp102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koehl P, Delarue M. A self consistent mean field approach to simultaneous gap closure and side-chain positioning in homology modelling. Nat. Struct. Biol. 1995;2:163–170. doi: 10.1038/nsb0295-163. [DOI] [PubMed] [Google Scholar]
- Lee S, Blundell TL. Ulla: a program for calculating environment-specific amino acid substitution tables. Bioinformatics. 2009;25:1976–1977. doi: 10.1093/bioinformatics/btp300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt M. Accurate modeling of protein conformation by automatic segment matching. J. Mol. Biol. 1992;226:507–533. doi: 10.1016/0022-2836(92)90964-l. [DOI] [PubMed] [Google Scholar]
- Li W, Godzik A. Cd-hit: a fast program for clustering and comparing large sets of protein or nucleotide sequences. Bioinformatics. 2006;22:1658–1659. doi: 10.1093/bioinformatics/btl158. [DOI] [PubMed] [Google Scholar]
- Lomize MA, et al. Opm: orientations of proteins in membranes database. Bioinformatics. 2006;22:623–625. doi: 10.1093/bioinformatics/btk023. [DOI] [PubMed] [Google Scholar]
- Michino M, et al. Community-wide assessment of gpcr structure modelling and ligand docking: Gpcr dock 2008. Nat. Rev. Drug Discov. 2009;8:455–463. doi: 10.1038/nrd2877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizuguchi K, et al. Joy: protein sequence-structure representation and analysis. Bioinformatics. 1998;14:617–623. doi: 10.1093/bioinformatics/14.7.617. [DOI] [PubMed] [Google Scholar]
- Moult J, et al. Critical assessment of methods of protein structure prediction—Round VIII. Proteins. 2009;77:1–4. doi: 10.1002/prot.22589. [DOI] [PubMed] [Google Scholar]
- Murzin AG, et al. SCOP: a structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol. 1995;247:536–540. doi: 10.1006/jmbi.1995.0159. [DOI] [PubMed] [Google Scholar]
- Müller DJ, et al. Vertebrate membrane proteins: structure, function, and insights from biophysical approaches. Pharmacol. Rev. 2008;60:43–78. doi: 10.1124/pr.107.07111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrey D, et al. Using multiple structure alignments, fast model building, and energetic analysis in fold recognition and homology modeling. Proteins. 2003;53:430–435. doi: 10.1002/prot.10550. [DOI] [PubMed] [Google Scholar]
- Punta M, et al. Membrane protein prediction methods. Methods. 2007;41:460–474. doi: 10.1016/j.ymeth.2006.07.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reddy ChS, et al. Homology modeling of membrane proteins: a critical assessment. Comput. Biol. Chem. 2006;30:120–126. doi: 10.1016/j.compbiolchem.2005.12.002. [DOI] [PubMed] [Google Scholar]
- Rost B. Twilight zone of protein sequence alignments. Protein Eng. 1999;12:85–94. doi: 10.1093/protein/12.2.85. [DOI] [PubMed] [Google Scholar]
- Sali A, Blundell TL. Comparative protein modelling by satisfaction of spatial restraints. J. Mol. Biol. 1993;234:779–815. doi: 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]
- Sali A, Overington JP. Derivation of rules for comparative protein modeling from a database of protein structure alignments. Protein Sci. 1994;3:1582–1596. doi: 10.1002/pro.5560030923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sánchez R, Sali A. Advances in comparative protein-structure modelling. Curr. Opin. Struct. Biol. 1997;7:206–214. doi: 10.1016/s0959-440x(97)80027-9. [DOI] [PubMed] [Google Scholar]
- Saxena AK, et al. Internet resources in gpcr modelling. SAR QSAR Environ. Res. 2008;19:11–25. doi: 10.1080/10629360701844126. [DOI] [PubMed] [Google Scholar]
- Schulz GE. The structure of bacterial outer membrane proteins. Biochim. Biophys. Acta. 2002;1565:308–317. doi: 10.1016/s0005-2736(02)00577-1. [DOI] [PubMed] [Google Scholar]
- Schwede T, et al. Swiss-model: an automated protein homology-modeling server. Nucleic Acids Res. 2003;31:3381–3385. doi: 10.1093/nar/gkg520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott KA, et al. Coarse-grained md simulations of membrane protein-bilayer self-assembly. Structure. 2008;16:621–630. doi: 10.1016/j.str.2008.01.014. [DOI] [PubMed] [Google Scholar]
- Shi J, et al. Fugue: sequence-structure homology recognition using environment-specific substitution tables and structure-dependent gap penalties. J. Mol. Biol. 2001;310:243–257. doi: 10.1006/jmbi.2001.4762. [DOI] [PubMed] [Google Scholar]
- Stevens TJ, Arkin IT. Are membrane proteins ‘inside-out’ proteins? Proteins. 1999;36:135–143. doi: 10.1002/(sici)1097-0134(19990701)36:1<135::aid-prot11>3.0.co;2-i. [DOI] [PubMed] [Google Scholar]
- Tusnády GE, et al. Pdb_tm: selection and membrane localization of transmembrane proteins in the protein data bank. Nucleic Acids Res. 2005;33:D275–D278. doi: 10.1093/nar/gki002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulmschneider MB, Sansom MS. Amino acid distributions in integral membrane protein structures. Biochim. Biophys. Acta. 2001;1512:1–14. doi: 10.1016/s0005-2736(01)00299-1. [DOI] [PubMed] [Google Scholar]
- Wallin E, von Heijne G. Genome-wide analysis of integral membrane proteins from eubacterial, archaean, and eukaryotic organisms. Protein Sci. 1998;7:1029–1038. doi: 10.1002/pro.5560070420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallner B, Elofsson A. All are not equal: a benchmark of different homology modeling programs. Protein Sci. 2005;14:1315–1327. doi: 10.1110/ps.041253405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu CH, et al. The universal protein resource (uniprot): an expanding universe of protein information. Nucleic Acids Res. 2006;34:D187–D191. doi: 10.1093/nar/gkj161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Q, et al. Modeling the binding modes of kv1.5 potassium channel and blockers. J. Mol. Graph. Model. 2008;27:178–187. doi: 10.1016/j.jmgm.2008.04.002. [DOI] [PubMed] [Google Scholar]
- Yarov-Yarovoy V, et al. Multipass membrane protein structure prediction using rosetta. Proteins. 2006;62:1010–1025. doi: 10.1002/prot.20817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zemla A, et al. Processing and analysis of casp3 protein structure predictions. Proteins. 1999;37:22–29. doi: 10.1002/(sici)1097-0134(1999)37:3+<22::aid-prot5>3.3.co;2-n. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Skolnick J. Tm-align: a protein structure alignment algorithm based on the tm-score. Nucleic Acids Res. 2005;33:2302–2309. doi: 10.1093/nar/gki524. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.