Advances in Analysis of Longitudinal Data

Abstract

In this review, we explore recent developments in the area of linear and nonlinear generalized mixed-effects regression models and various alternatives, including generalized estimating equations for analysis of longitudinal data. Methods are described for continuous and normally distributed as well as categorical (binary, ordinal, nominal) and count (Poisson) variables. Extensions of the model to three and four levels of clustering, multivariate outcomes, and incorporation of design weights are also described. Linear and nonlinear models are illustrated using an example involving a study of the relationship between mood and smoking.

OVERVIEW

Since the pioneering work of Laird & Ware (1982), statistical methods for the analysis of longitudinal data have advanced dramatically. Prior to this time, the standard approach to analysis of longitudinal data principally involved using the longitudinal data to impute end-points (e.g., last observation carried forward; LOCF) and then to simply discard the valuable intermediate time-point data, favoring the simplicity of analyses of change scores from baseline to study completion (or the last available measurement treated as if it was what would have been obtained had it been the end of the study), in some cases adjusting for baseline severity as well. Laird & Ware (1982) showed that generalized mixed-effects regression models could be used to perform a more complete analysis of all of the available longitudinal data under much more general assumptions regarding the missing data (i.e., missing at random; MAR). The net result was a more powerful set of statistical tools for analysis of longitudinal data that led to more powerful statistical hypothesis tests, more precise estimates of rates of change (and differential rates of change between experimental and control groups), and more general assumptions regarding missing data, for example because of study dropout. This early work has led to considerable related advances in statistical methodology for analysis of longitudinal data (for excellent reviews of this growing literature, see Diggle et al. 2002, Fitzmaurice et al. 2004, Goldstein 1995, Hedeker & Gibbons 2006, Longford 1993, Raudenbush & Bryk 2002, Singer & Willett 2003, and Verbeke & Molenberghs 2000). Notable among these advances and relevant to this review are generalizations of the original Laird-Ware type model to the nonlinear case (relevant for analysis of binary, ordinal, nominal, count, and time-to-event outcomes), even more general forms of missing data (not missing at random; NMAR), higher levels of nesting such as three-level models (e.g., repeated observations nested within subjects and subjects nested within hospitals or clinics), alternative distributional assumptions for residual errors of measurement, correlated residual errors of measurement, multivariate mixed-effects regression models, and advances in sample size determination in the context of longitudinal studies. Computational advances in parameter estimation have also been seen, particularly in the area of nonlinear mixed effects regression models, where numerical evaluation of the likelihood function is more complex and requires high dimensional numerical integration (e.g., adaptive quadrature or Monte Carlo–type integration for full Bayes estimation of model parameters).

In the following sections, we provide a general and nontechnical overview of these recent advances and then illustrate some of their uses by applying them in analysis of several example datasets.

PROBLEMS INHERENT IN LONGITUDINAL DATA

Although longitudinal studies provide far more information than their cross-sectional counterparts and are therefore now in widespread use, they are not without limitations. In the following sections we review some of the major challenges associated with longitudinal data analysis.

Heterogeneity

Particularly in the behavioral sciences, individual differences are the norm rather than the exception. The overall mean response in a sample drawn from a population tells us little regarding the experience of the individual. In contrast to cross-sectional studies in which it is reasonable to assume that there are random fluctuations at each measurement occasion, when the same subjects are repeatedly measured over time, their responses are correlated over time, and their estimated trend line or curve can be expected to deviate systematically from the overall mean trend line. For example, behavioral and/or biological subject-level characteristics can increase the likelihood of a favorable response to a particular experimental intervention (e.g., a new pharmacologic treatment for depression), leading subjects with those characteristics to have a trend with higher slope (i.e., rate of change) than the overall average rate of change for the sample as a whole. In many cases, these personal characteristics may be unobservable, leading to unexplained heterogeneity in the population. Modeling this unobserved heterogeneity in terms of variance components that describe subject-level effects (or alternatively cluster-level effects such as classrooms, schools, clinics, etc.) is one way to accommodate the correlation of the repeated responses over time and to better describe individual differences in the statistical characterization of the observed data. These variance components are often termed “random effects,” leading to terms like random-effects or mixed-effects regression models.

Correlated Errors of Measurement

In addition to heterogeneity in the population that leads to subject-specific deviations from the overall temporal response pattern, there is also often short-term correlated errors of measurement that are produced by the psychological state that a subject is in during measurement occasions that are close in time. This type of short-term residual correlation tends to decrease exponentially with the temporal distance between the measurement occasions. The addition of autocorrelated residuals (Chi & Reinsel 1989, Hedeker 1989) to mixed-effects regression models allows for a more parsimonious analysis of the more subtle features of the longitudinal response process and results in more accurate estimates of uncertainty in parameter estimates, improved tests of hypotheses, and more accurate interval estimates.

Missing Data

Perhaps the most dramatic difficulty is the presence of missing data. Stated quite simply, not all subjects remain in the study for the entire length of the study. Reasons for discontinuing the study may be differentially related to the treatment. For example, some subjects may develop side effects to an otherwise effective treatment and must discontinue the study. Alternatively, some subjects might achieve the full benefit of the study early on and discontinue the study because they feel that their continued participation will provide no added benefit. The treatment of missing data in longitudinal studies is itself a vast literature, with major contributions by Laird (1988), Little (1995), Little & Rubin (2002), and Rubin (1976), to name a few. The basic problem is that even in a randomized and well-controlled clinical trial, the subjects who were initially enrolled in the study and randomized to the various treatment conditions may be quite different from the subjects who are available for analysis at the end of the trial. If subjects drop out because they already have derived full benefit from an effective treatment, an analysis that only considers those subjects who completed the trial may fail to show that the treatment was beneficial relative to the control condition. This type of analysis is often termed a “completer” analysis. To avoid this type of obvious bias, investigators often resort to an “intent-to-treat” analysis, in which the last available measurement is carried forward to the end of the study as if the subject had actually completed the study. This type of analysis, often termed an “end-point” analysis, introduces its own set of problems in that (a) all subjects are treated equally regardless of the actual intensity of their treatment over the course of the study, and (b) the actual response that would have been observed at the end of the study, if the subject had remained in the study until its conclusion, may in fact be quite different from the response made at the time of discontinuation. Returning to our example of the study in which subjects discontinue when they feel that they have received full treatment benefit, an endpoint analysis might miss the fact that some of these subjects may have had a relapse had they remained on treatment. Many other objections have been raised about these two simple approaches of handling missing data in longitudinal data, which have led to many more modern and far better motivated approaches to analysis of longitudinal data with missing observations.

Irregularly Spaced Measurement Occasions

It is not at all uncommon in real longitudinal studies, either in the context of designed experiments or naturalistic cohorts, for individuals to vary in the number of repeated measurements they contribute and even in the time at which the measurements are obtained. This may be due to dropout or simply due to different subjects having different schedules of availability. Although this can be quite problematic for traditional analysis-of-variance-based approaches (leading to highly unbalanced designs that can produce biased parameter estimates and tests of hypotheses), more modern statistical approaches to the analysis of longitudinal data are all but immune to the “unbalancedness” that is produced by having different times of measurement for different subjects. Indeed, this is one of the most useful features of the regression approach to this problem, namely the ability to use all of the available data from each subject, regardless of when it was specifically obtained.

Subjects Clustered in Centers

In addition to correlation produced by repeated measurements with the same individual, the clustering of individuals within ecological units (schools, classrooms, clinics, hospitals, counties, etc.) produces an additional source of correlation that violates the independence assumption of traditional fixed-effects models. Simultaneous analysis of both clustered and longitudinal data leads to three-level (and even higher level) versions of the traditional two-level (repeated measurements nested with subjects) hierarchical or multilevel models. Although the magnitude of the variance component produced by clustering is typically much smaller than that produced by sampling repeated measurements within the same individual, ignoring this important source of variability leads to underestimates of standards errors of model parameters and tests of hypotheses with elevated Type I error rates (i.e., false positive rates). Three-level models are capable of simultaneously decomposing the overall variance into components related to within-subject effects and within-cluster effects. For example, a simple longitudinal study of patients within clinics may be based on the assumption that the intercept and slope of the linear time trend vary systematically from subject to subject, and the means of those time trends vary systematically from clinic to clinic.

STATISTICAL MODELS FOR ANALYSIS OF LONGITUDINAL AND/OR CLUSTERED DATA

In an attempt to provide a more general treatment of longitudinal data, with more realistic assumptions regarding the longitudinal response process and associated missing data mechanisms, statistical researchers have developed a wide variety of more rigorous approaches to the analysis of longitudinal data. Among these, the most widely used include mixed-effects regression models (Laird & Ware 1982) and generalized estimating equation (GEE) models (Zeger & Liang 1986). Variations of these models have been developed for both discrete and continuous outcomes and for a variety of missing data mechanisms. The primary distinction between the two general approaches is that mixed-effects models are full-likelihood methods and GEE models are partial-likelihood methods. The advantage of statistical models based on partial likelihood is that (a) they are computationally easier than full-likelihood methods, and (b) they generalize quite easily to a wide variety of outcome measures with quite different distributional forms. The price of this flexibility, however, is that partial likelihood methods are more restrictive in their assumptions regarding missing data than are their full-likelihood counterparts. In addition, full-likelihood methods provide estimates of person-specific effects (e.g., person-specific trend lines) that are quite useful in understanding interindividual variability in the longitudinal response process and in predicting future responses for a given subject or set of subjects from a particular subgroup (e.g., a county, a hospital, or a community). The distinctions between the various alternative statistical models for analysis of longitudinal data are fully explored in the following sections.

Mixed-Effects Regression Models

Generalized mixed-effects regression models are now quite widely used for analysis of longitudinal data. These models can be applied to both normally distributed continuous outcomes as well as categorical outcomes and other nonnormally distributed outcomes such as counts that have a Poisson distribution. Mixed-effects regression models are quite robust to missing data and irregularly spaced measurement occasions, and can easily handle both time-invariant and time-varying covariates. As such, they are among the most general of the methods for analysis of longitudinal data. As previously noted, they are sometimes called full-likelihood methods because they make full use of all available data from each subject. The advantage is that missing data are ignorable if the missing responses can be explained either by covariates in the model or by the available responses from a given subject. The disadvantage is that full-likelihood methods are more computationally complex than are quasi-likelihood methods, such as GEE.

Linear models

Traditional analysis of variance (ANOVA) methods, both univariate (repeated measures ANOVA) and multivariate (growth curve models), are of limited use because of restrictive assumptions concerning missing data across time and the variance-covariance structure of the repeated measures (Hedeker & Gibbons 2006, chapters 2 and 3). The univariate mixed-model or so-called repeated measures ANOVA assumes that the variances and covariances of the dependent variable across time are equal (i.e., compound symmetry). Alternatively, the multivariate analysis of variance for repeated measures only includes subjects with complete data across time. Also, these procedures focus on estimation of group mean trends across time and provide little help in understanding how specific individuals change across time. For these and other reasons, mixed-effects regression models (MRMs) have increasingly become popular for modeling longitudinal data.

Variants of MRMs have been developed under a variety of names: random-effects models (Laird & Ware 1982), variance component models (Dempster et al. 1981), multilevel models (Goldstein 1995), two-stage models (Bock 1989), random coefficient models (de Leeuw & Kreft 1986), mixed models (Longford 1987, Wolfinger 1993), empirical Bayes models (Hui & Berger 1983, Strenio et al. 1983), hierarchical linear models (Bryk & Raudenbush 1992), and random regression models (Bock 1983a,b; Gibbons et al. 1988). A basic characteristic of these models is the inclusion of random subject effects into the regression model in order to account for the influence of subjects on their repeated observations. These random subject effects thus describe each person’s trend across time and explain the correlational structure of the longitudinal data. Additionally, they indicate the degree of subject variation that exists in the population of subjects.

Several features make MRMs especially useful in longitudinal research. First, subjects are not assumed to be measured on the same number of time-points; thus, subjects with incomplete data across time are included in the analysis. The ability to include subjects with incomplete data across time is an important advantage relative to procedures that require complete data across time because (a) by including all data, the analysis has increased statistical power, and (b) complete-case analysis may suffer from biases to the extent that subjects with complete data are not representative of the larger population of subjects. Because time is treated as a continuous variable in MRMs, subjects do not have to be measured at the same time-points. This is useful for analysis of longitudinal studies where follow-up times are not uniform across all subjects. Both time-invariant and time-varying covariates can be included in the model. Thus, changes in the outcome variable may be due to both stable characteristics of the subject (e.g., their gender or race) and characteristics that change across time (e.g., life events). Finally, whereas traditional approaches estimate average change (across time) in a population, MRMs can also estimate change for each subject. These estimates of individual change across time can be particularly useful in longitudinal studies where a proportion of subjects exhibit change across time that deviates from the average trend.

Consider the following simple linear mixed-effects regression model for the measurement y of individual i (i = 1, 2, … N subjects) on occasion j (j = 1, 2, … n _j occasions):

$$y_{ij}={\beta }_0+{\beta }_1{t}_{ij}+{\epsilon }_{ij}.$$

Ignoring subscripts, this model represents the regression of the outcome variable y on the independent variable time (denoted t). The subscripts keep track of the particulars of the data, namely whose observation it is (subscript i) and when this observation was made (the subscript j). The independent variable t gives a value to the level of time and may represent time in weeks, months, etc. Since y and t carry both i and j subscripts, both the outcome variable and the time variable are allowed to vary by individuals and occasions.

In linear regression models, the errors ε_{i j} are assumed to be normally and independently distributed in the population with zero mean and common variance σ². This independence assumption makes the typical general linear regression model unreasonable for longitudinal data. This is because the outcomes y are observed repeatedly from the same individuals, and so it is much more likely to assume that errors within an individual are correlated to some degree. Furthermore, the above model posits that the change across time is the same for all individuals since the model parameters (β₀, the intercept or initial level, and β₁, the linear change across time) do not vary by individuals. For both of these reasons, it is useful to add individual-specific effects into the model that will account for the data dependency and describe differential time trends for different individuals. This is precisely what MRMs do. The essential point is that MRMs therefore can be viewed as augmented linear regression models.

Random Intercept Model

A simple extension of the simple linear regression model is the random intercept model, which allows each subject to deviate from the overall mean response by a person-specific constant that applies equally over time:

$$y_{ij}={\beta }_0+{\beta }_1{t}_{ij}+{\upsilon }_{0i}+{\epsilon }_{ij},$$

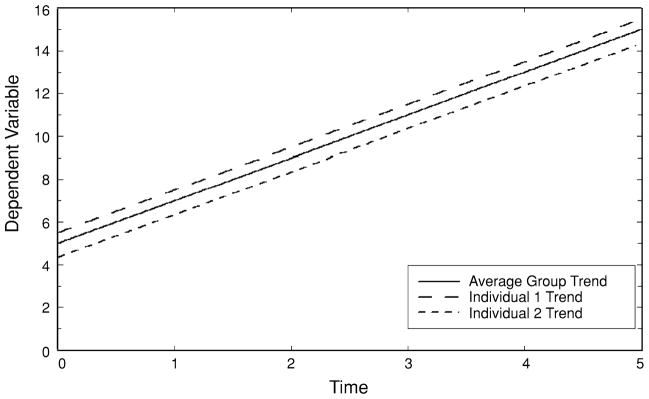
where υ_0i represents the influence of individual i on his/her repeated observations. Notice that if individuals have no influence on their repeated outcomes, then all of the υ_0i terms would equal 0. However, it is more likely that subjects will have positive or negative influences on their longitudinal data, and so the υ_0i terms will deviate from 0. Since individuals in a sample are typically thought to be representative of a larger population of individuals, the individual-specific effects υ_0i are treated as random effects. That is, υ_0i are considered to be representative of a distribution of individual effects in the population. The most common form for this population distribution is the normal distribution with mean 0 and variance ${\sigma }_{\upsilon }^2$. In addition, the model assumes that the errors of measurement are conditionally independent, which implies that the errors of measurement are independent conditional on the random individual-specific effects υ_0i. Since the errors now have an influence due to individuals removed from them, this conditional independence assumption is much more reasonable than the ordinary independence assumption associated with the general linear model. The random intercept model is depicted graphically in Figure 1.

Figure 1.

Random intercept model.

As mentioned, individuals deviate from the regression of y on t in a parallel manner in this model (since there is only one subject effect υ_0i). Thus, it is sometimes referred to as a random-intercepts model, with each υ_0i indicating how individual i deviates from the population trend. In this figure, the solid line represents the population average trend, which is based on β₀ and β₁. Also depicted are two individual trends, one below and one above the population (average) trend. For a given sample, there are N such lines, one for each individual. The variance term ${\sigma }_{\upsilon }^2$ represents the spread of these lines. If ${\sigma }_{\upsilon }^2$ is near zero, then the individual lines would not deviate much from the population trend. In this case, individuals do not exhibit much heterogeneity in their change across time. Alternatively, as individuals differ from the population trend, the lines move away from the population trend line and ${\sigma }_{\upsilon }^2$ increases. In this case, there is more individual heterogeneity in time trends.

Random Intercept and Trend Model

For longitudinal data, the random intercept model is often too simplistic for a number of reasons. First, it is unlikely that the rate of change across time is the same for all individuals. It is more likely that individuals differ in their time trends; not everyone changes at the same rate. Furthermore, the compound symmetry assumption of the random intercept model is usually untenable for most longitudinal data. In general, measurements at points close in time tend to be more highly correlated than measurements further separated in time. Also, in many studies, subjects are more similar at baseline and grow at different rates across time. Thus, it is natural to expect that variability will increase over time.

For these reasons, a more realistic MRM allows both the intercept and time-trend to vary by individuals:

$$y_{ij}={\beta }_0+{\beta }_1{t}_{ij}+{\upsilon }_{0i}+{\upsilon }_{1i}{t}_{ij}+{\epsilon }_{ij}.$$

In this model,

• β₀ is the overall population intercept,

• β₁ is the overall population slope,

• υ_0i is the intercept deviation for subject i, and

• υ_1i is the slope deviation for subject i.

As before, ε_{i j} is an independent error term distributed normally with mean 0 and variance σ².

The assumption regarding the independence of the errors is one of conditional independence, that is, they are independent conditional on υ_0i and υ_1i. With two random individual-specific effects, the population distribution of intercept and slope deviations is assumed to be bivariate normal N(0, Σ_υ), with the random-effects variance-covariance matrix given by

$${\mathrm{\sum }}_{\upsilon }=\left[\begin{array}{ll}{\sigma }_{{\upsilon }_0}^2\hfill & {\sigma }_{{\upsilon }_0{\upsilon }_1}\hfill \\ {\sigma }_{{\upsilon }_0{\upsilon }_1}\hfill & {\sigma }_{{\upsilon }_1}^2\hfill \end{array}\right].$$

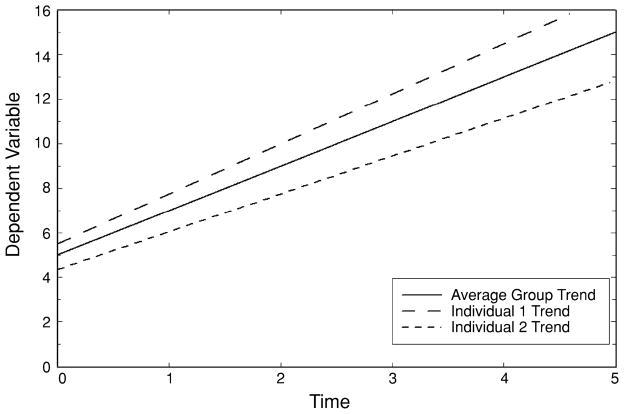
This model can be thought of as a personal trend or change model since it represents the measurements of y as a function of time, both at the individual υ_0i and υ_1i and population β₀ and β₁ levels. The intercept parameters indicate the starting point, and the slope parameters indicate the degree of change over time. The population intercept and slope parameters represent the overall (population) trend, while the individual parameters express how subjects deviate from the population trend. Figure 2 represents this model graphically.

Figure 2.

Random intercept and trend model.

The interested reader is referred to Hedeker & Gibbons (2006, chapters 4–7) for a more detailed coverage of various linear mixed-effects regression models.

Non-linear models

Reflecting the usefulness of mixed-effects modeling and the importance of categorical outcomes in many areas of research, generalization of mixed-effects models for categorical outcomes has been an active area of statistical research. For dichotomous response data, several approaches adopting either a logistic or probit regression model and various methods for incorporating and estimating the influence of the random effects have been developed (Conaway 1989, Gibbons 1981, Gibbons & Bock 1987, Goldstein 1991, Stiratelli et al. 1984, Wong & Mason 1985). We now describe a mixed-effects logistic regression model for the analysis of binary data. Extensions of this model for analysis of ordinal, nominal, and count data are described in detail by Hedeker & Gibbons (2006).

To formulate the logistic model, let p_i represent the probability of a positive outcome (i.e., Y_i = 1) for the ith individual. The probability of a negative outcome (i.e., Y_i = 0) is then 1 − p_i. Denote the set of covariates as x_i = (1, x_i1, …, x_{i p}), where β = (β₀, β₁, …, β_p) is a (p + 1) × 1 vector of corresponding regression coefficients. Then the logistic regression model is written as:

$$p_i=Pr(Y_i=1)=\frac{exp({\mathbf{x}}_i^{\prime }\mathbf{\beta })}{1+exp({\mathbf{x}}_i^{\prime }\mathbf{\beta })}$$

or

$$p_i=\frac{1}{1+exp(-{\mathbf{x}}_i^{\prime }\mathbf{\beta })}=\psi ({\mathbf{x}}_i^{\prime }\mathbf{\beta })$$

where ψ(.) is the logistic cumulative distribution function (cdf), namely 1

$$\psi (z)=\frac{1}{1+exp(-z)}.$$

This model can also be represented in terms of the log odds or logit of the probabilities; namely,

$$log\left[\frac{p_i}{1-p_i}\right]={\mathbf{x}}_i^{\prime }\mathbf{\beta }$$

The numerator in the logit is the probability of a 1 response, and the denominator equals the probability of a 0 response. The ratio of these probabilities is the odds of a 1 response, and the log of this ratio is the log odds, or logit, of a 1 response. Notice that the log odds is equal to 0 when the probability of a 1 response equals 0.5 (i.e., equal odds of a response in category 0 and 1), is negative when the probability is less than 0.5 (i.e., odds favoring a response in category 0), and is positive when the probability is greater than 0.5 (i.e., odds favoring a response in category 1).

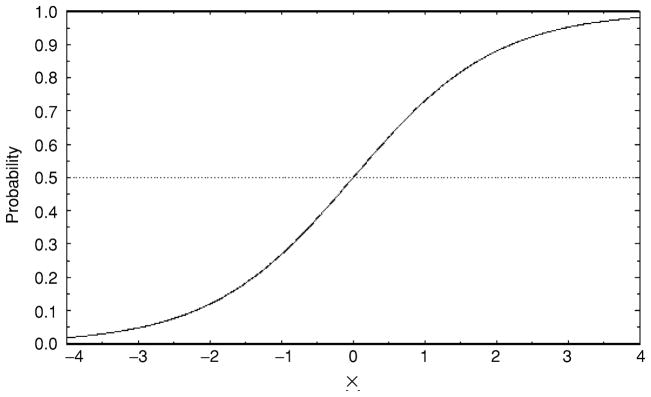
In logistic regression, the logit is called the link function because it maps the (0,1) range of probabilities unto the (−∞, ∞) range of linear predictors. The logit is linear in its parameter vector and so has many of the desirable properties of a linear regression model, albeit in terms of the logits. Note, however, that the logistic regression model is linear in terms of the logits and not the probabilities. In terms of the probabilities, the logistic regression model posits an s-shaped logistic relationship between the values of x and the probabilities as illustrated in Figure 3.

Figure 3.

Logistic relationship between x and the response probability.

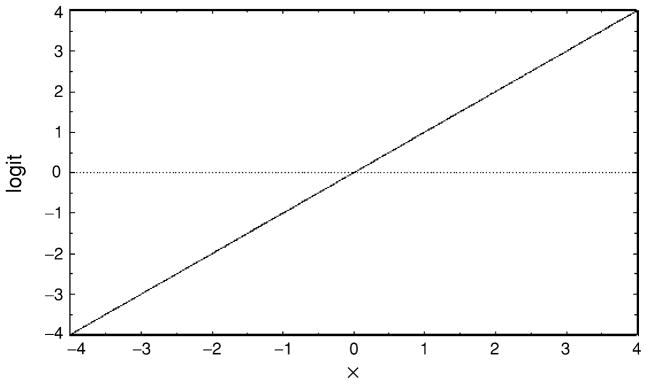
In contrast, the relationship between x and the logit is linear as shown in Figure 4.

Figure 4.

Linear relationship between x and the logit.

Since the model is linear in terms of the logits, interpretation of the parameters of the logistic regression model is in terms of the logits. Thus, the intercept β₀ is the log odds of a positive outcome for an individual with a set of covariates x_i = 0, and β_p measures the change in the log odds for a unit change in x_p holding all other covariates constant. Often the regression coefficients in logistic regression models are expressed in exponential form, namely exp(β_p). This transformation yields an odds ratio interpretation for the regressors, namely the ratio of the odds of a positive response for a unit change in x.

When the binary responses are clustered, for example repeatedly measured within individuals, or clustered within clinics, schools, or other social or ecological strata, the fixed-effects logistic regression model fails in its assumptions to accurately characterize the dependency in the data. Basically, the fixed-effects model assumes that the observations are independent, which they clearly are not when they are clustered within individuals. As described previously for the linear mixed-effects regression model, one solution to this problem is to generalize the model to the case of a combination of fixed (e.g., treatment) and random (e.g., time-trend coefficients) effects. The random effects allow the correlation between the clustered (e.g., repeated) measurements to be incorporated into the estimates of parameters, standard errors, interval estimates, and tests of hypotheses. One can conceptualize the random effects as representing subject-specific differences in the propensity to respond over time. Those subjects with higher response propensity will exhibit an increased probability of a positive response, conditional on their values of the fixed-effects (e.g., treatment group) included in the model.

To set the notation, let i denote the level-2 units (individuals) and let j denote the level-1 units (nested observations). Assume that there are i = 1, …, N level-2 units and j = 1, …, n_i level-1 units nested within each level-2 unit. The total number of level-1 observations across level-2 units is given by $n={\sum }_{i=1}^n{n}_i$. Let y_{i j} be the value of the dichotomous outcome variable, coded 0 or 1, associated with level-1 unit j nested within level-2 unit i. The logistic regression model is written in terms of the log odds (i.e., the logit) of the probability of a response, denoted p_{i j}. Considering first a random-intercept model, augmenting the logistic regression model with a single random effect yields:

$$log\left[\frac{p_{ij}}{1-p_{ij}}\right]={\mathbf{x}}_{ij}^{\prime }\mathbf{\beta }+{\upsilon }_i,$$

where x_{i j} is the (p + 1) × 1 covariate vector (includes a 1 for the intercept), β is the (p + 1)× 1 vector of unknown regression parameters, and υ is the random subject effect (one for each level-2 subject). These are assumed to be distributed in the population as $N(0,{\sigma }_{\upsilon }^2)$. For convenience and computational simplicity, in models for categorical outcomes the random effects are typically expressed in standardized form. For this, υ_i = σ_υθ_i and the model is given as:

$$log\left[\frac{p_i}{1-p_i}\right]={\mathbf{x}}_{ij}^{\prime }\mathbf{\beta }+{\sigma }_{\upsilon }{\theta }_i.$$

Notice that the random-effects variance term (i.e., the population standard deviation σ_υ is now explicitly included in the regression model). Thus, it and the regression coefficients are on the same scale, namely, in terms of the log-odds of a response. In terms of the underlying latent y, the model is written as:

$$log\left[\frac{p_i}{1-p_i}\right]={\mathbf{x}}_{ij}^{\prime }\mathbf{\beta }+{\sigma }_{\upsilon }{\theta }_i+{\epsilon }_{ij}.$$

This representation helps to explain why the regression coefficients from a mixed-effects logistic regression model do not typically agree with those obtained from a fixed-effects logistic regression model, or for that matter from a GEE logistic regression model which has regression coefficients that agree in scale with the fixed-effects model. In the mixed model, the conditional variance of the latent y given x equals ${\sigma }_{\upsilon }^2+{\sigma }_{\epsilon }^2$, whereas in the fixed-effects model this conditional variance equals only the latter term ${\sigma }_{\epsilon }^2$ (which equals either π²/3 or 1 depending on whether it is a logistic or probit regression model, respectively). As a result, equating the variances of the latent y under these two scenarios yields:

$${\mathit{\beta }}_{\mathit{M}}=\sqrt{\frac{{\mathbf{\sigma }}_{\mathbf{\upsilon }}^2+{\mathbf{\sigma }}_{\mathbf{\epsilon }}^2}{{\mathbf{\sigma }}_{\mathbf{\epsilon }}^2}}$$

where β_F and β_M represent the regression coefficients from the fixed-effects and (random-intercepts) mixed-effects models, respectively. In practice, Zeger et al. (1988) have found that (15/16)²π²/3 works better than π²/3 for ${\sigma }_{\epsilon }^2$ in equating results of logistic regression models.

Several authors have commented on the difference in scale and interpretation of the regression coefficients in mixed models and marginal models, like the fixed-effects and GEE models (Neuhaus 1991, Zeger et al. 1988). Regression estimates from the mixed model have been termed “subject specific” to reinforce the notion that they are conditional estimates, conditional on the random (subject) effect. Thus, they represent the effect of a regressor on the outcome controlling for or holding constant the value of the random subject effect. Alternatively, the estimates from the fixed-effects and GEE models are “marginal” or “population-averaged” estimates that indicate the effect of a regressor averaging over the population of subjects. This difference of scale and interpretation only occurs for nonlinear regression models like the logistic regression model. For the linear model, this difference does not exist.

The model can be easily extended to include multiple random effects. For this, denote z_{i j} as the r × 1 vector of random-effect variables (a column of ones is usually included for the random intercept). The vector of random effects υ_i is assumed to follow a multivariate normal distribution with mean vector 0 and variance-covariance matrix Σ_υ. To standardize the multiple random effects υ_i = Tθ_i where TT′ = Σ_υ is the Cholesky decomposition of Σ_υ. The model is now written as:

$$log\left[\frac{p_{ij}}{1-p_{ij}}\right]={\mathbf{x}}_{\mathbf{ij}}^{\prime }\mathbf{\beta }+{\mathbf{z}}_{\mathbf{ij}}^{\prime }\mathbf{T}{\mathbf{\theta }}_{\mathbf{i}}.$$

As a result of the transformation, the Cholesky factor T is usually estimated instead of the variance-covariance matrix Σ_υ. As the Cholesky factor is essentially the matrix square-root of the variance-covariance matrix, this allows more stable estimation of near-zero variance terms.

Two-level versus three-level models

Traditionally, mixed-effects regression models, both linear and nonlinear, are two-level models; for example, subjects repeatedly measured over time. Gibbons & Hedeker (1997) generalized the two-level mixed-effects logistic regression model to the case of three-level data (e.g., subjects repeatedly measured over time and clustered within clinics), and Hedeker & Gibbons (2006) reviewed a wide variety of linear and nonlinear three-level mixed-effects regression models and their application.

The amount of dependency in the data that is observable due to the clustering of the data is measured by the intraclass correlation. When the intraclass correlation equals 0, there is no association among subjects from the same cluster and analysis which ignores the clustering of the data is valid. For certain variables, however, intraclass correlation levels have been observed between 5% and 12% for data from spouse pairs and between 0.05% and 0.85% for data clustered by counties. As the intraclass correlation increases, the amount of independent information from the data decreases, inflating the Type I error rate of an analysis that ignores this correlation. Thus, statistical analysis that treats all subjects as independent observations may yield tests of significance that are too liberal.

The mixed model can be augmented to handle the clustering of data within centers. For this, consider a three-level model for the measurement y made on occasion k for subject j within center i. Relative to the previous two-level models, an additional random center effect, denoted γ_i, is included. This term indicates the influence that the center is having on the response of the individual. We assume that the distribution of the center effects is normal with mean 0 and variance ${\sigma }_{\gamma }^2$. To the degree that clustering of individuals within centers influences the individual outcomes, the center effects γ_i deviate from zero, and the population variance associated with these effects ${\sigma }_{\gamma }^2$ increases in value. Conversely, when the clustering of individuals within centers is having little influence on the individual outcomes, the center effects γ_i will all be near zero, and the population variance ${\sigma }_{\gamma }^2$ will approach zero. Empirical Bayes estimation can be used for the center effects γ_i, with marginal maximum likelihood estimation of the population variance term ${\sigma }_{\gamma }^2$.

Treatment of the center effects as a random term in the model means that the specific centers used in the study are considered to be a representative sample from a larger population of potential centers. Conversely, if interest is only in making inferences about the specific centers of a dataset (e.g., is there a difference between center A and center B?), the center could then be regarded as a “fixed” and not a “random” effect in the model. The random-effects approach is advised when there is interest in assessing the overall effect that any potential center may have on the data and, thus, in determining the degree of variability that the center accounts for in the data. This coincides with the manner in which the center is often conceptualized, that is, the center was drawn from a population of potential centers, and the 8 or 12 centers used in the study are not the population itself.

In addition to the random center effect, center-level covariates can be included in the model to assess the influence of, say, center size on the individual responses. Interactions between center-level, individual-level, and occasion-level covariates can also be included in the model. For example, the interaction of center size (center level) by treatment group (individual level) by time (occasion level) can be included in the model to determine whether, say, treated subjects from small centers improve over time more dramatically than treated subjects from large centers. In this way, the model provides a useful method for examining and teasing out potential center-related effects.

Regarding parameter estimates, for continuous and normally distributed outcomes, Hedeker et al. (1994) noted that the fixed effects estimates are not greatly affected by the choice of model. However, the estimates of the standard errors, which determine the significance of these parameter estimates, are influenced by the choice of model. In general, when a source of variability is present but ignored by the statistical model, the standard errors will be underestimated. Underestimation of standard errors results since the statistical model assumes that, conditional on the terms in the model, the observations are independent. However, when systematic variance is present but ignored by the model, the observations are not independent, and the amount of independent information available in parameter estimation is erroneously inflated.

Finally, when dealing with multilevel data, the number of levels of data must be considered. Often, pooling higher-order levels is determined prior to the analysis for pragmatic or conceptual reasons; at other times, the decision can be empirically tested. From the example, one could empirically argue that three-level analysis is unnecessary since the variance attributable to nesting of individuals within centers is not significant, so there is justification for pooling this additional level of the data. From a design perspective, on the other hand, there may be reason for including the center effect regardless of its statistical significance; for example, if centers were the unit of assignment in the randomization of treatment levels, one could argue that the random center term must remain in the model regardless of significance. When the variance attributable to a higher-order level is observed to be very small and nonsignificant and the sample is of moderate size, the parameter estimates and standard errors will not differ greatly whether or not the higher-order level is included in the model.

In the nonlinear case, the three-level generalization of the traditional two-level model is conceptually quite similar to that for linear mixed-effects regression models. Computationally, however, likelihood evaluation is far more complicated because the number of random effects is increased and therefore the dimensionality of the integration increases as well. Unlike the linear mixed-model, where the integrals associated with the random effect distributions do not play a role in performing maximum likelihood estimation in the marginal distribution, there is no simplification for nonlinear models such as mixed-effects binary or ordinal logistic regression, mixed-effects multinomial logistic regression, or mixed-effects Poisson regression. Here we must either evaluate the likelihood numerically (e.g., adaptive quadrature) or via simulation (Markov Chain Monte Carlo; MCMC). The interested reader is referred to Hedeker & Gibbons (2006) for detailed coverage of the technical aspects of linear and nonlinear mixed-effects regression models.

Generalized Estimating Equation Models

During the 1980s, alongside the development of mixed-effects regression models for incomplete longitudinal data, the generalized estimating equation (GEE) models were developed (Liang & Zeger 1986 and Zeger & Liang 1986). Essentially, GEE models extend generalized linear models (GLMs) to the case of correlated data. Thus, this class of models has become very popular, especially for analysis of categorical and count outcomes, although they can be used for continuous outcomes as well. One difference between GEE models and MRMs is that GEE models are based on quasi-likelihood estimation, and so the full likelihood of the data is not specified. GEE models are termed marginal models, and they model the regression of y on x and the within-subject dependency (i.e., the association parameters) separately. The term “marginal” in this context indicates that the model for the mean response depends only on the covariates of interest and not on any random effects or previous responses. In terms of missing data, GEE assumes that the missing data are missing completely at random (MCAR) as opposed to MAR, which is assumed by the models employing full-likelihood estimation.

Conceptually, GEE reproduces the marginal means of the observed data, even if some of those means have limited information because of subject dropout. Standard errors are adjusted (i.e., inflated) to accommodate the reduced amount of independent information produced by the correlation of the repeated observations over time (or within clusters). By contrast, mixed-effects models use the available data from all subjects to model temporal response patterns that would have been observed had the subjects all been measured to the end of the study. Because of this, estimated mean responses at the end of the study can be quite different for GEE versus MRM if the future observations are related to the measurements that were made during the course of the study. If the available measurements are not related to the missing measurements (e.g., following dropout), GEE and MRM will produce quite similar estimates. This is the fundamental difference between GEE and MRM; that is, the assumption that the missing data are dependent on the observed responses for a given subject during that subject’s participation in the study. It is hard to imagine that a subject’s responses that would have been obtained following dropout would be independent of their observed responses during the study. This leads to a preference for full-likelihood approaches over quasi- or partial-likelihood approaches, and MRM over GEE, at least for longitudinal data. There is certainly less of an argument for a preference for data that are only clustered (e.g., children nested within classrooms), in which case advantages of MAR over MCAR are more difficult to justify.

A basic feature of GEE models is that the joint distribution of a subject’s response vector y_i does not need to be specified. Instead, it is only the marginal distribution of y_ij at each time point that needs to be specified. To clarify this further, suppose that there are two time points and suppose that we are dealing with a continuous normal outcome. GEE would only require us to assume that the distribution of y_i1 and y_i2 are two univariate normals, rather than assuming that y_i1 and y_i2 form a (joint) bivariate normal distribution. Thus, GEE avoids the need for multivariate distributions by only assuming a functional form for the marginal distribution at each time point.

METHODS TO BE AVOIDED

Unfortunately, despite progress in the use of longitudinal designs in research studies, analysis of the resulting longitudinal data has not always been commensurate with the increased value of the data. Several approaches that are of historical interest only remain in routine practice today, and methods that unnecessarily reduce the longitudinal nature of the data into a cross-sectional summary unfortunately also remain in use despite enormous statistical progress in this area.

One of the worst examples of loss of valuable statistical information is “endpoint” analysis. The idea here is that although high-quality longitudinal data may be available, if they are used at all, it is only to fill in the blanks left by patients who have discontinued the study.

Completer Analysis

In some cases a “completer analysis” is performed in which only those patients who completed the study are the focus of the analysis. Of course, in the presence of missing data produced by patients who discontinue the study, the sample that is randomized may be quite different from the sample that is analyzed. If patients who complete the study are more compliant than those who do not, valuable information regarding treatment-related effects may be obscured. Completer analyses will generally lose the critically important advantages afforded by randomization.

Last Observation Carried Forward

A second approach that remains in reasonably widespread use is to impute the measurement at the end of the study using the last available measurement obtained from the subject during the study. This approach is termed “last observation carried forward” (LOCF). Here we assume that once subjects drop out of a study, their level of response would remain unchanged. Furthermore, no distinction in the analysis is made between those patients who actually had a valid measurement at the end of the study and those subjects for whom the study endpoint was imputed based on an earlier available measurement. Although it has been suggested that the LOCF approach is conservative and that is why it continues to be used by the U.S. Food and Drug Administration for the approval of new drugs, this is clearly not the case (Lavori et al. 2008, Molenberghs et al. 2004). As noted by Lavori et al. (2008, p. 789), “The most serious effect of LOCF is that it lulls the designer into a false sense of security about the need to resolve complex issues of nonadherence, as well as the consequences of unrestrained missingness for precision and bias. This ‘moral hazard’ has led investigators to underdesign studies in the mistaken belief that LOCF cures all.”

Despite enormous progress in the development of new and statistically more rigorous methods for analysis of longitudinal data, older and far less general methods remain in use. A historical foundation is presented by Hedeker & Gibbons (2006), who review these methods in detail.

Repeated Measures ANOVA

The traditional mixed-model ANOVA or so-called repeated-measures ANOVA was essentially a random intercept model that assumed that subjects could only deviate from the overall mean response pattern by a constant that was equivalent over time. A more reasonable view is that the subject-specific deviation is both in terms of the baseline response (i.e., intercept) and in terms of the rate of change over time (i.e., slope or set of trend parameters). This more general structure could not be accommodated by the repeated measures ANOVA. The random intercept model assumption leads to a compound-symmetric variance-covariance matrix for the repeated measurements in which the variances and covariances of the repeated measurements are constant over time. In general, we find that variances increase over time and covariances decrease as time-points become more separated in time. Finally, based on the use of least-squares estimation, the repeated measures ANOVA breaks down for unbalanced designs, such as those in which the sample size decreases over time due to subject discontinuation. Based on these limitations, the repeated measures ANOVA and related approaches should no longer be used for analysis of longitudinal data.

Multivariate Growth Curve Models

An improvement over the traditional repeated measures ANOVA was the multivariate growth curve model (Bock 1975, Potthoff & Roy 1964). The primary advantage of the multivariate analysis of variance (MANOVA) approach versus the ANOVA approach is that the MANOVA assumes a general form for the correlation of repeated measurements over time, whereas the ANOVA assumes the much more restrictive compound-symmetric form. The disadvantage of the MANOVA model is that it requires complete data. Subjects with incomplete data must be removed from the analysis, leading to potential bias. In addition, both MANOVA and ANOVA models focus on comparison of group means and provide no information regarding subject-specific growth curves. Finally, both ANOVA and MANOVA models require that the time-points are fixed across subjects (either evenly or unevenly spaced) and are treated as a classification variable in the ANOVA or MANOVA model. This precludes analysis of unbalanced designs in which different subjects are measured on different occasions. Finally, the MANOVA approach precludes use of time-varying covariates that are often essential to modeling dynamic relationships between predictors and outcomes.

SAMPLE SIZE DETERMINATION

Despite the now widespread use of longitudinal designs in behavioral research, surprisingly little statistical research has been conducted on sample size determination for longitudinal studies. Hedeker et al. (1999) developed sample size formulas for two-level models, and more recently, Roy et al. (2007) developed a general approach to sample size determination for three-level models. All of this work is for linear mixed effects models, though methods are also emerging for nonlinear mixed models (Dang et al. 2008). Based on the work of Roy et al. (2007) and Bhaumik et al. (2009), we illustrate some of the interesting features of sample size determination for three-level mixed effects regression models using a typical psychiatric application and computed using the RMASS Web-based application (www.healthstats.org).

Bhaumik et al. (2009) consider three-level data from the now classic National Institute of Mental Health schizophrenia collaborative study, which was one of the last large-scale multicenter studies to randomize schizophrenic patients to placebo. The study consisted of nine centers and seven repeated measurements over the course of six weeks. Bhaumik et al. (2009) fitted a three-level linear mixed effects regression model to the data from two arms of the study (placebo and chlorpromazine) and used the estimated model parameters and random effect variance estimates to determine sample size for a wide variety of future studies. In the following, we summarize a few of these results of interest.

For subject-level randomization, power of 95%, attrition of 5% per week, and E S = 0.5 SD units at the end of the study, with six centers, n = 34 subjects per center are required for a total of 204 subjects. Decreasing power to 80% decreases the number of subjects per center to n = 19 or a total of 114 subjects. Note that for subject-level randomization, if we double the number of centers from 6 to 12, one-half of the number of subjects per center are required (e.g., n = 17 for power of 95%). This result is expected because when using subject-level randomization, the sample size formula does not involve center-level random effect variances. This is not true if we were to randomize centers to different interventions. With cluster randomization, power of 80% is achieved for a study with six centers and n = 47 subjects per center; a total of 282 subjects as compared to 114 subjects for subject-level randomization. Increasing the number of centers to 12 decreases the number of subjects per center to n = 14, or a total of only 168 subjects. Under cluster randomization, there is a substantial tradeoff between number of centers and number of subjects per center, which can affect the total number of subjects required. If we were to require power of 95%, then a minimum of eight centers are required. With eight centers, n = 114 subjects per center are required, or a total of 912 subjects. This is over four times as many subjects as are required for subject-level randomization (n = 204). However, increasing the number of centers to 12 decreases the number of subjects per center to 35 (420 total), and increasing the number of centers to 50 decreases the total sample size to n = 250 (i.e., n = 5 per center). As can be seen, cluster randomization imposes a substantial tradeoff between numbers of centers and total number of subjects.

Finally, decreasing the ES to 0.3 SD units further increases sample size requirements as expected. Under subject-level randomization, power of 80% is achieved for any combination of centers and number of subjects within centers that totals to n = 320, and for 95% power, a total of n = 560 subjects are required. For cluster randomization, a minimum of 11 centers are required for power of 80% (n = 290 per center) and a minimum of 19 centers for power of 95% (n = 355 per center). More conservatively, assuming 25 centers, power of 80% is achieved for n = 21 per center, and power of 95% is achieved for n = 73 per center. As such, cluster-level randomization increases the total number of subjects from 320 for subject-level randomization to a total of 525 subjects, assuming that 25 centers are available. For the same 25 centers, requiring power of 95% more than triples the total sample size.

Bhaumik and colleagues present the following guidelines:

While it should be clear that sample size determination is study-specific, it is possible to provide some general guidelines. For example, consider a study involving 5 measurement occasions (e.g., baseline and 4 weekly measurements during the active treatment/intervention phase of the study), and a two-group comparison (e.g., drug versus placebo). For subject-level randomization with no variation in impact as a function of center, the total number of centers provides a negligible effect on statistical power and sample size. As such, we can compute the total number of subjects that are required for a given ES at the final time-point, under the assumption of a linear time by treatment interaction. For example, assuming subject-level randomization, five time-points, power of 80%, a Type I error rate of 5% and no attrition, to detect a one-half standard deviation unit difference at the end of the study requires a total sample size of 90 subjects or 45 per treatment arm. To detect a one-third standard deviation unit difference at the end of the study assuming all of the other conditions remained the same, a total of 200 subjects or 100 subjects per treatment arm are required (e.g., 40 subjects in each of 5 centers or 20 subjects in each of 10 centers). Adding attrition of 5% per wave increases the required sample size by about 15% and adding attrition of 10% per wave increases the required sample size by about 30% relative to no attrition.

For cluster-level randomization, the results are more complicated. Assuming the same conditions as above, and 10 centers, to detect a one-half standard deviation unit difference at the end of the study would require a total sample size of 200 subjects (20 per center) or 100 per treatment arm. To detect a one-third standard deviation unit difference at the end of the study assuming all of the other conditions remained the same, would require a minimum of 14 centers, regardless of the number of subjects per center. Conservatively, if we increase the number of centers to 20, a total of 560 subjects (28 per center) or 280 subjects per treatment arm are required. Similar to subject-level randomization, adding attrition of 5% per wave increases the required sample size by about 15% and adding attrition of 10% per wave increases the required sample size by about 30% relative to no attrition. (Bhaumik et al. 2009, pp. 769–770)

RECENT ADVANCES IN GENERALIZED MIXED-EFFECTS REGRESSION MODELS

In the following sections, we consider several recent advances in the analysis of linear and nonlinear mixed-effects regression models. The level of statistical presentation is at a higher level than in previous sections owing to the increased complexity of these newer methodologies.

Three-Level Models

In a previous section, we provided a general overview of three-level models. In the following, we review some of the more specific statistical details corresponding to linear and nonlinear three-level models.

Sampling design

Let y_{i j} denote a n_{i j} × 1 vector of outcomes with typical element y_{i j k}, where i denotes the level-3 units, j denotes the level-2 units nested within the i-th level-3 unit, and k denotes the level-1 units nested within i j. Assume further that there are N level-3 units so that i = 1, 2, …, N. Within a typical level-3 unit there are n_i level-2 units, j = 1, 2, …, n_i, and nested within i j there are n_{i j} level-1 units, so that k = 1, 2, …, n_{i j}. There are, therefore, ${\sum }_{i=1}^N{n}_i$ level-2 units and ${\sum }_{i=1}^N{\sum }_{j=1}^{n_i}{n}_{ij}$ level-1 units.

Linear Models

Let

$$y_{\mathit{ijk}}={{\mathbf{x}}^{\prime }}_{\mathit{ijk}}\mathbf{\beta }+{{\mathbf{z}}^{\prime }}_{(3)\mathit{ijk}}{\mathbf{v}}_i+{{\mathbf{z}}^{\prime }}_{(2)\mathit{ijk}}{\mathbf{u}}_{ij}+e_{\mathit{ijk}},$$

where β is an (m × 1) vector of regression coefficients, and where v_i, u_{i j}, and e_{i j k} denote level-3, level-2, and level-1 random effects, respectively. We assume that v₁, v₁, …, v_N are i.i.d. N(0, ψ), independent of u₁₁, u₁₂, …, u_Nni which are i.i.d. N(0, Φ). We further assume that the v_i and the u_{i j} effects are independent of e₁₁₁, e₁₁₂, …, e_{Nnini j} which are i.i.d. N(0, σ²).

The set of regression equations, k = 1, 2, …, n_{i j} can be written as

$$\begin{array}{l}{\mathbf{y}}_{ij}={\mathbf{X}}_{ij}\mathbf{\beta }+{\mathbf{Z}}_{(3)ij}{\mathbf{v}}_i+{\mathbf{Z}}_{(2)ij}{\mathbf{u}}_{ij}+{\mathbf{e}}_{ij},\\ j=1,2,\dots ,n_i,\end{array}$$

where y_{i j k}, x′_{i j k}, z′ _{(3)i j k}, z′ _{(2)i j k} and e _{i j} are typical rows of y_{i j}, X_{i j}, Z_{(3)i j}, Z_{(2)i j} and e_{i j} and where X_{i j}, Z_{(3)i j}, and Z_{(2)i j} are the design matrices for the predictors, random level-3, and random level-2 effects, respectively.

In turn, the set of regression equations is

$${\mathbf{y}}_i^{\ast }={\mathbf{X}}_i\mathbf{\beta }+{{\mathbf{Z}}_i}^{\ast }{\mathbf{v}}_i^{\ast }+{\mathbf{e}}_i^{\ast }$$

where

$$\begin{array}{c}{\mathbf{y}}_i^{\ast }=({\mathbf{y}}_{1i},{\mathbf{y}}_{2i},\dots ,{{\mathbf{y}}^{\prime }}_{{in}_i}),\\ {\mathbf{X}}_i=\left(\begin{array}{c}{X}_{i1}\\ X_{i1}\\ ⋮\\ X_{{in}_i}\end{array}\right),\\ {\mathbf{Z}}_i^{\ast }=\left(\begin{array}{ccccc}{\mathbf{Z}}_{(3)i1}& {\mathbf{Z}}_{(3)i1}& \mathbf{0}& \cdots & \mathbf{0}\\ {\mathbf{Z}}_{(3)i1}& \mathbf{0}& {\mathbf{Z}}_{(2)i2}& \cdots & \mathbf{0}\\ ⋮& ⋮& ⋮& \ddots & \mathbf{0}\\ {\mathbf{Z}}_{(3){in}_i}& \mathbf{0}& \mathbf{0}& \cdots & {\mathbf{Z}}_{(2){in}_i}\end{array}\right),\\ {\mathbf{v}}_i^{\ast }={({\mathbf{v}}_i,{\mathbf{u}}_{i1},{\mathbf{u}}_{i2},\dots ,{\mathbf{u}}_{{in}_i})}^{\prime },\end{array}$$

and

$${\mathbf{e}}_i^{\ast }={({\mathbf{e}}_i,{\mathbf{e}}_{i1},{\mathbf{e}}_{i2},\dots ,{\mathbf{e}}_{{in}_i})}^{\prime }.$$

From the distributional assumptions imposed on v_i, u_{i j} and e_{i j k}, it follows that

$${\mathbf{y}}_i\sim N({\mathbf{\mu }}_i,{\mathrm{\sum }}_i)$$

where μ_i = X_i β (the fixed part of the model) and

$${\mathrm{\sum }}_i={\mathbf{Z}}_i^{\ast }cov({\mathbf{v}}_i^{\ast }){{\mathbf{Z}}_i^{\ast }}^{\prime }+{\sigma }^{2}I$$

where

$$cov({\mathbf{v}}_i^{\ast })=\left(\begin{array}{cccc}\psi & 0& \cdots & 0\\ 0& \mathrm{\Phi }& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & \mathrm{\Phi }\end{array}\right).$$

The unknown parameters are the elements of the vector β of fixed regression coefficient and the nonduplicated elements of the variance component matrices ψ and Φ and the level-1 error variance σ². The log-likelihood function of y₁, y₂, …, y_N is

$$lnL=-\frac{1}{2}\sum _{i=1}^N\{n_{i}ln2\pi +ln\mid {\mathbf{\sum }}_i\mid +tr{\mathbf{\sum }}_i^{-1}({\mathbf{y}}_i-{\mathbf{\mu }}_i){({\mathbf{y}}_i-{\mathbf{\mu }}_i)}^{\prime }\}.$$

Nonlinear Models

A multilevel model with a nonnormal outcome variable is transformed to a linear model by using a link function that defines the relationship between the dependent variable η_{i j k} of the linear model and the mean μ_{i j k} of the distribution selected. More specifically, the linear model of a multilevel generalized linear model is given by

$${\eta }_{\mathit{ijk}}={\mathbf{x}}_{\mathit{ijk}}^{\prime }\mathbf{\beta }+{\mathbf{z}}_{(2)\mathit{ijk}}^{\prime }{\mathbf{u}}_{ij}+{\mathbf{z}}_{(3)\mathit{ijk}}^{\prime }{\mathbf{v}}_i,$$

where x_{i j k} is a p × 1 vector of predictors and z_{(2)i j k} is a q × 1 design vector associated with the level-2 random effects u_{i j}. Likewise, z_{(3)i j k} is a r × 1 design vector associated with the level-3 random effects v_i. Typically, the elements of z_{(3)i j k} and z_{(2)i j k} are subsets of the elements of x_{i j k}.

It is further assumed that the level-3 and level-2 random effect vectors are uncorrelated and also that v_i ~ N(0, ψ) and that u_{i j} ~ N(0, Φ).

Quadrature is a numeric method for evaluating multidimensional integrals. For mixed-effect models with count and categorical outcomes, the log-likelihood function is expressed as the sum of the logarithm of integrals, where the summation is over higher-level units, and the dimensionality of the integrals equals the number of random effects.

Quadrature entails the approximation of the definite integral of a function, usually stated as a weighted sum of function values at specified points within the domain of integration. Adaptive quadrature generally requires fewer points and weights to yield estimates of the model parameters and standard errors that are as accurate as would be obtained with more points and weights in nonadaptive quadrature. The reason for that is that the adaptive quadrature procedure uses the empirical Bayes means and covariances, updated at each iteration to essentially shift and scale the quadrature locations of each higher-level unit in order to place them under the peak of the corresponding integral.

A brief description of quadrature follows below, assuming a level-2 mixed effects model. Using the rules for joint and conditional distributions, it follows that

$$f({\mathbf{y}}_i,{\mathbf{v}}_i)=f({\mathbf{y}}_i\mid {\mathbf{v}}_i)f({\mathbf{v}}_i),$$

and that the marginal distribution of y_i can be obtained as the solution to the multidimensional integral

$$f({\mathbf{y}}_i)=\underset{v_1}{\int }\cdots \underset{v_r}{\int }f({\mathbf{y}}_i\mid {\mathbf{v}}_i)f(\mathbf{v})d{v}_1\dots .d{v}_r.$$

Since it is assumed that v_i ~ N(0, Φ), it follows, for example, that

$$f({\mathbf{v}}_i)={(2\pi )}^{-r/2}{\mid \mathbf{\Phi }\mid }^{-1/2}exp\left[-\frac{1}{2}{\mathbf{v}}_i^{\prime }{\mathbf{\Phi }}^{-1}{\mathbf{v}}_i\right].$$

In general, a closed-form solution to this integral does not exist. To evaluate integrals of the type described above, we use a direct implementation of Gauss-Hermite quadrature (see, e.g., Krommer & Ueberhuber 1994, section 4.2.6, and Stroud & Sechrest 1966, section 1). With this rule, an integral of the form

$$I(t)=\int f(t)exp[-t^2]dt$$

is approximated by the sum

$$I(t)\approx \sum _{u=1}^Q{w}_{u}f(z_u),$$

where w_u and z_u are weights and nodes of the Hermite polynomial of degree Q. A Q-point adaptive quadrature rule is a quadrature rule constructed to yield an exact result for polynomials of degree 2Q − 1, by a suitable choice of the n points x_i and n weights w_i.

Estimates of the variance components of the random effects and estimates of the fixed parameters are obtained by iteratively solving the equations

$$\frac{\partial }{\partial {\gamma }_k}lnf({\mathbf{y}}_i)=0,$$

where γ_k is a typical element of the vector γ of unknown parameters φ₁₁, φ₂₁, …, φ_rr and β₁, β₂, …, β_p.

Clinic	Patient	y1	y2	y3	x1	x2
1	1	0	2	1	22	−1
1	2	1	3	−9	30	1
1	3	−9	2	1	26	−1
2	1	0	1	1	23	−1
2	2	0	2	0	29	1
2	3	0	1	1	26	1
2	4	1	2	1	33	−1

To create a data set that can be analyzed within a level-3 linear model framework, dummy variables are created for each response variable in the data set. For the example above, this translates to three dummy-coded variables: d_k = 1 if y_k is measured, k = 1, 2, 3, and 0 otherwise. Using these dummy variables, we construct a new data set, shown below for clinic number 1, patients 1, 2, and 3.

Clinic	Patient	y	d1	d2	d3	x1*d1	x1*d2	x1*d3	x2*d1	x2*d2	x2*d3
1	1	0	1	0	0	22	0	0	−1	0	0
1	1	2	0	1	0	0	22	0	0	−1	0
1	1	1	0	0	1	0	0	22	0	0	−1
1	2	1	1	0	0	30	0	0	1	0	0
1	2	3	0	1	0	0	30	0	0	1	0
1	3	2	0	1	0	0	26	0	0	−1	0
1	3	1	0	0	1	0	0	26	0	0	−1

Multivariate Mixed Models

In mental health research, researchers often have data sets containing more than one response variable. A typical example is counts of inpatient (y₁), outpatient (y₂), and emergency room (y₃) visits for mental health care. There is thus a need to fit multivariate response variables to a linear mixed-effects model. It turns out that, with the use of dummy variables, a multivariate level-2 model can be fitted to the data using a level-3 model with a single response variable and no level-1 random effects.

For the variables y₁, y₂, and y₃ considered above, the following represents a typical data set, where x₁ = depressive severity and x₂ = type of insurance coverage (coded 1 for public and −1 for private). Missing values are coded −9.

In the level-3 framework, y is the response variable, d1, d2, d3, x1^*d1, …., x2^*d3 are typical rows of the fixed-effects design matrix X. The fixed-effects part consists of intercept coefficients (corresponding to d1, d2, and d3), slope coefficients for depressive severity (corresponding to x1^*d1, x1^*d2, and x1^*d3), and insurance coverage coefficients (corresponding to x2^*d1, x2^*d2, and x2^*d3). Alternatively, one can use depression and insurance as level-2 covariates, in which case the data set (shown for Clinic 1, Patient 1 only) has the form:

Clinic	Patient	y	d1	d2	d3	x1	x2
1	1	0	1	0	0	22	−1
1	1	2	1	1	0	22	−1
1	1	1	1	0	1	22	−1

The difference between the two approaches is that in the first approach, different slopes are assumed for the three service utilization outcome variables, whereas we assume equal slopes for depression and equal slopes for insurance type in the second approach.

Four-Level Models

Consider a clinical study designed to measure the impact of hormone therapy on memory and cognition in elderly women. Suppose that 50 hospitals (level-4 units) participated in the study. For each of the hospitals, data are available for five types of hormone treatments (level-3 units) obtained from the female patients (level-2 units) who were tested twice a year for a period of up to six years (level-1 units).

Let y_{i j kl} denote a cognition score at occasion l for patient k on treatment j at hospital i.

A typical mixed-effects model for data of this type is

$$y_{\mathit{ijkl}}={\beta }_0+{\beta }_1{x}_{1,\mathit{ijkl}}+{\beta }_2{x}_{2,\mathit{ijkl}}+\cdots +{\beta }_{r}xr{,}_{\mathit{ijkl}}+w_i+v_{ij}+u_{\mathit{ijk}}+e_{\mathit{ijkl}},$$

where w_i denotes a level-4 (hospital-level) variance component; v_{i j}, a level-3 (treatment-level) variance component; u_{i j k}, a level-2 (patient-level) variance component; and e _{i j kl}, the level-1 measurement error. It is further assumed that there are r covariates x₁, x₂, …, x_r (such as age, weight, and percentage fat) that may influence the cognition score.

The set of regression equations can be rewritten as

$${\mathbf{y}}_{\mathit{ijkl}}={\mathbf{X}}_{\mathit{ikl}}\mathbf{\beta }+{\mathbf{Z}}_{(3)\mathit{ikl}}{\mathbf{v}}_i^{\ast }+{\mathbf{Z}}_{(2)\mathit{ikl}}{\mathbf{v}}_{ik}+{\mathbf{Z}}_{(1)\mathit{ikl}}{\mathbf{e}}_{\mathit{ikl}},$$

where

$$\begin{array}{l}{\mathbf{X}}_{\mathit{ikl}}=\left[\begin{array}{cccc}1& x_{1,i1kl}& \dots & x_{r,i1kl}\\ 1& x_{1,i2kl}& \dots & x_{r,i2kl}\\ 1& x_{1,i3kl}& \dots & x_{r,i3kl}\\ 1& x_{1,i4kl}& \dots & x_{r,i4kl}\\ 1& x_{1,i5kl}& \dots & x_{r,i5kl}\end{array}\right]·\left[\begin{array}{c}{\beta }_0\\ {\beta }_1\\ ⋮\\ {\beta }_r\end{array}\right],\\ {\mathbf{Z}}_{(3)\mathit{ikl}}{\mathbf{v}}_i^{\ast }=\left[\begin{array}{cccccc}1& 1& 0& 0& 0& 0\\ 1& 0& 1& 0& 0& 0\\ 1& 0& 0& 1& 0& 0\\ 1& 0& 0& 0& 1& 0\\ 1& 0& 0& 0& 0& 1\end{array}\right]·\left[\begin{array}{c}{w}_i\\ v_{i1}\\ v_{i2}\\ v_{i3}\\ v_{i4}\\ v_{i5}\end{array}\right],\\ {\mathbf{Z}}_{(2)\mathit{ikl}}{\mathbf{v}}_{ik}=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right]·\left[\begin{array}{c}{v}_{i1k}\\ v_{i2k}\\ v_{i3k}\\ v_{i4k}\\ v_{i5k}\end{array}\right].\end{array}$$

We note that, except for column 1 of the design matrix Z₍₃₎, the remaining columns correspond to dummy variables T ₁, T ₂, …, T ₅, where T_j = 1 if treatment number is j and 0 otherwise. If only treatments 2, 3, and 5 are available at hospital i, the design matrices X_ikl, Z_(3)ikl, and Z_(2)ikl are defined as above, but with rows 1 and 4 removed. For example,

$${\mathbf{Z}}_{(3)\mathit{ikl}}=\left[\begin{array}{cccccc}1& 0& 1& 0& 0& 0\\ 1& 0& 0& 1& 0& 0\\ 1& 0& 0& 0& 0& 1\end{array}\right].$$

For the level-3 model to be equivalent to the level-4 model, the following patterned covariance specifications are required:

$$\left[\begin{array}{cccccc}1& & & & & \\ 0& 3& & & & \\ 0& 0& 3& & & \\ 0& 0& 0& 3& & \\ 0& 0& 0& 0& 3& \\ 0& 0& 0& 0& 0& 3\end{array}\right].$$

The advantage of this presentation is that one can allow for cross-level correlation(s). For example, if there is reason to believe that there are differences in the way patients react to the treatments due to some hospital effect, then we may want to assume that cov(w_i, v_{i j}) ≠ 0. These covariance terms may be included in the model by using the following covariance pattern:

$$\left[\begin{array}{cccccc}1& & & & & \\ 2& 3& & & & \\ 2& 0& 3& & & \\ 2& 0& 0& 3& & \\ 2& 0& 0& 0& 3& \\ 2& 0& 0& 0& 0& 3\end{array}\right].$$

Design Weights

Under the assumption that the sampling weights at a specific level are independent of the random effects at that level, Pfeffermann et al. (1998) adopted the following procedure. Consider the case of a two-level model. Denote by w_i the weight attached to the i-th level-2 unit and by w _j|i the weight attached to the j-th level-1 unit within the i-th level-2 unit such that

$$\sum _j{w}_{j\mid i}=n_i,\sum _i{w}_i=I$$

where I is the total number of level-2 units and N = Σ_i n_i the total number of level-1 units. That is, the lower-level weights within each immediate higher-level unit are scaled to have a mean of unity, and likewise for higher levels. For each level-1 unit, we now form the final, or composite, weight

$$\begin{array}{l}{w}_{ji}={Nw}_{j\mid i}{w}_i/\sum _j\sum _i{w}_{j\mid i}{w}_i\\ ={Nw}_{j\mid i}{w}_i/\sum _i{n}_i{w}_i.\end{array}$$

Denote by z_u and z_e, respectively, the sets of explanatory variables defining the level-2 and level-1 random coefficients and form

$$\begin{array}{l}{\mathbf{z}}_u^{\ast }={\mathbf{W}}_i{\mathbf{z}}_u,{\mathbf{W}}_i=\mathit{Diag}\{{\omega }_i^{-0.5}\}\\ {\mathbf{z}}_e^{\ast }={\mathbf{W}}_{ji}{\mathbf{z}}_e,{\mathbf{W}}_{ji}=\mathit{Diag}\{{\omega }_{ji}^{-0.5}\}.\end{array}$$

We now carry out a standard estimation, but using ${\mathbf{z}}_u^{\ast }$ and ${\mathbf{z}}_e^{\ast }$ as the random coefficient explanatory variables. For a three-level model, with an obvious extension to notation, we have the following

$$\begin{array}{c}\sum _j{w}_{j\mid ik}=n_{ik},\sum _i{w}_{i\mid k}=I_k,\sum _k{w}_k=K,\\ N=\sum _i\sum _k{n}_{ik},I=\sum _k{I}_k\\ w_{\mathit{jik}}={Nw}_{j\mid ik}{w}_{i\mid k}{w}_k/\sum _j\sum _i\sum _k{w}_{j\mid ik}{w}_{i\mid k}{w}_k,\\ w_{ik}={Iw}_{i\mid k}{w}_k/\sum _i\sum _k{w}_{i\mid k}{w}_k.\end{array}$$

Goldstein (1995) also pointed out that in survey work, analysts often have access only to the final level-1 weights w _{j i}. In this case, say for a two-level model, we can obtain the w_i by computing $w_i^{\prime }=W_{i}I/{\sum }_i{W}_i$, W_i = (Σ_j w_ji)/n_i. For a three-level model, the procedure is carried out for each level-3 unit, and the resulting $w_{ik}^{\prime }$ are transformed analogously.

Examples

Subjects

The data are drawn from a natural history study of adolescent smoking. Participants included in this study were in either ninth or tenth grade at baseline and reported on a screening questionnaire 6–8 weeks prior to baseline that they had smoked at least one cigarette in their lifetimes. The majority (57.6%) had smoked at least one cigarette in the past month at baseline. A total of 461 students completed the baseline measurement wave.

The study utilized a multimethod approach to assess adolescents, including self-report questionnaires, a week-long time/event sampling method via hand-held computers (ecological momentary assessment; EMA), and detailed surveys. Adolescents carried the hand-held computers with them at all times during a data collection period of seven consecutive days and were trained both to respond to random prompts from the computers and to event record (initiate a data collection interview) in conjunction with smoking episodes. Random prompts and the self-initiated smoking records were mutually exclusive; no smoking occurred during random prompts. Questions concerned place, activity, companionship, mood, and other subjective variables. The hand-held computers dated and time-stamped each entry. Following the baseline EMA assessment period, subjects also completed similar week-long EMA assessments at 6- and 15-month follow-ups.

A question of interest concerned comparing mood from random prompts and smoking events, and the degree to which this varied was examined across the three measurement waves. For this, subjects who had at least one smoking event at two or more measurement waves were selected for analysis. In all, there were 165 such subjects with data from a total of 14,540 random prompts and smoking events; 81 of these subjects were measured at all three waves, and the remaining 84 were measured at two waves. The numbers of subjects at each wave were 152, 141, and 118, respectively. Across the waves, the average number of random prompts per subject was approximately 30 (median = 30, range = 8 to 71), 28 (median = 29, range = 4 to 47), and 28 (median = 28, range = 5 to 48), respectively. Similarly, the average number of smoking events per subject was about 6 (median = 3.5, range = 1 to 42), 5 (median = 3, range = 1 to 32), and 8 (median = 4, range = 1 to 43), respectively, across the three waves. The Spearman correlation between the number of random prompts and number of smoking events was not significant at any wave (r = −0.16, −0.07, and −0.05, respectively).

Dependent Measures

Negative and positive affect

Two mood outcomes were considered: measures of the subject’s negative and positive affect (denoted NA and PA, respectively) at each random prompt and at each smoking episode. Both of these measures consisted of the average of several individual mood items, each rated from 1 to 10, that were identified via factor analysis. Specifically, PA consisted of the following items that reflected subjects’ assessments of their positive mood just before the prompt signal: I felt happy, I felt relaxed, I felt cheerful, I felt confident, and I felt accepted by others. Similarly, NA consisted of the following items assessing pre-prompt negative mood: I felt sad, I felt stressed, I felt angry, I felt frustrated, and I felt irritable. Subjects rated each item on a 1–10 Likert-type scale, with 10 representing very high levels of the attribute. For the smoking events, participants rated their mood right after smoking. Over all prompts and events, both random and smoking, and ignoring the clustering of the data within subjects, the mean of PA was 6.70 (sd = 1.96), 6.75 (sd = 1.92), and 6.86 (sd = 1.88) across the three waves. Similarly, for NA, the means were 3.57 (sd = 2.33), 3.43 (sd = 2.27), and 3.31 (sd = 2.18). Thus, overall, positive affect increased and negative affect decreased over time.

Inspection of the marginal distributions of these two variables indicated approximate normality for PA, but not for NA, which had a large proportion of responses with values of 1. Thus, we will describe analysis using a linear mixed-effects regression model for PA and an ordinal logistic mixed-effects regression model for NA. These models were estimated using the software program SuperMix (Hedeker et al. 2008)

Three-Level Linear Mixed-Effects Regression Model for Changes in PA Associated with Smoking Events Across Waves

Consider the following linear mixed model for the PA mood measurement y of individual i (i = 1, 2, …, N level-3 subjects) at wave j (j = 1, 2, …, n_i level-2 waves), and occasion k (k = 1, 2, …, n_{i j} level-1 prompts and events). Let Wave denote the measurement wave (coded 0, 1, and 2.5; each unit represents a six-month time interval), and SmkE represent a variable indicating whether the occasion is from a random prompt (= 0) or a smoking event (= 1):

$$y_{\mathit{ijk}}=({\beta }_0+v_{0i}+u_{0ij})+({\beta }_1+v_{1i}){\text{Wave}}_{ij}+({\beta }_2+v_{2i}){\text{SmkE}}_{\mathit{ijk}}+{\beta }_3({\text{SmkE}}_{\mathit{ijk}}\times {\text{Wave}}_{ij})+{\epsilon }_{\mathit{ijk}}.$$

In this model, there are three random subject effects to allow subjects to vary in their intercept (v_0i), time trend (v_1i), and effect of smoking (v_2i) on their mood. Also, a random effect for measurement wave within subjects (u_{0i j}) is included to account for additional within-wave mood correlation of the subject responses. Note that these random effects are all deviations relative to the model fixed effects. In terms of the fixed effects, the model includes effects of wave (β₁), smoke event (β₂), and the interaction of smoke event by wave (β₃). This latter term indicates the degree to which the mood effect of smoking varies across waves. Finally, the model also includes ε_{i j k}, which is an independent (level-1) error term distributed normally with mean 0 and variance ${\sigma }_{\epsilon }^2$.

The level-1 errors are independent conditional on the random effects (v_0i, v_1i, and v_2i at the subject level, and u_{0i j} at the wave level). With three random subject effects, the population distribution of intercept and slope deviations is assumed to be a trivariate normal N(0, Σ_v), where Σ_v is the 3 × 3 variance-covariance matrix given as:

$${\mathrm{\sum }}_v=\left(\begin{array}{ccc}{\sigma }_{v_0}^2& {\sigma }_{v_0{v}_1}& {\sigma }_{v_0{v}_2}\\ {\sigma }_{v_0{v}_1}& {\sigma }_{v_1}^2& {\sigma }_{v_1{v}_2}\\ {\sigma }_{v_0{v}_2}& {\sigma }_{v_1{v}_2}& {\sigma }_{v_2}^2\end{array}\right).$$

These variances indicate the heterogeneity in the population of subjects in terms of intercepts, and effects of time and smoking on mood. Likewise, the covariances represent association of these subject-specific random effects in the population of subjects. The additional level-2 variance ${\sigma }_{u_0}^2$ represents between-wave (and within-subjects) variation, over and above the random subject effects.

Three-Level Ordinal Logistic Mixed-Effects Regression Models for Changes in Negative Affect Associated with Smoking Events Across Waves

As indicated above, the distribution of the mood outcome for negative affect was not approximately normally distributed, and so we present an analysis treating the outcome as an ordinal variable. Three-level models for ordinal outcomes are described in Raman & Hedeker (2005) and Liu & Hedeker (2006), building upon the development of the three-level model for binary outcomes in Gibbons & Hedeker (1997). Here, the ordinal outcome Y_{i j k} can take on values c = 1, 2, …, C, and the model is written in terms of the cumulative logit, namely:

$$ln\left[\frac{Pr(Y_{\mathit{ijk}}\le c)}{1-Pr(Y_{\mathit{ijk}}\le c)}\right]={\gamma }_c-[(v_{0i}+u_{0ij})+({\beta }_1+v_{1i}){\text{Wave}}_{ij}+({\beta }_2+v_{2i}){\text{SmkE}}_{\mathit{ijk}}+{\beta }_3({\text{SmkE}}_{\mathit{ijk}}\times {\text{Wave}}_{ij})]$$

with C − 1 strictly increasing model thresholds γ_c (i.e., γ₁ < γ₂ · · · < γ_C−1). These thresholds reflect the marginal frequencies in the C categories of the ordinal outcome. For identification, either one of the thresholds or the model intercept must be fixed to zero. In the above, we have specified the latter. Otherwise, the model for NA includes the fixed and random effects as in the analysis of the continuous outcome PA. The interpretation for the covariates and random effects is in terms of the logit scale. Note that none of these carry the category subscript c, and so their effects are constant across the cumulative logits. McCullagh (1980) calls this assumption of identical odds ratios across the C − 1 cut-offs the proportional odds assumption.

We should note that for both PA and NA, we also investigated the decomposition of the effect of the occasion-varying SmkE on mood, as described in Begg & Parides (2003), by including the subject’s mean ${\overline{\text{SmkE}}}_{ij}$ at each wave as an additional covariate. Notice that because SmkE_ijk is simply a binary variable, taking on values of 0 or 1, ${\overline{\text{SmkE}}}_{ij}$ simply equals the proportion of occasions (i.e., both random prompts and smoking events) at a wave that were smoking events for a subject. By so doing, the effect of SmkE indicates how a person’s mood differs between a random prompt and smoking event controlling for the proportion of smoking events that the person has at the given wave. Inclusion of this additional covariate (as well as its interaction with wave) had minimal effect and did not alter the conclusions. Thus, for simplicity we leave this out in the results described below.

Results

Results for both (continuous) positive and (ordinal) negative affect are listed in Table 1.

Table 1.

Positive and negative affect model estimates, standard errors (se), and p-values

Parameter	Positive affect linear mixed model			Negative affect ordinal logistic mixed model
	Estimate	se	p <	Estimate	se	p <
Intercept β0	6.570	0.093	0.0001
Wavei j β1	0.091	0.041	0.03	−0.092	0.037	0.02
SmkEi j k β2	0.454	0.061	0.0001	−0.320	0.077	0.0001
SmkEi j k × Wavei j β3	−0.106	0.035	0.003	0.035	0.044	0.43
Intercept variance (level-3) ${\sigma }_{v_0}^2$	1.157	0.168	0.0001	2.603	0.374	0.0001
Wave variance (level-3) ${\sigma }_{v_1}^2$	0.089	0.032	0.006	0.167	0.062	0.007
SmkE variance (level-3) ${\sigma }_{v_2}^2$	0.127	0.037	0.001	0.198	0.073	0.007
Intercept, Wave covariance σv0v1	−0.043	0.054	0.44	−0.183	0.117	0.12
Intercept, SmkE covariance σv0v2	−0.169	0.059	0.005	−0.215	0.112	0.06
Wave, SmkE covariance σv1v1	−0.051	0.269	0.03	−0.062	0.043	0.14
Between-wave (level-2) variance ${\sigma }_{u_0}^2$	0.284	0.047	0.0001	0.554	0.094	0.0001
Error (level-1) variance ${\sigma }_{\epsilon }^2$	2.230	0.027	0.0001

Despite the different scales and models of these two variables, the results are relatively consistent for the two mood outcomes, albeit in opposite directions in terms of the mean. In terms of time, the effect of Wave on mood indicates that PA increases and NA decreases across the study waves. The effect of smoking on mood is such that positive mood is significantly increased and negative mood significantly decreased for smoking events, relative to random prompts. Thus, subjects’ moods are significantly different, and in the more desired direction, just after smoking, relative to their random prompts. The interaction indicates that the positive mood benefit associated with smoking events decreases significantly across time, whereas the beneficial effect on NA does not vary across time. The decrease in positive mood boost over time may reflect the development of tolerance, as smoking also increases in these adolescents. The continued reduction in NA, relative to random times, following smoking may reflect relief from nicotine withdrawal, which may also be increasing as these adolescents continue to develop higher levels of nicotine dependency.

In terms of the variance parameters, there is considerable subject heterogeneity for both PA and NA in terms of their intercepts and slopes for Wave and SmkE. Thus, the effects of time and smoking on mood vary considerably across subjects. Also, there is significant between-wave mood variation, both for PA and NA, in addition to the variation at the subject level. The covariances are in the same direction for PA and NA, albeit none of the covariances for the ordinal NA reach statistical significance. The negative covariance of the intercept and SmkE effect is particularly interesting. For PA, it suggests that subjects with higher random PA have less PA benefit (i.e., lower PA scores) associated with a smoking event. For NA, this negative covariance suggests that subjects with higher random NA have greater NA benefit (i.e., lower NA scores) for smoking events. Although these could be due to ceiling and floor effects of measurement, respectively, these negative covariances are consistent with previously reported results (Hedeker et al. 2009).

EXAMPLE APPLICATIONS IN THE BEHAVIORAL SCIENCES

Applications of mixed-effects regression models are steadily increasing and can be found in many different fields, including studies on alcohol (Curran et al. 1997), smoking (Niaura et al. 2002), HIV/AIDS (Gallagher et al. 1997), drug abuse (Carroll et al. 1994, Halikas et al. 1997), psychiatry (Elkin et al. 1995, Serretti et al. 2000), and child development (Campbell & Hedeker 2001, Huttenlocher et al. 1991), to name a few. Not only do these articles illustrate the wide applicability of mixed-effects regression models, they also give a sense of how mixed-effects regression model results are typically reported in the various literatures. Thus, they can be very useful for investigators who are new to mixed-effects regression models and their usage.

SUMMARY

In summary, generalized mixed-effects regression models have fundamentally changed the way we conceptualize the analysis of longitudinal data. The ability to model and compare longitudinal response patterns for continuous and categorical outcomes using a unified family of statistical models and to be able to estimate person-specific trends are major strengths of this general methodology. Robustness to missing data both under default MAR assumptions and extensions for NMAR further enhance the utility of these full likelihood procedures. Current limitations are largely related to the number of random effects that can be included in nonlinear models, where an explicit representation of the high dimensional integral must be obtained. Full Bayesian approaches provide one possible solution to this problem, and this should be an area of further statistical research.

Generalized mixed-effects regression models extend beyond analysis of longitudinal data and have been widely used for analysis of non-longitudinal clustered data as well. More recently, these models have even been applied to large-scale spontaneous reporting system data as tools to evaluate the safety of pharmaceuticals (Gibbons et al. 2008).

SUMMARY POINTS.

1. Generalized mixed-effects regression models (MRMs) are ideally suited to analysis of longitudinal data.

2. MRMs are available for continuous, binary, ordinal, nominal, count, and time-to-event data.

3. Linear MRMs are less computationally intensive than nonlinear MRMs because the integrals corresponding to the random effects are not a part of the estimation.

4. Full likelihood methods such as MRM are more robust to the presence of missing data than are partial likelihood methods such as generalized estimating equations.

5. Extensions of the general MRM include three and four levels of clustering, multivariate extensions, and the inclusion of design weights.

6. New computer software such as SuperMix is now available for routine estimation of two-level and three-level linear (continuous normal) and nonlinear (binary, ordinal, nominal, count, and time-to-event) models.

LOCF

last observation carried forward

MAR

missing at random

NMAR

not missing at random

GEE

generalized estimating equations

ANOVA

analysis of variance

MRMs

mixed-effects regression models

MCMC

Markov Chain Monte Carlo

GLMs

generalized linear models

MCAR

missing completely at random

MANOVA

multivariate analysis of variance

NA

negative affect

PA

positive affect