Abstract
Perennial plants monitor seasonal changes through changes in environmental conditions such as the quantity and quality of light. To ensure a correct initiation of critical developmental processes, such as the initiation and cessation of growth, plants have adapted to a spatially variable light regime and genes in the photoperiodic pathway have been implicated as likely sources for these adaptations. Here we examine genetic variation in genes from the photoperiodic pathway in Populus tremula (Salicaceae) for signatures diversifying selection in response to varying light regimes across a latitudinal gradient. We fail to identify any loci with unusually high levels of genetic differentiation among populations despite identifying four SNPs that show significant allele frequency clines with latitude. We do, however, observe large covariance in allelic effects across populations for growth cessation, a highly adaptive trait in P. tremula. High covariance in allelic effects is a signature compatible with diversifying selection along an environmental gradient. We also observe significantly higher heterogeneity in genetic differentiation among SNPs from the photoperiod genes than among SNPs from randomly chosen genes. This suggests that spatially variable selection could be affecting genes from the photoperiod pathway even if selection is not strong enough to cause individual loci to be identified as outliers. SNPs from three genes in the photoperiod pathway (PHYB2, LHY1, and LHY2) show significant associations with natural variation in growth cessation. Collectively these SNPs explain 10–15% of the phenotypic variation in growth cessation. Covariances in allelic effects across populations help explain an additional 5–7% of the phenotypic variation in growth cessation.
SPECIES occupying heterogeneous environments are often subjected to spatially variable natural selection, that is, natural selection that differs among populations that a species inhabits. Such spatially variable selection is expected to have important consequences for how phenotypic variation is partitioned within and among populations and also for genetic differentiation at the underlying loci controlling these traits (Latta 1998; Le Corre and Kremer 2003; Whitlock 2008). A major motivation for studying the genetic consequences of local adaptation is to identify loci that control local adaptation. The identification of loci (and traits) subjected to spatially variable selection is complicated by the fact that genetic drift introduces heterogeneity among loci. However, it should be possible to identify putative targets of spatially variable selection by searching for loci with unusually high levels of genetic differentiation (Lewontin and Krakauer 1973; Beaumont 2005). Although the initial idea championed by Lewontin and Krakauer (1973) has attracted much criticism, the general principle of searching for loci with unusually high levels of genetic differentiation has proved to be quite successful in identifying loci subject to spatially variable selection, especially when selection is strong relative to migration (e.g., Beaumont and Balding 2004; Beaumont 2005).
However, even though spatially variable selection acting on a quantitative trait conferring local adaptation may be strong, selection on the underlying causal loci can often be quite weak because individual loci contribute only a small proportion to the total phenotypic variation (Latta 1998; Le Corre and Kremer 2003). In such cases migration may overwhelm local selection acting on the underlying QTL (that is, m > s) and genetic differentiation at these loci is actually well approximated by genetic differentiation at neutral loci, even though genetic differentiation at the quantitative traits themselves can be high (Latta 1998; Whitlock 2002; Le Corre and Kremer 2003). The reason for this is that selection generates linkage disequilibrium between loci and the combined effect of multiple loci changing in parallel is much greater than what can be predicted from the effects of individual loci alone (Latta 1998; Le Corre and Kremer 2003). This potentially limits the utility of FST-based outlier detection methods for identifying loci controlling quantitative traits involved in mediating local adaptation.
A classic example of local adaptation in the face of substantial gene flow is adaptation to local photoperiod seen in many boreal forest trees (Chen et al. 2002). Trees alternate between growth when conditions allow and dormancy during periods of unfavorable environmental conditions and a correct timing of growth initiation and growth cessation represents a crucial trade-off between growth and survival. In boreal trees the onset of winter dormancy is largely determined by seasonal changes in photoperiod (Chen et al. 2002) and genes in the photoperiodic pathway have been implicated in the control of growth cessation (Frewen et al. 2000; Böhlenius et al. 2006; Gyllenstrand et al. 2007; Ingvarsson et al. 2008). The photoperiodic pathway has been dissected in great detail in the model plant Arabidiopsis thaliana and this has resulted both in the identification of individual genes making up the pathway and the interactions among these genes (Eriksson and Millar 2003; Hayama and Coupland 2003). Although distinct photoperiodic responses appear to have evolved independently several times in the evolutionary history of plants, the photoperiodic pathway is conserved between monocots and dicots (Cremer and Coupland 2003) and even between angiosperms and gymnosperms (Gyllenstrand et al. 2007).
Ingvarsson et al. (2008) recently showed that two mutations in the phytochrome photoreceptor PHYB2 are independently associated with naturally occurring variation in the timing of bud set or growth cessation in European aspen (Populus tremula, Salicaceae). However, these mutations explain only a few percent of the observed phenotypic variation in growth cessation. As this trait appears to be under tight genetic control with little environmental influence in P. tremula (Hall et al. 2007; Luquez et al. 2008), other genes besides PHYB2 must be involved in mediating natural variation in growth cessation. Here we use a candidate gene approach to search for signs of local adaptation and phenotypic associations to growth cessation in genes from the photoperiod pathway. Our goal is to identify loci involved in controlling natural variation in growth cessation and to study to what degree genes from the photoperiodic pathway show evidence for divergent natural selection. Finally, we test the predictions from Latta (1998) and Le Corre and Kremer (2003) of how divergent selection on adaptive traits influences genetic differentiation at the underlying QTL.
MATERIALS AND METHODS
PCR amplification and DNA sequencing:
All plant material used in this study was selected from the Swedish Aspen Collection (the SwAsp collection), which consists of 120 trees collected from 12 sites throughout Sweden (10 trees per population) along a latitudinal gradient spanning approximately 10 latitude degrees. The SwAsp collection is described in more detail in Hall et al. (2007) and Luquez et al. (2008).
Total genomic DNA was extracted from frozen leaf tissue using the DNeasy plant mini prep kit (QIAGEN, Valencia, CA). Sequences for 25 genes from the photoperiod pathway were taken from Hall (2010). Briefly, for a subset of 13 genes all exons (excluding short exons, <80 bp) were sequenced directly from PCR-amplified fragments from genomic DNA. For these genes we sequenced 24 individuals. The remaining 12 genes were PCR amplified from 12 individuals and cloned into the pCR2.1 vector using a TA-cloning kit from Invitrogen (Carlsbad, CA). All fragments were sequenced on a Beckman CEQ 2000 capillary sequencer at the Umeå Plant Science Centre sequencing facility. Sequences were verified manually and contigs were assembled using the computer program Sequencer v 4.0 (Gene Codes, Ann Arbor, MI). For genes that were directly sequenced, polymorphic sites were directly visible from double peaks in the chromatograms generated by the sequencer. For cloned genes, four or more colonies for each individual were sequenced in an attempt to identify the two haplotypes present within an individual and to control for Taq polymerase transcription errors. We also obtained the homologous gene regions from the P. trichocarpa genome sequence and used these as outgroup sequences to polarize mutations into ancestral and derived states on the basis of the allelic state in P. trichocarpa.
We selected all SNPs from these genes that had a frequency >15% in the sample of sequences we obtained. We developed proofreading allele-specific extension (PRASE) assays for these SNPs (Di Giusto and King 2004) and they were scored from the complete SwAsp collection (Hall et al. 2007; Luquez et al. 2008). Using these criteria we managed to score a total of 110 SNPs from 23 of the 25 genes, for an average of 4.8 SNPs per gene (minimum 1, maximum 14; see supporting information, Table S1 for information on the number of SNPs scored per gene). In addition, we included the three most common alleles from a short, trinucleotide microsatellite located in the coding region of the COL2B gene (Hall et al. 2007). Alleles at this microsatellite show variable numbers of poly(E) (Glu) repeats with repeat numbers ranging from 5 to 10 Glu amino acids (St. Onge 2006; Hall et al. 2007). These alleles were coded as “pseudo-SNPs,” where the presence of the SSR allele was coded as 0, 1, or 2, depending on the number of copies of that allele an individual carried. Two low-frequency alleles (frequencies 0.5 and 1.3%) at the COL2B microsatellite were not included in the analyses. For two genes (TOC1 and COL2A) no SNP passed our frequency criteria to be included in our scoring assay.
We also scored 93 SNPs from 21 genes that are not thought to be involved in the photoperiodic control of phenology. These genes were taken from the 77 genes analyzed in Ingvarsson (2008) and SNPs were selected using the same criteria that were used to select SNPs from the photoperiod genes. For brevity we refer to the first set of SNPs as “photoperiod SNPs” and the latter as “control SNPs” throughout this article.
Data analyses:
Genetic diversity was estimated for each population by calculating observed (Ho) and expected (He) heterozygosities. Tests for Hardy–Weinberg equilibrium were performed for each SNP using the genetics package in R (R Development Core Team 2008). This package was also used to test for pairwise linkage disequilibrium between individual SNPs using a maximum-likelihood approach as the genotype data are unphased and individual haplotypes cannot be distinguished. We also tested for clinal variation in SNP frequencies by regressing population allele frequencies on latitude of origin.
Genetic differentiation among populations for individual SNPs was estimated using the Bayesian method of Foll and Gaggiotti (2008). This method models allele frequency counts at a specific locus in a population using a multinomial-Dirichlet distribution that captures the underlying genealogical structure of the migration process among populations (Foll and Gaggiotti 2008; see also Beaumont and Balding 2004). This method allows for the estimation of both locus-specific effects (αi) and population-specific effects (βj) on genetic differentiation and these effects are estimated using logistic regression and subsequently used to calculate locus-specific estimates of FST. In the method of Foll and Gaggiotti (2008) the effects of selection at a locus are evaluated by fitting two alternative models to the data. One model (M0) includes only population-specific effects (βi) whereas the alternative model (M1) includes both population- and locus-specific effects (αi and βi). These models are compared using their respective posterior probabilities by calculating the Bayes factor (BF), which is the ratio of posterior probabilities for the two alternative models [that is, BF = P(M1 | D)/P(M0 | D)] (Foll and Gaggiotti 2008). We analyzed the SNP data using the BayesScan program that implements the method of Foll and Gaggiotti (2008) (available at http://www-leca.ujf-grenoble.fr/logiciels.htm). Since this analysis is clearly exploratory and is aimed at identifying possible loci under diversifying selection, we used a relatively modest threshold for identifying outliers. Foll and Gaggiotti (2008) showed that biallelic markers, like SNPs, have lower power to detect selection than multiallelic markers (e.g., SSRs) and we therefore used a rather liberal cutoff limit for regarding loci as potential outliers. In practice we used a posterior probability for the selection model (M1) of 86% [corresponding to a log10(Bayes factor) of 0.79] to identify potential outlier loci. Simulations have shown that for SNPs this cutoff limit yields an ∼5% false discovery rate (Foll and Gaggiotti 2008).
FST values for QTL are expected to show greater heterogeneity than putative neutral loci (Le Corre and Kremer 2003) and to test this hypothesis we compared the heterogeneity of FST values between the photoperiod SNPs and the control SNPs using the method of Lewontin and Krakauer (1973). Among-locus heterogeneity, k, was calculated as
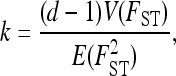 |
(1) |
where d is the number of populations and where E and V denote expectation and variance, respectively. For neutral loci, k is expected to be close to 2 (Lewontin and Krakauer 1973). We tested the differences in heterogeneity in FST values between photoperiod and control SNPs in two ways. First we compared the variance in FST between the two groups of SNPs using Bartlett's test of homogeneity of variances. Second, we used a resampling test to account for the fact that the number of SNPs differs between the two groups. We generated the null distribution of k by randomly assigning SNPs (without replacement) to the candidate gene and control groups and calculating k using Equation 1 for these two groups. This procedure was repeated 104 times and the observed value of k was compared to this distribution.
Theory suggests that in species experiencing diversifying selection in the face of high levels of gene flow, positive covariance (i.e., linkage disequilibrium) may build up across loci, so that even when allele frequency changes are relatively modest across populations, the combined effect of many loci, changing in parallel, can be substantial for quantitative traits controlled by these loci (Latta 1998; Le Corre and Kremer 2003). We therefore estimated the covariance of allele frequencies across populations for all pairwise combinations of SNPs. The covariance of allelic effects is
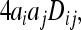 |
(2) |
where ai and aj are the additive effects of loci i and j, respectively and Dij is the linkage disequilibrium between the two loci (Latta 1998). As shown by Ohta (1982; see also Latta 1998; Le Corre and Kremer 2003), total linkage disequilibrium can be partitioned into within- and between-population components where the between-population component of linkage disequilibrium is given by
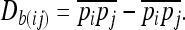 |
(3) |
This method is virtually identical to that used in Storz and Kelly (2008) (their Equation 3) with the exception that their estimator is standardized with respect to allele frequencies and is squared to remove the sign of the linkage disequilibrium (LD). Since we are specifically interested in loci showing positive covariance across populations (Latta 1998), we choose to preserve the sign in our calculations. Also, to avoid inflated covariances between SNPs because of intragenic LD, we performed only pairwise comparisons between SNPs from different genes. The additive effects of loci i and j in Equation 1 were calculated from our association analyses (see below).
We calculated the covariance of allelic effects across populations for all SNP pairs using Equation 2 for both control and photoperiod SNPs, using additive effects (a) estimated from data on growth cessation in these populations (Ingvarsson et al. 2008). To explore the expected distribution of the covariance among SNPs we simulated 113 SNPs using the approach of Nicholson et al. (2002). Briefly, this method simulates multipopulation unlinked genotype data from a multinomial Dirichlet model (see Nicholson et al. 2002 for more details). The simulations were tailored to give an expected value of FST equal to the average value of FST we observed in our sample of SNPs. All simulations were performed using the simmD function from the popgen package in R. The simulated SNPs were then used to calculate additive effects from the growth cessation data and subsequently to calculate the covariance among allelic effects using Equation 2. The simulated SNP data were used to estimate the expected distribution of covariance of allelic effects under no diversifying selection.
Phenotypic associations:
We used single-marker association tests assuming a model of additive effects of alleles within a marker locus. To control for possible spurious associations caused by genetic structuring of the sample, we used the mixed-model method of Yu et al. (2006), which allows for both population structure and more diffuse familial structure within the sample. Population structure and pairwise kinship coefficients were estimated using 26 putatively neutral SSR markers, using the program Structure (Pritchard et al. 2000) to estimate population membership for each individual using K = 2 (Ingvarsson et al. 2008). Similarly, the matrix of pairwise kinship coefficients was calculated according to Ritland (1996), using the software package SpaGeDi (Hardy and Vekemans 2002). The mixed model we used was
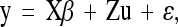 |
where y is a vector of observed phenotypes, β is a vector on parameters for fixed effects (including SNP effects), and u and ɛ are vectors that capture (random) variation due to unmeasured polygenic contributions (u) or environmental effects (ɛ). X and Z are design matrices relating fixed and random effects to individual observations. The variance of polygenic (clone) effects equals V(u) = 2KVG, where K is the matrix of kinship coefficients. Finally, the variance of the residual effects is V(ɛ) = RVR, where R is a matrix with zeros for all off-diagonal elements and the reciprocal of the number of observations along the diagonal. VG and VR measure the genetic and residual variances for the trait.
We combined phenotypic data on growth cessation from our two common garden sites (Luquez et al. 2008) across all years of our survey (2004–2008). We therefore included fixed effects for block, site, and year in the mixed model, in addition to variables included to control for population structure into the vector of fixed effects (β). We implemented our association analyses using the kinship library in R and fitted the model using restricted maximum-likelihood methods. We used the false discovery rate (FDR) (Storey and Tibshirani 2003) to control for multiple testing across the 206 SNPs.
RESULTS
Genetic differentiation at SNPs:
We analyzed 113 SNPs from 23 genes in the photoperiod pathway and 93 SNPs from 21 control genes. We could not reject Hardy–Weinberg equilibrium within populations for either photoperiod or control SNPs (data not shown). However, the power of these tests is quite low with only 10 individuals sampled per population. For the pooled samples, across populations, 19 SNPs from the photoperiodic pathway genes show significant deviations from Hardy–Weinberg expectations after multiple-test correction. All but 2 of these show a slight excess of heterozygotes across the 12 populations. For the 93 SNPs from the control loci we found 2 SNPs where we could reject Hardy–Weinberg equilibrium and both show an excess of homozygotes across populations. We cannot rule out that these minor deviations observed are caused by experimental artifacts. The PRASE assay is highly specific and we do not expect that misamplification of the alternate allele in each SNP pair is a contributing factor (Di Giusto and King 2004). A possible experimental error would be failed amplification due to polymorphisms in the primer binding sites. This would result in either failed amplification from some individuals or an excess of homozygotes if amplification failed in heterozygous individuals. We observe neither of these patterns and in fact we observe an excess of heterozygotes, suggesting that PCR amplification errors are not causing the slight deviations from Hardy–Weinberg we observe in our data set. In line with earlier results (Ingvarsson 2008; Ingvarsson et al. 2008) we find relatively little LD between SNPs. A total of 139 of 1741 pairwise comparisons (7.9%) between SNPs showed evidence for significant LD after multiple-test corrections. However, we do not observe any clear physical clustering of sites in LD and sites in close physical proximity often showed negligible levels of LD (data not shown).
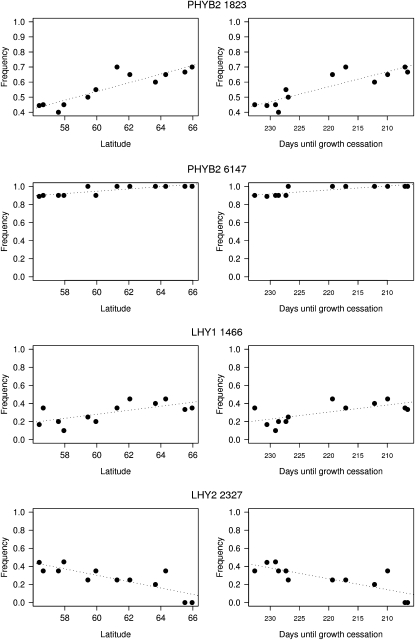
We detect four SNPs where allele frequencies vary with latitude after multiple-test correction using a false discovery rate of 0.1 (Figure 1). Two of these SNPs, PHYB 1823 (T608N) and PHYB2 6147 (Y1117F) from the phytochrome gene PHYB2, have already been shown to exhibit clinal variation in earlier studies (Ingvarsson et al. 2006). In this study we identified two additional SNPs showing significant clinal variation. These two SNPs are located in the circadian clock genes LHY1 and LHY2, respectively. The LHY1 1466 mutation is an A-to-T transversion that results in a synonymous mutation located in exon 4 of the LHY1 gene. The derived allele (T) is most common in northern populations, increasing from a frequency of ∼10% in the southernmost population to ∼40% in the northernmost population. The LHY2 2327 SNP is a G-to-A transition in exon 6 of LHY2 resulting in Ser → Asn replacement (S681N) in the translated protein sequence. For the LHY2 mutation, the derived allele (A) is most frequent in the southern populations and is virtually absent in the northernmost populations. This contrasts with mutations showing clinal variation in PHYB2 (Ingvarsson et al. 2006) and LHY1 where the derived allele increases in frequency with latitude. Interestingly, the LHY2 SNP shows a third allelic state (C) in P. nigra, which results in the incorporation of a Thr amino acid into the LHY2 protein (Takata et al. 2009).
Figure 1.—
Plots of derived allele frequency clines for four SNPs showing clinal variation. The left column shows population allele frequencies vs. latitude and the right column shows population allele frequencies vs. population means for growth cessation (in days). Note that populations are arranged from south to north along the x-axis to allow for easy comparison between them. The dotted line is the least-squares regression line of mean allele frequency vs. either latitude or population mean of growth cessation.
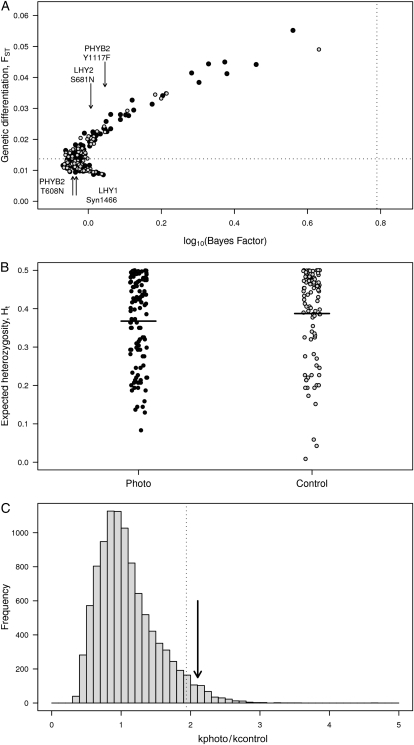
The average genetic differentiation across populations (mean FST) over all 206 SNPs was 0.017, which is very close to estimates of FST based on microsatellite data (FST = 0.015) (Hall et al. 2007). There was also no significant difference in mean FST between photoperiod and control SNPs (0.018 and 0.016, respectively; Wilcoxon's two-sample test, P = 0.33). We failed to identify any SNPs with significantly enhanced genetic differentiation due to the action of natural selection (Figure 2). It is interesting to observe that none of the four loci where we demonstrate significant clinal variation are identified as outliers. In fact, these four loci have FST values that fall right in the middle of the distribution of FST values (Figure 2).
Figure 2.—
(A) Analysis of genetic differentiation using the method of Foll and Gaggiotti (2008). Estimates of FST for photoperiod (solid circles) and reference SNPs (open circles) are plotted against empirical P-values for each SNP. The vertical dashed line denotes a posterior probability for an outlier caused by natural selection of 86% [corresponding to a log10(Bayes factor) of 0.79]. SNPs showing significant allele frequency clines are indicated by arrows. (B) Distribution of heterozygosities for photoperiod and control SNPs. The data points have been jittered horizontally to increase visibility of individual data points. (C) The distribution of the ratio of among-locus heterogeneity for photoperiod and control SNPs (kphoto/kcontrol) from 104 samples where SNPs were randomly assigned to the two groups. The resulting distribution of k was compared to the value of k observed in the data (arrow).
We quantified heterogeneity in FST values among loci for the photoperiod and control SNPs, respectively, using the approach outlined by Lewontin and Krakauer (1973). We find evidence for substantially greater heterogeneity in genetic differentiation among photoperiod SNPs (k = 4.27) than among control SNPs (k = 2.03) and this difference is significant using either a parametric test (Bartlett's test of homogeneity of variances, K2 = 11.7, d.f. = 1, P < 0.001) or a permutation test to account for differences in the number of loci in the two sets of SNPs (P = 0.025, Figure 2C). Since estimates of FST are intimately tied to expected heterozygosity (Beaumont and Nichols 1996), we also tested whether the heterozygosity differed between the two classes of SNPs to ensure that the differences in FST we observe are not simply caused by differences in heterozygosity at the underlying loci (Figure 2B). However, we found no significant difference in either the expected heterozygosity (HT) between photoperiod and control SNPs (t = 0.498, d.f. = 60, P = 0.62) or the heterogeneity of heterozygosity values between the two classes (Bartlett's test of homogeneity of variances, K2 = 0.344, d.f. = 1, P = 0.558). This demonstrates that the increased heterogeneity in genetic differentiation we observe in photoperiod SNPs is not caused by differences in genetic diversity between SNPs from the two classes of genes.
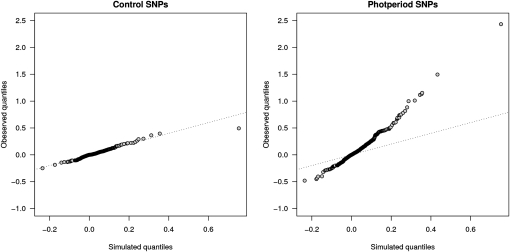
In the absence of diversifying selection, simulations suggest that among-population LD should generally be low. The data from the control SNPs also show a good correspondence with the simulated data. In the SNPs from the photoperiod pathway, however, we observe a substantial number of locus pairs that show unusually large (positive and negative) covariances of allelic effects, when compared to either simulated values or control SNPs (Figure 3). A total of 239 SNP pairs from the photoperiod pathway (5.5%) have covariances that fall outside of the 99% confidence interval calculated from the reference SNPs. Interestingly, of the 5 SNP pairs that show the highest covariance in allelic effects across populations, all but 1 involve at least one SNP showing significant clinal variation (Table 1).
Figure 3.—
Quantile–quantile plots of the distributions of covariance of allelic effects for pairs of control SNPs or photoperiod SNPs against simulated data. Data for the control SNPs show a good correspondence with the simulated data whereas the photoperiod SNPs show an excess of pairs with unusually large positive or negative covariances of allelic effects.
TABLE 1.
Pairs of SNPs showing the highest covariance of allelic effects for growth cessation
| Locus | SNP | FST | Pclinea | Locus | SNP | FST | Pclinea | Covb |
|---|---|---|---|---|---|---|---|---|
| LHY2 | 2327 | 0.023 | 0.002 | PHYB2 | 6030 | 0.019 | 0.021 | 2.433 |
| LHY2 | 2327 | 0.023 | 0.002 | CRY2.1 | 375 | 0.021 | 0.213 | 1.495 |
| APRR5 | 1291 | 0.012 | 0.035 | LHY2 | 2327 | 0.002 | 0.002 | 1.154 |
| PHYB2 | 6030 | 0.019 | 0.021 | CRY2.1 | 375 | 0.021 | 0.213 | 1.133 |
| APRR5 | 1291 | 0.012 | 0.035 | PHYB2 | 6030 | 0.019 | 0.021 | 1.115 |
| COL2B | Poly(E)9 | 0.066 | 0.113 | PHYB2 | 6030 | 0.019 | 0.021 | 1.011 |
| LHY2 | 2327 | 0.023 | 0.002 | GA20ox1 | 516 | 0.014 | 0.329 | 0.999 |
Probability of clinal variation of allele frequency with latitude.
Covariance of allelic effects (calculated using Equation 2).
Phenotypic associations:
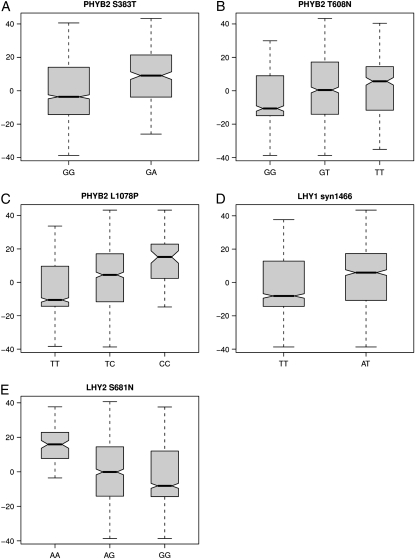
After correcting for multiple testing, six SNPs show significant associations with growth cessation (Table 2). Two of these SNPs are the nonsynonymous mutations (T608N and L1078P) located in the PHYB2 gene that we have previously shown to be significantly associated with growth cessation in P. tremula (Ingvarsson et al. 2008). In addition to the two PHYB2 SNPs we identified an additional SNP in PHYB2, S383T, that is also associated with onset of growth cessation in P. tremula. Furthermore, two SNPs in the circadian clock genes LHY1 (syn1466) and LHY2 (S681N) also show significant association with natural variation in growth cessation. Like the T608N SNP in PHYB2, the LHY1 and LHY2 SNPs both show significant allele frequency clines with latitude. The two mutations explain 6.7 and 12.7% of the observed phenotypic variation in growth cessation (Table 2, Figure 4), although these estimates are likely overestimating the true effect sizes by two- to threefold (Ingvarsson et al. 2008) (see also discussion below). Finally, one allele at the coding poly(E)-repeat SSR in COL2B, E9, is also associated with growth cessation.
TABLE 2.
Significant associations with growth cessation for SNPs in the photoperiodic pathway
| SNP | Type | β | P | q | Pmultiplea | R2b |
|---|---|---|---|---|---|---|
| col2b.poly(E)9 | SSR | 4.94 | 0.0070 | 0.087 | 0.1988 | 0.063 |
| lhy1.1466 | syn | 5.12 | 0.0052 | 0.064 | 0.0237 | 0.067 |
| lhy2.2327 | Ser → Asn | −5.55 | 0.0001 | 0.001 | 0.0002 | 0.127 |
| phyB2.1152 | Ser → Thr | 6.59 | 0.0077 | 0.095 | 0.0477 | 0.062 |
| phyB2.1823 | Thr → Asn | 3.45 | 0.0062 | 0.076 | 0.0081 | 0.064 |
| phyB2.6030 | Leu → Pro | −5.17 | 0.0008 | 0.010 | 0.0269 | 0.096 |
| All significant SNPs | 0.325 | |||||
| All significant SNPs and interactions | 0.423 | |||||
Only SNPs showing significant associations after correction for multiple testing using the false discovery rate (FDR) are shown.
P-value controlling for effects of other significant SNPs.
Percentage of variation explained.
Figure 4.—
Box plots of genotypic means of days until growth cessation for SNPs from (A) PHYBE S383T, (B) PHYB2 T608N, (C) PHYB2 L1078P, (D) LHY1 (syn1466), and (E) LHY2 (S681N). Means are calculated from the residuals after removing the effects of fixed effects of site, year, and block.
We included all SNPs into a single model to test for the effect of each SNP individually while statistically controlling for variation at the other putative causal SNPs. This analysis shows that all SNPs, except the poly(E)-repeat allele at COL2B, are independently associated with growth cessation (Table 2). Together the five SNPs that remain significant in the full model explain almost 33% of the phenotypic variation in growth cessation. To further take into account the positive covariances we observe among SNPs, we also analyzed a model including the five SNPs and their pairwise interactions and with this model the amount of variation explained increased to 42.5%. Again, we expect that these effects are overestimating the true effects of the SNPs due to the small size of our association mapping population.
DISCUSSION
Clines and detection of outlier loci:
In addition to the SNPs in PHYB2 where we already documented allele frequency clines (Ingvarsson et al. 2006), we identified two additional SNPs showing strong clinal variation with latitude, one each in the two circadian clock-associated genes LHY1 and LHY2 (Figure 1). The presence of such allele frequency clines is a strong sign of spatially variable selection acting directly at or near these mutations (Barton 1999). Two possible factors that are relevant for our identification of allele frequency clines in P. tremula are worth mentioning here. First, we sampled only 10 individuals per population and the rather low number of individuals can have a substantial effect on the estimation of allele frequencies. However, such sampling noise likely acts to reduce our power to detect allele frequency clines. Second, Swedish populations of P. tremula show evidence for recent admixture between lineages originating from different glacial refugia (De Carvalho et al. 2010). The clines we observe could therefore be a product of gene flow between two partly divergent populations (De Carvalho et al. 2010), a view that is further supported by the presence of weak, but significant, isolation by distance we found in our study populations based on microsatellite data (Hall et al. 2007). We do not, however, observe any isolation by distance in the SNP data presented here (Mantel's test, P = 0.413). Furthermore, if clines were the product of admixture, we would expect a substantially greater number of loci to show clinal variation. The fact that we observe only four loci suggests that clinal variation is not common in P. tremula and these loci are hence more likely the product of spatially variable selection rather than admixture. De Carvalho et al. (2010) also showed that the cline for growth cessation in P. tremula is much steeper than linear at the center of the cline and the data are better described by a step cline. Steep phenotypic clines are expected on theoretical grounds (Barton 1999), but it is not clear whether clines at the underlying loci are also expected to be steeper than linear. To explore this, we fitted the nonlinear model from De Carvalho et al. (2010), which allows for a steeper slope in the center of the cline, to the individual SNPs showing allele frequency clines (Figure 1). However, in all cases allele frequency clines were best described by a simple linear change in allele frequency with latitude (data not shown), consistent with much weaker selection acting on individual QTL (Latta 1998; Barton 1999; Le Corre and Kremer 2003).
Theory predicts that when a quantitative trait is subject to diversifying selection in the face of substantial migration, average levels of genetic differentiation at individual loci controlling quantitative trait variation (QTL) can be hard to distinguish from genetic differentiation at completely neutral loci (Latta 1998; Whitlock 2002; Le Corre and Kremer 2003), suggesting that it might be difficult to identify QTL as outlier loci with unusually high levels of genetic differentiation. In accordance with this prediction we do not find any loci that show unexpectedly high levels of population structure among either the photoperiod or the control loci (Figure 2). Perhaps surprisingly this also applies to the four SNPs for which we demonstrate significant allele frequency clines and that hence are clear candidates for being influenced by spatially variable selection. The near complete lack of outlier loci can, at least partly, be ascribed to an ascertainment effect since we purposely selected SNPs that were relatively common across the sample range and that therefore are perhaps less likely to show large frequency differences between populations.
A growing number of studies have identified outlier loci exhibiting unusually high levels of genetic differentiation among populations, using genome-wide approaches (see, for instance, Nosil et al. 2009, for a recent review), while relatively few studies have taken a more targeted candidate gene approach that includes loci with known or suspected effects on the trait conferring local adaptation. Our results suggest that a genome-wide scan for loci with higher than expected FST values would have failed to identify all four SNPs that show clinal variation and hence strong evidence for spatially variable selection. We can think of two possible reasons for this: either our data from P. tremula are atypical in some way or genome-wide approaches will identify only a subset of loci subjected to divergent selection. In this respect, allele-frequency clines provide substantially stronger evidence for diversifying selection at, or near, these SNPs than patterns of genetic differentiation among populations.
Heterogeneity in levels of genetic differentiation:
Gene flow among populations in P. tremula is very high [genetic differentiation at neutral markers is FST = 0.018 (Hall et al. 2007), and the mean FST for the SNPs in this study is 0.017], and it is likely that the effects of migration overwhelm selection acting on individual causal SNPs and thus limit our ability to detect a signal of diversifying selection by yielding loci with unusually high levels of genetic differentiation. One observation supporting this interpretation is the significantly higher heterogeneity we observe among FST values for the photoperiod SNPs (k = 4.27) compared to control SNPs (k = 2.03, see also Figure 3). Thus, even though selection is not strong enough to generate FST values that are different enough from the background level of genetic differentiation to be classified as outliers, the variance in FST among QTL is higher than at putative neutral markers (Le Corre and Kremer 2003; Whitlock 2008). This suggests that diversifying selection is acting on at least a few of the photoperiod SNPs, but that selection is not strong enough to result in the identification of clear outlier loci using FST-outlier methods (Le Corre and Kremer 2003).
Parallel clines and the covariance of allelic effects:
Under strong diversifying selection and high levels of gene flow, theory predicts that population differences in the mean of a quantitative trait will partly be caused by positive covariances (that is, linkage disequilibrium) that build up between individual QTL (Latta 1998; Le Corre and Kremer 2003). We can also confirm this observation in our data, where several pairs of loci show what appears to be unusually large covariation of allelic effects on growth cessation across the latitudinal cline (Figure 3, Table 1). As predicted by theory, at least one locus, and in some cases both loci, from the five SNP pairs displaying the highest covariances also shows significant latitudinal allele frequency clines (Table 1). For instance, the locus pair with the highest observed covariance consists of the S681N SNP from LHY2 and the T1078P SNP from PHYB2 (Table 1). The covariance of allelic effects of the S681N/T1078P SNP pair is ∼25 standard deviations greater than the mean covariance seen among reference SNPs.
A similar approach to what we used here to study the effects of spatially divergent selection on allelic associations across populations was recently proposed by Storz and Kelly (2008). Storz and Kelly (2008) showed that spatially variable selection among altitudinal populations of deer mice (Peromyscus maniculatus), driven by differences in the partial oxygen pressure at low and high-altitude populations, results in strong between-population linkage disequilibrium at two α-globins. These α-globins were previously shown to contribute to differences in aerobic capacity between mice from low- or high-altitude populations and are hence likely candidate genes mediating local adaptation to variation in oxygen pressure (Storz et al. 2007). They also showed that while genetic differentiation between functionally distinct allelic classes at the two α-globin genes was strong, genetic differentiation between populations was not exceptionally high, presumably due to high levels of gene flow between populations (Storz and Kelly 2008). Storz and Kelly (2008) also concluded that causal substitutions would not have been identified on the basis of patterns of genetic differentiation alone, a pattern similar to what we observe in P. tremula (see above).
Phenotypic associations in the photoperiod pathway:
We identified five SNPs, three in PHYB2 and one each in LHY1 and LHY2, that are independently associated with naturally occurring variation in growth cessation (Table 2, Figure 4). Individually these SNPs explain between 6 and 12% of the observed genotypic variation in growth cessation and together the total variation explained is >30%. The naive estimation of the variation explained is likely overestimating the true effects of the mutations at least by two- to threefold, since these effects are estimated from a relatively small mapping population. In a previous study we used an ad hoc method (Allison et al. 2002) to show that the phenotypic effects of mutations are overestimated by two- to threefold (Ingvarsson et al. 2008). However, even if we take this into account, the five mutations likely explain 10–15% of the naturally occurring variation in growth cessation. Furthermore, this measures only the amount of variation explained by allelic variation at these five SNPs. As discussed above, theory predicts that a large fraction of the observed phenotypic variation is actually explained by positive covariances among causal SNPs that build up as allele frequencies change in parallel across populations (Latta 1998; Le Corre and Kremer 2003). Taking covariances between loci into account increases the variation explained to 42.5%, which corresponds to 14–21% after correcting for overestimation. This shows that 20–25% of the phenotypic variation observed in growth cessation cannot be attributed directly to individual SNPs but is rather explained by covariances among among individual causal mutations. Such covariances could thus make an important contribution to the proportion of variation explained in many quantitative traits and partly explain why the amount of variation explained is usually far below that predicted on the basis of heritabilities of the traits, a phenomenon highlighted in the human-genetics community as the “missing heritability problem” (Manolio et al. 2009).
Another potential bias affecting the amount of variation explained is that the SNPs we have identified may not be causal but are in fact only in imperfect LD with the true causal SNPs. These true causal SNPs can either be segregating at a lower frequency or occur in an unsampled region of the gene (e.g., regulatory regions in introns or untranslated regions) and in such cases the true QTL effect of the gene can be substantially larger than what we detected using the sampled SNPs. Given the low levels of LD observed in P. tremula, extending only a few hundred base pairs, we believe this is unlikely and we are reasonably confident that the SNPs we identified are the causal mutations. However, all associations will necessarily have to be verified either in an independent mapping population or using detailed functional studies.
Phytochrome signaling is known to be mediated through physical interactions between the Pfr form of the phytochrome protein and transcriptional regulators that are constitutively present in the nuclei before light signal perception (Martinez-Garcia et al. 2000). Interestingly, the phytochrome interacting protein PIF3 has been shown to bind to elements in the LHY promoters and PHYB then interacts with the promoter-bound PIF3, thereby inducing LHY expression (Martinez-Garcia et al. 2000). In view of these possible interactions between the PHYB and LHY genes, it interesting to note that the by far strongest covariance in effects across populations we observe among SNPs is between the L1078P SNP in PHYB2 and the S681N SNP in LHY2. The PHYB2 SNP (L1078P) occurs in a region of the PHY protein with poorly characterized function but that is possibly involved in mediating downstream signaling (Chen et al. 2004). The residue in LHY2 harboring the mutation that is significantly associated with growth cessation in P. tremula is highly conserved among other angiosperms. Interestingly, the same residue is segregating yet another amino acid in the closely related species P. nigra, and the mutation responsible for this amino acid substitution occurs at the same site that is polymorphic in P. tremula, although P. nigra harbors a third allelic state at this site (Takata et al. 2009).
The LHY protein itself is a core component of the central oscillator of the circadian clock and is crucial for sustaining circadian rythms in plants (Alabadi et al. 2001). In Arabidopsis and rice two homologous genes, LHY and CCA1, together with TOC1 make up the central oscillator of the circadian clock (Hayama and Coupland 2003;). The Arabidopsis LHY and CCA1 genes have partially redundant function but both are crucial for maintaining sustained circadian rhythms (Alabadi et al. 2001). Interestingly, Populus lacks a homolog of the CCA1 gene and it is possible that the two LHY homologs in Populus share the role that LHY/CCA1 has in other plants (Takata et al. 2009). Both LHY1 and LHY2 are functional in Populus, although LHY2 shows roughly fivefold higher expression than LHY1 in P. nigra (Takata et al. 2009). The Populus LHY1 paralog also has a mutation at a highly conserved Ser residue located upstream of the Myb DNA-binding domain of LHY1 that is likely involved in controlling protein phosphorylation (Takata et al. 2009). The loss of such a site has been hypothesized to contribute to altered functions of a protein and altogether this suggests that LHY2 is the primary LHY gene functioning in the circadian clock of Populus (Takata et al. 2009). However, both LHY paralogs retain a diurnal expression pattern it is therefore not clear whether the function of LHY1 is redundant to or distinct from that of LHY2 (Takata et al. 2009). Why both LHY homologs in P. tremula appear to be targets of natural selection in P. tremula is not clear at present. A more detailed functional characterization of the two LHY homologs is clearly needed to evaluate what possible function the two LHY mutations have in controlling natural variation in growth cessation in Populus.
Conclusions:
Most traits that influence fitness in natural populations are quantitative in nature and are hence controlled by many genes. Furthermore, these genes often interact in regulatory networks, and although most of these genes are potentially important in controlling the expression of a given trait, only a small fraction of these genes actually have ecologically relevant variation segregating in natural populations. For instance, >30 genes have been shown to be involved in regulating flowering time in Arabidopsis, and crossing experiments have identified at least 14 unique QTL (Koornneef et al. 2004). Nevertheless, two genes, FRI and FLC, explain >70% of the natural variation in flowering time among Arabidopsis accessions collected from the wild (Koornneef et al. 2004; although see Scarcelli et al. 2007 for a different view).
In this article we have shown that segregating variation in only three genes from the photoperiod pathway explains a significant proportion of naturally occurring variation in growth cessation, a highly adaptive trait in P. tremula. We also show that three of these SNPs can be identified as targets of spatially variable selection as indicated by the presence of allele frequency clines across a latitudinal gradient. However, none of these loci are identified as targets of diversifying selection on the basis of FST-outlier approaches. These seemingly contradictory observations actually fit theoretical predictions, which show that even fairly strong diversifying selection on a quantitative trait will have only relatively minor effects on allele frequencies at the underlying QTL (Latta 1998; Le Corre and Kremer 2003). Our analyses also show that even if selection at individual QTL is weak enough, relative to migration, to not identify individual loci as outliers in FST-based tests, selection is still strong enough to generate substantial heterogeneity in genetic differentiation among loci. This suggests that searching only for outlier loci, showing enhanced levels of genetic differentiation, can miss a large number of potential loci contributing to local adaptation, especially in species experiencing high levels of gene flow.
Acknowledgments
We are indebted to Carin Olofsson for DNA sequencing and SNP scoring. We are also grateful to O. Savolainen and two anonymous reviewers for constructive criticism on earlier versions of the manuscript. This study was funded by grants from the Swedish Research Council and the Research School in Forest Genetics and Breeding to P.K.I.
Supporting information is available online at http://www.genetics.org/cgi/content/full/genetics.110.120873/DC1.
References
- Alabadi, D., T. Oyama, M. J. Yanovsky, F. G. Harmon, P. MÁS et al., 2001. Reciprocal regulation between TOC1 and LHY/CCA1 within the Arabidopsis circadian clock. Science 293 880–883. [DOI] [PubMed] [Google Scholar]
- Allison, D. B., J. R. Fernadez, M. Heo, S. Zhu, C. Etzel et al., 2002. Bias in estimates of quantitative-trait-locus effect in genome scans: demonstration of the phenomenon and a method-of-moments procedure for reducing bias. Am. J. Hum. Genet. 70 575–585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barton, N. H., 1999. Clines in polygenic traits. Genet. Res. 74 223–236. [DOI] [PubMed] [Google Scholar]
- Beaumont, M. A., 2005. Adaptation and speciation: What can FST tell us? Trends Ecol. Evol. 20 435–440. [DOI] [PubMed] [Google Scholar]
- Beaumont, M. A., and D. J. Balding, 2004. Identifying adaptive genetic divergence among populations from genome scans. Mol. Ecol. 13 969–980. [DOI] [PubMed] [Google Scholar]
- Beaumont, M. A., and R. A. Nichols, 1996. Evaluating loci for use in the genetic analysis of population structure. Proc. R. Soc. Lond. B 263 1619–1626. [Google Scholar]
- Böhlenius, H., T. Huang, L. Charbonnel-Campaa, A. M. Brunner, S. Jansson et al., 2006. CO/FT regulatory module controls timing of flowering and seasonal growth cessation in trees. Science 312 1040–1043. [DOI] [PubMed] [Google Scholar]
- Chen, M., J. Chory and C. Frankhauser, 2004. Light signal transduction in higher plants. Annu. Rev. Genet. 38 87–117. [DOI] [PubMed] [Google Scholar]
- Chen, T. H. H., G. T. Howe and H. D. Bradshaw, 2002. Molecular genetic analysis of dormancy-related traits in poplars. Weed Sci. 50 232–240. [Google Scholar]
- Cremer, F., and G. Coupland, 2003. Distinct photoperiodic responses are conferred by the same genetic pathway in Arabidopsis and in rice. Trends Plant Sci. 8 405–407. [DOI] [PubMed] [Google Scholar]
- De Carvalho, D., P. K. Ingvarsson, J. Joseph, L. Suter, C. Sedivy et al., 2010. Admixture facilitates adaptation from standing variation in the European aspen (P. tremula L.), a widespread forest tree. Mol. Ecol. 19 1638–1650. [DOI] [PubMed] [Google Scholar]
- Di Giusto, D. A., and G. C. King, 2004. Strong positional preference in the interaction of LNA oligonucleotides with DNA polymerase and proofreading exonuclease activities: implications for genotyping assays. Nucleic Acids Res. 32 e32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eriksson, M. E., and A. J. Millar, 2003. The circadian clock. A plant's best friend in a spinning world. Plant Physiol. 132732–738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foll, M., and O. Gaggiotti, 2008. A genome-scan method to identify selected loci appropriate for both dominant and codominant markers: a Bayesian perspective. Genetics 180977–993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frewen, B. E., T. H. H. Chen, G. T. Howe, J. Davis, A. Rohde et al., 2000. Quantitative trait loci and candidate gene mapping of bud set and bud flush in Populus. Genetics 154837–845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gyllenstrand, N., D. Clapham, T. Källman and U. Lagercrantz, 2007. A Norway Spruce FLOWERING LOCUS T homolog is implicated in control of growth rhythm in conifers. Plant Physiol. 144248–257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall, D., 2010. Tracing selection and adaptation along an environmental gradient in Populus tremula. Ph.D. Thesis, Umeå University, Umeå, Sweden.
- Hall, D., V. Luquez, V. M. Garcia, K. R. St Onge, S. Jansson et al., 2007. Adaptive population differentiation in phenology across a latitudinal gradient in European aspen (Populus tremula, L.): a comparison of neutral markers, candidate genes and phenotypic traits. Evolution 612849–2860. [DOI] [PubMed] [Google Scholar]
- Hardy, O. J., and X. Vekemans, 2002. SPAGeDi: a versatile computer program to analyse spatial genetic structure at the individual or population levels. Mol. Ecol. Notes 2 618–620. [Google Scholar]
- Hayama, R., and G. Coupland, 2003. Shedding light on the circadian clock and the photoperiodic control of flowering. Curr. Opin. Plant Biol. 613–19. [DOI] [PubMed] [Google Scholar]
- Ingvarsson, P. K., 2008. Multilocus patterns of polymorphism and the demographic history of Populus tremula. Genetics 180329–340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingvarsson, P. K., M. V. Garcia, D. Hall, V. Luquez and S. Jansson, 2006. Clinal variation in phyB2, a candidate gene for day-length-induced growth cessation and bud set, across a latitudinal gradient in European aspen (Populus tremula). Genetics 1721845–1853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingvarsson, P. K., M. V. Garcia, V. Luquez, D. Hall and S. Jansson, 2008. Nucleotide polymorphism and phenotypic associations within and around the phytochrome B2 locus in European aspen (Populus tremula, Salicaceae). Genetics 1782217–2226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koornneef, M., C. Alonso-Blanco and D. Vreugdenhil, 2004. Naturally occurring genetic variation in Arabidopsis thaliana. Annu. Rev. Plant Biol. 55141–172. [DOI] [PubMed] [Google Scholar]
- Latta, R. G., 1998. Differentiation of allelic frequencies at quantitative trait loci affecting locally adaptive traits. Am. Nat. 151283–292. [DOI] [PubMed] [Google Scholar]
- Le Corre, V., and A. Kremer, 2003. Genetic variability at neutral markers, quantitative trait loci and trait in a subdivided population under selection. Genetics 164 1205–1219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewontin, R. C., and J. Krakauer, 1973. Distribution of gene frequency as a test of the theory of the selective neutrality of polymorphisms. Genetics 74 175–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luquez, V., D. Hall, B. R. Albrectsen, J. Karlsson, P. Ingvarsson et al., 2008. Natural phenological variation in aspen (Populus tremula): the SwAsp collection. Tree Genet. Genomes 4 279–292. [Google Scholar]
- Manolio, T. A., F. S. Collins, N. J. Cox, D. B. Goldstein, L. A. Hindorff et al., 2009. Finding the missing heritability of complex diseases. Nature 461 747–753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martínez-García, J. F., E. Huq and P. H. Quail, 2000. Direct targeting of light signals to a promoter element-bound transcription factor. Science 288 859–863. [DOI] [PubMed] [Google Scholar]
- Nicholson, G., A. V. Smith, F. Jónsson, Ó. Gústafsson, K. Stefánsson et al., 2002. Assessing population differentiation and isolation from single-nucleotide polymorphism data. J. R. Stat. Soc. Ser. B 64 695–715. [Google Scholar]
- Nosil, P., D. J. Funk and D. Orritz-Barrientos, 2009. Divergent selection and heterogeneous genomic divergence. Mol. Ecol. 18 375–402. [DOI] [PubMed] [Google Scholar]
- Ohta, T., 1982. Linkage disequilibrium with the island model. Genetics 101 139–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard, J. K., M. Stephens and P. J. Donnelly, 2000. Inference of population structure using multilocus genotype data. Genetics 155 945–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team, 2008. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna. http://www.R-project.org.
- Ritland, K., 1996. Estimators for pairwise relatedness and individual inbreeding coefficients. Genet. Res. 67 175–185. [Google Scholar]
- Scarcelli, N., J. M. Chevrud, B. A. Schaal and P. X. Kover, 2007. Antagonistic pleiotropic effects reduce the adaptive value of the FRIDIDA locus. Proc. Natl. Acad. Sci. USA 104 16986–16991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- St. Onge, K. R., 2006. Natural variation in Populus tremula flowering time gene PtCO2B. M.Sc. Thesis, Umeå Plant Science Centre, Umeå University, Umeå, Sweden.
- Storey, J. D., and R. Tibshirani, 2003. Statistical significance for genome-wide studies. Proc. Natl. Acad. Sci. USA, 100 9440–9445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storz, J. F, and J. K. Kelly, 2008. Effects of spatially varying selection on nucleotide diversity and linkage disequilibrium: insights from deer mouse globin genes. Genetics 180 367–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storz, J. F., S. J. Sabatino, F. G. Hoffman, E. J. Gering, H. Moriyama et al., 2007. The molecular basis of high-altitude adaptation in deer mice. PLoS Genet. 3 e45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takata, N., S. Saito, C. Tanaka Saito, T. Nanjo, K. Shinohara et al., 2009. Molecular phylogeny and expression of poplar circadian clock genes, LHY1 and LHY2. New Phytol. 181 808–819. [DOI] [PubMed] [Google Scholar]
- Whitlock, M. C., 2002. Selection, load and inbreeding depression in a large metapopulation. Genetics 160 1191–1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitlock, M. C., 2008. Evolutionary inference from QST. Mol. Ecol. 17 1885–1896. [DOI] [PubMed] [Google Scholar]
- Yu, J., G. Pressoir, W. H. Briggs, I. V. Bi, M. Yamasaki et al. 2006. A unified mixed-model method for association mapping accounting for multiple levels of relatedness. Nat. Genet. 38 203–208. [DOI] [PubMed] [Google Scholar]