Abstract
Background Meta-analysis of individual participant time-to-event data from multiple prospective epidemiological studies enables detailed investigation of exposure–risk relationships, but involves a number of analytical challenges.
Methods This article describes statistical approaches adopted in the Emerging Risk Factors Collaboration, in which primary data from more than 1 million participants in more than 100 prospective studies have been collated to enable detailed analyses of various risk markers in relation to incident cardiovascular disease outcomes.
Results Analyses have been principally based on Cox proportional hazards regression models stratified by sex, undertaken in each study separately. Estimates of exposure–risk relationships, initially unadjusted and then adjusted for several confounders, have been combined over studies using meta-analysis. Methods for assessing the shape of exposure–risk associations and the proportional hazards assumption have been developed. Estimates of interactions have also been combined using meta-analysis, keeping separate within- and between-study information. Regression dilution bias caused by measurement error and within-person variation in exposures and confounders has been addressed through the analysis of repeat measurements to estimate corrected regression coefficients. These methods are exemplified by analysis of plasma fibrinogen and risk of coronary heart disease, and Stata code is made available.
Conclusion Increasing numbers of meta-analyses of individual participant data from observational data are being conducted to enhance the statistical power and detail of epidemiological studies. The statistical methods developed here can be used to address the needs of such analyses.
Keywords: Meta-analysis, epidemiological studies, individual participant data, statistical methods, survival analysis
Introduction
Combining information across several studies using meta-analysis can enhance precision for quantitative summaries of evidence.1 Re-analysis of individual participant data (IPD) from multiple epidemiological studies has several advantages compared with meta-analysis of aggregated published data, including harmonization of definitions for risk markers as well as disease outcomes; ability to update follow-up information; consistent approaches to adjustment for confounding; characterization of the shape of exposure–risk relationships; greater ability to correct for regression dilution bias; and determination of how exposure–risk relationships depend on age, sex and other potential effect modifiers.2–4 This article describes and illustrates statistical methods that are being used in the Emerging Risk Factors Collaboration (ERFC), an analysis of individual records from more than 1.2 million participants in 116 prospective studies in predominantly Western populations of major cardiovascular disease outcomes.5–8 The ERFC includes mostly prospective cohort studies (a few based in randomized trials), as well as some nested case–control and case–cohort studies. For each participant in the ERFC, the coordinating centre has collated, verified and harmonized individual records on baseline risk markers, confounders, other characteristics, major cardiovascular morbidity and cause-specific mortality.5 Available repeat survey data, which provide serial measurements, have also been collected to help address measurement error and within-person variability.3,9
As the ERFC subsumes the Fibrinogen Studies Collaboration,10 we have illustrated the statistical methods used in the ERFC by analysis of plasma fibrinogen concentration and the risk of coronary heart disease (CHD) in the Fibrinogen Studies Collaboration dataset involving individual data on 154 211 participants from 31 prospective studies. CHD is defined as first non-fatal myocardial infarction or coronary death in those without known cardiovascular disease at the initial examination.10 A total of 7118 CHD events occurred during an average of 9 years of follow-up. Across the 31 studies, the number of CHD events ranged from 17 to 1474 and the follow-up ranged from 4 to 33 years; the crude mean fibrinogen was 3.02 g/l [pooled within-study standard deviation (SD) 0.65 g/l].
Methods and illustrative analyses
Principal meta-analysis methods
This exposition initially assumes all data are derived from prospective cohorts; other designs are addressed towards the end of the article. The main analyses are based on Cox proportional hazards (PH) models,11 estimated for each study separately. The PH models are stratified by sex and, if applicable, randomized group. So separately for each study s = 1 … S, with strata k = 1 … Ks (for most studies, Ks = 2 just for the two sexes) and individuals i = 1 … ns, with exposure of interest Esi and other covariates Xsi, the hazard at time t after baseline is modelled as
| (1) |
The evolution of risk over time is thus modelled independently for each stratum in each study, as represented by the non-parametric baseline hazards h0sk(t). The βs are the parameters of interest, being the log hazard ratios (HRs) per unit increase in the exposure in study s, adjusted for the confounding effects of the covariates Xsi.
These estimated log HRs can be combined over studies using random-effects meta-analysis,12 which incorporates heterogeneity between studies as described below. Fixed-effects meta-analysis can also be used3,13,14 and has been employed in parallel analyses in the ERFC. Writing the variance of the estimated βs as vs, the random-effects meta-analysis model is given by
| (2) |
Here β is the average log HR, the estimate of which combines within-study information on the relationship between exposure and risk, while allowing for heterogeneity in the true log HRs between studies as represented by the variance τ2. A standard moment estimator of τ2 is used,15 although other estimation methods are available.16 The statistical significance of the standard test for heterogeneity17 reflects the strength of evidence for heterogeneity. The impact of heterogeneity on the imprecision of the overall log HR is expressed in terms of I2, the percentage of variance in the point estimates of the study-specific log HRs that is attributable to between-study variation as opposed to sampling variation,18 for which a confidence interval (CI) is also available.19 Values of I2 close to 0% correspond to lack of heterogeneity. In addition, specific sources of heterogeneity are explored by investigating the impact of various factors (e.g., age, sex and other potential effect modifiers) on the strength of the association between exposure and risk, as described in later sections.
The above procedure is a two-step method: first, each study is analysed separately in (1) and then the log HRs are combined in (2). A one-step method would be preferable in principle, writing a combined model as
| (3) |
Computational problems are, however, formidable in a dataset the size of the ERFC.20 A two-step analysis has only the slight disadvantage that the first-step variances vs in a two-step analysis are not in general exactly those implied in a one-step method, although one-step and two-step methods usually produce very similar results.21,22
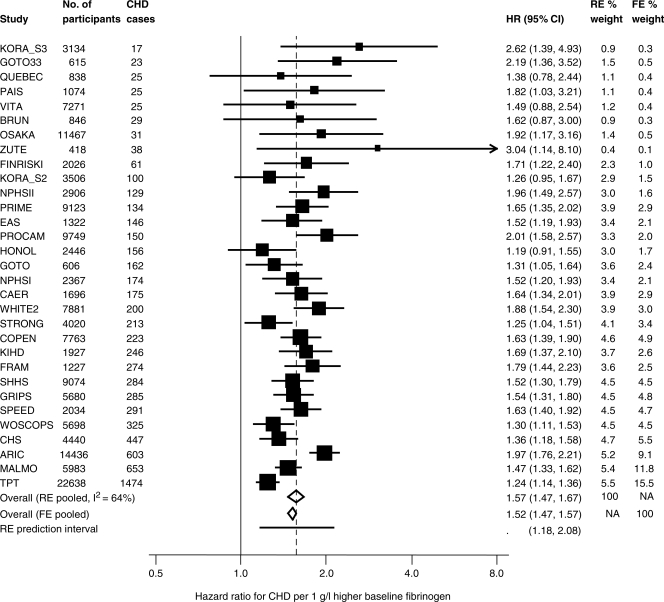
For the case of fibrinogen and the risk of CHD, adjusting only for the linear effect of age at baseline in each study, these analyses are summarized in the upper part of Table 1. The study-specific HRs are shown in Figure 1. The random-effects combined HR exp(β) is estimated as 1.57 (95% CI 1.47–1.67) per 1 g/l higher baseline fibrinogen concentration, and an I2 of 64% (95% CI 48–76) indicates substantial heterogeneity across studies (test for heterogeneity, P < 0.0001). By comparison, a fixed-effects meta-analysis estimate gives a lower point estimate of 1.52 with a narrower 95% CI of 1.47–1.57.
Table 1.
Combined HRs for the relationship between baseline fibrinogen (g/l) and CHD risk, adjusted for a linear effect of age at baseline in each study separately
| Method | HR (95% CI) | Log HR, 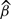 (SE) (SE) |
Heterogeneity |
||
|---|---|---|---|---|---|
Between-study variance 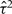
|
P-value | I2 (95% CI) | |||
| Untransformed fibrinogen: log HRs per 1 g/l increase | |||||
| Random-effects meta-analysis | 1.57 (1.47–1.67) | 0.450 (0.033) | 0.018 | <0.0001 | 64% (48, 76) |
| Fixed-effects meta-analysis | 1.52 (1.47–1.57) | 0.419 (0.018) | NA | <0.0001 | NA |
| Transformed fibrinogen: log HRs per SD increase—random-effects meta-analysis | |||||
| Untransformed fibrinogen | 1.34 (1.29–1.40) | 0.294 (0.022) | 0.008 | <0.0001 | 64% (48, 76) |
| Log fibrinogen | 1.38 (1.32–1.45) | 0.325 (0.025) | 0.010 | <0.0001 | 65% (48, 76) |
| Study-specific SD score fibrinogen | 1.34 (1.29–1.40) | 0.292 (0.021) | 0.007 | <0.0001 | 63% (45, 75) |
| Study-specific SD score log fibrinogen | 1.37 (1.31–1.44) | 0.316 (0.024) | 0.009 | <0.0001 | 64% (47, 76) |
| Untransformed fibrinogen | |||||
| Quadratic term for fibrinogen | 0.96 (0.91–1.01) | −0.045 (0.027) | 0.007 | 0.013 | 40% (7, 61) |
NA: not applicable; SE: standard error.
Figure 1.
Study-specific HRs and 95% CIs (log scale) for the relationship of baseline fibrinogen with CHD in 31 studies, and meta-analysis. A 95% prediction interval for the true HR in a new study is also shown. Results are adjusted for age at baseline as a linear term. For acronyms to studies, see Ref. 10. RE, random effects; FE, fixed effects; NA, not applicable.
The above estimates and CIs relate to the overall mean HR across all studies. Also of interest is the range of true HRs across studies, representing those in different contexts or populations. It can be expressed by the 95% prediction interval for the true HR in a new study and is estimated from the random-effects meta-analysis by 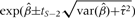 , where t is the 2.5-percentile of a t-distribution and S is the number of studies.12 In the case of the fibrinogen data, this 95% prediction interval is 1.18–2.08. Because of the presence of heterogeneity, this interval is much wider than the 95% CI for exp(β), as shown at the bottom of Figure 1, but remains above 1, indicating that the relationships in different studies are consistently positive.
, where t is the 2.5-percentile of a t-distribution and S is the number of studies.12 In the case of the fibrinogen data, this 95% prediction interval is 1.18–2.08. Because of the presence of heterogeneity, this interval is much wider than the 95% CI for exp(β), as shown at the bottom of Figure 1, but remains above 1, indicating that the relationships in different studies are consistently positive.
Choice of exposure scale
An assumption of the above model is that the log HR increases linearly with the exposure. It might be more appropriate, however, to choose a log scale for some exposures to improve linearity. Alternatively, the use of a study-specific SD score might reduce heterogeneity of the risk association between studies. In the case of fibrinogen, for example, the distributions were slightly positively skewed and the SD varied considerably between studies.23 It is also important to assess the possibility of non-linear risk relationships that could indicate a threshold or a plateau for risk.
To assess linearity, as in previous studies,3 the distributions of the exposure are divided into quantile groups such as fifths; such quantile groups can be defined within each study or across all studies. HRs in each quantile group, compared with the bottom group, are estimated by using Cox PH regression in each study separately. These log HRs within each study are not independent (their correlations are available from standard regression software), because they are all relative to the same reference group. So the set of log HRs are pooled across studies using a multivariate version of random-effects meta-analysis24,25 to allow for their inter-correlations both within and between studies. These pooled log HRs are plotted against the mean exposure level in each quantile group. Assessing linearity is easier using CIs derived by floating absolute risk methods26,27 so that each estimate (including that for the reference category) has a measure of uncertainty and is less correlated with the others. Judging linearity visually from strongly correlated estimates can be misleading: for example, if the reference group is small, then all the standard CIs will be wide and non-linearity cannot be ruled out. Sensitivity analyses, employing different scales for the exposure (e.g. log, SD score) or assessing curvature using polynomial terms, are also used to investigate whether heterogeneity between studies is reduced or the substantive conclusions affected.
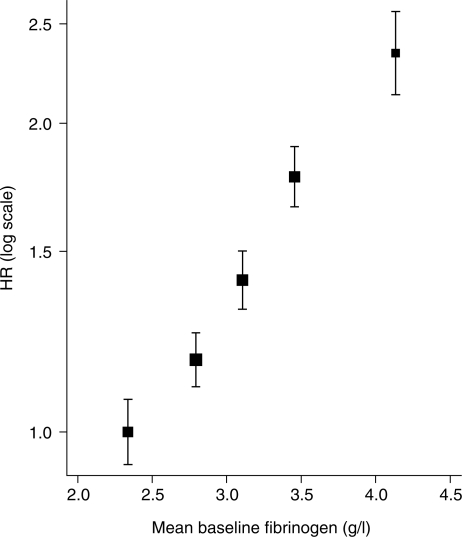
Figure 2 shows the results of an analysis by study-specific fifths of fibrinogen in relation to CHD risk, which suggests that a log-linear model for risk is satisfactory.10 Examples of sensitivity analyses are shown in the lower part of Table 1. These compare untransformed fibrinogen, log fibrinogen, study-specific SD fibrinogen score, and study-specific SD log fibrinogen score. For comparability, results are expressed as the HR per 1-SD higher baseline fibrinogen; in the first two analyses, this refers to the pooled within-study SD (0.65 g/l for untransformed fibrinogen). The results from all analyses are quantitatively similar, including the extent of heterogeneity. Including a quadratic term for untransformed fibrinogen in the first analysis provides little evidence of curvature in the risk relationship (P = 0.09). In the case of fibrinogen, therefore, the heterogeneity between studies is not due to the choice of exposure scale.
Figure 2.
Combined log HRs with 95% CIs based on floating absolute risks for the relationship between baseline fibrinogen (g/l) and CHD risk, plotted against mean baseline fibrinogen in fifths. From multivariate random-effects meta-analysis, adjusted for a linear effect of age at baseline in each study separately.
A few technical issues in such analyses merit consideration. First, the visual assessment of linearity and the comparison between different exposure scales are informal. Second, although it might be preferable to use fractional polynomials28 or splines29 to investigate curvature, this is not straightforward in a two-step random-effects meta-analysis, because different functional forms might be appropriate for different studies. These problems would be reduced if one-step meta-analysis methods were computationally feasible. Thirdly, in Figure 2, the choice of fifths is rather arbitrary, and it is not entirely clear what levels of fibrinogen the log HRs should be plotted against; for example, this could be the mean fibrinogen in each fifth weighted by the number of events rather than by the number of participants. Finally, the effect of measurement error and within-person variation in fibrinogen may distort the shape of the exposure–disease relationship, as discussed later.
Covariate adjustment
Age is the most important confounder in many epidemiological applications, so adjustment for age demands particular attention. For linear terms, age-at-baseline in a PH model is equivalent to including current age as a time-dependent variable, but the latter is computationally more difficult to fit. Assuming a simple linear term for age at baseline may, however, be inadequate, resulting in residual confounding. Alternatives include adjustment or stratification by age categories at baseline, as well as inclusion of polynomial terms and interactions with other covariates (especially sex). Empirical comparison of alternatives as sensitivity analyses is useful to check for adequate age adjustment. In principle, similar considerations apply to other covariates, but in practice, the use of linear terms is usually sufficient unless the covariates are both highly prognostic and substantially correlated with the exposure of interest. One important practical problem often encountered is that not all studies measure all the desired confounders; an approach to this situation is described under section ‘Discussion’.
The ERFC’s two-step approach allows the confounding effects (γs in model 1) to be different in each study. Examples of age and other confounder adjustments for the fibrinogen dataset are given in Table 2. In this case, linear adjustment for age at baseline appears to be adequate, because more complex forms of adjustment hardly change the results. No precision is lost by stratification using narrow age bands. The overall HR for fibrinogen is reduced towards unity on adjusting for four additional covariates (last row in Table 2), and the extent of heterogeneity decreases. Thus, some of the original heterogeneity between studies seems to be due to differing impacts of these confounders in different studies. The age-adjusted HR per 1 g/l higher baseline fibrinogen falls from 1.57 to 1.38 on adjusting for these covariates, so 29% [calculated as (log 1.57−log 1.38)/log 1.57] of the effect is ‘explained’ by the observed values of these confounders. The change in the respective Wald 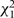 statistics reflects a slight decrease in the strength of evidence for an association.3
statistics reflects a slight decrease in the strength of evidence for an association.3
Table 2.
Combined HRs for CHD per 1 g/l increase in baseline fibrinogen: random-effects meta-analysis adjusting for baseline confounding variables
| With adjustment for | HR (95% CI) | Log HR 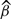 (SE) (SE) |
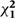 |
Heterogeneity |
||
|---|---|---|---|---|---|---|
Between-study variance 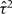
|
P-value | I2 (95% CI) | ||||
| Age | 1.57 (1.47–1.67) | 0.450 (0.033) | 181 | 0.018 | <0.0001 | 64% (48, 76) |
| Age as 5-year age bands | 1.57 (1.47–1.68) | 0.451 (0.033) | 183 | 0.018 | <0.0001 | 64% (48, 76) |
| Stratification by 5-year age bands | 1.57 (1.47–1.68) | 0.451 (0.033) | 182 | 0.018 | <0.0001 | 64% (48, 76) |
| Age sex × age | 1.57 (1.47–1.68) | 0.450 (0.034) | 180 | 0.018 | <0.0001 | 65% (48, 76) |
| Age age2 | 1.56 (1.46–1.67) | 0.447 (0.033) | 179 | 0.018 | <0.0001 | 64% (48, 76) |
| Age age2 sex × age sex × age2 | 1.57 (1.47–1.67) | 0.448 (0.034) | 177 | 0.019 | <0.0001 | 65% (49, 76) |
| Age smoking tchol sbp bmia | 1.38 (1.31–1.45) | 0.320 (0.026) | 156 | 0.006 | 0.028 | 35% (0, 58) |
SE: standard error.
aSmoking coded as current vs other; tchol: total cholesterol; sbp: systolic blood pressure; bmi: body mass index.
Joint effects
An important advantage of IPD is that it provides the opportunity for systematic investigation of the exposure–risk relationship at different levels of other variables. This evaluation of factors that modify the overall log HRs estimated above involves assessing their interactions on this scale with the exposure of interest. When effect modifiers are variables measured in individuals, such as age or other risk markers, these interactions are most effectively assessed using within-study information.4,30 Here a two-step procedure has again been adopted, first estimating the interaction in each study separately. For example, for a single potential effect modifier Xsi, the model in study s is
| (4) |
The estimates of the interaction terms δs are combined using random-effects meta-analysis, as in (2). The overall interaction, δW, is then based on only within-study information. Model (4) can be extended by including adjustments for other confounders, and indeed their interactions with the exposure of interest; this enables investigation of whether, as is possible, a particular interaction is confounded by other main effects or interactions.
Some potential effect modifiers are assessed only at the study level; for example, the type of population recruited or the laboratory methods used for measuring the exposure. For such variables, any information on interactions relies entirely on between-study comparisons, which are assessed using random-effects meta-regression.31 Using the estimates of βs from (1), model (2) is extended to include a study level covariate Xs by writing
| (5) |
δB is the between-study interaction term, with statistical significance assessed allowing for the residual between-study heterogeneity τ2.
A few variables, notably sex and ethnic group, have potential interactions for which both within-study and between-study information may be important. For example, studies involving both men and women provide within-study information on sex interactions, whereas studies that comprise members of one sex alone can only be used to assess interactions across studies. In this case, the within-study interaction δW is estimated as in model (4) based on studies of both sexes, and the between-study interaction δB is estimated using model (5) in which Xs is the proportion of women in each study. Provided they are similar, these two asymptotically independent estimates of interaction can themselves be combined. As between-study information on interactions is prone to numerous potential sources of between-study confounding,32 there is a trade-off between increased precision and possible bias in choosing whether to use between-study information in addition to within-study information.22,33,34
Presenting interactions in a way that is intelligible to readers is not easy. For a binary variable identifying two subgroups, the exponent of the interaction term is a ratio of HRs, but it is simpler to present two separate meta-analyses, one in each subgroup. However, because the between-study heterogeneity, τ2 in (2), now affects each of these estimates, the (multivariate) meta-analytic weighting of study-specific subgroup estimates is different from the weighting of study-specific interactions. So neither the estimates nor the CIs of the subgroup-specific estimates are necessarily compatible with the estimate and CI of the interaction term. In practice, this problem is not usually severe. For continuous variables, the exponent of the interaction term is a ratio of HRs per unit increase in the effect modifier. Similarly, for presentation, it is easier to present the HR estimates according to study-specific quantile groups (e.g. thirds or fifths) of the effect modifier distribution.
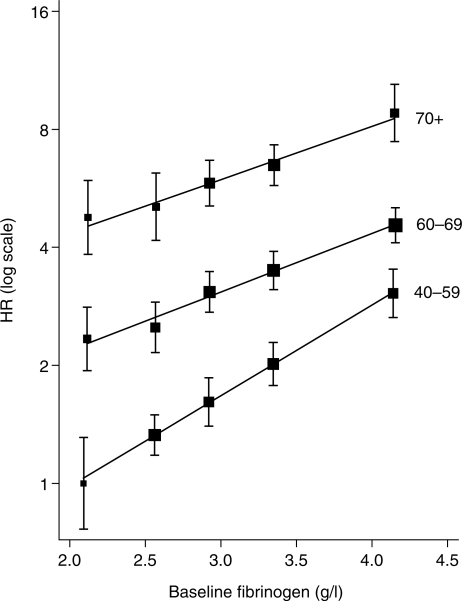
Examples of interaction analyses for fibrinogen are shown in Table 3. The interactions with body mass index and age at baseline are clear, but the interactions with other variables are less marked. Including the body mass index and age interactions simultaneously hardly affect their respective estimates. There is more consistency in the interaction terms across studies than for the main effect of fibrinogen, as indicated by the lower values of I2. For investigating a possible sex interaction, δB is estimated from a meta-regression of the study-specific log HRs on the proportion of women in each study. The SE of the interaction term is smaller for δW than δB, so the majority (73%) of the information comes from within-study information. It is sensible to rely on the within-study pooled interaction estimate, especially when it contributes the majority of the information, because of the potential for bias in the between-study estimate.22 The sex-specific combined log HRs (not shown) and the combined sex interaction term are similar but not identical. The sex interaction term represents the correct analysis, whereas the sex-specific HRs are probably the preferable method of presentation in applied publications, especially when given in a diagram. As noted above, effect modification is being assessed on the HR scale. Thus, although the HRs per unit higher fibrinogen decrease with increasing age, the absolute risk gradients increase (Figure 3).
Table 3.
Interactions between baseline fibrinogen (g/l) and potential effect modifiers for risk of CHD: differences in log HRs adjusted for the main effects of baseline age, smoking, total cholesterol, systolic blood pressure and body mass index
| Potential effect modifier | Estimated interaction between the potential effect modifier and fibrinogen |
||||
|---|---|---|---|---|---|
| Number of cohorts | Number of subjects | Estimate δ (SE) | P-value | Heterogeneity I2 (95% CI) | |
| Age (10 years) | 31 | 154 211 | −0.095 (0.029) | 0.001 | 0% (0, 40) |
| Systolic blood pressure (10 mmHg) | 31 | 154 211 | −0.021 (0.010) | 0.032 | 21% (0, 50) |
| Body mass index (5 kg/m2) | 31 | 154 211 | −0.079 (0.023) | <0.0001 | 3% (0, 31) |
| Total cholesterol (1 mmol/l) | 31 | 154 211 | −0.025 (0.014) | 0.081 | 1% (0, 41) |
| Sex: women vs men | |||||
| Between-study interaction | 31 | 154 211 | 0.120 (0.092) | 0.21 | NA |
| Within-study interaction | 16 | 90 529 | 0.089 (0.061) | 0.15 | 0% (0, 52) |
| Overall pooled interactiona | 31 | 154 211 | 0.098 (0.051) | 0.054 | NA |
NA: not applicable; SE: standard error.
aMeta-analysis of between-study and within-study interactions.
Figure 3.
Interaction of baseline fibrinogen and age, derived from a proportional hazards model with time-dependent effect of age in each study and combined using multivariate random-effects meta-analysis. Log HRs with 95% CIs based on floating absolute risks, plotted against mean baseline fibrinogen in fifths.
Proportional hazards
An assumption of all the models considered so far is of PH, meaning that the regression coefficients in model (1) do not change with time since baseline measurement. Although the effect of any covariate measured at baseline may plausibly decrease over time, the prime interest is whether the PH assumption is appropriate for the exposure of interest. This can be evaluated in each study separately by including an interaction between the exposure and time, or by the commonly used diagnostic tool based on Schoenfeld residuals.35 These independent 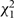 statistics can be summed across the S studies, yielding a
statistics can be summed across the S studies, yielding a 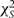 statistic testing the hypothesis that PH holds in each study.
statistic testing the hypothesis that PH holds in each study.
This approach is, however, not a powerful test against the plausible alternative hypothesis that HRs tend to decline over time in all studies. A better method is to combine the interaction terms between the exposure and time over studies. Using random-effects meta-analysis, and assuming linear time-dependence, the model is given by
| (6) |
where βs are separate fixed effects, and the focus is on the estimate of ξ, which can be tested using a 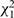 statistic.
statistic.
The results of these analyses for fibrinogen are shown in Table 4. The summed 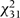 statistics are less than expectation, as is the more powerful
statistics are less than expectation, as is the more powerful 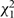 statistic. So, in this case (and perhaps surprisingly given the extent of data), there is no evidence of departures from PH for fibrinogen and no evidence of heterogeneity between studies in this regard. The final method provides an estimate of the non-PH parameter ξ, which indicates that over a 20-year period the estimated change in the exposure log HR is small. In ERFC, this random-effects pooling of the interaction terms between exposure and time is used to assess the PH assumption. It provides extra power against a plausible alternative hypothesis and is consistent with the approach described above for quantifying other interactions. If there was substantial evidence against the PH assumption, it would be necessary to summarise the exposure–risk relationship either in discrete intervals of time or as a trend over time.
statistic. So, in this case (and perhaps surprisingly given the extent of data), there is no evidence of departures from PH for fibrinogen and no evidence of heterogeneity between studies in this regard. The final method provides an estimate of the non-PH parameter ξ, which indicates that over a 20-year period the estimated change in the exposure log HR is small. In ERFC, this random-effects pooling of the interaction terms between exposure and time is used to assess the PH assumption. It provides extra power against a plausible alternative hypothesis and is consistent with the approach described above for quantifying other interactions. If there was substantial evidence against the PH assumption, it would be necessary to summarise the exposure–risk relationship either in discrete intervals of time or as a trend over time.
Table 4.
Non-PHs for CHD risk assessed by the interaction of baseline fibrinogen (g/l) and time (years)
| Method | Estimated non-PH parameter, ξ (SE) | χ2 test |
Heterogeneity | |
|---|---|---|---|---|
| χ2 (df) | P-value | I2 (95% CI) | ||
Summed 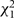 statistics of non-PH parameter from each study statistics of non-PH parameter from each study |
NA | 24 (31) | 0.80 | NA |
Summed 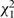 statistics from tests of Schoenfeld residuals in each study statistics from tests of Schoenfeld residuals in each study |
NA | 21 (31) | 0.90 | NA |
| Random-effects meta-analysis of study-specific non-PH parameters | 0.0016 (0.0045) | 0.12 (1) | 0.73 | 0% (0, 40) |
The models include adjustment for age at baseline as a linear term. NA: not applicable; SE: standard error; df: degrees of freedom.
Other topics
When the focus is on estimating underlying aetiological associations, it is necessary to adjust for the effect of measurement error and within-person variation. For the exposure of interest, this addresses the often serious underestimation caused by regression dilution bias,9,36,37 and for covariates it reduces residual confounding.38 Methods exist to correct for regression dilution bias in exposure variables in IPD meta-analysis.3,13,14 Novel methods that enable concurrent adjustment for measurement error both in the exposure of interest and in covariates have been developed for use in the multiple study context of the ERFC, but they are technically demanding and have been described in full elsewhere.39,40 Examples of these analyses for fibrinogen are shown in Table 5. Because the within-person correlation of fibrinogen measurements on different occasions is ∼0.5,39 the overall log HR corrected for measurement error in fibrinogen alone is about twice the uncorrected estimate (leading to a corrected HR of 1.96 vs 1.38 uncorrected). Multivariate correction for measurement error in four confounders makes the log HR for fibrinogen slightly less extreme, as expected because residual confounding is reduced, with an estimated HR of 1.85 per 1 g/l higher ‘usual’ (i.e. long-term average) fibrinogen level. As methods that correct for regression dilution cannot correct for unmeasured covariates, residual confounding may persist after their use.
Table 5.
Combined HRs for CHD per 1 g/l increase in fibrinogen, corrected for measurement error
| Measurement error correction | HR (95% CI) | Log HR (SE) |
|---|---|---|
| No measurement error correction | 1.38 (1.31–1.45) | 0.320 (0.026) |
| Measurement error in fibrinogen | 1.96 (1.76–2.17) | 0.672 (0.053) |
| Measurement error in fibrinogen, smoking, total cholesterol, systolic blood pressure and body mass index | 1.85 (1.66–2.06) | 0.617 (0.055) |
SE: standard error. All analyses are adjusted for age at baseline, sex, smoking, total cholesterol, systolic blood pressure and body mass index.
Some cohorts in the ERFC have analysed particular risk markers in a nested case–control or case–cohort design. Nested case–control studies are analysed with similar methods to those described for cohort studies, but they involve logistic regression.41 For individually matched studies, conditional logistic regression is appropriate. For frequency-matched studies, ordinary logistic regression is used with the matching factors as covariates. Such analyses either provide estimates of HRs (if matched controls were selected to be disease-free at the time the case had an event) or odds ratios (if the selected controls were disease-free at the end of the study).42 Provided the disease is relatively rare (say <10% of the study participants), odds ratios approximate HRs and it is reasonable to combine them in a meta-analysis. For nested case–cohort studies, the analysis should allow for the fact that some members of the randomly selected cohort also become cases.43 A modified PH regression model then provides estimates of log HRs with robust standard errors,44 although this modification generally has only a small effect.
Although some participants may have multiple events (e.g. two CHD events at separate time points, or a CHD event followed by another type of event, such as a stroke or death from cancer), analyses in the ERFC focus on first events by censoring participants after their first CHD event, after another non-fatal event such as stroke (when cohorts have recorded them), and after death from any cause. The rationale for this approach is that major cardiovascular disease events may disrupt the association between baseline risk factors and subsequent disease risk. The ERFC does not, however, censor individuals at the time of cardiovascular investigations or interventions (such as angiography or coronary bypass operations) or at the diagnosis of angina because the incidence of such occurrences is not recorded reliably enough in sufficient studies. Sensitivity analyses that implement alternative censoring criteria can assess potential biases that might arise through these decisions on censoring.
The constraints on comprehensiveness in IPD meta-analyses mainly relate to the identification of relevant studies and provision of data. In the ERFC, studies have been identified from publications, extensive literature searches, and correspondence with authors of relevant reports. The ERFC has included the large majority of Western prospective studies with any relevant exposure markers and >20 000 person-years of follow-up. Hence, although publication and reporting biases are potential concerns in all meta-analyses, they may be less so in the ERFC.
Discussion
The statistical methods used in the ERFC have been explicitly described and illustrated in this article to facilitate their adoption by others; example programs in Stata45 are available from http://www.phpc.cam.ac.uk/MEU/ERFC/Software.html. The ERFC methods extend previous approaches in several respects.46–48 Strategies being used in the ERFC to adjust for measurement error concurrently in levels of both confounders and exposures should help improve estimates of the underlying aetiological association between exposures and disease outcomes by reducing residual confounding. Methods used in the ERFC give specific consideration to the analysis of interactions for characteristics that vary both within and between studies and to assessment of the PH assumption.
A common practical problem in IPD meta-analyses is how to adjust for confounders that are measured only in a subset of the studies. For the fibrinogen example, age and four other confounders (Table 2) were measured in all participants in all studies. However, additional confounders, such as lipid fractions (high-density lipoprotein cholesterol, low-density lipoprotein cholesterol and triglycerides), were available in only about half of the studies.10 More comprehensive adjustment for confounding can only be easily achieved by restricting the dataset to the latter studies, but such restriction omits information on partial adjustment from the other studies. We have previously described an approach that uses the partially adjusted HRs, which can be estimated in all studies, and the more comprehensively adjusted log HRs, which can be estimated only in a subset of studies, in a bivariate meta-analysis.49 This approach acknowledges the correlations between the partially and the more comprehensively adjusted log HRs within studies in which both can be estimated but uses the full dataset to contribute to the estimation of a combined more comprehensively adjusted log HR.
An unresolved issue concerns the estimation of a possibly non-linear exposure–risk relationship when the exposure is measured with error. Homogeneous measurement error, with a variance that does not depend on level of the exposure, will tend to make a non-linear association appear more linear. Conversely, measurement error that, for example, increases with level of the exposure will make a linear association appear non-linear. Characterizing the shape of the underlying exposure–disease relationship, while taking into account possibly heterogeneous measurement error, is not well studied, especially in the context of IPD meta-analysis.50 One approach may be to model the underlying association using fractional polynomials or splines, while carefully estimating measurement error variance as a function of exposure level.
As distinct from characterizing the shape, magnitude and independence of associations between risk factors and disease (which may be relevant to judgements about an exposure’s potential aetiological relevance), IPD meta-analyses of multiple studies can provide additional useful information. For example, we have previously described the ERFC’s approach to characterizing the cross-sectional correlates (and, hence, potential determinants) of risk markers.23 Although this article has not addressed issues related to risk prediction (i.e. the extent to which measuring an additional exposure could better identify the risk of disease outcomes for individuals), there is considerable interest in the use of information from multiple prospective studies to help inform risk stratification and/or screening strategies. A separate literature exists that involves discussion of how the ‘area under an Receiver operating characteristic (ROC) curve’ can be adapted for time-to-event data51 and the extent to which individuals are re-classified into risk groups that would affect the subsequent intervention offered.52,53 We have adapted and illustrated some of these predictive metrics for use in the multiple study situation,54 and further such work comprises a future methodological research agenda.
Increasing numbers of IPD meta-analyses of observational data are being conducted in order to enhance the statistical power and detail of epidemiological studies. The scientific value of such approaches has now been demonstrated in relation to various exposures and disease outcomes in many different consortia, exemplified by the Prospective Studies Collaboration,3 the Asia Pacific Cohort Studies Collaboration,55 the Breast Cancer Genetics Linkage Consortium,56 the Collaborative Group on Hormonal Factors in Breast Cancer,57 the US Pooling Project of Prospective Studies of Diet and Cancer47 and the GENOMOS Genetic Markers for Osteoporosis Consortium.58 The statistical methods developed here can be used to address the needs of such analyses. Appropriate meta-analytical methods may also have applications to analyses of large purpose-designed multi-centre prospective observational studies, such as the pan-European EPIC study,59 UK Biobank60,61 and the subsequent planned meta-analysis of such studies.62
Funding
Methodological work in the ERFC has been supported by specific grants from the UK Medical Research Council. The ERFC Coordinating Centre is underpinned by a programme grant from the British Heart Foundation and supported by the BUPA Foundation and unrestricted educational grants from GlaxoSmithKline. Various sources have supported recruitment, follow-up and laboratory measurements in the cohorts contributing to the ERFC. Investigators of several of these studies have contributed to a list naming some of these funding sources, which can be found at http://www.phpc.cam.ac.uk/MEU/.
Conflict of interest: None declared.
KEY MESSAGES.
Summarizing exposure–risk relationships on the basis of individual time-to-event data from multiple studies enhances the detail and power of epidemiological analyses.
A two-step meta-analysis method is proposed to combine study-specific associations estimated by using Cox regression.
These methods allow investigation of the appropriate exposure scale, adjustment for confounders, and checking the proportional hazards assumption.
Within-study and between-study information for interactions need to be distinguished.
More technically demanding issues include adjustment for measurement error and within-person variation, and handling confounders that are not measured in all studies.
Appendix
List of Authors: (Appendix 1 in Ref. 5 lists the study acronyms).
Writing Committee: SG Thompson DSc, MRC Biostatistics Unit, UK; S Kaptoge PhD, University of Cambridge, UK; IR White MSc, MRC Biostatistics Unit, UK; AM Wood PhD, University of Cambridge, UK; PL Perry MBChB, University of Cambridge, UK; J Danesh FRCP, University of Cambridge, UK.
Author contributions: All authors contributed to the conception and design of this work; S.G.T. and I.R.W. proposed the methods; S.K. and P.L.P. analysed the data; S.G.T. drafted the paper; all authors critically revised the paper and approved the final version. S.G.T. is the guarantor. The authors declare no conflicts of interest.
Investigators/contributors: AFTCAPS: RW Tipping MS, Merck Research Laboratories, USA; ALLHAT: CE Ford PhD, University of Texas School of Public Health, USA; LM Simpson PhD, University of Texas School of Public Health, USA; AMORIS: G Walldius MD, Karolinska Institutet, Sweden; I Jungner MD, Karolinska Institutet, Sweden; ARIC: LE Chambless PhD, University of North Carolina, USA; ATTICA: DB Panagiotakos MD, Harokopio University, Greece; C Pitsavos MD, University of Athens, Greece; C Chrysohoou MD, University of Athens, Greece; C Stefanadis MD, University of Athens, Greece; BHS: M Knuiman PhD, University of Western Australia, Australia; BIP: U Goldbourt PhD, Sheba Medical Center, Israel; M Benderly PhD, Sheba Medical Center, Israel; D Tanne MD, Sheba Medical Center, Israel; BRHS: PH Whincup FRCP, University of London, UK; SG Wannamethee PhD, University College London, UK; RW Morris PhD, University College London, UK; BRUN: J Willeit MD, Medical University Innsbruck, Austria; S Kiechl MD, Medical University Innsbruck, Austria; P Santer MD, Bruneck Hospital, Italy; A Mayr MD, Bruneck Hospital, Italy; BWHHS: DA Lawlor PhD, University of Bristol, UK; CaPS: JWG Yarnell MD, Queen’s University of Belfast, UK; J Gallacher PhD, Cardiff University, UK; CASTEL: E Casiglia MD, University of Padova, Italy; V Tikhonoff MD, University of Padova, Italy; CHARL: PJ Nietert PhD, Medical University of South Carolina, USA; SE Sutherland PhD, Medical University of South Carolina, USA; DL Bachman MD, Medical University of South Carolina, USA; JE Keil DrPH, Medical University of South Carolina, USA; CHS: M Cushman MD, University of Vermont, USA; RP Tracy PhD, University of Vermont, USA; (see http://chs-nhlbi.org for acknowledgements); COPEN: A Tybjærg-Hansen MD, University of Copenhagen, Denmark; BG Nordestgaard MD, University of Copenhagen, Denmark; M Benn MD, University of Copenhagen, Denmark; R Frikke-Schmidt MD, University of Copenhagen, Denmark; CUORE: S Giampaoli MD, Istituto Superiore di Sanità, Italy; L Palmieri DrStat, Istituto Superiore di Sanità, Italy; S Panico MD, Federico II University, Italy; D Vanuzzo MD, Centre for Cardiovascular Prevention, Italy; DRECE: A Gómez de la Cámara MD, Hospital 12 de Octubre, Spain; JA Gómez-Gerique PhD, Hospital Marqués de Valdecilla, Spain; DUBBO: L Simons MD, University of NSW, Australia; J McCallum DPhil, Victoria University, Melbourne, Australia; Y Friedlander PhD, Hebrew University, Israel; EAS: FGR Fowkes MBChB, University of Edinburgh, UK; AJ Lee PhD, University of Edinburgh, UK; EPESEBOS: J Taylor MD, East Boston Neighborhood Health Center, USA; JM Guralnik MD, US National Institute on Aging, USA; EPESEIOW: R Wallace MD, University of Iowa, USA; J Guralnik MD, US National Institute on Aging, USA; EPESENCA: DG Blazer MD, Duke University Medical Centre, USA; JM Guralnik MD, US National Institute on Aging, USA; EPESENHA: JM Guralnik MD, US National Institute on Aging, USA; EPICNOR: K-T Khaw MBBChir, University of Cambridge, UK; ESTHER: H Brenner MD, German Cancer Research Center, Germany; E Raum MD, German Cancer Research Center, Germany; H Müller DrScHum, German Cancer Research Center, Germany; D Rothenbacher MD, German Cancer Research Center, Germany; FIA: JH Jansson MD, Umeå University, Sweden; P Wennberg MD, Umeå University, Sweden; FINE_FIN: A Nissinen MD, National Institute for Health and Welfare, Finland; FINE_IT: C Donfrancesco DrStat, Istituto Superiore di Sanità, Italy; S Giampaoli MD, Istituto Superiore di Sanità, Italy; FINRISK92, FINRISK97: V Salomaa MD, National Institute for Health and Welfare, Finland; K Harald MA, National Institute for Health and Welfare, Finland; P Jousilahti MD, National Institute for Health and Welfare, Finland; E Vartiainen MD, National Institute for Health and Welfare, Finland; FLETCHER: M Woodward PhD, Mount Sinai School of Medicine, USA; FRAMOFF: RB D’Agostino PhD, Boston University, USA; RS Vasan MD, Boston University School of Medicine, USA; MJ Pencina PhD, Boston University School of Medicine, USA; GLOSTRUP: EM Bladbjerg PhD, University of Southern Denmark, Denmark; T Jørgensen, MD, University of Copenhagen, Denmark; L Møller MD, World Health Organization; J Jespersen DSc, University of Southern Denmark, Denmark; GOH: R Dankner MD, Gertner Institute for Epidemiology and Health Policy Research, Israel; A Chetrit MSc, Gertner Institute for Epidemiology and Health Policy, Israel; F Lubin RD, Gertner Institute for Epidemiology and Health Policy, Israel; GOTO33, GOTO43: A Rosengren MD, Göteborg University, Sweden; G Lappas BSc, Göteborg University, Sweden; GOTOW: C Björkelund MD, Göteborg University, Sweden; L Lissner PhD, Göteborg University, Sweden; C Bengtsson MD, Göteborg University, Sweden; GRIPS: P Cremer MD, Klinikum der Universität München LMU, Germany; D Nagel PhD, University of Munich, Germany; HELSINAG: RS Tilvis MD, Helsinki University Hospital, Finland; TE Strandberg MD, Oulu University Hospital, Finland; HISAYAMA: Y Kiyohara MD, Kyushu University, Japan; H Arima MD, Kyushu University, Japan; Y Doi MD, Kyushu University, Japan; T Ninomiya MD, Kyushu University, Japan; HONOL: B Rodriguez MD, University of Hawaii, USA; HOORN: JM Dekker PhD, VU University Medical Center, The Netherlands; G Nijpels MD, Vrije Universiteit Medical Center, The Netherlands; CDA Stehouwer MD, Maastricht University Medical Centre, The Netherlands; HPFS: E Rimm ScD, Harvard University, USA; JK Pai ScD, Brigham and Women’s Hospital, USA; IKNS: S Sato MD, Osaka Medical Center for Health Science and Promotion, Japan; H Iso MD, Osaka University, Japan; A Kitamura MD, Osaka Medical Center for Health Science and Promotion, Japan; H Noda MD, Osaka University, Japan; ISRAEL: U Goldbourt PhD, Sheba Medical Center, Israel; NORTH KARELIA: V Salomaa MD, National Institute for Health and Welfare, Finland; K Harald MA, National Institute for Health and Welfare, Finland; P Jousilahti MD, National Institute for Health and Welfare, Finland; E Vartiainen MD, National Institute for Health and Welfare, Finland; KIHD: JT Salonen MD, University of Kuopio, Finland; T-P Tuomainen MD, University of Kuopio, Finland; LASA: DJH Deeg MD, VU University Medical Centre, The Netherlands; JL Poppelaars, VU University Medical Centre, The Netherlands; LEADER: TW Meade FMedSci, London School of Hygiene and Tropical Medicine, UK; JA Cooper MSc, University College London, UK; MALMO: B Hedblad MD, Lund University, Sweden; G Berglund MD, Lund University, Sweden; G Engstrom; MD, Lund University, Sweden; MCVDRFP: WMM Verschuren PhD, National Institute of Public Health and the Environment, The Netherlands; A Blokstra MSc, National Institute for Public Health and the Environment, The Netherlands; MESA: M Cushman MD, University of Vermont, USA; S Shea MD, Columbia University, USA; MOGERAUG1, MOGERAUG2, MOGERAUG3: A Döring MD, German Research Center for Environmental Health, Germany; W Koenig MD, University of Ulm Medical Center, Germany; C Meisinger MD, German Research Center for Environmental Health, Germany; W Mraz MD, Klinikum der Universität München, Institute of Clinical Chemistry, Munich, Germany; MORGEN: WMM Verschuren PhD, National Institute of Public Health and the Environment, The Netherlands; A Blokstra MSc, National Institute for Public Health and the Environment, The Netherlands; H Bas Bueno-de-Mesquita PhD, National Institute for Public Health and the Environment, The Netherlands; MOSWEGOT: A Rosengren MD, Göteborg University, Sweden; G Lappas MD, Göteborg University, Sweden; MRFIT: LH Kuller MD, University of Pittsburgh, USA; G Grandits MS, University of Minnesota, USA; NCS: R Selmer PhD, Norwegian Institute of Public Health, Norway; A Tverdal PhD, Norwegian Institute of Public Health, Norway; W Nystad PhD, Norwegian Institute of Public Health, Norway; NHANES I, NHANES II, NHANES III: R Gillum MD, Centers for Disease Control and Prevention, USA; M Mussolino PhD, National Institutes of Health, USA; NHS: E Rimm ScD, Harvard University, USA; S Hankinson ScD, Harvard School of Public Health, USA; JE Manson MD, Harvard Medical School, USA; JK Pai ScD, Brigham and Women's Hospital, USA; NPHS I: TW Meade FMedSci, London School of Hygiene and Tropical Medicine, UK; JA Cooper MSc, University College London, UK; C Knottenbelt MD, London School of Hygiene and Tropical Medicine, UK; NPHS II: JA Cooper MSc, University College London, UK; KA Bauer MD, Harvard Medical School, USA; OSAKA: S Sato MD, Osaka Medical Center for Health Science and Promotion, Japan; A Kitamura MD, Osaka Medical Center for Health Science and Promotion, Japan; Y Naito MD, Mukogawa Women's University, Japan; H Iso MD, Osaka University, Japan; OSLO: I Holme PhD, Oslo University Hospital, Norway; R Selmer PhD, Norwegian Institute of Public Health, Norway; A Tverdal PhD, Norwegian Institute of Public Health, Norway; W Nystad PhD, Norwegian Institute of Public Health, Norway; OYABE: H Nakagawa MD, Kanazawa Medical University, Japan; K Miura MD, Shiga University of Medical Science, Japan; PARIS1: P Ducimetiere PhD, INSERM, France; X Jouven MD, INSERM, France; PRHHP: CJ Crespo DrPH, Portland State University, USA; MR Garcia Palmieri MD, University of Puerto Rico, USA; PRIME: P Amouyel MD, Institut Pasteur de Lille, France; D Arveiler MD, Université de Strasbourg, France; A Evans MD, The Queens University of Belfast, UK; J Ferrieres MD, University of Toulouse, France; PROCAM: H Schulte PhD, Assmann-Stiftung für Prävention, Germany; G Assmann FRCP, Assmann-Stiftung für Prävention, Germany; PROSPER: J Shepherd MD, Glasgow Royal Infirmary, UK; CJ Packard DSc, University of Glasgow, UK; N Sattar FRCPath, University of Glasgow, UK; I Ford PhD, University of Glasgow, UK; QUEBEC: B Cantin MD, Institut de Cardiologie de Québec, Hôpital Laval, Canada; J-P Després PhD, Centre de recherche de l'Institut universitaire de cardiologie et de pneumologie de Québec, Canada; GR Dagenais MD, Institut universitaire de cardiologie et pneumologie de Québec, Canada; RANCHO: E Barrett-Connor MD, University of California, USA; DL Wingard PhD, University of California, USA; R Bettencourt MS, University of California, USA; REYK: V Gudnason MD, University of Iceland, Iceland; T Aspelund PhD, University of Iceland, Iceland; G Sigurdsson, MD, University of Iceland, Iceland; B Thorsson MD, Icelandic Heart Association, Iceland; RIFLE: M Trevisan MD, Nevada System of Higher Education, USA; ROTT: J Witteman PhD, Erasmus MC, The Netherlands; I Kardys MD, Erasmus MC, The Netherlands; M Breteler MD, Erasmus MC, The Netherlands; A Hofman MD, Erasmus MC, The Netherlands; SHHEC: H Tunstall-Pedoe MD, University of Dundee, UK; R Tavendale PhD, University of Dundee, UK; GDO Lowe DSc, University of Glasgow, UK; M Woodward PhD, Mount Sinai School of Medicine, USA; SPEED: Y Ben-Shlomo PhD, University of Bristol, UK; G Davey-Smith MD, University of Bristol, UK; SHS: BV Howard PhD, Medstar Research Institute, USA; Y Zhang MD, University of Oklahoma Health Sciences Center, USA; J Umans MD, Georgetown University Medical Centre, USA; TARFS: A Onat MD, Istanbul University, Turkey; TPT: TW Meade FMedSci, London School of Hygiene and Tropical Medicine, UK; TROMSØ: T Wilsgaard PhD, University of Tromsø, Norway; ULSAM: E Ingelsson MD, Karolinska Institutet, Sweden; L Lind PhD, Department of Medical Sciences, Uppsala University, Uppsala, Sweden; V Giedraitis PhD, Department of Public Health and Geriatrics, Uppsala University Hospital, Uppsala, Sweden; L Lannfelt MD, Department of Public Health and Geriatrics, Uppsala University Hospital, Uppsala, Sweden; USPHS: JM Gaziano MD, Brigham and Women's Hospital, USA; P Ridker MD, Brigham and Women's Hospital, USA; USPHS2: JM Gaziano MD, Brigham and Women's Hospital, USA; P Ridker MD, Brigham and Women’s Hospital, USA; VHMPP: H Ulmer PhD, Innsbruck Medical University, Austria; G Diem MD, Agency for Preventive and Social Medicine, Austria; H Concin MD, Agency for Preventive and Social Medicine, Austria; VITA: A Tosetto MD, San Bortolo Hospital, Italy; F Rodeghiero MD, San Bartolo Hospital, Italy; WHI: S Wassertheil-Smoller PhD, Albert Einstein College of Medicine, New York, USA; JE Manson MD, Harvard Medical School, USA; WHITE I: M Marmot FMedSci, University College London, UK; R Clarke MD, University of Oxford, UK; R Collins FMedSci, University of Oxford, UK; WHITE II: E Brunner PhD, University College London, UK; M Shipley MSc, University College London, UK; WHS: P Ridker MD, Brigham and Women's Hospital, USA; J Buring ScD, Brigham and Women’s Hospital, USA; WOSCOPS: J Shepherd MD, Glasgow Royal Infirmary, UK; SM Cobbe FMedSci, BHF Glasgow Cardiovascular Research Centre, UK; I Ford PhD, University of Glasgow, UK; M Robertson BSc, University of Glasgow, UK; XIAN: Y He MD, Chinese PLA General Hospital, China; ZARAGOZA: A Marín Ibañez MD, San Jose Norte Health Centre, Spain; ZUTE: EJM Feskens MD, Division of Human Nutrition, Wageningen University, Wageningen, The Netherlands; D Kromhout PhD, Division of Human Nutrition, Wageningen University, The Netherlands.
Coordinating centre: R Collins FMedSci, University of Oxford, UK; E Di Angelantonio MD, University of Cambridge, UK; S Erqou MD, University of Cambridge, UK; S Kaptoge PhD, University of Cambridge, UK; S Lewington DPhil, University of Oxford, UK; L Orfei MSc, University of Cambridge, UK; L Pennells MSc, University of Cambridge, UK; PL Perry MBChB, University of Cambridge, UK; KK Ray MD, University of Cambridge, UK; N Sarwar PhD, University of Cambridge, UK; M Alexander MPhil, University of Cambridge, UK; A Thompson PhD, University of Cambridge, UK; SG Thompson DSc, MRC Biostatistics Unit, UK; M Walker PhD, University of Cambridge, UK; S Watson MMath, University of Cambridge, UK; F Wensley MSc, University of Cambridge, UK; IR White MSc, MRC Biostatistics Unit, UK; AM Wood PhD, University of Cambridge, UK; J Danesh FRCP, University of Cambridge, UK (principal investigator).
References
- 1.Egger M, Smith DG, Altman DG, editors. Systematic Reviews in Health Care: Meta-Analysis in Context. London: BMJ Books; 2001. [Google Scholar]
- 2.Stewart LA, Clarke MJ. Practical methodology of meta-analyses (overviews) using updated individual patient data. Stat Med. 1995;14:2057–79. doi: 10.1002/sim.4780141902. [DOI] [PubMed] [Google Scholar]
- 3.Prospective Studies Collaboration. Age-specific relevance of usual blood pressure to vascular mortality: a meta-analysis of individual data for one million adults in 61 prospective studies. Lancet. 2002;360:1903–13. doi: 10.1016/s0140-6736(02)11911-8. [DOI] [PubMed] [Google Scholar]
- 4.Thompson SG, Higgins JPT. Can meta-analysis help target interventions at individuals most likely to benefit? Lancet. 2005;365:341–46. doi: 10.1016/S0140-6736(05)17790-3. [DOI] [PubMed] [Google Scholar]
- 5.Emerging Risk Factors Collaboration. Collaborative meta-analysis of individual data on over 1 million participants in 96 prospective cohorts of lipid and inflammatory markers in cardiovascular diseases. Eur J Epidemiol. 2007;22:839–69. doi: 10.1007/s10654-007-9165-7. [DOI] [PubMed] [Google Scholar]
- 6.Emerging Risk Factors Collaboration. Major lipids, apolipoproteins and risk of vascular disease. J Am Med Assoc. 2009;302:1993–2000. doi: 10.1001/jama.2009.1619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Emerging Risk Factors Collaboration. Lipoprotein(a) concentration and the risk of coronary heart disease, stroke and nonvascular mortality: individual data analysis of 121,944 participants from 34 prospective studies. J Am Med Assoc. 2009;302:412–23. doi: 10.1001/jama.2009.1063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Emerging Risk Factors Collaboration. C-reactive protein concentration and the risk of coronary heart disease, stroke and mortality: an individual participant meta-analysis. Lancet. 2010;375:132–40. doi: 10.1016/S0140-6736(09)61717-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.MacMahon S, Peto R, Cutler J, et al. Blood pressure, stroke, and coronary heart disease. Part 1, Prolonged differences in blood pressure: prospective observational studies corrected for the regression dilution bias. Lancet. 1990;335:765–74. doi: 10.1016/0140-6736(90)90878-9. [DOI] [PubMed] [Google Scholar]
- 10.Fibrinogen Studies Collaboration. Plasma fibrinogen and the risk of major cardiovascular diseases and nonvascular mortality: an individual participant meta-analysis. JAMA. 2005;294:1799–809. doi: 10.1001/jama.294.14.1799. [DOI] [PubMed] [Google Scholar]
- 11.Cox DR. Regression models and life tables. J Roy Stat Soc B. 1972;74:187–220. [Google Scholar]
- 12.Higgins JPT, Thompson SG, Spiegelhalter DJ. A re-evaluation of random-effects meta-analysis. J Roy Stat Soc A. 2009;172:137–59. doi: 10.1111/j.1467-985X.2008.00552.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Prospective Studies Collaboration. Collaborative overview ('meta-analysis') of prospective observational studies of the associations of usual blood pressure and usual cholesterol levels with common causes of death: protocol for the second cycle of the Prospective Studies Collaboration. J Cardiovasc Risk. 1999;6:315–20. doi: 10.1177/204748739900600508. [DOI] [PubMed] [Google Scholar]
- 14.Prospective Studies Collaboration. Blood cholesterol and vascular mortality by age, sex, and blood pressure: a meta-analysis of individual data from 61 prospective studies with 55,000 vascular deaths. Lancet. 2007;370:1829–39. doi: 10.1016/S0140-6736(07)61778-4. [DOI] [PubMed] [Google Scholar]
- 15.DerSimonian R, Laird N. Meta-analysis in clinical trials. Control Clin Trials. 1986;7:177–88. doi: 10.1016/0197-2456(86)90046-2. [DOI] [PubMed] [Google Scholar]
- 16.DerSimonian R, Kacker R. Random-effects model for meta-analysis of clinical trials: an update. Contemp Clin Trials. 2007;28:105–14. doi: 10.1016/j.cct.2006.04.004. [DOI] [PubMed] [Google Scholar]
- 17.Cochran WG. The combination of estimates from different experiments. Biometrics. 1954;10:101–29. [Google Scholar]
- 18.Higgins JPT, Thompson SG, Deeks JJ, Altman DG. Measuring inconsistency in meta-analysis. BMJ. 2003;327:557–60. doi: 10.1136/bmj.327.7414.557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Higgins JP, Thompson SG. Quantifying heterogeneity in a meta-analysis. Stat Med. 2002;21:1539–58. doi: 10.1002/sim.1186. [DOI] [PubMed] [Google Scholar]
- 20.Tudur-Smith C, Williamson PR, Marson AG. Investigating heterogeneity in an individual patient data meta-analysis of time to event outcomes. Stat Med. 2005;24:1307–19. doi: 10.1002/sim.2050. [DOI] [PubMed] [Google Scholar]
- 21.Olkin I, Sampson A. Comparison of meta-analysis versus analysis of variance of individual patient data. Biometrics. 1998;54:317–22. [PubMed] [Google Scholar]
- 22.Riley RD, Lambert PC, Staessen JA, et al. Meta-analysis of continuous outcomes combining individual patient data and aggregate data. Stat Med. 2008;27:1870–93. doi: 10.1002/sim.3165. [DOI] [PubMed] [Google Scholar]
- 23.Fibrinogen Studies Collaboration. Associations of plasma fibrinogen levels with established cardiovascular risk factors, inflammatory markers and other characteristics: individual participant meta-analysis of 154 211 adults in 31 prospective studies. Am J Epidemiol. 2007;166:867–79. doi: 10.1093/aje/kwm191. [DOI] [PubMed] [Google Scholar]
- 24.Riley RD, Abrams KR, Lambert PC, Sutton AJ, Thompson JR. An evaluation of bivariate random-effects meta-analysis for the joint synthesis of two correlated outcomes. Stat Med. 2007;26:78–97. doi: 10.1002/sim.2524. [DOI] [PubMed] [Google Scholar]
- 25.White IR. Multivariate random-effects meta-analysis. Stata J. 2009;9:40–56. [Google Scholar]
- 26.Easton DF, Peto J, Babiker AG. Floating absolute risk: an alternative to relative risk in survival and case-control analysis avoiding an arbitrary reference group. Stat Med. 1991;10:1025–35. doi: 10.1002/sim.4780100703. [DOI] [PubMed] [Google Scholar]
- 27.Plummer M. Improved estimates of floating absolute risk. Stat Med. 2004;23:93–104. doi: 10.1002/sim.1485. [DOI] [PubMed] [Google Scholar]
- 28.Royston P, Ambler G, Sauerbrei W. The use of fractional polynomials to model continuous risk variables in epidemiology. Int J Epidemiol. 1999;28:964–74. doi: 10.1093/ije/28.5.964. [DOI] [PubMed] [Google Scholar]
- 29.Govindarajulu US, Spiegelman D, Thurston SW, Ganguli B, Eisen EA. Comparing smoothing techniques in Cox models for exposure–response relationships. Stat Med. 2007;26:3735–52. doi: 10.1002/sim.2848. [DOI] [PubMed] [Google Scholar]
- 30.Lambert PC, Sutton AJ, Abrams KR, Jones DR. A comparison of summary patient-level covariates in meta-regression with individual patient data meta-analysis. J Clin Epidemiol. 2002;55:86–94. doi: 10.1016/s0895-4356(01)00414-0. [DOI] [PubMed] [Google Scholar]
- 31.Thompson SG, Sharp Explaining heterogeneity in meta-analysis: a comparison of methods. Stat Med. 1999;18:2693–708. doi: 10.1002/(sici)1097-0258(19991030)18:20<2693::aid-sim235>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- 32.Thompson SG, Higgins JPT. How should meta-regression analyses be undertaken and interpreted? Stat Med. 2002;21:1559–73. doi: 10.1002/sim.1187. [DOI] [PubMed] [Google Scholar]
- 33.Simmonds MC, Higgins JP. Covariate heterogeneity in meta-analysis: criteria for deciding between meta-regression and individual patient data. Stat Med. 2007;26:2982–99. doi: 10.1002/sim.2768. [DOI] [PubMed] [Google Scholar]
- 34.Jackson C, Best N, Richardson S. Improving ecological inference using individual-level data. Stat Med. 2006;25:2136–59. doi: 10.1002/sim.2370. [DOI] [PubMed] [Google Scholar]
- 35.Collett D. London: Chapman & Hall; 1994. Modelling Survival Data in Medical Research. [Google Scholar]
- 36.Clarke R, Shipley M, Lewington S, et al. Underestimation of risk associations due to regression dilution in long-term follow-up of prospective studies. Am J Epidemiol. 1999;150:341–53. doi: 10.1093/oxfordjournals.aje.a010013. [DOI] [PubMed] [Google Scholar]
- 37.Rosner B, Willett WC, Spiegelman D. Correction of logistic regression relative risk estimates and confidence intervals for systematic within-person measurement error. Stat Med. 1989;8:1051–69. doi: 10.1002/sim.4780080905. [DOI] [PubMed] [Google Scholar]
- 38.Rosner B, Spiegelman D, Willett WC. Correction of logistic regression relative risk estimates and confidence intervals for measurement error: the case of multiple covariates measured with error. Am J Epidemiol. 1990;132:734–45. doi: 10.1093/oxfordjournals.aje.a115715. [DOI] [PubMed] [Google Scholar]
- 39.Fibrinogen Studies Collaboration. Regression dilution methods for meta-analysis: assessing long-term variability in plasma fibrinogen among 27,247 adults in 15 prospective studies. Int J Epidemiol. 2006;35:1570–78. doi: 10.1093/ije/dyl233. [DOI] [PubMed] [Google Scholar]
- 40.Fibrinogen Studies Collaboration. Correcting for multivariate measurement error by regression calibration in meta-analyses of epidemiological studies. Stat Med. 2009;28:1067–92. doi: 10.1002/sim.3530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Breslow NE, Day NE. Volume 1: The Analysis of Case-Control Studies. Volume 1. Lyon: IARC Scientific Publications; 1980. Statistical Methods in Cancer Research. [PubMed] [Google Scholar]
- 42.Rodrigues L, Kirkwood BR. Case-control designs in the study of common diseases: updates on the demise of the rare disease assumption and the choice of sampling scheme for controls. Int J Epidemiol. 1990;19:205–13. doi: 10.1093/ije/19.1.205. [DOI] [PubMed] [Google Scholar]
- 43.Prentice RL. A case-cohort design for epidemiologic cohort studies and disease prevention trials. Biometrika. 1986;73:1–11. [Google Scholar]
- 44.Barlow WE, Ichikawa L, Rosner D, Izumi S. Analysis of case-cohort designs. J Clin Epidemiol. 1999;52:1165–72. doi: 10.1016/s0895-4356(99)00102-x. [DOI] [PubMed] [Google Scholar]
- 45.Stata: Data Analysis and Statistical Software. Texas, USA: StataCorp; 2009. [(31 March 2010, date last accessed)]. http://www.stata.com. [Google Scholar]
- 46.Simmonds MC, Higgins JPT, Stewart LA, Tierney JF, Clarke MJ, Thompson SG. Meta-analysis of individual patient data from randomised trials: a review of methods used in practice. Clin Trials. 2005;2:209–17. doi: 10.1191/1740774505cn087oa. [DOI] [PubMed] [Google Scholar]
- 47.Pooling Project of Prospective Studies of Diet and Cancer (Smith-Warner SA et al) Methods for pooling results of epidemiologic studies. Am J Epidemiol. 2006;163:1053–64. doi: 10.1093/aje/kwj127. [DOI] [PubMed] [Google Scholar]
- 48.Bennett DA. Review of analytical methods for prospective cohort studies using time to event data: single studies and implications for meta-analysis. Stat Methods Med Res. 2003;12:297–319. doi: 10.1191/0962280203sm319ra. [DOI] [PubMed] [Google Scholar]
- 49.Fibrinogen Studies Collaboration. Systematically missing confounders in individual participant data meta-analysis of observational cohort studies. Stat Med. 2009;28:1218–37. doi: 10.1002/sim.3540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Carroll RJ, Stefanski LA. Measurement error, instrumental variables and corrections for attenuation with applications to meta-analyses. Stat Med. 1994;13:1265–82. doi: 10.1002/sim.4780131208. [DOI] [PubMed] [Google Scholar]
- 51.Harrell FE, Jr, Lee KL, Mark DB. Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat Med. 1996;15:361–87. doi: 10.1002/(SICI)1097-0258(19960229)15:4<361::AID-SIM168>3.0.CO;2-4. [DOI] [PubMed] [Google Scholar]
- 52.Cook NR. Use and misuse of the receiver operating characteristic curve in risk prediction. Circulation. 2007;115:928–35. doi: 10.1161/CIRCULATIONAHA.106.672402. [DOI] [PubMed] [Google Scholar]
- 53.Pencina MJ, D’Agostino RB, Sr, D’Agostino RB, Jr, Vasan RS. Evaluating the added predictive ability of a new marker: from area under the ROC curve to reclassification and beyond. Stat Med. 2008;27:157–72; discussion 207–12. doi: 10.1002/sim.2929. [DOI] [PubMed] [Google Scholar]
- 54.Fibrinogen Studies Collaboration. Measures to assess the prognostic ability of the stratified Cox proportional hazards model. Stat Med. 2009;28:389–411. doi: 10.1002/sim.3378. [DOI] [PubMed] [Google Scholar]
- 55.Asia Pacific Cohort Studies Collaboration. Determinants of cardiovascular disease in the Asia Pacific region: protocol for a collaborative overview of cohort studies. CVD Prevention. 1999;2:281–89. [Google Scholar]
- 56.Breast Cancer Linkage Consortium (Thompson D, Easton DF) Cancer Incidence in BRCA1 mutation carriers. J Natl Cancer Inst. 2002;94:1358–65. doi: 10.1093/jnci/94.18.1358. [DOI] [PubMed] [Google Scholar]
- 57.Collaborative Group on Hormonal Factors in Breast Cancer (Beral V, Bull D, Doll R, Peto R, Reeves G) Breast cancer and abortion: collaborative reanalysis of data from 53 epidemiological studies, including 83,000 women with breast cancer from 16 countries. Lancet. 2004;363:1007–16. doi: 10.1016/S0140-6736(04)15835-2. [DOI] [PubMed] [Google Scholar]
- 58.Uitterlinden AG, Ralston SH, Brandi ML, et al. The association between common vitamin D receptor gene variations and osteoporosis: a participant-level meta-analysis. Ann Intern Med. 2006;145:255–64. doi: 10.7326/0003-4819-145-4-200608150-00005. [DOI] [PubMed] [Google Scholar]
- 59.Bingham S, Riboli E. Diet and cancer—the European Prospective Investigation into Cancer and Nutrition. Nat Rev Cancer. 2004;4:206–15. doi: 10.1038/nrc1298. [DOI] [PubMed] [Google Scholar]
- 60.UK Biobank. The UK Biobank sample handling and storage protocol for the collection, processing and archiving of human blood and urine. Int J Epidemiol. 2008;37:234–44. doi: 10.1093/ije/dym276. [DOI] [PubMed] [Google Scholar]
- 61.UK Biobank Protocol. [(31 March 2010, date last accessed)]. http://www.ukbiobank.ac.uk. [Google Scholar]
- 62.Knoppers BM, Fortier I, Legault D, Burton P. The Public Population Project in Genomics (P3G): a proof of concept? Eur J Hum Genet. 2008;16:664–65. doi: 10.1038/ejhg.2008.55. [DOI] [PubMed] [Google Scholar]