Solving the aerodynamics of fungal flight: How air viscosity slows spore motion

Abstract

Viscous drag causes the rapid deceleration of fungal spores after high-speed launches and limits discharge distance. Stokes' law posits a linear relationship between drag force and velocity. It provides an excellent fit to experimental measurements of the terminal velocity of free-falling spores and other instances of low Reynolds number motion (Re<1). More complex, non-linear drag models have been devised for movements characterized by higher Re, but their effectiveness for modeling the launch of fast-moving fungal spores has not been tested. In this paper, we use data on spore discharge processes obtained from ultra-high-speed video recordings to evaluate the effects of air viscosity predicted by Stokes' law and a commonly used non-linear drag model. We find that discharge distances predicted from launch speeds by Stokes' model provide a much better match to measured distances than estimates from the more complex drag model. Stokes' model works better over a wide range projectile sizes, launch speeds, and discharge distances, from microscopic mushroom ballistospores discharged at <1 m/s over a distance of <0.1 mm (Re<1.0), to macroscopic sporangia of Pilobolus that are launched at >10 m/s and travel as far as 2.5 m (Re>100).

Introduction

Fungal spores vary greatly in shape and size (Fig. 1). While the spores of many species are spherical, others are ellipsoidal, polyhedral, fusiform to filiform, and star-shaped (Kirk et al. 2008). Spore morphology is further modified in many species by elaborate surface ornamentation and appendages. Spore size ranges from the 3 μm-long basidiospores of certain bracket fungi, to the “giant” spores of lichenized Ascomycota that measure up to 300 × 100 μm (Ingold 1971; Fischer et al. 2010). Corresponding estimates of spore mass, based on density measurements between 1.0 × 10³ and 1.3 × 10³ kg m^-3 (Gregory 1973), range from 1 pg to 2 μg. Across this diversity of morphology, tens of thousands of species utilize active launch mechanism that propel their spores into the air. In many fungi, multiple spores are attached to one another, or are formed within sporangia, producing larger projectiles. Pressurized squirt guns blast spores individually, tethered together, or within sporangia over distances of up to 2.6 meters (Yafetto et al. 2008); a catapult powered by fluid movement discharges single spores of mushroom-forming fungi and their relatives over a maximum distance of 1.3 mm (Stolze-Rybczynski et al. 2009), and the explosive formation of gas bubbles (cavitation) launches conidia a few millimeters from the parent colony (Meredith 1963; Money and Fischer 2009).

Fig 1.

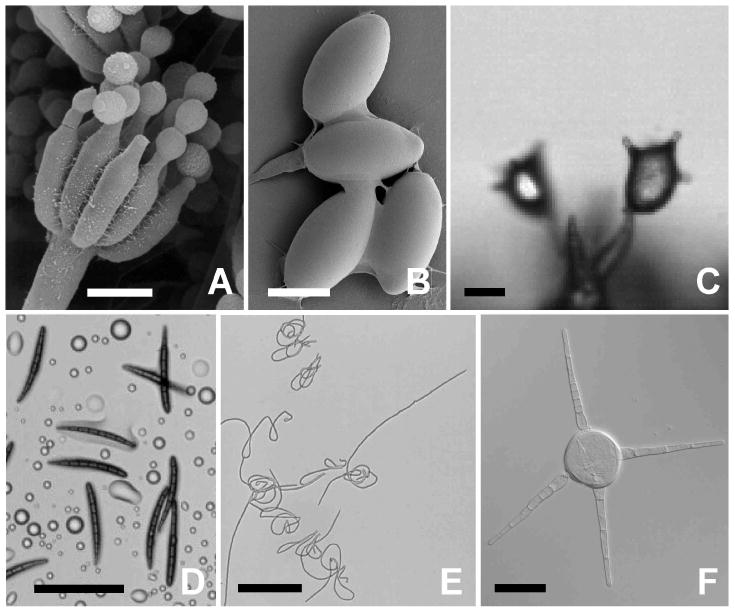
Sampling of morphological diversity of fungal spores. A, Spherical conidia of Penicillium sp. produced by subtending phialides. B, Ellipsoidal ascospores of Podospora anserina. C, Polyhedral basidiospores of Aleurodiscus oakesii. D, Fusiform ascospores of Geoglossum nigritum. E, Filamentous ascospores of Cordyceps militaris. F, Star-shaped aquatic conidium of Brachiosphaera tropicalis. Scale bars A, B, C, 10 μm, D, E, 100 μm, F, 20 μm. Image A, courtesy M. Duley, R. Edelmann; F, courtesy H. Raja.

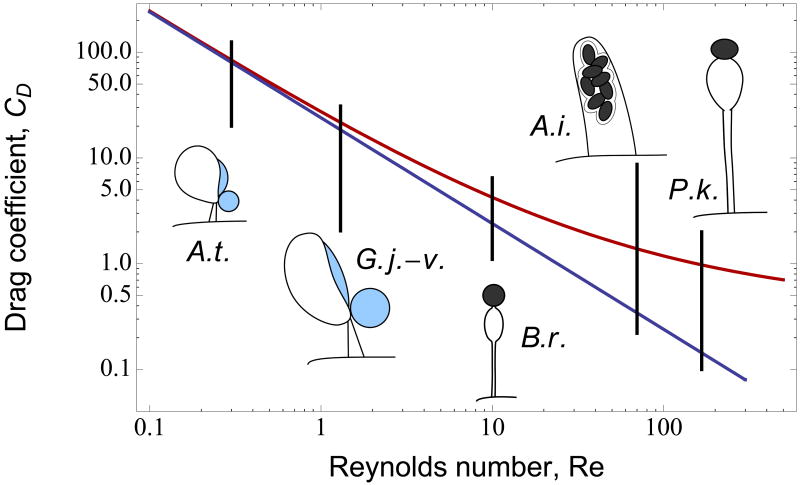
Differences in discharge distance among the fungi are due to a combination of launch speed, projectile mass, and projectile surface area. For the same launch speed, larger projectiles travel farther than smaller ones, because larger and heavier objects have greater momentum. When spores are launched at high speeds (maximum velocities of up to 25 m s^-1 were measured by Yafetto et al. 2008) the effects of viscous drag have a much greater influence upon their motion than gravity. This drag force becomes increasingly significant as spore size decreases (Fig. 3).

Fig 3.

Relationship between Reynolds number (Re) and drag coefficient (C_D) according to simple Stokes model (blue curve) and more complex interpolation model (red curve) for range of Re values corresponding to spore discharge mechanisms evaluated in this study. Divergence between the two models is apparent at Re = 10 (Basidiobolus) and increases at higher Re values (Re = 70 for Ascobolus and 167 for Pilobolus).

To explore the motion of spores it is essential to identify an effective model for the drag force. Until recently, it was impossible to evaluate the utility of different models for spore movement because there was so little empirical data on launch speeds. The recent use of ultra-high-speed video cameras has allowed researchers to capture unprecedented information on spore discharge processes in a variety of fungi (Pringle et al. 2005; Yafetto et al. 2008; Roper et al. 2008; Stolze-Rybczynski et al. 2009). In light of these studies, we offer analysis of two approaches to estimating the effects of viscous drag and demonstrate that the simpler model based on Stokes is superior to a more complex, but more commonly used, interpolation model of drag.

Methods and additional background

Approaches to drag modeling

In the absence of high-speed video data, earlier studies on fungal movement predicted initial launch speeds from observed discharge distances (e.g., Buller 1909; Turner and Webster 1991; Trail et al. 2005; Vogel 2005). Typically, the calculated launch speed was then used to deduce other properties of the system, including the pressure or energy required for launch. The validity of these studies was predicated upon the accuracy of the underlying model used to calculate the viscous drag acting on the projectile. In general, the force due to viscous drag, F_D, is derived from the following expression:

$$F_D=C_D\frac{\pi }{8}{\rho }_{\mathit{\text{gas}}}{d}^2{V}^2$$

where V is the velocity of the projectile through the surrounding fluid, ρ_gas is the density of that fluid, and d is the characteristic size of the projectile. For most motional regimes, C_D, the drag coefficient itself is velocity dependent. Although the particle velocity, V, appears above, movements through viscous fluids are typically characterized by the dimensionless Reynolds number, Re:

$$\text{Re}=\frac{{\rho }_{\mathit{\text{gas}}}Vd}{\eta }$$

where η is the viscosity of the surrounding fluid. To model the viscous drag effectively, the appropriate dependence of the drag coefficient upon Re must be determined.

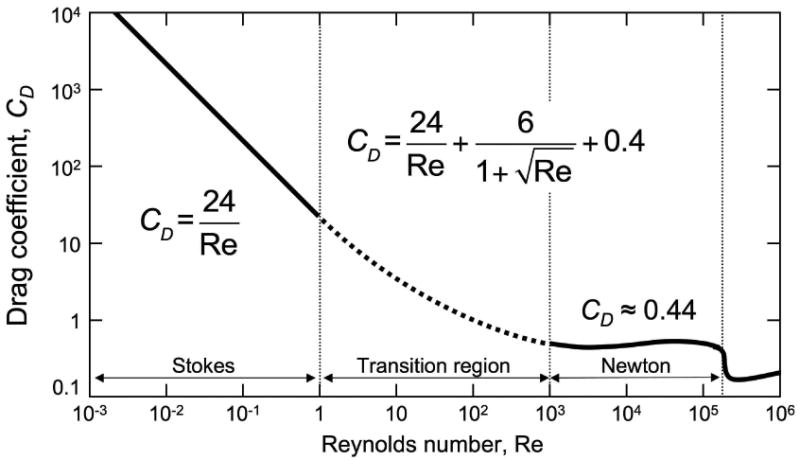
Unfortunately, the relationship between C_D and Re is complicated in the motional regime in which many spore flights occur. In the slow speed, creeping flow, small particle, low Re regime, viscous drag is accurately modeled by Stokes' law:

$$C_D=\frac{24}{\text{Re}}$$

At the fast motion, high Re limit, drag is reasonably well represented by a constant value of the drag coefficient, C_D = 0.44. This regime is also known as the Newtonian limit.

For intermediate Re, many quasi-empirical, interpolating models have been proposed (Clift et al. 2005), including the following, proposed by White (1974) and utilized by Vogel (2005):

$$C_D=\frac{24}{\text{Re}}+\frac{6}{1+\sqrt{\text{Re}}}+0.4$$

The first term of this expression is Stokes' law and the third term reflects the Newtonian limit. The second term provides the smooth transition between these two limits (Fig 2).

Fig 2.

Relationship between Reynolds number and drag coefficient.

Irrespective of the model chosen to represent drag, the ultimate goal is to relate the initial velocity of a projectile as characterized by the Re to the range achieved by that projectile. If Stokes model of drag is adopted, this can be done analytically.

Equations describing the motion of a projectile of mass, m, can be obtained by integrating Newton's second law:

$$\overrightarrow{F}=m\overrightarrow{a}\text{or}\{\begin{array}{c}{F}_x=m\frac{d^{2}x}{d{t}^2}\\ F_y=m\frac{d^{2}y}{d{t}^2}\end{array}$$

In the x-direction, taken to be horizontal, the only force acting on the projectile (radius = r) after its launch, is the x-component of the viscous drag:

$$F_x\left(t\right)=-\frac{6\pi r\eta }{m}{V}_x\left(t\right)$$

Thus, the differential equation to be solved for x(t) is,

$$-\frac{6\pi r\eta }{m}\frac{dx}{dt}=m\frac{d^{2}x}{d{t}^2}$$

which can be solved analytically to yield:

$$x\left(t\right)=x_i+\frac{m{V}_i\text{cos}\left(\theta \right)}{6\pi r\eta }-\frac{e^{-\frac{6\pi r\eta }{m}t}m{V}_i\text{cos}\left(\theta \right)}{6\pi r\eta }$$

where,

• x_i is the initial x-position of the projectile at launch,

• V_i is the launch speed,

• θ is the launch angle (horizontal=0°, vertical straight up = 90°),

• t is time after launch,

• r is the aerodynamic radius of the projectile, and

• g is the acceleration due to gravity.

Similarly, the forces in the vertical y-direction are the y-component of the viscous drag and gravity (assumed to be constant). The differential equation to be solved for y(t) is as follows:

$$-g-\frac{6\pi r\eta }{m}\frac{dy}{dt}=m\frac{d^{2}y}{d{t}^2}$$

where g is the acceleration due to gravity. This can be solved analytically to yield

$$y\left(t\right)=y_i-\frac{\mathit{\text{mgt}}}{6\pi r\eta }+\left(1-e^{\frac{-6\pi r\eta }{m}t}\right)\left(\frac{g{m}^2}{{\left(6\pi r\eta \right)}^2}+\frac{m{V}_i\text{sin}\left(\theta \right)}{6\pi r\eta }\right)$$

Here, y_i is the initial y-position of the particle. These x- and y-coordinates of the particle position, parameterized by time, can be combined to produce an expression for the range of the launched particle as a function of the launch speed and launch angle:

$$\mathit{\text{Range}}=xi+\frac{m{v}_i\text{cos}\theta }{6\pi r\eta }\left(1-e^{-\text{ProductLog}\left[e^{-1-\frac{6\pi r\eta \left(6\pi r\eta y_i+m{v}_i\text{sin}\theta \right)}{g{m}^2}}\left(-1-\frac{6\pi r\eta v_i\text{sin}\theta }{gm}\right)\right]-\frac{g{m}^2+36{\pi }^2{r}^2{\eta }^2{y}_i+m6\pi r\eta v_i\text{sin}\theta }{g{m}^2}}\right)$$

The preceding expressions appear complicated due to their generality. They can be greatly simplified by making a few assumptions and substitutions. For a horizontal launch and letting

$$c=\frac{6\pi r\eta }{m},$$

• R = maximum horizontal range attained by projectile, and

• V_sed = steady-state sedimentation rate of the particle,

the equations above simplify as:

$$x\left(t\right)=R\left(1-e^{-ct}\right)$$

$$y\left(t\right)=-V_{\mathit{\text{Sed}}}\left(t-\frac{1}{c}\left(1-e^{-ct}\right)\right)$$

$$R=\frac{V_i}{c}$$

Buller (1909) offered the same simple formula.

If the more complicated, interpolation model of drag is used, analytical expressions for the trajectory cannot be obtained, even when the simplifying assumptions described above are applied. Instead, Newton's second law must be numerically integrated. Using this approach, the forces on the projectile at a time, t, are used to estimate the velocity and position at time t +Δt. If the time step, Δt, is sufficiently small, a picture of the projectile flight can be built up iteratively. This computationally intensive process is repeated with different initial velocity values until the observed projectile range is discovered. The time step, Δt, should be as small as possible because the velocity and, therefore, the drag force decrease rapidly after the launch. Consequently, the drag force at time t will always overestimate the true drag force acting at time t +Δt. Thus, the predicted initial velocity will be overestimated for any Δt > 0.

Information from ultra-high-speed video microscopy

Recently, spore discharge processes in fungi have been studied using ultra-high-speed video cameras (Pringle et al. 2005; Yafetto et al. 2008; Stolze-Rybczynski et al. 2009; Noblin et al. 2009; Fischer et al. 2010). Image capture at camera speeds ranging from 50,000 to one million frames per second has allowed the first direct observations of the motion of discharged spores. Analysis of these recordings provides precise measurements of launch speeds and the deceleration of spores after their launch. Comparisons between observed speeds and speeds predicted from the distances at which spores are deposited after discharge, provide an objective basis for evaluating different drag models.

For the present analyses, we utilized measurements of launch speed from five species of fungi whose spores, and sporangia, cover a broad size range and whose discharge processes are characterized by a 500-fold range in Re (Table 1). This range in Re was critical for our study, because Stokes' law has been considered applicable only for Re less than or equal to 1.0 (Dusenbery 2009). Above Re = 1.0, the interpolation model predicts a greater increase in drag force than the Stokes model (Fig 2). The analysis of spore discharge in these fungi using highspeed video has been described by Yafetto et al. (2008) and Stolze-Rybczynski et al. (2009). Armillaria tabescens (Basidiomycota, Agaricomycetes) is a wood-decay fungus that produces gilled mushrooms. Gymnosporangium juniperi-virginianae (Basidiomycota, Pucciniomycetes) is a pathogenic rust fungus that causes cedar-apple rust. Active discharge of basidiospores in both species of Basidiomycota is powered by the rapid movement of a droplet of fluid, called Buller's drop, over the spore surface (Fischer et al. 2010). The basidiospores of A. tabescens are discharged for a distance of <0.1 mm from the surfaces of its gills; the spores of G. juniperi-virginianae are discharged >1.0 mm from the surface of orange gelatinous horns that emerge from galls that it forms on various juniper species. Basidiobolus ranarum (Zygomycota, Mucorales) flourishes in the dung of amphibians and reptiles and causes rare infections in mammalian hosts, including humans. It discharges a single conidium from the tip of a fluid-filled pressurized stalk that travels up to 2 cm (horizontal distance) from the substrate. Ascobolus immersus (Ascomycota, Pezizomycetes) is a coprophilous ascomycete that discharges eight ascospores from each of its multiple asci that are exposed on the surface of a gelatinous ascoma. Its spores often fly together as a single projectile embedded in mucilage and travel as far as 30 cm. Pilobolus kleinii (Zygomycota, Mucorales) produces a fluid-filled sporangiophore that squirts a spore-filled sporangium from the dung on which the fungus thrives. The sporangium can travel a maximum distance of 2.5 m.

Table 1. Comparisons between measured launch speeds and discharge distances and predictions based upon competing models for the effects of viscous drag on the motion of fungal spores.

Fungal genus	Armillaria		Gymnosporangium		Basidiobolus		Ascobolus		Pilobolus
Measured launch speed (m s-1), range, mean (sample size)	0.1-0.9, 0.6 (9)		0.7-1.4, 1.1 (18)		2-9, 4 (10)		5-18, 14 (12)		2-13, 9 (14)
Aerodynamic radius (μm)	3		9		20		40		141
Reynolds number	0.3		1.3		10		70		167
Measured maximum discharge distance	60 μm		1-2 mm		20 mm		0.3 m		2.5 m
	Stokes	White	Stokes	White	Stokes	White	Stokes	White	Stokes	White
Launch speed (m s-1) required to match discharge distance	0.4	0.4	0.9-1.7	1.0-2.0	3.4	5.2	14	84	9	210
Predicted discharge distance based on measured launch speed	0.1 mm	0.1 mm	1.3 mm	1.1 mm	22 mm	15 mm	0.3 m	0.1 m	2.6 m	0.7 m

Note: Shaded cells in table highlight superiority of simple Stokes model for the effect of viscous drag over the more complex interpolation model of White (1974).

Results

The published velocity measurements for each species obtained from high-speed video analyses, Reynolds' numbers, and maximum discharge distances are shown in Table 1. To evaluate the competing drag models, launch speeds required to produce the observed discharge distances were calculated using Stokes' model for drag and the more complicated interpolation model (Table 1). Similarly, the distances that would result from the observed launch speeds were also calculated using both models.

For A. tabescens, the species with the lowest launch speed, the initial motion of the spore is characterized by a small Reynolds number, Re = 0.3. As expected for low Re motion (Fig 2), both drag models predict that the same launch speed, 0.4 m s^-1, is necessary to achieve the observed discharge distance of 0.06 mm. These predictions are consistent with the range of directly observed launch speeds: 0.12 to 0.91 m s^-1 with mean 0.64 m s^-1. The launch of G. juniperi-virginianae is characterized by Re = 1.3. A precise value for the discharge distance was difficult to obtain for this species, because its spores traveled well beyond the microscope field of view. Measurements from spore deposits provide estimates of 1-2 mm for the maximum discharge distance. Again there was excellent agreement between the discharge distances predicted from velocity data, and vice versa, for the Stokes and interpolation model of White.

For the remaining species, whose launches are characterized by larger Re, the predictions of the two models diverge (Fig 3). For B. ranarum, with Re = 10, there is a nearly two-fold difference in the launch speeds predicted from discharge distances; the interpolation model suggests that drag forces would reduce the travel to 75% of the measured distance. For A. immersus, Re = 70, the difference between the models increases to a six-fold mismatch between observed and predicted speeds, and to 23-fold for P. kleinii, with Re = 167 (Table 1, Fig 3). As Re increases, the White model drastically overestimates the drag on the projectiles and predicts unrealistic launch speeds. The superior performance of the Stokes model is apparent from the fact that it continues to predict discharge distances consistent with experimental measurements. These findings are highlighted by predicting spore trajectories based on the two models (Fig 4).

Fig 4.

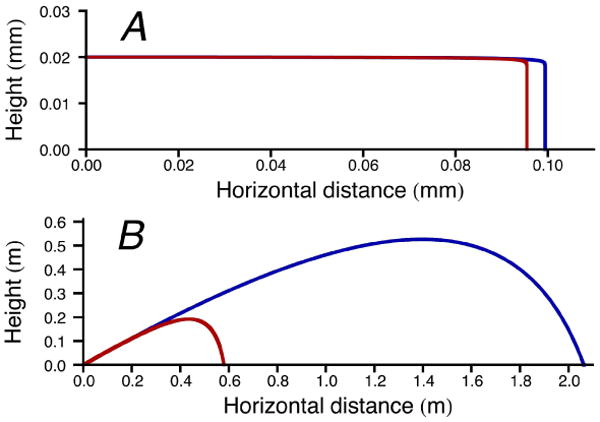
Predicted trajectories of discharged spores according to the simple Stokes model (blue curve) and more complex interpolation model (red curve). A, Armillaria tabescens; B, Pilobolus kleinii.

Discussion

For the low Reynolds number spore movement examined in this study (A. tabescens, G. juniperi-virginianae, and B. ranarum) the Stokes and White models predict discharge distances consistent with experimental measurements (Table 1). As Re increases, however, the overestimation of the drag by the White model is evident from the underestimation of discharge distance based on the measured launch speeds in A. immersus and P. kleinii. The continued effectiveness of Stokes' law in quantifying the drag on spores of these species that are moving in the transitional velocity regime (Fig 2), particularly at Reynolds numbers greater than 100 (Re = 167 for Pilobolus) is surprising, because it is generally assumed that Stokes is valid only for Re<1. Until recently, the lack of reliable measurements of the velocity of discharged spores precluded empirical evaluation of the competing drag models as applied to fungal systems. The present results do not argue against the need for a reliable theoretical model for Re>1, but they do require further exploration of the reason that the effects of drag are less extreme than the non-linear models, and other researchers, have suggested. The agreement between the experimental measurements and Stokes may be coincidental, but it is clear that the more complex models fail to provide useful predictions.

There are a number of possible explanations for these findings. One important consideration is that spores are launched at considerably higher speeds than their terminal velocities. Initial launch speeds can exceed sedimentation rates by several orders of magnitude. For example, mushroom ballistospores are discharged from their basidia at maximum speeds of 1 m s^-1, but they sediment at a rate of a few mm s^-1 (Gregory 1973; McCartney and West 2007). The faster discharge processes examined in this paper may generate turbulence behind the projectile. It has been suggested that this wake may overtake the projectile and decrease the effective drag (Wakaba and Balachandar 2007). This added mass effect and the related Basset or viscous history effect contribute to a reduction in drag, but are not sufficient to explain the success of the Stokes model.

A second consideration is the asymmetrical shape of most fungal projectiles. A crucial observation from high-speed video microscopy is that the spores of A. immersus, and other Ascomycota, are jettisoned along with a considerable volume of fluid from the ascus (Yafetto et al. 2008). The eight spores discharged from each ascus of A. immersus, and the surrounding fluid, are launched in single-file before coalescing into a more globular form during flight as they decelerate (Yafetto et al. 2008). The form of the projectile diverges from a spherical model even further in P. kleinii, in which the fluid within the sporangiophore is ejected as a lengthy column behind the sporangium. The White model predicted the least realistic launch speeds and discharge distances for these species, which suggests that the complex shape of the projectile may reduce the drag. In these fungi, the airflow that moves around the spores or sporangium does not close directly behind them, but remains separated around the subtending stream of fluid. It has been suggested that this trailing fluid may exert a streamlining effect, reducing drag (Vogel 2005). The extended form of the projectile and associated fluid in many Ascomycota and in species of Pilobolus may reduce the turbulence in the closing airflow, which may also reduce the drag.

Roper and Brenner (2009) developed a novel approach for calculating fluid flow around microscopic bodies of various shapes based upon an earlier recommendation by Carrier (1953). They used Oseen's approximation for drag (C_D = 24/Re + 3/16), which is a simple modification of Stokes (C_D = 24/Re), and a renormalized or Re-dependant viscosity term. The function for renormalized viscosity was found by fitting the results of the Oseen approximation to data obtained from the solution of the complete Navier-Stokes equations that describe fluid flow. It is encouraging, from the standpoint of the results of the present paper, that this model was successful in modeling fluid flow because Oseen and Stokes are very similar. But despite the apparent utility of the Ossen model, it is not clear whether the conclusions reached by Roper and Breener (2009) are fully applicable to the analysis of spore trajectories. In common with many previous studies on the drag on tiny projectiles, Roper and Brenner (2009) were concerned with steady-state conditions. The high-speed movements addressed in our work are far from steady-state, being characterized by an initial high acceleration from rest followed by fast deceleration.