Statistical prediction of single-stranded regions in RNA secondary structure and application to predicting effective antisense target sites and beyond

Abstract

Single-stranded regions in RNA secondary structure are important for RNA–RNA and RNA–protein interactions. We present a probability profile approach for the prediction of these regions based on a statistical algorithm for sampling RNA secondary structures. For the prediction of phylogenetically-determined single-stranded regions in secondary structures of representative RNA sequences, the probability profile offers substantial improvement over the minimum free energy structure. In designing antisense oligonucleotides, a practical problem is how to select a secondary structure for the target mRNA from the optimal structure(s) and many suboptimal structures with similar free energies. By summarizing the information from a statistical sample of probable secondary structures in a single plot, the probability profile not only presents a solution to this dilemma, but also reveals ‘well-determined’ single-stranded regions through the assignment of probabilities as measures of confidence in predictions. In antisense application to the rabbit β-globin mRNA, a significant correlation between hybridization potential predicted by the probability profile and the degree of inhibition of in vitro translation suggests that the probability profile approach is valuable for the identification of effective antisense target sites. Coupling computational design with DNA–RNA array technique provides a rational, efficient framework for antisense oligonucleotide screening. This framework has the potential for high-throughput applications to functional genomics and drug target validation.

INTRODUCTION

In the last two decades several important approaches have been developed for the prediction of secondary structure from an RNA sequence. The popular mfold program, developed with dynamic programming algorithms, predicts optimal structure and suboptimal structures through free energy minimization (1–3; http://bioinfo.math.rpi.edu/~zukerm/rna/). The partition function approach by McCaskill (4) computes base pair probabilities and the binding probability for any base. A C program for this algorithm is available in a suite of RNA secondary structure software known as the Vienna RNA package. This package was developed by a theoretical chemistry group at the University of Vienna (5; http://www.tbi.univie.ac.at/~ivo/RNA/). Ding and Lawrence (6) formulated the RNA folding problem in a Bayesian statistical framework and extended the partition function method by generating a statistically representative sample of the probable structures. Heuristic Monte Carlo algorithms based on kinetics and genetic principles have also been described (7–10).

In this paper, we explore the use of a sampling approach for the prediction of single-stranded regions in an RNA molecule. While we focus on the important antisense application, single-stranded regions, particularly destabilizing loops, can play many important functional roles. These include, for example, protein binding (11,12), ribozyme binding and catalysis (13), regulation of cellular processes (14,15), pseudoknot formation and tertiary interactions for kissing hairpins, bulge–loop complexes, hairpin loop–internal loop complexes, etc. (16). For these applications, computational prediction of single-stranded regions can also be helpful for experimental design for structure probing by RNases or chemical means.

A novel regulatory mechanism was recognized about two decades ago: an oligodeoxynucleotide can bind to an mRNA through complementary base pairing to block its translation (17). The discovery that oligonucleotides can play a regulatory role in gene expression led to the development of the antisense strategy to artificially control gene expression. Although variable degrees of success have been achieved in the application of antisense methods to the research of biological phenomena and human disease treatment, it has been proven that antisense oligonucleotides (ASOs) are able to modulate gene expression in both prokaryotes and eukaryotes (18). In recent years, several antisense compounds for disease treatment have been evaluated in clinical trials with promising results, and more compounds are being evaluated in clinical trials (19,20). In 1998, Vitravene (Isis Pharmaceuticals, Carlsbad, CA) became the first antisense drug approved by the Food and Drug Administration. It is used to treat cytomegalovirus retinitis in AIDS patients.

For ASOs to be effective, the complementary target sequence on mRNA must be available for hybridization. RNA nucleotides can be inaccessible when they are sequestered in secondary structure. The usually weaker tertiary interactions and RNA–protein interactions can also be factors that affect accessibility. The identification of regions likely to remain single-stranded in RNA secondary structure can be an important part of antisense technology.

Lima et al. (21) concluded that the tightest binding of ASOs occurs at target sites for which disruption of the target structure is minimal, and single-stranded regions should be selected over double-stranded regions in the consideration of target sites. Vickers et al. (22) directly demonstrated that mRNA structures play a significant role in determining antisense oligonucleotide efficacy in vivo. They concluded that discovery of active ASOs requires identification of unstructured sites in the cellular mRNA. Matveeva et al. (23) also found that there is a correlation between single-stranded specific probes and accessible sites for antisense targeting, but there are a few exceptions, probably due to steric hindrance that limits RNase H access. It has been speculated that duplex formation is initiated at an accessible substructure that includes a site for nucleation with unpaired bases and then propagates from the nucleation site through a ‘zippering’ process (24,25). A hairpin of four unpaired bases can be involved in hybrid formation (26).

A few secondary-structure-prediction based computational approaches to the evaluation of potential antisense targets have been reported. Stull et al. (27) presented thermodynamic indices by averaging relevant free energies of secondary structures generated from a Monte Carlo RNA folding algorithm based on an evolutionary heuristic (7,28). Because this algorithm does not guarantee the generation of a valid statistical sample of low energy structures, the most likely structure is not necessarily the lowest free energy structure.

For the genomic RNA (∼9700 nt) and the complementary RNA strand of the human immunodeficiency virus type 1 (HIV-1), Sczakiel et al. (29) found that local folding potential can shed light on effective antisense targets. The local folding potential was computed for each of successive overlapping segments of a chosen window width (ranging from 50 to 400 nt) along the RNA chain, by folding each segment with mfold and computing its minimum free energy. This method was proposed by Le et al. (30) for assessing stable structures in HIV-1. Because long distance interactions and short term interactions between the nucleotides near the ends of the segment and the neighboring nucleotides outside the segment are ignored, this method appears to be reasonable only for relatively long window width, as it cannot address the hybridization potential of individual nucleotides or short segments.

Zhao and Lemke (31) performed a comparative analysis on 22 RNAs using mfold. The RNAs were previously studied for selective gene inactivation by ASOs and ribozymes, small catalytical RNA molecules that specifically bind to and cleave target RNAs. Despite limited representation of alternative structures by four or five suboptimal foldings, they found a correlation between the predicted base-pairing accessibility of the targets and the experimental efficacy of the antisense reagents. They recommend that the cleavage site for ribozymes should fall within a loop of at least four nucleotides, and one, preferably both, of the 5′- and 3′-ends of the antisense segment should fall within a single-stranded rather than a stem region. Despite the inherent difficulty in selecting a representative sample of the suboptimal foldings, James and Cowe (32) proposed addressing the hybridization potential using suboptimal foldings from mfold and showed that their procedure works well for the rat OX40 mRNA.

These findings lend additional support to the importance of exploring secondary structure in the selection of antisense targets. Our strategy is to focus on single-stranded regions in RNA secondary structure, in particular those of at least four consecutive unpaired bases. The Vienna package can calculate the probability of a single base being unpaired; however, it cannot address the hybridization potential of a region. This is not a problem for the sampling-based probability profile approach we propose in this work, which can overcome limitations of existing computational approaches. We illustrate our approach with applications to representative RNA sequences and an antisense application to rabbit β-globin mRNA.

MATERIALS AND METHODS

Statistical sampling of RNA secondary structures

The structure sampling algorithm of Ding and Lawrence (6) yields a representative statistical sample of secondary structures. This algorithm was based on free energies for stacking in helices. The sampling probabilities are computed using partition functions calculated in the forward step of the algorithm. For more sophisticated and realistic energy rules, we have developed an extended algorithm. The forward step of this algorithm is a recursive algorithm for partition functions. This recursive algorithm extends the work of McCaskill (4) by including single base stacking energies and other up-to-date free energy parameters. The backward step takes the form of a sampling algorithm; the sampling probabilities are computed using the partition functions computed in the forward step.

The extended algorithm accommodates the up-to-date free energy rules and parameters developed by Turner’s group (33,34) with the exception of coaxial stacking. These include free energies for stacking in a helix, stacking for a terminal mismatch in a hairpin loop (size ≥4 nt) or an interior loop, and penalties for hairpin, bulge, interior and multi-branched loops. Free energies for single base stacking (dangling ends) are used for exterior and multi-branched loops. For hairpins, a bonus for UU and GA first mismatches (included in the terminal stacking data) and a bonus for G·U closure preceded by two G nucleotides in base pairs are applied, and a penalty for oligo-C loops (all unpaired nucleotides are C) are used. A table is consulted for tetraloops (hairpin loops with four unpaired nucleotides). For a bulge of 1 nt, the stacking energy of the adjacent pairs is added. For interior loops, tables for 1 × 1, 1 × 2 and 2 × 2 loops are consulted and a penalty for asymmetry is applied. A terminal A-U, G·U penalty is explicitly applied to exterior loop, multi-branched loops, bulges longer than 1 nt and triloops (hairpin loops with three unpaired nucleotides), while this penalty is included in the terminal stacking data for hairpin loops (size ≥4 nt) and interior loops. These free energy parameters are for 37°C and 1 M NaCl; however, this algorithm can be used with any set of nearest neighbor parameters derived for other conditions.

The Boltzmann distribution in statistical mechanics gives the probability of a secondary structure I at equilibrium as (1/U)exp[–E(I)/RT], where E(I) is the free energy of the structure, R is the gas constant, T is the absolute temperature and U is the partition function for all admissible secondary structures of the RNA sequence. The extended algorithm samples exactly according to the Boltzmann distribution, i.e. it can generate a statistical sample of any desired size from the Boltzmann ensemble of secondary structures. The sampling process is similar to the traceback algorithm employed in the dynamic programming algorithms (1–3) but differs in that the base pairing is randomly sampled from Boltzmann probabilities rather than chosen to yield a minimum free energy structure. Because the probability of a structure decreases exponentially with increasing free energy, the structure with highest frequency in the sample is most likely the minimum free energy structure. When long interior loops (e.g. size >30 nt) are disallowed, the forward step of the algorithm is cubic. The sampling step of the algorithm is stochastically quadratic in the worst case, thus it can quickly generate a large number of secondary structures.

Probability profiles of single-stranded bases and sequences

From recursively derived partition functions for an RNA sequence of n bases, McCaskill (4) also presented recursions for marginal base pairing probability,

P_ij = Prob(base i and base j form a pair);

then the probability that base i is unbound, i.e. single-stranded, is

q_i = 1 – Σ_{(i + 1) ≤ j ≤ n} P_ij – Σ_{1 ≤ j ≤ i} P_ji.

As emphasized by McCaskill (4), the base pair binding probabilities are not locally determined by the RNA sequence, rather they reflect a sum over all equilibrium-weighted structures in which the chosen base pair occurs. Therefore, {q_i} statistically describe the antisense hybridization potential for every nucleotide in the sequence. Alternatively, the sampling method presents a means to estimate q_i with the sampling frequency for the unbound base i. This avoids the cubic algorithm required to compute the probabilities analytically. A probability profile is then displayed by plotting {q_i} against the nucleotide position.

However, probabilities {q_i} do not provide a suitable means to assess the potential of a sequence to be single-stranded and available for hybridization. More specifically, for a fragment from base i to base j, Q_ij, the probability of the fragment being single-stranded is not simply the product of individual probabilities {q_m}, i ≤ m ≤ j, because independence is invalidated by the nearest-neighbor interactions. However, a probabilistic measure of the hybridization potential of a sequence can be obtained from a sample of secondary structures. Because the sample is representative of the Boltzmann ensemble of secondary structures, the fraction of the sample in which all the nucleotides in the sequence are single-stranded provides an unbiased estimate of the probability of the sequence being single-stranded. For all successive overlapping sequences of width W, the sampling estimate for the probability that a sequence is single-stranded can be plotted against the first nucleotide of the sequence for a probability profile of single-stranded sequences with width W. Based on the rule-of-thumb of at least four unpaired bases (26,31), we set W = 4 for antisense application.

RESULTS

Examples of probability profiles

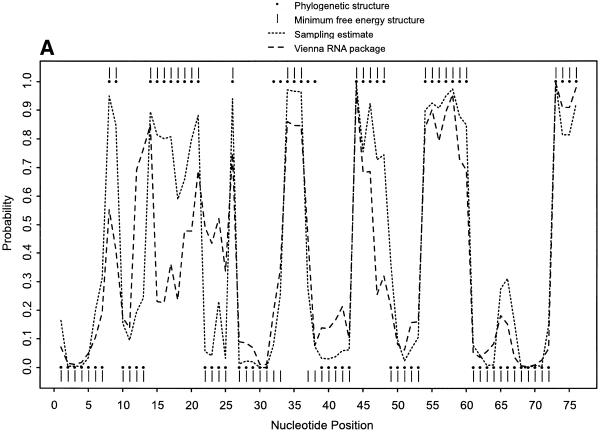
For single-stranded bases in Escherichia coli tRNA^Ala, Figure 1A demonstrates the probability profile estimated from 1000 sampled secondary structures, the probability profile computed by the Vienna RNA package, the profile indicated by the minimum free energy (MFE) structure computed with version 3.1 of mfold (33,34; http://bioinfo.math.rpi.edu/~mfold/rna/form1.cgi) and that indicated by the phylogenetically-determined structure (35). A sample size of 1000 was found to be adequate because the profile estimates from this sample and a larger sample of 10 000 structures were not readily distinguishable. For the unpaired individual bases, the probability profile and the profile by the MFE structure are comparable. This is generally expected because the MFE structure is the most probable structure in the sample. However, the MFE structure substantially underpredicts the width of the region around nucleotide G³⁵ of the anticodon loop, while a significant portion of the sample adequately reveals the width. For the region between nucleotide G³⁰ and A⁷⁶, the sampling approach and version 1.3.1 of the Vienna RNA package gave comparable results; however, for the region between nucleotides C⁵ and C²⁵, the sampling profile predicted the phylogenetic structure substantially better than the Vienna profile. This version of Vienna package is based on an earlier compilation of Turner’s free energy parameters described by Walter et al. (36). It has been shown that the latest update improves the prediction of secondary structure (33). This explains the better performance by our sampling algorithm.

Figure 1.

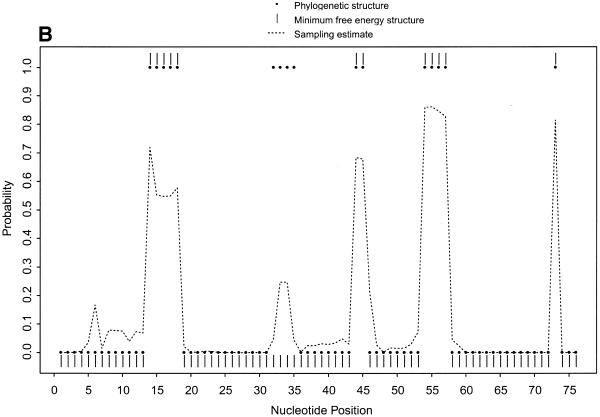
Probability profiles for E.coli tRNA^Ala, with sampling estimates computed from 1000 sampled secondary structures. (A) The probability profiles for single-stranded nucleotides (sequence width W = 1) indicated by the phylogenetic structure (large dots) and by the minimum free energy structure (vertical bars), estimated by the sampling algorithm (short dashed line) and computed by the Vienna RNA package (long dashed line). For the region between C⁵ and C²⁵, the sampling estimate predicts the phylogenetic structure substantially better than the Vienna RNA package. (B) The probability profiles for single-stranded sequences of four consecutive nucleotides (sequence width W = 4) in E.coli tRNA^Ala indicated by the phylogenetic structure (large dots) and by the minimum free energy structure (vertical bars) and estimated by the sampling algorithm (dashed line). The probability profile cannot be computed by the Vienna RNA package or other existing algorithms.

Figure 1B shows the probability profile of the sample for single-stranded sequences with a sequence width of 4 nt. For comparison with the phylogenetic structure, a dot with coordinates (i, 1) is shown in Figure 1B if the 4 nt sequence starting at nucleotide i is single-stranded, and a dot with coordinates (i, 0) is plotted if any of the four nucleotides is base paired. Similarly, the MFE structure is plotted. The unstructured region of the anticodon loop is missed by the MFE structure, but is revealed by the sampling profile through a peak of substantial probability. For the two sampling profiles in Figure 1A and B, not only do the single-stranded regions in the phylogenetic structure correspond well to the local peaks of the probability profiles, but also the width of the regions matches the width of the peaks with only one exception, region ³²AUGGCAU³⁸ of the anticodon loop. The peak for this region in the phylogenetic structure is slightly narrower because two Watson–Crick pairs A³²–U³⁸ and U³³–A³⁷ are likely to be predicted by any free-energy based algorithm, while these two base pairs are absent in the phylogenetic structure. In Figure 1B, the peak of the sampling profile between A³² and U³⁸ is much lower than the corresponding peak in Figure 1A because, while the single-stranded probability for each of G³⁴, G³⁵ and C³⁶ is >0.96, the probabilities for U³³ and A³⁷ are <0.28. Thus, for identifying a single-stranded region of at least 4 nt, a high peak in the profile of single-stranded bases can be visually misleading when the width of the peak is <4 nt. The probability profile of single-stranded sequences presents a clearer picture of potential antisense sites, because it has fewer and narrower peaks than the profile of single-stranded bases. This probability profile cannot be obtained by the Vienna RNA package or any other existing computational methods.

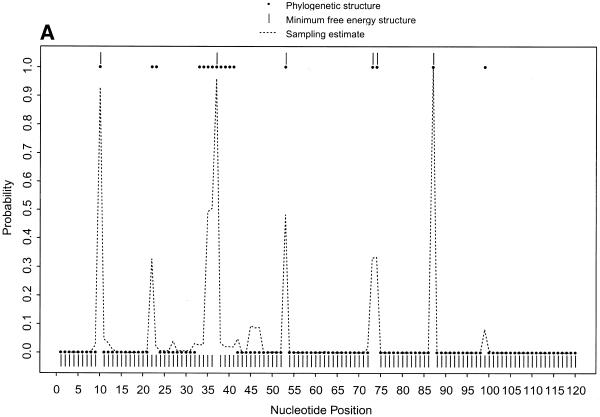
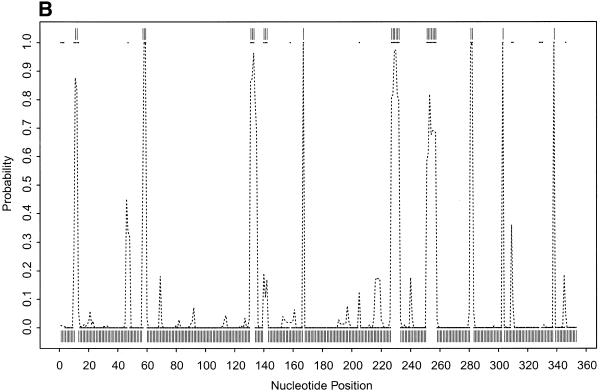
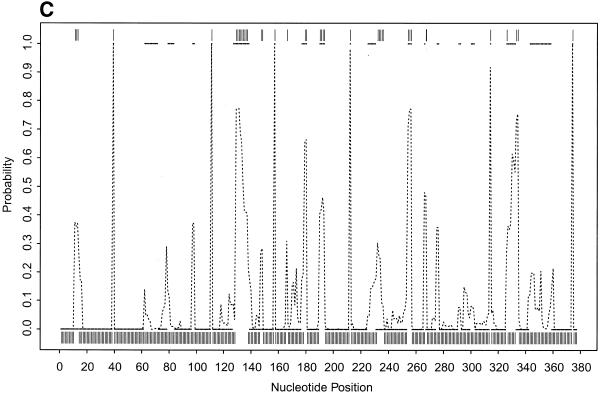
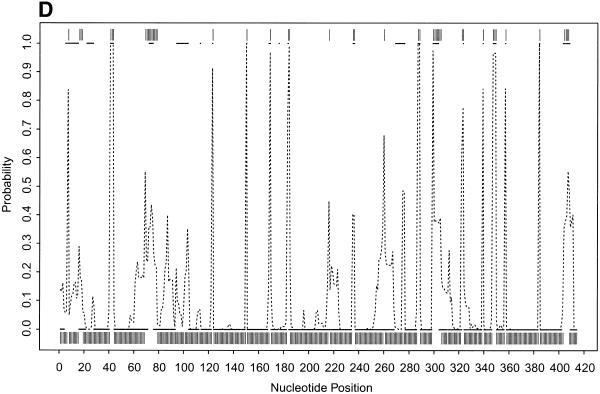
To further illustrate our approach, we present the probability profiles in Figure 2A–D for the following representative RNA sequences with phylogenetically-determined secondary structures: Xenopus laevis oocyte (Xlo) 5S rRNA (37), domain II of E.coli 16S rRNA (38), E.coli RNase P (39) and group I intron from 26S rRNA of Tetrahymena thermophila (40,41). For these sequences, phylogenetically-determined single-stranded regions correspond to peaks in the probability profile with near certainty (Fig. 2; P_C in Table 1). On the other hand, peaks with at least a maximum probability of 0.5 almost certainly point to single-stranded regions (P_C1 in Table 1); peaks with a maximum probability between 0.2 and 0.5 have at least a 50% chance of correctly indicating single-stranded regions (P_C2 in Table 1), whereas there is a far smaller but appreciable chance for peaks with a maximum probability <0.2 (P_C3 in Table 1) to correctly indicate single-stranded regions. As in the case of E.coli tRNA^Ala, for all these RNA sequences, the probability profile reveals more single-stranded regions in the phylogenetic structure than the MFE structure (P_I in Table 1). The substantial improvement is because the alternative structures in the sample are able to reveal structural motifs not predicted by the MFE structure. On the other hand, the motifs in the MFE structure are well reported by the sample because it is the most probable structure in the sample. The improvement is noticeably greater for E.coli RNase P, which has the highest percentage of nucleotides in pseudoknots, a motif not allowed by either mfold or our current algorithm.

Figure 2.

(Opposite and above) Probability profiles (sequence width W = 4) for other representative RNA sequences, with sampling estimates computed from 1000 sampled secondary structures. For X.laevis oocyte 5S rRNA (A, opposite), the large dots present the profile indicated by the phylogenetic structure, the dashed line is the sampling estimate and the vertical bars represent the minimum free energy structure. For E.coli 16S rRNA domain II (B, opposite), E. coli RNase P (C, above) and Group I intron from 26S rRNA of T.thermophila (D, above), the small solid squares (adjacent squares appear to form line segments) present the profile indicated by phylogenetic structure, the dashed line is the sampling estimate and the vertical bars represent the minimum free energy structure. For the Tetrahymena Group I intron, a 6 bp double-stranded region called P3 (38) in the phylogenetic structure is not considered here because of the creation of a pseudoknot. The current sampling algorithm needs to be extended to predict certain types of pseudoknots.

Table 1. Correspondence between phylogenetically-determined single-stranded regions and peaks on the probability profile and improvement in predictions over minimum free energy structure.

RNA sequence	Accession no.	Length (nt)	PC (%)a	PC1 (%)b	PC2 (%)c	PC3 (%)d	PI (%)e
Escherichia coli tRNAAla	X66515	76	100	100	100	0	20
Xenopus laevis oocyte 5S rRNA	K02695	120	100	100	100	25	28
Escherichia coli 16S rRNA domain II	J01695	353	82	100	50	33	29
Escherichia coli RNase P	V00338	377	100	100	58	50	40
Tetrahymena thermophila LSU group I intron	V01416	413	95	88	67	29	19

^aP_C is the percentage of phylogenetically-determined single-stranded regions (region here is either a sequence of four consecutive nucleotides or several such sequences in a row) that correspond to peaks (regardless of the magnitude of the maximum probability) in the probability profile in Figure 2.

^bFor peaks with a maximum probability ≥0.5, P_C1 is the percentage of these peaks that correspond to single-stranded regions.

^cP_C2 is the percentage of the correspondence for peaks with a maximum probability between 0.2 and 0.5.

^dP_C3 is the percentage of the correspondence for peaks with maximum probability <0.2.

^eA probability profile predicts more single-stranded regions in the phylogenetic structure than the minimum free energy structure (Figs 1B and 2). P_I is the percentage of improvement in the prediction by the probability profile over the MFE structure. This is computed by the number of regions missed by the MFE structure but predicted by the probability profile divided by the total number of single-stranded regions in the phylogenetic structure (e.g., seven for Xlo 5S RNA) and multiplied by 100%.

The results reveal variation in the reliability of prediction among different RNAs. For free energy minimization for the prediction of RNA secondary structure, variability in the reliability of prediction for different RNAs has been well documented (33,42,43). Because our sampling algorithm is also based on free energies, it is not surprising to observe a similar phenomenon in our context. There is also substantial variability in the maximum probabilities for the peaks that correspond to single-stranded regions. Similarly, for minimum free energy prediction of secondary structure, there is variability in the reliability of predictions for different regions of a sequence (43). The summary in Table 1 indicates that single-stranded regions predicted by high probability peaks are ‘well-determined’ by the probability profile. In other words, these regions are highly stable and, thus, are present with high probability in a sample of probable secondary structures. For regions of lower stability, their probabilities are either moderate or low, because alternative structural motifs will be more likely to be present in the sample. Our sampling algorithm gives a complete statistical presentation of probable competing alternative structures. Thus, the probability profile provides a statistical delineation of single-stranded regions with varying stabilities.

Antisense application

The rabbit β-globin mRNA (589 nt, GenBank accession V00879, coding region 54–497) has been well studied for antisense inhibition of protein synthesis (24,44,45). Cazenave et al. (44) used an 11mer and three 17mers targeted to rabbit β-globin mRNA in a wheatgerm extract as well as in microinjected Xenopus oocytes. Goodchild et al. (45) examined the inhibition of cell-free translation by eight phosphodiester ASOs targeted to this mRNA. Milner et al. (24) described a combinatorial oligonucleotide array technique for hybridization assessment of oligonucleotides within a given region. For the rabbit β-globin mRNA, an array of 1938 oligonucleotides up to a length of 17 bases was used to measure the ASO:mRNA hybridization potential. These oligonucleotides were complementary to the first 122 bases of the mRNA. Three oligomers, BG1, BG2 and BG3, were chosen for study by in vitro translation in wheatgerm extract and the RNase H assay.

In our analysis, the results for BG1, BG2 and BG3 are directly compared to the data from the other two groups, because all these ASOs were studied in cell-free translation systems and the percentages of translation inhibition were reported (Table 2). The inhibition percentages facilitate a quantitative comparison and assessment of the correlation between inhibition of cell-free translation and computational predictions. The qualitative array hybridization data of Milner et al. (24) and the computational predictions were summarized and compared separately (Table 3).

Table 2. Comparison of inhibition of rabbit β-globin synthesis in cell-free translation systems and hybridization potential predicted by probability profile for rabbit β-globin mRNA.

ASO name	Target sequence/site	% Inhibitiona	Hybridization	Reference
(length in nt)	on mRNA		potential
β1 (20)	A14–C33/5′-UTR	23 (5.2)	high	45
β2 (20)	C46–G65/start	61 (5.2)	high	45
β3 (20)	A144–C163/coding	18 (5.2)	moderate	45
β4 (20)	G207–A226/coding	43 (5.2)	high	45
β5 (22)	A1–G22/cap	67 (5.2)	high	45
β6 (23)	U23–A45/5′-UTR	47 (5.2)	high	45
β7 (CCC+β5, 25)	A1–G22/cap	75 (5.2)	high	45
β8 (β7β6, 48)	A1–A45/cap	89 (2.6)	high	45
β6+β7 (mixture)	A1–A45/cap	89 (2.6)	high	45
BG1 (17)	C46–U62/start	50 (0.1)	high	24
BG2 (17)	A51–C67/start	50 (0.5)	high	24
BG3 (15)	C85–U95/coding	0 (1)	low	24
17 Glo[3-19] (17)	A3–A19/cap	72 (0.5)	high	44
17 Glo[51–67] (17)	U51–C67/start	95 (0.5)	high	44
11 Glo (11)	A44–A54/start	65 (0.5)	high	44
17 Glo[113–129] (17)	U113–G129 / coding	95 (0.5)	low	44

^aNumbers in parentheses represent ASO concentration in µM.

Table 3. Comparison of the intensity of ASO:mRNA hybridization on the oligodeoxynucleotide array and the probability profile for the first 122 bases of rabbit β-globin mRNA.

Region	Hybridization intensity	Probability profile (peak feature)
A1–C37	not detectable	high peaks (narrow)
C46–C60 a	high	high peak (wide)
A61–C91	weak but detectable	low
A76–A90	not detectable	low
C94–G110	moderate	moderate

^aC⁴⁶–C⁶⁰ is contained in two 16mers C⁴⁶–A⁶¹ and A⁴⁵–C⁶⁰, and three 17mers C⁴⁶–U⁶² (BG1), A⁴⁴–C⁶⁰ and A⁴⁵–A⁶¹. The hybridization yields for ASOs complementary to these six sequences are at least three times that of any other oligonucleotides in the array (24).

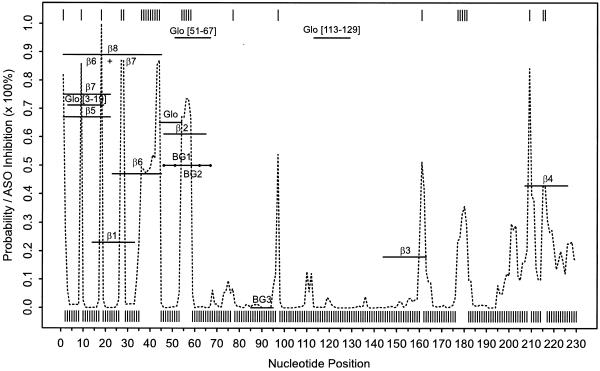
The probability profile with a sequence width of 4 nt was computed with a sample of 1000 secondary structures for the rabbit β-globin mRNA. The probability profile and the profile by the MFE structure for the region A¹–U²³⁰ are shown in Figure 3, as the ASOs in these studies were targeted to this part of the mRNA. The target sites on the mRNA, the inhibition effect in cell-free translation systems in the three studies, and the hybridization potential predicted by the probability profile are summarized in Table 2. For this analysis, the hybridization potential was assessed as high if, for the target site, there was at least one peak with probability ≥0.6; the potential was considered moderate for a peak with probability between 0.3 and 0.6; and the potential was low for a site with a probability <0.3 of being partly single-stranded. For ASOs described by Cazenave et al. (44), the inhibition figures for wheatgerm extract were estimated from figures 3 and 7 in that report. The region A¹–A⁴⁵ was targeted by five of eight ASOs described by Goodchild et al. (45). There are three high probability sequences in this region: A¹–C⁴, A¹⁸–U²¹ and U³⁶–A⁴⁵. They explain the predicted high hybridization potential for β5, β6, β7, β8 and β6 + β7. The moderate inhibition by β1 indicates that A¹⁸–U²¹ alone is not as effective as the other two. One explanation is that the two adjacent nucleotides, C¹⁷ and G²², are predicted to almost certainly engage in G·C pairing and, thus, they might present a substantial energy barrier for hybridization elongation by ‘zippering’. The high inhibition by β8 and β6 + β7 suggests that an antisense effect can be enhanced by simultaneously targeting several high potential sites. We also found consistent results for BG1, BG2 and BG3 reported by Milner et al. (24). Clear inconsistency between our predictions and the observed inhibition was found for 17 Glo[113–129] of Cazenave et al. (44), which appears to be an exception to the rule-of-thumb of at least four unpaired bases (26,31). In the case of an effective antisense site with less than four unpaired bases, the site would not be predicted by the probability profile with a sequence width of 4 nt. On the target site of 17 Glo[113–129], the probabilities of being unpaired for U¹²⁵ and G¹²⁶ are 0.61 and 0.56, respectively, but the probabilities are <0.1 for adjacent bases U¹²⁴ and G¹²⁷. Among many other potential reasons for poor prediction in this case could be tertiary interactions and RNA–protein interactions, and self-folding of the oligomer that are unaccounted for by the current algorithm.

Figure 3.

The probability profile for single-stranded sequences of four consecutive nucleotides (sequence width W = 4) estimated by 1000 sampled secondary structures (dashed line) and the profile indicated by the minimum free energy structure (vertical bars) for rabbit β-globin mRNA and the experimentally measured inhibition of ASOs in cell-free translation systems. The profile is shown for the region of the first 230 nt that is targeted by the ASOs. The length and binding sites of the ASOs are indicated by horizontal lines with the names of the ASOs centered above or below the lines. These lines also indicate the inhibition of translation through their position on the vertical axis. The vertical axis also shows the probability for the profile with inhibition corresponding to probability multiplied by 100%.

If we associate low, moderate and high hybridization potential with inhibition of 0–19, 20–39 and 40–100%, respectively, then for 13 of the 16 ASOs (81%) examined here, the hybridization potential revealed by the probability profile is indicative of the antisense inhibitory effect. For all the ASOs, there is a significant correlation (P = 0.0147, correlation coefficient = 0.597) between the hybridization potential predicted by the probability profile and the degree of translation inhibition. For β1–β8, there is a substantially higher correlation (P = 0.0037, correlation coefficient = 0.882). In contrast, Stull et al. (27) found no significant correlations between observed inhibition and any predictive indices for β1–β8. For ASOs described by Cazenave et al. (44), Stull et al. (27) found a correlation between Dscore, one of their indices, and inhibition for oligomer concentration at 6 µM, but no significant correlation for oligomer concentrations <6 µM. The probability profile and the MFE structure give comparable predictions of single-stranded regions. However, without an associated measure of confidence, there is a lack of correlation between the binary prediction by the MFE structure and the degree of translation inhibition (P = 0.567, correlation coefficient = 0.155). This exemplifies the observation that there is limited success in using MFE structure for antisense design (46). Because the sampling profile provides a statistical measure of confidence in the predictions, it is not surprising that the profile is found to be generally indicative of the degree of translation inhibition.

For the hybridization intensity data of Milner et al. (24), there is very good agreement between the hybridization intensity and the probability profile for regions C⁴⁶–C⁶⁰, A⁷⁶–C⁹⁰ and G⁹⁴–G¹¹⁰ (Table 3). The hybridization intensity for region A⁶¹–C⁹¹ is in reasonable agreement with the probability profile. In this region, the maximum probability of a peak is ∼0.1. For a peak with a maximum probability <0.2, there is an appreciable chance for the peak to correctly predict single-stranded regions (Table 1). Thus, weak hybridization is possible for low but appreciable probabilities. For region A¹–C³⁷, it is an intriguing contrast that the hybridization data are in disagreement both with the data described by Goodchild et al. (45) and with the probability profile, but the probability profile is in good agreement with the data of Goodchild et al. (45). The length of the oligomers, 20–45 nt discussed by Goodchild et al. (45), and at most 17 nt in the report of Milner et al. (24), offers an explanation for the conflicting results. Goodchild et al. (45) indicated that a greater inhibition could be obtained by covering a longer portion of the mRNA. This is evidenced by the greater inhibition of β8 or a mixture of β6 and β7 than either β6 or β7 alone (Table 2). There are several sharp peaks in the probability profile for this region. Thus, a plausible explanation from the profile is that substantially longer ASOs cover more peaks in this region and hence enhance the chance of both nucleation and propagation of duplex formation. Although oligomer length has a positive effect on translation inhibition in this case, this may not be generally true (24). We also note that the conclusion of insignificant hybridization by Milner et al. (24) for region A¹–C³⁷ appears to be based on the lack of a continuous subregion with detectable hybridization. In this region, there are two isolated intensity bands in figure 1 of Milner et al. (24), indicating substantial hybridization at sequence positions that were also targeted by Glo[3–19] of Cazenave et al. (44).

The six oligomers containing bases C⁴⁶–C⁶⁰ (Table 3), and BG2, β2, Glo[51–67] in Table 2 share one common feature on the profile: a relatively wide, high probability peak between A⁵⁴ and U⁵⁸, with ⁵⁴AUG⁵⁶ being the initiation codon. This suggests that a smooth and relatively wide peak on the probability profile can be a high potency antisense site because the chance of hybridization is improved for a wider single-stranded region.

DISCUSSION

Prediction of single-stranded regions

In this work, we have demonstrated the probability profile approach for the prediction of single-stranded regions in RNA secondary structure. The results on the test sequences show good correspondence between single-stranded regions by phylogenetic structure and predictions by the probability profile. In particular, high probability peaks correspond to single-stranded regions with high reliability. The variability in the reliability of predictions suggests that the results from the test sequences may not indicate the reliability of prediction for other RNA sequences. Poor predictions for a particular RNA or regions of the sequence can be partly attributed to uncertainties in thermodynamic parameters, pseudoknots and other tertiary interactions and RNA–protein interactions. These factors are not taken into account in the current algorithm. These caveats are associated with other efficient and free-energy based algorithms for RNA secondary structure prediction. In future work, we plan to extend the sampling algorithm to address certain types of pseudoknots.

The sampling stage of the algorithm is rather fast, although the implementation of the algorithm in Fortran 77 is not yet highly optimized. For the rabbit β-globin mRNA, it took 527 s to complete the partition function calculation, and 75 s to generate 1000 structures on a 300 MHz CPU of an Ultra 2 SPARC workstation. The computation time for the partition function calculation can be substantially improved if simpler multibranched loop evaluation is made possible, as was done for version 3.1 of mfold (33). This will be investigated. The sampling algorithm can be used for estimating the probability of any structural motif, such as helices, hairpin loops, bulges or interior loops, in addition to single-stranded regions.

Computational screening of effective antisense sites

For long mRNA sequences, there are many suboptimal foldings with free energies close to the minimum free energy. It has been a practical problem for antisense experimentalists to select one of the low free energy structures as the basis for antisense design. Furthermore, the suboptimal foldings from mfold do not guarantee a statistically unbiased sample of probable secondary structures. This makes it difficult to assign a statistical measure of confidence for predictions based on these suboptimal foldings. By summarizing a statistical sample of probable structures in a single plot, the probability profile approach overcomes these difficulties. The ‘well-determined’ single-stranded regions are revealed by peaks with high probabilities on the profile. While the test RNA sequences in Figures 1 and 2 probably have a single well-defined structure, it is possible that mRNAs do not. Statistical sampling of probable structures provides a suitable means to address this uncertainty. This is demonstrated by the substantial improvement in predictions over the minimum free energy structure. The sampling method also has the advantage that it does not require the generation of a huge number of all possible structures, as suggested previously (47).

The probability profile approach offers a comprehensive computational screening of the entire mRNA. For several other mRNA sequences with length ranging from 1 to 3 kb, we observed 15–20 high hybridization sites per kilobase (data not shown). These sites provide ample opportunities for rational design of antisense oligomers. An antisense oligomer is the reversed complement of a target sequence. The identification of optimal oligomers could be particularly important for antisense drug development. In applications, one can focus on sites within a particular mRNA region (e.g., coding region) of interest. In designing antisense oligomers, some basic rules are applicable for avoiding non-antisense effects and for enhancing antisense potency. Three or more Gs in a row should be avoided (48). To minimize the possibility of binding to a non-targeted mRNA with strong sequence homology at the binding site, a BLAST search for a prospect oligomer can be performed to ensure no appreciable overlapping with other mRNAs in the experimental system (49). In particular, investigators need to be aware that translation initiation sites can have good homology in both related and non-related genes (46). To avoid stable intra-molecular structure within oligomers, oligomers that contain self-complementary regions (i.e. palindromic sequences) should not be used. Other suggestions for experimental design can be found in the literature (49–51).

The results with rabbit β-globin mRNA suggest that relatively wide, high probability peaks on the probability profile are very likely to be effective antisense sites. In some cases, relatively long oligonucleotides covering narrow high probability peaks in a region can be effective, because the chance of nucleation and propagation of duplex formation is enhanced with several single-stranded sites, despite their short length. In other cases, increasing oligomer length may not improve hybridization, because intramolecular base pairing within the oligomer may hinder hybridization (24). The finding of a significant correlation between the degree of translation inhibition in cell-free systems and predicted hybridization potential is consistent with results from in vitro and in vivo studies (21–23). This further supports the belief that the accessibility of the target site through complementary base pairing is a very important factor in determining the efficacy of an antisense oligonucleotide.

The antisense analysis is based on data from cell-free translation systems and an oligonucleotide array. A correlation between in vitro accessibility data and oligonucleotide intracellular activity has been documented for several RNAs (23,52–54) and a significant correlation by statistical analysis on a large number of oligonucleotides has been reported (55). Also, for oligonucleotide array, good correspondence between hybridization yield on the array and in vivo and in vitro antisense activities has been reported (23,54).

Similar to several existing procedures, our approach to antisense application is also based on mRNA secondary structure, one of several factors that can affect the accessibility and efficacy of an antisense molecule. Tertiary structure and RNA–protein interaction are not addressed. Cellular concentrations of the ASO and the mRNA are also important variables that can dictate how likely it is that the target mRNA and the antisense oligonucleotide will encounter and hybridize. Our finding reiterates the belief that secondary structure is perhaps the most important variable.

The approach presented in this work does not address the potential impact of secondary structure around single-stranded regions. In view of the multi-step process of nucleation and propagation for duplex formation (24,25), the probability profile presents a statistical delineation of the potential for nucleation. The initial pairing from the nucleation step needs to be stable enough to allow propagation (25). While the free energy gained can be computed, some empirical rule for minimum free energy gain required for propagation will be helpful for selecting sites with propagation potential from the profile. Propagation can more readily proceed by strand invasion of stems, while propagation through a single-stranded region may involve considerable reorientation of the strand (25). This striking observation suggests that it does not require too great a free energy price to invade a helically-ordered strand for propagation. It also suggests that for a sizable loop, sites on the ends of the loop may be more efficient for propagation. Furthermore, duplex propagation is affected by features in the target structure that are not well understood (25). The ‘zippering’ process for propagation stops when it meets an energy barrier such as the ends of stems or sharp turns in the folded RNA (24,25). These observations offer some clues as to how a quantitative score based on the profile might be developed to assess the potential of propagation. The algorithm can be expanded to include the free energy change attributed to oligomer–target duplex formation and to assess its impact on the predictions. A lack of apparent correlation between the measured free energy change and the measured hybridization has been demonstrated (24). However, correlation between the free energy change and antisense efficacy has been indicated by computational studies (27,56). With a better understanding of the contributions of structures around single-stranded regions, an extension to the present work may improve the reliability of the predictions.

Functional genomics and drug target validation

Functional genomics, the determination of the function of DNA sequence on a genomic scale, is a fast-growing field in biotechnology. Recently, the first assembly of 3.12 billion base pairs for the human genome was completed by Celera Genomics, and a working draft of the human genome by the publicly funded Human Genome Project has been finished. Definitive functions have been assigned to less than 1000 of the estimated 100 000 genes in the genome. While every technique for the determination of gene function has its own strengths and weaknesses, ASOs are given the most favorable assessment on all attributes in a comprehensive comparison of techniques (57). These attributes include broad applicability, usage of primary sequence, time, cost and resource requirement, chance of success, relevance to human disease and the possibility the technique will result in a drug product. For example, gene knockout is not broadly applicable. Routine gene knockout in mammals has been performed only in mice. In addition to the lengthy duration of the procedure, mammalian gene knockout often leads to an embryonic lethal phenotype, providing very little information about the gene function. Mutagenesis has not been shown to be feasible in mammals. For mice, antisense strategy has been demonstrated to inhibit gene expression in utero, permitting the stage-specific analysis of gene function and identification of secondary phenotypes (58). This technique is expected to be applicable to other mammalian species (59). At relatively low cost, antisense not only offers high specificity of gene expression inhibition and rapid detection of antisense effects, but it also enables determination of gene function in adult animals by bypassing the potentially lethal embryonic stage. For functional genomics in the post-genomic era, traditional tools can no longer keep pace with new sequence information rapidly accumulated from various genome projects. The antisense technique has emerged as an important tool both in vitro and in vivo. When properly used, it has the potential to meet the need of large-scale functional genomics.

Antisense technique is also a very important tool for drug target validation. This is also well illustrated by the most favorable assessment on all attributes in a comparison of drug target validation techniques (57). Thousands of new potential therapeutic targets have emerged from human genome sequencing. The selection and validation of molecular targets are of paramount importance for drug development in the new millennium (60). Although phenotypes of many diseases are well known, the identification of the genes responsible for these phenotypes is a major challenge in the drug development process.

An ASO, by specifically blocking the synthesis of a prospective protein drug target, provides a fast, inexpensive and often definitive assessment of the biological effect achieved by a drug targeted against that protein. The antisense technology offers a rational alternative to the typical strategy of designing small molecules for the inhibition of a particular gene, which requires substantially more information than antisense design. Furthermore, the interactions between many small molecules and multiple members of a gene family can confound the assessment of a gene as a drug target (20).

Complicated multi-component biological systems can be studied by using an appropriate set of ASOs to independently block the synthesis of each individual protein in the system. Antisense also promises to reveal genetic pathways through expression arrays. By antisense inhibition of protein expression and target mRNA, and through the evaluation of inhibitory effects on expression of genes on DNA arrays, insight will be gained on gene interaction and regulatory pathways (20).

High-throughput antisense applications

DNA expression arrays have emerged as major high-throughput experimental tools in the post-genomic era which allow the measurement of gene expression patterns of tens of thousands of genes in parallel (61,62). DNA expression arrays can provide important clues to gene function. Genes of similar expression behavior suggest that they are likely to be co-regulated or possibly functionally related. Indeed, statistical clustering analysis has revealed that gene expression data tend to organize genes into functional categories (63). Genes with unknown function can be assigned tentative functions or a role in a biological process based on the known function of genes in the same cluster.

Single nucleotide polymorphisms (SNPs) show promise in the progression of pharmacogenomics, the emerging field concerned with the dissection of the genetic basis of disease and therapeutic response. Assembly of large SNP databases has been undertaken by the next phase of the Human Genome Project (64), a non-profit SNP Consortium of 10 pharmaceutical companies and the Wellcome trust (65; http://snp.cshl.org/data/), and by several industrial efforts. SNPs enable studies of association between a SNP and risk of a disease or drug response (66,67). The associations are valuable for the identification of candidate genes for disease phenotypes.

The eventual determination of the functions of the candidate genes and confirmation of gene functional predictions based on analysis of DNA expression arrays will require experimental analysis in a systematic and high-throughput fashion to keep pace with the fast growing genome, expression array and SNP databases. Antisense technology is well suited for this endeavor. Expression array and SNP databases can provide the basis for high-throughput antisense applications to functional genomics and drug target validation.

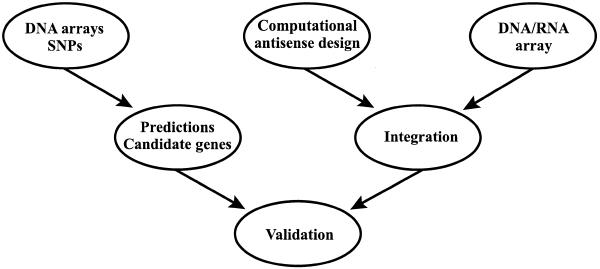
Experimental approaches for finding effective ASOs are expensive, time consuming and laborious, and are usually limited to a region of the mRNA. Published work suggests that, at the very best, only one in eight ASOs is effective (68). To realize the promise of antisense technique for high-throughput functional genomics and drug target validation, efficient screening for identifying active antisense target sites on the mRNA is necessary. This must be based on the combination of a high-throughput experimental platform and rational antisense design by a computational method. The combinatorial DNA–RNA oligonucleotide array technique appears to be an adequate experimental approach (25,69). With labeled transcripts, hybridization intensity can be measured and visualized (25). However, there are seemingly two practical limitations. First, the number of all possible oligomers up to a preset length is huge for an mRNA. Secondly, large mRNAs can be hampered by their bulky size from approaching the oligomers densely distributed on the array surface (69). Use of selective oligomers designed by comprehensive computational screening provides a solution. Hence, we advocate the strategy of integrating computational predictions and the array technique for a rational, efficient and comprehensive platform for ASO screening (Fig. 4). This platform needs to be extensively tested by experimentalists in both academia and industry to assess its potential for high-throughput applications.

Figure 4.

A potential high-throughput antisense framework for functional genomics, drug target validation and elucidation of genetic pathways. Systematic statistical analysis of DNA expression arrays and SNP databases can provide the basis for high-throughput functional analysis. Integration of computational antisense design and oligonucleotide array presents a rational, efficient, high-throughput platform for antisense oligonucleotide screening.