Abstract
Muscles actuate running by developing forces that propel the body forward while supporting the body's weight. To understand how muscles contribute to propulsion (i.e., forward acceleration of the mass center) and support (i.e., upward acceleration of the mass center) during running we developed a three-dimensional muscle-actuated simulation of the running gait cycle. The simulation is driven by 92 musculotendon actuators of the lower extremities and torso and includes the dynamics of arm motion. We analyzed the simulation to determine how each muscle contributed to the acceleration of the body mass center. During the early part of the stance phase, the quadriceps muscle group was the largest contributor to braking (i.e., backward acceleration of the mass center) and support. During the second half of the stance phase, the soleus and gastrocnemius muscles were the greatest contributors to propulsion and support. The arms did not contribute substantially to either propulsion or support, generating less than 1% of the peak mass center acceleration. However, the arms effectively counterbalanced the vertical angular momentum of the lower extremities. Our analysis reveals that the quadriceps and plantarflexors are the major contributors to acceleration of the body mass center during running.
Introduction
Experimental studies have characterized human running using kinematic, kinetic, and electromyographic (EMG) measurements (e.g., Cavagna et al., 1976; Winter, 1983; McClay, 1990; McMahon and Cheng, 1990; Novacheck, 1998). Recordings of mass center positions and velocities have shown that in steady state running the body mass center travels downward and its forward speed decreases during early to mid-stance (i.e., the braking phase of stance) (Cavagna et al., 1964). The body mass center travels upward and its forward speed increases during mid- to late stance (i.e., the propulsive phase of stance). While it is possible to measure muscle activities, joint angles, and acceleration of the body mass center during running, it is difficult to determine how individual muscles contribute to the motion of the body mass center.
Analyses of mass center trajectories and ground reaction forces have suggested that elastic storage of energy is important for running efficiency (Cavagna et al., 1976; Dickinson et al., 2000). This finding has motivated the development of models of running dynamics in which all of the lower extremity muscles are represented by a single spring. These spring-mass models have been used to gain valuable insights into the dynamics and energetics of human running (e.g., Blickhan, 1989; McMahon and Cheng, 1990; Seyfarth et al., 2002). Although spring-mass models of running provide a useful theoretical framework for examination of running dynamics, these models are not intended to describe the actions of individual muscles or to study muscle coordination during running.
Muscle-actuated simulations complement experimental analyses and spring-mass models by providing a systematic methodology for determining muscle contributions to propulsion and support (Liu et al., 2008; Neptune et al., 2008). For example, Sasaki and Neptune (2006) created two-dimensional muscle-actuated simulations of walking and running at the walk-run transition speed (1.96 m/s) and used a ground reaction force decomposition method with a segment power analysis to quantify muscle contributions to propulsion and support. This study provided the first estimates of muscle contributions to mass center accelerations in the sagittal plane at a slow running speed. However, muscle activity (Nilsson et al., 1985; Mann et al., 1986; Cappellini et al., 2006), joint kinematics (Mann and Hagy, 1980), and relative joint work (Novacheck, 1998) change with running speed, which suggests muscle contributions to propulsion and support may also change with speed. Additionally, the two-dimensional running simulation by Sasaki and Neptune (2006) did not include arms or a separate torso segment, yet arm and torso motions may affect running dynamics (Hinrichs et al., 1987).
The purpose of this study was to determine how muscles contribute to propulsion and support of the body mass center during running at 3.96 m/s (6:46 min/mile), including the effects of the torso and arms. To achieve this, we developed a three-dimensional muscle-actuated simulation of running that included 92 musculotendon actuators representing 76 muscles of the lower extremities and torso. Using a model that included lower extremity muscles, a torso, and arms we were able to quantify the contribution of muscles and arm dynamics to mass center accelerations in three dimensions, which provided insights into the actions of muscles during running. The simulation is freely available (simtk.org/home/RunningSim) allowing researchers to reproduce our results and perform additional analyses.
Methods
We collected marker trajectories and ground reaction forces and moments of a subject running on a treadmill and used these data to generate a subject-specific simulation. A single healthy male subject (height 1.83 m, mass 65.9 kg) had 41 reflective markers placed on anatomical landmarks (Kadaba et al., 1990). Experimental data was collected while the subject ran at 3.96 m/s, three times his self-selected walking speed. Marker positions were measured at 60 Hz using a six-camera motion capture system (Motion Analysis Corporation, Santa Rosa, CA, USA). The ground reaction forces and moments were measured at 600 Hz using a force-plate instrumented treadmill (Bertec Corporation, Columbus, OH, USA). Marker positions and ground reaction forces and moments were low-pass filtered at 20 Hz with a finite impulse response filter. EMG data were collected at 600 Hz using surface electrodes (Noraxon, Scottsdale, AZ, USA) for eight muscles: erector spinae, gluteus maximus, gluteus medius, semitendinosus, vastus lateralis, gastrocnemius medialis, soleus, and tibialis anterior.
The simulation was generated using OpenSim (Delp et al., 2007; see Supplemental Movie 1 for an animation of the simulation). A 12 segment, 29 degree-of-freedom (dof) musculoskeletal model was used to create the simulation (Fig. 1). Each lower extremity had five degrees-of-freedom (Supplemental Figure 1); the hip was modeled as a ball-and-socket joint (3 dofs), the knee was modeled as a custom joint with 1 dof (Seth et al., 2010), and the ankle was modeled as a revolute joint (1 dof) (Delp et al., 1990). Lumbar motion was modeled as a ball-and-socket joint (3 dofs) (Anderson and Pandy, 1999). Each arm consisted of 5 degrees-of-freedom; the shoulder was modeled as a ball-and-socket joint (3 dofs), and the elbow and forearm rotation were each modeled with revolute joints (1 dof) (Holzbaur et al., 2005). Mass properties for the arms were estimated from de Leva (1996; Supplemental Table 1). The lower extremity and back joints were actuated by 92 musclotendon actuators (Delp et al., 1990; Anderson and Pandy, 1999) and the arms were driven by torque actuators.
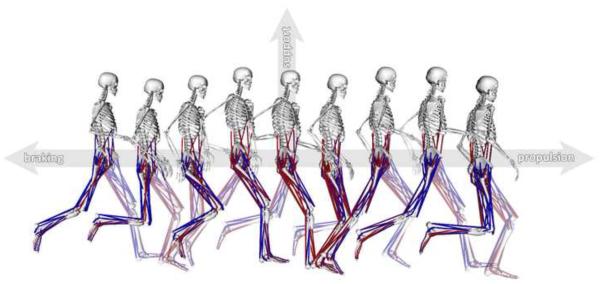
Figure 1.
Snapshots from a simulation of the running gait cycle. The simulation starts at left foot contact and ends at subsequent left foot contact, with a total duration of 0.683 s. Muscle color indicates simulated activation level from fully activated (red) to fully deactivated (blue). Axes show propulsion as forward acceleration of the body mass center, braking as backward acceleration of the mass center, and support as upward acceleration of the mass center.
The model was scaled to match the subject's anthropometry based on experimentally measured markers placed on anatomical landmarks. A virtual marker set was placed on the model based on these anatomical landmarks. An inverse kinematics algorithm solved for the joint angles that minimized the difference between the experimentally measured marker positions and the virtual markers on the model. Joint moments needed to track the subject's motion were calculated using a residual reduction algorithm (RRA) (Delp et al., 2007). With traditional inverse dynamics, a non-physical external force and moment (i.e., residuals) are applied to a body in the model (e.g., the pelvis) to resolve dynamic inconsistency between the measured kinematics and ground reactions (Kuo, 1998). RRA uses the inverse dynamics result, calculated from joint kinematics and experimentally measured ground reactions, and reduces the magnitude of the residuals by slightly adjusting the joint kinematics and model mass properties (see Supplemental Figure 2 for changes in residuals). The computed muscle control algorithm (Thelen et al., 2003; Thelen and Anderson, 2006) was then used to compute the muscle excitations required to track the kinematics produced by RRA. Computed muscle control solved a static optimization problem (Crowninshield and Brand, 1981) to resolve muscle redundancy by minimizing the sum of the square of muscle activations, while accounting for muscle activation and contraction dynamics (Zajac, 1989). Computed muscle control estimated the initial states for each muscle such that the muscle fiber and tendon force equaled the musculotendon force, which was calculated by solving a static optimization problem using experimental joint kinematics and kinetics.
To test the accuracy of the simulation we compared simulated quantities to experimental data. The joint angles from inverse kinematics, joint moments from RRA, and experimentally measured ground reaction forces were compared to averaged data from previous studies (Cavanagh and Lafortune, 1980; Winter, 1983; Novacheck, 1998; Swanson and Caldwell, 2000; Yokozawa et al., 2007; Supplemental Figure 3). Simulated muscle activations were compared to the subject's recorded EMG and to speed-matched experimental EMG data averaged from eight subjects (Cappellini et al., 2006). We compared simulated muscle forces to muscle forces derived from an EMG-driven musculoskeletal model of running (Lloyd and Besier, 2003; Besier et al., 2009; Supplemental Figure 4).
An induced acceleration analysis was used to compute the contributions of individual muscles to the acceleration of the body mass center (Zajac and Gordon, 1989; Riley and Kerrigan, 1999; Anderson and Pandy, 2003). A challenge of this analysis was to capture the rapid changes in acceleration at foot contact. To meet this challenge we modeled the foot-floor interaction using a combination of a non-penetrating unilateral constraint (i.e., no floor penetration but the foot can be lifted off the floor) and a pure rolling constraint (i.e., no slipping and no twisting) (Kane, 1961). To perform the induced acceleration analysis, we described the general form of the constrained multibody dynamic system with equations of motion:
| (1) |
where M is the mass matrix, q are the generalized coordinates (e.g., joint angles), C is the constraint matrix, λ are the constraint forces, G are the gravitational generalized forces, V are the generalized forces due to velocity effects (i.e., centrifugal and Coriolis forces), R is the matrix of muscle moment arms, and Fm are the muscle forces. The constraint matrix, C, maps from constraint forces, λ, to system generalized forces.
To simultaneously solve for constraint forces, λ, and system accelerations, q̈ the constraint conditions at the acceleration level:
| (2) |
where B is a vector describing the position and velocity terms of the constraint equations. Both C and B are derived by differentiating kinematic constraint Equations 3-6. The constraint conditions were comprised of one position and three velocity constraint equations:
| (3) |
| (4) |
| (5) |
| (6) |
where ρ is the position of the point of contact on the foot segment expressed in ground, ρ velocity, ω is the angular velocity of the foot segment expressed in ground, x is the fore-aft direction, y is the vertical direction, and z is the mediolateral direction. Equation (3) describes a non-penetrating constraint, which was active only if the vertical reaction force was upward (i.e., the floor cannot pull downward). Equations (4) and (5) describe rolling constraints (i.e., no slip), which were active if the non-penetrating constraint was active and the magnitude of the reaction force was less than the product of a coefficient of static friction, μ, and the non-penetrating constraint force, λ1. Equation (6) describes the pure rolling constraint, which was active if the vertical reaction moment was less than the moment due to the resultant no-slip force acting within a specified contact radius, rc. Specific parameters used for these constraints were a coefficient of static friction (μ) of 0.65 and a contact radius (rc) of 0.01 m. Differentiating the constraint equations enabled us to formulate the system constraints in Equation (2):
We solved Equations (1) and (2) for the contact constraint reaction forces, λ, and the system acceleration, q̈
Throughout the simulated running trial, the effect of each force (i.e., muscle forces, gravity, and forces due to velocity effects) on musculoskeletal dynamics was calculated by solving Equations (1) and (2) for the accelerations caused by that force. During the stance phase (i.e., ground contact) we constrained the foot to the floor using the constraint described by Equations (3) through (6). We verified that the sum of all the accelerations due to muscles, gravity, and velocity effects equaled the total acceleration of the body mass center (Supplemental Figure 5).
Results
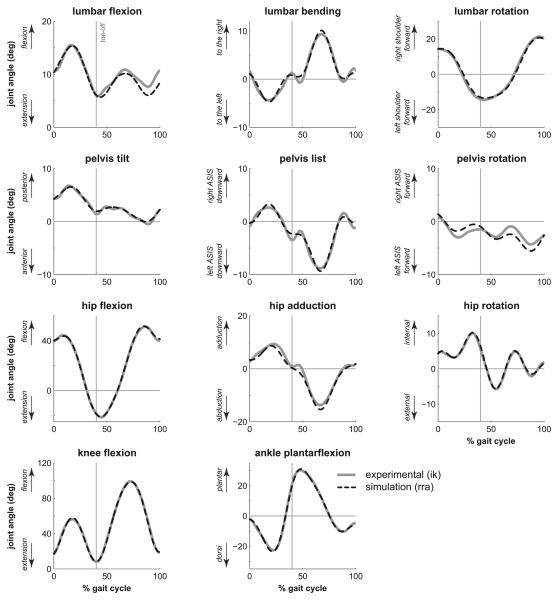
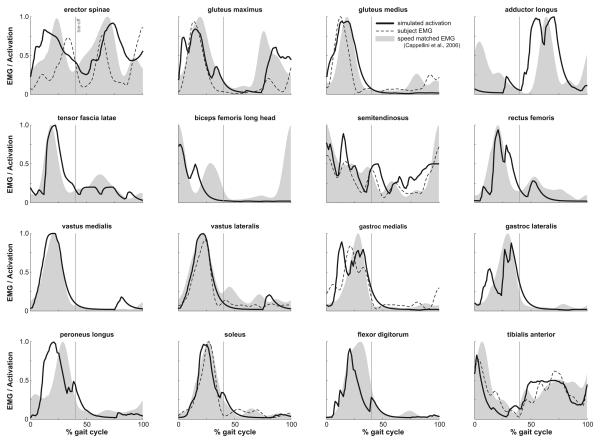
The muscle-actuated simulation tracked the joint angles calculated from the experimental marker positions with a maximum RMS deviation of 1.5° for all joint angles over the gait cycle (Fig. 2). The sum of joint moments generated by all muscles, computed as the product of each muscle's force and moment arm, closely matched the joint moments calculated with inverse dynamics after residuals were reduced (Fig. 3). Simulated activations, experimental EMG data recorded for this subject, and speed-matched experimental EMG averaged from eight subjects (Cappellini et al., 2006) showed similar features (Fig. 4), including strong activation of the quadriceps (i.e., rectus femoris and the vasti) and hamstrings (i.e., semitendinosus and biceps femoris long and short heads) in early to mid-stance, and activation of soleus and gastrocnemius in mid- to late stance. Simulated activations lacked anticipatory activation seen in the EMG recordings of biceps femoris just before foot strike.
Figure 2.
Kinematics of the back, pelvis, and lower extremities during the running gait cycle. The gray line represents experimental joint angles calculated by inverse kinematics, while the dashed line represents simulated joint angles produced by computed muscle control. Toe-off is indicated by a vertical line at 40% of the gait cycle.
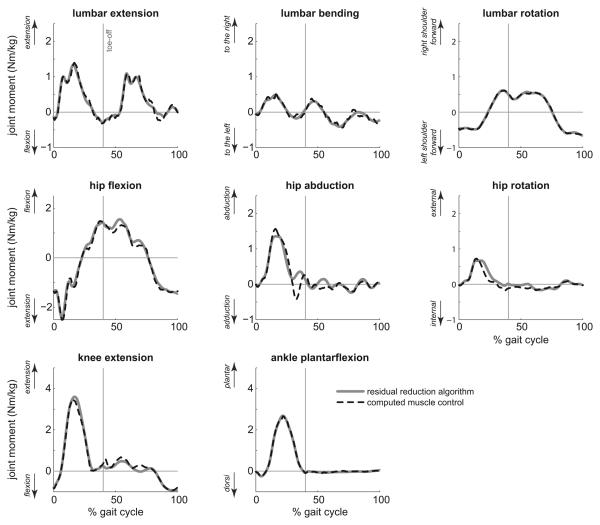
Figure 3.
Comparison of moments about the lumbar and lower extremity joints during the running gait cycle, normalized by body mass, computed using the residual reduction algorithm (solid line), and by summing the moments generated by muscle forces in the simulation (dashed line). Toe-off is indicated by a vertical line at 40% of the gait cycle.
Figure 4.
Comparison of simulated muscle activations from computed muscle control (solid line), experimental EMG collected from the subject (dashed line), and speed-matched experimental EMG data (Cappellini et al., 2006) (gray area). The experimental EMG data are individually normalized to the maximum recorded signal of each muscle over the trial and simulated activations are defined to be between 0 (fully deactivated) and 1 (fully activated). Toeoff is indicated by a vertical line at 40% of the gait cycle.
The horizontal and vertical mass center accelerations (i.e., propulsion and support) during running were generated primarily by muscles, as skeletal structures contributed very little to support (Fig. 5, see All Muscles). Muscles accelerated the mass center backward during the first 60% of stance phase (i.e., the braking phase of stance) and the muscles accelerated the mass center forward during the remaining 40% of the stance phase (i.e., propulsion phase of stance) (Supplemental Figure 6, see total fore-aft mass center acceleration).
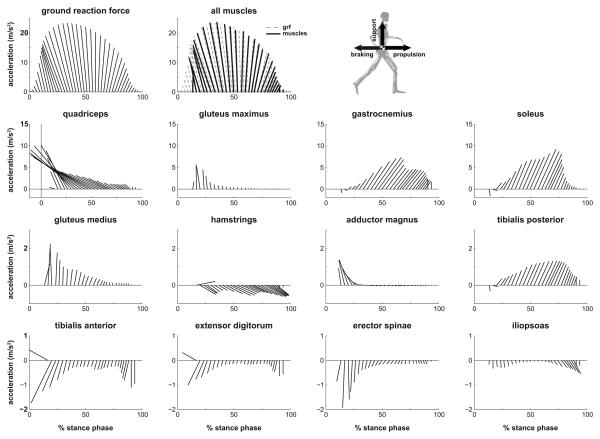
Figure 5.
Muscle contributions to propulsion and support of the body mass center during the stance phase of running. Stance is defined as 0-40% of the running gait cycle. Each ray is the resultant vector of the vertical and fore-aft accelerations (axes scaled equally). The body mass center acceleration, calculated from the experimentally measured ground reaction force, is shown at the top left. “All muscles” represents the sum of contributions from all muscle actuators in the model, which is plotted on top of the body mass center acceleration due to ground reaction forces (gray).
During the braking phase of stance, the main contributor to both braking and support was the quadriceps muscle group, which contributed twice the peak braking acceleration and nearly half of the peak vertical support of the body mass center (Fig. 5, see quadriceps). Gluteus maximus, gluteus medius, and adductor magnus together contributed about half of the peak vertical support after initial contact.
During the propulsion phase of stance, soleus and gastrocnemius were the two main contributors to propulsion and support; together they provided over twice the peak forward acceleration and over half of the peak vertical support of the body mass center (Fig. 5). During the propulsive phase, the quadriceps continued to resist forward motion (Supplemental Movie 2). The hamstrings, tibialis anterior, and iliopsoas accelerated the mass center downward at the end of stance.
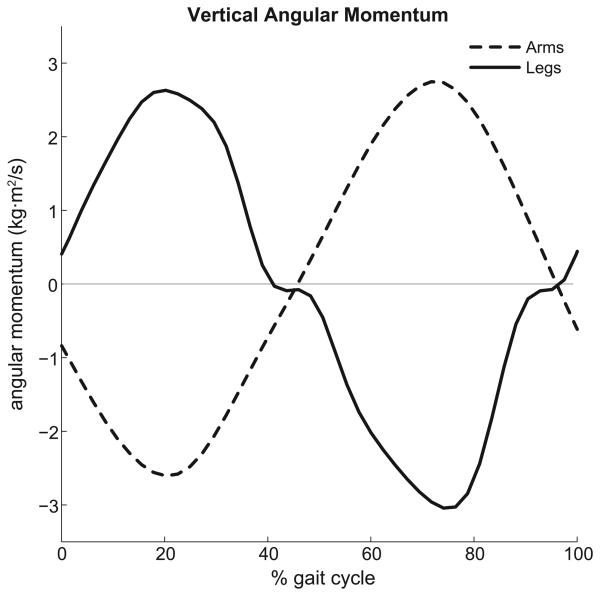
The arms did not contribute substantially to either propulsion or support, with a maximum contribution of less than 1% of both the peak horizontal and vertical mass center accelerations. However, the angular momentum of the arms about a vertical axis passing through the center of mass counterbalanced (i.e., was equal and opposite to) the angular momentum of the lower extremities about the vertical axis (Fig. 6).
Figure 6.
The angular momentum of the arms (dashedline) and legs (solidline) computed about the vertical axis passing through the body mass center during the running gait cycle.
Discussion
The purpose of this study was to determine how muscles contribute to propulsion and support during running by creating and analyzing a three-dimensional muscle-actuated simulation of the running gait cycle. During the braking phase of stance, the quadriceps muscle group is the largest contributor to both braking and support of the body mass center. During the propulsive phase of stance, soleus and gastrocnemius become the greatest contributors to both forward propulsion and support.
As highlighted by Sasaki and Neptune (2006), previous studies have disagreed on the role of the ankle plantarflexors (i.e., soleus and gastrocnemius) during the late stance phase of running. Some researchers suggest that the plantarflexors provide propulsion and support (Novacheck, 1998), while others suggest that plantarflexor activation ceases well before toe-off and thus cannot contribute to propulsion (Reber et al., 1993). Similar to Sasaki and Neptune (2006), our simulation reveals that the ankle plantarflexors are the primary contributors to both propulsion and support of the body mass center during late stance. In contrast to Sasaki and Neptune (2006), however, our results show that the quadriceps muscle group (i.e., vastus lateralis, vastus intermedius, vastus medialis, and rectus femoris), not soleus, is the largest contributor to braking the body mass center during early stance. The difference in fore-aft accelerations induced by soleus between Sasaki and Neptune (2006) and our simulation could arise for several reasons, including different simulated activation of soleus, different musculoskeletal models (e.g., 2D or 3D, arms or no arms), or different models of the foot-floor interaction. Our analysis revealed that the fore-aft accelerations induced by soleus are sensitive to the model of foot-floor interaction. With the current model, the sum of the mass center accelerations produced by muscles closely matched the mass center acceleration caused by the measured ground reaction force (Supplemental Figure 5), a necessary condition for accurate muscle-induced accelerations.
Muscle contributions to propulsion and support of our subject were similar to muscle contributions reported for fast walking by Liu et al. (2008). During early stance, both simulations revealed that the quadriceps decrease forward speed of the body mass center and provide body weight support, with gluteus medius and maximus providing additional support. During mid- and late stance, both simulations show soleus and gastrocnemius as the primary contributors to propulsion and support of the body mass center. These results suggest that muscles have similar actions on the body mass center during fast waking (Liu et al., 2008), running at the walk-run transition speed (Sasaki and Neptune, 2006), and running at 3.96 m/s, as studied here, especially during mid- to late stance. Forces transmitted through the skeleton contribute substantially to body weight support during slow and free-speed walking (Liu et al., 2008), yet skeletal forces contribute much less to body weight support during fast walking (Liu et al., 2008) and running because the lower extremity joints are more flexed during these activities.
The contributions of arm dynamics to propulsion and support of the body mass center were negligible (less than 1% of the total mass center acceleration), which disagrees with Hinrichs et al. (1987), who utilized a relative momentum approach that attributed 5-10% of the total vertical impulse to the arms. This discrepancy may be due to differences in how contributions were computed. As highlighted by Hara et al. (2006), the relative momentum approach attributes all arm motion relative to the torso to the ground reaction impulse, yet arm motion can induce changes in kinematics of the lower extremities through mechanical coupling, an effect that the relative momentum approach does not capture. Contribution of arms to propulsion and support may also be sensitive to running speed and style. We also found that the arms counterbalanced the change in angular momentum of the legs, which agrees with the findings of Hinrichs (1987) and Pontzer et al. (2009) who presented that angular momentum balance of the arms reduces torso rotations. Although the arms have less mass than the legs, they are able to balance the angular momentum of the legs due to a greater distance of the arm segments from the body mass center (Hinrichs, 1987).
Modeling arms improved the dynamic consistency of our simulation by reducing residual forces and moments, especially the vertical force and sagittal moment. This caused differences in the calculated back and hip moments, which improved accuracy of the simulated activations for muscles crossing the back and hip in comparison to EMG recordings. While arms do not significantly contribute to propulsion and support, modeling arm dynamics may be necessary to produce accurate full-body simulations of running. Additionally, a three-dimensional model allowed us to examine muscle contributions to the mediolateral acceleration of the body mass center. Unlike propulsion and support of the mass center, individual muscles or muscle groups did not have distinct roles in producing the small net mediolateral acceleration of the body mass center observed during running (Supplemental Figure 5, see mediolateral mass center acceleration).
Several limitations should be kept in mind when interpreting our results. We studied a single subject running at a single speed. Therefore, the results do not represent a general running strategy, as different runners may adopt different strategies based on their anthropometry, level of training, and performance goal (e.g., sprinting versus long-distance running). However, we did compare the joint angles, joint moments, ground reaction forces, and EMG data from our subject and simulation to results from previous studies with larger populations to ensure our subject had a typical running gait pattern (Fig. 4; Supplemental Figure 3). To more thoroughly characterize muscle actions during running, the methodology used here could be applied to more subjects over a range of speeds (e.g., 2-9 m/s), as there is evidence that movement strategy varies with running speed (Novacheck, 1998).
A challenge in simulating human running is modeling the transition from the flight phase to the initial contact of the stance phase. As the forward speed of a runner increases, peak ground reaction forces and the rate of loading increase (Weyand et al., 2000). Modeling the foot-floor interaction becomes more difficult with such a rapid transition and requires more robust and accurate contact models during high-speed running. While we have designed a contact model using rigid body constraints that was able to match the accelerations due to ground reaction forces for a majority of stance phase, better modeling is still required to accurately analyze effects at initial foot contact (i.e., the first 5-10% of the stance phase).
We have created a three-dimensional muscle-actuated simulation of a complete running gait cycle and quantitatively described how individual muscles accelerate the body mass center. To promote the utilization and acceptance of simulations in movement science our simulation is freely available in OpenSim (Delp et al., 2007; simtk.org/home/RunningSim), so others may reproduce our results, perform additional analyses, and gain further insight into running dynamics.
Supplementary Material
Joint definitions for the 12 segment, 29 degree-of-freedom musculoskeletal model created for this study.
Residual forces and moments acting on the pelvis resulting from inverse dynamics (dashed line) and after residual reduction (solid line). The residual reduction algorithm was successful in substantially reducing the magnitude of the residual forces and moments.
Comparison of joint angles, joint moments, and ground reaction forces from the simulation to experimental data from previous studies. Joint angles calculated by inverse kinematics for our subject were compared to data from Winter (1983), Novacheck (1998), and Swanson and Caldwell (2000). Joint moments computed using the residual reduction algorithm were compared to data from Winter (1983), Novacheck (1998), and Yokozawa (2007). Experimentally measured ground reaction forces were compared to data from Cavanagh and Lafortune (1980, 4.5 m/s). The average running speed for each study is shown in the figure legend.
Comparison of estimated muscle forces from computed muscle control (solid line) with results averaged across 16 subjects running at 2.7 ± 0.3 m/s (Besier et al. 2009; dashed line with grey area representing ±1 standard deviation), which were computed using an EMG-based model. Muscle forces were individually normalized by the maximum isometric force of each muscle.
Comparison of mass center acceleration calculated from experimental measurements (dashed line) with the sum of individual muscle contributions (solid line) computed by the induced acceleration analysis (i.e., superposition) during the stance phase.
Animation of the simulated running gait cycle. The simulation starts at left foot contact and ends at subsequent left foot contact, with a total duration of 0.683 s. Muscle color indicates simulated activation level from fully activated (red) to fully deactivated (blue). The simulation is shown in real time followed by half-speed.
Animation showing the action of soleus and quadriceps with respect to the body mass center during late stance. The individual muscle force is perturbed, with no other forces acting on the system, during late stance to illustrate how each muscle affects the acceleration of the mass center. Muscle color indicates activation level from fully activated (red) to fully deactivated (blue). The mass center acceleration due to the action of an individual muscle is shown as a green arrow.
Muscle contributions of major contributing muscle groups to total mass center acceleration during the stance phase of running. Muscle groups include the quadriceps (vastus lateralis, vastus intermedius, vastus medialis, and rectus femoris), ankle plantarflexors (soleus and gastrocnemius), hamstrings (semimembranosus, semitendinosus, and biceps femoris long and short heads), and all other muscles.
Mass properties of the generic musculoskeletal model created for this study.
Acknowledgements
We gratefully thank Chand John and Jill Higginson for data collection. We also thank Ayman Habib, Pete Loan, Edith Arnold, Jeff Reinbolt, Amy Silder, and Clay Anderson. Authors are supported by Fellowships from the National Science Foundation, and NIH Grants U54 GM072970 and R01 HD046814.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflicts of interest
None of the authors had any financial or personal conflict of interest with regard to this study.
References
- Anderson FC, Pandy MG. A Dynamic Optimization Solution for Vertical Jumping in Three Dimensions. Comput Methods Biomech Biomed Engin. 1999;2(3):201–231. doi: 10.1080/10255849908907988. [DOI] [PubMed] [Google Scholar]
- Anderson FC, Pandy MG. Individual muscle contributions to support in normal walking. Gait Posture. 2003;17(2):159–169. doi: 10.1016/s0966-6362(02)00073-5. [DOI] [PubMed] [Google Scholar]
- Besier TF, Fredericson M, Gold GE, Beaupre GS, Delp SL. Knee muscle forces during walking and running in patellofemoral pain patients and pain-free controls. J Biomech. 2009;42(7):898–905. doi: 10.1016/j.jbiomech.2009.01.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blickhan R. The spring-mass model for running and hopping. J Biomech. 1989;22(11):1217–1227. doi: 10.1016/0021-9290(89)90224-8. [DOI] [PubMed] [Google Scholar]
- Cappellini G, Ivanenko YP, Poppele RE, Lacquaniti F. Motor patterns in human walking and running. J Neurophysiol. 2006;95(6):3426–3437. doi: 10.1152/jn.00081.2006. [DOI] [PubMed] [Google Scholar]
- Cavagna GA, Saibene FP, Margaria R. Mechanical Work in Running. J Appl Physiol. 1964;19:249–256. doi: 10.1152/jappl.1964.19.2.249. [DOI] [PubMed] [Google Scholar]
- Cavagna GA, Thys H, Zamboni A. The sources of external work in level walking and running. J Physiol. 1976;262:639–657. doi: 10.1113/jphysiol.1976.sp011613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavanagh PR, Lafortune MA. Ground reaction forces in distance running. J Biomech. 1980;13(5):397–406. doi: 10.1016/0021-9290(80)90033-0. [DOI] [PubMed] [Google Scholar]
- Crowninshield RD, Brand RA. A physiologically based criterion of muscle force prediction in locomotion. J Biomech. 1981;14(11):793–801. doi: 10.1016/0021-9290(81)90035-x. [DOI] [PubMed] [Google Scholar]
- de Leva P. Adjustments to Zatsiorsky-Seluyanov's segment inertia parameters. J. Biomech. 1996;29(9):1223–1230. doi: 10.1016/0021-9290(95)00178-6. [DOI] [PubMed] [Google Scholar]
- Delp SL, Anderson FC, Arnold AS, Loan P, Habib A, John CT, Guendelman E, Thelen DG. OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE Trans Biomed Eng. 2007;54(11):1940–1950. doi: 10.1109/TBME.2007.901024. [DOI] [PubMed] [Google Scholar]
- Delp SL, Loan JP, Hoy MG, Zajac FE, Topp EL, Rosen JM. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Trans Biomed Eng. 1990;37(8):757–767. doi: 10.1109/10.102791. [DOI] [PubMed] [Google Scholar]
- Dickinson MH, Farley CT, Full RJ, Koehl MAR, Kram R, Lehman S. How Animals Move: An Integrative View. Science. 2000;288(5463):100–106. doi: 10.1126/science.288.5463.100. [DOI] [PubMed] [Google Scholar]
- Hara M, Shibayama A, Takeshita D, Fukashiro S. The effect of arm swing on lower extremities in vertical jumping. J. Biomech. 2006;39(13):2503–2511. doi: 10.1016/j.jbiomech.2005.07.030. [DOI] [PubMed] [Google Scholar]
- Hinrichs R, Cavanagh PR, Williams KR. Upper Extremity Function in Running I: Center of Mass and Propulsion Considerations. International Journal of Sport Biomechanics. 1987;3:222–241. [Google Scholar]
- Hinrichs RN. Upper Extremity Function in Running II: Angular Momentum Considerations. International Journal of Sport Biomechanics. 1987;3:242–263. [Google Scholar]
- Holzbaur KR, Murray WM, Delp SL. A model of the upper extremity for simulating musculoskeletal surgery and analyzing neuromuscular control. Ann Biomed Eng. 2005;33(6):829–840. doi: 10.1007/s10439-005-3320-7. [DOI] [PubMed] [Google Scholar]
- Kadaba MP, Ramakrishnan HK, Wootten ME. Measurement of lower extremity kinematics during level walking. J Orthop Res. 1990;8(3):383–392. doi: 10.1002/jor.1100080310. [DOI] [PubMed] [Google Scholar]
- Kane TR. Analytical Elements of Mechanics: Dynamics (Volume 2) Academic Press; New York: 1961. [Google Scholar]
- Kuo AD. A least-squares estimation approach to improving the precision of inverse dynamics computations. J Biomech Eng. 1998;120(1):148–159. doi: 10.1115/1.2834295. [DOI] [PubMed] [Google Scholar]
- Liu MQ, Anderson FC, Schwartz MH, Delp SL. Muscle contributions to support and progression over a range of walking speeds. J Biomech. 2008;41(15):3243–3252. doi: 10.1016/j.jbiomech.2008.07.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lloyd DG, Besier TF. An EMG-driven musculoskeletal model to estimate muscle forces and knee joint moments in vivo. J Biomech. 2003;36(6):765–776. doi: 10.1016/s0021-9290(03)00010-1. [DOI] [PubMed] [Google Scholar]
- Mann RA, Hagy J. Biomechanics of walking, running, and sprinting. Am J Sports Med. 1980;8(5):345–350. doi: 10.1177/036354658000800510. [DOI] [PubMed] [Google Scholar]
- Mann RA, Moran GT, Dougherty SE. Comparative electromyography of the lower extremity in jogging, running, and sprinting. Am J Sports Med. 1986;14(6):501–510. doi: 10.1177/036354658601400614. [DOI] [PubMed] [Google Scholar]
- McClay I, Lake MJ, Cavanagh PR. Muscle Activity in Running. In: Cavanagh PR, editor. Biomechanics of Distance Running. Human Kinetics Books; Champaign, IL: 1990. pp. 165–186. [Google Scholar]
- McMahon TA, Cheng GC. The mechanics of running: how does stiffness couple with speed? J Biomech. 1990;23(Suppl 1):65–78. doi: 10.1016/0021-9290(90)90042-2. [DOI] [PubMed] [Google Scholar]
- Neptune RR, Sasaki K, Kautz SA. The effect of walking speed on muscle function and mechanical energetics. Gait Posture. 2008;28(1):135–143. doi: 10.1016/j.gaitpost.2007.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nilsson J, Thorstensson A, Halbertsma J. Changes in leg movements and muscle activity with speed of locomotion and mode of progression in humans. Acta Physiol Scand. 1985;123(4):457–475. doi: 10.1111/j.1748-1716.1985.tb07612.x. [DOI] [PubMed] [Google Scholar]
- Novacheck TF. The biomechanics of running. Gait Posture. 1998;7(1):77–95. doi: 10.1016/s0966-6362(97)00038-6. [DOI] [PubMed] [Google Scholar]
- Pontzer H, Holloway JH, Raichlen DA, Lieberman DE. Control and function of arm swing in human walking and running. J Exp Biol. 2009;212(Pt 4):523–534. doi: 10.1242/jeb.024927. [DOI] [PubMed] [Google Scholar]
- Reber L, Perry J, Pink M. Muscular control of the ankle in running. Am J Sports Med. 1993;21(6):805–810. doi: 10.1177/036354659302100608. discussion 810. [DOI] [PubMed] [Google Scholar]
- Riley PO, Kerrigan DC. Kinetics of stiff-legged gait: induced acceleration analysis. IEEE Trans Rehabil Eng. 1999;7(4):420–426. doi: 10.1109/86.808945. [DOI] [PubMed] [Google Scholar]
- Sasaki K, Neptune RR. Differences in muscle function during walking and running at the same speed. J Biomech. 2006;39(11):2005–2013. doi: 10.1016/j.jbiomech.2005.06.019. [DOI] [PubMed] [Google Scholar]
- Seth A, Sherman M, Eastman P, Delp S. Minimal formulation of joint motion for biomechanisms. Nonlinear Dynamics. 2010 doi: 10.1007/s11071-010-9717-3. DOI: 10.1007/s11071-010-9717-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seyfarth A, Geyer H, Günther M, Blickhan R. A movement criterion for running. J Biomech. 2002;35:649–655. doi: 10.1016/s0021-9290(01)00245-7. [DOI] [PubMed] [Google Scholar]
- Swanson SC, Caldwell GE. An integrated biomechanical analysis of high speed incline and level treadmill running. Med Sci Sports Exerc. 2000;32(6):1146–1155. doi: 10.1097/00005768-200006000-00018. [DOI] [PubMed] [Google Scholar]
- Thelen DG, Anderson FC. Using computed muscle control to generate forward dynamic simulations of human walking from experimental data. J Biomech. 2006;39(6):1107–1115. doi: 10.1016/j.jbiomech.2005.02.010. [DOI] [PubMed] [Google Scholar]
- Thelen DG, Anderson FC, Delp SL. Generating dynamic simulations of movement using computed muscle control. J Biomech. 2003;36(3):321–328. doi: 10.1016/s0021-9290(02)00432-3. [DOI] [PubMed] [Google Scholar]
- Weyand PG, Sternlight DB, Bellizzi MJ, Wright S. Faster top running speeds are achieved with greater ground forces not more rapid leg movements. J Appl Physiol. 2000;89(5):1991–1999. doi: 10.1152/jappl.2000.89.5.1991. [DOI] [PubMed] [Google Scholar]
- Winter DA. Moments of force and mechanical power in jogging. J Biomech. 1983;16(1):91–97. doi: 10.1016/0021-9290(83)90050-7. [DOI] [PubMed] [Google Scholar]
- Yokozawa T, Fujii N, Ae M. Muscle activities of the lower limb during level and uphill running. J Biomech. 2007;40(15):3467–3475. doi: 10.1016/j.jbiomech.2007.05.028. [DOI] [PubMed] [Google Scholar]
- Zajac FE. Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Crit Rev Biomed Eng. 1989;17(4):359–411. [PubMed] [Google Scholar]
- Zajac FE, Gordon ME. Determining muscle's force and action in multi-articular movement. Exerc Sport Sci Rev. 1989;17:187–230. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Joint definitions for the 12 segment, 29 degree-of-freedom musculoskeletal model created for this study.
Residual forces and moments acting on the pelvis resulting from inverse dynamics (dashed line) and after residual reduction (solid line). The residual reduction algorithm was successful in substantially reducing the magnitude of the residual forces and moments.
Comparison of joint angles, joint moments, and ground reaction forces from the simulation to experimental data from previous studies. Joint angles calculated by inverse kinematics for our subject were compared to data from Winter (1983), Novacheck (1998), and Swanson and Caldwell (2000). Joint moments computed using the residual reduction algorithm were compared to data from Winter (1983), Novacheck (1998), and Yokozawa (2007). Experimentally measured ground reaction forces were compared to data from Cavanagh and Lafortune (1980, 4.5 m/s). The average running speed for each study is shown in the figure legend.
Comparison of estimated muscle forces from computed muscle control (solid line) with results averaged across 16 subjects running at 2.7 ± 0.3 m/s (Besier et al. 2009; dashed line with grey area representing ±1 standard deviation), which were computed using an EMG-based model. Muscle forces were individually normalized by the maximum isometric force of each muscle.
Comparison of mass center acceleration calculated from experimental measurements (dashed line) with the sum of individual muscle contributions (solid line) computed by the induced acceleration analysis (i.e., superposition) during the stance phase.
Animation of the simulated running gait cycle. The simulation starts at left foot contact and ends at subsequent left foot contact, with a total duration of 0.683 s. Muscle color indicates simulated activation level from fully activated (red) to fully deactivated (blue). The simulation is shown in real time followed by half-speed.
Animation showing the action of soleus and quadriceps with respect to the body mass center during late stance. The individual muscle force is perturbed, with no other forces acting on the system, during late stance to illustrate how each muscle affects the acceleration of the mass center. Muscle color indicates activation level from fully activated (red) to fully deactivated (blue). The mass center acceleration due to the action of an individual muscle is shown as a green arrow.
Muscle contributions of major contributing muscle groups to total mass center acceleration during the stance phase of running. Muscle groups include the quadriceps (vastus lateralis, vastus intermedius, vastus medialis, and rectus femoris), ankle plantarflexors (soleus and gastrocnemius), hamstrings (semimembranosus, semitendinosus, and biceps femoris long and short heads), and all other muscles.
Mass properties of the generic musculoskeletal model created for this study.