White matter maturation reshapes structural connectivity in the late developing human brain

Abstract

From toddler to late teenager, the macroscopic pattern of axonal projections in the human brain remains largely unchanged while undergoing dramatic functional modifications that lead to network refinement. These functional modifications are mediated by increasing myelination and changes in axonal diameter and synaptic density, as well as changes in neurochemical mediators. Here we explore the contribution of white matter maturation to the development of connectivity between ages 2 and 18 y using high b-value diffusion MRI tractography and connectivity analysis. We measured changes in connection efficacy as the inverse of the average diffusivity along a fiber tract. We observed significant refinement in specific metrics of network topology, including a significant increase in node strength and efficiency along with a decrease in clustering. Major structural modules and hubs were in place by 2 y of age, and they continued to strengthen their profile during subsequent development. Recording resting-state functional MRI from a subset of subjects, we confirmed a positive correlation between structural and functional connectivity, and in addition observed that this relationship strengthened with age. Continuously increasing integration and decreasing segregation of structural connectivity with age suggests that network refinement mediated by white matter maturation promotes increased global efficiency. In addition, the strengthening of the correlation between structural and functional connectivity with age suggests that white matter connectivity in combination with other factors, such as differential modulation of axonal diameter and myelin thickness, that are partially captured by inverse average diffusivity, play an increasingly important role in creating brain-wide coherence and synchrony.

Most real-world networks do not arise all at once but, guided by rules, develop through a growth process that progressively fine-tunes the configuration of nodes and edges. Thus, an important aspect in the analysis of large-scale networks is the characterization of their dynamic development and evolution. From a theoretical point of view growth rules have been shown to have a significant effect on the emergent behavior of the final large-scale structural topology. For example, the emergence of scale-free networks can be explained by a preferential attachment rule (1, 2), with important functional consequences (3). If we can measure the growth and reshaping of connectivity that occurs with maturation during the developmental process, we can begin to infer growth rules governing this complex process and examine their functional consequences. These growth rules need to be instantiated in a biological system, and therefore the functional consequences would provide hypotheses linking emergent network properties to underlying cellular and molecular mechanisms.

Real-world networks rarely grow according to simple statistical models, thus necessitating empirical sampling over time. Empirical studies have examined evolving social networks from scientific collaborations (4) and the time evolution of Internet dating communities (5). Similar concepts of network growth can be applied to developmental biology and in particular to the organogenesis of the human brain. In the present study we focus on the largely unexplored field of network refinement during late human development, defined as the time period between early childhood and late adolescence (2–18 y of age). Although the pattern of axonal projections in the human brain has not been fully documented, nonhuman primate literature shows that during this period synaptic pruning continues but the wiring pattern of white matter axonal connections is relatively constant, with only limited axonal removal (6–8). However, during this time in the human brain, the white matter undergoes progressive increases in volume and changes in composition due to increases in axonal diameter and increasing myelination (9–14). These white matter changes likely play a significant role in establishing interregional processing and neuronal synchrony in humans (15, 16). Nonhuman primate literature suggests that further developmental changes in neuronal functional specification likely occur through intracortical dendritic and neurochemical modulation (17).

Our current understanding of changes in structural and functional networks during this period of late human brain development is still incomplete. In particular, rules that govern interactions between structural brain plasticity and functional specification during development are largely unknown. Imaging experiments in humans have demonstrated that functional networks reorganize significantly during this age period, with short-range functional connectivity (FC) decreasing and long-range FC increasing, providing evidence that brain networks progressively refine to decrease segregation and increase integration (18–20). One plausible hypothesis is that these functional phenomena are driven through structural network refinement, such as regionally specific increases in myelination, axonal diameter, remodeling of dendritic arborization, and neurochemical changes. The extent to which each of these factors contributes to the currently established functional network refinement is unclear. However, animal and human experiments have shown that white matter rewiring through the significant growth of new axonal pathways or axonal pruning is unlikely to occur in late development, particularly in the absence of a major injury (21, 22).

Over the last few years several studies have focused on the relationship between resting-state FC and structural connectivity (SC). These studies showed largely convergent results (23–26), indicating that at the regional as well as at the connectome (27, 28) level, the strength of FC is positively correlated with the strength of SC, when direct or indirect SC is present and measurable. There is further evidence that there is significant correlation between structural white matter coherence and EEG FC in healthy controls and patients with amnesic mild cognitive impairment (29).

Yet important questions remain unanswered. (i) Are there sensitive MRI contrast mechanisms that capture changes of white matter structure and composition occurring between early childhood and late adolescence? (ii) How does white matter maturation affect network topology with increasing age? Do developmental changes in white matter increase total connectivity? How do topological network metrics such as small-world attributes or efficiency change during development? Are there changes in the spatial distribution of modules and hubs? (iii) Finally, does the coupling between structural and functional networks remain constant across age?

Results

We report results from a cohort of 30 subjects within an age range from 18 mo to 18 y, examined with high-resolution T1-weighted imaging, diffusion tensor imaging at b-values of 1,000 and high angular resolution diffusion imaging at 3,000 s/mm² and, for a subset of 14 subjects, resting-state blood oxygen level–dependent (BOLD) MRI.

We used two cortical parcellations, called the “low resolution” and the “high resolution.” In the low-resolution parcellation, 66 cortical regions of varying sizes were identified in each participant using an automated landmark-based algorithm (30). The high-resolution parcellation is a refinement of the low-resolution surface partition and is composed of 241 regions of interest (ROIs) of approximately equal area (≈6 cm²) that are identified according to the same method as for the low resolution parcellation (25).

The size or importance of a given white matter pathway was determined by computing connection densities between each pair of ROIs performing MRI tractography in each individual subject (25). To model physiological changes in the SC that occur with white matter maturation, we used as a connection weight the product between the connection density of a given pathway (which captures the relative importance of a fiber path and which is known to be relatively stable across developmental age) and the inverse average apparent diffusion coefficient (ADC) measured along the entire length of the same pathway. We chose ADC as a marker of white matter maturation (myelin and axonal diameter changes) because these factors are the major determinants of white matter water diffusion restriction (31). A pattern of decreasing ADC with increasing white matter maturation and increasing age has been reported in numerous studies (32–34). However, the relationship between white matter maturation and connection efficacy (i.e., conduction speed) is extremely complex (10, 16, 35) and impossible to fully characterize for all axonal pathways in vivo. As a first approximation to test the hypothesis that modulation of connection efficacy through maturation alters connectivity profiles, we used 1/ADC as a multiplicative factor in determining the strengths of interregional pathways. We did not use fractional anisotropy (FA) as a marker of maturation for two reasons. First, we noticed that ADC at high b-value exhibits much higher age dependence. Second, FA is a ratio and therefore can be misleading when dealing with multiple fiber compartments, in particular at high b-value.

Resting-state FC was calculated in each subject from pair-wise Pearson's correlation coefficients of BOLD time series obtained for each ROI by averaging across voxels within the ROI (26).

Both SC and FC were calculated for each subject individually at the high resolution (241 ROIs) and then down-sampled by averaging across ROIs within each of the 66 predefined anatomical regions. Similar networks were built including deep gray matter structures as additional nodes. Corresponding results are included as supplementary material. It is important to note that every subject was processed independently in terms of cortical parcellation and tractography. No registration on a common template was necessary. Further details for each of the above-mentioned steps are provided in Materials and Methods.

Changes in ADC with Age.

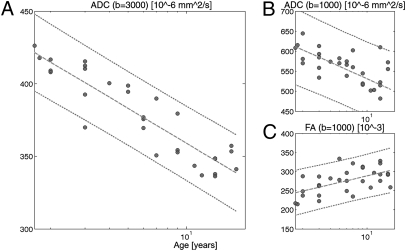
As demonstrated previously, white matter ADCs decrease logarithmically with age, but changes after 24 mo are essentially linear and weak when investigated with standard diffusion imaging methods using a b-value of 1,000 s/mm² or below (34, 36, 37). For each subject we computed the average ADC and FA at b = 1,000 s/mm² and average ADC at b = 3,000 s/mm² over all connections and plotted the results according to developmental age (Fig. 1). FA at b = 3,000 s/mm² is not depicted because of highly variable and trendless changes with respect to age. Although significant (P < 0.005), the correlation was relatively weak between age and ADC at b = 1,000 (R = −0.62) and FA at b = 1,000 (R = 0.56). However, we found that there is a strong (R = −0.91) and highly reliable (P < 10⁻¹¹) correlation between age and ADC at b = 3,000 s/mm². Theoretically, ADC has an increased ability to resolve diffusivity in the lower range, such as in the range of myelinated white matter, by an increased sensitivity to slow diffusing molecules at high b-value (38). Therefore, these diffusion changes suggest that significant structural changes occur in the cerebral white matter even beyond 24 mo of age that are likely driven by increasing myelin thickness and axonal diameter (10, 32–34). Obviously, high b-value ADC is more sensitive for detecting these late developmental changes. In the rest of this article we only refer to results computed with ADC at b = 3,000 s/mm². We also noticed that when considering the top 10% longest vs. the bottom 10% lowest fibers, their ADC time evolution was translated in time. Longer fibers reach a low-level ADC later than their shorter counterpart (Fig. S1), a result that was also suggested elsewere (39). This dependence in fiber length is likely to have a significant effect on the time evolution of structural network properties.

Fig. 1.

Change of several diffusion MRI parameters with respect to developmental age averaged over all brain white matter connections at low resolution. (A) ADC at b = 3,000 s/mm² (R = −0.9078, P < 10⁻¹¹), (B) ADC at b = 1,000 s/mm² (R = −0.6204, P < 0.0005), and (C) FA at b = 1,000 s/mm² (R = 0.5659, P < 0.005). R is the Pearson correlation coefficient.

Increased Average Node Strength and Efficiency with Age.

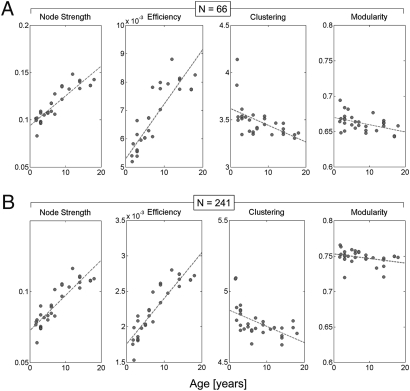
An expected consequence of the coupled myelin and axonal maturation is an increased physiological efficacy of fiber pathways, which is at least partly related to increased conduction velocity. In weighted network theory, these changes in edge properties can be captured at the node level with node strength (40). Node strength is the sum of all of the weights attached to a specific node. The average node strength over all nodes of the structural network shows a strong and highly significant age-dependent increase (Table 1). This nodal tendency is observed for both low- and high-resolution partitions and for the cortex considered in isolation (Fig. 2), as well as for the entire brain, including subcortical gray matter regions (Fig. S2).

Table 1.

Relationship of network metrics and developmental age

Network measure	Low resolution		High resolution
	wb (83 nodes)	ctx (66 nodes)	wb (258 nodes)	ctx (241 nodes)
Node strength	0.92*	0.90*	0.90*	0.89*
Efficiency	0.90*	0.87*	0.91*	0.90*
Clustering coefficient	−0.41†	−0.55‡	−0.42†	−0.55‡
Path length	0.02 n.s.	−0.18 n.s.	0.09 n.s.	−0.21 n.s.
Small-world index	−0.49*	−0.22 n.s.	−0.48‡	−0.03 n.s.
Modularity	−0.31 n.s.	−0.45†	−0.21 n.s.	−0.33 n.s.

Values are Pearson correlation coefficients for five network measures (efficiency, clustering coefficient, small-world index, node strength, and modularity) obtained from 30 structural brain networks, from subjects aged 2–18 y. Data are for both low and high resolution, partitions recorded here for whole brain (wb, n = 83 and n = 258) and cortex only (ctx, n = 66 and n = 241). n.s., not significant.

*P < 0.001;

^†P < 0.05;

^‡P < 0.01.

Fig. 2.

Relationship of network metrics and developmental age. Results shown are for cerebral cortex at two spatial resolutions: (A) n = 66 and (B) n = 241 nodes. For whole-brain data (cortex and deep gray structures) see Fig. S2. Scatter plots show node strength, global efficiency, clustering coefficient, and modularity (left to right). All measures are computed from the weighted SC matrices of individual subjects. Values for clustering coefficient and small-world index are scaled relative to populations of 100 random networks with preserved degree and weight distributions. For R and P values, see Table 1.

The observed global changes in ADC are expected to have effects on the modulation of structural network topology. We computed measures designed to characterize the capacity of the structural network to carry out functional segregation and functional integration via modulation of connection strength (1/ADC). Functional integration is the ability of the brain to rapidly combine specialized information from distributed regions and is strongly related to the efficiency of a network (40). Age and efficiency were found to be strongly and positively correlated (Table 1, Fig. 2, and Fig. S2).

Decrease in Structural Clustering Coefficient with Age.

The mean clustering coefficient of a network reflects, on average, the prevalence of clustered connectivity around individual nodes and hence is a measure of segregation (40). The higher the clustering, the greater the tendency for nodes to form numerous strongly connected communities. In our data, we observed a significant age-dependent decrease in clustering coefficient after scaling the empirically obtained value relative to a population of random networks (Materials and Methods and Table 1, Fig. 2, and Fig. S2). This observation supports the idea that local SC and thus functional segregation decreases with age as a result of modulations in connection strength. Unlike the scaled clustering coefficient, the scaled path length did not exhibit significant trends between 2 and 18 y of age.

Small-world networks are more clustered than equivalent random graphs yet have similar characteristic path length, thus combining high segregation and high integration. The small-world index is a compact metric that captures both of these effects. Consistent with previous work conducted in the adult brain (25, 41), we found that brain structural networks exhibit robust small-world properties across the entire range of development examined. The small-world index generally decreased with age, with significant negative correlations found for individual cortical hemispheres and whole-brain networks, at both low and high resolutions (Table 1).

Modularity and Module Composition as a Function of Age.

Modularity, measured from the expected density of structural connections within and between communities (42), did not exhibit consistent significant trends with age (Fig. 2, Table 1, and Fig. S2). Across all ages examined in this study, modularity remained high. At both low and high resolution, module membership of nodes was highly correlated across all ages, as indicated by uniformly high normalized mutual information (≈0.8–0.9) for pairs of node partitions obtained at different ages. Major reorganizations of structural modules did not occur after 2 y of age. A closer examination of the lengths of fiber pathways linking 66 cortical regions revealed that regardless of age, the lengths of fiber pathways linking regions within the same module were significantly shorter than pathways linking regions in different modules (Fig. S3A). This pattern of fiber length distribution reflects the tendency, conserved across development, of spatially adjacent regions to belong to the same module. The aggregate connection efficacy of within- and between-module pathways grew with age, and the proportion of connection efficacy found between modules increased significantly (R = 0.42, P < 0.05; Fig. S3B). This effect was due to developmental changes in the ADC of long-range pathways linking modules to each other (Fig. S1). Similar results were seen for the 241 cortical ROIs constituting the higher-resolution partition. Thus, over the course of development structural modules remain composed of spatially close regions but become increasingly interlinked by the maturation of long fiber pathways.

Centrality as a Function of Age.

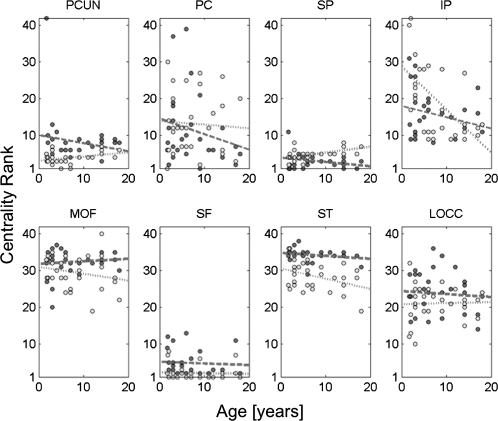
Consistent with the stability of most structural modules across development, the centrality of brain regions, measured here as the betweenness centrality estimated from the SC, remained largely unchanged. The centrality ranks of a number of hub regions such as the precuneus, posterior cingulate cortex, superior frontal cortex, and superior parietal cortex remained high between ages 2 and 18 y (Fig. 3), in both cerebral hemispheres and at both resolutions examined in this study. The structural backbone exhibited a postero-medial core with extensions into the temporo-parietal junction and fronto-medial cortices for subjects across the entire age range (Fig. S4). Roughly half of all shortest paths across the cortical network were found to pass through nodes located in the structural core, and there was no significant tendency for this proportion to either increase or decrease over development.

Fig. 3.

Relationship of the rank of node betweenness centrality for several cortical regions and developmental age. Dark dots and dashed regression lines represent the right hemisphere and light dots and stippled lines the left hemisphere. Centrality ranks remain largely unchanged. None of the relationships shown here exhibit significant trends, with the exception of the left IP. PCUN, precuneus; PC, posterior cingulate cortex; SP, superior parietal cortex; IP, inferior parietal cortex; MOF, medial orbitofrontal cortex; SF, superior frontal cortex; ST, superior temporal cortex; LOCC, lateral orbital cortex.

Structure–Function Relationship.

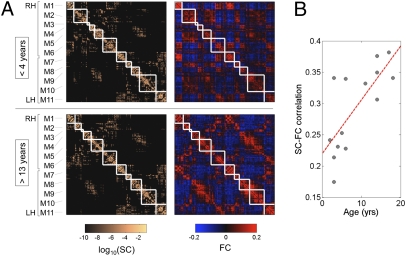
Previous work indicated that, after averaging data across participants, the SC and FC strengths across cortical region-pairs that were structurally linked were significantly and positively correlated (25, 26). This SC–FC statistical dependence was replicated with our current data. Correlation coefficients for SC–FC connections ranged between ≈0.2 and 0.4 for individual participants, at both high and low resolution. Comparing cortical SC and FC matrices averaged over groups of younger (<4 y) and older (>13 y) participants, we found a significant relationship at both high and low resolutions between SC and FC (Fig. 4A), with R = 0.30 and R = 0.43 at the low resolution and R = 0.36 and R = 0.46 at the high resolution, respectively (all P < 0.001). For SC and FC matrices recorded in 14 individual participants, the relationship exhibited a tendency to significantly increase in strength with age at the low resolution (R = 0.62, P < 0.05) and at the high resolution (R = 0.74, P < 0.005; Fig. 4B). Importantly, the observation of an increase in the relationship between SC and FC over development did not depend on the use of a mean connection density matrix derived from older participants (>16 y). When mean connection density is derived from the youngest participants (<4 y), the SC–FC relationship continued to exhibit a significant increase with age (R = 0.59, P < 0.05), and the correlation between SC and FC at young age did not improve (R ≈ 0.2).

Fig. 4.

Modularity and SC–FC correlation. (A) Cortical (n = 241) SC and FC matrices averaged over the younger (<4 y) and older (>13 y) age group. Structural modules are delineated by the superimposed white grid. Although modules are highly conserved (normalized mutual information = 0.82), there is a notable increase in SC–FC correspondence from younger to older brains. Eleven modules (M1–M6 in the right hemisphere, M7–M11 in the left hemisphere) were identified, and the two sets of SC and FC matrices are displayed such that modules correspondence across age is maximized. Modules are centered on the following anatomical locations: M1, occipital cortex; M2, parietal cortex; M3, parietal cortex; M4, orbitofrontal cortex; M5, frontal cortex; M6, temporal cortex; M7, occipital cortex; M8, parietal cortex; M9, orbitofrontal cortex; M10, frontal cortex; and M11, temporal cortex. (B) Increasing statistical relationship between SC and FC across age (R = 0.74, P < 0.005). Data reported in this plot are for SC that was resampled into a Gaussian distribution as described in ref. 26, and for FC corresponding to raw Pearson cross-correlations between time series. The relationship persists for unresampled SC (R = 0.66, P < 0.01), whole-brain unresampled SC (R = 0.59, P < 0.05), or for FC that has been Fisher z-transformed and normalized (R = 0.74, P < 0.005).

Discussion

The present work builds on concepts from several different disciplines, including developmental neurobiology, noninvasive brain imaging, and network theory, to characterize how late myelin and axonal maturation (43–45) may reshape global brain network topology over time and influence the synchronization of functional brain networks by modulating the efficacy and conduction velocity of long-range projections (16, 44).

We found that imaging at higher b-values significantly improved our sensitivity to age-related modifications of the ADC. By increasing the diffusion-sensitizing gradients from a b-value of 1,000 to 3,000 s/mm², the relation between developmental age and ADC is significant even in a small cohort of subjects, and changes continue to unfold into late adolescence. By increasing the b-value, the imaging signal is more heavily weighted toward slow-moving molecules, whereas the contributions of fast-diffusing water molecules almost vanish from the signal and the ADC measurement. Therefore maximal contrast is created for changes of diffusion speed in the slow-diffusing regime. The concepts of slow- and fast-diffusing compartments are relatively old, based on the observation that signal decay in biological tissue, typically white matter, is not mono- but rather biexponential with respect to b-value (46, 47). The fast-diffusing component is classically related to extracellular water, whereas the slow-diffusing component is likely related to intraaxonal and macromolecular bounded water. In the case of late myelination processes, the gross axonal diameter and myelin thickness increase to maintain a constant ratio, while compaction and reduction of extracellular space occurs in addition to small chemical modifications and other non–well-characterized modifications (44). We hypothesized that these maturational changes result in detectable decreases in ADC with high b-value imaging.

We decided to combine this sensitive way to measure white matter maturation with the simultaneous ability of diffusion imaging to map brain connectivity. Although the white matter wiring pattern is almost fixed after the first 2 y of life, with only minimal pruning during the first 2 decades of life, the physiological characteristics of these connections are known to undergo dramatic changes, most likely through changes in axonal diameter and myelin thickness (48, 49). Several functional studies have illustrated modification of resting and task-related functional networks not only in early life but also through adolescence and early adulthood. A recently published example is the constitution of the default mode network and of task-related executive networks (18, 50). Going from childhood to adolescence, the functional topology evolves toward higher global integration and less local segregation. We wanted to test how the underlying structural substrate is reshaped by white matter maturation during this important developmental period and how these structural modifications parallel these established functional trends.

First, progressive white matter maturation leads to significant increases in the average node strength of brain structural networks with age. Increased node strength reflects greater physiological efficacy, particularly of long pathways. Reports have suggested that between childhood and early adulthood functional integration increases because the average path length of functional networks decreases (20), and that the phenomenon was related to increased axonal diameter and myelin thickness of long association fiber tracts. In the same study based on resting-state functional MRI (fMRI), it was also suggested that short-range connectivity decreases its relative importance with increasing age. The reshaping of SC by white matter maturation reported in the present article supports this set of ideas, previously suggested by observation of functional brain networks. We found that structural efficiency when modulated by white matter maturation significantly increases with age, indicating greater functional integration across the entire brain. Furthermore the structural clustering coefficient exhibited a marked decrease with age in our study. The two latter findings, combined with an increase in global node strength with age, suggest that maturation of interregional pathways results in topological changes in structural brain networks. Long-range connections mature later than short-range connections (Fig. S1) (39), hence contributing to an opposing trend of increasing efficiency (integration) and decreasing clustering (segregation).

With increasing integration we would expect related increasing neural synchrony. To determine how neural synchrony behaves as a function of our structural measures we compared SC and FC as well as average functional connection strength. Surprisingly, we found that not only are SC and FC significantly correlated at all ages we examined but also that this relationship, instead of remaining constant, strengthens with age.

At this stage we can only offer some hypotheses that might explain this intriguing finding while also considering the limitations of our technique. White matter maturation is a complex process combining changes in axonal diameter and packing, myelin thickness, and composition (44). 1/ADC is only a crude reflection of these phenomena. Increased physiological coupling may not only be related to white matter maturation but also differential maturation to improve synchrony according to fiber length (16). At this stage we are unable to provide a comprehensive model for this process. Furthermore, the particular role of the deep gray nuclei in modulating cortical activity through topographically segregated loops linking cortex, striatum, and thalamus is not modeled specifically in our study (51). It is also known that, during the developmental period considered in this study, white matter structural changes are accompanied by synaptic plasticity and neurochemical modifications. Development of GABAergic neurotransmission is known to be reflected in increased synchrony in the γ band frequency (52), which is thought to be related to BOLD signals (53), possibly including those seen in resting-state fMRI. Therefore the increasing correlation we observed may be attributable to combined additional structural and chemical phenomena occurring in late development that are not modeled in our data. Ways to test such a hypothesis exist, for example by combining electrophysiological measurements, with SC (diffusion and magnetic transfer MRI) across development.

In summary, our study suggests that changes in connection strengths likely to occur with white matter maturation significantly reshape SC. The overall effect on network properties is increased integration and decreased segregation. Although inverse diffusivity is unlikely to capture the full complexity of maturational changes in connection strength, this approach provides a first step toward capturing these fundamental principles in a network-based analysis and results in network properties consistent with other studies. In addition, these findings emphasize the important role developmental white matter differential maturation may play in optimizing connectivity. If these growth rules are correct, connectivity analysis can provide a framework for expressing and monitoring brain development. In turn these frameworks may allow detection of early abnormalities in neuronal synchronization and integration, fundamental differences that are thought to underlie many neurological/psychiatric disorders associated with subtle structural differences.

Materials and Methods

Thirty subjects aged 18 mo to 18 y were selected a posteriori from a large cohort of patients scanned for various indications at the Massachusetts General Hospital. The clinical follow-up of these patients showed no subsequent significant psychiatric, neurological, or systemic disease, and all neuroimaging studies were clinically void of relevant findings after review by two neuroradiologists (Table S1 provides detailed patient information). This study was approved by our institutional review board.

MRI Acquisition.

Subjects were scanned with a 3-Tesla MRI scanner (Trio; Siemens) using a 12-channel head coil. Among other imaging sequences depending on the indication, a high-resolution T1-weighted image was acquired using a magnetization prepared rapid gradient echo sequence with a matrix size of 512 × 512 × 128 and 1-mm isotropic voxels. Diffusion tensor imaging was performed using 12 diffusion-weighted directions with a b-value of 1,000 s/mm² (and two b0 images) with a matrix size of 128 in plane and 64 slices and 2-mm isotropic voxels (54). We also acquired a second diffusion experiment with a q-ball scheme using 60 diffusion-weighted directions with a b-value of 3,000 s/mm² and identical geometry (55). Finally a 6-min resting-state fMRI experiment was performed successfully in 14 patients using a gradient echo echo planar imaging sequence with time to echo of 30 ms and time to repetition of 2,600 ms, a matrix size of 72 × 72 in plane and 42 slices with isotropic voxels of 3 mm (56, 57).

Diffusion MRI Preprocessing and Tractography.

The diffusion tensor imaging (DTI) data were preprocessed using a freely available software package Diffusion Toolkit (trackvis.org) to obtain b-value = 1,000 s/mm² ADC maps and FA maps for every subject (58).

Q-ball data were processed with the same software package to obtain b-value = 3,000 s/mm² ADC and FA maps for every subject. In addition, orientation distribution functions (ODFs) were calculated and then used for tractography.

Structural Connectivity Mapping.

The path from q-ball imaging to structural connection matrix is made of several processing steps that are described in detail elsewhere (25) and include gray and white matter segmentation, partition of the gray matter in multiple regions of interest (ROI), and tractography between each pairs of ROIs. We summarize the key steps and the specific aspects related to the present study in SI Materials and Methods.

SC Model.

SC in this study is composed of two components: connection density and connection efficacy. Connection density takes into account the physiological importance of a pathway (its size), and the mean diffusivity represents the level of pathway maturation. On the basis of empirical evidence from other studies, we started from the assumption that the pattern of SC does not change within the age range considered (i.e., no new fiber tracts grow from one cortical region to another, and none are eliminated). Therefore we built an average matrix for the connection density (at both high and low resolutions) by averaging together the connection density matrices of the three oldest subjects (ages 17 to 18 y). Results reported in this study were robust with respect to averaging over wider age ranges. The resulting average connection density matrix was applied to all subjects.

The second component was provided by the ADCs of neural pathways collected in an individual participant-specific matrix. ADC values were clipped at 100 and 800 × 10⁻⁶ mm²/s to exclude outliers, and the data matrix was normalized to a range of [0 1]. Connection efficacy was then computed as the inverse ADC (1/ADC)-1. Using other transforms (e.g., 1-ADC) did not affect our main conclusions. SC for each individual participant was then computed as the product of the average connection density and the individual connection efficacy. Some pathways were detected in older participants and hence included in the average density, but were not detected in younger subjects, presumably owing to varying brain size or their immature myelin status. Rather than excluding these pathways from the analysis, we assumed that they were physically present but inefficacious. They were assigned an ADC value equivalent to the individual's 95th percentile. Hence, all structural connection matrices maintained an equal number of pathways but with individual variations in connection efficacy.

fMRI Preprocessing and Correlations.

The raw fMRI images were registered onto the b0 image of the DTI experiment using the rigid body registration tool from the FSL package (www.fmrib.ox.ac.uk/fsl). After slice time correction the BOLD time series were computed as the average signal in each of the predefined 241 ROIs. These time series were then piecewise linearly detrended (every 50 s), and mean ventricular, white matter, and cortical signals were regressed out from each time series. On these signals, Pearson correlations were computed between each region pair. Such correlation coefficients define FC at high resolution (241 ROIs). To get the low-resolution FC maps (66 ROIs), we computed average correlations from the high-resolution matrix.

Network Metrics.

All graph theoretical analyses were carried out on weighted SC using the Brain Connectivity Toolbox, as described in ref. 40. For more details see SI Materials and Methods.