On the swimming of Dictyostelium amoebae

The conventional mode for amoeboid locomotion is crawling. Barry and Bretscher (1) recently showed that Dictyostelium amoebae are also capable of swimming to chemoattractants. They hypothesized that the mechanism for swimming is intimately related to crawling. When crawling, the cell front bifurcates, and protrusions move backward, relative to the cell. The authors (1) conjecture that floating cells executing these same motions will swim. In this letter, we show that, indeed, the shape changes of a crawling cell are sufficient for swimming.

To obtain cell geometries, we flattened developed D. discoideum (cytosolic GFP in AX2) in an ∼4-μm-tall chamber (2). Cells were imaged using confocal microscopy (f_image = 1/s) for 500 ± 140 s. From these images, cell contours were retrieved (3).

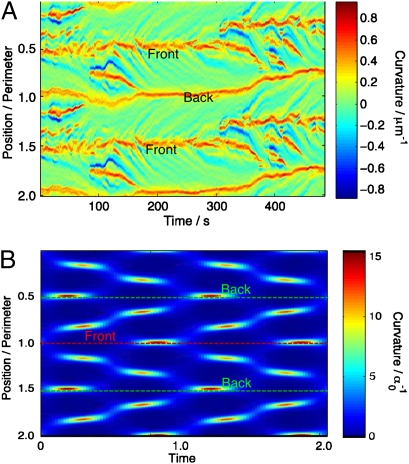
The contour curvature plot (Fig. 1A) shows that, indeed, protrusions move from the cell front to the back. This behavior can also be seen in the 2D, low Reynolds number swimming model of Shapere and Wilczek (4). Therefore, the crawling motion seems consistent with swimming.

Fig. 1.

Curvature space-time plots for the contours of (A) a typical crawling cell and (B) the Shapere–Wilczek swimmer. To prevent a loss of detail at the edges, the curvature has been plotted over two contour lengths. Note the herringbone structure—regions of high curvature bifurcate at the front and travel to the back.

To more rigorously evaluate this claim, we solved the Stokes flow with no-slip boundary conditions at the cell and an open boundary, zero normal stress, at a distance 250 μm away. By calculating the appropriate counterflow (cf. ref. 4), we were able to determine the translational and rotational velocities for the cell if the cell were attached to a substrate.

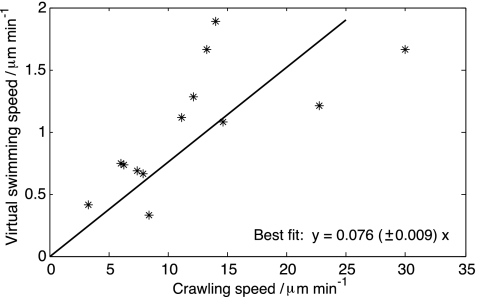
We analyzed the virtual swimming velocity of n = 13 cells and found that, for all cells, the time-averaged component along the direction of polarization was positive (defined as the direction from the cell's tail to its centroid). The average directed swimming speed was 1.0 ± 0.5 μm/min. The crawling speed was found to be 12 ± 7 μm/min. The correlation coefficient was r = 0.69, with P = 0.009. Therefore, cells that crawl faster are also faster swimmers (Fig. 2).

Fig. 2.

The crawling and virtual swimming velocities along the direction of polarization. Constrained least squares regression shows that the cells crawl 12 times faster than they swim.

In ref. 1, the cells swim at 4.2 μm/min and crawl at 3.8 μm/min. Our measured crawling speed is three times higher, and our virtual swimming speed is four times lower. The difference in speeds can be attributed to the vertical confinement of our cells, because flattened cells migrate faster and have a lower rate of pseudopod production. There may also be a contribution to swimming from a membrane flow, which has not been included here. We expect the result to hold for neutrophils by analog.