Information-geometric measure of 3-neuron firing patterns characterizes scale-dependence in cortical networks

Abstract

To understand the functional connectivity of neural networks, it is important to develop simple and incisive descriptors of multineuronal firing patterns. Analysis at the pairwise level has proven to be a powerful approach in the retina, but it may not suffice to understand complex cortical networks. Here we address the problem of describing interactions among triplets of neurons. We consider two approaches: an information-geometric measure (Amari, 2001), which we call the “strain,” and the Kullback-Leibler divergence. While both approaches can be used to assess whether firing patterns differ from those predicted by a pairwise maximum-entropy model, the strain provides additional information. Specifically, when the observed firing patterns differ from those predicted by a pairwise model, the strain indicates the nature of this difference – whether there is an excess or a deficit of synchrony – while the Kullback-Leibler divergence only indicates the magnitude of the difference. We show that the strain has technical advantages, including ease of calculation of confidence bounds and bias, and robustness to the kinds of spike-sorting errors associated with tetrode recordings.

We demonstrate the biological importance of these points via an analysis of multineuronal firing patterns in primary visual cortex. There is a striking scale-dependent behavior of triplet firing patterns: deviations from the pairwise model are substantial when the neurons are within 300 microns of each other, and negligible when they are at a distance of > 600 microns. The strain identifies a consistent pattern to these interactions: when triplet interactions are present, the strain is nearly always negative, indicating that there is less synchrony than would be expected from the pairwise interactions alone.

Introduction

The organization of neurons into networks and the resultant emergence of functional circuits is a central theme in neuroscience. To understand this process, it is important to determine the rules which govern how individual neurons interact with each other to form a network. Most often, these interactions are studied at the level of correlations between pairs of neurons (Kohn & Smith, 2005, Meister, Lagnado & Baylor, 1995). Even though this is the simplest possible interaction, pairwise interactions have been shown to account, nearly completely, for the patterns of population activity in an important model system, the retina (Schneidman, Berry, Segev & Bialek, 2006, Shlens, Field, Gauthier, Grivich, Petrusca, Sher, Litke & Chichilnisky, 2006). However, this simplification may not suffice in general, and pairwise couplings – which could simply arise from shared synaptic input – are only the first step in understanding network interaction rules.

With this in mind, here we focus on an approach to characterize firing patterns among triplets of neurons. This level of analysis is significant because it points to active processing by the neural circuitry. For instance, the activity of logic gates (Feinerman, Rotem & Moses, 2008, Vogels & Abbott, 2005), cell assemblies (Pastalkova, Itskov, Amarasingham & Buzsaki, 2008) and synfire chains(Abeles, 1991), would lead to an excess or shortage of synchrony, compared to the predictions of purely pairwise interactions.

To determine whether an excess or shortage of synchrony is present in experimental data, we employ an information-geometric measure (Amari, 2001) to characterize firing patterns of triplets of neurons, which we call the “strain.” We compare this approach with one based on the application of a goodness-of-fit measure to pairwise maximum-entropy models (Schneidman et al., 2006, Shlens et al., 2006, Tang, Jackson, Hobbs, Chen, Smith, Patel, Prieto, Petrusca, Grivich, Sher, Hottowy, Dabrowski, Litke & Beggs, 2008, Yu, Huang, Singer & Nikolic, 2008). Both approaches indicate the extent to which triplet firing patterns cannot be predicted from pairwise statistics. However, for the purpose of characterizing ensemble behavior, the strain has an important advantage: it is a signed quantity, rather than a measure of fit. That is, the strain describes how the pairwise model fails (an excess vs. a shortage of synchrony), not just whether it fails. Additionally, the strain has practical advantages: as we show, its statistics are simple to calculate, it is asymptotically independent of bin size, and it is relatively immune to the “lockout” problem that can affect multineuronal recordings.

To illustrate these points, we use the strain to analyze multineuronal recordings in macaque visual cortex. We analyze triplet firing patterns among groups of neurons separated by <300, ~600 and >1000 microns in area V1 of the anesthetized macaque. We find that the strain identifies a consistent kind of departure of cortical firing patterns from the pairwise model, that this departure is strongly scale-dependent, and that it is correlated with the strength of pairwise interactions within the cluster.

Methods

Physiological preparation

All procedures were in accordance with the National Institutes of Health guidelines for the use and care of experimental animals and were approved by the Weill Cornell Medical College Institutional Animal Care and Use Committee. We recorded from area V1 of 12 anesthetized, paralyzed macaque monkeys (Macaca mulatta) using single tetrodes and a three-tetrode recording array. The tetrode array had a T-configuration, with the near pair 600 microns apart and the third tetrode at an adjustable position, but no less than 1000 microns from their midpoint.

Full details of the experimental preparation have been previously provided (Schmid, Purpura, Ohiorhenuan & Victor, 2009, Victor, Mechler, Repucci, Purpura & Sharpee, 2006). Recordings of extracellular action potentials were made only during periods when the animal was held at a constant plane of anesthesia (an intravenous infusion containing 10 mg/ml of propofol and 0.25 to 0.50 mcg/ml sufentanil, initially delivered at 2 mg/kg/hr propofol then titrated based on heart rate and blood pressure). EEG was monitored from frontal leads in 5 animals, and was characterized by mixed delta and theta activity.

Analysis of multineuronal firing patterns was based on responses to pseudorandom checkerboards (Reid, Victor & Shapley, 1997) presented at a frame rate of 67.6 or 100 Hz, for 16 to 32 epochs of approximately 1 min each. Typically, the checkerboard consisted of a 13×13 array of checks, each of which typically subtended 0.25×0.25 degrees. As a check on stability of overall responsiveness, we verified that firing rate was similar for the first and second half of the collection period, and that the coefficient of variation in each epoch was small (Figure S1). Orientation tuning was determined from responses to sinusoidal luminance gratings of near-optimal spatial and temporal frequency prior to collection of responses to pseudorandom checkerboards.

Data analysis

Single cell spiking activity was sorted from the raw extracellular recordings using an algorithm based on principal components (Fee, Mitra & Kleinfeld, 1996). After spike sorting, spike times were binned into 10 ms or 14.8 ms bins, depending on the frame rate of the stimulus, yielding ~10⁵ bins for each analysis. In each of our datasets, there were more than 100 counts of each of the eight possible triplet firing patterns. Similar bin sizes (10–20 ms) have been used to characterize multi-neuron firing patterns in the retina (Schneidman et al., 2006, Shlens, Field, Gauthier, Greschner, Sher, Litke & Chichilnisky, 2009, Shlens et al., 2006), ex vivo cortex (Tang et al., 2008) and cat area 17 (Yu et al., 2008).

When multiple units isolated by a tetrode fire nearly simultaneously, their spike waveforms sum at the recording tetrode, creating, at short timescales, events that cannot be spike-sorted. This leads to a lockout window of 1.2 ms within which it is difficult to accurately measure the frequency of near simultaneous activity from multiple neurons. We correct for these missed simultaneous events by calculating (for an n-spike event) the number of possible events assuming an independent assortment of spikes into a bin (10 ms or 14.8 ms), bin and the number of events that can be observed given the constraint that no two neurons fire simultaneously in a 1.2 ms slot. The ratio between these two numbers is a correction-factor which conservatively assumes that neurons are no more correlated at timescales of ~1 ms than they are at 10 ms. Further details on the lockout correction are provided in the Appendix. Unless otherwise stated, the lockout correction has been applied to all analyses.

Characterization of neuronal firing patterns

We use two methods to characterize neuronal firing patterns, both based on how actual firing patterns compare to the predictions of pairwise maximum-entropy models. The first kind of approach – based on the Kullback-Leibler divergence – is identical to the one used by several recent authors (Schneidman et al., 2006, Shlens et al., 2006, Tang et al., 2008, Yu et al., 2008); the second, the “strain”, is based on the notions of information geometry (Amari, 2001).

To describe these approaches and facilitate a comparison of them, we set up a common notation. Our data consist of a set of observations of a network of M neurons (here, typically M = 3). Each observation is a state vector, σ⃗ = (σ₁, σ₂, …, σ_M), with the convention that σ_k =+1 means that neuron k is firing, and σ_k = −1 means that it is not. We use N(σ⃗) to denote the number of observations in the state σ⃗, and N to be the total number of observations (i.e., the total number of analysis bins in the experiment). Thus, p(σ⃗), the probability that the network is in the state σ⃗ is estimated by N(σ⃗)/N. With this notation, the probability of firing for the jth neuron, which we will denote p(j), is a sum over all p(σ⃗) for which σ_j = 1:

$$p(j)=\sum _{{\sigma }_j=1}p(\overrightarrow{\sigma }),$$ (1)

and the probability of joint firing for neurons j and k, which we will denote p(j,k), is a sum over all p(σ⃗) for which σ_j =1 and σ_k =1:

$$p(j,k)=\sum _{{\sigma }_j=1,{\sigma }_k=1}p(\overrightarrow{\sigma }).$$ (2)

Kullback-Leibler approach

In the approach based on the Kullback-Leibler divergence, the initial step is to fit the observations p(σ⃗) to a pairwise maximum-entropy model:

$$p_{\mathit{model}}(\overrightarrow{\sigma };{\mathbf{\alpha }}^{\mathit{model}},{\mathbf{\beta }}^{\mathit{model}})=\frac{1}{Z}exp\left(\sum _{j=1}^M{\alpha }_j^{\mathit{model}}{\sigma }_j+\sum _{j<k}^M{\beta }_{jk}^{\mathit{model}}{\sigma }_j{\sigma }_k\right),$$ (3)

where

$$Z=\sum _{\overrightarrow{\sigma }}exp\left(\sum _{j=1}^M{\alpha }_j^{\mathit{model}}{\sigma }_j+\sum _{j<1}^M{\beta }_{jk}^{\mathit{model}}{\sigma }_j{\sigma }_k\right).$$ (4)

The model parameters α ={α_j} describe the tendency of each neuron to fire, and the parameters β ={β_jk} describe their pairwise interactions. The parameter values are determined by the requirement that the firing probabilities p_model(j) and pairwise firing probabilities p_model(j,k) match those observed. The goodness of fit of the model to the observations is quantified by the Kullback-Leibler divergence,

$$D_{KL}(P||P_{\mathit{model}})=\sum _{\overrightarrow{\sigma }}p(\overrightarrow{\sigma })log\frac{p(\overrightarrow{\sigma })}{p_{\mathit{model}}(\overrightarrow{\sigma })}.$$ (5)

The Kullback-Leibler divergence is a non-negative quantity - effectively a squared distance. Following Shlens et al. (Shlens et al., 2006), we convert the Kullback-Leibler divergence into a log likelihood ratio (LLR) per minute, according to the formula

$$\mathit{LLR}=-{RD}_{KL}(P||P_{\mathit{model}})$$ (6)

where R is the number of bins (snapshots) per minute. The LLR thus indicates the relative plausibility of the pairwise maximum-entropy model. Large negative values of the LLR indicate that it is unlikely that the pairwise model accounts for the data, and hence, indicate that higher-than-second-order multineuronal structure is present in the firing patterns. We use base-2 logarithms for LLR values, so, for example, a LLR of -5 means that the likelihood ratio for the pairwise model is 1/32 = 2⁻⁵.

We calculate confidence limits for the LLRs according to the method of Kennel et al. (Kennel, Shlens, Abarbanel & Chichilnisky, 2005) We use a Markov Chain Monte Carlo process to sample from the a posteriori distribution under a Dirchlet prior given the observed joint firing counts. We then recalculate the pairwise maximum-entropy models from 200 of these resampled datasets, and construct 95% confidence intervals from the Kullback-Leibler divergences of those models. We quote values obtained with a Dirichlet β-parameter of 0; similar results were obtained with Dirichlet parameters of 0.5, 1, and 2. Bias correction is calculated from the mean of these 200 resampled datasets. For our data, which were well-sampled (~ 10⁵ bins, >100 counts of each triplet firing pattern), confidence limits were narrow and bias correction was negligible (see Figure 1). For further discussion on these issues and alternative approaches in the undersampled regime, which are particularly relevant for analyses of smaller datasets and larger populations of neurons, see (Kennel et al., 2005, Martignon, Deco, Laskey, Diamond, Freiwald & Vaadia, 2000, Martignon, Von Hasseln, Grun, Aertsen & Palm, 1995, Schneidman et al., 2006, Shlens et al., 2006).

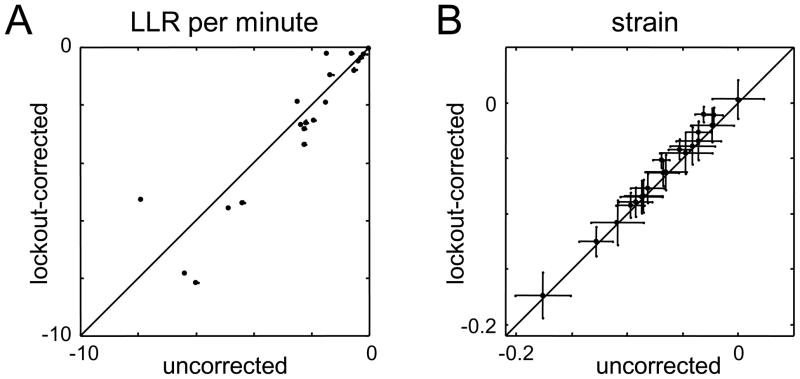
Figure 1.

Comparison of two indices of firing patterns for triplets of neurons recorded by a single tetrode. Panel A: LLR per minute for the pairwise model; Panel B: strain. Each quantity is calculated without (abscissa) and with (ordinate) the lockout correction. The strain is virtually unaffected by the lockout correction, but has much larger confidence limits. Both measures reveal significant departures from the predictions of a pairwise model. In Panel A, the bias correction is shown by the small points (small points are bias-corrected), barely visible next to the larger symbols; in panel B, the bias correction is negligible (< 3×10⁻⁴). In Panel B, error bars represent 95% confidence limits; in panel A, they are comparable to the size of the plotted points (±0.05)

The “strain”

The second approach we use to describe multineuronal firing patterns is based on notions of information geometry (Amari, 2001). It applies most readily to analyses of joint firing patterns of three neurons. Our datasets consist of recordings of M = 3, 4, and 5 neurons; for recordings of >3 neurons, we apply this analysis to all three-neuron subsets. (See the Appendix for alternative ways to extend this approach to >3 neurons.)

For three neurons (M = 3), any set of firing patterns can be recast in the form:

$$p(\overrightarrow{\sigma })=\frac{1}{Z}exp\left(\sum _{j=1}^M{\alpha }_j{\sigma }_j+\sum _{j<k}^M{\beta }_{jk}{\sigma }_j{\sigma }_k+\gamma {\sigma }_j{\sigma }_k{\sigma }_l\right).$$ (7)

where

$$Z=\sum _{\overrightarrow{\sigma }}exp\left(\sum _{j=1}^M{\alpha }_j{\sigma }_j+\sum _{j<k}^M{\beta }_{jk}{\sigma }_j{\sigma }_k+\gamma {\sigma }_j{\sigma }_k{\sigma }_l\right).$$ (8)

Eq. (7) is identical to that of the pairwise maximum-entropy model (eq. (3)), except for the addition of a γ-term that parameterizes the interactions of three firing states.

We note that the right-hand-side of eq. (7) is the first three terms of the complete exponential expansion of the probability distribution p(σ⃗), written for the special case of M = 3. In the general case of M neurons, the r th term has M!/(M − r)!r! parameters, one for each way of choosing r of the M neurons. For the case of interest (M = 3), there is only one third-order term, so we can simply write γ=γ₁₂₃. Thus, for M = 3, eq. (7) is the full exponential expansion, and is therefore guaranteed to provide an exact fit for the probability distribution p(σ⃗).

The exponential expansion approach has used by many authors in another form: with states denoted by s_k ∈ {0,1} and the r-th order parameters denoted by θ’s with r subscripts (Amari, 2001, Gutig, Aertsen & Rotter, 2003, Martignon et al., 2000, Martignon et al., 1995, Nakahara & Amari, 2002). We use the {−1,1} designation here because it leads to a simpler form for many of the equations below, and because it is natural for the Ising formulation (Schneidman et al., 2006).

For the reader’s convenience, we summarize how these two forms are related. To begin, we note that an expansion that terminates at order m has, as its exponent, a general polynomial of order m in the M state variables (s_k ∈ {0,1} or σ_k ∈{−1,1}). Moreover, these polynomials differ by a simple change of variables: s_k = (σ_k +1)/2. Thus, an expansion that terminates at order m in one convention is equivalent to an expansion that terminates at the same order m in the other. This change of variables indicates the relationship between the θ-parameters and the parameters of eq. (7). Specifically, a parameter of order r in one expansion is a linear combination of the corresponding parameter in the other expansion, along with parameters whose order is > r and ≤ m. As an example with r = 2 and M = 3: θ₁₂= 4β₁₂ − 4γ₁₂₃ and β₁₂=θ₁₂/4+θ₁₂₃/8. For the highest-order parameters in the two expansions (i.e., the parameter of rank r = m), the relationship is particularly simple: the parameters differ only by a scale factor, for example, γ₁₂₃=θ₁₂₃/8. The scale factor, 8, is 2^r; the 2 corresponds to the difference in the numerical values (+1 and −1) used to label the states.

For a complete exponential expansion – that is, when the termination order m equals the number of neurons, M – the highest-order parameter in eq. (7) can be determined from the state probabilities p(σ⃗) in simple closed form. In our case of interest, r = M = M = 3. Here, the value of this parameter (γ in eq. (7)) is given by

$$\gamma =\frac{1}{8}\sum _{\overrightarrow{\sigma }}{\sigma }_1{\sigma }_2{\sigma }_{3}logp(\overrightarrow{\sigma }).$$ (9)

See for example eq. 124 of (Amari, 2001). Eq. (9) is also derived in the Appendix.

We call the quantity in eq. (9) the “strain.” Since it is logarithmic in the probabilities, it is an example of a “surprise” (e.g., (Martignon et al., 1995, Palm, 1981, Palm, Aertsen & Gerstein, 1988)). We give it a special designation to emphasize that we are not considering the general case of a full exponential expansion for M neurons, but focusing specifically on the third-order term for triplets. We use the term “strain” to emphasize that it quantifies how a pairwise-only model must be “strained” to accommodate the observed triplet firing patterns – i.e., how a triangular interaction is not fully described by the pairwise interactions corresponding to its edges.

For convenience, we rewrite eq. (9) in a notation in which state probabilities are denoted by p_s1s2···sM, where s_k = 1 corresponds to σ_k =1 (firing), and s_k = 0 corresponds to σ_k = −1:

$$\gamma =\frac{1}{8}log\frac{p_{100}{p}_{010}{p}_{001}{p}_{111}}{p_{000}{p}_{011}{p}_{101}{p}_{110}}.$$ (10)

As indicated above, other than the factor of 1/8, this is identical to the information-geometric coordinate θ₁₂₃ of (Amari, 2001).

The quantity γ quantifies the extent of departure of the observed probabilities from the predictions of the pairwise model, but it does so in a manner that differs in several ways from the Kullback-Leibler divergence. The most important difference is that it is a coordinate, not a distance – so it can be positive, negative, or zero. When it is zero, the exact parameterization (eq. (7)) reduces to the pairwise maximum-entropy model (eq. (3)), but when it is nonzero, its sign describes how the observed probabilities depart from the pairwise model. For instance, γ > 0 means that there are more simultaneous-firing events than expected from the pairwise firing probabilities, while γ< 0 means that there are fewer. Other differences between γ and the Kullback-Leibler divergence are discussed below.

Since γ is readily related to the estimated probabilities of each kind of event (via eq. (9)), there are simple asymptotic forms for its bias and variance (see Appendix). The bias of the naïve (plug-in) estimate is

$$B\approx -\frac{1}{16N}\sum _{\overrightarrow{\sigma }}\frac{{\sigma }_j{\sigma }_k{\sigma }_l}{p(\overrightarrow{\sigma })}$$ (11)

and its variance is

$$V\approx \frac{1}{64N}\sum _{\overrightarrow{\sigma }}\frac{1}{p(\overrightarrow{\sigma })}+O(N^{-2}),$$ (12)

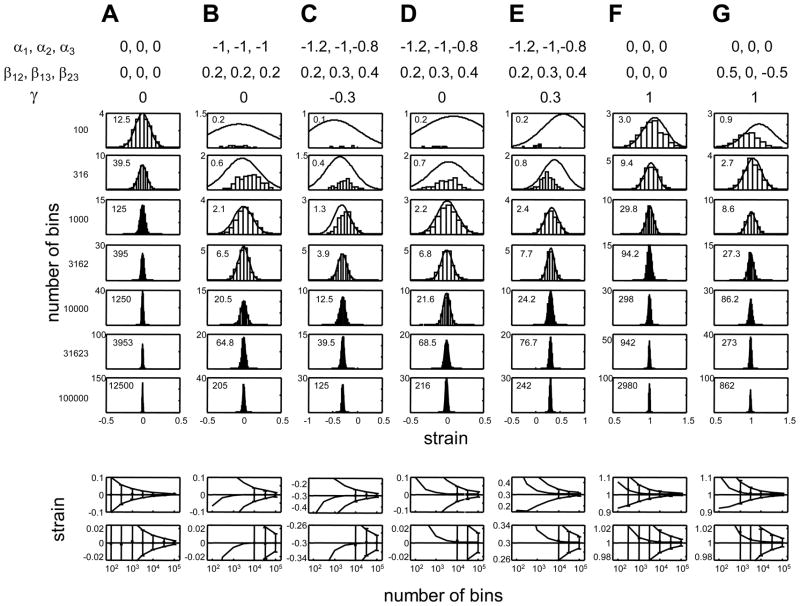
where (as above) N is the total number of observations. We debias estimates of γ by subtracting the quantity in eq. (11), and use $\pm 1.96\sqrt{V}$ for 95% confidence limits on values. As shown in the Appendix and Figure A1, these asymptotic estimates are highly accurate provided that there are at least 10 counts of each firing pattern.

Figure A1.

The asymptotic distribution of bias and variance estimates of the plug-in estimator for the strain are highly accurate, provided that there are at least 10 counts of each firing pattern. In the upper half of the Figure, the asymptotic Gaussian distribution (smooth curve) is compared to the empirical distribution of the plug-in estimator, eq. (A11). The Gaussian has a mean given by the asymptotically debiaser (A21) and variance corresponding to the asymptotic estimate (A24). The histograms show the empirical distribution of the plug-in estimator (A11) for 1000 simulated experiments. In each set of simulations, spike pattern counts are distributed in a Poisson fashion according to the probabilities given by eq. (7), with the parameters for the right-hand-side indicated at the top of each column. From top to bottom, the number of bins in the experiment increases from 10² to 10⁵; the latter value is comparable to the number of bins used in the experiments reported here. Note that when the number of bins is small (upper rows), some of the spike patterns are not encountered, so the plug-in estimator diverges; these counts are not included in the histograms. The numbers inset into each plot indicate the expected number of counts of the least likely firing pattern. Note that when there are at least 10 counts of each firing pattern, the asymptotic Gaussian provides an excellent approximation to the empirical distribution.

The lower half of the Figure shows the mean (points) and standard deviation (error bars) of the empirical distribution of the plug-in estimator, as a function of the number of bins in the simulated experiment. Points are only plotted when all of the 1000 simulated experiments had at least one count of all patterns. The horizontal line indicates the true value of the strain. The three smooth curves indicate the asymptotic estimates of the mean and standard deviation, according to eqs. (A21) and (A24). The two rows show the same data plotted on different vertical scales, so that the biases can be clearly seen.

Quantification of orientation tuning

Orientation tuning of individual neurons was determined from their responses to drifting sine gratings of near-optimal spatial and temporal frequency, presented at each of 16 directions, φ_k = 2πk/16, k = 0, ···, 15 in pseudorandom order. (Schmid et al., 2009, Victor et al., 2006). To quantify the orientation bandwidth of a neuron, we used the circular variance of the firing rate r_k obtained at the direction φ_k (Ringach, Shapley & Hawken, 2002):

$$CV=1-\left|\sum _k{r}_k{e}^{2i{\varphi }_k}/\sum _k{r}_k\right|.$$ (13)

The extreme values correspond to a neuron that responds to only one orientation (CV = 0), and to a neuron that responds equally well to all orientations (CV=1). A typical oriented V1 neuron whose orientation tuning is a von Mises distribution with orientation bandwidth (half-width at half-height) of π/8 (22.5 deg) has CV = 0.25.

To compare the orientation tuning of n neurons in a cluster, we calculated the orientation bandwidth of each neuron (CV(j), j =1, … M), and compared this with the orientation bandwidth of an “average” neuron, CV_avg, whose response to each direction at each direction is the average of the responses of the n neurons. This yielded an “orientation tuning difference index” (ODI):

$$\mathit{ODI}=C{V}_{\mathit{avg}}-\frac{1}{M}\sum _{j=1}^{M}CV(j).$$ (14)

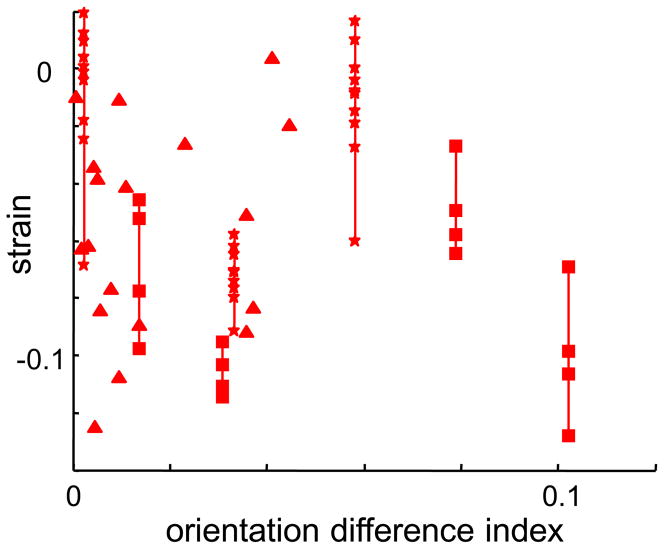
The extreme values of the ODI correspond to a cluster of neurons that have identical orientation tuning (ODI = 0), and to a cluster of neurons each of which are narrowly tuned but together cover all orientations ODI=1). For a triplet of neurons whose orientation tuning half-width is π/8 (22.5 deg) and whose preferred orientations differ in steps of π/10 (18 deg), ODI = 0.1; this corresponds approximately to the upper limit of our observed values (Figure 3).

Figure 3.

In local clusters of neurons, strain is not correlated with the similarity of their orientation tuning. The abscissa is the orientation tuning difference index (ODI), eq. (14). Plotting conventions as in Figure 2.

Results

To analyze multineuronal firing patterns and determine how they depend on distance, we made recordings with a T-shaped array of three tetrodes (near pair 600 microns apart, third tetrode >1000 microns from their midpoint) in primary visual cortex of the macaque. In total, 102 neurons were recorded. Groups of simultaneously-recorded neurons were used to form three categories of datasets: three or more neurons recorded at a single tetrode (27 datasets), at two nearby tetrodes (56 datasets) or three separate tetrodes (24 datasets). We designate these categories according to the range of distances between the recorded neurons: “<300 microns” refers to clusters of three neurons recorded at the same tetrode; “600 microns” refers to recordings of two neurons at one tetrode and a third neuron at a second tetrode 600 microns away; “>1000 microns” refers to clusters in which each neuron was at a separate tetrode. Each neuron was typically included in datasets belonging to two or more of these distance categories. The single-tetrode data included four datasets in which four neurons were simultaneously recorded, and three datasets in which five neurons were simultaneously recorded.

Our specific focus is on how firing patterns depend on distance, and this means that we need to compare recordings of neurons at multiple tetrodes with recordings obtained at a single tetrode. As described in Methods, simultaneous recordings at one tetrode are potentially confounded by a “lockout” – that when two neurons fire nearly simultaneously, spike-sorting algorithms fail to identify them because the waveforms superimpose. (We note that recently-developed spike-sorting algorithms may be able to resolve these overlaps (Franke, Natora, Boucsein, Munk & Obermayer, 2009); nevertheless, it is desirable to have analytic approaches that are insensitive to these errors.) We therefore begin with an analysis of how the lockout impacts measures of multineuronal firing patterns.

Figure 1 illustrates the impact of the lockout correction on the LLR (Figure 1A) and the strain (Figure 1B). For each measure, we compare the value obtained from the raw count probabilities (abscissa), with the value obtained after lockout correction (ordinate). For the log likelihood ratio, there is substantial scatter; for the strain, all points cluster very tightly on the diagonal. That is, the strain is relatively unaffected by alteration in firing patterns due to the lockout. There is an intuitive reason for this based on the nature of lockouts and the formula for the strain, eq. (10). Typical lockouts cause two-neuron events to be misinterpreted as a zero-neuron event, or a three-neuron event to be misinterpreted as a one-neuron event. This is because in a lockout event, the waveforms of two spikes superimpose, and thus prevent either one from being recognized. In eq. (10), these occlusions will shift probabilities within the numerator, or within the denominator, but will not move a count from the numerator to the denominator. Thus, miscounts due to occlusion of a pair have a smaller effect on the strain than generic miscounts, because the strain recognizes relationships between the 8 possible firing patterns. In contrast, the LLR, which is based on the Kullback-Leibler divergence, does not recognize any relationship between the firing patterns, and therefore cannot selectively discount the effects of pair occlusions.

Although the purpose of Figure 1 was to examine the impact of the lockout, it has another obvious feature: the confidence limits for the LLR are proportionally much smaller than for the strain. The larger confidence limits for the strain are a consequence of how these two measures depend on the observed firing pattern probabilities. For the strain, all 8 probabilities p(σ⃗) are weighted equally. Since counting statistics govern the uncertainty of the estimates of p(σ⃗), the uncertainty of the strain will be dominated by the uncertainty of the most infrequent configuration, typically p₁₁₁. In contrast, in the calculation of the Kullback-Leibler divergence (eq. (5)), the discrepancies between observed probabilities p(σ⃗) and the model probabilities p_model(σ⃗) are weighted by the observed probabilities themselves. Consequently, the values that are most uncertain (i.e., the probabilities of the rarest events) contribute the least to the LLR. However, even though the confidence limits for the strain are substantially larger than for the LLR, the conclusions one can draw from the strain are sharper, as we will see below. Finally, we note that for both measures, the bias is negligible – because our data are well-sampled (~ 10⁵ bins, >100 counts of each triplet firing pattern).

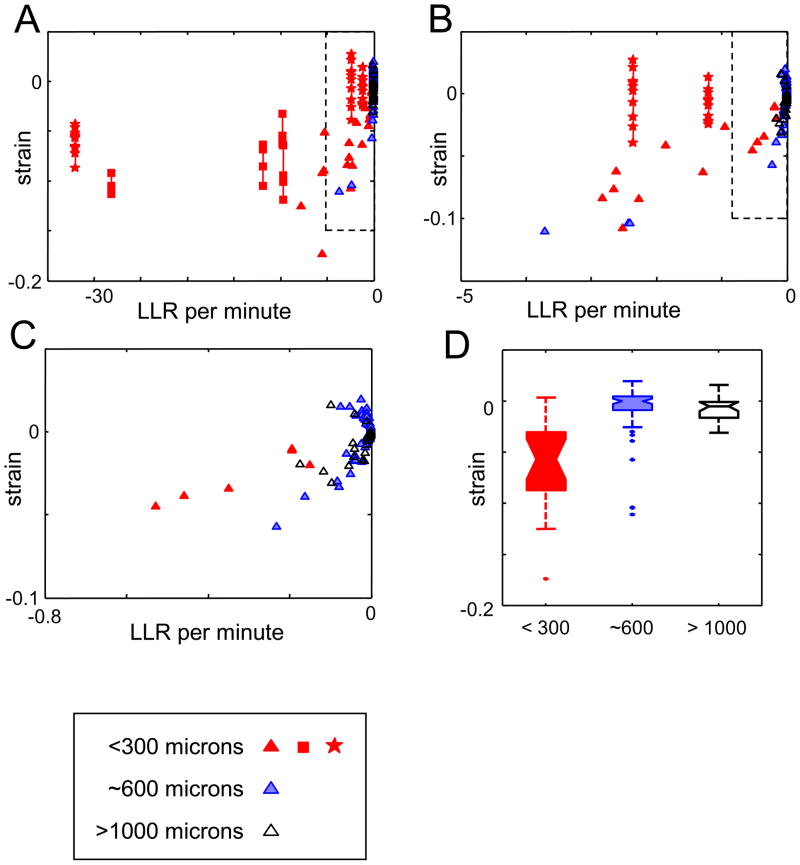
To determine how firing patterns depend on the distance between the recorded neurons, we apply these measures to the three groups of datasets (<300 microns, 600 microns, >1000 microns). Figure 2 shows the results of the analysis, and reveals a striking dependence on scale. In the <300 micron group (red symbols), the LLR per minute is often quite negative; it is the only group for which values <−5 are found (Ohiorhenuan & Victor, 2007). This means that the pairwise maximum-entropy model is a poor fit for many of the datasets, so we anticipate that the strain will be significantly different from zero. This is in fact what is found: for 55 of the 66 triplets in the <300 micron group, 95% confidence limits for the strain excluded zero. Conversely, a nonzero value of the strain was found in only 6/56 recordings in the 600-micron group (blue symbols), and 4/24 recordings in the >1000-micron group (black symbols).

Figure 2.

Triplet firing patterns show a strong dependence on spatial scale. Panels A–C: LLR per minute for the pairwise model and the strain for clusters recorded within 300 microns (red filled symbols), at a distance of ~600 microns (blue shaded symbols) and > 1000 microns (black open symbols). Three magnifications are shown: the dashed box in Panel A is enlarged to form Panel B, and the dashed box in panel B is enlarged to form Panel C. For the 300-micron clusters but not the others, the LLR and the strain is often large and negative. Note that the LLR must be negative and hence its sign is uninformative, while a negative value for the strain indicates that there is a deficit of triplet-firing events, compared to the expectation of a pairwise model. The four- and five-neuron datasets are indicated by squares and stars, respectively; for these, LLR values are calculated for all neurons together, and strain values are calculated separately for each 3-neuron subset. Confidence limits are not shown; for the LLR, they are approximately ±0.05; for the strain, they are approximately ±0.02 (see Figure 1). Panel D: boxplots of the distribution of strain values.

The <300 micron datasets include several clusters of M ≥ 4 neurons. For these datasets, the LLR calculation reflects the fit to all 2^M firing patterns, while the strain is calculated separately for each 3-neuron subset. As shown in Figure 2, the strains for these datasets are generally similar to those for the M = 3 datasets, while the LLR’s are much more negative. This allows for two inferences. First, our finding that the strain values are similar for the M ≥ 4 - and the M = 3- datasets is further empirical evidence for the robustness of the strain in the face of spike-sorting artifacts, which are more severe when more neurons are recorded on the same tetrode. Second, the finding that the LLR is generally more negative for the M ≥ 4 -datasets indicates that the failure of the pairwise model is not simply an artifact of examining only three neurons.

Importantly, the strain allows us to go beyond saying that the pairwise model fails: it tells us how it fails. Specifically, in 52 of 55 triplets in the <300 micron group for which the strain is nonzero, it is negative. That is, in the overwhelming majority of recordings of local clusters, the number of triplet firing events is less than anticipated from the number of pairwise firings. In the 600-micron group, all 6 of the significantly nonzero values of strain were negative too (Figure 2C). In the >1000 micron group, there was no evident bias: 3/20 values of the strain were significantly negative, and 1/20 was significantly positive. In sum, we find a highly consistent pattern in local clusters – fewer multineuronal firing events than expected from the pairwise statistics – and that this pattern falls off rapidly with distance. This behavior is summarized by the boxplots of Figure 2D.

We considered two kinds of origins for these triplet interactions: common stimulus driving, and intrinsic network interactions. Common stimulus driving could occur if the neurons have similar receptive fields, and are therefore simultaneously driven by the same subset of stimuli. Since all neurons’ receptive fields had approximately the same location, we indexed the similarity of their receptive fields by comparing their orientation tuning (eq. (14)). As shown in Figure 3, strain values are uncorrelated with the similarity in orientation tuning, thus suggesting that common stimulus driving is not responsible for our observations.

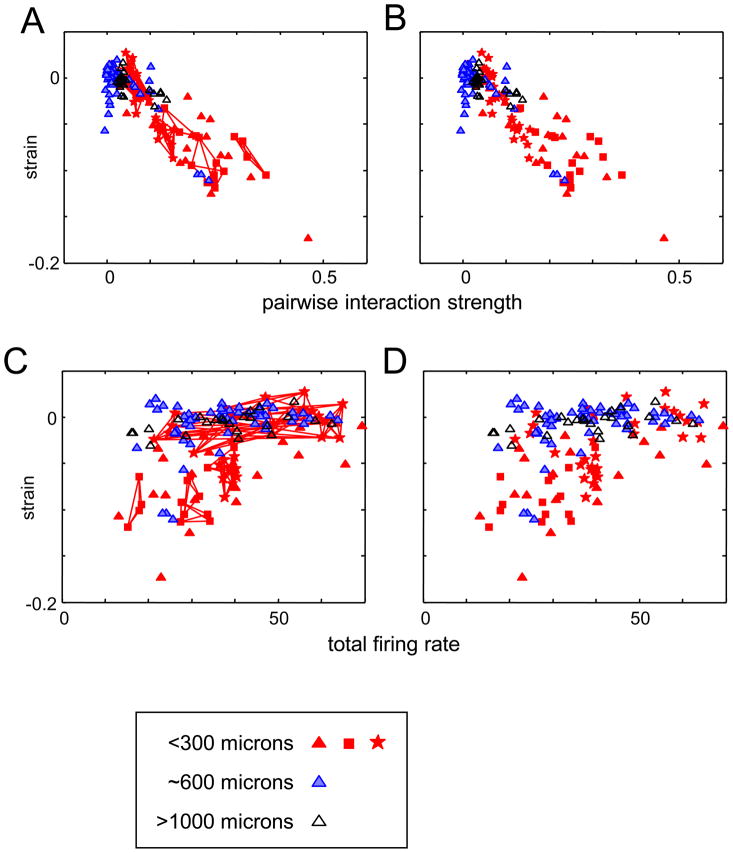
If, on the other hand, the strain reflects intrinsic network interactions, we would expect that the strain is correlated with the extent of pairwise coupling between the neurons. To test this idea, we used a measure for pairwise interaction strength based on the firing patterns of pairs of neurons, $\frac{1}{4}log\frac{p_{00}{p}_{11}}{p_{01}{p}_{10}}$. As Figure 4 shows, the strain is most negative when the pairwise interaction strengths are large (Figure 4A, C). Strain is not correlated with overall firing rate (Figure 4B, D), so the correlation between strain and pairwise interactions is not merely a matter of having enough spikes to make the measurement, or overall levels of excitation. Note also that the few recordings in the 600 micron group with significantly negative values of the strain are the recordings for which the pairwise interaction strengths are largest, and in the range of the <300 micron group.

Figure 4.

The strain is correlated with pairwise interaction strength (panels A and B) but not with firing rate (panels C and D). Clusters recorded within 300 microns shown as red filled symbols, at a distance of ~600 microns as blue shaded symbols, and at > 1000 microns as black open symbols. Pairwise interaction strength (panels A and B) is quantified by the average of the quantities $\frac{1}{4}log\frac{p_{00}{p}_{11}}{p_{01}{p}_{10}}$ for each neuron in the cluster. Firing rate (panels C and D) is the total firing rate across the three neurons. In Panels A and C, data from three-neuron subsets of four- and five-neuron recordings are connected by lines (as in Figure 2); Panels B and D show the same data with the connecting lines suppressed so that all data points are visible.

As has been noted (Nakahara & Amari, 2002), the information-geometric coordinates of different orders are not independent. That is, when the third-order interaction terms are not zero, the partitioning of firing statistics into second- and third-order interactions is somewhat arbitrary. However, this lack of independence cannot account for our results: no matter how we quantify the second-order interactions, the maximum-entropy prediction is that the third-order interactions are zero, which is not what we find. Moreover, if the third-order interactions were simply a result of common driving of many cells, we would expect that the strain would be larger when pairwise joint firings are more frequent, and this is the opposite of what we find.

Discussion

The general problem: describing population firing patterns

A central goal of systems neuroscience is to understand the function of populations of neurons. To achieve this goal, it is crucial to have descriptions of multineuronal firing patterns that highlight their important qualitative features. Achieving such descriptions is a challenge, because of the obvious dimensional explosion: for M neurons, there are 2^M possible firing patterns. Thus, it is noteworthy that in several neural systems (Schneidman et al., 2006, Shlens et al., 2006, Tang et al., 2008, Yu et al., 2008), the probabilities of these 2^M firing patterns can be accounted for on the basis of far fewer parameters – the M(M+1)/2 pairwise firing probabilities. This dimensional reduction is achieved via maximum-entropy modeling: to a very good approximation, the multineuronal firing patterns are the most random possible set of firing patterns that are consistent with the observed pairwise correlations.

Here, we take the next step, focusing on triplet correlations. We quantify these correlations with the “strain”, an algebraic combination of the probabilities of the eight firing patterns that can be manifest by a three-neuron group. There are two reasons to focus on this level: one that is data-driven, and one that is theoretically motivated. The data-driven reason is that in our recordings (macaque visual cortex), pairwise interactions do not account for multineuronal firing patterns. Thus, even for a phenomenological fit to the data, triplet firing patterns must be taken into account. The second reason is more general: triplet firing patterns provide insight into network behavior and represent constraints that mechanistic models must satisfy. For example, if all three-neuron subsets have a positive strain, synchrony across the entire population is facilitated, while if all three-neuron subsets have a negative strain (as we observe here), global synchrony is suppressed. Positive and negative strain, if specific to particular subsets of neurons within the network, can be interpreted as logic operations (Feinerman et al., 2008, Vogels & Abbott, 2005): a positive strain among three neurons corresponds to an AND gate, while a negative strain corresponds to an XOR gate.

Note that even if a pairwise maximum-entropy model for the entire population is exact, nonzero values of the strain may be encountered in three-neuron subsets. At a formal level, this is because for M>3, marginalization of the pairwise maximum-entropy distribution (eq. (3)) over one or more neurons does not yield a pairwise maximum-entropy distribution over the remaining neurons. The intuition behind this is that the firing patterns manifest by a subset of neurons can be primarily a result of pairwise interactions with the other (unobserved) neurons within the network. This observation is a general one, not restricted to the strain, or to the size of the observed subset (Roudi, Tyrcha & Hertz, 2009b): even at the pairwise level, the observed coupling coefficients that account for firing patterns in a set of recorded neurons may differ from the couplings that would be identified, were it possible to sample the entire network. An analogous consideration applies across time as well: although the present study and most others focus on snapshots of responses (for an exception, see (Marre, El Boustani, Fregnac & Destexhe, 2009)), the underlying biophysical processes that shape the observed firing patterns necessarily involve interactions not only with un-recorded neurons, but also across time (Rulkov & Bazhenov, 2008, Vogels & Abbott, 2005).

Characterizing triplet interactions via the strain and the Kullback-Leibler divergence

At the level of three-neuron firing patterns, there are two natural measures of the departure from a pairwise model: the Kullback-Leibler divergence, and the strain. There is an obvious conceptual difference: the Kullback-Leibler divergence is unsigned, so it can only indicate the magnitude of deviation from the pairwise model. In contrast, (as emphasized above), the strain is a signed quantity, so it indicates the direction of this deviation. But there are other differences as well, because the Kullback-Leibler divergence and the strain measure the departure from a pairwise model in different ways.

The basic difference is that the Kullback-Leibler divergence compares the observed data with the specific pairwise model that matches the observed pairwise correlations, while the strain compares the observed firing probabilities with any pairwise model. As a consequence, the Kullback-Leibler divergence compares probabilities in an additive fashion, while the strain compares probabilities in a multiplicative fashion. To see this, we note that for three neurons, equating pairwise probabilities to that of a model – which is the basis of the Kullback-Leibler measure – implies that the model probabilities p_model(σ⃗) and the observed probabilities p(σ⃗) are related by

$$p_{\mathit{model}}(\overrightarrow{\sigma })=p(\overrightarrow{\sigma })+k{\sigma }_1{\sigma }_2{\sigma }_3.$$ (15)

for some value of the free parameter k. (This is because after the pairwise marginals have been specified, all that remains is one degree of freedom. See, for example, Appendix 1 of (Martignon et al., 2000)). The Kullback-Leibler divergence is a differentiable non-negative function of the parameter k. It is zero only for k = 0, and thus for small k, it is proportional to k². Thus, the Kullback-Leibler divergence determines the quantity that must be added or subtracted to observed probabilities, in order to obtain a pairwise maximum-entropy model that accounts for the observed pairwise correlations. In contrast, the strain determines the multiplicative or divisive factor that needs to be applied to the observed probabilities, so that they match a pairwise model. This can be seen directly from eqs. (7) and (8): the strain, γ, is the quantity for which the probabilities p(σ⃗)exp(−γσ₁σ₂σ₃), followed by renormalization, satisfy a pairwise maximum-entropy model.

A consequence of this difference is that the Kullback-Leibler divergence necessarily approaches 0 as bin size decreases, while the strain can have a meaningful nonzero value in this limit. To see this, we consider the limit of infinitesimally small bins, i.e., bins whose width δt is finer than the firing precision of any neuron, and in which each neuron’s firing is infrequent. (This is the asymptotic limit of Roudi et al. (Roudi, Nirenberg & Latham, 2009a), and corresponds to small values of their quantity ῡδt, the mean firing rate per neuron per bin.) In this limit, the probabilities of the three states in which one neuron fires (p₁₀₀, p₀₁₀, and p₀₀₁) are proportional to δt; the probabilities of the three states in which two neurons fire (p₀₁₁, p₁₀₁, and p₁₁₀) are proportional to (δt)², and the probability of the triplet firing state p₁₁₁ is proportional to (δt)³. Consequently, the Kullback-Leibler divergence for the pairwise model is proportional to (δt)³ -- since the divergence for the best-fitting pairwise model can be no worse than the divergence for a pairwise model that fits the singlet and doublet events exactly (see (Roudi et al., 2009a) for further details). As Roudi et al. (Roudi et al., 2009a) showed, this obligate approach to 0 when ῡδt is small affects not only the Kullback-Leibler divergence, but also, measures based on the Kullback-Leibler divergence when normalized by the connected information (Schneidman et al., 2006). On the other hand, the strain tends to a stable value as bin size decreases, since the δt-terms counterbalance. This can be seen from eq. (10): the numerator has three factors of δt from the singlet probabilities and one factor of (δt)³ from the triplet term, resulting in (δt)⁶; the denominator has three factors of (δt)² from each of the doublet terms, also resulting in (δt)⁶. Thus, the strain is anticipated to be independent of δt in the asymptotic regime of (Roudi et al., 2009a). Figure 4C, D shows that meaningful values of the strain can be measured in this asymptotic regime: significantly negative values of the strain were obtained in datasets for which firing rates were as small as 25 spikes per second across all 3 neurons, which corresponds to firing rates per neuron per bin (ῡδt) less than 0.1.

The above advantages of the strain are balanced by two tradeoffs. First, extension of the strain to > 3 neurons is likely to be impractical (see Appendix). Second, even for 3 neurons, the strain is more difficult to estimate than the Kullback-Leibler divergence (Figure 1). The reason is related to the fact that the strain retains a nonzero value in the limit of small bins: it is based on a ratio of probabilities, including the probability of triplet firing events. As bin size decreases, the number of such events will become progressively smaller, so the strain will become progressively more difficult to estimate. The uncertainty in estimation is readily quantified (see eq. (12)), and is dominated by Poisson counting statistics for the rarest state.

The strain identifies a distinctive feature of local cortical networks

The experimental component of this paper consists of an analysis of three-neuron cortical firing patterns, obtained from tetrode recordings in V1 of the macaque monkey. During visual stimulation with pseudorandom checkerboards, we found a scale-dependence to triplet firing patterns: nearby neurons (<300 microns) displayed fewer triplet events than predicted from their pairwise interactions, while more distant neurons (600 and >1000 microns) displayed firing patterns consistent with the expectation from pairwise statistics (Figure 2). The difference between the number of triplet events and the expectation based on pairwise statistics is strongly correlated with the strength of pairwise interactions in the network (Figure 4A and 4B), but not firing rate (Figure 4C and 4D). Since our findings of a negative strain are specific to local clusters, it is unlikely that they are the result of global state changes, such as fluctuations between “up-states” and “down-states”, which typically extend over at least several millimeters (Li, Poo & Dan, 2009).

Our finding that networks of nearby neurons display a negative, and often large, strain suggests a network-level mechanism that reduces synchrony. This is behavior has evident functional utility, as it would act to prevent runaway synchrony in strongly coupled recurrent networks. We speculate that this behavior is mediated by small inhibitory GABA-ergic neurons (Bonifazi, Goldin, Picardo, Jorquera, Cattani, Bianconi, Represa, Ben-Ari & Cossart, 2009). Since cortical extracellular recordings generally record the activity of large, excitatory pyramidal cells (Buzsaki, 2004), the activity of these inhibitory neurons would be largely hidden, so only their indirect effects would be seen in typical extracellular recordings such as we report here.

Other strategies for examining multineuronal firing patterns

We have chosen to focus on the strain because it allows for an examination of multineuronal firing patterns beyond the pairwise level, while remaining in a regime in which large numbers of counts of the relevant events can be accumulated.

Other studies have taken a different approach to the problem of going beyond the pairwise level, developing methods for analyzing all orders of interaction in the simultaneous activity of four or more neurons (Gutig et al., 2003, Martignon et al., 2000, Martignon et al., 1995, Nakahara & Amari, 2002). Two of these studies have included an application to experimental data (Martignon et al., 2000, Martignon et al., 1995). As in the present study, evidence of high-order interactions was found, as manifest by nonzero coefficients of terms in the exponential probability expansion. However, it is difficult to make a more detailed comparison with our data, because of numerous experimental differences. First, our main finding – a negative strain – was only present among neurons recorded within 300 microns of each other at a single tetrode; the above studies relied on multi-electrode arrays (500 to 1000 microns: (Prut, Vaadia, Bergman, Haalman, Slovin & Abeles, 1998); 400 to 600 microns: (Vaadia, Bergman & Abeles, 1989)), and were unlikely to contain three or more neurons within 300 microns. Second, our studies were carried out under anesthesia; the latter studies were carried out in awake animals, during various phases of a behavioral task. Finally, our conclusions are based on several dozen datasets each of which typically contained >1000 sec of data; the above studies only considered a handful of datasets (one dataset of 6 neurons in frontal cortex (Martignon et al., 1995); “several” datasets in frontal cortex and two in visual cortex (Martignon et al., 2000)) and each contained <200 sec of data. Thus, while the above studies illustrated how the approach could be applied to small datasets, they stopped short of determining what is typical of local networks.

Another related approach is that of (Montani, Ince, Senatore, Arabzadeh, Diamond & Panzeri, 2009), who also examined interactions of all orders, in recordings (Arabzadeh, Petersen & Diamond, 2003) made with an electrode array (400 micron spacing) in mouse somatosensory cortex. To reduce the number of parameters in the exponential expansion of the probability distribution, they assumed that all neurons are equivalent. Given this assumption of homogeneity, interactions of each order are summarized by a single number, providing a very strong dimensional reduction: only M parameters are needed to characterize all possible 2^M firing patterns. This study found evidence of triplet interactions, and also showed that these interactions contributed to coding. However, the analysis was based on entropy differences, so it is unclear whether their findings correspond to a positive vs. a negative strain, and the conclusions hinged on the assumption of homogeneity across neurons.

Appendix

This Appendix expands on a number of technical points mentioned in the main text. First, we demonstrate the basic formula for the strain, eq. (9); this is well-known ((Amari, 2001) (Nakahara & Amari, 2002)) and we demonstrate it here for the reader’s convenience and to illustrate the notation used in the remainder of the Appendix. We then develop asymptotic expressions for the bias and variance of the “plugin” estimator for the strain (eqs. (11) and (12) of the main text), and for the effect of a lockout correction. Finally, we comment on ways that the strain can be applied to recordings from more than three neurons.

Our notational setup is the same as in the main text: we consider a network of M neurons and population state vectors σ⃗ = (σ₁,σ₂,…,σ_M), with the convention that σ_k =+1 means that neuron k is firing, and σ_k=−1 means that it is not. We also use s(σ⃗) to represent the parity of σ⃗,

$$s(\overrightarrow{\sigma })=\prod _j{\sigma }_j.$$ (A1)

s(σ⃗) is +1 if all neurons fire, or if an even number of neurons do not fire, and −1 otherwise.

For a three-neuron network (M = 3), the firing probabilities can always be expressed in the form

$$p(\overrightarrow{\sigma })=\frac{Z(\overrightarrow{\sigma })}{Z},$$ (A2)

where

$$Z(\overrightarrow{\sigma })=exp\left(\sum _{j=1}^M{\alpha }_j{\sigma }_j+\sum _{j<k}^M{\beta }_{jk}{\sigma }_j{\sigma }_k+\gamma {\sigma }_1{\sigma }_2{\sigma }_3\right)$$ (A3)

and

$$Z=\sum _{\overrightarrow{\sigma }}Z(\overrightarrow{\sigma }).$$ (A4)

See, for example, (Amari, 2001, Nakahara & Amari, 2002). For notational simplicity, we focus on the three-neuron case, but the derivations immediately extend to M > 3 neurons, as we indicate.

Calculating the strain from the firing probabilities

Our first objective is to derive eq. (9) of the main text. With the above notation, it can be written

$$\gamma =\frac{1}{2^M}\sum _{\overrightarrow{\sigma }}s(\overrightarrow{\sigma })logp(\overrightarrow{\sigma }).$$ (A5)

To demonstrate eq. (A5), we proceed as follows. First, we note that exactly half of the σ⃗’s have even parities (s(σ⃗) =+1), and half have odd parities (s(σ⃗) = −1). Thus, ${\displaystyle \sum _{\overrightarrow{\sigma }}}s(\overrightarrow{\sigma })=0$, and therefore (using eq. (A2))

$$\frac{1}{2^M}\sum _{\overrightarrow{\sigma }}s(\overrightarrow{\sigma })logp(\overrightarrow{\sigma })=\frac{1}{2^M}\sum _{\overrightarrow{\sigma }}s(\overrightarrow{\sigma })(logp(\overrightarrow{\sigma })+logZ)=\frac{1}{2^M}\sum _{\overrightarrow{\sigma }}s(\overrightarrow{\sigma })logZ(\overrightarrow{\sigma }).$$ (A6)

We now use eq. (A3) for Z(σ⃗):

$$\frac{1}{2^M}\sum _{\overrightarrow{\sigma }}s(\overrightarrow{\sigma })logp(\overrightarrow{\sigma })=\frac{1}{2^M}\sum _{\overrightarrow{\sigma }}{\sigma }_1{\sigma }_2{\sigma }_3\left(\sum _{j=1}^M{\alpha }_j{\sigma }_j+\sum _{j<k}^M{\beta }_{jk}{\sigma }_j{\sigma }_k+\gamma {\sigma }_1{\sigma }_2{\sigma }_3\right).$$ (A7)

Expanding the right-hand-side leads to a simplification, because σ_k=±1, and therefore σ_k²=1:

$$\frac{1}{2^M}\sum _{\overrightarrow{\sigma }}s(\overrightarrow{\sigma })logp(\overrightarrow{\sigma })=\frac{1}{2^M}\sum _{\overrightarrow{\sigma }}({\alpha }_1{\sigma }_2{\sigma }_3+{\alpha }_2{\sigma }_1{\sigma }_3+{\alpha }_3{\sigma }_2{\sigma }_3+{\beta }_{12}{\sigma }_3+{\beta }_{13}{\sigma }_2+{\beta }_{23}{\sigma }_1+\gamma ).$$ (A8)

In calculating the sum over all 2^M network states σ⃗, the α-terms vanish because each of the alternatives σ_jσ_k =±1 occurs half of time, and the β-terms vanish because each of the alternatives σ_k =±1 occur half the time. Thus,

$$\frac{1}{2^M}\sum _{\overrightarrow{\sigma }}s(\overrightarrow{\sigma })logp(\overrightarrow{\sigma })=\frac{1}{2^M}\sum _{\overrightarrow{\sigma }}\gamma ,$$ (A9)

which is equivalent to eq. (A5) and eq. (9) of the main text.

Note that the above derivation immediately generalizes to the highest coefficient of a complete exponential expansion, e.g., the coefficient of σ₁σ₂σ₃σ₄ for M = 4, etc.

Asymptotic estimates of bias and variance

In this section, we determine the asymptotic bias and variance of estimates of γ, based on the “plug-in” estimator corresponding to eq. (A5).

To formalize the problem, we assume that our data consist of N observations (“bins”), each of which are independent, and (as in the main text) that the number of observations that are in the state σ⃗ is N(σ⃗), so N =ΣN(σ⃗). Our estimate of p(σ⃗) is the naïve one, namely

$$p_{\mathit{est}}(\overrightarrow{\sigma })=\frac{N(\overrightarrow{\sigma })}{N}.$$ (A10)

With this estimate for p(σ⃗), the “plug-in” estimator corresponding to eq. (A5) is

$${\gamma }_{\mathit{est}}=\frac{1}{2^M}\sum _{\overrightarrow{\sigma }}s(\overrightarrow{\sigma })log\frac{N(\overrightarrow{\sigma })}{N}.$$ (A11)

The bias of the estimator γ_est is, by definition, the expected departure of the estimator from its true value γ:

$$B\equiv \langle {\gamma }_{\mathit{est}}\rangle -\gamma ,$$ (A12)

where 〈 〉 denotes an average over all experiments with N observations, and true state probabilities p(σ⃗). Its variance is, by definition,

$$V\equiv \langle {({\gamma }_{\mathit{est}}-\langle {\gamma }_{\mathit{est}}\rangle )}^2\rangle ,$$ (A13)

Thus, our goal is to determine the mean and variance of γ_est, as defined by eq. (A11).

We begin by noting that eq. (A11) simplifies, because half of the σ⃗’s have even parities, and half have odd parities. Thus,

$${\gamma }_{\mathit{est}}=\frac{1}{2^M}\sum _{\overrightarrow{\sigma }}s(\overrightarrow{\sigma })logN(\overrightarrow{\sigma }).$$ (A14)

The right-hand-side of eq. (A14) is a linear combination of logarithms of values drawn from a multinomial process of 2^M symbols (the states σ⃗), each with probability p(σ⃗). Therefore, to determine the mean and variance of γ_est, we determine the mean and variance of the logarithms of values drawn from a multinomial distribution.

We determine these quantities from the well-known expressions for the mean, variance, and covariance of a multinomial process. In N observations, the expected number of times that a symbol with probability p(σ⃗) is encountered is

$$\langle N(\overrightarrow{\sigma })\rangle =Np(\overrightarrow{\sigma }).$$ (A15)

With δ(σ⃗) = N(σ⃗)− 〈N(σ⃗)〉, the variance of each count is given by

$$\langle \delta {(\overrightarrow{\sigma })}^2\rangle =Np(\overrightarrow{\sigma })(1-p(\overrightarrow{\sigma }))$$ (A16)

and the covariances are given by

$$\langle \delta (\overrightarrow{\sigma })\delta ({\overrightarrow{\sigma }}^{\prime })\rangle =-NP(\overrightarrow{\sigma })p({\overrightarrow{\sigma }}^{\prime }),\overrightarrow{\sigma }\ne {\overrightarrow{\sigma }}^{\prime }.$$ (A17)

We now calculate the corresponding statistics of the logarithms asymptotically:

$$<logN(\overrightarrow{\sigma })>=\langle log(\langle N(\overrightarrow{\sigma })\rangle +\delta (\overrightarrow{\sigma }))\rangle =log\langle N(\overrightarrow{\sigma })\rangle +\langle log\left(1+\frac{\delta (\overrightarrow{\sigma })}{\langle N(\overrightarrow{\sigma })\rangle }\right)\rangle$$

Expanding the logarithm via a Taylor series yields

$$\langle logN(\overrightarrow{\sigma })\rangle =log\langle N(\overrightarrow{\sigma })\rangle +\langle \frac{\delta (\overrightarrow{\sigma })}{\langle N(\overrightarrow{\sigma })\rangle }\rangle -\frac{1}{2}\langle {\left(\frac{\delta (\overrightarrow{\sigma })}{\langle N(\overrightarrow{\sigma })\rangle }\right)}^2\rangle +O(N{(\overrightarrow{\sigma })}^{-3/2}),$$ (A18)

or

$$\langle logN(\overrightarrow{\sigma })\rangle =log\langle N(\overrightarrow{\sigma })\rangle -\frac{Np(\overrightarrow{\sigma })(1-p(\overrightarrow{\sigma }))}{2{(Np(\overrightarrow{\sigma }))}^2}+O(N^{-3/2})=log\mathit{NP}(\overrightarrow{\sigma })-\frac{1-p(\overrightarrow{\sigma })}{2NP(\overrightarrow{\sigma })}+O(N^{-3/2}),$$ (A19)

where we have used 〈δ(σ⃗)〉 = 0, eq. (A15), and eq. (A16).

So the bias in the logarithm of the counts of the state σ⃗ is

$$B(\overrightarrow{\sigma })\equiv \langle logN(\overrightarrow{\sigma })\rangle -log\langle N(\overrightarrow{\sigma })\rangle =-\frac{1-p(\overrightarrow{\sigma })}{2Np(\overrightarrow{\sigma })}+O(N^{-3/2}).$$ (A20)

The bias estimate (text eq. (11)) now follows from the definition (A12) by combining eq. (A20) with eq. (A14):

$$B\equiv \langle {\gamma }_{\mathit{est}}\rangle -\gamma =\frac{1}{2^M}\sum _{\overrightarrow{\sigma }}s(\overrightarrow{\sigma })B(\overrightarrow{\sigma })=-\frac{1}{2^{M+1}N}\sum _{\overrightarrow{\sigma }}\frac{s(\overrightarrow{\sigma })}{p(\overrightarrow{\sigma })}+O(N^{-3/2})$$ (A21)

with a simplification resulting from the fact that the parities sum to zero (Σs(σ⃗)= 0).

Similar algebra provides asymptotic expressions for the variances of the logarithms of the counts,

$$V(\overrightarrow{\sigma },\overrightarrow{\sigma })\equiv \langle {(logN(\overrightarrow{\sigma })-\langle logN(\overrightarrow{\sigma })\rangle )}^2\rangle =\langle {\left(\left(log\langle N(\overrightarrow{\sigma })\rangle +log\left(1+\frac{\delta (\overrightarrow{\sigma })}{\langle N(\overrightarrow{\sigma })\rangle }\right)\right)-\left(log\langle N(\overrightarrow{\sigma })\rangle -\frac{1-p(\overrightarrow{\sigma })}{2Np(\overrightarrow{\sigma })}\right)\right)}^2\rangle +O(N^{-3/2})=\langle {\left(log\left(1+\frac{\delta (\overrightarrow{\sigma })}{\langle N(\overrightarrow{\sigma })\rangle }\right)-\frac{1-p(\overrightarrow{\sigma })}{2Np(\overrightarrow{\sigma })}\right)}^2\rangle +O(N^{-3/2})=\frac{1}{Np(\sigma )}-\frac{1}{N}+O(N^{-3/2})$$ (A22)

and their covariances,

$$V(\overrightarrow{\sigma },{\overrightarrow{\sigma }}^{\prime })\equiv \langle (logN(\overrightarrow{\sigma })-\langle logN(\overrightarrow{\sigma })\rangle )(logN({\overrightarrow{\sigma }}^{\prime })-\langle logN({\overrightarrow{\sigma }}^{\prime })\rangle )\rangle =-\frac{1}{N}+O(N^{-3/2}),\overrightarrow{\sigma }\ne {\overrightarrow{\sigma }}^{\prime }.$$ (A23)

The variance estimate (text eq. (12)) follows from the definition (A13) by combining eqs. (A22) and (A23) with eq. (A14):

$$V\equiv \langle {({\gamma }_{\mathit{est}}-\langle {\gamma }_{\mathit{est}}\rangle )}^2\rangle =\frac{1}{2^{2M}}\sum _{\overrightarrow{\sigma },{\overrightarrow{\sigma }}^{\prime }}s(\overrightarrow{\sigma })s({\overrightarrow{\sigma }}^{\prime })V(\overrightarrow{\sigma },{\overrightarrow{\sigma }}^{\prime })=\frac{1}{2^{2M}N}\sum _{\overrightarrow{\sigma }}\frac{1}{p(\overrightarrow{\sigma })}+O(N^{-3/2}).$$ (A24)

In practice, γ_est is approximately Gaussian-distributed, and the above asymptotic expressions for bias (eq. (A21)) and variance (eq. (A24)) are accurate provided that the minimum number of counts, N min_σ⃗p(σ⃗), is at least ~10. Simulations that support this approximation are shown in Figure A1.

The effect of the lockout correction

As mentioned in the main text, spike-sorting introduces a potential confound into the analysis of multineuronal data. The source of the problem is that when two spikes overlap in time, their waveforms sum, and neither can be reliably identified. When this happens, a bin that actually contains two firing events will be registered as containing none; this is known as a “lockout.” (We note that recently, spike-sorting algorithms that may be able to resolve these overlaps have been developed (Franke et al., 2009); the applicability of such methods is likely to depend on the details of the recording situation, such as firing rates and noise. Thus, even with the availability of advanced spike-sorting algorithms, it is desirable to have analytic approaches that are insensitive to spike-sorting errors.)

As described in Methods, an approximate correction for lockout can be constructed, by making use of the fact that in a typical recording, the analysis bin (the interval of time used for tallying spiking states) is many times larger than the spike width. Figure 1 shows that the strain is nearly independent of the lockout correction, indicating that it is relatively insensitive to the effects of the lockout. Our goal here is to show why this is the case.

We do this by first describing the lockout correction strategy in detail, and then deriving a formula that relates the lockout-corrected value of the strain to the observed probability of each spiking state.

The lockout correction is based on an estimate of how many events are miscounted due to overlapping spikes. To obtain this estimate, we assume that firing rates are constant for the duration of the analysis bin, that spikes occur in a Poisson fashion, and that no bin contains more than one spike from each neuron. We then partition each analysis bin into W sub-intervals, where each sub-interval corresponds to the spike width. (In the data presented here, W = 8 for the datasets analyzed with 10 ms bins and W=12 for the datasets analyzed with 14.8-ms bins.) We estimate the miscounts by relating the total frequency of multineuronal events to the observed frequency of the multineuronal events. In order for a multineuronal event to be observed, each sub-interval can contain no more than one spike.

Consider, for example, an event in which neurons 1 and 2 fire. The spikes from neurons 1 and 2 can fall into the W sub-intervals in W² equally-likely ways, since each of the W sub-intervals is equally likely to contain either spike. Usually, the spikes from the two neurons fall into different sub-intervals, so both are registered; these events properly contribute to the estimate of p₁₁₀. This happens in W(W−1) of the W² possible configurations in which the spikes can fall into sub-intervals. But in the remaining W configurations, both spikes fall into the same subinterval, so neither spike is registered, and the event is an erroneous contribution to p₀₀₀. As a result of these overlap events, p₁₁₀ is under-estimated by a factor of $\frac{W^2}{W(W-1)}\approx 1+1/W$; the resulting undercounts contribute to p₀₀₀. (Here, we write p₁₁₀ as the probability of a state in which σ₁= +1, σ₂ = +1, and σ₃ = −1, etc.).

Similarly, triplet firing events can populate the W sub-intervals in W³ ways, but only W(W−1)(W−2) of these are observed configurations, in which no sub-interval has 2 or more spikes. Thus, p₁₁₁ is undercounted by a factor of $\frac{W^3}{W(W-1)(W-2)}\approx 1+3/W$. Most of the undercounts occur when two spikes occur in one sub-interval, and a third occurs in another subinterval. The two spikes that occur in the same sub-interval occlude each other. The third spike, which occurs in its own sub-interval, is correctly detected. Thus, the three-spike event appears to contain only one spike, and contributes to one of the singleton event probabilities p₁₀₀, p₀₁₀, and p₀₀₁. A small number of undercounts are events in which all three spikes occur within the same sub-interval. The three spikes occlude each other and thus the event contributes to p₀₀₀. We neglect these events, since their proportion is O(W⁻²).

Putting the above facts together leads to formulas that relate the raw estimates of the state probabilities to those that would have been encountered in the absence of a lockout. We add the undercounts to the triplet firing events

$${p_{111}}^{\mathit{corrected}}={p_{111}}^{\mathit{raw}}(1+\frac{3}{W}),$$ (A25)

and to the doublet firing events

$${p_{110}}^{\mathit{corrected}}={p_{110}}^{\mathit{raw}}(1+\frac{1}{W}),{p_{101}}^{\mathit{corrected}}={p_{101}}^{\mathit{raw}}(1+\frac{1}{W}),\text{and}{p_{011}}^{\mathit{corrected}}={p_{011}}^{\mathit{raw}}(1+\frac{1}{W}).$$ (A26)

The counts that are added to the triplet firing events (eq. (A25)) are removed from the singlet firing events

$${p_{100}}^{\mathit{corrected}}={p_{100}}^{\mathit{raw}}-\frac{{p_{111}}^{\mathit{raw}}}{W},{p_{010}}^{\mathit{corrected}}={p_{010}}^{\mathit{raw}}-\frac{{p_{111}}^{\mathit{raw}}}{W},\text{and}{p_{001}}^{\mathit{corrected}}={p_{001}}^{\mathit{raw}}-\frac{{p_{111}}^{\mathit{raw}}}{W},$$ (A27)

and the counts that are added to the doublet firing events (eq. (A26)) are removed from the null events

$${p_{000}}^{\mathit{corrected}}={p_{000}}^{\mathit{raw}}-\frac{{p_{011}}^{\mathit{raw}}+{p_{101}}^{\mathit{raw}}+{p_{110}}^{\mathit{raw}}}{W}.$$ (A28)

Thus, (as mentioned in the main text), we anticipate that the lockout correction will be small: it shifts events within the numerator (eqs. (A25) and (A27)) or within the denominator (eqs. (A26) and (A28)), but not between numerator and denominator.

To formalize this observation, we substitute the above formulae (eqs. (A25) to (A28)) into

$${\gamma }^{\mathit{corrected}}=\frac{1}{8}log\frac{{p_{111}}^{\mathit{corrected}}{p_{100}}^{\mathit{corrected}}{p_{010}}^{\mathit{corrected}}{p_{001}}^{\mathit{corrected}}}{{p_{011}}^{\mathit{corrected}}{p_{101}}^{\mathit{corrected}}{p_{011}}^{\mathit{corrected}}{p_{000}}^{\mathit{corrected}}}$$ (A29)

to obtain (after some algebra)

$${\gamma }^{\mathit{corrected}}={\gamma }^{\mathit{raw}}+\frac{1}{8W}\left(\left(\frac{{p_{011}}^{\mathit{raw}}}{{p_{000}}^{\mathit{raw}}}-\frac{{p_{111}}^{\mathit{raw}}}{{p_{100}}^{\mathit{raw}}}\right)+\left(\frac{{p_{101}}^{\mathit{raw}}}{{p_{000}}^{\mathit{raw}}}-\frac{{p_{111}}^{\mathit{raw}}}{{p_{010}}^{\mathit{raw}}}\right)+\left(\frac{{p_{110}}^{\mathit{raw}}}{{p_{000}}^{\mathit{raw}}}-\frac{{p_{111}}^{\mathit{raw}}}{{p_{001}}^{\mathit{raw}}}\right)\right)+O(W^{-2}).$$ (A30)

Eq. (A30) provides further reasons that the lockout correction is small: γ^corrected − γ^raw is a sum of three terms, each of which is a difference of probability ratios. These differences are nonzero only to the extent to which triplet interactions are present. For example, the first term is nonzero only if the probability of joint firing neuron 2 and 3 depends on whether neuron 1 fires. Moreover, each of these ratios has a quadratic dependence on the analysis bin width, and their total contribution is attenuated by the multiplier1/W.

More than 3 neurons

In the final section, we mention ways in which the strain can be extended to analyses of M > 3 neurons. Above we have taken the simple approach of analyzing larger datasets by considering only three neurons at a time, but other approaches are possible. Perhaps the most natural alternative is to enlarge the pairwise maximum-entropy model (text eq.(3)) to include all third-order terms:

$$p_{\mathit{model}}(\overrightarrow{\sigma };{\mathbf{\alpha }}^{\mathit{model}},{\mathbf{\beta }}^{\mathit{model}},{\mathbf{\gamma }}^{\mathit{model}})=\frac{1}{Z}exp\left(\sum _{j=1}^M{\alpha }_j^{\mathit{model}}{\sigma }_j+\sum _{j<k}^M{\beta }_{jk}^{\mathit{model}}{\sigma }_j{\sigma }_k+\sum _{j<k<l}^M{\gamma }_{jk}^{\mathit{model}}{\sigma }_j{\sigma }_k{\sigma }_l\right).$$ (A31)

The resulting model is again maximum-entropy model, but now subject to the constraints of matching all triplet firing probabilities p(j,k,l) to those observed in the data, as well as matching the singlet firing probabilities p(j) and the pairwise firing probabilities p(j,k). The M (M−1)(M−2)/6 third-order parameters γ_jkl are a comprehensive description of how triplet firing patterns depart from the predictions of the pairwise model. Note that for M>3, there is no explicit formula comparable to eq. (9) for calculating the parameters γ_jkl from the state probabilities p(σ⃗); they must be determined via fitting the third-order model.

In order to preserve the feature that γ can be calculated directly from the state probabilities p(σ⃗), a different generalization is necessary. This generalization is based on including terms up to Mth order in a maximum-entropy model. (At this point it is no longer a “model”; it is guaranteed to fit the set of state probabilities p(σ⃗) exactly (Amari, 2001)). Once terms of all orders are included, the highest-order term (i.e., the coefficient of σ₁σ₂σ₃···σ_M) can be calculated explicitly, as

$${\gamma }_{[M]}\equiv \frac{1}{2^M}\sum _{\overrightarrow{\sigma }}s(\overrightarrow{\sigma })logp(\overrightarrow{\sigma }).$$ (A32)

γ_[M] indicates how the network’s firing patterns differ from those that could be predicted from the interactions up to order M−1. Like γ≡γ_[3], its sign indicates whether there is an excess or a deficit of synchronous events. As is the case for γ, estimation of γ_[M] requires sufficient data so that even the rarest event occurs often enough (e.g., 50 times) for its probability can be accurately estimated. This is likely to be on the edge of practicality for M = 4, and impractical for larger M. We do not advocate estimating γ_[M] unless all firing patterns have been observed many times, and thus, do not address the situation in which the plug-in estimator corresponding to eq. (A32) diverges.