Abstract
A functional model of biological neural networks, called temporal hierarchical probabilistic associative memory (THPAM), is proposed in this paper. THPAM comprises functional models of dendritic trees for encoding inputs to neurons, a first type of neuron for generating spike trains, a second type of neuron for generating graded signals to modulate neurons of the first type, supervised and unsupervised Hebbian learning mechanisms for easy learning and retrieving, an arrangement of dendritic trees for maximizing generalization, hardwiring for rotation-translation-scaling invariance, and feedback connections with different delay durations for neurons to make full use of present and past informations generated by neurons in the same and higher layers. These functional models and their processing operations have many functions of biological neural networks that have not been achieved by other models in the open literature and provide logically coherent answers to many long-standing neuroscientific questions. However, biological justifications of these functional models and their processing operations are required for THPAM to qualify as a macroscopic model (or low-order approximate) of biological neural networks.
Keywords: Neuron model, Hebb learning, Spike train, Unsupervised learning, Dendritic tree model
Introduction
Biological neural networks are known to have such structures as hierarchical networks with feedbacks, neurons, denritic trees and synapses; and perform such functions as supervised and unsupervised Hebbian learning, storing knowledge in synapses, encoding information by dendritic trees, and detecting and recognizing spatial and temporal multiple/hierarchical causes. However, descriptions of these structures and functions are mostly fragmental and sometimes controversial in the literature on neuroscience (Arbib 2003; Dayan and Abbott 2001; Kandel et al. 2000; Koch 1999; Levitan and Kaczmarek 1993; Stuart et al. 2008) (Two examples related with this paper are logic gates vs. low-order polynomials in dendritic processing (Mel 1994), Hebbian vs. not Hebbian in learning (Mel 2002)) and on artificial neural networks (Bishop 2006; Dayan and Abbott 2001; Hawkins 2004; Hecht-Nielsen 2007; Hecht-Nielsen and McKenna 2003; Principe et al. 2000; Rieke et al. 1999; O’Reilly and Munakata 2000; Hassoun 1993; Hinton and Anderson 1989; Kohonen 1988). A single mathematical model that provides an integration of these structures and functions, and explains how the structures interact to perform the functions may shed some light to what processing operations might be required for each structure and function, suggest corresponding experiments to perform, and thereby enhance understanding of biological neural networks as systems whole. In fact, neuroscientists have long hypothesized a common cortical algorithm, and researchers on artificial neural networks have long searched for an ideal learning machine that learns and retrieves easily, detects and recognizes multiple temporal and spatial causes, and generalizes adequately on noisy, distorted, occluded, rotated, translated and scaled patterns. A common cortical algorithm and, more often than not, an ideal learning machine is intended to be a single mathematical model. To the best of this author’s knowledge, the former was first mentioned by Vernon Mountcastle (1978) and the latter was first suggested by John von Neumann (1958).
This paper is intended to provide such a mathematical model. The model, called temporal hierarchical probabilistic associative memory (THPAM), comprises novel models of dendritic trees; neurons communicating with spike trains; a mechanism for unsupervised and supervised learning; a structure for detecting and recognizing noised, distorted and occluded patterns; hard-wiring for detecting and recognizing rotated, translated and scaled patterns; and feedback neural fibers for processing temporal data. Although biological justifications of these models have not been established, these models are logically coherent and integrate into the model, THPAM, of biological neural networks. Before the biological justifications are obained, THPAM can only be termed a functional model rather than a macroscopic model.
Derivation of THPAM is guided by the following four neurobiological postulates:
The biological neural networks are recurrent multilayer networks of neurons.
Most neurons output a spike train.
Knowledge is stored in the synapses between neurons.
Synaptic strengths are adjusted by a version of the Hebb rule of learning. (In his 1949 book, The Organization of Behavior, Donald Hebb posited: “When one cell repeatedly assists in firing another, the axon of the first cell develops synaptic knobs (or enlarges them if they already exist) in contact with the soma of the second cell.” A natural extension of this (alluded to by Hebb as the decay of unused connections) is to decrease the synaptic strength when the source and target neurons are not active at the same time.) [http://www.en.wikipedia.org/wiki/Hebbian_theory].
As a matter of fact, in the development of artificial neural networks, Postulates 1 and 3 led to multilayer perceptrons and recurrent multilayer perceptrons (Rieke et al. 1999; O’Reilly and Munakata 2000; Dayan and Abbott 2001; Hecht-Nielsen and McKenna 2003; Hawkins 2004; Hecht-Nielsen 2007; Principe et al. 2000; Bishop 2006; Haykin 2009), and Postulates 3 and 4 led to associative memories (Kohonen 1988; Hinton and Anderson 1989; Hassoun 1993). However, multilayer perceptrons exclude Postulates 2 and 4; and associative memories exclude Postulate 1. As useful as multilayer perceptrons and associative memories are in engineering, they have limited capabilities and offer little insight into the inner workings of biological neural networks.
The construction of a functional model of biological neural networks based on all the four postulates has broken the barriers confining the multilayer perceptrons and the associative memories. A first contribution of this paper lies in each of the following features of THPAM (temporal hierarchical probabilistic associative memory) that such existing models as the recurrent multilayer perceptron and associative memories do not have:
a recurrent multilayer network learning by the Hebb rule;
fully automated unsupervised and supervised Hebbian learning mechanisms (involving no differentiation, error backpropagation, optimization, iteration, cycling repeatedly through all learning data, or waiting for asymptotic behavior to emerge);
dendritic trees encoding inputs to neurons;
neurons communicating with spike trains carrying subjective probability distributions;
masking matrices facilitating recognition of corrupted, distorted, and occluded patterns; and
feedbacks with different delay durations for fully utilizing temporally and spatially associated information.
A second contribution of this paper lies in the integration of not only the above unique features but also the following additional features in a single model of biological neural networks:
detecting and recognizing multiple/hierarchical causes; and
hard-wired learning for detecting and recognizing rotated, translated and scaled patterns.
A third contribution of this paper is providing logically coherent answers jointly to the following long-standing questions by using a single functional model of biological neural networks:
What is the information that neurons communicate by spike trains?
How do spike trains carry this information?
In what form is this information stored in the synapses? How are the synapses updated to learn this information in supervised learning and unsupervised learning in accordance with the Hebb rule of learning?
How is this information stored in synapses retrieved and converted into spike trains?
How does a biological neural network generalize on corrupted, distorted or occluded input?
What enables a biological neural network to recognize rotated, translated or scaled patterns?
How do the spike generation and travel times affect the network processing?
What are the functions of dendritic nodes and trees? How are dendritic nodes connected into trees to perform their function?
However, we note that even if all its component models are biologically justified, THPAM is only a “first-order approximate” of biological neural networks, which is not intended to explain all the biological structures and phenomena observed in biological neural networks. Some biological structures or phenomena can undoubtedly be found that are seemingly or apparently missing in THPAM. Nevertheless, the 16 numbered list items above are like 16 pieces of a jigsaw puzzle. The fact that they fit together nicely into one piece whole for the first time indicates that THPAM is worth pursuing further as a candidate macroscopic model.
The components and processing operations in THPAM can be viewed as hypotheses about the macroscopic properties of biological neural networks. Some issues that need to be resolved to biologically justify or dismiss these hypotheses are mentioned in this paper. In recent years, we have seen rapid progress in technology for measuring dendritic, synaptic and neuronal quantities, and we expect to see more. It is hoped that those outstanding issues will soon be resolved in one way or another. (It may be appropriate to recall that when it was first published, the special theory of relativity was not more than a set of logically coherent mathematical results. The claims of bizarre space/time relativity and mass-energy conversion had not even been thought of, much less experimentally confirmed. Yet the theory led to experiments, and the bizarre space/time relativity and mass-energy conversion were eventual proven to be true.)
A current major research thrust on learning machines is the development of those with a deep architecture such as the convolutional networks (LeCun et al. 1989, 1998; Simard et al. 2003), deep belief networks (Hinton et al. 2006; Hinton and Salakhutdinov 2006) and deep Boltzmann machines (Salakhutdinov and Hinton 2009). Better versions and good understandings have been reported in (Bengio and LeCun 2007; Ranzato et al. 2007; Bengio et al. 2007; Desjardins and Bengio 2008; Erhan et al. 2010). The deep belief networks and their improved version, the deep Boltzmann machines, can learn without a supervisor by a ingenious technique called greedy layer-wise learning strategy. The convolutional networks capture the spatial topology of the input images and can recognize translated patterns very well. All these deep learning machines have good generalization capabilities for recognizing distorted, rotated and translated patterns. On the well-known and widely used “MNIST Database” of handwritten digits, the deep Boltzmann machine achieved an error rate of 0.95% in recognizing handwritten digits (without using training tricks such as supplementing the data set with lightly transformed versions of the training data) (Salakhutdinov and Hinton 2009). After about 20 years of evolution, the convolutional networks’ latest version, “LeNet-6+ unsupervised training,” achieved a recognition error of 0.39% on the same “MNIST Database” (Bengio and LeCun 2007). Performances of these deep learning machines are expected to continue improving even further, especially when feedback structures are added in them.
To appreciate these performances, we note that the error rate of human performance in recognizing handwritten numerals is 1.56% at about 1 digit per second (Wilkinson et al. 1992) and 0.91% (0.56% rejection and 0.35% error) in two rounds with no time limit in the second round (Geist et al. 1994). Nevertheless, none of the deep learning machines existing in the open literature has any of the first seven features listed above.
Several models of cortical circuits, which attempt to integrate neurobiological findings into a model of the cortex, have been reported (Martin 2002; Granger 2006; Grossberg 2007; George and Hawkins 2009). Martin (2002) states: “It is clear that we simply do not understand much of the detailed structure of cortical microcircuits or their relation to functions.” (Granger 2006) provides a computational instruction set to establish a unified formalism for describing human faculties ranging from perception and learning to reasoning and language. Grossberg (2007) explains how laminar neocortical circuits, which embody two computational paradigms—complementary computing and laminar computing, give rise to biological intelligence. George and Hawkins (2009) describes how Bayesian belief propagation in a spatio-temporal hierarchical model can lead to a mathematical model for cortical circuits. The models of cortical circuits in (Granger 2006; George and Hawkins 2009) exhibit interesting pattern recognition capabilities in certain numerical examples. However, they have not been tested or compared with learning machines on those widely used databases. Granger (2006), Grossberg (2007) contain no numerical results. None of the models of cortical circuits has any of the first six features listed above.
A brief summary of the results on THPAM together with the organization of this paper follows: THPAM can be viewed as an organization of a biological neural network into a recurrent multilayer network of processing units (PUs). Section "A recurrent multilayer network of processing units" briefly describes this network and establishes notations of the inputs and outputs of PUs in the network.
The first two questions are answered in "Information carried by spike trains". It is argued that the ideal informations for neurons to communicate are the subjective probability distributions (SPDs) of the labels of patterns appearing in the receptive domains of neurons. Therefore, we hypothesize that the SPDs are said ideal informations to facilitate our derivation of THPAM. The resulting integrity of THPAM and impossibility to replace SPDs suggests that the hypothesis is likely to be valid. It is further argued that under the four postulates, the SPD is the average frequency of the spikes in the spike train.
A processing unit (PU) is a two-layer pattern recognizer, which learns and generates aforementioned SPDs. To achieve these, the PU uses not-exclusive-or (NXOR) logic gates to transform its input vectors into general orthogonal expansions (GOEs). GOEs are described in "Orthogonal expansion". The transformation by a large number of NXOR gates can be looked upon as a functional model of the dendritic trees of the neurons in the PU.
By a crude version of the Hebb rule, outer products of the GOEs (general orthogonal expansions) and their respective labels are accumulated to form general expansion correlation matrices (GECMs), which are the synaptic strengths stored in the PU (processing unit). GECMs are discussed in "Expansion correlation matrices". Simple multiplication of the GECMs and the GOE of the input pattern and simple manipulation of the resultant products yield the SPD of the label of the input pattern. This generation of SPDs together with an example is given in "Representations of probability distributions".
Each processing unit (PU) uses a masking matrix to automatically select a maximum number of components of its input feature subvector that matches those of a stored feature subvector and determine the SPD of the label involved. The masking matrix and how it works is described in "Masking matrices". The masking matrix can be viewed as mathematical idealization and organization of a large number of overlapped and nested dendritic trees.
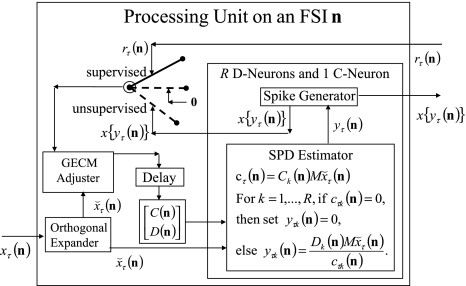
As shown in Fig. 2, a processing unit (PU) comprises an Orthogonal Expander, a label SPD (subjective probability distribution) Estimator, a Spike Generator, a GECMs (general expansion correlation matrices) Adjuster, and a storage of 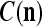 and
and 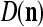 . A PU has essentially two functions, retrieving “point estimates” of the label of a feature subvector
. A PU has essentially two functions, retrieving “point estimates” of the label of a feature subvector 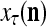 from the memory (i.e., GECMs) and learning a feature subvector and its label that is either provided from outside the PU (in supervised learning) or generated by itself (in unsupervised learning). The structural diagram of an example PU is shown in Fig. 3. Both supervised and unsupervised learning by the PU follow a crude version of the Hebb rule. Spike trains generated by each PU facilitate unsupervised learning. This simple novel modeling of the Hebbian unsupervised learning in biological neural networks is a major underpin of THPAM as a functional model of biological neural networks. The PU and its functions of retrieving and learning are explained in "Processing units and supervised and unsupervised learning".
from the memory (i.e., GECMs) and learning a feature subvector and its label that is either provided from outside the PU (in supervised learning) or generated by itself (in unsupervised learning). The structural diagram of an example PU is shown in Fig. 3. Both supervised and unsupervised learning by the PU follow a crude version of the Hebb rule. Spike trains generated by each PU facilitate unsupervised learning. This simple novel modeling of the Hebbian unsupervised learning in biological neural networks is a major underpin of THPAM as a functional model of biological neural networks. The PU and its functions of retrieving and learning are explained in "Processing units and supervised and unsupervised learning".
Fig. 2.
A processing unit, PU(n), with a feature subvector index n, comprising an Orthogonal Expander, a label SPD (subjective probability distribution) Estimator, a Spike Generator, a GECM (general expansion correlation matrix) Adjuster, and a storage of 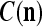 and
and 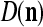 . PU(n) has essentially two functions, retrieving a “point estimate” or a sequence of “point estimates” (i.e., spike trains) of the label of a feature subvector
. PU(n) has essentially two functions, retrieving a “point estimate” or a sequence of “point estimates” (i.e., spike trains) of the label of a feature subvector 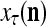 from the memory, GECMs, and learning a feature subvector and its label that is either provided from outside the PU (in supervised learning) or generated by the PU itself (in unsupervised learning)
from the memory, GECMs, and learning a feature subvector and its label that is either provided from outside the PU (in supervised learning) or generated by the PU itself (in unsupervised learning)
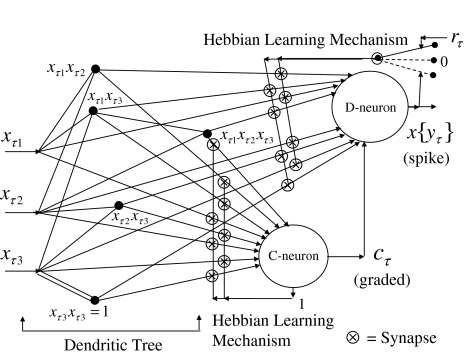
Fig. 3.
The structural diagram of the PU (processing unit) in Example 3 and Example 4. The dendritic tree is the orthogonal expansion of the input feature subvector xτ. The tree nodes are NXORs. A Hebbian learning mechanism for the D-neuron can perform supervised or unsupervised depending on whether the label rτ is provided from outside the PU or is the output x{yτ} of the D-neuron. A “pseudo-Hebbian” learning mechanism for the C-neuron performs only unsupervised learning and always uses 1 in so doing. While the D-neuron output spike trains, the C-neuron generates graded signals to modulate the D-neuron
The brain is known to be able to recognize rotated, translated and scaled patterns. To achieve this, each PU in THPAM learns a rotation, translation and scaling suite of its input feature subvector. Such suites are described in "Learning to recognize rotated, translated or scaled patterns". Some translations, rotation, compression and expansion of an example pattern are shown in Fig. 4.
Fig. 4.
A receptive domain is shown in (a), and a translation in (b). A rotation, compression and expansion of the translation are shown in (c), (d), (e). (f) shows five receptive domains that are translations of one another
Spike trains propagated among the PUs are one of the postulates leading to THPAM. In "Spike trains for each exogenous feature vector", the necessity of spike trains for the foregoing parts of THPAM to work properly is discussed. So is how the spike trains are feedbacked with delays. Typical feedback connections with delays are shown in Fig. 5.
Fig. 5.
Layer l and layer l +2 of an example THPAM with feedback connections from layer l to layer l and from layer l +2 to layer l. For each exogenous feature vector 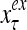 , ζ rounds of retrieving and learning are performed by each PU in THPAM at times, τ + i/ζ,, i = 0, 1,…, ζ −1. The outputs of a PU form R spike trains
, ζ rounds of retrieving and learning are performed by each PU in THPAM at times, τ + i/ζ,, i = 0, 1,…, ζ −1. The outputs of a PU form R spike trains
A recurrent multilayer network of processing units
The temporal hierarchical probabilistic associative memory (THPAM) can be looked upon as an organization of a biological neural network into a recurrent hierarchical network of PUs (processing units). Each PU is a pattern recognizer that comprises dendritic trees, neurons of two types, synaptic weights, and a learning mechanism for updating these synaptic weights by a version of the Hebb rule in unsupervised or supervised learning.
Spike trains propagating through biological neural networks are assumed to be sequences of unipolar binary numbers, 0’s and 1’s. A group of M spike trains can be viewed as a sequence of M-dimensional unipolar binary vectors, vt, t = 1, 2,…, where 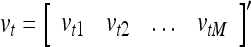 . In this paper, we convert vt, t = 1, 2,…, into a sequence of M-dimensional bipolar binary vectors, xt, t = 1, 2,…, by xtm = 2vtm −1, for m = 1,…, M and t = 1, 2,…. We will use xt to simplify our description and discussion in this paper. Since xt is only a mathematical representation of vt, and xtm can easily be converted back into vtm by vtm = (xtm +1)/2, we also call the components of xt, t = 1, 2,…, spike trains with the understanding that they are mathematical representations of the “biological” spike trains, vt, t = 1, 2,….
. In this paper, we convert vt, t = 1, 2,…, into a sequence of M-dimensional bipolar binary vectors, xt, t = 1, 2,…, by xtm = 2vtm −1, for m = 1,…, M and t = 1, 2,…. We will use xt to simplify our description and discussion in this paper. Since xt is only a mathematical representation of vt, and xtm can easily be converted back into vtm by vtm = (xtm +1)/2, we also call the components of xt, t = 1, 2,…, spike trains with the understanding that they are mathematical representations of the “biological” spike trains, vt, t = 1, 2,….
A vector input to THPAM is called an exogenous feature vector, and a vector input to a layer of PUs is called a feature vector. A feature vector input to a layer usually contains not only feedforwarded outputs from a preceding layer but also feedbacked outputs from the same or higher layers with a time delay. A feature vector may contain components from an exogenous feature vector. For simplicity, we assume that the exogenous feature vector is only input to layer 1 and is thus a subvector of a feature vector input to layer 1. These vectors over time form groups of spike trains.
A subvector of a feature vector that is input to a PU is called a feature subvector. Trace the feedforward connections backward from neurons of a PU to a subvector of the exogenous feature vector. This feature subvector is called the receptive domain of the PU. The collection of neurons in layer l −1 that have a feedforward connection to a neuron in a PU in layer l and the delay devices that hold a feedback for direct input to the same PU in layer l are called the immediate receptive domain of the PU.
The feature vector input to layer l at time or numbering t is denoted by 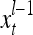 , and the output from the layer at t is denoted by
, and the output from the layer at t is denoted by 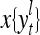 , where
, where 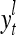 and
and 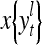 are specified in more detail later in this section. An exogenous feature vector is denoted by
are specified in more detail later in this section. An exogenous feature vector is denoted by 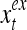 . It is a subvector of
. It is a subvector of 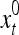 , which may contain feedbacked components. For notational simplicity, the superscript l −1 in
, which may contain feedbacked components. For notational simplicity, the superscript l −1 in 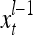 and dependencies on l −1 or l in other symbols are sometimes suppressed in the following when no confusion is expected.
and dependencies on l −1 or l in other symbols are sometimes suppressed in the following when no confusion is expected.
Let xt, t = 1, 2,…, denote a sequence of M-dimensional feature vectors 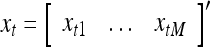 , whose components are ternary numbers. Let
, whose components are ternary numbers. Let 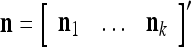 be a subvector
be a subvector  such that
such that 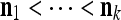 . The subvector
. The subvector 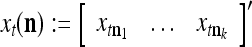 of xt is a feature subvector of the feature vector xt. n is called a feature subvector index (FSI), and
of xt is a feature subvector of the feature vector xt. n is called a feature subvector index (FSI), and 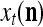 is said to be a feature subvector on the FSI n or have the FSI n. Each PU is associated with a fixed FSI n and denoted by PU
is said to be a feature subvector on the FSI n or have the FSI n. Each PU is associated with a fixed FSI n and denoted by PU 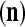 . Using these notations, the sequence of subvectors of xt, t = 1, 2,…, that is input to PU(n) is
. Using these notations, the sequence of subvectors of xt, t = 1, 2,…, that is input to PU(n) is 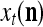 , t = 1, 2,…. The FSI n of a PU usually has subvectors,
, t = 1, 2,…. The FSI n of a PU usually has subvectors, 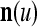 , u = 1,…, U, on which subvectors
, u = 1,…, U, on which subvectors 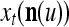 of
of 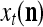 are separately processed by PU(
are separately processed by PU(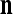 ) at first. The subvectors,
) at first. The subvectors, 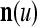 , u = 1,…, U, are not necessarily disjoint, but all inclusive in the sense that every component of n is included in at least one of the subvectors
, u = 1,…, U, are not necessarily disjoint, but all inclusive in the sense that every component of n is included in at least one of the subvectors 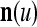 . Moreover, the components of
. Moreover, the components of 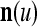 are usually randomly selected from those of n.
are usually randomly selected from those of n.
The PUs in layer l have FSIs (feature subvector indices) denoted by 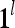 ,
, 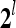 ,…,
,…,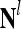 . Upon receiving a feature vector
. Upon receiving a feature vector 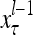 by layer l, the feature subvectors,
by layer l, the feature subvectors, 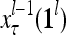 ,
, 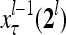 ,…,
,…,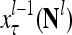 , are formed and processed by the PUs, PU
, are formed and processed by the PUs, PU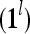 , PU
, PU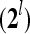 ,…,PU
,…,PU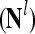 , to compute
, to compute 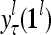 ,
, 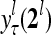 ,…,
,…,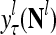 first and then generate
first and then generate 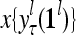 ,
, 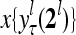 ,…,
,…,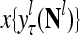 , respectively. Here
, respectively. Here 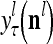 denotes a representation of the subjective probability of the label
denotes a representation of the subjective probability of the label 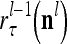 of
of 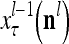 , and
, and 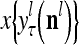 denotes the output of
denotes the output of 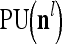 based on
based on 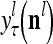 . These representations and outputs are grouped into the representation
. These representations and outputs are grouped into the representation 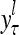 of subjective probabilities and the output vector
of subjective probabilities and the output vector 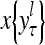 of layer l as follows:
of layer l as follows:
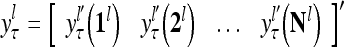 |
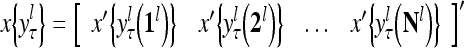 |
The components of a feature vector 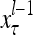 input to layer l at time (or with numbering) τ comprise components of ternary vectors generated by PUs in layer l −1 and those generated at a previous time by PUs in the same layer l or PUs in higher layers with layer numberings l +k for some positive integers k. The time delays may be of different durations.
input to layer l at time (or with numbering) τ comprise components of ternary vectors generated by PUs in layer l −1 and those generated at a previous time by PUs in the same layer l or PUs in higher layers with layer numberings l +k for some positive integers k. The time delays may be of different durations.
Once an exogenous feature vector is received by THPAM, the PUs perform functions of retrieving and/or learning from layer to layer starting with layer 1, the lowest layer. After the PUs in the highest layer, layer L, complete performing their functions, THPAM is said to have completed one round of retrievings and/or learnings (or memory adjustments). For each exogenous feature vector, THPAM will continue to complete a certain number of rounds of retrievings and/or learnings.
We note that retrieving and learning by a PU are performed locally, meaning that only the feature subvector input to the PU and its label are involved in the processing by the PU. In "Orthogonal expansion, Expansion correlation matrices, Representations of probability distributions, 7, 8 and Learning to recognize rotated, translated or scaled patterns", the subscripts t and τ denote the time or numbering of a feature vector or subvector that is input to a layer or a PU, whereas, in "Spike trains for each exogenous feature vector", they denote the time or numbering of an exogenous vector that is input to THPAM.
Information carried by spike trains
Since the immediate receptive domain (defined in Section "A recurrent multilayer network of processing units") of a PU may be shared by more than one cause (or pattern) or may contain parts from more than one cause, and may contain corruption, distortion, occludion or noise from the PU’s receptive domain (defined in Section "A recurrent multilayer network of processing units") or the sensor measurements, image pixels, or sound recordings that are transformed into the receptive domain; the PU’s immediate receptive domain can completely be described or represented only by a probability distribution (or a relative frequency distribution). Therefore, probability distributions are the most desirable information for the PUs to communicate among them. Since probability distributions can be learned by the PU only from “experiences,” they must be subjective probability distributions (SPDs). As will be seen in "Representations of probability distributions", SPDs of the labels of a PU’s immediate receptive domain can be generated by the PU.
There are three possible ways spike trains can carry an SPD: (1) The SPD is carried by the shapes of the spikes. (2) The spike trains at an instant of time form a binary representation of the SPD. (3) The SPD is represented by the frequencies of spikes in spike trains.
Shapes of the spikes cannot be learned by the Hebb rule. Besides, SPDs output from a layer of PU are input to the next layer of PUs. In the process of learning, such SPDs for causes or patterns change. The learning and retrieving mechanisms of PUs must be able to tolerate such changes. It is not clear how changes in spike shapes can be tolerated. Hence, way (1) is ruled out for PUs in THPAM.
In way (2), each SPD is represented by a certain number of bits (or tets), the number depending on the level of accuracy required. The higher the accuracy level, the larger the dimensionality of the output vector of the processing unit.
Again, in the process of learning, the SPD for a certain cause changes. For the learning and retrieving mechanisms to tolerate changes in the codes for the SPDs, the codes must vary gradually as the SPD changes gradually. Such codes are known to consist of large numbers of bits, requiring a large dimensionality of the output vector of the PU. Furthermore, it is not clear how unsupervised learning can be performed with such binary codes by the Hebb rule. For instance, when feature subvectors (or their variants) that have not been learned are input to a PU, the SPDs output by the PU are the same, namely the uniform distribution, which is therefore represented by the same binary code and giving all such input vectors the same label in Hebbian learning, failing to learn to distinguish different feature subvectors without supervision.
Way (3) can be easily obtained by using a pseudo-random number generator to convert a subjective probability into a +1 spike with said subjective probability and a mathematical −1 spike (i.e., biological 0) otherwise. Using this representation, the rate of +1 spikes in a spike train is on the average the subjective probability generated by the PU that outputs the spike train. The dimensionality of this representation is the dimensionality of the label. At any instant of time, the spike trains output by the processing units in a layer form an image of +1, −1 and 0 (for simplicity in certain cases). Gradual change in the subjective probabilities changes the distribution of the ternary digits in the image gradually, which can be tolerated by the use of the masking matrices to be described in "Masking matrices. When a feature subvector (or a variant thereof) that has never been learned is input to a PU, a random label is assigned to the vector. Different new input feature subvectors are usually assigned different labels in unsupervised learning. Occasional coincidences of different feature subvectors assigned with the same label do not cause a problem, if the label is used as part of a feature subvector input to a higher-layer PU. For example, “loo” as a part of “look,” “loot,” and “loop” does not cause confusion.
Therefore, under the four postulates, the subjective probability of a component of a label being +1 is represented by the average spike rate of a spike train. It follows that if the dimensionality of the label is at most R, R neurons form a group whose R spike trains carry the SPD of the label.
Orthogonal expansion
As discussed in the preceding section, SPDs (subjective probability distributions) are the most desirable information for PUs to communicate among themselves. Can SPDs be learned and retrieved by PUs under the four postulates? Subjective probabilities are relative frequencies. We need to find out whether and how relative frequencies can be learned and retrieved.
Orthogonal expansion of ternary vectors from the coding theory (Slepian 1956) plays an important role in learning and retrieving of the relative frequencies. The following example motivates and explains the definition of orthogonal expansion of bipolar vectors.
Example 1 Given 2-dimensional bipolar vectors, 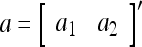 and
and 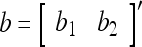 , let
, let
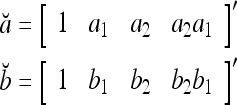 |
By simple algebra, 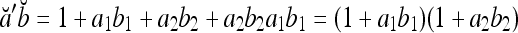 . It follows that
. It follows that 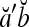 = 1, if a = b; and
= 1, if a = b; and 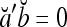 , if a ≠ b.
, if a ≠ b. 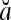 and
and 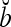 are therefore called orthogonal expansions of a and b. Generalizing this idea of orthogonal expansion yields the following definition.
are therefore called orthogonal expansions of a and b. Generalizing this idea of orthogonal expansion yields the following definition.
Definition Given an m-dimensional ternary vector 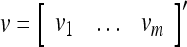 , define
, define 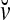 recursively by
recursively by
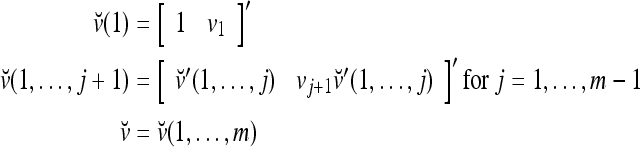 |
1 |
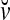 is called the orthogonal expansion of v.
is called the orthogonal expansion of v.
The above definition is justified by the following theorem.
Theorem 1 Let 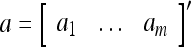 and
and 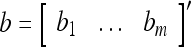 be two m-dimensional ternary vectors. Then the inner product
be two m-dimensional ternary vectors. Then the inner product 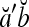 of their orthogonal expansions,
of their orthogonal expansions, 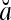 and
and 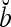 , can be expressed as follows:
, can be expressed as follows:
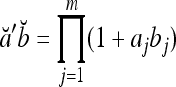 |
2 |
which have the following properties:
If akbk = −1 for some k ∈ {1,…, m}, then
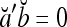 .
.If akbk = 0 for some k ∈ {1,…, m}, then
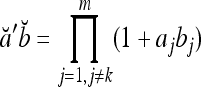 .
.If
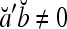 , then
, then 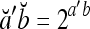 .
.If a and b are bipolar vectors, then
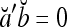 if a ≠ b; and
if a ≠ b; and 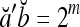 if a = b.
if a = b.
Proof Applying the recursive formula (1), we obtain
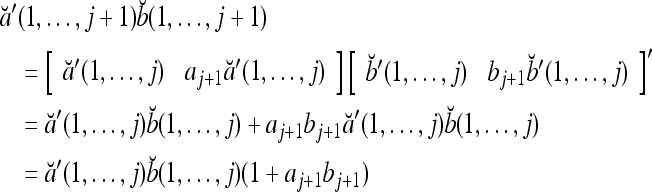 |
The formula in (2) follows. The four properties above are easy consequences.
We remark that if some components of a are set equal to zero to obtain a vector c and the nonzero components of c are all equal to their corresponding components in b, then we still have 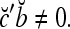 This property is used to construct masking matrices in "Masking matrices" for learning and recognizing corrupted, distorted and occluded patterns and for facilitating generalization on such patterns.
This property is used to construct masking matrices in "Masking matrices" for learning and recognizing corrupted, distorted and occluded patterns and for facilitating generalization on such patterns.
Expansion correlation matrices
In this section, it is shown how orthogonal expansions of subvectors of feature subvectors input to a PU are used to construct synaptic weights in the PU, and how such synaptic weights, in the form of matrices, are adjusted in the PU to learn feature subvectors.
Let the label of 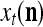 be denoted by
be denoted by 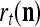 , which is an R-dimensional ternary vector. All subvectors,
, which is an R-dimensional ternary vector. All subvectors, 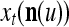 , u = 1,…, U, of
, u = 1,…, U, of 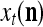 share the same label
share the same label 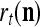 . In supervised learning,
. In supervised learning, 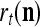 is provided from outside THPAM, and in unsupervised learning,
is provided from outside THPAM, and in unsupervised learning, 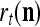 is generated internally in the PU itself.
is generated internally in the PU itself.
The pairs (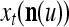 ,
, 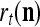 ), t = 1, 2,…, are learned by the PU to form expansion correlation matrices (ECMs),
), t = 1, 2,…, are learned by the PU to form expansion correlation matrices (ECMs), 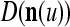 and
and 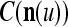 on
on 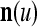 . After the first T pairs are learned, these matrices are
. After the first T pairs are learned, these matrices are
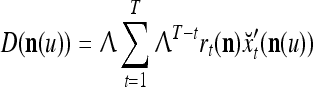 |
3 |
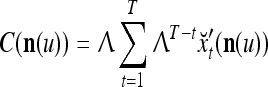 |
4 |
where 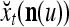 are orthogonal expansions of
are orthogonal expansions of 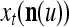 ,
, 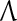 is a scaling constant that is selected to keep all numbers involved in THPAM manageable, λT-tI is a weight matrix, where I is the identity matrix, and λ(0 < λ < 1) is a forgetting factor. Other matrix
is a scaling constant that is selected to keep all numbers involved in THPAM manageable, λT-tI is a weight matrix, where I is the identity matrix, and λ(0 < λ < 1) is a forgetting factor. Other matrix 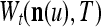 can be used as the weight matrix instead. Note that the matrix
can be used as the weight matrix instead. Note that the matrix 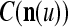 has only one row.
has only one row.
The ECMs, 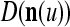 and
and 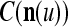 , are adjusted as follows: If
, are adjusted as follows: If 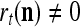 ,
,
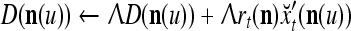 |
5 |
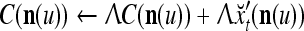 |
6 |
If 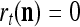 , then
, then 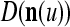 and
and 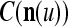 are unchanged. These update formulas are discussed in terms of supervised and unsupervised Hebbian learning in "Processing units and supervised and unsupervised learning". We note here that learning an input feature subvector using the above formulas is instantaneous. No differentiation, backpropagation, iteration, optimization, cycling repeatedly through training material or waiting for asymptotic convergence is required.
are unchanged. These update formulas are discussed in terms of supervised and unsupervised Hebbian learning in "Processing units and supervised and unsupervised learning". We note here that learning an input feature subvector using the above formulas is instantaneous. No differentiation, backpropagation, iteration, optimization, cycling repeatedly through training material or waiting for asymptotic convergence is required.
Orthogonal expansions (OEs) 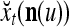 and ECMs,
and ECMs, 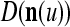 ,
, 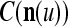 , u = 1,…, U, are assembled into a general orthogonal expansion (GOE)
, u = 1,…, U, are assembled into a general orthogonal expansion (GOE) 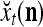 and general expansion correlation matrices (GECMs),
and general expansion correlation matrices (GECMs), 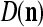 and
and 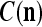 , for PU
, for PU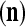 (the PU on the FSI n) as follows:
(the PU on the FSI n) as follows:
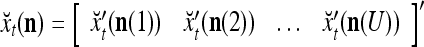 |
7 |
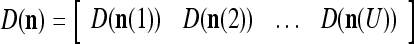 |
8 |
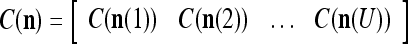 |
9 |
Note that while 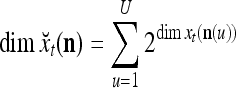 , the dimensionality of the orthogonal expansion of
, the dimensionality of the orthogonal expansion of 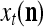 is
is 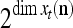 . The former can be made much smaller than the latter by setting
. The former can be made much smaller than the latter by setting 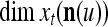 small. If the components of a subvector
small. If the components of a subvector 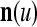 of the feature subvector index (FSI) n are selected from the FSI n at random, then the components of
of the feature subvector index (FSI) n are selected from the FSI n at random, then the components of 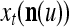 are a random sample of
are a random sample of 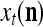 , and
, and  is a “lower-resolution” representation of
is a “lower-resolution” representation of 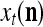 . Hence, a sufficient number U of
. Hence, a sufficient number U of 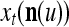 , which may have common components, can sufficiently represent
, which may have common components, can sufficiently represent 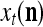 . Since subvectors
. Since subvectors 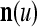 are all inclusive,
are all inclusive, 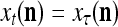 if and only if
if and only if 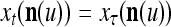 for u = 1,…, U. However, even if
for u = 1,…, U. However, even if 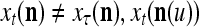 may still be equal to
may still be equal to 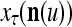 for some values of u. Therefore, the use of the GOE
for some values of u. Therefore, the use of the GOE 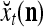 has not only the advantage of having the much smaller dimensionality of
has not only the advantage of having the much smaller dimensionality of 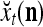 and thereby the much smaller dimensionality of the GECMs, but also the advantage of helping enhance the generalization capability of the PU. This advantage is further discussed in "Masking matrices".
and thereby the much smaller dimensionality of the GECMs, but also the advantage of helping enhance the generalization capability of the PU. This advantage is further discussed in "Masking matrices".
Note that the components of 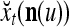 are actually all the products that can be obtained from those of
are actually all the products that can be obtained from those of 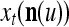 . Each product is obtained by successive two-factor multiplications. For example,
. Each product is obtained by successive two-factor multiplications. For example,
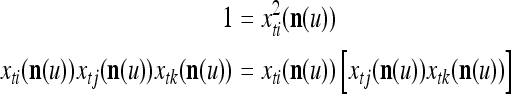 |
Because of commutativity and associativity of multiplication, the successive two-factor multiplication for a component of 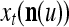 is not unique. Missing or repeating components in
is not unique. Missing or repeating components in 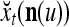 in the GECMs,
in the GECMs, 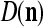 and
and 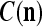 , or in the GOE of the input feature subvectors
, or in the GOE of the input feature subvectors 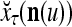 cause only graceful degradation of subjective probability distribution representation
cause only graceful degradation of subjective probability distribution representation 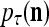 .
.
Each two-factor multiplication can be looked upon as an NXOR operation on the two factors involed. Note that NXOR operations can be replaced with XOR operations without affecting the generation of subjective probability distribution representation 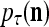 . XOR gates were found in dendritic trees by Zador et al. (1992), Fromherz and Gaede (1993), and the existence of logic gates and low-order polynomials in dendritic trees were discussed in Mel (1994).
. XOR gates were found in dendritic trees by Zador et al. (1992), Fromherz and Gaede (1993), and the existence of logic gates and low-order polynomials in dendritic trees were discussed in Mel (1994).
Representations of probability distributions
How the expansion correlation matrices are used to generate representations of SPDs (subjective probability distributions) is shown in this section. The following example illustrates the idea.
Example 2 Given two different feature subvectors, 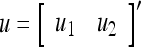 and
and 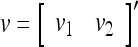 , which are 2-dimensional bipolar vectors. Then,
, which are 2-dimensional bipolar vectors. Then, 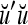 = 4,
= 4, 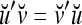 = 0, and
= 0, and 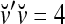 . Let a training data set consists of 8 copies of u with label +1 and 2 copies of u with label −1; and 3 copies of v with label +1 and 27 copies of v with label −1. This training data set is learned by a PU with
. Let a training data set consists of 8 copies of u with label +1 and 2 copies of u with label −1; and 3 copies of v with label +1 and 27 copies of v with label −1. This training data set is learned by a PU with 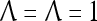 [in (3) and (4)] to form the GECMs (general expansion correlation matrices) with U = 1:
[in (3) and (4)] to form the GECMs (general expansion correlation matrices) with U = 1:
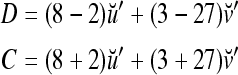 |
By simple algebra, 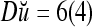 ,
, 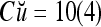 ,
, 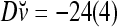 ,
, 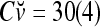 . It follows that
. It follows that 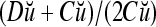 = 8/10 is the relative frequency that u has been learned with label +1 by the PU; and
= 8/10 is the relative frequency that u has been learned with label +1 by the PU; and 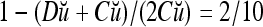 is the relative frequency that u has been learned with label −1 by the PU. Similary,
is the relative frequency that u has been learned with label −1 by the PU. Similary,  is the relative frequency that v has been learned with label +1; and
is the relative frequency that v has been learned with label +1; and 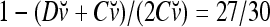 is the relative frequency that v has been learned with label −1.
is the relative frequency that v has been learned with label −1.
We now generalize the idea illustrated in Example 2 in the following. Let us first define the symbols 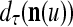 ,
, 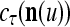 ,
, 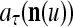 :
:
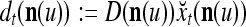 |
10 |
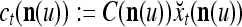 |
11 |
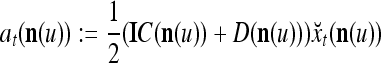 |
12 |
and the symbols 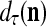 ,
, 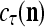 ,
, 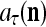 :
:
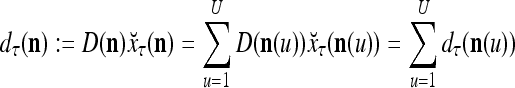 |
13 |
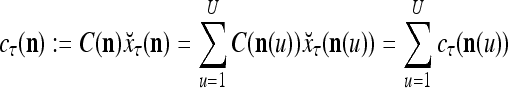 |
14 |
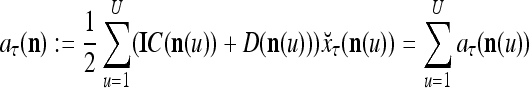 |
15 |
where 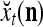 is a general orthogonal expansion (GOE) and
is a general orthogonal expansion (GOE) and 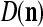 and
and 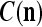 are general expansion correlation matrices (GECMs) for PU
are general expansion correlation matrices (GECMs) for PU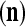 . It is easy to see that
. It is easy to see that 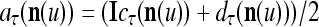 , and
, and 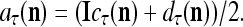
As a special case, Example 2 shows that 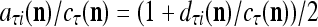 is an approximate of the subjective probability that the i-th component of the label of
is an approximate of the subjective probability that the i-th component of the label of  is +1. The general case is examined in the following.
is +1. The general case is examined in the following.
Assume that all  and
and 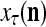 are bipolar binary vectors. By (11), (12), (3) and (4),
are bipolar binary vectors. By (11), (12), (3) and (4),
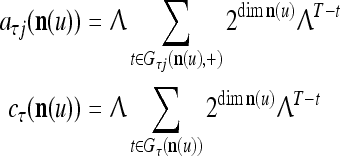 |
where
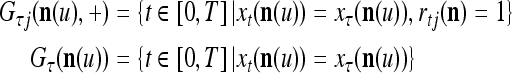 |
Assume further that 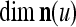 , u = 1,…, U are all the same. Then if
, u = 1,…, U are all the same. Then if 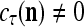 ,
,
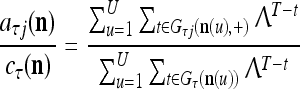 |
16 |
For example, if λ and U are set equal to 1, the above expression becomes
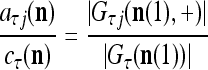 |
where 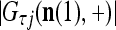 is the number of
is the number of 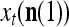 ’s with
’s with 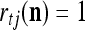 that have been learned and are equal to
that have been learned and are equal to 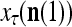 , and
, and 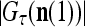 is the number of
is the number of 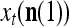 ’s that have been learned and are equal to
’s that have been learned and are equal to 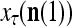 . Hence, the ratio
. Hence, the ratio 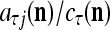 is a relative frequence that the input feature subvector
is a relative frequence that the input feature subvector 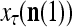 has a label with its j-th component
has a label with its j-th component 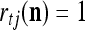 . The example also shows that if λ equal to 1, the memory,
. The example also shows that if λ equal to 1, the memory, 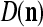 and
and 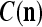 , never degrades. However, in this case, if learning continues, the memory can get saturated, causing memory “overflow.”
, never degrades. However, in this case, if learning continues, the memory can get saturated, causing memory “overflow.”
The closer λ is to 1 and the smaller U is, the closer the above expression (16) approximates the subjective probability that the label 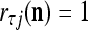 , based on the GECMs,
, based on the GECMs, 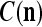 and
and 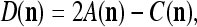 which are constructed with pairs
which are constructed with pairs  t = 1, 2,…, T. Here
t = 1, 2,…, T. Here 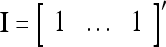 with R components. (note that I is not the identify matrix I.) The forgetting factor λ de-emphasizes past pairs gradually. It does not have to be applied each time a feature subvector
with R components. (note that I is not the identify matrix I.) The forgetting factor λ de-emphasizes past pairs gradually. It does not have to be applied each time a feature subvector 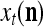 is learned by PU(n) as above. It can be applied once after a certain number, say 1,600 of feature subvectors are learned by the PU.
is learned by PU(n) as above. It can be applied once after a certain number, say 1,600 of feature subvectors are learned by the PU.
All the statements concerning a probability in this paper are statements concerning a subjective probability, and the word “subjective” is sometimes omitted. If 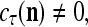 then
then 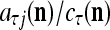 is approximately the probability
is approximately the probability 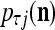 that the j-th component
that the j-th component 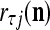 of the label
of the label 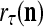 of
of 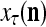 is +1 based on
is +1 based on 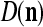 and
and 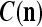 . If
. If 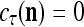 , then we set
, then we set 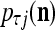 = 1/2. The vector
= 1/2. The vector
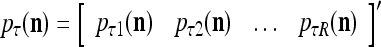 |
is a representation of a probability distribution of the label 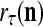 of the feature subvector
of the feature subvector 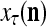 input to PU(n). Since
input to PU(n). Since  , if
, if 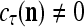 , the ratio
, the ratio 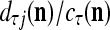 is equal to
is equal to 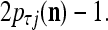 If
If 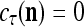 , set 2
, set 2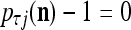 . Denote
. Denote 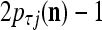 by
by 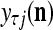 . Then the vector
. Then the vector 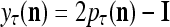 satisfies
satisfies
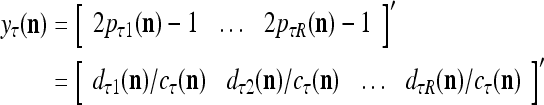 |
and is also a representation of a probability distribution of the label 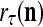 of the feature subvector
of the feature subvector 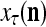 . Here,
. Here, 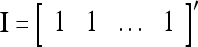 .
.
A point estimate of the label 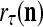 can be obtained by converting each component
can be obtained by converting each component 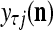 of
of 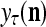 into a ternary number
into a ternary number 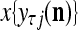 by the following steps: For k = 1, R, set
by the following steps: For k = 1, R, set 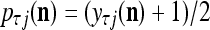 , and generate a pseudo-random number in accordance with the probability distribution of a random variable
, and generate a pseudo-random number in accordance with the probability distribution of a random variable 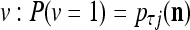 and
and 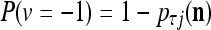 , and set
, and set 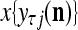 equal to the resultant pseudo-random number. Assemble
equal to the resultant pseudo-random number. Assemble 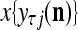 , j = 1,…, R, into
, j = 1,…, R, into 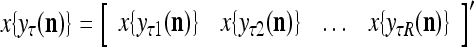 , which is a point estimate of the label
, which is a point estimate of the label 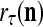 .
.
Masking matrices
Let a feature subvector that deviates from each of a group of feature subvectors that have been learned by the PU due to corruption, distortion or occlusion be presented to the PU. If the PU is able to automatically find the largest subvector of the presented subvector that matches at least one subvector among the group and generate the SPD of the label of the largest subvector, the PU is said to have a maximal generalization capability. This capability is achieved by the use of masking matrices described in this section.
Let a subvector 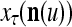 be a slightly different (e.g., corrupted, distorted, occluded) version of
be a slightly different (e.g., corrupted, distorted, occluded) version of 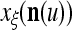 , which is one of the subvectors,
, which is one of the subvectors, 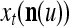 , t = 1, 2,…, T, stored in ECMs,
, t = 1, 2,…, T, stored in ECMs, 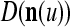 and
and 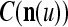 , on
, on 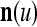 . Assume that
. Assume that 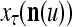 is very different from other subvectors stored in the ECMs. Since
is very different from other subvectors stored in the ECMs. Since 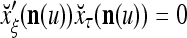 , the information stored in
, the information stored in 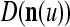 and
and 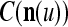 about the label
about the label 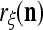 cannot be obtained from
cannot be obtained from 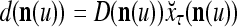 and
and 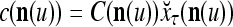 . This is viewed as failure of
. This is viewed as failure of 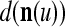 and
and 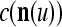 to generalize. Because of property 2 in Theorem 1, if the corrupted, distorted and occluded components in
to generalize. Because of property 2 in Theorem 1, if the corrupted, distorted and occluded components in 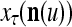 are set equal to zero, then the information stored in the ECMs about the label
are set equal to zero, then the information stored in the ECMs about the label 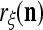 can be obtained in part from the remaining components of
can be obtained in part from the remaining components of 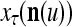 . This observation motivated masking matrices.
. This observation motivated masking matrices.
Let us denote the vector 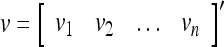 with its i1-th, i2-th,…, and ij-th components set equal to 0 by
with its i1-th, i2-th,…, and ij-th components set equal to 0 by 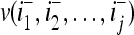 , where 1 ≤ i1 < i2 < ⋅⋅⋅ < ij ≤ n. For example, if
, where 1 ≤ i1 < i2 < ⋅⋅⋅ < ij ≤ n. For example, if 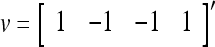 , then
, then 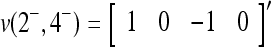 . Denote the n-dimensional vector
. Denote the n-dimensional vector 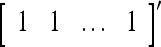 by I (not the identity matrix I) and denoting the orthogonal expansion of v(i−1, i−2,…, i−j) by
by I (not the identity matrix I) and denoting the orthogonal expansion of v(i−1, i−2,…, i−j) by 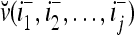 . We note that v(i−1, i−2,…, i−j) = diag(I(i−1, i−2,…, i−j)) v and
. We note that v(i−1, i−2,…, i−j) = diag(I(i−1, i−2,…, i−j)) v and 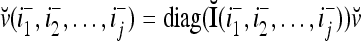 , where
, where 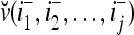 and
and 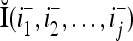 denote the orthogonal expansions of v(i−1, i−2,…, i−j) and
denote the orthogonal expansions of v(i−1, i−2,…, i−j) and 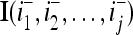 respectively (not the orthogonal expansions of v and I with their i1-th, i2-th, and ij-th components set equal to 0).
respectively (not the orthogonal expansions of v and I with their i1-th, i2-th, and ij-th components set equal to 0).
Using these notations, a feature subvector 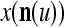 with its i1-th, i2-th, and ij-th components set equal to 0 is
with its i1-th, i2-th, and ij-th components set equal to 0 is 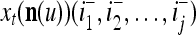 , and the orthogonal expansion of
, and the orthogonal expansion of 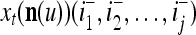 is diag
is diag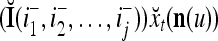 . Hence, the matrix diag
. Hence, the matrix diag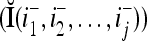 , as a matrix transformation, sets the i1-th, i2-th, and ij-th components of xt(n(u)) equal to zero in transforming
, as a matrix transformation, sets the i1-th, i2-th, and ij-th components of xt(n(u)) equal to zero in transforming 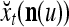 (i.e., in diag
(i.e., in diag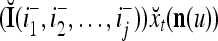 ).
).
Two important properties of the matrix diag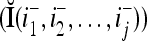 are the following:
are the following:
If diag
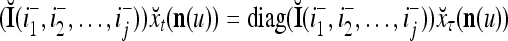 , then
, then 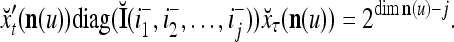
If diag
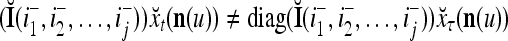 , then
, then 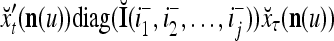 = 0.
= 0.
The following example illustrates how such matrices diag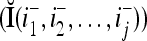 can be used by a PU (processing unit) to generalize.
can be used by a PU (processing unit) to generalize.
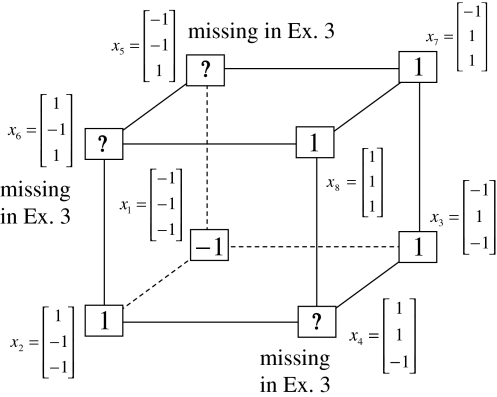
Example 3 Consider a cube shown in Fig. 1. The coordinate vectors of its eight vertices, xt, t = 1, 2,…, 8, and their corresponding labels, rt, t = 1, 2,…, 8, are shown at the vertices and in the squares, respectively, where the question marks indicate unknown labels. The training data consists of the pairs, (xt, rt), t = 1, 2, 3, 7, 8.
Fig. 1.
Data for training and testing the PU (processing unit) in Example 3 and Example 4 are shown as the vertices of a cube. Their bipolar binary labels are the numbers or question marks for unknown labels in the squares at the vertices. x4, x5, x6 are unavailable in the data set for Example 3. They are learned one by one without supervision (i.e., with labels generated by the PU) in Example 4
The pairs, 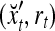 , t = 1, 2, 3, 7, 8, are listed as rows in the following table:
, t = 1, 2, 3, 7, 8, are listed as rows in the following table:
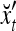 |
1 | xt1 | xt2 | xt2xt1 | xt3 | xt3xt1 | xt3xt2 | xt3xt2xt1 | rt |
|---|---|---|---|---|---|---|---|---|---|
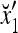 |
1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | −1 |
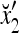 |
1 | 1 | −1 | −1 | −1 | −1 | 1 | 1 | 1 |
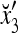 |
1 | −1 | 1 | −1 | −1 | 1 | −1 | 1 | 1 |
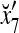 |
1 | −1 | 1 | −1 | 1 | −1 | 1 | −1 | 1 |
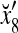 |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Assume U = 1 and 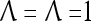 in (5), (6), (3) and (4) in a PU (processing unit). The general expansion correlation matrices, D and C, of the PU is the following:
in (5), (6), (3) and (4) in a PU (processing unit). The general expansion correlation matrices, D and C, of the PU is the following:
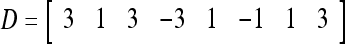 |
17 |
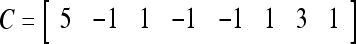 |
18 |
Let
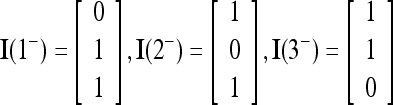 |
Orthogonal expansion of them yields
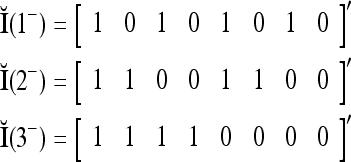 |
We introduce the following matrix
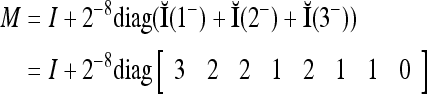 |
19 |
where the weight 2−8 is selected to de-emphasize the effect of the second term above as compared with the first term. The orthogonal expansion of the three vertices of the cube in Fig. 1 that are not included in the training data are listed as follows:
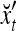 |
1 | xt1 | xt2 | xt2xt1 | xt3 | xt3xt1 | xt3xt2 | xt3xt2xt1 |
|---|---|---|---|---|---|---|---|---|
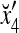 |
1 | 1 | 1 | 1 | −1 | −1 | −1 | −1 |
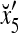 |
1 | −1 | −1 | 1 | 1 | −1 | −1 | 1 |
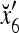 |
1 | 1 | −1 | −1 | 1 | 1 | −1 | −1 |
From the following examples,
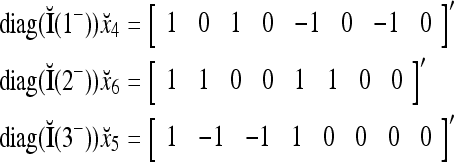 |
we see that diag sets the k-th component xtk of
sets the k-th component xtk of 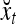 equal to 0 for t = 1,…, 8, k = 1, 2, 3.
equal to 0 for t = 1,…, 8, k = 1, 2, 3.
Simple matrix-vector multiplication yields 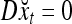 and
and 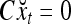 for t = 4, 5, 6. Hence no information is provided on xt by
for t = 4, 5, 6. Hence no information is provided on xt by 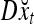 and
and 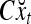 for t = 4, 5, 6. This shows that if xt has not been learned, then no information on it is provided by the general expansion matrices. Recall that if
for t = 4, 5, 6. This shows that if xt has not been learned, then no information on it is provided by the general expansion matrices. Recall that if 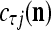 ≠ 0, the subjective probability
≠ 0, the subjective probability  , where
, where 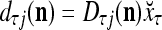 and
and 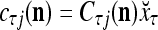 . With M, we will use
. With M, we will use 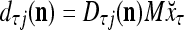 and
and 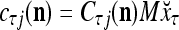 instead.
instead.
Assume that x1 is input to the PU with the above D and C. By matrix multiplication,
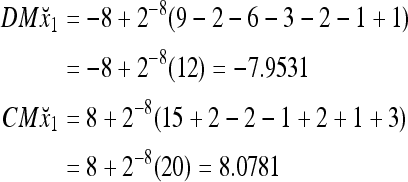 |
Then the subjective probability that the label of x4 is 1 is 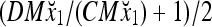 = 0.0077, and the subjective probability that the label of x4 is −1 is 0.9923. Note that x1 with a label of −1 has been learned. The subjective probability that the label of x4 is −1 should be 1. The use of M causes a very small amount of error to the subjective probability, which can be adjusted by changing the weight, 2−8.
= 0.0077, and the subjective probability that the label of x4 is −1 is 0.9923. Note that x1 with a label of −1 has been learned. The subjective probability that the label of x4 is −1 should be 1. The use of M causes a very small amount of error to the subjective probability, which can be adjusted by changing the weight, 2−8.
Assume that x4 is input to the PU with the above D and C. By matrix multiplication,
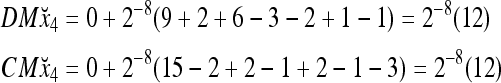 |
Then the subjective probability that the label of x4 is 1 is 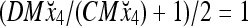 . From Fig. 1, we see that all the three vertices neighboring x4 have been learned and have a label of 1. It is a good generalization that a label of 1 is assigned to x4.
. From Fig. 1, we see that all the three vertices neighboring x4 have been learned and have a label of 1. It is a good generalization that a label of 1 is assigned to x4.
Assume that x6 is presented to the same PU. By matrix multiplication,
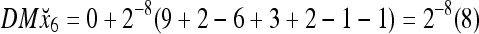 |
20 |
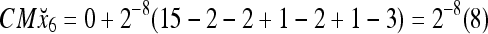 |
21 |
Then the subjective probability that the label of x6 is 1 is 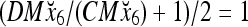 . From Fig. 1, we see that only two vertices neighboring x4 have been learned, and they both have a label of 1. It is a good generalization that a label of 1 is assigned to x6.
. From Fig. 1, we see that only two vertices neighboring x4 have been learned, and they both have a label of 1. It is a good generalization that a label of 1 is assigned to x6.
Assume that x5 is input to the same PU. By matrix multiplication,
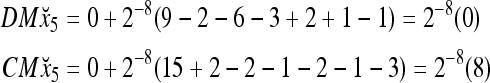 |
Then the subjective probability that the label of x5 is 1 is 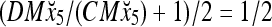 . From Fig. 1, we see that only two vertices neighboring x4 have been learned, and one of them has a label of 1, and the other has a label of −1. No generalization is possible. A label of 1 is assigned to x6 with a subjective probability of 1/2 and that a label of −1 is assigned to x6 with equal subjective probability.
. From Fig. 1, we see that only two vertices neighboring x4 have been learned, and one of them has a label of 1, and the other has a label of −1. No generalization is possible. A label of 1 is assigned to x6 with a subjective probability of 1/2 and that a label of −1 is assigned to x6 with equal subjective probability.
In the general case, we combine all such matrices diag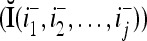 that set less than or equal to a selected positive integer
that set less than or equal to a selected positive integer 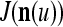 of components of
of components of 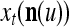 equal to zero into the following masking matrix
equal to zero into the following masking matrix
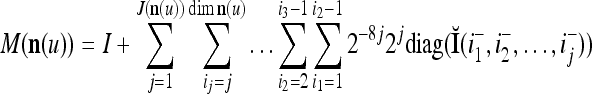 |
22 |
where 2j is used to compensate for the factor 2−j in 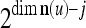 in the important property stated above, and 2−8j is an example weight selected to differentiate between different levels j of maskings. What this weight really is in biological neural networks needs to be found by biological experiments. So is the positive integer
in the important property stated above, and 2−8j is an example weight selected to differentiate between different levels j of maskings. What this weight really is in biological neural networks needs to be found by biological experiments. So is the positive integer 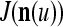 .
.
Let us denote 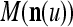 by M here for abbreviation. Note that for k = 1,…, R, we have the following:
by M here for abbreviation. Note that for k = 1,…, R, we have the following:
- If
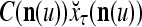 ≠ 0, then
≠ 0, then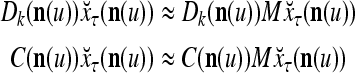
- If
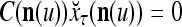 , but
, but  , then
, then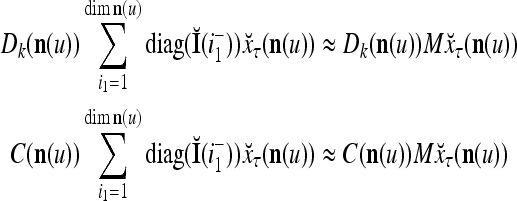
- If
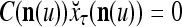 ,
, 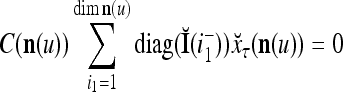 , but
, but 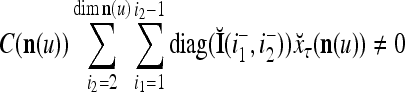 , then
, then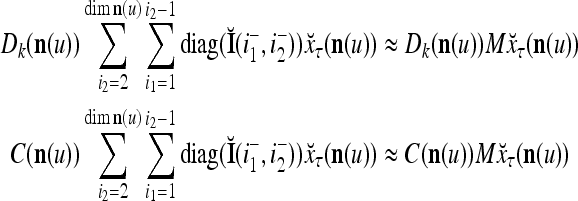
Continuing in this manner, it is seen that 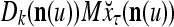 and
and 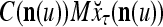 always use the greatest number of uncorrupted, undistorted or unoccluded components of
always use the greatest number of uncorrupted, undistorted or unoccluded components of 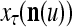 in estimating
in estimating 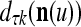 ,
, 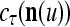 , and
, and 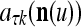 .
.
Corresponding to 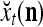 ,
, 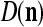 and
and 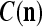 defined in (7), (8) and (9), a general masking matrix is defined as follows:
defined in (7), (8) and (9), a general masking matrix is defined as follows:
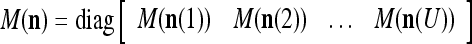 |
23 |
where the right side is a matrix with 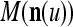 , u = 1, 2, U, as diagonal blocks and zero elsewhere.
, u = 1, 2, U, as diagonal blocks and zero elsewhere.
If the masking matrix 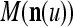 is used, the symbols
is used, the symbols 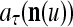 ,
, 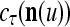 ,
, 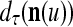 are defined as follows:
are defined as follows:
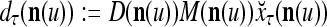 |
24 |
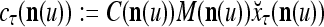 |
25 |
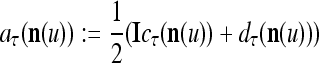 |
26 |
With the masking matrix  , the symbols
, the symbols 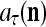 ,
, 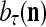 ,
, 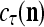 ,
, 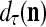 are in turn defined as follows:
are in turn defined as follows:
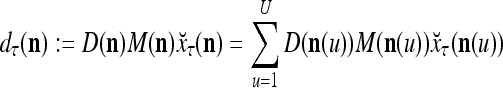 |
27 |
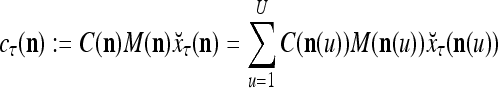 |
28 |
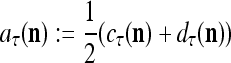 |
29 |
where 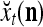 is a general orthogonal expansion (GOE) and
is a general orthogonal expansion (GOE) and 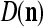 and
and 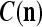 are general expansion correlation matrices (GECMs) for PU
are general expansion correlation matrices (GECMs) for PU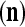 . It follows that
. It follows that
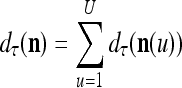 |
30 |
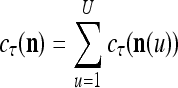 |
31 |
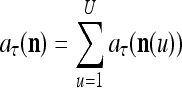 |
32 |
It is easy to see that 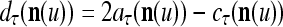 , and
, and 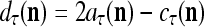 . If
. If 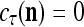 , then we set
, then we set 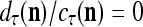 . If
. If 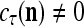 , then
, then 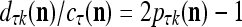 , where
, where 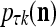 is the probability that the k-th component
is the probability that the k-th component 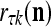 of the label
of the label 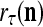 of
of 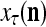 is +1 based on
is +1 based on 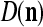 and
and 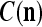 . It follows that
. It follows that
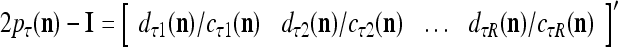 |
is a representation of a probability distribution of the label 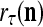 of
of 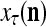 .
.
It is mentioned in "Expansion correlation matrices" that selecting sufficiently small subvectors 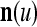 , u = 1,…, U, has the advantage of making
, u = 1,…, U, has the advantage of making 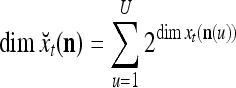 sufficiently small. The formula (22) shows that selecting sufficiently small subvectors
sufficiently small. The formula (22) shows that selecting sufficiently small subvectors 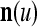 , u = 1,…, U, also has the advantage of making the number of terms in the formula sufficiently small. The use of subvectors
, u = 1,…, U, also has the advantage of making the number of terms in the formula sufficiently small. The use of subvectors 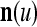 , u = 1,…, U, has another way to help enhancing the generalization capability of PU
, u = 1,…, U, has another way to help enhancing the generalization capability of PU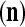 : If the number of corrupted, distorted or occluded components of a subvector
: If the number of corrupted, distorted or occluded components of a subvector 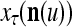 of
of 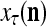 exceeds
exceeds 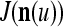 , then
, then 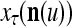 does not contribute to
does not contribute to 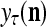 or the output
or the output 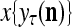 of PU(n). This eliminates the effect of a subvector
of PU(n). This eliminates the effect of a subvector 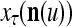 that contains too many errors and allows PU(n) to produce a better estimate of the subjective probability distribution of a label on better subvectors of
that contains too many errors and allows PU(n) to produce a better estimate of the subjective probability distribution of a label on better subvectors of 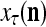 .
.
If some terms in (22) are missing, PU(n) suffers only graceful degradation of its generalization capability. We hypothesize that a masking matrix is a mathematical idealization and organization of a large number of nested and overlapped dendritic trees.
Processing units and supervised and unsupervised learning
We are ready to assemble a PU (processing unit) and see how supervised and unsupervised learning are performed. A processing unit, PU(n), on a feature subvector index n, is shown in Fig. 2. It has essentially two functions, retrieving a “point estimate” of the label of a feature subvector 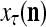 from the memory (i.e., GECMs) and learning a feature subvector and its label that is either provided from outside the PU (in supervised learning) or generated by itself (in unsupervised learning). PU(n) comprises an Orthogonal Expander, a label SPD (subjective probability distribution) Estimator, a Spike Generator, a GECM (general expansion correlation matrix) Adjuster, and a storage of the GECMs, C(n) and
from the memory (i.e., GECMs) and learning a feature subvector and its label that is either provided from outside the PU (in supervised learning) or generated by itself (in unsupervised learning). PU(n) comprises an Orthogonal Expander, a label SPD (subjective probability distribution) Estimator, a Spike Generator, a GECM (general expansion correlation matrix) Adjuster, and a storage of the GECMs, C(n) and 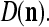 The Orthogonal Expander models dendritic trees with NXORs (or XORs) as tree nodes,
The Orthogonal Expander models dendritic trees with NXORs (or XORs) as tree nodes, 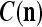 and
and 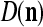 model the synaptic weights in a biological neural network, and the label SPD Estimator and Spike Generator jointly model R neurons of one type and 1 neuron of another type in the same layer of a biological neural network. These two types of neuron will be described below.
model the synaptic weights in a biological neural network, and the label SPD Estimator and Spike Generator jointly model R neurons of one type and 1 neuron of another type in the same layer of a biological neural network. These two types of neuron will be described below.
During retrieving, a feature subvector 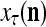 on the FSI (feature subvector index) n is first expanded into a GOE (general orthogonal expansion)
on the FSI (feature subvector index) n is first expanded into a GOE (general orthogonal expansion) 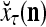 by the Orthogonal Expander.
by the Orthogonal Expander. 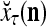 is then processed by the SPD (subjective probability distribution) Estimator, using the GECMs (general expansion correlation matrices),
is then processed by the SPD (subjective probability distribution) Estimator, using the GECMs (general expansion correlation matrices), 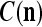 and
and 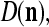 to obtain a representation
to obtain a representation 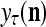 of an SPD of the label of the feature subvector
of an SPD of the label of the feature subvector 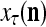 . The Spike Generator converts
. The Spike Generator converts 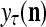 into a ternary vector
into a ternary vector 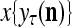 , which is the output of the PU. This process of generating
, which is the output of the PU. This process of generating 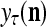 and
and 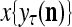 by PU(n) is called retrieval of a label of the feature subvector
by PU(n) is called retrieval of a label of the feature subvector 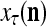 by PU(n).
by PU(n).
The SPD Estimator and Spike Generator may be viewed as R neurons of one type and one neuron of another type that jointly output a “point estimate” 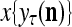 of the label of
of the label of 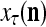 . The former type is called D-neurons and the latter C-neuron. The C-neuron does a simple multiplication
. The former type is called D-neurons and the latter C-neuron. The C-neuron does a simple multiplication
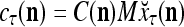 |
For j = 1,…, R, D-neuron j performs the following tasks:
Input
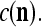 If
If 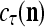 = 0, set
= 0, set 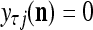 ; else compute
; else compute 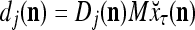 and set
and set 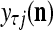 equal to
equal to 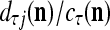 .
.Compute the subjective probability
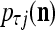 = (
= (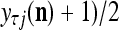 that the j-th component of the label of
that the j-th component of the label of 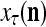 is +1.
is +1.Generate a pseudo-random number in accordance with the probability distribution of a random variable
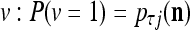 and
and 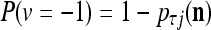 , and set
, and set 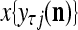 equal to the resultant pseudo-random number. This is a point estimate of the j-th component of the label of
equal to the resultant pseudo-random number. This is a point estimate of the j-th component of the label of 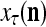 .
.
Figure 2 provides a “flow chart” of the general PU. A structural diagram of an example PU is shown in Fig. 3, where the PU is that of Example 3. Input to the PU is the feature subvector 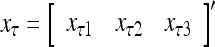 . An dendritic tree encode xτ into the orthogonal expansion
. An dendritic tree encode xτ into the orthogonal expansion 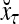 , whose components are multiplied by the synapses, denoted by ⊗, and the resultant multiples are distributed to the D-neuron and C-neuron. In learning, the general expansion correlation matrices, D and C, are incremented by
, whose components are multiplied by the synapses, denoted by ⊗, and the resultant multiples are distributed to the D-neuron and C-neuron. In learning, the general expansion correlation matrices, D and C, are incremented by  and
and 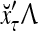 , respectively. In supervised learning of D, rτ is provided from outside the PU. In unsupervised learning of D, rτ is set equal to x{yτ}, which is generated by D-neurons. C is the accumulation of
, respectively. In supervised learning of D, rτ is provided from outside the PU. In unsupervised learning of D, rτ is set equal to x{yτ}, which is generated by D-neurons. C is the accumulation of 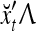 . A possible way to perform this accumulation by the Hebb rule is for the C-neuron to have a second output that is always equal to the constant 1.
. A possible way to perform this accumulation by the Hebb rule is for the C-neuron to have a second output that is always equal to the constant 1.
If a label 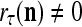 of
of 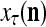 from outside the PU is available for learning, and learning
from outside the PU is available for learning, and learning 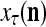 and
and 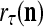 is wanted, supervised learning is performed by the PU. In supervised learning, the class label
is wanted, supervised learning is performed by the PU. In supervised learning, the class label 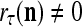 is received through a lever represented by a thick solid line with a solid dot at its end in Fig. 2 by the GECM Adjuster, which receives also
is received through a lever represented by a thick solid line with a solid dot at its end in Fig. 2 by the GECM Adjuster, which receives also 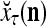 from the Orthogonal Expander and adjusts ECMs by formulas (5)–(6) and assembles the resultant ECMs,
from the Orthogonal Expander and adjusts ECMs by formulas (5)–(6) and assembles the resultant ECMs, 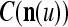 and
and 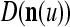 , u = 1,…,U, into general ECMs,
, u = 1,…,U, into general ECMs, 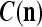 and
and 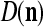 , by (8) and (9).
, by (8) and (9).
These 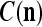 and
and 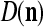 are then stored, after a one-numbering delay (or a unit-time delay), in the storage, from which they are sent to the SPD Estimator.
are then stored, after a one-numbering delay (or a unit-time delay), in the storage, from which they are sent to the SPD Estimator.
If a label 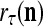 of
of 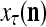 from outside the PU is unavailable but learning
from outside the PU is unavailable but learning 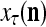 is wanted, unsupervised learning is performed by the PU. In this case, the lever in Fig. 2 should be in the unsupervised training position represented by the lower dashed line with a solid dot at its end in Fig. 2. The feature subvector
is wanted, unsupervised learning is performed by the PU. In this case, the lever in Fig. 2 should be in the unsupervised training position represented by the lower dashed line with a solid dot at its end in Fig. 2. The feature subvector 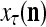 is first processed by the Orthogonal Expander, SPD Estimator, and Spike Generator as in performing retrieval described above. The resultant bipolar vector
is first processed by the Orthogonal Expander, SPD Estimator, and Spike Generator as in performing retrieval described above. The resultant bipolar vector 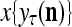 , which is a point estimate of the lable of
, which is a point estimate of the lable of 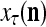 is received, through the lever in the unsupervised training position, and used by the GECM Adjuster as the label
is received, through the lever in the unsupervised training position, and used by the GECM Adjuster as the label 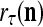 of
of 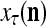 . The GECM Adjuster receives
. The GECM Adjuster receives 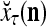 also and adjusts GECMs,
also and adjusts GECMs, 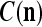 and
and 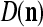 , using the update formulas, (5)–(6), in the same way as in supervised learning.
, using the update formulas, (5)–(6), in the same way as in supervised learning.
Let us now see how a “vocabulary” is created by the PU through unsupervised learning: If a feature subvector 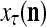 or a slightly different version of it has not been learned by PU
or a slightly different version of it has not been learned by PU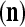 , and
, and 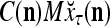 = 0; then
= 0; then 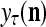 = 0 and
= 0 and 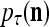 = (1/2)I, where I =
= (1/2)I, where I = 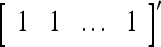 . The SPD Estimator and Spike Generator uses this probability vector to generate a purely random label
. The SPD Estimator and Spike Generator uses this probability vector to generate a purely random label 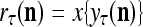 . Once this
. Once this 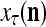 has been learned and stored in
has been learned and stored in 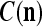 and
and 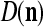 , if
, if 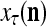 is input to PU(n) and to be learned without supervision for the second time, then
is input to PU(n) and to be learned without supervision for the second time, then 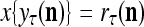 and one more copy of the pair (
and one more copy of the pair (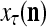 ,
, 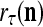 ) is included in
) is included in 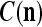 and
and 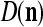 .
.
If a feature subvector 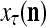 or a slightly different version of it has been learned by PU(n) with different labels for different numbers of times, then
or a slightly different version of it has been learned by PU(n) with different labels for different numbers of times, then 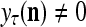 and
and 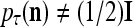 . For example, assume that two labels,
. For example, assume that two labels, 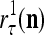 and
and 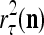 of the same feature subvector
of the same feature subvector 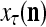 have been learned with relative frequencies, 0.7 and 0.3, respectively. Since these two labels may have common components, the point estimate of the label resembles
have been learned with relative frequencies, 0.7 and 0.3, respectively. Since these two labels may have common components, the point estimate of the label resembles 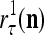 with a probability of higher that 70% and resembles
with a probability of higher that 70% and resembles 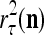 with a probability of greater than 30%. To learn this probability, a number of such point estimates need to be learned. This is one of the reasons for each PU to generate multiple spikes for each exogenous feature vector, which is to be discussed in "Spike trains for each exogenous feature vector".
with a probability of greater than 30%. To learn this probability, a number of such point estimates need to be learned. This is one of the reasons for each PU to generate multiple spikes for each exogenous feature vector, which is to be discussed in "Spike trains for each exogenous feature vector".
If no learning is to be performed by PU(n), the lever represented by a thick solid line with a solid dot in Fig. 2 is placed in the neutral position, through which 0 is sent as the label 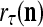 of
of 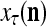 to the GECM Adjuster, which then keeps
to the GECM Adjuster, which then keeps 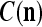 and
and 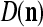 unchanged. Here is a condition for setting
unchanged. Here is a condition for setting 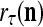 = 0 to skip learning (supervised or unsupervies): If
= 0 to skip learning (supervised or unsupervies): If 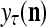 generated by a PU’s estimation means in retrieving is a bipolar vector or sufficiently close to a bipolar vector by some criterion, which indicates that the input feature subvector
generated by a PU’s estimation means in retrieving is a bipolar vector or sufficiently close to a bipolar vector by some criterion, which indicates that the input feature subvector 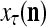 is adequately learned, then the lever is placed in the middle position and no learning is performed. This avoids “saturating” the expansion correlation matrices with too many copies of one feature subvector and its label.
is adequately learned, then the lever is placed in the middle position and no learning is performed. This avoids “saturating” the expansion correlation matrices with too many copies of one feature subvector and its label.
We note that a well-known unsupervised learning method based on a kind of Hebb rule is the Oja learning algorithm that generates the principal components of the input vectors (Oja 1982). Oja’s method gets the principal components only asymptotically and the principal components must taper down fast enough, which is true only if the input vectors do not have too many major features.
We use the PU of Example 3 to illustrate unsupervised learning in the following example.
Example 4 In this example, the PU in Example 3 with D, C, M in (17), (18), (19) will learn x6 and then x5 without supervision.
Recall that
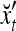 |
1 | xt1 | xt2 | xt2xt1 | xt3 | xt3xt1 | xt3xt2 | xt3xt2xt1 |
|---|---|---|---|---|---|---|---|---|
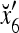 |
1 | 1 | −1 | −1 | 1 | 1 | −1 | −1 |
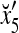 |
1 | −1 | −1 | 1 | 1 | −1 | −1 | 1 |
and
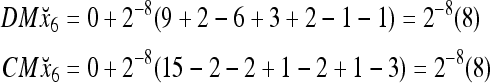 |
and the subjective probability that the label of x6 is 1 is 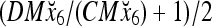 = 1. Hence,
= 1. Hence, 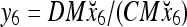 = 1 and thus the spike x{y6} generated by the PU is 1. To learn x6 without supervision, the GECM adjuster in Fig. 2 (i.e., Hebbian learning mechanism in Fig. 3) uses this spike as r6 in (5) and (6) and updates D and C in (17) and (18) into
= 1 and thus the spike x{y6} generated by the PU is 1. To learn x6 without supervision, the GECM adjuster in Fig. 2 (i.e., Hebbian learning mechanism in Fig. 3) uses this spike as r6 in (5) and (6) and updates D and C in (17) and (18) into
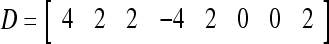 |
33 |
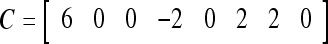 |
34 |
To learn x5, the SPD Estimator in Fig. 2 (i.e., D- and C-neurons in Fig. 3) first processes it to obtain
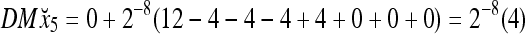 |
35 |
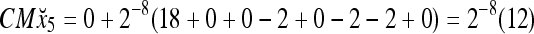 |
36 |
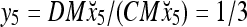 . The Spike Generator then uses the subjective probability p5 = (y5 + 1) /3 = 2/3 to output the spike +1 with probability 2/3 and −1 with probability 1/3. The resultant spike is then used as r5 in (5) and (6) to updates D and C in (35) and (36) into
. The Spike Generator then uses the subjective probability p5 = (y5 + 1) /3 = 2/3 to output the spike +1 with probability 2/3 and −1 with probability 1/3. The resultant spike is then used as r5 in (5) and (6) to updates D and C in (35) and (36) into
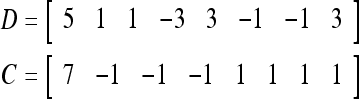 |
or
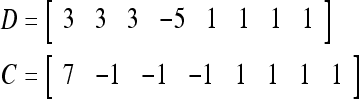 |
depending on whether r5 = 1 or r5 = −1, respectively. For D and C to learn the subjective probability p5 = 2/3, the feature subvector x5 needs to be learned a number of times. This is one of the motivations of PUs generating spike trains for each exogenous feature vector input to the THPAM. Generating spike trains in a THPAM are discussed in "Spike trains for each exogenous feature vector".
Learning to recognize rotated, translated or scaled patterns
In this section, we describe a method for PUs (processing units) to learn to recognize rotated, translated and scaled patterns. The method can be modified for PUs to learn to recognize translated and scaled temporal patterns such as speech and music. Since the method is valid for both supervised and unsupervised learning, labels 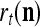 to be referred to may be provided from outside THPAM in supervised learning or generated by the PUs in unsupervised learning. It is assumed in this section that feature vectors are arrays of ternary pixels.
to be referred to may be provided from outside THPAM in supervised learning or generated by the PUs in unsupervised learning. It is assumed in this section that feature vectors are arrays of ternary pixels.
Locations of ternary pixels in an array are assumed to be dense relative to the locations of the pixels selected as components of a feature subvector 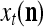 input to a PU. We identify the FSI (feature subvector index) n of a feature subvector with the locations of the pixels in
input to a PU. We identify the FSI (feature subvector index) n of a feature subvector with the locations of the pixels in 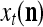 . In other words, the components of n are also the numberings of the locations of the pixels included as components of
. In other words, the components of n are also the numberings of the locations of the pixels included as components of 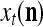 .
.
Imagine a thin rubber disk with small holes at the locations of the pixels of the feature subvector with the FSI n. We translate the disk in some directions (e.g., 0, 15, 30, 45,…, 330, 345 degrees) a number of steps (e.g., 0, 1, 2,…), rotate the disk clockwise and counterclockwise a number (e.g., 0, 1, 2,…) of angles (e.g., 0, 5, 10, 15 degrees) at each translation, and expand and compress the rubber disk uniformly for a number of times (e.g., 0, 1, 2,…) at each translation for some percentages (e.g., 0, 5, 10%,…), to obtain other feature subvector indices of the same dimensionality as n. Note that in using the rubber disk to determine an FSI, if a hole in the rubber disk contains more than one pixel in the image, the one nearest to the center of the hole is included in the FSI.
Figure 4 shows examples of rotation, translations and scalings in an RTS (rotation, translation and scaling) suite of a feature subvector index n, which is shown in Fig. 4a. The components of n are the numberings (of a feature subvector) shown in the small circles within the retangular box. The cross without arrow heads indicate the orientation and position of n. Figure 4b shows a translation to the right. Figure 4c shows a rotation of the translation in Fig. 4b. Figure 4d and e show a compression and an expansion of the translation in Fig. 4b. Five examples of translations of n are shown in Fig. 4f.
Let 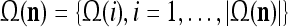 be a set of FSIs ω(i) identified with such rotations, translations, and scalings of n including n.
be a set of FSIs ω(i) identified with such rotations, translations, and scalings of n including n. 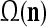 is called a rotation/translation/scaling (RTS) suite of n, and
is called a rotation/translation/scaling (RTS) suite of n, and 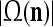 denotes the number of elements in
denotes the number of elements in 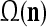 . Notice the digit 0 in the parentheses (e.g., 0, 1, 2,…) in the last paragraph. It indicates a rotation, a translation, or a scaling that is the feature subvector itself.
. Notice the digit 0 in the parentheses (e.g., 0, 1, 2,…) in the last paragraph. It indicates a rotation, a translation, or a scaling that is the feature subvector itself.
Although ω(i) is a rotation, translation, or scaling of n, this dependence on n is not indicated in the symbol ω(i) for notational simplicity. As n is rotated, translated or scaled into ω(i), 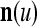 as a subvector of n is rotated, translated or scaled into a subvector of ω(i). This subvector of ω(i) is denoted by
as a subvector of n is rotated, translated or scaled into a subvector of ω(i). This subvector of ω(i) is denoted by 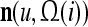 . The set
. The set 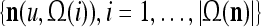 of such subvectors of
of such subvectors of 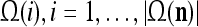 , is denoted by
, is denoted by 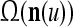 and called a rotation/translation/scaling (RTS) suite of
and called a rotation/translation/scaling (RTS) suite of 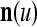 . Note that
. Note that 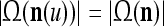 . The set
. The set 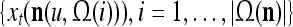 , which is also denoted by
, which is also denoted by 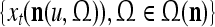 , is called the rotation/translation/scaling (RTS) suite of
, is called the rotation/translation/scaling (RTS) suite of 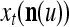 on
on 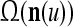 . In generating and summing orthogonal expansions on an RTS suite
. In generating and summing orthogonal expansions on an RTS suite 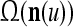 , elements in the RTS suite of
, elements in the RTS suite of 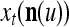 on
on 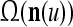 first go through orthogonal expansion. The resultant orthogonal expansions
first go through orthogonal expansion. The resultant orthogonal expansions 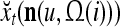 are then added up to form the sum
are then added up to form the sum 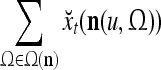 on the RTS suite
on the RTS suite 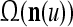 of
of 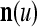 .
.
In both the supervised learning and unsupervied learning, the subvectors, 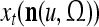 ,
,  , on
, on 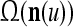 are assigned the label
are assigned the label 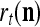 of
of 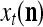 . ECMs (expansion correlation matrices),
. ECMs (expansion correlation matrices), 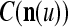 and
and 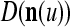 , on
, on 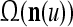 are defined by
are defined by
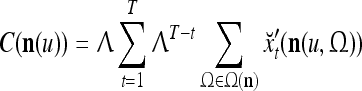 |
37 |
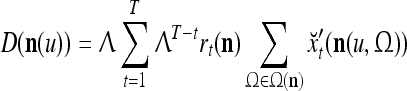 |
38 |
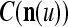 and
and 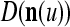 can be adjusted to learn a pair
can be adjusted to learn a pair 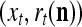 , where λ is a forgetting factor, and Λ is a scaling constant. If
, where λ is a forgetting factor, and Λ is a scaling constant. If 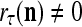 ,
, 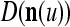 and
and 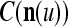 are replaced respectively with
are replaced respectively with 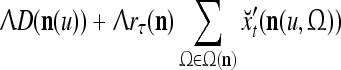 and
and 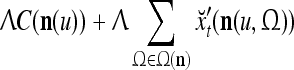 . If
. If 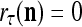 , then
, then 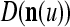 and
and 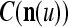 are unchanged.
are unchanged.
Sums 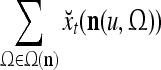 of orthogonal expansions (OEs), and ECMs,
of orthogonal expansions (OEs), and ECMs, 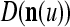 and
and 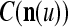 , u = 1,…, U, are respectively assembled into a general orthogonal expansion (GOE)
, u = 1,…, U, are respectively assembled into a general orthogonal expansion (GOE) 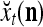 and general expansion correlation matrices (GECMs),
and general expansion correlation matrices (GECMs), 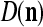 and
and  , for PU(n) (the PU on the feature vector n) as follows:
, for PU(n) (the PU on the feature vector n) as follows:
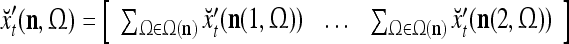 |
39 |
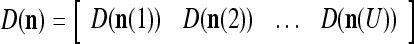 |
40 |
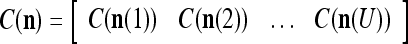 |
41 |
If these are used in PU(n), Fig. 2 should be modified: 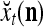 should be replaced with
should be replaced with 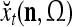 .
. 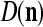 and
and 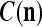 in Fig. 2 should denote those
in Fig. 2 should denote those 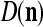 and
and 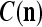 above. Note that the input feature subvector
above. Note that the input feature subvector 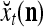 in Fig. 2 is not adequate. It should be replaced with
in Fig. 2 is not adequate. It should be replaced with 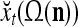 to provide the the RTS suite of
to provide the the RTS suite of 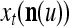 on
on 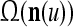 for u = 1,…, U.
for u = 1,…, U.
Spike trains for each exogenous feature vector
Recall that a ternary vector 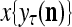 output from a processing unit, PU(n), is obtained by converting a representation
output from a processing unit, PU(n), is obtained by converting a representation 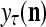 of a probability distribution of a label
of a probability distribution of a label 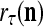 of a feature subvector
of a feature subvector 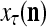 . The spike generator in PU(n) uses a pseudo-random number generator to do the conversion. If some components of
. The spike generator in PU(n) uses a pseudo-random number generator to do the conversion. If some components of 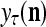 are greater than −1 and less than 1, then the corresponding components of
are greater than −1 and less than 1, then the corresponding components of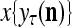 generated by the pseudo-random number generator contain uncertainty (i.e., pseudo-randomness), which reflects probabilistic information contained in
generated by the pseudo-random number generator contain uncertainty (i.e., pseudo-randomness), which reflects probabilistic information contained in 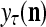 .
.
In retrieving, when a PU receives a feature subvector with such components with uncertainty, it uses masking matrices or general masking matrices to suppress or “filter out” those components that make the received feature subvector inconsistent with those stored in its ECMs or GECMs and to find a match between the received feature subvector and feature subvectors stored in those ECMs or GECMs. Masking matrices are described in "Masking matrices".
However, there is a chance for pseudo-random number generators to generate a ternary vector 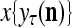 that is an outlier for the probability distribution
that is an outlier for the probability distribution 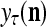 . As
. As 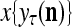 is used as a label in unsupervised learning in PU(n) and is feedforwarded or feedbacked as inputs to PUs, such an outlier may have undesirable effects on learning and retrieving of THPAM in spite of masking matrices. To minimize such undesirable effects and to represent the subjective probabilities involved in the PUs, we let a THPAM complete a certain number of rounds of retrieving and learning for each exogenous feature vector
is used as a label in unsupervised learning in PU(n) and is feedforwarded or feedbacked as inputs to PUs, such an outlier may have undesirable effects on learning and retrieving of THPAM in spite of masking matrices. To minimize such undesirable effects and to represent the subjective probabilities involved in the PUs, we let a THPAM complete a certain number of rounds of retrieving and learning for each exogenous feature vector 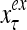 so that many versions of
so that many versions of 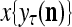 are generated and learned by each PU for the same
are generated and learned by each PU for the same 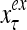 .
.
The subscript t or τ in 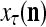 ,
, 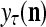 , and
, and 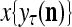 denote the time or numbering of the quantities going through PU(n) in Sections "A recurrent multilayer network of processing units" and "Expansion correlation matrices to Learning to recognize rotated, translated or scaled patterns". In the rest of this section, assume that each exogenous feature vector is presented to THPAM for one unit of time, and that during this one unit of time, there are ζ spikes in each spike train. Here, the subscript t or τ denotes only the time the exogenous feature vector
denote the time or numbering of the quantities going through PU(n) in Sections "A recurrent multilayer network of processing units" and "Expansion correlation matrices to Learning to recognize rotated, translated or scaled patterns". In the rest of this section, assume that each exogenous feature vector is presented to THPAM for one unit of time, and that during this one unit of time, there are ζ spikes in each spike train. Here, the subscript t or τ denotes only the time the exogenous feature vector 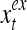 or
or 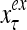 arrives at the input terminals of THPAM. For each exogenous feature vector
arrives at the input terminals of THPAM. For each exogenous feature vector 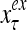 , ζ rounds of retrieving and learning are performed by THPAM at times, τ + i/ζ,, i = 0, 1, ζ −1. Consequently, PU(n) generates a sequence of ternary vectors denoted by
, ζ rounds of retrieving and learning are performed by THPAM at times, τ + i/ζ,, i = 0, 1, ζ −1. Consequently, PU(n) generates a sequence of ternary vectors denoted by 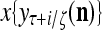 , i = 0, 1,…, ζ −1, for each exogenous feature vector
, i = 0, 1,…, ζ −1, for each exogenous feature vector 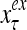 . This sequence consists of R spike trains, each having ζ spikes each of 1/ζ unit of time.
. This sequence consists of R spike trains, each having ζ spikes each of 1/ζ unit of time.
A feedback connection from layer l +k to layer l for k ≥ 0 must have at least one delay device to ensure stability. Each delay device holds a spike for 1/ζ unit of time before it is allowed to pass. Causes in patterns, temporal or spatial, usually form a hierarchy. Example 1: Phonemes, words, phrases, sentences, and paragraphs in speech. Example 2: Notes, intervals, melodic phrases, and songs in music. Example 3: Bananas, apples, peaches, salt shaker, pepper shaker, Tabasco, fruit basket, condiment tray, table, refrigerator, water sink, and kitchen in a house. Note that although Example 3 is a spatial hierarchy, when one looks around in the kitchen, the images received by the person’s retina form a temporal hierarchy.
The higher a layer in THPAM is, the higher in the hierarchy the causes the PUs in the layer treat, and the more time it takes for the causes to form and be recognized by the PUs. Therefore, the number of delay devices on a feedback connection is a monotone increasing function of k. This requirement is consistent with the workings in a biological neural network in the cortex. Note that it takes time (1) for PUs to process feature subvector, (2) for spikes to travel along feedforward connections from a layer to the next layer, and (3) for spikes to travel along feedback connections from a layer to the same or lower-numbered layer. Note also that the times taken for (1) and (2) can be ignored in the feedforward connections, because the subscripts of the input vector 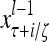 and output vector
and output vector 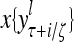 of all layers are the same. However, a feedback
of all layers are the same. However, a feedback 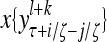 from layer l +k to layer l for inclusion in
from layer l +k to layer l for inclusion in 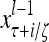 must have a delay j that is proportional to the sum of the times taken for (1), (2) and (3) from the input terminals of layer l back to the same input terminals.
must have a delay j that is proportional to the sum of the times taken for (1), (2) and (3) from the input terminals of layer l back to the same input terminals.
For illustration, two examples are given in the following:
Example 5 Let us set the number Nd of delay devices on the feedback connection from layer l +k to layer l, and the number ζ of learning and retriving rounds to be equal to 1 + 2k and 8 respectively, and consider the feedback connections for k = 0, 2, 3 and 7. Figure 5 shows layer l +2 and layer l in the THPAM. The feature subvector 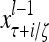 input to layer l consists
input to layer l consists 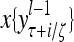 feedforwarded from layer l −1 and feedbacks from layer l and layers above it. Only the feedback
feedforwarded from layer l −1 and feedbacks from layer l and layers above it. Only the feedback 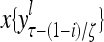 from layer l and the feedback
from layer l and the feedback 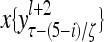 from layer l +2 are shown in the figure. The boxes containing 1/ζ are delay devises with delay duration 1/ζ.
from layer l +2 are shown in the figure. The boxes containing 1/ζ are delay devises with delay duration 1/ζ.
On the feedback connection from layer l to layer l (k = 0): There is 1 delay device on the connection. At the time τ, the exogenous feature vector
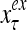 arrives, the feedback
arrives, the feedback 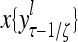 is the last output from layer l in response to the preceding exogenous feature vector
is the last output from layer l in response to the preceding exogenous feature vector 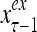 . At time τ + i/ζ for i = 1,…, 7, the feedback is
. At time τ + i/ζ for i = 1,…, 7, the feedback is 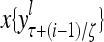 , which is an output from layer l in response to the same exogenous feature vector
, which is an output from layer l in response to the same exogenous feature vector 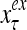 . This feedback connection is shown on the right side of Fig. 5.
. This feedback connection is shown on the right side of Fig. 5.On the feedback connection from layer l +2 to layer l (k = 2): There are five delay devices on the connection. At time τ, the exogenous feature vector
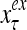 arrives at the input terminals of THPAM, and the five delay devices on the feedback connection holds the 5 feedbacks,
arrives at the input terminals of THPAM, and the five delay devices on the feedback connection holds the 5 feedbacks, 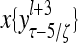 ,
, 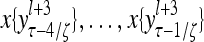 , which are outputs from layer l +2 in response to the preceding exogenous feature vector
, which are outputs from layer l +2 in response to the preceding exogenous feature vector 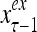 . During the presence of
. During the presence of 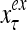 , these five feedbacks are respectively included in the first five feature vectors,
, these five feedbacks are respectively included in the first five feature vectors, 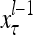 ,
, 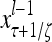 ,…,
,…,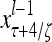 , input to layer l. The next 3 inputs,
, input to layer l. The next 3 inputs, 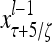 ,
, 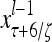 ,
, 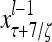 , to layer l include respectively the feedbacks,
, to layer l include respectively the feedbacks, 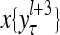 ,
, 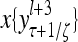 ,
, 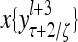 , output from layer l +3 in response to
, output from layer l +3 in response to 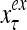 . This feedback connection is shown on the right side of Fig. 5.
. This feedback connection is shown on the right side of Fig. 5.On the feedback connection from layer l +3 to layer l (k = 3): There are 7 delay devices on the connection. At time τ, the exogenous feature vector
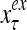 arrives at the input terminals of THPAM, and the 7 delay devices on the feedback connection holds the 7 feedbacks,
arrives at the input terminals of THPAM, and the 7 delay devices on the feedback connection holds the 7 feedbacks, 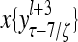 ,…,
,…,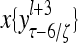 ,…,
,…,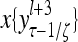 , which are outputs from layer l +3 in response to the preceding exogenous feature vector
, which are outputs from layer l +3 in response to the preceding exogenous feature vector 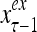 . During the presence of
. During the presence of 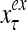 , these 7 feedbacks are respectively included in the first 7 feature vectors,
, these 7 feedbacks are respectively included in the first 7 feature vectors, 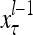 ,
, 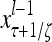 ,
, 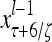 , input to layer l. The eighth input
, input to layer l. The eighth input 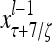 to layer l includes the feedback
to layer l includes the feedback 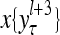 output from layer l +3 in response to
output from layer l +3 in response to 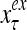 .
.On the feedback connection from layer l +3 to layer l (k = 7): There are 15 delay devices on the connection. At time τ, the exogenous feature vector
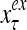 arrives at the input terminals of THPAM, and the 15 delay devices on the feedback connection holds the 15 feedbacks,
arrives at the input terminals of THPAM, and the 15 delay devices on the feedback connection holds the 15 feedbacks, 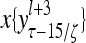 ,…,
,…,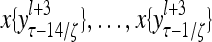 . The first 7 of them are outputs from layer l +7 in response to the exogenous feature vector
. The first 7 of them are outputs from layer l +7 in response to the exogenous feature vector 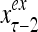 . The next 1 of them,
. The next 1 of them, 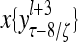 , is the first output from layer l +7 in response to the exogenous feature vector
, is the first output from layer l +7 in response to the exogenous feature vector 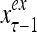 . During the presence of
. During the presence of 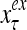 , these 8 feedbacks are respectively included in the 8 feature vectors,
, these 8 feedbacks are respectively included in the 8 feature vectors, 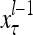 ,
, 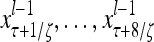 , input to layer l in response to
, input to layer l in response to 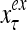 .
.
During the presence of the exogenous feature vector 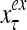 , the feedbacks, output from layer l +k in response to
, the feedbacks, output from layer l +k in response to 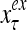 , provide spatial associative information; and the feedbacks, output from layer l +k in response to
, provide spatial associative information; and the feedbacks, output from layer l +k in response to 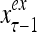 provide less spatial and more temporal associative information. The further back that feedbacks are from, the less spatial and more temporal associative information is used in processing the current
provide less spatial and more temporal associative information. The further back that feedbacks are from, the less spatial and more temporal associative information is used in processing the current 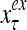 . Of course, if an exogenous feature vector is presented to THPAM for a large number of time units, all the feedbacks are actually from the same exogenous feature vector, and spatial associative information is thoroughly utilized by the use of the feedback connections.
. Of course, if an exogenous feature vector is presented to THPAM for a large number of time units, all the feedbacks are actually from the same exogenous feature vector, and spatial associative information is thoroughly utilized by the use of the feedback connections.
Conclusion
The temporal hierarchical probabilistic associative memory (THPAM), proposed in this paper, is the only single mathematical model of biological neural networks that has all the eight features and answers coherently all the eight questions listed in the introductory section "Introduction". John von Neumann said: “We require exquisite numerical precision over many logical steps to achieve what brains accomplish in very few short steps” in his well-known 1958 book, The Computer and the Brain (von Neumann 1958). Showing that it is possible to achieve so many functions of biological neural networks in a few short logical steps by a single functional model is a small but perhaps significant step towards unraveling the brain.
THPAM’s mathematical structures, functions and their processing operations are hypothesized to be low-order approximates of those of biological neural networks. The integration of them, THPAM, is hypothesized to be a low-order approximate of the biological neural networks themselves. These hypotheses have been under examination. Insight into the inner workings and interactions of the components of a biological neural network is expected to be gained through the examination.
The work reported in this paper points to three research directions:
Examine the components and processing operations of THPAM as biological hypotheses. If possible, justify these hypotheses to establish THPAM as a macroscopic model or low-order approximate of biological neuronal models.
Expand and modify THPAM into functional models of the visual, auditory, somatosensory and (premotor, primary and supplementary) motor cortices.
Test and apply THPAM to such applications as face detection and recognition, radiograph reading, baggage examination, financial time series prediction, video monitoring, text understanding, prostheses, etc.
Abbreviations
- ECM
Expanded correlation matrix
- FSI
Feature subvector index
- GECM
General expanded correlation matrix
- GOE
General orthogonal expansion
- NXOR
Not-exclusive-or
- OE
Orthogonal expansion
- PU
Processing unit
- PU(n)
Processing unit on feature subvector index n
- RTS
Rotation, translation and scaling
- SPD
Subjective probability distribution
- THPAM
Temporal hierarchical probabilistic associative memory
- XOR
Exclusive-or
Footnotes
An erratum to this article can be found at http://dx.doi.org/10.1007/s11571-010-9127-8
References
- Arbib MA. The handbook of brain theory and neural networks, 2. Cambridge: The MIT Press; 2003. [Google Scholar]
- Bengio Y, Lamblin P, Popovici D, Larochelle H (2007) Greedy layer-wise training of deep networks. In: Advances in neural information processing systems. The handbook of brain theory and neural networks, MIT Press, Cambridge
- Bengio Y, LeCun Y (2007) Scaling learning algorithms towards AI. In: Bottou et al. (eds) Large-scale kernel machines. The MIT Press, Cambridge
- Bishop CM. Pattern recognition and machine learning. New York: Springer Science; 2006. [Google Scholar]
- Dayan P, Abbott LF. Theoretical neuroscience: computational and mathematical modeling of neural systems. Cambridge: The MIT Press; 2001. [Google Scholar]
- Desjardins G, Bengio Y (2008) Empirical evaluation of convolutional rbms for vision. Technical Report 1327, Département d’Informatique et de Recherche Opérationnelle, Université de Montréal
- Erhan D, Bengio Y, Courville A, Manzagol P, Vincent P, Bengio S (2010) Why does unsupervised pre-training help deep learning? J Mach Learn Res Appear
- Fromherz P, Gaede V. Exclusive-or function of single arborized neuron. Biol Cybern. 1993;69:337–334. doi: 10.1007/BF00203130. [DOI] [PubMed] [Google Scholar]
- Geist J, Wilkinson R, Janet S, Grother P, Hammond B, Larsen N, Klear R, Matsko M, Burges C, Creecy R, Hull J, Vogl, Wilson C (1994) The second census optical charater recognition systems conference. Technical Report NIST 5452, National Institute of Standards and Technology, May 1994
- George D, Hawkins J. Towards a mathematical theory of cortical micro-circuits. PLoS Comput Biol. 2009;5(10):1–26. doi: 10.1371/journal.pcbi.1000532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Granger R. Engines of the brain: the computational instruction set of human cognition. AI Mag. 2006;27:15–31. [Google Scholar]
- Grossberg S. Towards a unified theory of neocortex: laminar cortical circuits for vision and cognition. Prog Brain Res. 2007;165:79–104. doi: 10.1016/S0079-6123(06)65006-1. [DOI] [PubMed] [Google Scholar]
- Hassoun MH. Associative neural memories, theory and implementation. New York: Oxford University Press; 1993. [Google Scholar]
- Hawkins J. On intelligence. New York: Henry Holt and Company; 2004. [Google Scholar]
- Haykin S. Neural networks and learning machine, 3. Upper Saddle River: Pretice Hall; 2009. [Google Scholar]
- Hecht-Nielsen R. Confabulation theory. New York: Springer; 2007. [Google Scholar]
- Hecht-Nielsen R, McKenna T. Computational models for neuroscience. New York: Springer; 2003. [Google Scholar]
- Hinton GE, Anderson JA. Parallel models of associative memory. Hllsdale: Lawrence Erlbaum Associates; 1989. [Google Scholar]
- Hinton GE, Osindero S, Teh Y. A fast learning algorithm for deep belief nets. Neural Comput. 2006;313:504–507. doi: 10.1162/neco.2006.18.7.1527. [DOI] [PubMed] [Google Scholar]
- Hinton GE, Salakhutdinov RR. Reducing the dimensionality of data with neural networks. Science. 2006;18:1527–1554. doi: 10.1126/science.1127647. [DOI] [PubMed] [Google Scholar]
- Kandel ER, Schwartz JH, Jessell TM. Principles of neural science. New York: McGraw-Hill; 2000. [Google Scholar]
- Koch C. Biophysics of computation. Oxford: Oxford University Press; 1999. [Google Scholar]
- Kohonen T. Self-organization and associative memory. New York: Springer; 1988. [Google Scholar]
- LeCun Y, Bose B, Denker JS, Henderson D, Howard RE, Hubbard W, Jackel LD. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989;1(4):541–551. doi: 10.1162/neco.1989.1.4.541. [DOI] [Google Scholar]
- LeCun Y, Bottou L, Bengio Y, Haffner P (1998) Gradient-based learning applied to document recognition. In: Proceedings of The IEEE 86(11):2278–2324
- Levitan IB, Kaczmarek LK. Simulated annealing and boltzmann machines. London: Wiley; 1993. [Google Scholar]
- Martin KAC. Microcircuits in visual cortex. Curr Opinion Neurobiol. 2002;12(4):418–425. doi: 10.1016/S0959-4388(02)00343-4. [DOI] [PubMed] [Google Scholar]
- Mel BW. Information processing in dendritic trees. Neural Comput. 1994;6:1031–1085. doi: 10.1162/neco.1994.6.6.1031. [DOI] [Google Scholar]
- Mel BW. Have we been hebbing down the wrong path? Neuron. 2002;34:275–288. doi: 10.1016/S0896-6273(02)00669-4. [DOI] [PubMed] [Google Scholar]
- Mountcastle VB. An organizing principle for cerebral function: the unit model and the distributed system. In: Edelman GM, Mountcastle VB, editors. The mindful brain. Cambridge: MIT Press; 1978. [Google Scholar]
- Oja E. A simplified neuron nodel as a principal component analyzer. J Math Biol. 1982;15:267–273. doi: 10.1007/BF00275687. [DOI] [PubMed] [Google Scholar]
- O’Reilly R, Munakata Y. Computational explorations in cognitive neuroscience. Cambridge: The MIT Press; 2000. [Google Scholar]
- Principe JC, Euliano NR, Lefebvre WC. Neural and adaptive systems: fundamentals through simulations. New York: Wiley; 2000. [Google Scholar]
- Ranzato M, Huang F, Boureau Y, LeCun Y (2007) Unsupervised learning of invariant feature hierarchies with applications to object recognition. In: Proceedings of computer vision and pattern recognition conference (CVPR 2007). IEEE Press, New York
- Rieke F, Warland D, Ruyter R, van Steveninck, Bialek W. Spikes: exploring the neural code. Cambridge: The MIT Press; 1999. [Google Scholar]
- Salakhutdinov R, Hinton G (2009) Deep Boltzmann machines. In: Proceedings of the 12th international conference on artificial intelligence and statistics (AISTATS) volume 5. Clearwater Beach, Florida, pp 448–455
- Simard P, Steinkraus D, Platt JC (2003) Best practices for convolutional neural networks. In: Proceedings of the seventh international conference on document analysis and recognition 2:958–962
- Slepian D. A class of binary signaling alphabets. Bell Syst Tech J. 1956;35:203. [Google Scholar]
- Stuart G, Nelson S, Hausser M. Dendrites, 2. New York: Oxford University Press; 2008. [Google Scholar]
- Neumann J. The computer and the brain. New Haven: Yale University Press; 1958. [Google Scholar]
- Wilkinson R, Geist J, Janet S, Grother P, Burges C, Creecy R, Hammond B, Hull J, Larsen N, Vogl, Wilson C (1992) The first census optical charater recognition systems conference. Technical Report NIST 4912, National Institute of Standards and Technology, August 1992
- Zador AM, Clairborne BJ, Brown TH (1992) Nonlinear pattern separation in single hippocampal neurons with active dendritic membrane. In: Moody J, Lippmann R (eds) Advances in neural information processing systems, vol. 4. Morgan Kaufmann, San Mateo, pp 51–58