Analysis of Relationships Between Solid-State Properties, Counterion, and Developability of Pharmaceutical Salts

Abstract

The solid-state properties of pharmaceutical salts, which are dependent on the counterion used to form the salt, are critical for successful development of a stable dosage form. In order to better understand the relationship between counterion and salt properties, 11 salts of procaine, which is a base, were synthesized and characterized using a variety of experimental and computational methods. Correlations between the various experimental and calculated physicochemical properties of the salts and counterions were probed. In addition to investigating the key factors affecting solubility, the hygroscopicity of the crystalline salts was studied to determine which solid-state and counterion properties might be responsible for enhancements in moisture uptake, thus providing the potential for adverse chemical stability. Multivariate principal components and partial least squares projection to latent structures analyses were performed in an attempt to establish predictive models capable of describing the relationships between these characteristics and both measured and calculated properties of the counterion and salt. Some success was achieved with respect to modeling crystalline salt solubility and the glass transition temperature of the amorphous salts. Through the modeling, insight into the relative importance of various descriptors on salt properties was achieved. The solid-state properties of crystalline and amorphous salts of procaine are highly dependent on the nature of the counterion. Important properties including aqueous solubility, melting point, hygroscopicity, and glass transition temperature were found to vary considerably between the different salts.

INTRODUCTION

Pharmaceutical salts are important solid-state modifications, and salt screening and selection strategies are of great value for finding solid-state forms with the appropriate properties for successful pharmaceutical development. Recently, a number of studies have been dedicated to improving salt selection strategies and to developing predictive capabilities for the properties of the final form through better understanding the crystallization behavior of salts and interrelationships between structure and physical properties (1–11). The importance of this knowledge is also obvious in the emerging discipline of crystal engineering (12,13).

Some of the most important properties measured during early screening are solubility and dissolution rate, hygroscopicity, melting point and crystallinity, mechanical properties, and chemical/physical stability (6,14). Such properties are key because of their effect on processing, therapeutic efficacy, toxicity, and bioavailability. Of these properties, aqueous solubility of the salt is often considered one of the most important and may be the underlying reason for salt formation. It is therefore of great interest to understand the relationship between counterion and crystal properties and salt solubility.

One attractive notion is that higher salt solubilities can be attained by selecting more hydrophilic counterions (15,16). However, Anderson and Conradi (17) found a lack of strong correlation between the salt solubility product, K_sp, and counterion hydrophilicity for a series of amine and metal salts of the drug flurbiprofen. In studies of the solubility behavior of alkali and alkaline earth metal salts of organic carboxylic acids and of naproxen, Chowhan (18) noted unpredictability in the effect of salt species on the solubilities. Fini et al. (19) found that an increase in the number of hydroxyl groups in the cation for diclofenac salts showed no simple relationship with the solubility of the salt, and the presence of a hydroxyl group in the cation was not enough to increase the solubility of the salt above that of the sodium salt. The solubility of the salt of the tris(methylol)aminomethane (TRIS) base, which has three hydroxyl groups, was the lowest of any salt measured. Agharkar et al. (15) suggested the vastly increased solubilities of the 2-hydroxyethane-1-sulfonate and lactate salts of an antimalarial agent relative to the hydrochloride salt were due to both the decreased lattice energies evidenced by their lower melting points, as well as hydrogen bonding between the counterions and water molecules. Such findings suggest there are multiple factors which contribute to salt solubility which depend on the structure and properties of both the salt formers and drug molecules as well as the solid-state properties of the resultant salt. In particular, a simplistic prediction of salt solubility based on counterion hydrophilicity neglects the fact that the polarity of the counterion may contribute to stronger lattice interactions. Thus, although hydrogen bond-forming ability is expected to produce stronger solute–solvent interactions, the presence of hydrogen bonds has been shown to decrease solubility by providing stronger crystalline bonds (20).

Although the crystalline form is most often preferred because of the enhanced stability provided by the more thermodynamically stable form, it is sometimes advantageous to develop an amorphous form of the drug as evidenced by the increasing numbers of amorphous formulations reaching the market and existing within the development portfolios of the pharmaceutical industry (21). Amorphous salts provide an opportunity to enhance dissolution behavior in biological fluids via both a higher solubility of the ionized form relative to the free form, as well as the higher apparent solubility of the amorphous solid. The amorphous form, however, has a tendency to crystallize since it is a metastable form. A higher glass transition temperature, T_g, is generally considered to be a favorable property, since at a given temperature, compounds with higher T_g values will typically have a reduced ability to crystallize due to lower molecular mobility relative to those with a lower T_g (22).

Salt formation and the nature of the counterion have been shown to influence the properties of the amorphous solid. The sodium salt of indomethacin was observed to have a T_g which was about 75°C higher than that of the corresponding free acid form (23), which was attributed to stronger intermolecular interactions in the salt form as a result of electrostatic interactions between the sodium ion and the indomethacin carboxylate anion. The lower mobility of the salt form was also supported by its reduced free volume relative to the free acid form, evidenced by an increase in density. The choice of counterion was also found to influence the value of the T_g of a series of amorphous indomethacin salts formed with various alkali metal counterions (24). The value of T_g exhibited an inverse relationship with the ionic radius of the cation, increasing with reduced size. Stronger electrostatic interactions between the carboxylate ion and the alkali metal cation for smaller radii were postulated to exist due to the higher charge densities of the latter. An increase in ion–ion interaction would result in reduced molecular mobility and thereby a higher T_g. Other examples whereby the salt forms had a higher T_g relative to the free form have also been reported (25).

The main objective of this work was to investigate the effect of the counterion on important solid-state properties including solubility and hygroscopicity of the crystalline state and the T_g of the amorphous counterparts. An additional goal was to attempt to establish structure–property relationships using various fundamental physicochemical properties and molecular descriptors in combination with multivariate analysis. Partial least squares (PLS) projection to latent structures is a bilinear modeling and computational method whereby blocks of variables are connected and quantitative relationships established via projection of the data matrix onto a small set of latent variables. These latent variables represent the main variation in the data set and are similar to principal components (PCs) in principal component analysis (PCA). A series of predominately molecular salts of the pharmaceutical compound procaine, a local anesthetic, were investigated. Procaine is a weak base with a pK_a of 9.0 and an intrinsic solubility of approximately 5 mg/mL. The counterions were selected to achieve high molecular diversity; a series of sulfonic acids were included in the set.

MATERIALS AND METHODS

Materials

Procaine, procaine hydrochloride, and 2-napthalene sulfonic acid were purchased from Spectrum Chemicals (New Brunswick, NJ, USA). Phosphoric acid, para-toluenesulfonic acid, ethanesulfonic acid, methanesulfonic acid, oxalic acid, citric acid, formic acid, and sulfuric acid were supplied by Sigma-Aldrich Chemical Co. (St Louis, MO, USA). Benzenesulfonic acid was supplied by Fluka (Buchs, Switzerland). Sodium acetate, glacial acetic acid, tetrahydrofuran, chloroform, ethyl acetate, isopropanol, toluene, ethanol, and high performance liquid chromatography (HPLC)-grade acetonitrile were obtained from Mallinckrodt Chemical (Phillipsburg, NJ, USA).

Methods

Salt Preparation and Characterization

Eleven crystalline salts of procaine, the formic, mesylate, esylate, bisulfate, citrate, napsylate, besylate, phosphate, tosylate, oxalate, and hydrochloride, were prepared. Organic solvents were used to prevent hydrate formation or hydrolysis during the crystallization procedures. Salts were formed by addition of counterion solution to a solution of procaine free base in equimolar concentrations; crystallization either occurred immediately or was induced by cooling to 5°C and/or evaporation. Procaine hydrochloride was recrystallized from solution from the commercially available salt form. Salts were dried via suction filtration and washed with an organic solvent, followed by a second recrystallization procedure in organic solvents to increase purity. The crystalline salts were stored under temperature and humidity conditions which were shown to induce recrystallization of the amorphous form (26), followed by storage under vacuum before further characterization. The absence of hydrates or solvates was established using thermal gravimetric analysis. Formation of monovalent 1:1 salts was confirmed using both nuclear magnetic resonance spectroscopy and quantitative HPLC analysis.

Moisture Sorption and Surface Areas

Water vapor sorption profiles of the salts (10–50 mg) were generated at 25°C using an automated gravimetric analyzer (SGA-100; VT Corporation, Hialeah, FL, USA). Samples were initially dried at 50°C and 0% relative humidity (RH) in the sorption analyzer. For deliquescent salts, the deliquescence RH, RH₀, was measured by extrapolating the linear parts of the vapor sorption plot before and after the deliquescence event (27). Equilibration at each RH step was deemed to have been achieved once weight change was measured to be less than 0.001% over 5 min with a maximum exposure time of 90 min. The sample weights used were based on preliminary moisture sorption measurements; larger sample sizes were used for samples which gained the least amounts of moisture.

The specific surface areas of the procaine salts were measured by nitrogen adsorption using the BET (Brunauer-Emmett-Teller) method (28) with a Micromeritics ASAP 2000. Samples (1–2 g) were degassed under vacuum (<10 mbar) at 50°C for at least 8 h, to remove any residual or physically adsorbed water. The sample weight was adjusted for any loss during degassing, and the tube was then immersed in a liquid nitrogen dewar for measurement. The adsorption isotherm data across a range of partial pressures (0.05–0.30) were fitted to the BET model to determine the corresponding amount of adsorbate for an adsorbed monolayer, and a linearized form of the BET isotherm equation was used to determine the surface area based on the cross-sectional area of a nitrogen molecule (0.162 nm²).

Enthalpies of Solution

The heats of solution were measured using a 2225 Precision Solution Calorimeter (Thermometric AB, Järfälla, Sweden) with a Thermometric 2227 Thermal Activity Monitor (TAM). For each experiment, the samples were equilibrated in a vacuum desiccator for 10–15 min and then weighed into the crushing ampoules. The crushing ampoules are sealed with a silicon stopper and beeswax, and the experiment was conducted using a 100-mL solution calorimeter vessel and deionized water (Reagent grade, Ricca Chemical Co., Arlington, TX, USA). A calibration was performed for each experiment by pulsing a known amount of power into the system and measuring the change in temperature. The heat capacity is calculated from this data and, together with the change in temperature upon the breaking of the ampoule, is used to determine the heat flow of the process.

Differential Scanning Calorimetry

Differential scanning calorimetry (DSC) measurements were taken using a TA Instruments Q10 DSC. Samples (5–10 mg) were accurately weighted into aluminum pans, which were hermetically sealed and punctured with a needle immediately preceding the experiment to allow any water or solvent evolved during the experiment to escape. The melting temperature, T_m, and heat of fusion, ΔH_fus, of the crystalline salts were measured from DSC scans collected at a heating rate of 5°C/min. The melting points were confirmed by hot-stage microscopy, with the values agreeing within 3°C.

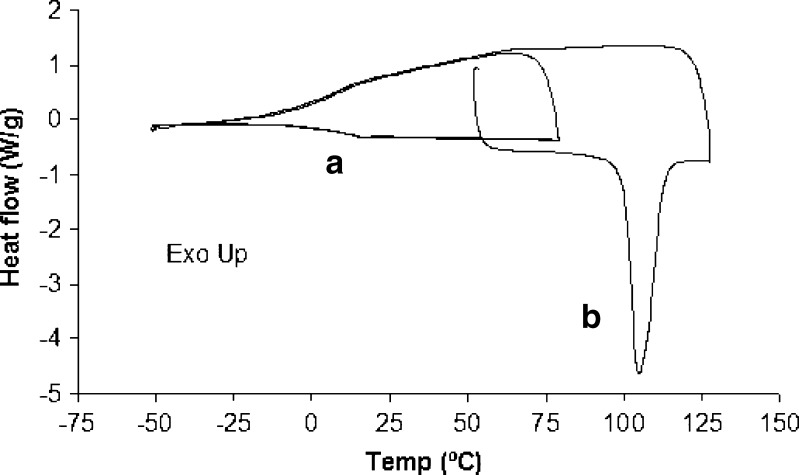
Amorphous samples of the crystalline salts were prepared directly in DSC pans by heating at 20°C/min to a few degrees beyond T_m to allow complete melting, followed by rapid cooling at 40°C/min to −40°C, with equilibration for 3 min. The next step was heating at 10°C/min to a temperature below T_m but at least 50°C above T_g. Traces were then inspected for an initial value of T_g and to rule out any recrystallization event during the cooling segment. The experiment was then repeated, adding a second rapid cooling and subsequent heating cycle to erase thermal history and ensure all moisture had escaped, and the T_g was taken from the second and final heating segment. A DSC trace illustrating these events is shown in Fig. 1. The difference between the initial and final measured T_g was less than 1°C in all cases.

Fig. 1.

DSC trace of procaine besylate for measurement of T _g. Labeled are a T _g and b melting endotherm

Molecular Modeling

Electronic properties of single molecules of the counterions used to form salts were calculated by quantum mechanical methods using a single-energy calculation for the neutral and ionized forms of the molecules, following full optimization. Values for certain counterions from a study by Towler et al. (25) were used where available and were calculated for the remaining counterions. The software program Gaussian 03 was used to obtain the total energy of the counterion; the methods and basis sets utilized were B3LYP/6–311++g(2d,p)//B3LYP/6–311g(d,p). Other general molecular descriptors such as flex index and logD were calculated using ChemBioDraw Ultra 11.0 software (CambridgeSoft). The molecular descriptors of the counterions are given in Tables I and II.

Table I.

General Molecular Descriptors of Acids Used as Counterions

Counterion (acid)	M (g/mol)	pK a1	Vol (cm3/mol)	CMR	ClogP	PSA	Rotatable bonds	logD	Flex index	H acc	H don
Phosphoric	98.0	1.96	69.4	1.427	−2.174	77.8	0	−6.3	0.0	3	4
Citric	192.1	3.13	160.9	3.680	−1.998	132.1	5	−10	26.0	4	7
Benzenesulfonic	158.2	0.7	128.1	3.714	−0.645	54.4	1	−4.6	6.3	1	3
Oxalic	90.0	1.27	68.7	1.483	−1.745	74.6	1	−8.8	11.1	2	4
Sulfuric	98.1	−3	61.7	1.356	−2.174	74.6	0	−10.2	0.0	2	4
Ethanesulfonic	110.1	−2.05	91.2	2.131	−1.895	54.4	1	−5.9	9.1	1	3
Naphthalenesulfonic	208.2	0.17	174.4	5.402	0.529	54.4	1	−3.5	4.8	1	3
Toluenesulfonic	172.2	−1.34	147.2	4.178	−0.146	54.4	1	−4.1	5.8	1	3
Formic	46.0	3.75	39.8	0.830	−1.316	37.3	0	−3.8	0.0	1	2
Methanesulfonic	96.1	−1.2	72.0	1.667	−2.424	54.4	0	−6.4	0.0	1	3
HCl	36.5	−6	29.1	0.000	−1.316	0.7	0	–	0.0	0	0

Table II.

Calculated Molecular Descriptors of Counterions Using DFT

Counterion (acid)	A (eV)	I (eV)	η (eV)	S (eV−1)	μ (eV)	ω (eV)
Phosphoric	0.012	10.498	10.486	0.095	−5.255	1.317
Citric	0.426	9.507	9.081	0.110	−4.967	1.358
Benzenesulfonic	0.353	9.569	9.216	0.109	−4.961	1.335
Oxalic	0.714	10.407	9.692	0.103	−5.561	1.595
Sulfuric	0.771	11.359	10.587	0.094	−6.065	1.737
Ethanesulfonic	0.103	12.134	12.032	0.083	−6.119	1.556
Naphthalenesulfonic	0.945	8.306	7.361	0.136	−4.625	1.453
Toluenesulfonic	0.305	9.122	8.817	0.113	−4.713	1.260
Formic	−0.986	11.100	12.086	0.083	−5.057	1.058
Methanesulfonic	0.321	10.769	10.448	0.096	−5.545	1.471
HCl	−0.486	12.765	13.251	0.075	−6.139	1.422

Multivariate Data Analysis

PCA was performed to establish the existence of outliers in the data set, as well as to establish groupings based on molecular diversity of the counterions. PCA is a projection method whereby linear combinations of a set of variables are sought which can explain the variation in the data. These directions in space are called PCs. PLS projection to latent structures was used to identify relationships between various salt properties and other physicochemical properties and molecular descriptors. PLS is a multivariate modeling and computational method which relates two data matrices. Both PCA and PLS modeling were conducted using the software package SIMCA-P +11.0 (Umetrics AB, Umeå, Sweden). Each of the variables in the dataset were autoscaled by unit variance and mean-centered before performing any statistical analysis.

RESULTS AND DISCUSSION

The calculated molecular descriptors as well as physicochemical properties such as molar mass and pK_a for the counterions used in this study are given in Tables I and II. The measured aqueous solubility (25°C) (26), melting temperature T_m, enthalpy of fusion ΔH_fus, and enthalpy of solution ΔH_sol for each of the crystalline procaine salts are given in Table III, as well as the glass transition temperatures (T_gs) of the amorphous salts.

Table III.

Measured Physicochemical Properties of Procaine Salts

Procaine salt	pH of saturated solution at 25°C	Solubility at 25°C (mol/L)	T m (°C)	Enthalpy of fusion (kJ/mol)	Enthalpy of solution (kJ/mol)	T g (°C)	T g/T m
Phosphate	4.50	0.488	188.6	43.8	25.6	–a	–
Citrate	3.72	0.697	128.2	52.0	39.1	22.9	0.74
Besylate	5.99	0.901	100.9	39.5	37.1	12.9	0.76
Oxalate	3.47	0.067	162.3	60.3	47.6	23.4	0.68
Bisulfate	1.35	2.644	96.6	40.9	19.2	31.2	0.82
Esylate	6.02	2.329	101.5	34.9	20.2	7.6	0.75
Napsylate	6.54	0.026	164.7	41.0	35.9	30.7	0.69
Tosylate	5.66	0.068	153.0	50.2	36.7	21.9	0.69
Formate	6.42	2.891	73.4	37.4	19.2	−14.9	0.75
Mesylate	4.68	2.780	104.2	29.1	22.2	12.2	0.76
HCl	4.82	2.583	157.3	38.6	32.5	33.3	0.71

^aSince the phosphate salt showed evidence of decomposition upon melting from the DSC thermogram, its T _g is excluded

Aqueous Solubility

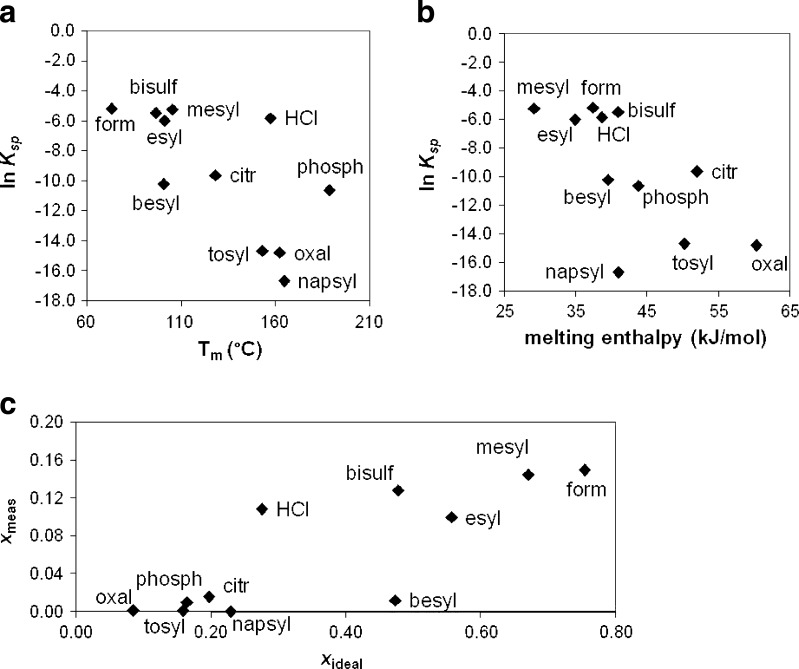
The molar solubilities of the various salts vary by more than two orders of magnitude, illustrating the importance of the counterion in influencing aqueous solubility. Generally, a decrease in salt solubility accompanies increases in melting point (T_m) and enthalpy of fusion (ΔH_fus), which is at least partially attributable to the higher crystal lattice energies for a material with a higher melting point. The melting points of the various salts range from 73°C (formate) to 188°C (phosphate) and ΔH_fus values vary by a factor of approximately 2. Although far from a linear correlation, the general trend between solubility and fusion properties can be seen from Fig. 2a, b, where the solubility in terms of the solubility product is plotted versus T_m and ΔH_fus.

Fig. 2.

Correlations of salt solubility (ln K _sp) of procaine salts with a melting temperature T _m and b melting enthalpy. c The relationship between measured and ideal solubilities (mole fraction)

The following relationships (Eqs. 1 and 2) can be used to estimate the ideal solubility (29,30):

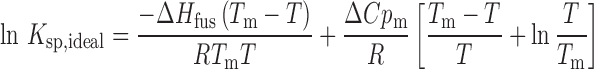1

where K_sp is the solubility product on a mole fraction scale, ΔCp_m is the molar heat capacity difference between the crystalline and liquid forms of the solute, T is temperature, and R is the gas constant. Here, we have used entropy of fusion to estimate the value of ΔCp_m (31). For a 1:1 salt, K_sp can be related to the ideal mole fraction solubility by Eq. 2:

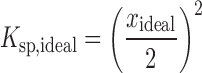2

The correlation between measured and ideal solubility, calculated using Eqs. 1 and 2, is illustrated in Fig. 2c, and the values are given in Table IV. The ideal solubility describes the contribution of the solute crystallinity to the solubility. The ratio of the ideal solubility to the experimental solubility gives the activity coefficient, γ, which represents non-idealities in mixing of the solute with the solvent. These non-idealities can arise either from a non-zero enthalpy of mixing or an entropy of mixing that is not purely combinatorial. Values of the activity coefficient are listed in Table IV.

Table IV.

Solubilities and Estimated Thermodynamic Properties of Procaine Salts

	Ideal solubility (x ideal)	Measured solubility (x meas)	ln γ	ΔHfus (kJ/mol) at 298 K	ΔHmix (kJ/mol)
Phosphate	0.165	0.010	2.8	28.3	−2.7
Citrate	0.198	0.016	2.5	38.6	0.5
Besylate	0.473	0.012	3.7	31.5	5.6
Oxalate	0.085	1.2 × 10−3	4.2	41.3	6.3
Bisulfate	0.478	0.128	1.3	33.0	−13.8
Esylate	0.557	0.100	1.7	27.8	−7.6
Napsylate	0.230	4.7 × 10−4	6.2	27.9	8.0
Tosylate	0.159	1.3 × 10−3	4.8	35.1	1.6
Formate	0.754	0.150	1.6	32.2	−13.0
Mesylate	0.671	0.145	1.5	23.0	−0.7
HCl	0.276	0.108	0.9	26.8	5.7

It is apparent from Table IV that all of the salts have activity coefficients greater than unity. In order to better understand the origin of the non-idealities for these systems, additional thermodynamic parameters were calculated. The dissolution process can be represented by the following conceptual process (31,32):

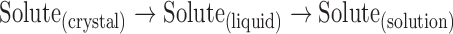3

Here, the dissolution process is described by considering the thermodynamics of melting the crystalline solid to a supercooled liquid (at the temperature of interest) and mixing the liquid with the solvent to the equilibrium concentration. Employing the approach outlined in Eq. 3 and using the experimentally determined melting and solution enthalpies shown in Table III, the enthalpy of mixing could be estimated, as shown by Eq. 4:

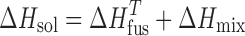4

where 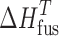represents the heat of fusion at the temperature of interest and can be determined from the relationship (29)

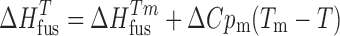5

The individual enthalpic contributions to solution, namely of fusion and mixing, are given in Table IV. The overall enthalpy contribution to the solution process is positive in all cases and, therefore, contributes negatively to solubility. While ΔH_fus is always positive, ΔH_mix is either positive or negative depending on the counterion, indicating non-ideal mixing. Thus, it is clear that the solubility of the salt is also strongly influence by the solute–solvent interactions, which can either promote solubility (negative ΔH_mix) or reduce solubility (positive ΔH_mix).

The compound with the most negative ΔH_mix value is the bisulfate salt, while the salt with the most endothermic mixing is the napsylate salt. While the napsylate salt is the least soluble salt (Table III), the bisulfate salt was not as soluble as the mesylate salt, which had a much lower ΔH_mix. This observation can most likely be explained by the higher enthalpy of fusion of the bisulfate salt relative to that of the mesylate salt, illustrating the interplay between crystal lattice properties and solute–solvent interactions on the solution process. For the sulfonic acid series, it is interesting to note that the counterions that are dominated by the sulfate group with only a moderate number of hydrocarbon groups, namely, the bisulfate, mesylate, and esylate, yield negative ΔH_mix values, indicating favorable interactions with water. In contrast, the counterions with larger, more hydrophobic structures, that is the besylate, tosylate, and napsylate salts, result in positive ΔH_mix values. In general, more endothermic enthalpies of mixing correspond to increased ln γ values as shown in Table IV, suggesting that ΔH_mix is a major contributor to the non-ideal behavior manifested in experimental solubility of the salts relative to the ideal solubilities. However, a plot of ln γ versus ΔH_mix (data not shown) does not show a linear correlation, suggesting that entropy effects also contribute to the non-ideal solubilities observed. This is readily understandable if the clustering of water around large hydrophobic residues is considered. For instance, the large value of ln γ for the napsylate salt may be due in some part to the more unfavorable entropic contribution exhibited by aromatic compounds (33,34).

Multivariate Modeling of Aqueous Solubility

Because of the direct relationship between aqueous solubility, absorption, and bioavailability for some compounds, there is a growing interest in methods capable of explaining and predicting the solubility of pharmaceutical compounds. Predicting the dependence of solubility of a salt on both crystalline and counterion properties is no simple task. Despite early reports attempting to establish strong predictive relationships with such properties as melting point, numerous inconsistencies due to the complicated nature of such dependencies have emerged and are evident upon review of the relevant literature. Attempts to correlate aqueous solubility with single properties such as melting point have produced mixed results; for instance, Gould (3) observed log solubility was linearly related to the reciprocal of absolute melting temperature for data collected for a series of salts of an antimalarial drug (15), while others generally yield qualitative relationships. Gu and Strickley (4), in studies of the physical properties of four analgesic/anti-inflammatory agents, found no simple relationship between the melting point and solubility of the sodium and tris(hydroxymethyl)aminomethane (THAM) salts of each compound. Our results (Fig. 2a, b) show a general trend between melting enthalpy and melting temperature with solubility, although it is clear other factors are involved.

A number of approaches attempting to approximate aqueous solubility either by multivariate techniques with various descriptors/properties, by employing semi-empirical equations, or in one case by a group contribution method, have achieved varying levels of success (35–48), some using impressive datasets of compounds and/or descriptors. Many of these studies involve descriptors based merely on structure, where quantitative structure–property relationships (QSPR) are sought, and many researchers have studied groups of compounds with related or un-complex structures. However, few literature reports are available involving salts (49–51), particularly salts with a series of commonly used pharmaceutical counterions. The objective of our multivariate analysis is to identify suitable descriptors/properties which will allow derivation of an appropriate model for aqueous solubility of a series of salts of a pharmaceutical compound, thus elucidating the characteristics accurately dictating aqueous solubility.

Molecular descriptors attempt to quantify the structural features of a compound and can be subdivided into three categories based on the types of information they encode—topological, geometric, and electronic—and are related to the size, shape, and polarity of the compound. Geometric descriptors include solvent-accessible molecular surface area and volume, while atom counts and polar surface area (PSA) typify examples of topological and electronic descriptors. Considerable overlap between the various types of descriptors is evident and thus many descriptors can be regarded as combination descriptors. However, the purpose of using such descriptors is to provide some characterization of the solute–solvent interaction and the lattice energy. For our PLS modeling, we chose to utilize heat of solution, heat of fusion, temperature of melting (T_m), molecular volume (Vol), molar mass (M), calculated molar refractivity (CMR), PSA, number of hydrogen bond donors (H don) and acceptors (H acc), and calculated logP (ClogP).

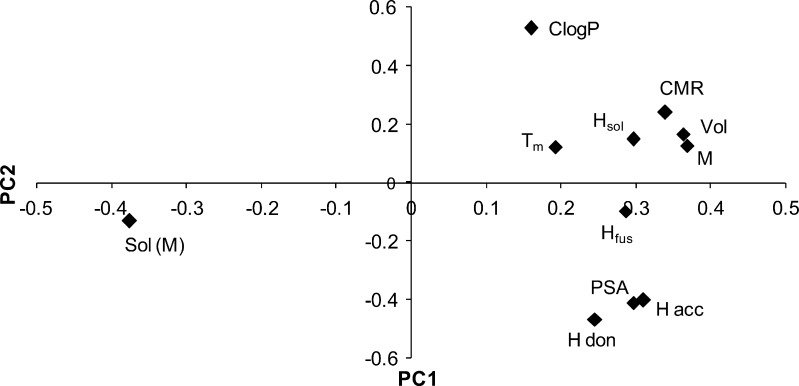
Initial PCA analysis including all components showed expected results, with M, Vol, and CMR in close proximity, T_m, ΔH_sol, and ΔH_fus as a second group, and the number of hydrogen bond donors and acceptors and PSA grouped closely as a third collection in the plot of PCs (Fig. 3), and finally ClogP on its own. Solubility showed the expected relationships with the first two groups mentioned above, where higher values of the parameters correlated with lower solubilities. The phosphate salt was excluded from the model as it showed degradation on melting. The resultant PLS model, constructed using all these descriptors, gave less than adequate predictability with an R² of 0.835 and Q² of 0.793. From the observed versus predicted values, it was observed that the oxalate, napsylate, and tosylate salts, with the lowest solubilities, were not predicted well, having much lower observed values. These three exhibited by far the largest negative deviations from ideal solubility (Table IV). Excluding these produced a model with excellent predictability, with an R² of 0.994 and Q² of 0.96.

Fig. 3.

PCA scatter plot for analysis of solubility of procaine salts showing the two PCs plotted against each other

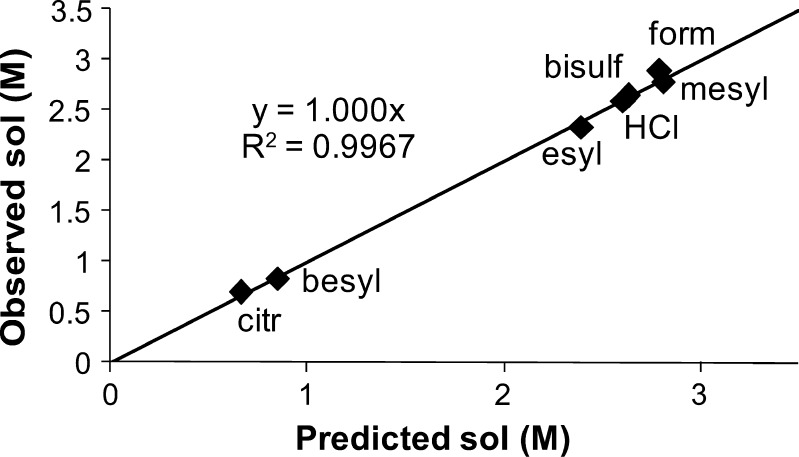
The model was then further refined by reducing the number of descriptors (a model with fewer descriptors is generally desired). The least important variables based on the variable importance in the projection (52) values, T_m, number of hydrogen bond donor and acceptors, were thus excluded. The resultant simpler model had slightly improved predictability and acceptable validity by response permutation. The observed vs. predicted plot for this final model is given in Fig. 4, while the VIP values showed that the relative importance of the model variables were, in decreasing order, Vol, CMR, M, ΔH_sol, ΔH_fus, PSA, and ClogP. All of these parameters showed a negative effect on solubility, i.e., increasingly positive values translate to lower values of solubility.

Fig. 4.

Observed vs. predicted values of solubility (M) for procaine salts from final PLS model

Although only able to model the solubility of some of the salts, the PLS results highlight the importance of both solution and crystal chemistry in determining the solubility of this series of salts. The variables used to build the model can affect solubility through their influence on both interaction energies in the crystalline lattice as well as solute–solvent interactions. For example, the negative effect, i.e., decreasing solubility with larger values of H_sol, can be rationalized by the contribution of higher crystalline lattice energies in the form of more positive heat of fusion and/or less favorable solute–solvent interactions (more positive heat of mixing) to lower solubilities. In the case of M, Vol, and CMR, the negative effect on solubility is likely due in part to the fact that the hydrophilic ionic portion is counterbalanced by an increasing number of carbons atoms/structures, which translates to reduced net solute–solvent interactions—this is most easily rationalized with the sulfonic acid series. The most likely reason for the failure of the model to deal with all the salts is that the importance of the entropic contributions to the solution process has not been considered. The complicated effects of structure on solvent disorder thus may explain why it was impossible to build a good model for all of the salts—a descriptor describing solution entropy effects has not been identified.

Moisture Sorption

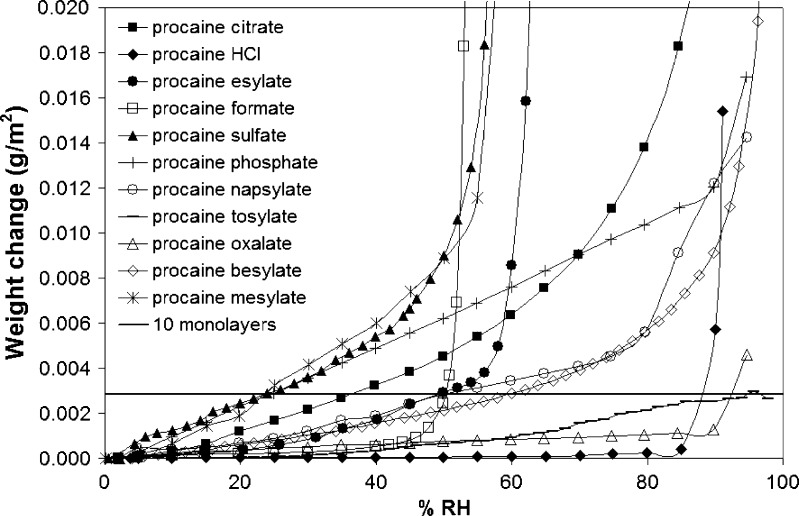
The next developability parameter of interest was the hygroscopicity of the salts. It is widely recognized that more hygroscopic salts are likely to be less chemically stable, and hygroscopicity is frequently used as a criterion in salt screening procedures (6). The procaine salts exhibited a broad range of hygroscopicities, as shown in Fig. 5, where the weight gain has been normalized to the surface area of the salts. The hydrochloride salt was the least hygroscopic, with the moisture uptake equivalent to one monolayer at 90% RH, while the mesylate salt had the greatest moisture sorption with 200 equivalent monolayers at 40% RH. A number of the salts exhibited deliquescence, namely, the besylate, hydrochloride, bisulfate, mesylate, esylate, and formate salts. The values of the deliquescent RH (i.e., the RH where the salt dissolved in the atmospheric moisture to form a solution), RH₀, ranged from 53% to 94% RH, and values are given in Table V. The equivalent weight gain per unit surface area for ten monolayer coverage, based on a molecular surface area of water of 0.106 nm², is represented by the horizontal line in Fig. 5. It is apparent that the various salts reach this level of moisture coverage at very different relative humidities.

Fig. 5.

Moisture sorption profiles for crystalline salts of procaine; data is normalized to surface area

Table V.

Measured and Predicted RH₀ of Deliquescent Procaine Salts

	Ideal a w (Raoult's law)	RH0/100 (measured)	Meas/ideal
Besylate	0.99	0.94	0.95
Bisulfate	0.87	0.60	0.69
Esylate	0.90	0.65	0.72
Formate	0.85	0.53	0.62
Mesylate	0.86	0.60	0.70
HCl	0.89	0.90	1.01

It is of interest to determine if the varying salt hygroscopicities can be explained by any readily measurable parameter. First, it should be noted that the difference in hygroscopicities between the various salts cannot be accounted for by minor amounts of bulk amorphous material, since none of the salts except the mesylate salt could be maintained as the amorphous form in the presence of even moderate relative humidities (26). Second, it is apparent that there is no correlation between salt solubility and the surface area normalized moisture sorption below RH₀. Indeed, we were entirely unsuccessful in modeling the hygroscopicity of the salts using any of the descriptors described above. The origin of the hygroscopicity thus appears to be complex and is most likely dependent to some extent on the surface structure of the various salts (disorder is known to enhance moisture sorption (53,54)), in addition to other factors such as trace levels of impurities (55). The lack of correlation between hygroscopicity and solubility is illustrated by considering two of the sparingly soluble salts, the napsylate and tosylate salts. These two salts have similarly low solubilities; the napyslate salt, whose acid counterion includes a large hydrophobic moiety, has the lower solubility value. However, the napsylate salt is the more hygroscopic of the two (Fig. 5), reaching ten monolayers at an RH of approximately 49% compared to 95% RH for the tosylate salt.

The phenomenon of deliquescence, the process by which crystalline solids undergo a phase transformation to a solution state via dissolution within sorbed moisture (56,57), is a particularly egregious occurrence involving interaction of solid API or formulation with moisture. Thus, avoidance of the conditions promoting deliquescence is vital. There was no apparent relationship between hygroscopicity below RH₀ and deliquescence tendency. The most and least hygroscopic salts, the mesylate and the HCl salt, both underwent deliquescence, albeit at vastly different relative humidities. Deliquescence, however, is related to the solubility of the salt. Deliquescent compounds often follow a general trend, where the critical RH (RH₀) at which the phase transformation occurs is lower for compounds with increasing solubilities (58). Of the 11 salts investigated, the six crystalline procaine salts exhibiting deliquescence had the highest solubilities. Solution thermodynamics can be employed to predict RH₀. By assuming ideal solution behavior of the water-soluble material, application of Raoult's law provides an estimation of the water activity a_w of a solution (59) based on concentration, and thus the solubilities can be used to estimate the deliquescence RH (invoking the assumption that the estimated a_w is the same as RH₀/100).

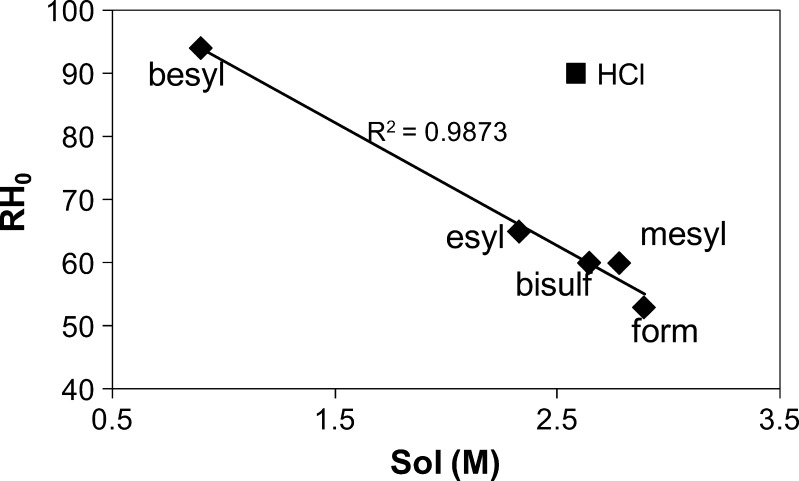
The RH₀s predicted for five of the six deliquescent procaine salts were higher than the observed values (Table V), while RH₀ for the hydrochloride salt was close to the predicted value. Furthermore, the RH₀ values for these five salts exhibited a linear relationship with solubility as shown in Fig. 6. Since water activity can be regarded as a measure of the escaping tendency of water, higher strengths of interactions between solute and solvent will result in lower activity coefficients and increased negative deviation from ideality. The negative heats of mixing values for these five (Table V) provide additional evidence for the favorable interactions of these five salts with water. The fact that HCl is an outlier may be due to its lack of strong hydrogen bond-forming potential, as the counterions of the other five salts all have multiple H bond donors/acceptors and very strong H bond acceptors. The observation that RH₀ is related to the salt solubility (as also noted previously) is important, since salt selection criteria might favor more soluble salt forms.

Fig. 6.

Plot of measured RH₀ vs. solubility for deliquescent procaine salts

Glass Transition Temperatures of Amorphous Counterparts

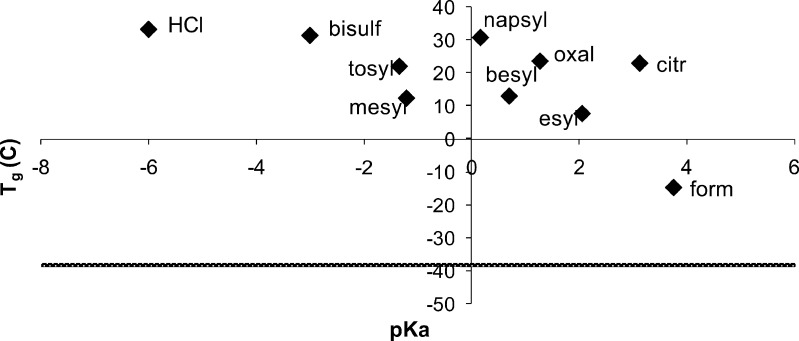
The final developability parameter investigated was the glass transition temperature (60) of the amorphous salt forms. T_g is important if a non-crystalline formulation is being developed, e.g., a lyophilized product for parenteral administration, as well as from the perspective of the unintentional introduction of amorphous material. The T_gs of the amorphous salts were found to depend on the nature of the counterion, and the values are shown in Table III. The T_g of each procaine salt was substantially higher than the T_g of the free base, which was around −38°C. Furthermore, it is apparent that the T_g varies considerably with the counterion, with the formate salt showing the lowest T_g (−15°C) and the HCl the highest value of 33°C. Thus, it is clear that T_g can be manipulated through the choice of the counterion. Interestingly, the ratio T_g/T_m varies substantially between the different counterions, from 0.68 for the oxalate salt to the 0.82 for the bisulfate salt (Table III). A plot of T_gversus pK_a of the counterion is shown in Fig. 7 where it can be seen that the T_g of the salt tends to increase as the counterion pK_a decreases, in agreement with previous observations for other amorphous salts (25). Thus, the formation of a salt is a convenient strategy to increase the T_g of a compound, with more acidic counterions offering greater T_g increases.

Fig. 7.

Glass transition temperature T _g of amorphous samples of procaine salts plotted with pK _a of the counterion. The line represents the T _g of procaine free base

Multivariate Analysis of T_gs

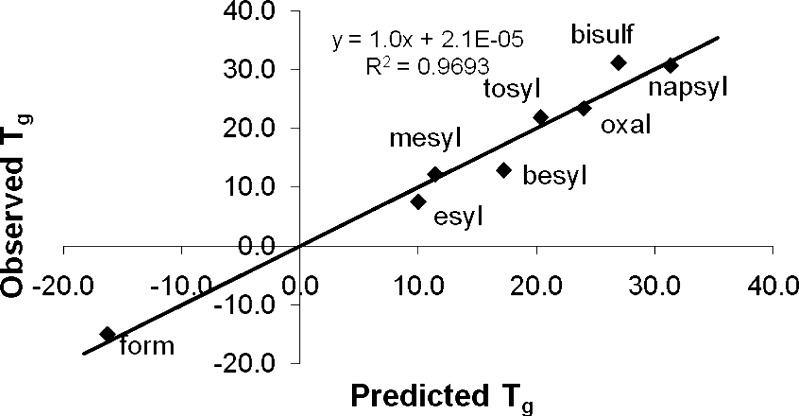
It is of interest to better understand which properties of the counterion are important in influencing the T_g values of the resultant salt. Initial PCA using all of the molecular descriptors in Tables I and II and the measured values of T_g for the ten procaine salts revealed the citrate and HCl salts to be outliers. The occurrence of the citrate salt as such is consistent with results for propranolol and nicardipine by Towler et al. (25) and was suggested to be due to the trivalent character of the counterion. The HCl salt was also found to be an outlier in the hygroscopicity analysis described above. Excluding the two outliers from further analysis, the glass transition temperature was described as a function of the descriptors for an initial PLS analysis. The resultant model with three PCs produced an R² of 0.99 and Q² of 0.94. Based on the VIP values and the loading plot, as well as the effect of their individual exclusions on the resultant Q² values, the descriptors ClogP, μ, and logD were excluded.

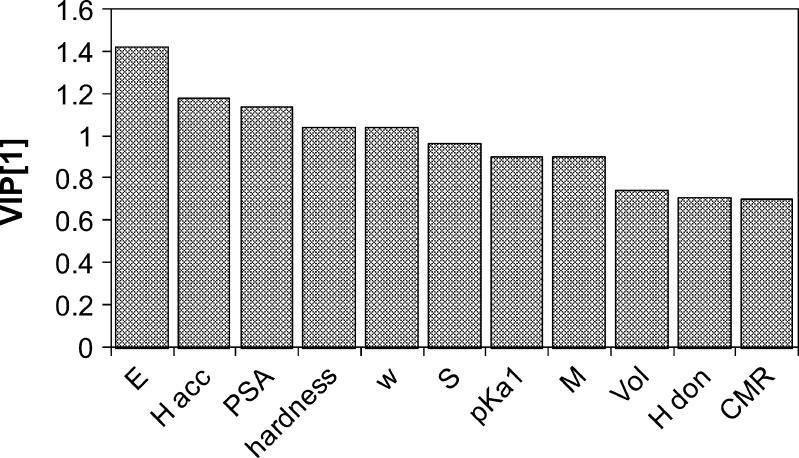
The subsequent model provided excellent predictability, with an R² of 0.99, a Q² of 0.956, and a root mean square error of the fit (RMSEE) of 2°C. However, validation of the model by response permutation gave intercept values of 0.58 and −0.41 for R² and Q², respectively, indicating perhaps an overfit since a valid model requires values below 0.3–0.4 and 0.05 for the R² and Q² intercepts, respectively. The three least significant variables, rotatable bonds, flex index, and ionization potential, were then excluded, resulting in a valid single-PC model by response permutation, with R²(intercept) = 0.139 and Q²(intercept) = −0.309. The observed versus predicted plot is given in Fig. 8. The goodness of fit parameters R² and Q² were 0.969 and 0.9, respectively, and the model had an RMSEE of 2.84. The VIP values for this final model are all above 0.7 (see Fig. 9), the approximate threshold of “importance.”

Fig. 8.

Observed vs. predicted values of T _g (°C) using PLS modeling

Fig. 9.

Variable of importance in the projection (52) plot from the final PLS model of T _g of procaine salts

Values of descriptors, which signify stronger interactions between the acid and base, are expected to correlate with higher values of T_g, due to the enhanced amounts of energy necessary to impart sufficient molecular mobility. Additionally, certain structural factors are expected to contribute to reduced mobility through steric and free volume effects. The descriptors used here to assess intermolecular interactions have been elucidated from density functional theory (DFT) (61,62) and represent some of the most prominent and universal concepts describing the flow of electrons. The electronic chemical potential μ is a measure of the strength of Lewis acids/bases or the escaping tendency of electrons, and is represented by the response in energy to a change in the number of electrons N in an external potential, ν, of fixed nuclear positions (63):

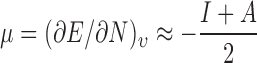9

where I is the ionization potential, and A is the electron affinity. The concepts of hardness and softness also originate from the interaction between acids and bases, representing a measure of the polarizability of electronic structure. Hardness (η) can be regarded as resistance to charge transfer or low polarizability and is represented by the second derivative of energy relative to electron number:

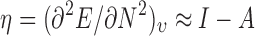10

Softness (S) is simply the reverse of hardness, where greater values represent relative ease of charge transfer. The covalent and polarization contributions to intermolecular interactions can be characterized by these concepts discussed above. Another concept which may be used as a measure of these types of interactions is that of electrophilicity index ω, which may be defined as (63):

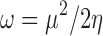11

Less polarizable structures should therefore yield smaller values of electrophilicity index and intuitively should favor the sharing of electrons less.

It is expected that values of these descriptors, which correspond to inherent increased ability to form electrostatic and polarization interactions, will translate to higher values of T_g via a reduction in molecular mobility. Towler et al. (25) found adequate predictability using identical descriptors, although those showing the highest influence were different in the cases of the two pharmaceutical bases used. Here, we have derived a validated PLS model with good predictability. The variables of most significance, in decreasing order of importance, are electron affinity, hydrogen bond acceptors, PSA, hardness, electrophilicity index, softness, and pK_a. Other descriptors appearing in the final model are molar mass and volume, CMR, and hydrogen bond donors. All of these variables exhibited positive distances from the origin for the loading weights (w*) in the direction of the regression coefficient, c (see Table VI) except for hardness, H bond acceptors, and pK_a. The importance is stated by the absolute value, while the sign represents positive and negative influence (i.e., a positive value of w*(c) signifies increasing values of the descriptor correlates to higher T_g, while the opposite is true for negative values where decreasing values of the descriptor correlate to a higher T_g). The contributions from the molar mass and volume descriptors are likely the result of steric or free volume limiting effects on molecular mobility or simply increased non-specific interactions. The large majority of the molecular descriptors representing intrinsic electronic properties intuitively agree with expectations, although in certain cases, the relationship is unclear. For instance, the number of hydrogen bond donors and acceptors and PSA would all be expected to enhance intermolecular interactions in the amorphous state, yielding a positive value of w*(c) relative to T_g. Thus, the relationship of the hydrogen bond acceptors is unexpected.

Table VI.

Distance of Loading Weights in the Direction of the Regression Coefficient for the Final PLS Model Predicting T _g with One PC

	A	H acc	PSA	η	ω	S	pKa1	M	Vol	H don	CMR
w*c[1]	0.430	−0.315	0.344	−0.315	0.314	0.290	−0.272	0.272	0.225	0.213	0.212
VIP[1]	1.426	1.177	1.141	1.043	1.042	0.962	0.902	0.901	0.745	0.707	0.703

CONCLUSIONS

It has been demonstrated that the solid-state properties of crystalline and amorphous salts of procaine are highly dependent on the nature of the counterion employed to form the salt. Important properties including aqueous solubility, melting point, hygroscopicity, and glass transition temperature were found to vary considerably between the different salts. Counterions, which lead to favorable properties such as high aqueous solubility, may not be so favorable with respect to other properties such as deliquescence tendency, where a clear relationship between the deliquescence RH and aqueous solubility was observed. Thus, the molecular structure of the counterion has important consequences on both the intermolecular interactions between acid and base as well as between counterion and water; these interactions impact properties essential for evaluating the developability of both crystalline and amorphous compounds.