Abstract
The present investigation was aimed at developing cytarabine-loaded poly(lactide-coglycolide) (PLGA)-based biodegradable nanoparticles by a modified nanoprecipitation which would have sustained release of the drug. Nine batches were prepared as per 32 factorial design to optimize volume of the co-solvent (0.22–0.37 ml) and volume of non-solvent (1.7–3.0 ml). A second 32 factorial design was used for optimization of drug: polymer ratio (1:5) and stirring time (30 min) based on the two responses, mean particle size (125 ± 2.5 nm), and percentage entrapment efficiency (21.8 ± 2.0%) of the Cyt-PLGA nanoparticles. Optimized formulation showed a zeta potential of −29.7 mV indicating good stability; 50% w/w of sucrose in Cyt-PLGA NP was added successfully as cryoprotectant during lyophilization for freeze-dried NPs and showed good dispersibility with minimum increase in their mean particle sizes. The DSC thermograms concluded that in the prepared PLGA NP, the drug was present in the amorphous phase and may have been homogeneously dispersed in the PLGA matrix. In vitro drug release from the pure drug was complete within 2 h, but was sustained up to 24 h from PLGA nanoparticles with Fickian diffusion. Stability studies showed that the developed PLGA NPs should be stored in the freeze-dried state at 2–8°C where they would remain stable in terms of both mean particle size and drug content for 2 months.
Key words: cytarabine, factorial design, modified nanoprecipitation method, nanoparticles, PLGA, stability studies
INTRODUCTION
Cytarabine (CYT) is an antimetabolite used primarily for acute myelogenous leukemia and meningeal leukemia. It is metabolized intracellularly into its active triphosphate form (cytosine arabinoside triphosphate) which damages DNA by multiple mechanisms, including the inhibition of alpha-DNA polymerase, inhibition of DNA repair through an effect on beta-DNA polymerase, and incorporation into DNA (1). Cytarabine is poorly absorbed from gastrointestinal tract with less than 20% bioavailability and has a short half life of 2–4 h (2). CYT is usually required to be administered intravenously and is available as multidose vials. The conventional parenteral therapy is painful to the patients even with as little as effective concentration and cause severe side effects. Thus improvement of treatment modalities for leukemia requires a drug delivery system which can provide sustained release of the drug.
The release of cytarabine has been earlier sustained by using different drug delivery systems such as slow releasing hydrogels (3), niosomes (4), liposomes (5), acryloylated polyaspartamide-based nanoparticles in without microemulsion (6) and comatrices of albumin microspheres (7) but poly(lactide-coglycolide) (PLGA)-based nanoparticles have not been reported.
The most widely used polymers for biodegradable nanoparticles have been poly(lactic acid) (PLA), poly(glycolic acid) (PGA), and their co polymers, PLGA (8). These polymers are known for their biocompatibility and resorbability through natural pathways. Additionally, the degradation rate and accordingly the drug release rate can be manipulated by varying the ratio of PLA to PGA (9). Since the biodegradable polymers are degraded in a certain period of time, they are not harmful to the human body. PLGA is degraded into non-toxic lactic acid and glycolic acid in the body. Therefore, drug delivery systems based on these polymers can be applied in the sustained release of drugs (10).
Nanoprecipitation is a simple method used for encapsulation of both hydrophilic and hydrophobic drugs in nanoparticles (11). The method results in instantaneous formation of nanoparticles, is easy to perform technique, can be easily scaled up and is a one-step procedure. The method requires addition of two solvents that are miscible with each other and results in spontaneous formation of nanoparticles on phase separation. From the two solvents ideally, the first one (solvent) is the one in which the polymer and the drug dissolves but not in the second system (the non-solvent) (12). Fessi and co-workers were the first to develop and patent the nanoprecipitation method for preparation of nanoparticles for use in drug delivery (13,14). A modified nanoprecipitation method utilizes use of a co-solvent to either increase the entrapment efficiency of the drug in nanoparticles or to reduce the mean particle size of the nanoparticles.
The present investigation was aimed at developing cytarabine-loaded PLGA-based biodegradable nanoparticles by a modified nanoprecipitation which would have sustained release of the drug. The prolonged drug release with the PLGA nanoparticles would reduce the side effects associated with the conventional leukemia therapy by reducing dosing frequency and reducing pain at the site of injection. The drug delivery would be given as a single-shot injection by intravenous route that would release the drug for a sustained period and would be beneficial in better control of leukemia therapy.
MATERIALS AND METHODS
Materials
Cytarabine was obtained as a gift sample from Biocon Ltd., Bangalore, poly(DL lactide-co-glycolide) PLGA 50:50 (inherent viscosity 0.22 dl/g) was obtained as a gift sample from Boehringer Ingelheim Limited, Germany, Pluronic F-68 (BASF) was obtained as a gift sample from Alembic Ltd, Vadodara. Chloroform, methanol, acetone, potassium dihydrogen phosphate, disodium hydrogen phosphate, hydrochloric acid and sodium hydroxide were obtained from SD fine Chemicals, Mumbai, Synthetic cellulose membrane with molecular weight cut-off (MWCO) of 12,000–14,000 D was procured from Himedia Labs, Mumbai.
Formulation Development of Cytarabine-Loaded PLGA Nanoparticles
Modified nanoprecipitation method was used for the preparation of nanoparticles (15). Hydrophilic drug (5 mg of CYT) was dissolved in an aqueous phase consisting of a solvent (0.3 ml of distilled water) and a co-solvent (0.6 ml of methanol). Polymer (25 mg of PLGA) was dissolved in an organic phase consisting of a non-solvent (4 ml of chloroform). The organic phase was then added drop wise to aqueous phase under stirring. Finally, the above mixture was added drop wise to 10 ml of distilled water containing 0.5% w/v of Pluronic F-68. Organic solvent was removed by stirring over night. Nanoparticles were then recovered from the nanodispersion by centrifugation (Sigma centrifuge) for 30 min at 25,000 rpm, washed two times with distilled water to remove unentrapped drug. The dispersion was finally lyophilized (Heto Dry Winner, Denmark) for 24 h to yield freeze-dried nanoparticles. Samples were frozen at −70°C and placed immediately in the freeze-drying chamber. Different concentrations of sucrose in 10%, 20%, 50%, 75%, and 100% w/w of the total solid content were used as cryoprotectant.
The method was first optimized for the choice of a co-solvent. Then a 32 factorial design was used to investigate the effect of volume of co-solvent and volume of non-solvent. Finally, a second 32 factorial design was used to investigate the effect of drug: polymer ratio and stirring time on mean particle size (MPS) and percentage of entrapment efficiency (%EE).
Investigation on Choice of Co-Solvent
The Choice of Co-solvent was Based on Least MPS
Three batches in triplicate were taken, first without a co-solvent, second with acetone, and third with methanol.
Use of 32 Factorial Design
Effect of Volume of Co-solvent and Non-solvent on MPS
Nine batches were prepared as per 32 factorial design to study the effect of two independent variables, volume of the co-solvent (X1) and volume of non-solvent (X2) on the response, MPS (Y1) of the Cyt-PLGA Nanoparticles. Each factor was tested at three levels designated as −1, 0 and +1. The regression equation for the response was calculated using Eq. 1.
Response:
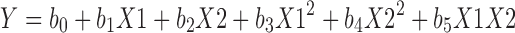 |
1 |
The responses in the above equation Y are the quantitative effect of the formulation components or independent variables X1 and X2; b is the co-efficient of the term X.
Effect of Drug: Polymer Ratio and Stirring Time on MPS and %EE
After investigation of volume of co-solvent and non-solvent nine batches were further prepared as per 32 factorial design to study the effect of two independent variables, ratio of drug and polymer (X1), stirring time (X2) on the two responses, MPS (Y2) and percentage entrapment efficiency (%EE; Y3) of the Cyt-PLGA Nanoparticles. Each factor was tested at three levels designated as −1, 0, and +1.
The values of the factors were transformed to allow easy calculation of co-efficient in polynomial equation. To identify the effect of significant variables, the reduced model was generated (16). Interactive multiple regression analysis and F statistics was utilized in order to evaluate the response.
The multiple regression was applied using Microsoft excel in order to deduce the factors having significant effect on the formulation properties. To identify the significant variables, the variables having p value >0.05 in the full model were discarded and then the reduced model was generated for both the independent variables and each type of formulation.
In this mathematical approach, each experimental response (Y) can be represented by a quadratic equation of the response surface. Y is the measured response and b is the estimated co-efficient for the factor X. The coefficients corresponding linear effects (X1 and X2), interaction (X1X2), and the quadratic effects (X12 and X22) were determined from the results of experiments.
Surface Response Plots
Surface response plots are diagrammatic representation of the values of the response. They are helpful in explaining the relationship between independent and dependent variables. Response surface methodology (RSM) shows relationship between an experimental response and a set of input variables. RSM sets a mathematical trend in the experimental design for determining the optimum level of experimental factors required for a given response (17). The reduced models were used to plot three dimension RSM using STATISTICA software at the values of X1 and X2 between −1 and +1 at predetermined values of responses.
Evaluation of Nanoparticles
Mean Particle Size
The freeze-dried nanoparticles were dispersed in distilled water for particle size analysis using Malvern Zetasizer 3000 (Malvern Instruments, UK). The measurement of nanoparticle size was based on photon correlation spectroscopy. Polydispersity index was studied to determine the narrowness of the particle size distribution. All the measurements were carried out in triplicate.
Surface Charge
Zeta potential was studied to determine the surface charge on the nanoparticles using Malvern Zetasizer 3000, (Malvern Instruments, UK). The zeta potential of the nanoparticles was determined using electrophoretic light scattering. Freeze-dried samples were suspended in distilled water and their zeta potential was determined. All the measurements were carried out in triplicate.
Differential Scanning Calorimetry Thermograms
Dry powder samples of the test samples (CYT, PLGA, and CYT-loaded PLGA NP) weighing 2–5 mg were placed in aluminum pans and were sealed with aluminum caps. Thermograms were taken on a differential scanning calorimeter (Mettler-Toledo, Switzerland) at a heating rate of 10°C/min in nitrogen atmosphere over a temperature range of 20–210°C.
Entrapment Efficiency
The entrapment efficiency was determined by extracting and quantifying the encapsulated drug using UV-spectroscopy; 100 mg of NPs were added to 10 ml of 1:1 mixture of chloroform and methanol. This dispersion was subjected to shaking at room temperature to ensure complete dissolution of the particles, the resulting solution was evaporated to dryness, and the dried residue was reconstituted with 5 ml of phosphate buffer saline. The reconstituted dispersion was centrifuged at 10,000 rpm for 15 min. In this extraction procedure, the drug was solubilised in PBS (pH 7.4) and the polymer which was not soluble remained in the pellet. The supernatant was analyzed for drug using UV-spectroscopy at λmax 271 nm using calibration curve of cytarabine in PBS. The %EE was calculated using the following formula-%EE = (amount of drug in the NPs/drug added in the formulation) × 100
Redispersibility of Lyophilized Nanoparticles
We used two methods for redispersing the lyophilized NP, manual shaking and sonication (18). First method used was manually shaking a weighed quantity of lyophilized NP (100 mg) in a test tube containing 5 ml of phosphate buffer saline pH 7.4. After gentle shaking for 2 min the nanosuspension was subjected to particle size measurement using Malvern zetasizer. Presences of particles of more than 1 μm were said to non-dispersible. In the second method, 100 mg of the lyophilized NP in a test tube containing 5 ml of phosphate buffer saline pH 7.4 was subjected to sonication for 2 min using a bath sonicator and redispersibility was checked as explained above.
In Vitro Drug Release Study
The dialysis bag diffusion technique was used to evaluate the in vitro drug release (19). The NP corresponding to 10 mg of cytarabine was placed in a dialysis bag with a Synthetic cellulose membrane tied and placed into 200 ml of phosphate buffer saline (PBS) pH 7.4 maintained at 37°C with continuous magnetic stirring in a beaker. At predetermined time intervals, aliquots were withdrawn from the acceptor compartment and replaced by the same volume of PBS. The drug content of the samples was determined by UV spectrophotometer at 271 nm. The tests were carried out three times and cumulative percentage drug release was calculated. The data was statistically analyzed using the Sigmastat software (Sigma Stat, USA).
Data obtained from in vitro release studies were fitted to Korsmeyer–Peppas equation (log Mt/M∞ = nlog t + k) to identify the mechanism of drug release from formulated NPs (20). Where Qt is the amount of drug released at time t and Q0 is the initial amount of drug present. Mt/M∞ is the fraction of drug released after time t in respect to amount of drug released at infinite time, k is the rate constant and n is the diffusional exponent which characterizes the transport mechanism.
Stability Studies
The optimized formulations were studied for their stability and their potential to withstand atmospheric/environmental changes. The freeze-dried (FD) samples and aqueous dispersion (AD) were sealed in Type-I amber colored glass vials. The samples were stored at 2–8°C, 25°C, and 40°C. Samples were withdrawn at 1, 2, and 3 months time interval and analyzed for mean particle size and drug content. Each study was performed in triplicate.
RESULTS AND DISCUSSIONS
In the nanoprecipitation method, an organic solution of the polymer is emulsified in an aqueous solution (with or without a surfactant). Then the organic solvent is removed by stirring (with or without vacuum) and this process allows nanoparticle formation. This method has drawback if the drug to be encapsulated is hydrophilic, because the drug may leak out in the aqueous solution. Hence, we modified the method and as suggested by Peltonen et al. (15) used a co-solvent in the aqueous phase.
Choice of Co-solvent
For the optimization of choice of co-solvent, the different formulation conditions and MPS obtained are shown in Table I. With acetone, the particle size achieved was higher compared with methanol because of the tendency of drug substance to precipitate in the presence of acetone. Based on the least MPS (138 nm) obtained for batch No. cytarabine-loaded PLGA NP (CPN)P3, methanol was chosen as the co-solvent.
Table I.
Effect of Co-solvent on Mean Particle Size of Cyt-PLGA NP
| Batch No. | Aqueous Phase (1 ml) | Organic phase (4 ml) | MPS (nm) ± SDa | ||
|---|---|---|---|---|---|
| Drug (mg) | Volume of co-solvent | Polymer PLGA (mg) | Volume of chloroform (ml) | ||
| CPNP1 | 5 | No co-solvent | 25 | 4 | 250 ±12.0 |
| CPNP2 | 5 | Acetone, 0.3 ml | 25 | 4 | 195 ± 6.2 |
| CPNP3 | 5 | Methanol, 0.3 ml | 25 | 4 | 138 ± 7.8 |
aStandard deviation (n = 3)
Effect of Volume of Co-solvent and Non-solvent on MPS
Table II displays the values of factors, their levels and transformed values and values of the response (Y1).
Table II.
Formulation of Cyt-PLGA NP for Optimization of Volume of Co-solvent and Non-solvent
| Batch No. | Real value | Transformed values | Response | |||||
|---|---|---|---|---|---|---|---|---|
| Volume of the co-solvent (ml) X1 | Volume of the non-solvent (ml) X2 | X1 | X2 | X12 | X22 | X1X2 | MPS (nm) ± SDa Y1 | |
| CPNP4 | 0.3 | 2 | −1 | −1 | 1 | 1 | 1 | 147 ± 7.1 |
| CPNP5 | 0.3 | 5 | −1 | 0 | 1 | 0 | 0 | 137 ± 2.3 |
| CPNP6 | 0.3 | 8 | −1 | 1 | 1 | 1 | −1 | 142 ± 6.2 |
| CPNP7 | 0.6 | 2 | 0 | −1 | 0 | 1 | 0 | 137 ± 7.6 |
| CPNP8 | 0.6 | 5 | 0 | 0 | 0 | 0 | 0 | 127 ± 3.1 |
| CPNP9 | 0.6 | 8 | 0 | 1 | 0 | 1 | 0 | 134 ± 5.2 |
| CPNP10 | 0.9 | 2 | 1 | −1 | 1 | 1 | −1 | 141 ± 3.4 |
| CPNP11 | 0.9 | 5 | 1 | 0 | 1 | 0 | 0 | 137 ± 2.5 |
| CPNP12 | 0.9 | 8 | 1 | 1 | 1 | 1 | 1 | 148 ± 5.6 |
Batches taken as per 32 factorial design: factors, their levels, transformed values and response: MPS
MPS mean particle size
aStandard deviation (n = 3)
Response-Mean Particle Size
The mean particle size of NP ranged from 127 ± 3.1 to 148 ± 5.6 nm. The lowest MPS was observed in middle level of X1 (0.6 ml) and middle level of X2 (5.0 ml) in batch CPNP8.
Table III shows model coefficients estimated by multiple linear regression for MPS. The regression coefficients having P value <0.05 are highly significant. The terms having coefficients with P value >0.05 are least contributing in the prediction of mean particle size and hence the factor X1 and X2 having P value >0.05 were removed from the full model to give the reduced model equation.
Table III.
Model Coefficients Estimated by Multiple Linear Regression for MPS
| Full model | Reduced model | ||
|---|---|---|---|
| Factor | Co-efficient value | P value | P value |
| Intercept | 127.444 | 1.18E-06 | 2E-10 |
| X1 | 0 | 1 | |
| X2 | −0.166 | 0.787 | |
| X12 | 9.333 | 0.002 | 6.79E-05 |
| X22 | 7.833 | 0.004 | 0.000158 |
| X1X2 | 3 | 0.022 | 0.002709 |
The Eq. 2 explains the reduced model for Y1 (MPS).
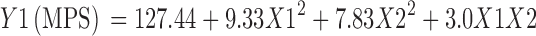 |
2 |
Analysis of variance (ANOVA) of full and reduced model for MPS is shown in Table IV. Model F value was assessed by the F statistic, which estimates the percentage of the variability in the outcome (21). Full model F value (34.5923) was more than the tabulated F value (Ftab = 9.01), implying that the model was significant. Model F value of the reduced model was 93.34891 and the Ftab value was 5.41, showing that the model was significant.
Table IV.
Regression Analysis of Variance (ANOVA) of Full and Reduced Model for MPS
| Full model regression | Reduced model regression | |
|---|---|---|
| F | 34.592 | 93.348 |
| Significance f | 0.00744 | 8.25E-05 |
| R 2 | 0.9829 | 0.9824 |
| Adj R 2 | 0.9545 | 0.9719 |
The R2 value is a measure of total variability explained by the model. The R2 value of 0.98295 for the full model indicated that the model was significant. That means the model can explain 98.29% of varibility around the mean. R2 of the reduced model was 0.982459, which was also high but slightly lower than the full model. The numbers of factors in the full model are more than the reduced model, therefore the R2 value increases (22). This explains the higher R2 value of the full model than the reduced model. In such cases, the term R2 adjusted has to be checked. It is called adjusted as the value has been adjusted for the size of the model. The R2 adjusted decreases when non-significant terms are added to the equation. Removal of non-significant terms improves the value of R2 adjusted. In our present model the value of R2 adjusted in the reduced model is 0.982459, which was greater than the R2 adjusted value of the full model (0.95453).
Table V shows each of the observed values of Y in both full and reduced model and was compared with the predicted values of Y from each model. The residual value and percent error was calculated to show the correlation between the observed and the predicted values. The low residuals values and the percentage error was less than 5% showed significance of the model used.
Table V.
Observed Responses and Predicted Values for Full and Reduced Model MPS
| Full model | Reduced model | ||||||
|---|---|---|---|---|---|---|---|
| Batch No. | Observed value | Predicted value | Residual value | %Error | Predicted value | Residual value | %Error |
| CPNP4 | 147 | 147.777 | −0.777 | 0.528 | 147.611 | −0.611 | 0.415 |
| CPNP5 | 137 | 136.777 | 0.222 | 0.162 | 136.777 | 0.222 | 0.162 |
| CPNP6 | 142 | 141.444 | 0.555 | 0.390 | 141.611 | 0.388 | 0.273 |
| CPNP7 | 137 | 135.444 | 1.555 | 1.095 | 135.277 | 1.722 | 1.256 |
| CPNP8 | 127 | 127.444 | −0.444 | 0.349 | 127.444 | −0.444 | 0.349 |
| CPNP9 | 134 | 135.111 | −1.111 | 0.829 | 135.277 | −1.277 | 0.952 |
| CPNP10 | 141 | 141.777 | −0.777 | 0.551 | 141.611 | −0.611 | 0.433 |
| CPNP11 | 137 | 136.777 | 0.222 | 0.162 | 136.777 | 0.222 | 0.162 |
| CPNP12 | 148 | 147.444 | 0.555 | 0.375 | 147.611 | 0.388 | 0.262 |
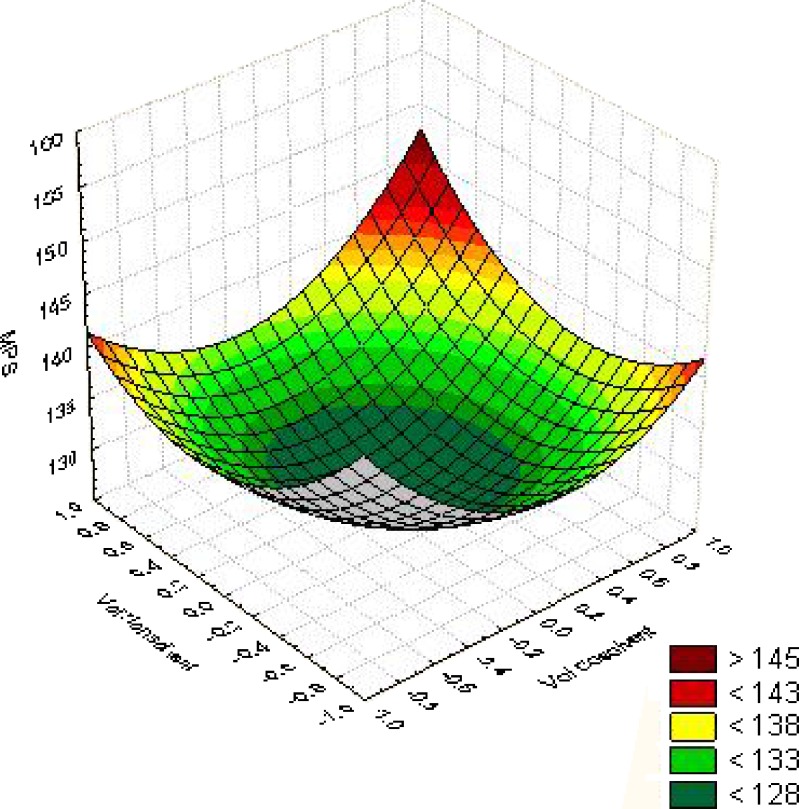
The response surface curves drawn at −1 level to 1 level of X1 and X2 for the values of the response is shown in Fig. 1 to give a diagrammatic representation of the same. The plots were found to be non-linear; therefore non-linear relationship exists between X1 and X2 variables. It was concluded from the non-linear plots that the MPS of 128 nm could be obtained with X1 range from 0.22 level (0.22 ml) to −0.22 level (0.37 ml) and X2 range from 0.23 (1.7 ml) to −0.24 (3.2 ml).
Fig. 1.
Surface response plot for optimization of volume of co-solvent and non-solvent, response-MPS
Effect of Drug: Polymer Ratio and Stirring Time on MPS and %EE
Nine batches were prepared as per 32 factorial design to study the effect of two independent variables, ratio of drug and polymer (X1), stirring time (X2) on the two responses, mean particle size (Y2) and percentage entrapment efficiency (Y3) of the Cyt-PLGA Nanoparticles. Table VI displays the values of Factors, their levels and transformed values and values of the responses, MPS and %EE as per 32 factorial design.
Table VI.
Formulation of Cyt-PLGA NP for Optimization of Drug: Polymer Ratio and Stirring Time
| Real value | Transformed values | Response | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Batch No. | Drug: polymer ratio (mg) X1 | Stirring time (min) X2 | X1 | X2 | X12 | X22 | X1X2 | MPS (nm) ± SDa Y2 | %EE ± SDa Y3 |
| CPNP13 | 1:5 | 10 | −1 | −1 | 1 | 1 | 1 | 142 ± 4.1 | 15.0 ± 2.3 |
| CPNP14 | 1:5 | 20 | −1 | 0 | 1 | 0 | 0 | 129 ± 3.2 | 17.8 ± 3.7 |
| CPNP15 | 1:5 | 30 | −1 | 1 | 1 | 1 | −1 | 125 ± 2.5 | 21.8 ± 2.0 |
| CPNP16 | 1:10 | 10 | 0 | −1 | 0 | 1 | 0 | 148 ± 2.9 | 19.6 ± 2.2 |
| CPNP17 | 1:10 | 20 | 0 | 0 | 0 | 0 | 0 | 135 ± 3.2 | 20.0 ± 2.1 |
| CPNP18 | 1:10 | 30 | 0 | 1 | 0 | 1 | 0 | 131 ± 4.0 | 21.6 ± 1.2 |
| CPNP19 | 1:15 | 10 | 1 | −1 | 1 | 1 | −1 | 151 ± 2.4 | 20.0 ± 2.1 |
| CPNP20 | 1:15 | 20 | 1 | 0 | 1 | 0 | 0 | 139 ± 0.9 | 21.6 ± 4.2 |
| CPNP21 | 1:15 | 30 | 1 | 1 | 1 | 1 | 1 | 134 ± 2.5 | 22.0 ± 2.1 |
Batches taken as per 32 factorial design: factors, their levels, transformed values and response: MPS and %EE
MPS mean particle size, %EE percentage entrapment efficiency
aStandard deviation (n = 3)
The concentration of drug was kept constant at 5 mg/batch, and the concentration of polymer was varied from 25, 50, and 75 mg to give drug: polymer ratio of 1:5, 1:10, and 1:15. These three different ratios were tested at three different stirring rates of 10, 20, and 30 min and in this way nine batches were prepared as per 32 factorial design.
Response-Mean Particle Size
The mean particle size of NP ranged from 125 ± 2.5 to 151 ± 2.4. The lowest MPS was observed in lowest level of X1 (1:5) and highest level of X2 (30 min) in batch CPNP15.
Table VII shows model coefficients estimated by multiple linear regression for MPS. The factor X1X2 having P value >0.05 was removed from the full model to give the reduced model Eq. 3 for Y2 (MPS).
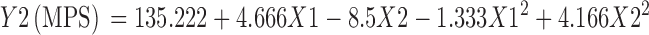 |
3 |
Table VII.
Model Coefficients Estimated by Multiple Linear Regression for MPS and %EE
| MPS | %EE | |||||
|---|---|---|---|---|---|---|
| Full model | Reduced model | Full model | Reduced model | |||
| Factor | Co-efficient value | P value | P value | Co-efficient value | P value | P value |
| Intercept | 135.222 | 2.11E-08 | 6.84E-11 | 19.777 | 1.56E-05 | 1.93E-07 |
| X1 | 4.666 | 8.38E-05 | 4.31E-06 | 1.166 | 0.011181 | 0.00332 |
| X2 | −8.5 | 1.39E-05 | 3.94E-07 | 1.333 | 0.007678 | 0.002019 |
| X12 | −1.333 | 0.0162 | 0.0048 | −0.166 | 0.674941 | |
| X22 | 4.1666 | 0.0006 | 6.02E-05 | 0.333 | 0.422826 | 0.360051 |
| X1X2 | 0 | 1 | −0.5 | 0.144294 | 0.093599 | |
ANOVA of full and reduced model for MPS is shown in Table VIII. The F values for both the full model (813.3) and the reduced model (1,355.5) were more than their tabulated value (Ftab = 9.01) suggesting that the models were significant. The R2 value was more than 0.99 for both the full and reduced models. The value of R2 adjusted in the reduced model (0.9992) was greater than the R2 adjusted value of the full model (0.9980).
Table VIII.
Regression Analysis of Variance (ANOVA) of Full and Reduced Model for MPS and %EE
| MPS | %EE | |||
|---|---|---|---|---|
| Full model regression | Reduced model regression | Full model regression | Reduced model regression | |
| F | 813.3 | 1,355.5 | 15.5142 | 24.066 |
| Significance f | 6.79E-05 | 1.63E-06 | 0.02358 | 0.0046 |
| R 2 | 0.999263 | 0.999262 | 0.962766 | 0.96010 |
| Adj R 2 | 0.99803 | 0.99852 | 0.900709 | 0.92021 |
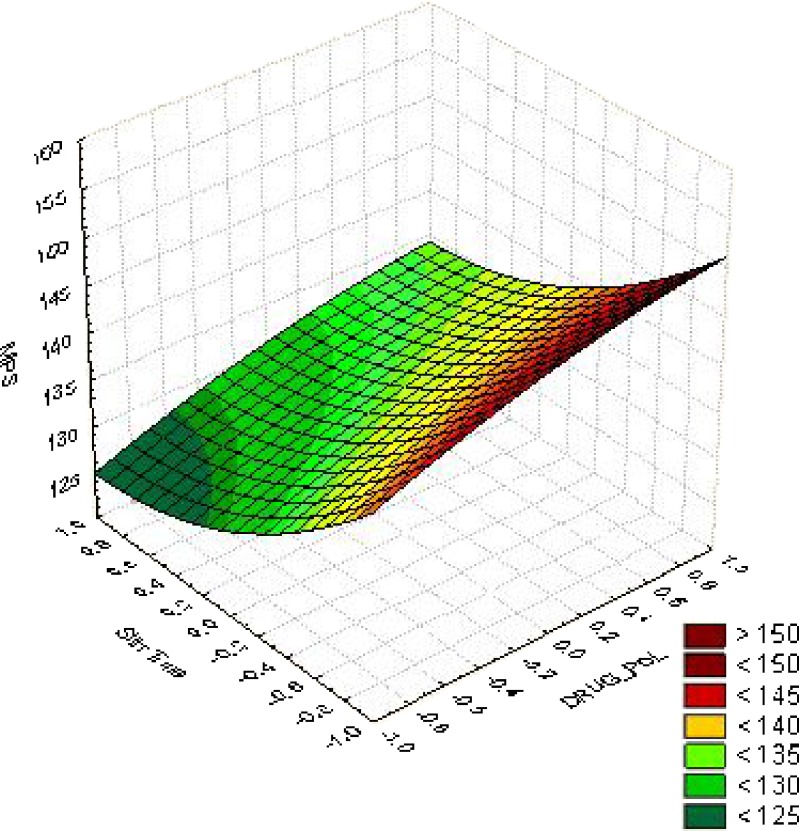
From the response surface curves for MPS (Fig. 2) it was concluded that the MPS of 125 nm could be obtained with X1 range from −0.6 level (1:7) to −1.0 level (1:5) and X2 range from 0.2 (22 min) to 1.0 (30 min).
Fig. 2.
Surface response plot for MPS for optimization of drug: polymer ratio and stirring time X1 (drug: polymer ratio) and X2 (stirring time) values ranging from −1 to +1
Response-Entrapment Efficiency
The %EE of CYT in PLGA NP varied from 15.0 ± 2.3% to 22.0 ± 2.1. Highest %EE of 22.0% was observed at the highest levels of X1 (1:15) and X2 (30 min) and %EE of 21.8%, was observed at the lowest level of X1 (1:5) and highest level of X2(30 min). We chose the batch which had the lower MPS (Batch No. CPN15, %EE of 21.8%).
Table VII shows model coefficients estimated by multiple linear regression for%EE. The factor X12, X22, and X1X2 having P value >0.05 were removed from the full model to give the reduced model Eq. 4.
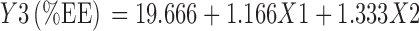 |
4 |
The results of the regression output and are presented in Table VII and ANOVA of the model is presented in Table VIII. Model F value for the full model (15.5142) and reduced model (24.0666) was more than the tabulated F value (Ftab = 9.01), implying that the models were significant. The value of R2 adjusted in the reduced model (0.9202) was greater than the R2 adjusted value of the full model (0.9007).
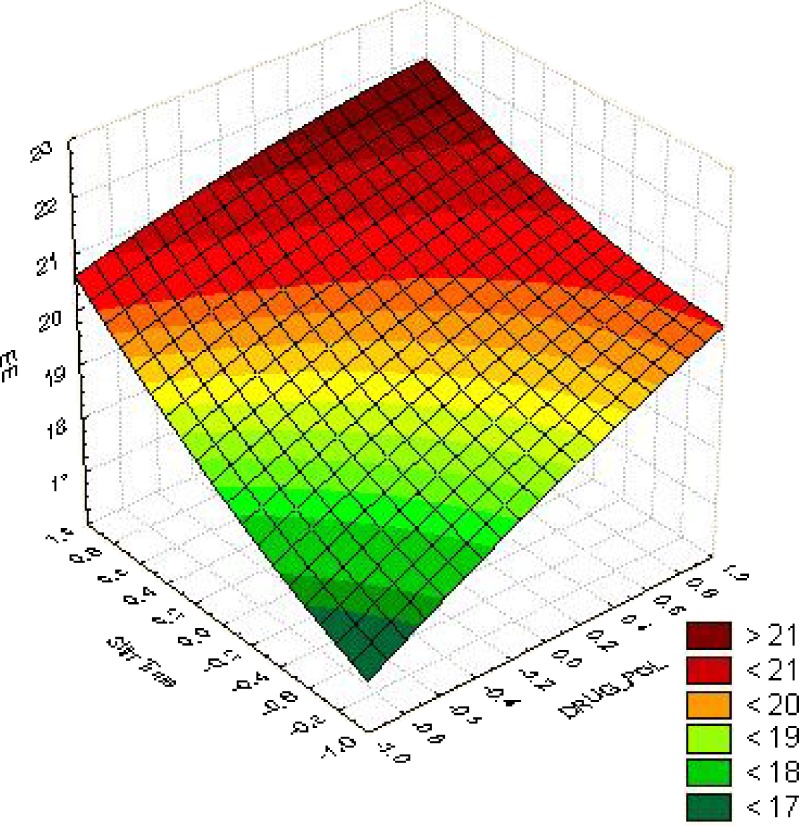
From the response surface curves for %EE (Fig. 3), it was concluded that the %EE of 21% could be achieved with X1 ranging from 1.0 (1: 15) to 0.6 (1:13) and X2 ranging from 0.8 (28 min) to 1.0 (30 min).
Fig. 3.
Surface response of EE for optimization of drug: polymer ratio and stirring time
Lyophilization and Optimization of Cryoprotectant
Lyophilization is the process in which freeze-drying is done to remove solvent from the formulation and therefore improve its stability upon storage. The process of freeze-drying is stressful and hence a cryoprotectant is added in the process, which also helps in redispersibility of the freeze-dried nanoparticle in a suitable solvent (23). One of the main challenges during the freeze-drying process is preserving or rather increasing the redispersibility of the nanoparticles upon reconstitution with distilled water or buffer saline. Redispersants are generally added to the nanoparticles prior to the drying step. Commonly used cryoprotectants such as sugars also act as redispersants. Cryoprotectants such as sorbitol, mannitol, glucose, trehalose can be used to increase the physical stability of nanoparticles during freeze-drying (24).
In the present study we have used sucrose in five different concentrations of 10%, 20%, 50%, 75%, and 100% w/w to act as both a cryoprotectant and a redispersant.
Freeze-drying has an effect of increasing particle size after lyophilization, probably due to aggregation of nanoparticles during this process; therefore we checked the redispersibility of the particles after lyophilization. If the aggregated particles do not separate during redispersion, then larger particle sizes would be observed which were not desired.
Table IX indicates the different concentrations of sucrose used and its effect on particle size after lyophilization. Optimization of the cryoprotectant was based on its ability to give minimum increase in MPS and dispersibility. An increase in size of the NPs was seen following freeze-drying with the use of sucrose as cryoprotectant. All the formulations above 50% w/w sucrose had good dispersibilty and it was seen that use of sucrose in a 50% w/w concentration showed minimum increase in particle size of the Cyt-PLGA NP. Use of higher concentrations of cryoprotectants made the NP dispersible but an increase in MPS was also observed. So higher concentrations of more than 50% w/w for Cyt-PLGA NP were not selected..
Table IX.
Optimization of Sucrose as Cryoprotectant and its Effect on Mean Particle Size and Redispersibility
| % w/w Sucrose | Cyt-PLGA NP | |||||||
|---|---|---|---|---|---|---|---|---|
| Mean particle Size (nm) ± SD | PDI ± SD | Zeta potential (mV) ± SD | Redispersibility | |||||
| BL | AL | BL | AL | BL | AL | MS | SO | |
| 0 | 125 ± 2.5 | 212 ± 2.1 | 0.092 ± 0.024 | 0.352 ± 0.081 | −29.6 ± 2.1 | −30.2 ± 1.1 | ND | ND |
| 10 | 125 ± 2.5 | 149 ± 1.3 | 0.092 ± 0.024 | 0.185 ± 0.054 | −29.6 ± 2.1 | −29.4 ± 1.8 | ND | ND |
| 20 | 125 ± 2.5 | 135 ± 0.9 | 0.092 ± 0.024 | 0.176 ± 0.051 | −29.6 ± 2.1 | −29.0 ± 1.3 | ND | D |
| 50 | 125 ± 2.5 | 129 ± 1.8 | 0.092 ± 0.024 | 0.071 ± 0.011 | −29.6 ± 2.1 | −28.3 ± 1.1 | D | D |
| 75 | 125 ± 2.5 | 147 ± 2.2 | 0.092 ± 0.024 | 0.189 ± 0.066 | −29.6 ± 2.1 | −28.2 ± 1.0 | D | D |
| 100 | 125 ± 2.5 | 152 ± 1.6 | 0.092 ± 0.024 | 0.182 ± 0.080 | −29.6 ± 2.1 | −27.8 ± 1.4 | D | D |
BL Before lyophilization, AL after lyophilization, PDI polydispersity index, MS manual shaking, SO sonication, D dispersible, ND non-dispersible
Effect of Lyophilization on Polydispersity Index and Zeta Potential
The other two parameters evaluated before and after lyophilization were polydispersity index and zeta potential.
Polydispersity index (PdI) is a measure of dispersion homogeneity and usually ranges from 0 to 1. Values close to 0 indicate a homogeneous dispersion while those greater than 0.3 indicate high heterogeneity (25). Table IX shows the effect of lyophilization on MPS and PdI on the formed nanoparticles of the six batches. PdI values were less than 0.3 for all batches except the batch in which there was no croprotectant. It was concluded that Batch using 50% sucrose had the least PdI (0.071) and was considered optimum as it also had least increase in MPS.
Zeta potential is the potential at the hydrodynamic shear plane and can be determined from the particle mobility under an applied electric field. The mobility will depend on the effective charge on the surface. Zeta potential information is helpful in predicting the storage stability of colloidal dispersions (26). In general, greater the zeta potential value of a nanoparticulate system better is the colloidal suspension stability due to repulsion effect between charged nanoparticles. The zeta potential value was −29.6 ± 2.1 before lyophilization and after lyophilization it was in the range of −30.2 ± 1.1 to −27.8 ± 1.4 mV. Zeta potential values in the −15 to −30 mV are common for well-stabilized nanoparticles (27). Hence it was concluded that the NPs would remain stable under storage. The presence of sucrose did not have a significant change on the surface charge of the NPs.
It was concluded that 50% w/w of sucrose in Cyt-PLGA NP can be added as cryoprotectant during lyophilization for freeze-dried NPs having good dispersibility with minimum increase in their mean particle sizes and with no significant change in PdI and surface charge.
Differential Scanning Calorimetry Studies
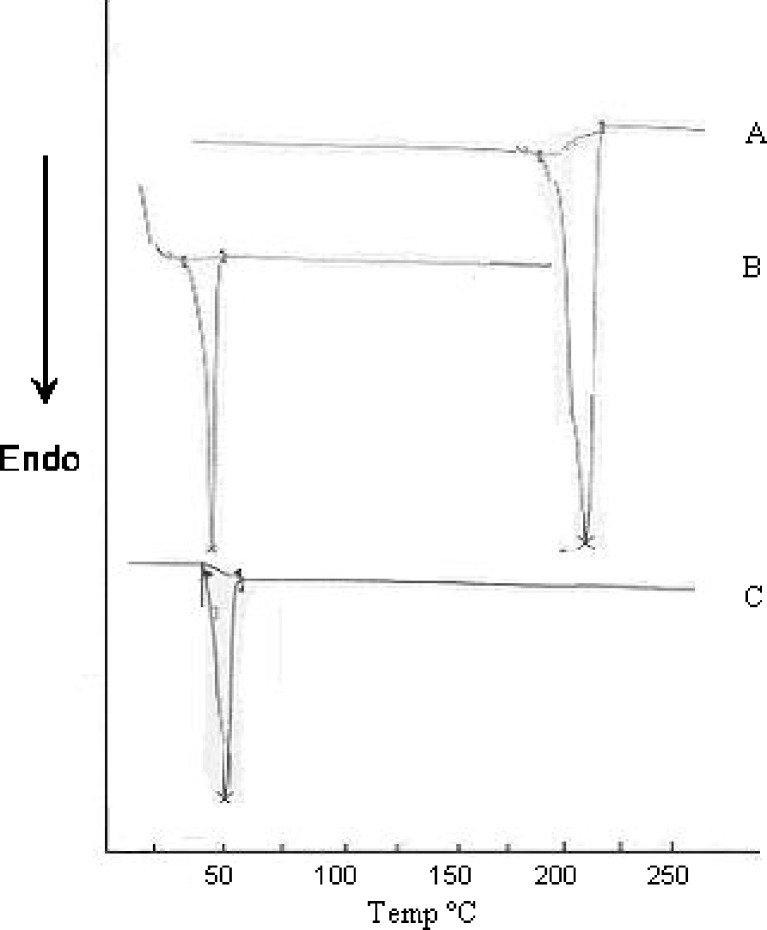
Differential scanning calorimetry (DSC) gives information regarding the physical properties like crystalline or amorphous nature of the samples. The DSC thermograms (Fig. 4) of cytarabine, PLGA and Cyt-PLGA NP depicted characteristic endothermic peaks. Onset of cytarabine was seen at 191.23°C, endset at 218.20°C, and the peak was at 211.94°C. PLGA had onset at 41.60°C, endset was seen at 51.17°C, and peak at 48.11°C. Cyt-PLGA NP had onset at 45.81°C, endset 54.04°C, and peak at 50.02°C. These endothermic curves showed that the drug peak was absent in nanoparticle formulation, indicating drug was dispersed as an amorphous state in the nanoparticle (28). Hence, it could be concluded that in the prepared PLGA NP, the drug was present in the amorphous phase and may have been homogeneously dispersed in the PLGA matrix.
Fig. 4.
DSC thermogram of a cytarabine, b PLGA, and c Cyt-PLGA NP
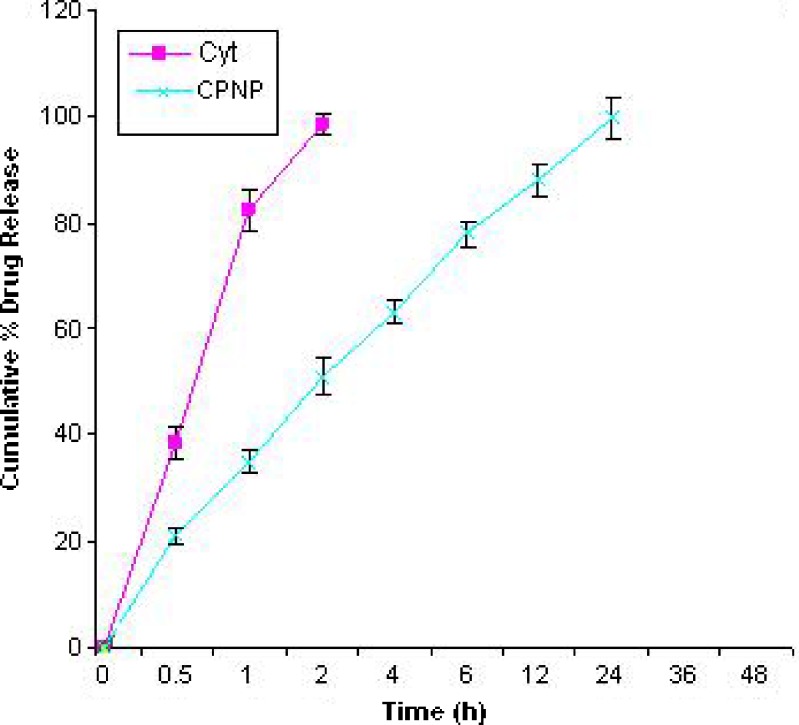
In Vitro Drug Release
In vitro drug release from the pure drug was complete within 2 h, but was sustained up to 24 h from PLGA nanoparticles. The release profile is shown in Fig. 5.
Fig. 5.
In vitro drug release profile of cytarabine pure drug (Cyt) and cytarabine-loaded PLGA nanoparticles (CPNP)
CPN released 34% in 1 h and 51% in 2 h. The release from Cyt-PLGA NP was sustained till 24 h. The sustained release of the drug may be attributed to the PLGA’s property to sustain the release of the entrapped drug in nanoparticles (29). The release data when fitted to Korsmeyer and Peppas equation found that the diffusion exponent (n value) was found to be 0.3754 for CPNP. The n value is the diffusional exponent which characterizes the transport mechanism and if its value is less than 0.43 it indicates a Fickian release (30). Hence the release mechanism from the NPs was Fickian.
It was concluded from the drug release studies that PLGA NP could sustain the release of CYT upto 24 h and the release mechanism was Fickian diffusion.
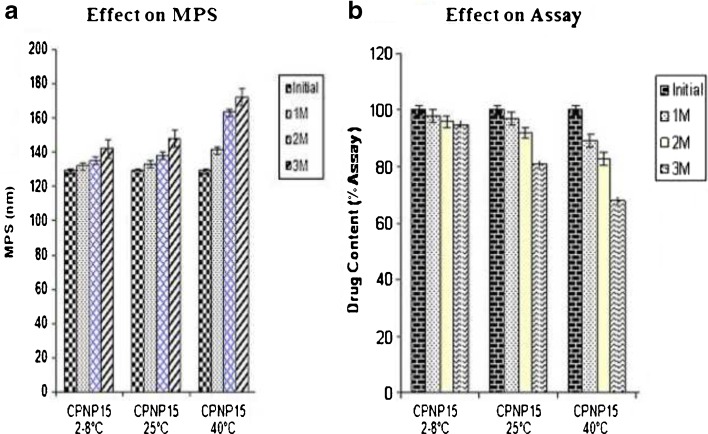
Stability Studies
Stability studies of polymeric nanoparticles were carried out to evaluate the change in mean particle size and drug content over a period of 3 months storage at 2–8, 25 and 40°C. The change in the mean particle size and drug content at 2–8°C for 1 and 2 M for cytarabine-loaded PLGA NP (CPNP15) (Fig. 6a, b) was not significant (P > 0.05). There was significant difference (P < 0.05) in the change in the mean particle size and drug content of CPNP15 at 3 M. The MPS of CPNP15 increased from initial 129 nm to 142 nm in 3 M. The drug content of CPNP15 decreased to 96% in the 3 M. After storage at 25°C, there was no significant change (P > 0.05) in the mean particle size and in drug content at 25°C for 1 M. But there was a significant change in the mean particle size and%EE of CPNP15 at 25°C for 2 and 3 M. The size of the particles increased significantly in the 2 and 3 M. The MPS of CPNP15 increased from initial 129 nm to 138 and 148 nm in 2 and 3 M, respectively. The drug content for CPNP15 decreased to 92% and 81% in the 2 and 3 M, respectively. After storage at 40°C CYT-loaded loaded PLGA NP (CPNP15) were not stable at 40°C as there was significant change (P < 0.05) in both the mean particle size and in the drug content. The MPS of CPNP15 increased from initial 129 nm to 141, 163 and 172 nm in 1, 2 and 3 M respectively. The drug content of CPNP15 decreased to 89%, 83%, and 68% in the 1, 2, and 3 M, respectively.
Fig. 6.
Effect of storage at 2–8°C, 25°C, and 40°C on lyophilized cytarabine-loaded PLGA NP (Batch-CPNP15). The values are mean of three batches with ± SD
It was observed from the stability studies that cytarabine-loaded PLGA NP were stable at 2–8°C for 2 M and at 25°C for 1 M as there was no significant change in the mean particle size and in the drug content. Nanoparticles are not stable at higher temperatures (>25°C) due to aggregation of particles and degradation of the polymer (31).
It was concluded that the developed PLGA NPs should be stored in the freeze-dried state at 2–8°C where they would remain stable in terms of both MPS and drug content.
CONCLUSION
It was concluded that cytarabine could be effectively entrapped in PLGA-based nanopartilces by using a modified nanoprecipitation method. The developed nanoparticles had a sustained release of drug for 24 h with Fickian diffusion. The PLGA-based cytarabine nanoparticles were stable in freeze-dried state at 2–8°C for 2 months. This sustained drug release of cytarabine would reduce the side effects associated with the conventional leukemia therapy by reducing dosing frequency and reducing pain at the site of injection. The drug delivery could be given as a single-shot injection by IV route that would release the drug for a sustained period and would be beneficial in better control of leukemia therapy. However, further studies are required to be carried out in animals to confirm the pharmacological activities.
Contributor Information
Khushwant S. Yadav, Email: khush.yadav@gmail.com
Krutika K. Sawant, Phone: +91-265-2434187, FAX: +91-265-2418927, Email: dr_krutikasawant@yahoo.co.in
References
- 1.Ho DHW, Frei E. Clinical pharmacology of 1-B-D arabinofuranosylcytosine. Clin Pharmacol Ther. 1971;12:944–954. doi: 10.1002/cpt1971126944. [DOI] [PubMed] [Google Scholar]
- 2.Knoester PD, Underberg WJM, Beijnen JH. Clinical pharmacokinetics and pharmacodynamics of anticancer agents in pediatric patients. Anticancer Res. 1993;13:1795–1808. [PubMed] [Google Scholar]
- 3.Blanco MD, Trigo RM, Teijón C, Gómez C, Teijón JM. Slow releasing of ara-C from poly(2-hydroxyethyl methacrylate) and poly(2-hydroxyethyl methacrylate-co-N-vinyl-2-pyrrolidone) hydrogels implanted subcutaneously in the back of rats. Biomaterials. 1998;19:861–869. doi: 10.1016/S0142-9612(97)00247-0. [DOI] [PubMed] [Google Scholar]
- 4.Ruckmani K, Jayakar B, Ghosal SK. Nonionic surfactant vesicles (Niosomes) of cytarabine hydrochloride for effective treatment of leukemias: encapsulation, storage, and in vitro release. Drug Dev Ind Pharm. 2000;26(2):217–222. doi: 10.1081/DDC-100100348. [DOI] [PubMed] [Google Scholar]
- 5.Subramanian N, Yajnik A, Murthy RSR. Artificial neural network as an alternative to multiple regression analysis in optimizing formulation parameters of cytarabine liposomes. AAPS PharmSciTech. 2004;5(1):1–9. doi: 10.1007/BF02830572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Craparo EF, Cavallaro G, Bondì ML, Giammona G. Preparation of polymeric nanoparticles by photo-crosslinking of an acryloylated polyaspartamide in w/o microemulsion. Macromol Chem Phys. 2004;205:1955–1964. doi: 10.1002/macp.200400128. [DOI] [Google Scholar]
- 7.Gómez C, Blanco MD, Bernardo MV, Olmo R, Muñiz E, Teijón JM. Cytarabine release from comatrices of albumin microspheres in a poly(lactide–co- glycolide) film: in vitro and in vivo studies. Eur J Pharm Biopharm. 2004;57:225–233. doi: 10.1016/S0939-6411(03)00154-1. [DOI] [PubMed] [Google Scholar]
- 8.Gliding DK, Reed AM. Biodegradable polymers for use in surgery: poly(glycolic)/poly (lactic acid) homo and co-polymers. Polymer. 1979;20:1459–1464. doi: 10.1016/0032-3861(79)90009-0. [DOI] [Google Scholar]
- 9.Wise DL, Fellmann TD, Sanderson JE, Wentworth RL. Lactic/glycolic acid polymers. In: Gregoridas G, editor. Drug carriers in biology and medicine. London: Academic; 1979. pp. 237–270. [Google Scholar]
- 10.Anderson JM, Shive MS. Biodegradation and biocompatibility of PLA and PLGA microspheres. Adv Drug Deliv Rev. 1997;28:5–24. doi: 10.1016/S0169-409X(97)00048-3. [DOI] [PubMed] [Google Scholar]
- 11.Barichello JM, Morishita M, Takayama K, Nagai T. Encapsulation of hydrophilic and lipophilic drugs in PLGA nanoparticles by the nanoprecipitation method. Drug Dev Ind Pharm. 1999;25(4):471–476. doi: 10.1081/DDC-100102197. [DOI] [PubMed] [Google Scholar]
- 12.Bilati U, Allemann E, Doelker E. Development of a nanoprecipitation method intended for the entrapment of hydrophilic drugs into nanoparticles. Eur J Pharm Sci. 2005;24:67–75. doi: 10.1016/j.ejps.2004.09.011. [DOI] [PubMed] [Google Scholar]
- 13.Fessi H, Puisieux F, Devissaguet JP, Ammoury N, Benita S. Nanocapsule formation by interfacial polymer deposition following solvent displacement. Int J Pharm. 1989;55:25–28. doi: 10.1016/0378-5173(89)90281-0. [DOI] [Google Scholar]
- 14.Fessi, H., Devissaguet, J.-P., Puisieux, F., Thies, C. 1992. Process for the preparation of dispersible colloidal systems of a substance in the form of nanoparticles. US Patent 593 522.
- 15.Peltonen L, Aitta J, Hyvönen S, Karjalainen M and Hirvonen J. Improved Entrapment Efficiency of Hydrophilic Drug Substance During Nanoprecipitation of Poly(l)lactide Nanoparticles. AAPS PharmSciTech 2004; 5 (1): Article 16. [DOI] [PMC free article] [PubMed]
- 16.Yadav KS, Sawant KK. Formulation optimization of etoposide loaded PLGA nanoparticles by double factorial design and their evaluation. Curr Drug Deliv. 2010;7:51–64. doi: 10.2174/156720110790396517. [DOI] [PubMed] [Google Scholar]
- 17.McCarron PA, Woolfson AD, Keating SM. Response surface methodology as a predictive tool for determining the effects of preparation conditions on the physicochemical properties of poly(isobutylcyanoacrylate) nanoparticles. Int J Pharm. 1999;193:37–47. doi: 10.1016/S0378-5173(99)00311-7. [DOI] [PubMed] [Google Scholar]
- 18.Freitas, Muller RH. Spray-drying of solid lipid nanoparticles (SLN™) Eur J Pharm Biopharm. 1998;46:145–151. doi: 10.1016/S0939-6411(97)00172-0. [DOI] [PubMed] [Google Scholar]
- 19.Levy MY, Benita S. Drug release from submicronized o/w emulsion: a new in vitro kinetic evaluation model. Int J Pharm. 1990;66:29–37. doi: 10.1016/0378-5173(90)90381-D. [DOI] [Google Scholar]
- 20.Korsmeyer RW, Gurny R, Doelker E, Buri P, Peppas NA. Mechanisms of solute release from porous hydrophilic polymers. Int J Pharm. 1983;15:25–35. doi: 10.1016/0378-5173(83)90064-9. [DOI] [PubMed] [Google Scholar]
- 21.Hocking RR. Analysis and selection of variables in linear regression. Biometrics. 1976;32:1–49. doi: 10.2307/2529336. [DOI] [Google Scholar]
- 22.Montegomery DC. Design and analysis of experiments. New York: Wiley; 2004. pp. 392–426. [Google Scholar]
- 23.Chacon M, Molpeceres J, Berges L, Guzman M, Aberturas MR. Stability and freeze-drying of cyclosporine loaded poly(D, L lactide-glycolide) carriers. Eur J Pharm Sci. 1999;8:99–107. doi: 10.1016/S0928-0987(98)00066-9. [DOI] [PubMed] [Google Scholar]
- 24.De Chasteigner S, Cave´ G, Fessi H, Devissaguet J-P, Puisieux F. Freeze-drying of itraconazoleloaded nanosphere suspensions: a feasibility study. Drug Dev Res. 1996;38:116–124. doi: 10.1002/(SICI)1098-2299(199606)38:2<116::AID-DDR6>3.0.CO;2-M. [DOI] [Google Scholar]
- 25.Ahlin P, Kristl J, Kristl A, Vrecer F. Investigation of polymeric nanoparticles as carriers of enalaprilat for oral administration. Int J Pharm. 2002;239:113–120. doi: 10.1016/S0378-5173(02)00076-5. [DOI] [PubMed] [Google Scholar]
- 26.Thode K, Muller RH, Kresse M. Two-time window and multiangle photon correlation spectroscopy size and zeta potential analysis-highly sensitive rapid assay for dispersion stability. J Pharm Sci. 2000;89:1317–1324. doi: 10.1002/1520-6017(200010)89:10<1317::AID-JPS9>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
- 27.Kesisoglou F, Panmai S, Wu Y. Nanosizing - Oral formulation development and biopharmaceutical evaluation. Adv Drug Deliv Rev. 2007;59:631–644. doi: 10.1016/j.addr.2007.05.003. [DOI] [PubMed] [Google Scholar]
- 28.Mandal TK, Bostanian LA, Graves RA, Chapman SR, Womack I. Development of biodegradable microcapsules as carrier for oral controlled delivery of amifostine. Drug Dev Ind Pharm. 2002;28(3):339–344. doi: 10.1081/DDC-120002849. [DOI] [PubMed] [Google Scholar]
- 29.Lamprecht A, Ubrich N, Hombreiro Pérez M, Lehr CM, Hoffman M, Maincent P. Influences of process parameters on nanoparticle preparation performed by a double emulsion pressure homogenization technique. Int J Pharm. 2000;196:177–182. doi: 10.1016/S0378-5173(99)00422-6. [DOI] [PubMed] [Google Scholar]
- 30.Peppas NA. Analysis of fickian and non-fickian drug release from polymers. Pharm Acta Helv. 1985;60:110. [PubMed] [Google Scholar]
- 31.Dunne M, Corrigan OI, Ramtoola Z. Influence of particle size and dissolution conditions on the degradation properties of polylactide-co-glycolide particles. Biomaterials. 2000;21:1659–1668. doi: 10.1016/S0142-9612(00)00040-5. [DOI] [PubMed] [Google Scholar]