Mechanism of Processive Movement of Monomeric and Dimeric Kinesin Molecules

Abstract

Kinesin molecules are motor proteins capable of moving along microtubule by hydrolyzing ATP. They generally have several forms of construct. This review focuses on two of the most studied forms: monomers such as KIF1A (kinesin-3 family) and dimers such as conventional kinesin (kinesin-1 family), both of which can move processively towards the microtubule plus end. There now exist numerous models that try to explain how the kinesin molecules convert the chemical energy of ATP hydrolysis into the mechanical energy to “power” their proceesive movement along microtubule. Here, we attempt to present a comprehensive review of these models. We further propose a new hybrid model for the dimeric kinesin by combining the existing models and provide a framework for future studies in this subject.

Introduction

Kinesin is a motor protein that transports cargo across cells by moving along microtubule (MT) filaments by hydrolysis of ATP ^1-5. Native kinesins generally have several forms of construct. This review focuses on two forms of them which have been studied extensively. One is the monomer such as KIF1A (kinesin-3 family ⁶) that has one N-terminal motor domain or head, whereas the other one is the dimer such as conventional kinesin (kinesin-1 family ⁶) that consists of two identical N-terminal motor domains or heads that are connected together by a rod-shaped, coiled-coil stalk through their neck linkers (NLs). Both forms can move towards the MT plus end.

For the two-headed kinesin-1, it has been determined that the dimer advances stepwise over the MT surface lattice in about 8 nm increments, the tubulin dimer repeat distance. A single molecule can generate hundreds of steps during a single encounter with a MT ^7,8 and can exert a maximal force of about 5-7.5 pN ^9-12. During the processive movement, the dimer only occasionally steps backwards under low backward loads ^13-15. It is now well known that the dimer moves along MT in a hand-over-hand manner ^16,17: a given head is displaced in discrete steps with a size of about 16 nm ¹⁷, resulting in the step size of the dimer of about 8 nm.

Among single-headed kinesins, it has been experimentally demonstrated that a single KIF1A molecule, like the dimeric kinesin-1 molecule, can also move processively along MT ^18,19. However, in contrast to the dimer, the step size of the monomer is distributed stochastically around multiples of 8 nm with a Gaussian-like envelope ²⁰. A single KIF1A molecule can only exert a maximal force of about 0.15 pN ²⁰. Interestingly, among truncated single-headed conventional kinesins, one has also been observed to move processively along MT ^21,22, similar to KIF1A, while others have been shown to have very low or no processivity ^23-26.

To understand the mechanism on how kinesin molecules convert chemical energy of ATP hydrolysis into mechanical energy to “power” their proceesive movement along MT, numerous models have been proposed for both monomeric and dimeric kinesin molecules ^{4,5,15-20,27-47}. In this review, we provide a broad classification to these models. We also present an intuitive description of each class of the models. The consistency and/or inconsistency between each class of the models and the available experimental data are discussed briefly. Based on these previous models, we propose a hybrid model for the dimeric kinesin and a framework for future studies.

Models for Processive Movement of Monomeric Kinesin

Broadly speaking, the models for the unidirectional motion of monomeric kinesin can be divided into two classes, which are described in the following two sections.

Brownian ratchet model with fluctuation of global potential

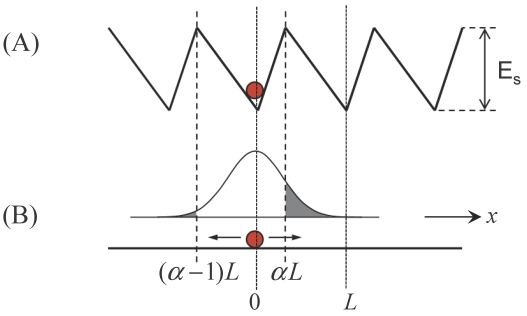
The prevailing model for the unidirectional motion of the monomeric kinesin along MT is described by the potentials as shown in Fig. 1 ^27,28 or those with minor variants ^18-20. Here, we take Fig. 1 as an example to discuss this class of models. For convenience, the model is termed as Brownian ratchet model with fluctuation of global potential (FGP model). In the model, the monomer is viewed as a Brownian particle moving in a periodic, piecewise but spatially asymmetric potential. The change in nucleotide states of the motor induces its conformational change ^48,49, which in turn induces the potential switching between “on” (corresponding to the kinesin in nucleotide-free, ATP or ADP.Pi state) and “off” states (corresponding to the kinesin in ADP state). When the potential is on, the particle is pinned near the bottom of one potential well (for example, at x = 0) (Fig. 1A). When the potential is off, the particle diffuses freely due to the thermal noise. After a time, t_off, the probability distribution of the particle's position has the form

Fig 1.

Brownian ratchet model with fluctuation of global potential (FGP model). The sphere represents monomeric kinesin. (A) Strong interaction potential of kinesin in nucleotide-free, ATP or ADP.Pi state with MT along a MT protofilament, i.e., the x direction. The potential is represented by a periodic, piecewise but spatially asymmetric form, with a period of L = 8 nm and an asymmetry ratio of α. (B) Weak interaction potential of kinesin in ADP state with MT, which is represented by a flat form. The Gaussian curve represents the probability distribution of the kinesin's position after the potential becomes flat.

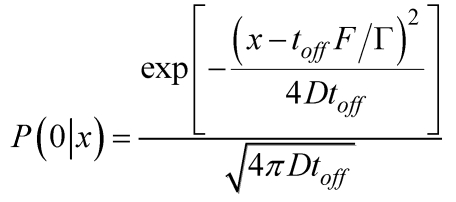(1)

Where D=k_BT/Γ, Γ=6πηr, is the drag coefficient, where η=0.01g cm^-1 s^-1 is the viscosity of the aqueous medium. The motor is approximated as a sphere of radius r and F is the external force acting on the motor and pointing towards the MT minus end.

Although the FGP model is very simple and elegant, it has the following problems when it is applied to monomeric KIF1A. First, as noted from Fig. 1, even under F = 0, the motor shows a much larger probability to stay in the original position than to make a forward step during one ATPase cycle. This gives a very small mechanochemical coupling efficiency. Secondly, using Eq. (1) one can easily obtain the stall force to be F_stall= Γ L(1/2-α)/ t_off. From the available measured ADP-release rate of about 250 s^{-1 4,50}, we have t_off ≈ 4ms. Taking r = 3 nm and L = 8 nm, we obtain F_stall ≈ 5.65×10^-5 pN even for α→0. This value is much smaller than the measured stall force of about 0.15 pN for monomeric KIF1A ²⁰. Finally, during the off state (Fig. 1B) with t_off ≈ 4 ms, since the kinesin has a very weak affinity for MT, the motor has 100% probability to detach from MT. Thus, the motor shows no processivity, which is inconsistent with the experiments, which showed KIF1A to be of high processivity ^18-20.

Brownian ratchet model with fluctuation of both global and local potential

More and more structural studies indicate that the kinesin conformation should also be investigated with MT to understand the moving mechanism of kinesin along MT ⁵¹. For example, in the absence of MT, the conformation of kinesin in ATP state ⁴⁸ has been observed in the presence of ADP, while the conformation in ADP state ⁴⁸ has been observed in the presence of AMP-PNP (an ATP analog) ⁵². The two conformations are independent of the bound nucleotide ^53,54. However, in the presence of MT, the conformation of the plus-end directed kinesin seems to be tightly coupled with the bound nucleotide, as reviewed by Kikkawa ⁵¹. Thus, the interaction of MT with kinesin seems to affect the conformation of the kinesin. Conversely, it has been reported that a significant structural change in MT is also induced by the strong binding of kinesin ^55-58. It is thus expected that both the conformational change of kinesin and that of MT induced by the strong binding of the kinesin should be taken into account in eliciting the mechanism of kinesin moving along MT.

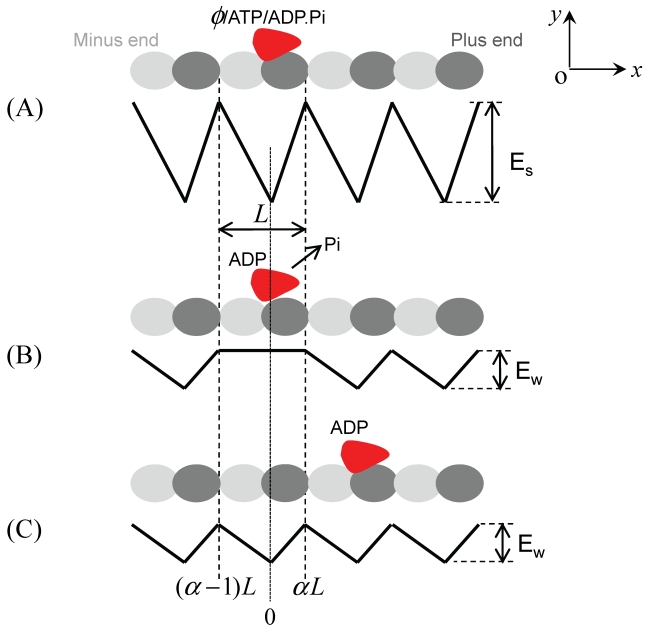
In light of the above results, the binding affinity of MT for kinesin due to nucleotide transitions is hypothesized to have the form shown in Fig. 2 ²⁹. In nucleotide-free, ATP or ADP.Pi state, the strong interaction potential of kinesin with MT has a periodic, piecewise but spatially asymmetric form (Fig. 2A), same as Fig. 1A. As just mentioned above, the strong interaction of kinesin with MT induces a significant structural change in the local binding site of MT where the kinesin is binding, making it different from other unaffected binding sites of MT. Thus the affinity of the local binding site on MT should be different from that of the other unaffected binding sites for the ADP-kinesin that has a different conformation near its MT-binding site from that in ATP or ADP.Pi state. It is reasonable to assume that the ADP-kinesin has a further weaker interaction with the local binding site on MT (Fig. 2B). In a time of t_r after Pi release from the kinesin, the local binding site of MT relaxes to its normal conformation and, thus, the interaction potential of ADP-kinesin with MT changes from that schematically shown in Fig. 2B to that shown in Fig. 2C. The model based on the potentials shown in Fig. 2 is termed as Brownian ratchet model with fluctuation of both global and local potential (FGLP model).

Fig 2.

Brownian ratchet model with fluctuation of both global and local potential (FGLP model). The top in each figure shows the position of kinesin relative to MT, while the bottom in each figure represents the interaction potential of the kinesin with MT along a MT protofilament, i.e., the x direction. (A) Strong interaction potential of kinesin in nucleotide-free, ATP or ADP.Pi states with MT. The potential depth E_s may be slightly different for the different nucleotide states. (B) Weak interaction potential of the kinesin in ADP state with MT immediately after Pi release. (C) Weak interaction potential of the kinesin in ADP state with MT in a time t_r after Pi release.

As demonstrated in Ref. 29, the numerical results based on the FGLP model have shown good quantitative agreement with the available experimental data for monomeric kinesin molecules. Some typical characteristics are stated as follows. (1) As noted evidently from Fig. 2B, the motor shows a very small probability to stay in the original position during one ATPase cycle. Moreover, the asymmetric potential provides a larger probability for forward stepping than backward stepping. This thus gives a large mechanochemical coupling efficiency, in contrast to the FGP model. (2) In the FGLP model, the stall force corresponds to the backward force under which the particle has equal probability to diffuse to x = αL and to x = (α-1)L from position x = 0 with the potential shown in Fig. 2B, which is very different from the case of FGP model (Fig. 1B). This thus gives a stall force much larger than that for the FGP model. (3) Another important conclusion deduced from the FGLP model is that the processivity of a monomeric kinesin is determined by its binding affinity for MT in ADP state: a weak affinity giving a low processivity while a high affinity giving a high affinity. Due to the presence of K loop, KIF1A shows a high affinity for MT, thus giving a high processivity. In particular, with the FGLP model the predicted binding affinity (~ 13 k_BT) of ADP-kinesin for MT which is obtained using the measured processivity ²⁹ is consistent with that (13±2 k_BT) which is obtained using the frictional drag coefficient measured recently by Bormuth et al. ⁵⁹.

Models for Processive Movement of Dimeric Kinesin

Since it has been determined that the dimeric kinesin moves hand-over-hand along MT ^16,17, we exclude here the discussion of models in which the dimer moves in other manners such as inchworm manner ⁶⁰ other than in the hand-over-hand manner. A lot of models have been proposed for the hand-over-hand motion of the dimer ^{4,5,16,17,30-47}. Broadly speaking, the models can be divided into two classes. One prevailing class, although each model in this class has minor variants, is that the forward movement of the trailing ADP-head to the leading position results mainly from the conformational change of the NL, with all binding sites on MT having the same affinity for the ADP-head. The other one is that the forward movement of the trailing ADP-head to the leading position is due mainly to the difference in the binding affinity for ADP-head between the next forward binding site on MT and the original one and to the affinity between the two heads.

Neck-linker-docking model

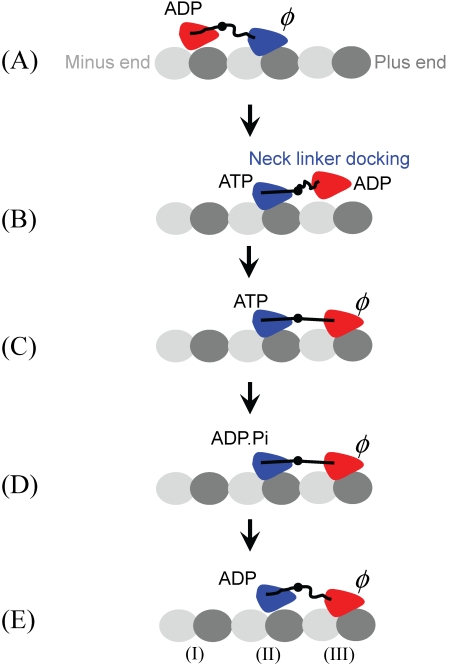
A pronounced conformational change in kinesin's NL has been observed ^61,62: the NL is mobile when the MT-bound kinesin is nucleotide free, but the NL becomes immobilized and extended towards the MT plus end after the binding of AMP-PNP. Based on this evidence, the neck-linker-docking (NLD) model has been proposed (Fig. 3) ^{5,16,30,34-40,46,47}. Recent computational modeling of MT-unbound kinesin suggested that the docking of the NL to the motor domain may be realized through the interaction between the N-terminal peptide and the NL in the ATP state ⁶³. More recently, based on their observations by using cryoelectron microscopy, Sindelar and Downing ⁶⁴ proposed a mechanism in which the switch loops of the MT-bound kinesin, triggering by ATP binding, propel their side of the motor domain down and thereby elicit docking of the NL on the opposite side of the seesaw. In the NLD model, the docking of the NL of the leading head upon ATP binding delivers the trailing ADP-head that is weakly bound to MT to the leading position (Fig. 3B). Then, due to the thermal noise, the tethered ADP-head diffuses to the nearest binding site (Fig. 3C).

Fig 3.

Neck-linker-docking (NLD) model. (A) We begin with the leading head (blue) in nucleotide-free state bound strongly to binding site (II) of MT and the trailing head (red) in ADP state bound weakly to MT. (B) The binding of ATP to the leading head (blue) induces the docking of its NL to the motor domain, delivering the trailing ADP-head (red) to the leading position. (C) Then, due to the thermal noise, the tethered ADP-head (red) diffuses to the nearest binding site (III), activating ADP release. (D) The strain between the two NLs induced by strong bindings of both heads to MT accelerates the hydrolysis of ATP to ADP.Pi in the trailing head (blue) but reduces the rate of ATP binding to the leading head (red). (E) After Pi is released from the trailing head (blue), the state of dimeric kinesin becomes that of (A) except that the dimer has moved forwards by one step.

The model requires that the tethered ADP-head can distinguish between forward- and backward-binding sites. The possible mechanism for this biased binding is supposed as follows. In the dimer, the kinesin heads are connected by the NLs and the binding of the tethered ADP-head to the forward-binding site induces a backward force on the ADP-head. If the backward force increases ADP-release rate, the ADP release and subsequent strong binding to the MT most probably happens at the forward-binding site. This is consistent with the experimental data on distributions of unbinding force for dimeric kinesin molecules, which showed that, at intermediate ADP concentrations where populations of strong and weak MT-binding kinesins coexist, backward loading increases the proportion of strong binding molecules, while forward loading increases the proportion of weak binding molecules ⁶⁵.

As mentioned elsewhere (see, Refs. ^5,51,66,67), a persistent problem for the NLD model is that the free energy change associated with the NL docking is only about 1.5 k_BT ⁶⁸. This implies that a small load of only 1 pN, which is much smaller than the stall force of about 7 pN, can prevent the NL docking which, based on the NLD model, should drive the trailing ADP head to move forwards by more than 8 nm. Indeed, it has been shown recently that, with the aid of only a 1.5-pN forward load, the walking behavior of the mutant kinesin with deletion of the N-terminal peptide, potentially defecting the docking of the NL, restored much of the character of the wild-type kinesin ⁶⁹. In addition, as mentioned above, using the measured frictional drag coefficient, Bormuth et al. ⁵⁹ have determined that the well depth of the interacting potential between the ADP-head and a binding site on MT is 13±2 k_BT. Consequently, the small free energy change of only about 1.5 k_BT associated with NL docking is far from being sufficient to drive the ADP-head to escape from the potential well of the ADP-head interacting with binding site (I) (see Fig. 3). Here it is interesting to note that recent molecular dynamics simulations showed a larger free energy change associated with NL docking upon ATP binding ⁶³. However, the molecular dynamics simulations were performed on kinesin alone. As mentioned above, both the experimental data ^61,62 and structural studies ^51-54 have showed that the docking or undocking of the NL seems to be independent of the nucleotide state of kinesin without bound to MT. Thus, the molecular dynamics simulations on the nucleotide-dependent conformational change of kinesin's NL in the absence of MT seem not to be credible.

Therefore, the docking of the NL upon ATP binding seems not to be the only mechanism for the forward stepping of the dimeric kinesin, and other mechanisms must be involved.

Two-heads-interacting model

An alternative model for the hand-over-hand walking of the dimer has been constructed based both on the difference in the binding affinity between the next binding site on MT and the original one (see Fig. 2), as argued above, and on the existence of the interaction between the two heads of the dimer ^42-45. This model is called two-heads-interacting (THI) model here.

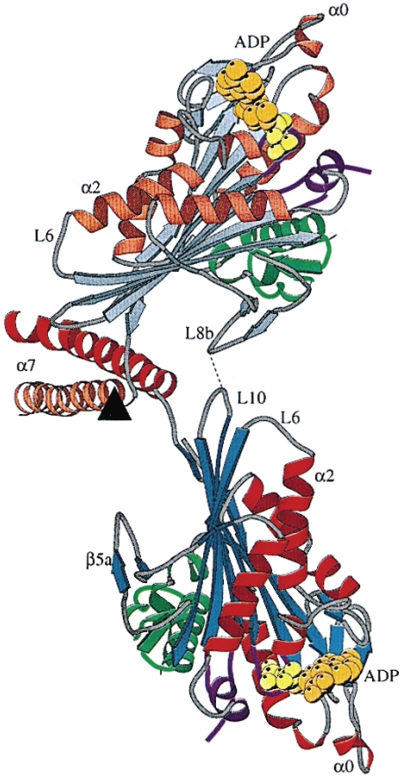
As noted from the crystal structure of dimeric kinesin determined by Kozielski et al. ⁷⁰, there exists a local interaction between loop L8b from one head and loop L10 from another head (Fig. 4). This local interaction maintains the dimer in the equilibrium conformation as shown in Fig. 4. Marx et al. ⁷¹ further revealed that the dimer has this equilibrium conformation in solution. Based on this evidence and the interaction potential of the kinesin head with MT, as argued above (Fig. 2), the THI model has been proposed (Fig. 5) ^42-45. In contrast to the NLD model, where the movement of the trailing ADP-head to the leading position follows ATP binding to the leading head (the leading head is gated) (Fig. 3B), in the THI model the movement of the trailing head to the leading position follows Pi release from the trailing head (the trailing head is gated) (Fig. 5B). This is similar to the kinetic model proposed by Cross and his coworkers ^4,15,72. To explain their experimental data on kinesin backsteps induced by nucleotide, Guydosh and Block ⁷³ have proposed that the leading head is gated. However, as shown in the Supplementary Material of Xie et al. ⁴⁵, the experimental data can also be well explained by using the THI model.

Fig 4.

Structure of dimeric kinesin from rat brain (taken from Kozielski et al. ⁷⁰).

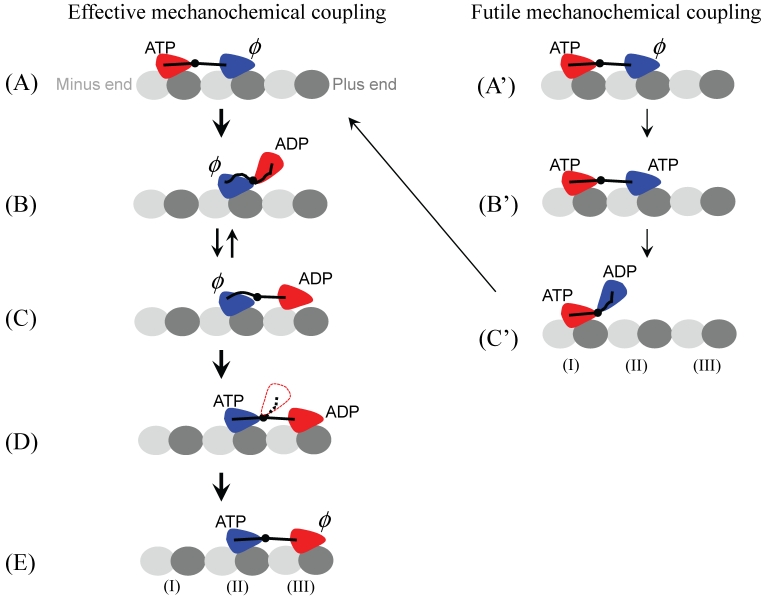
Fig 5.

Two-heads-interacting (THI) model. Effective mechanochemical cycle: (A) The cycle begins with both heads binding to MT with the trailing head (red) in ATP state and the leading head (blue) in nucleotide-free state. The strain between the two NLs induced by strong bindings of both heads to MT accelerates the ATP hydrolysis to ADP.Pi and Pi release in the trailing head (red) but reduces the rate of ATP binding to the leading head (blue). (B) After Pi is released, due to the very weak affinity between the ADP-head and the local binding site (I) (see Fig. 2B), the trailing ADP-head (red) is moved to the equilibrium position relative to the other head (blue) due to the affinity between two heads. (C) The new leading head (red) diffuses to the nearest binding site (III). Because the NL of the nucleotide-free new trailing head (blue) cannot be docked, the length of the NLs along MT is not long enough to allow the leading ADP head (red) binding appropriately to the binding site (III). Thus, the release of ADP from the leading head (red) is inhibited without the MT activation. Moreover, due to the weak interaction between ADP-head (red) and the binding site (III), the ADP-head (red) often diffuses backwards to the equilibrium position relative to the other head (blue), which is indicated by the arrow pointing from (C) to (B). (D) After an ATP binding to the trailing head (blue), its NL is docked, allowing the leading head (red) to bind appropriately to MT. Note that, before ADP release, the ADP-head (red) may also occasionally diffuse backwards to the equilibrium position (red head with dotted outline) relative to the other head (blue). (E) When ADP-head (red) binds appropriately to MT, activated by MT, ADP is released. Then, the state of dimeric kinesin becomes that of (A) except that the dimer has moved forwards by one step. Futile mechanochemical cycle: (A') Kinesin is in the same state as that in (A). (B') Consider an ATP binding to the leading head (blue) before ATP hydrolysis occurs in the trailing head (read). Note that, because the strain between the two NLs accelerates the hydrolysis of ATP in the trailing head (red) but reduces the rate of ATP binding to the leading head (blue), this case rarely occurs. (C') After ATP is hydrolyzed and Pi is released, the leading head (blue) diffuses to the equilibrium position. After the conformation of the binding site (II) relaxes to its normal form (see Fig. 2), the leading head (blue) rebinds to it and releases ADP. Then, the state of dimeric kinesin becomes that of (A). In this case, although an ATP is consumed, no mechanical step is made.

In the THI model, the interaction between the two heads makes a contribution to the movement of the trailing ADP-head to the leading position (Fig. 5B). Then, due to the thermal noise, the tethered ADP-head diffuses to the nearest binding site (III) by overcoming its interaction with the other head. Note that, in Fig. 5B, since the ADP-head is nearer to binding site (III) than to binding site (I), the ADP-head would have larger probability to diffuse to site (III) than to site (I) even if the two sites had the same affinity for the ADP-head. Thus, the interaction between the two heads in the model plays the similar role to the NL docking in the NLD model in the forward movement of the trailing ADP-head.

As in the NLD model, the THI model also requires that the tethered ADP-head can distinguish between forward- and backward-binding sites. Besides the possible biased-binding mechanism, as discussed in the NLD model, another more important mechanism is present in the THI model. Immediately after Pi release, the binding affinity of binding site (III) for ADP-head is higher than that of site (I) (see Figs. 2 and 5). This results in that the ADP release nearly always happens at the binding site (III), i.e., the forward-binding site. The two biased-binding mechanisms give a very high mechanochmeical coupling efficiency in the THI model.

Two-heads-interacting plus neck-linker-docking model

As discussed above, both the NL docking and the interaction between the two heads are determined characters for dimeric kinesin ^61,62,70,71. Thus, both characters should be included in the moving mechanism of the dimer along MT. Moreover, both the NL docking in NLD model and the interaction between the two heads in THI model play the same role in reducing the probability for the ADP-head in the leading position from moving backwards to the trailing position (see Figs. 3B and 5B). Based on these considerations, a hybrid model that is termed as “two-heads-interacting plus neck-linker-docking” (THI-NLD) model is proposed here (see also Fig. 5). As in the THI model, in the THI-NLD model the trailing ADP-head (red) also moves to the leading position after Pi release (Fig. 5B). Then the docking of the NL to the blue head after ATP binding further increases the energy barrier by ~ 1.5 k_BT ⁶⁸ to prevent the ADP-head (red) from moving backwards to the trailing position (Fig. 5D), but the docking has no effect on the energy barrier for the ADP-head to move from the equilibrium position (dotted red) to the MT-bound position (solid red).

Concluding Remarks and Perspectives

In this review we have focused on the models for unidirectional motion of both monomeric and dimeric kinesin molecules and models for other behaviors such as limping of the dimer ^16,74 have not been discussed. For either monomers or dimers, two classes of models for the unidirectional motion have been discussed. Moreover, a hybrid model has also been proposed based on the two classes of the model for the dimers.

For the monomer, while the FGP model is simpler than the FGLP model, it cannot explain several aspects of the dynamics of the monomeric kinesin. On the contrary, the latter model agrees with the available experimental data. For the dimer, though very differences between the NLD and THI models, most of the experimental observations for wild-type dimers can be well reproduced by using either of the two models ^41-46,75-77. However, the puzzling dynamic behaviors for a number of mutant homodimeric and heterodimeric kinesin molecules observed by Kaseda et al. ^78,79 could not be described by the NLD model ⁸⁰, but can be easily explained by the THI model ⁴³. Similarly, the experimental data for the wild-type dimers can also be well reproduced and the puzzling results for the mutant dimers can also be understandable by using the THI-NLD model. Moreover, based on the FGLP model for the monomer and the THI-NLD model for the dimer, it is evident that, whether the monomer is nonprocessive (corresponding to a weak binding affinity for MT in ADP state) or processive (corresponding to a high binding affinity), the dimerization can convert the diffusion motion along MT (monomeric mechanism) into the hand-over-hand motion (dimeric mechanism) ^81-83. If the neck linkers of the dimerized molecule are longer than 8 nm, no internal strain between the two heads would exist. As a result, the ATPase rates of the two heads are comparable, resulting in that the two heads are sometimes in ADP state simultaneously. Thus, the dimer would display motility properties of both diffusion and hand-over-hand walking along MT, consistent with the recent experimental data of Hammond et al. ⁸².

As discussed above, the FGLP and THI-NLD models are likely the best candidates to describe the mechanochemistry of monomeric and dimeric kinesin molecules, respectively. The basis for the two models is that the conformational change of MT induced by the strong interaction with kinesin plays a critical role in the kinesin motility, which has not been paid much attention up to now. Thus, in order to elucidate the moving mechanism of kinesin along MT, the future studies, besides on the more detailed and subtle kinetics and dynamics of wild-type and mutant kinesins, should also be on the effect of MT such as the effect of its conformational change on the affinity for kinesin in different nucleotide states.

For this purpose, we can resort to the structural studies, for example, using high-resolution cryoelectron microscopy to study the structural difference between MT decorated with AMP-PNP-kinesin and that with ADP-kinesin, and, more interestingly, using X-ray crystallography to study the difference between structure of α- and β-tubulin molecules complexed with AMP-PNP-kinesin and that with ADP-kinesin. We can also resort to biochemical assays. For example, in one assay, MT is preincubated with nucleotide-free KIF1A of very high density so that nearly all α- and β-tubulin molecules are bound strongly by KIF1A. After adding ATP into the solution, it would be expected that the kinesin molecules detach from MT after ATP hydrolysis and Pi release, because, based on the FGLP model, the affinity for ADP-kinesin of nearly all bare binding sites on MT surface now becomes very weak for a short time. In another assay, when mixing MT with preincubated ADP-KIF1A, one would expect to observe the cosedimentation between the ADP-kinesin and MT, because the interaction of the ADP-kinesin with the unaffected MT is not weak.