Abstract
Based on an extensive dataset analyzed by Benua et al., a whole-body retention threshold of 2.96 GBq (80 mCi) at 48 h has been used to limit the radioactivity of 131I administered to thyroid cancer patients with diffuse pulmonary metastases. In this work, the 80-mCi activity retention limit is used to derive lung-absorbed doses and dose rates. The resulting dose-rate–based limits make it possible to account for patient-specific differences in lung geometry. This is particularly important, for example, in pediatric patients exhibiting diffuse lung metastases. The approach also highlights the impact of altered radioiodine kinetics as seen with recombinant human thyroid-stimulating hormone.
Methods
The dose-rate constraint (DRC) was defined as the absorbed dose rate to the lungs of the adult female reference phantom when 80 mCi of 131I are in the body and 90% of this is uniformly distributed in the lungs. With this definition, the 80-mCi rule was generalized by calculating the activity required to yield a dose rate equal to DRC using lung-to-lung S factor values corresponding to different reference phantoms.
Results
A DRC value of 41.1 cGy/h was obtained. Applying this DRC to the adult male phantom and to the phantom of a 15-y-old yields equivalent 48-h activity limits of 3.73 GBq (101 mCi) and 2.46 GBq (66.4 mCi), respectively. Depending on model parameters, the absorbed doses to lungs ranged from 54 to 83 Gy; the photon-only portion, which better reflects the dose to normal lung parenchyma, ranged from 4.6 to 10.1 Gy.
Conclusion
A dose-rate–based version of the 80-mCi rule is derived and used to demonstrate application of this rule to pediatric patients and to adult male patients. The implications of the 80-mCi rule are also examined. The assumption of uniform energy deposition in the lungs leads to substantially overestimated absorbed doses. Severe radiation-induced lung toxicity, expected at normal lung absorbed doses of 25–27 Gy, is avoided, probably because most of the local electron dose is delivered to tumor tissue instead of to normal lung parenchyma. The possibility of using a DRC to adjust treatment for different clinical situations is illustrated.
Keywords: patient-specific dosimetry, thyroid carcinoma, 131I, lung metastases, pulmonary fibrosis
The observation that repeated 131I treatment of meta-static thyroid carcinoma with subtherapeutic doses often fails to cause tumor regression and can lead to loss of iodine avidity in metastases led Benua and Leeper to propose a dosimetry-based treatment-planning approach to 131I thyroid cancer therapy (1). The objective of the approach was to identify the largest administered 131I radioactivity that would be safe yet optimally therapeutic. Drawing on a large database of patient studies, they formulated the following constraints on the administered activity. First, the blood absorbed dose should not exceed 200 rad. This was recognized to be a surrogate for red bone marrow absorbed dose and was intended to decrease the likelihood of severe marrow depression, the dose-limiting toxicity in radioiodine therapy of thyroid cancer. Second, whole-body retention at 48 h should not exceed 4.44 GBq (120 mCi). This was shown to prevent release of 131I-labeled protein into the circulation from damaged tumor (2). Third, in the presence of diffuse lung metastases, the 48-h whole-body retention should not exceed 2.96 GBq (80 mCi). This constraint was chosen to avoid pneumonitis and pulmonary fibrosis.
The lung-related constraint is derived, primarily, from a series of 15 patients (11 female and 4 male) with pulmonary metastases (3) who were treated with 131I in the late 1950s. Two of these patients died of pulmonary fibrosis and pneumonitis after single administrations of 11.1 and 7.84 GBq of 131I to women 27 and 32 y old, respectively. Another 2 patients experienced dyspnea with radiographic evidence of fibrosis after single doses of 11.1 and 9.32 GBq; the patient receiving the latter dose had received 4.77 GBq 2.5 y earlier. Both these patients were first treated as teenagers, when 13 and 15 y old, respectively. Since these activity constraints were implemented, the incidence of life-threatening radiation-induced side effects has been reduced substantially. These treatment-planning guidelines were used to obtain a distribution of administered activities in 116 patients with 131I-avid metastases. The mean administered activity was 10.8 GBq (293 mCi), and the largest was 24.2 GBq (654 mCi). Benua and Leeper noted that had a fixed amount of 5.6–7.4 GBq (150–200 mCi) been applied, 92 of the administrations would have undertreated the patient. It is important to note, however, that there is still no evidence that a treatment-planning approach to 131I treatment of thyroid cancer yields results that are better than fixed-activity therapy when the endpoint is survival (4–6). This may reflect the lack of standardization in dosimetry methodologies, the state of sophistication of dosimetry, or possibly the reluctance to treat to a dosimetrically defined tolerance level; most likely, all 3 reasons are involved.
The lungs are the most common extracervical recurrence site in patients who fail radioiodine therapy; approximately half of these patients die of their disease (7–9). The guidelines regarding activity prescription in the presence of lung disease were formulated before the availability of nuclear medicine imaging and were based on urinary excretion measurements (3). Given the importance of pulmonary disease in thyroid cancer morbidity and mortality, a dosimetric analysis has been performed to place the activity-based Benua–Leeper constraints on a dosimetric foundation. In this work, we have examined the implications of the activity constraints in terms of lung dose rate and total absorbed dose.
MATERIALS AND METHODS
Dose-Rate Constraint (DRC)
The following equations are used to obtain the dose rate, DR(t), to lungs at time t in reference phantom P.
| Eq. 1 |
where
| Eq. 2 |
| Eq. 3 |
and
| Eq. 4 |
and where ALU(t) is lung activity at time t, is the lung-to-lung 131I S factor for reference phantom P, ARB(t) is the remainder-of-body activity (total-body – lung) at time t, is the remainder-of-body–to–lung 131I S factor for reference phantom P, AT is whole-body activity at time T, FT is the fraction of AT that is in the lungs at time T, λLU is the effective clearance rate from lungs (ln(2)/TE, with TE equal to effective half-life), λRB is the effective clearance rate from the remainder of the body (ln(2)/TRB, with TRB equal to effective half-life in the remainder of the body), is the total-body–to–lung 131I S factor for reference phantom P, is the total-body mass of reference phantom P, and is the lung mass of reference phantom P.
Equation 2 describes a model in which radioiodine uptake in tumor-bearing lungs is assumed instantaneous relative to the clearance kinetics. Clearance is modeled by an exponential expression with a clearance rate constant λLU and corresponding effective half-life TE. At a particular time T after administration, the fraction of whole-body activity that is in the lungs is given by the parameter FT. Activity that is not in the lungs (i.e., is in the remainder of the body) is also modeled by an exponential clearance (Eq. 3) but with a different rate constant, λRB. At time T, the fraction of whole-body activity in this compartment is 1 − FT. Equation 4 is obtained from Loevinger et al. (10).
When Equations 2 and 3 are used to replace for ALU(t) and ARB(t) in Equation 1, the dose rate to lungs at time T for phantom P is
| Eq. 5 |
Derived Activity Constraint
If we assume that the dose rate to the lungs at 48 h is the relevant constraint on avoiding prohibitive lung toxicity, then one may derive 48-h activity constraints for different reference phantoms that give a 48-h dose rate equal to a predetermined fixed dose-rate constraint, denoted DRC. By reordering expression 5 and renaming AT to , the activity constraint for phantom P, so that DRP(48 h) = DRC, we get
| Eq. 6 |
In Equation 6, depends on the fraction of whole-body activity in the lungs at 48 h and also on the reference phantom that best matches the patient characteristics.
Corresponding Administered Activity
Equation 6 gives the 48-h whole-body activity constraint so that the dose rate to lungs at 48 h does not exceed DRC. The corresponding constraint on the maximum administered activity, AAmax, can be derived by using Equations 2 and 3 to give an expression for the total-body activity as a function of time:
| Eq. 7 |
Replacing AT with and setting t = 0, we obtain the following expression for AAmax:
| Eq. 8 |
The denominator in each term of this expression scales the activity up to reflect the starting value needed to obtain . AAmax is shown to be dependent on λLU and λRB (or, equivalently, on TE and TRB).
Mean Lung Absorbed Dose
The mean lung absorbed dose may be obtained by integrating Equation 1 from zero to infinity:
| Eq. 9 |
Integrating the expressions for lung and remainder-of-body activity as a function of time (Eqs. 2 and 3, respectively), and replacing parameters with the 48-h constraint values, the following expressions are obtained for ÃLU and ÃRB:
| Eq. 10 |
and
| Eq. 11 |
In Equations 10 and 11, the λ values have been replaced to explicitly show the dependence of the cumulated activities on the clearance half-lives.
If TRB is kept constant and TE is varied, the minimum absorbed dose to the lungs will occur at a TE value that gives a minimum for Equation 9. This can be obtained by differentiating with respect to TE, setting the resulting expression to zero and solving for TE. This gives TE = ln(2)·48 h = 33 h.
Electron Versus Photon Contribution to Lung Dose
Because almost all activity in tumor-bearing lungs would be localized to tumor cells, it is instructive to separate the electron contribution to the estimated lung dose from the photon contribution. The electron contribution would be expected, depending on the tumor geometry (11), to irradiate tumor cells predominantly, whereas the photon contribution will irradiate lung parenchyma. The dose contribution from the remainder of the body is already limited to photon emissions. The photon-only lung-to-lung S value ( ) for a phantom P is obtained from the S factor value and the Δ-value for electron emissions of 131I:
| Eq. 12 |
where is total energy emitted as electrons per disintegration of 131I.
Replacing for in Equation 9 gives the absorbed dose to lungs from photon emissions only.
Parameter Values
Table 1 lists the reference phantom parameter values used in the calculations. The masses, lung-to-lung S values, and total-body–to–lung S values listed were obtained from the OLINDA dose calculation program (12,13). The remainder-of-body–to–lung and lung-to-lung photon-only S values were calculated using Equations 4 and 12, respectively. The effective clearance half-life of radioiodine activity not localized to the lungs, TRB, was set to 10 or 20 h. These values correspond to reported values for whole-body clearance with or without recombinant thyroid-stimulating hormone, respectively (14,15). The effective clearance half-life for activity in tumor-bearing lungs, TE, was varied from 20 to 100 h (16). The fraction of whole-body activity in the lungs at 48 h, F48, was varied from 0.6 to 1.
TABLE 1.
Values for Parameters in Reference Phantoms
| Reference phantom | MTB (kg) | MLU (kg) | SLU←LU (mGy/MBq-s) | SLU←TB (mGy/MBq-s) | SLU←RB (mGy/MBq-s) | SPLU←LU (mGy/MBq-s) |
|---|---|---|---|---|---|---|
| Male adult | 73.7 | 1.00 | 3.40 × 10−5 | 7.22 × 10−7 | 2.64 × 10−7 | 3.60 × 10−6 |
| Female adult | 56.9 | 0.80 | 4.28 × 10−5 | 9.34 × 10−7 | 3.37 × 10−7 | 4.80 × 10−6 |
| 15-y-old | 56.8 | 0.65 | 5.16 × 10−5 | 9.33 × 10−7 | 3.46 × 10−7 | 4.90 × 10−6 |
| 10-y-old | 33.2 | 0.45 | 7.34 × 10−5 | 1.48 × 10−6 | 4.85 × 10−7 | 6.29 × 10−6 |
RESULTS
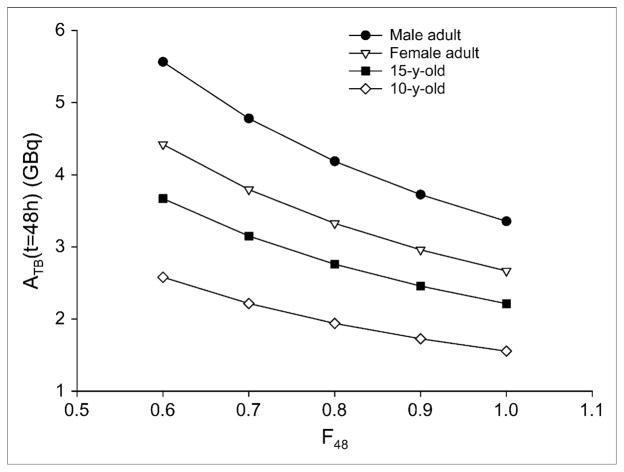
To derive the dose rate to lungs associated with the 80-mCi, 48-h constraint, we assume that 90% of the whole-body activity is uniformly distributed in the lungs (F48 = 0.9). The original reports describing the 80-mCi, 48-h limit do not provide a value for this parameter; the value chosen is consistent with the expected biodistribution in patients with disease that is dominated by diffuse lung metastases. As noted in the introduction, the 80-mCi activity constraint was derived primarily from results obtained in women. Accordingly, activity is converted to dose rate using S factors and masses for the adult female phantom. Using Equation 5, with F48 = 0.9, the DRC corresponding to the 48-h, 80-mCi limit is 41.1 cGy/h. This is the estimated dose rate to the lungs when 80 mCi of 131I are uniformly distributed in the lungs of a woman whose anatomy is consistent with the standard female adult phantom geometry. Implicit in the constraint of 80 mCi at 48 h is that radiation-induced pneumonitis and pulmonary fibrosis will be avoided as long as the dose rate does not exceed 41.1 cGy/h at 48 h after 131I administration. If we assume that this dose-rate–based constraint applies to pediatric patients, then using Equation 6, we may calculate the 48-h activity limitation if the patient anatomy is consistent with the standard phantom for a 15- or 10-y-old. Figure 1 provides the 48-h whole-body activity retention values for different phantoms and F48 values. Because the guidelines were developed with data from women, the 80-mCi rule applied to the adult male phantom gives a 48-h whole-body activity constraint of 3.73 GBq (101 mCi) at F48 = 0.9; corresponding values for the phantoms of a 15-y-old and 10-y-old are 2.46 GBq (66.4 mCi) and 1.73 GBq (46.7 mCi), respectively. It is important to note that DRC, because it is a dose rate, does not depend on the clearance parameters. The value chosen does, however, depend on the assumed lung fraction of whole-body activity. Table 2 lists the DRC values for different F48 values. All the results presented will scale linearly by DRC value.
FIGURE 1.
Whole-body 48-h activity retention limits for different phantoms and F48 values.
TABLE 2.
DRC Values for Different 48-Hour Lung–to–Whole-Body Activity Ratios*
| F48 | DRC (cGy/h) |
|---|---|
| 1.0 | 45.6 |
| 0.9 | 41.1 |
| 0.8 | 36.6 |
| 0.7 | 32.0 |
| 0.6 | 27.5 |
Derived so that total-body retention at 48 h in female adult reference phantom is 2.96 GBq (80 mCi).
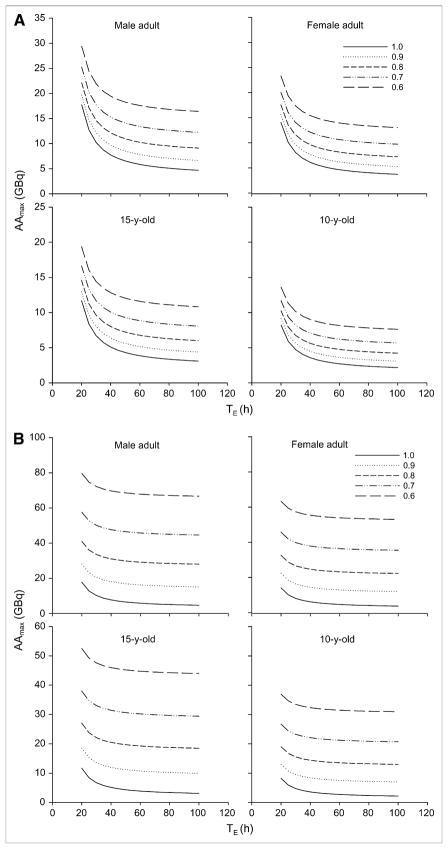
Most patients with diffuse 131I-avid lung metastases exhibit prolonged whole-body retention. In such cases, the whole-body kinetics are dominated by tumor-associated activity. Assuming that 90% of the whole-body activity is in the lungs and that this clears with an effective half-life of 100 h, whereas the remainder activity clears with an effective half-life of 20 h (corresponding to a treatment plant that includes hormone withdrawal (15)), one may use Equation 8 to calculate the administered activity that will yield the corresponding 48-h activity constraint for each phantom. The administered activity values are 6.64, 5.23, 4.37, and 3.08 GBq (180, 143, 118, and 83.2 mCi, respectively) for the standard phantom anatomies of an adult male, adult female, 15-y-old, and 10-y-old, respectively. These values depend on the assumed clearance half-life of activity in the remainder of the body. If an effective half-life of 10 h (consistent with use of recombinant human thyroid-stimulating hormone) is assumed, the respective administered activity values are 15.1, 12.0, 9.92, and 6.98 GBq (407, 323, 268, and 189 mCi, respectively). Figure 2A depicts administered activity limits for different phantoms and F48 values as a function of TE when TRB is set to 20 h. Figure 2B depicts corresponding results when TRB equals 10 h. The plots show that at TE greater than 3–4 times TRB, the administered activity limit is largely independent of lung clearance half-life but, as shown by the equidistant spacing of the curves with increasing F48, remains linearly dependent on the fraction of whole-body activity that is in the lungs at 48 h. When TE approaches the lower TRB value as in Figure 2A, AAmax increases rapidly and appears to converge. This reflects the condition of a partitioned activity distribution that clears from the lungs and remainder of the body at the same effective half-life; the AA values at TE = TRB = 20 h are not the same because the dose rate, which is used to determine AAmax, will be different because of the physical distribution of the activity even when the half-lives are the same. The rapid increase in AAmax at lower TE values reflects the need to increase administered activity as the clearance rate increases.
FIGURE 2.
Administered activity limits for different phantoms and F48 values as function of TE when TRB is set to 20 h (A) or 10 h (B).
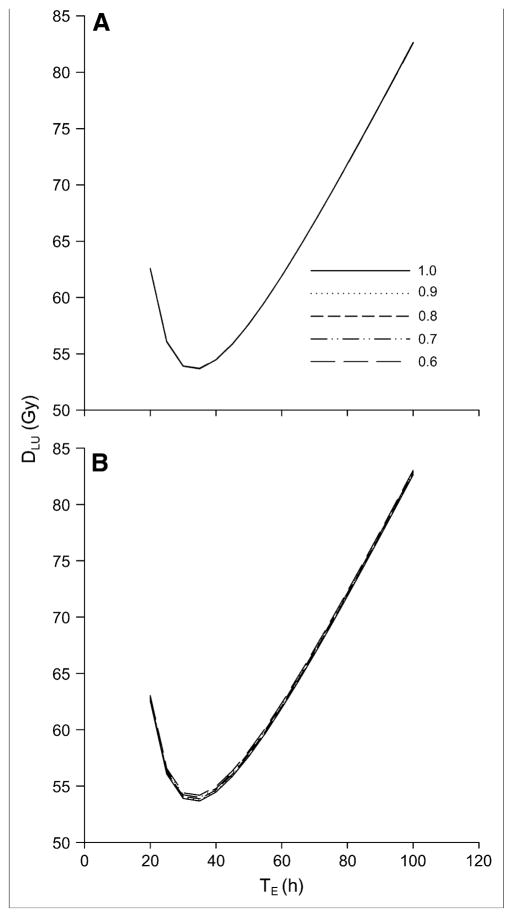
Figure 3 depicts the absorbed dose to lungs as a function of TE for different F48 values. Because the administered activities are adjusted to reach a constant 48-h dose rate in the lungs, the absorbed dose curves are essentially independent of phantom geometry, with less than a 2% difference in lung absorbed dose versus TE profiles across the 4 standard phantom geometries (data not shown). As shown in figure 3, the dose versus TE relationship is also independent of F48 and minimally sensitive to TRB. This is because the remainder-of-body contribution to the total lung absorbed dose is negligible relative to the self-dose.
FIGURE 3.
Absorbed dose to lungs as function of TE for different F48 values when TRB is set to 20 h (A) or 10 h (B). In A, the lung dose is insensitive to F48 and the curves are superimposed into a single curve.
Both sets of curves show a minimum absorbed dose at TE = 33.3 h (ln(2) × 48 h). The minimum absorbed dose is 53.6 for TRB = 20 h and ranges from 53.6 (F48 = 1) to 54.2 (F48 = 0.6) for TRB = 10 h.
Less is known about the effects of lung irradiation on pediatric patients or patients with already-compromised lung function. In such cases, a more conservative dose-rate limit may be appropriate. As noted earlier, the results shown in Figures 1–3 scale linearly with DRC. Table 3 summarizes the relevant results for the different phantoms at F48 = 0.9 when DRC = 20 cGy/h. In the adult female phantom, this corresponds to 1.44 GBq (38.9 mCi) retained in the whole body at 48 h.
TABLE 3.
Dosimetric Results When DRC = 20 cGy/Hour and F48 = 0.9
| Reference phantom | ATB(t = 48 h) (GBq) |
AAmax(GBq) |
DLU (Gy) |
||
|---|---|---|---|---|---|
| TRB = 20 h | TRB = 10 h | TRB = 20 h | TRB = 10 h | ||
| Male adult | 1.81 | 3.23 | 7.33 | 40.2 | 40.3 |
| Female adult | 1.44 | 2.57 | 5.82 | 40.2 | 40.3 |
| 15-y-old | 1.20 | 2.13 | 4.83 | 40.2 | 40.3 |
| 10-y-old | 0.84 | 1.50 | 3.40 | 40.2 | 40.3 |
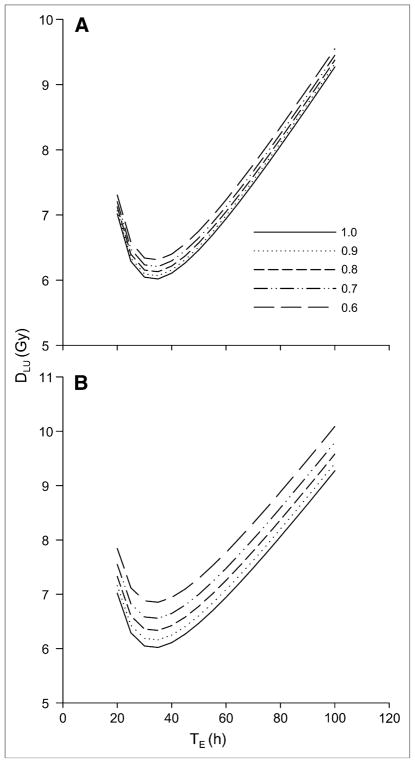
All the lung absorbed dose values shown in Figure 3 and listed in Table 3 are well above the reported 24- to 27-Gy maximum tolerated dose for adult lungs (17,18). The discrepancy may be explained by considering the photon and electron fraction of this absorbed dose. The electron emissions are deposited locally, most likely within the thyroid carcinoma cells that have invaded the lungs, whereas the photon contribution would irradiate the total lung volume. Using Equations 9 and 12, the lung absorbed dose attributable to photons may be calculated. Absorbed dose versus TE curves are depicted in Figure 4 for the adult female phantom and for the 2 different remainder-of-body effective clearance half-lives considered. As might be expected, the photon dose to lung is more sensitive to F48 than is the total lung dose (Fig. 3). This is because the remainder of body dose terms is dominated by the photon dose. Photon dose better reflects the absorbed dose to normal lung parenchyma and is generally below 10 Gy (at TRB = 10 h, TE = 100 h, and F48 = 0.6, the photon dose is 10.1 Gy). At TE = 100 h, the photon lung dose to the adult male phantom ranges from 8.75 Gy (F48 = 1.0) to 9.03 Gy (F48 = 0.6) when TRB = 20 h; the corresponding values when TRB = 10 h are 8.75 Gy (F48 = 1.0) and 9.56 Gy (F48 = 0.6). For the phantom of a 15-y-old, the respective values are 7.85, 8.10, 7.85, and 8.55 Gy; respective values for the phantom of a 10-y-old are 7.09, 7.33, 7.09, and 7.78 Gy.
FIGURE 4.
Absorbed dose vs. TE for adult female phantom for the 2 different remainder-of-body effective clearance half-lives considered. Effective remainder-of-body clearance half-life, TRB, is set to 20 h (A) or 10 h (B).
DISCUSSION
Benua et al. (1,2) found that the most effective approach for radioiodine treatment of thyroid cancer metastases was to deliver, in a single administration, the largest safe absorbed dose to tumor tissue. Their dosimetric approach placed constraints on the blood absorbed dose and on the whole-body activity retained at 48 h after 131I administration. If the patient was known to have diffuse lung metastases, the 48-h whole-body activity limit was set to 80 mCi. This value was arrived at primarily from toxicity observed in female patients.
In this work, we have translated the 80-mCi rule from an activity-based to a dose-rate–based limit. This translation has made it possible to mathematically extend the 80-mCi rule to pediatric patients and to show how it is influenced by the spatial distribution of activity at 48 h. The exercise has also revealed the possible need for a different activity limit in men from that in women. It is important to note that the underlying assumption with this approach is that lung radio-sensitivity is invariant across different geometries and ages. As illustrated, however, a formalism is provided for adjusting the dose-rate limit and estimating administered activities based on clinical considerations. As noted in the methodology and results, the dose-rate limits derived in this work make no assumptions regarding clearance kinetics. Such assumptions are required, however, in estimating maximum allowable administered activity and lung absorbed dose.
The total lung absorbed doses estimated were substantially greater than the 24- to 27-Gy maximum tolerated dose to the lungs for adults if the dose-rate equivalent of the 80-mCi rule is used to constrain the administered activity. The photon contribution to the absorbed dose, however, was within the 24- to 27-Gy limit in all except for the combination of a 10-h effective clearance half-life from the remainder of the body and a 48-h lung activity fraction of less than 0.9. The actual absorbed dose to the lungs will depend on the tumor cell distribution within the lungs (11).
The 80-mCi rule was established by Benua et al. (1,2) at a time when conventional nuclear medicine imaging was not available, when an internal dosimetry formalism did not exist, and when external radiotherapy was still in its infancy. It is remarkable, therefore, that this guideline, along with the blood-based absorbed dose limitation, has been so successful in limiting the morbidity associated with radioiodine therapy of thyroid cancer. The more difficult question in this regard is whether the approach is too conservative, potentially underdosing patients with diffuse lung metastases, which is a clinical stage often associated with treatment failure and one in which delivery of the maximum tolerated therapy is critical for a successful outcome. The analysis provided in this article is a possible first step in the direction of a treatment methodology that reduces the potential for underdosing in this population of thyroid cancer patients.
Acknowledgments
This work was supported by NIH/NCI grant R01CA116477.
References
- 1.Benua RS, Leeper RD. A method and rationale for treatment of thyroid carcinoma with the largest, safe dose of 131-I. In: Medeiros-Neto G, Gaitan E, editors. Frontiers in Thyroidology. New York, NY: Plenum Medical; 1986. p. 1317. [Google Scholar]
- 2.Benua RS, Rawson RW, Sonenberg M, Cicale NR. Relation of radioiodine dosimetry to results and complications in treatment of metastatic thyroid cancer. AJR. 1962;87:171–182. [PubMed] [Google Scholar]
- 3.Rall JE, Alpers JB, Lewallen CG, Sonenberg M, Berman M, Rawson RW. Radiation pneumonitis and fibrosis: complication of radioiodine treatment of pulmonary metastases from cancer of the thyroid. J Clin Endocrinol Metab. 1957;17:1263–1276. doi: 10.1210/jcem-17-11-1263. [DOI] [PubMed] [Google Scholar]
- 4.Robbins RJ, Schlumberger MJ. The evolving role of I-131 for the treatment of differentiated thyroid carcinoma. J Nucl Med. 2005;46(suppl):28S–37S. [PubMed] [Google Scholar]
- 5.Dorn R, Kopp J, Vogt H, Heidenreich P, Carroll RG, Gulec SA. Dosimetry-guided radioactive iodine treatment in patients with metastatic differentiated thyroid cancer: largest safe dose using a risk-adapted approach. J Nucl Med. 2003;44:451–456. [PubMed] [Google Scholar]
- 6.Gerard SK, Park HM. I-131 dosimetry and thyroid stunning. J Nucl Med. 2003;44:2039–2040. [PubMed] [Google Scholar]
- 7.Clark JR, Lai P, Hall F, Borglund A, Eski S, Freeman JL. Variables predicting distant metastases in thyroid cancer. Laryngoscope. 2005;115:661–667. doi: 10.1097/01.mlg.0000161337.46892.e0. [DOI] [PubMed] [Google Scholar]
- 8.Lin JD, Chao TC, Chou SC, Hsueh C. Papillary thyroid carcinomas with lung metastases. Thyroid. 2004;14:1091–1096. doi: 10.1089/thy.2004.14.1091. [DOI] [PubMed] [Google Scholar]
- 9.Mazzaferri EL, Kloos RT. Current approaches to primary therapy for papillary and follicular thyroid cancer. J Clin Endocrinol Metab. 2001;86:1447–1463. doi: 10.1210/jcem.86.4.7407. [DOI] [PubMed] [Google Scholar]
- 10.Loevinger R, Budinger TF, Watson EE. MIRD Primer for Absorbed Dose Calculations. New York, NY: Society of Nuclear Medicine; 1991. Revised ed. [Google Scholar]
- 11.Song H, Bin H, Prideaux A, et al. Lung dosimetry for radioiodine therapy treatment planning in the case of diffuse lung metastases. J Nucl Med. 2006;47:1985–1994. [PMC free article] [PubMed] [Google Scholar]
- 12.Stabin MG, Sparks RB, Crowe EB, Cremonesi M, Siegel JA. Olinda/Exm 1.0 and Radar [abstract] Eur J Nucl Med Mol Imaging. 2004;31(suppl):S471. [Google Scholar]
- 13.Stabin MG, Sparks RB. OLINDA: PC-based software for biokinetic analysis and internal dose calculations in nuclear medicine [abstract] J Nucl Med. 2003;44(suppl):103P. [Google Scholar]
- 14.North DL, Shearer DR, Hennessey JV, Donovan GL. Effective half-life of I-131 in thyroid cancer patients. Health Phys. 2001;81:325–329. doi: 10.1097/00004032-200109000-00013. [DOI] [PubMed] [Google Scholar]
- 15.Hanscheid H, Lassmann M, Luster M, et al. Iodine biokinetics and dosimetry in radioiodine therapy of thyroid cancer: procedures and results of a prospective international controlled study of ablation after rhTSH or hormone withdrawal. J Nucl Med. 2006;47:648–654. [PubMed] [Google Scholar]
- 16.Samuel AM, Rajashekharrao B, Shah DH. Pulmonary metastases in children and adolescents with well-differentiated thyroid cancer. J Nucl Med. 1998;39:1531–1536. [PubMed] [Google Scholar]
- 17.Emami B, Lyman J, Brown A, et al. Tolerance of normal tissue to therapeutic irradiation. Int J Radiat Oncol Biol Phys. 1991;21:109–122. doi: 10.1016/0360-3016(91)90171-y. [DOI] [PubMed] [Google Scholar]
- 18.Press OW, Eary JF, Appelbaum FR, et al. Radiolabeled-antibody therapy of B-cell lymphoma with autologous bone marrow support. N Engl J Med. 1993;329:1219–1224. doi: 10.1056/NEJM199310213291702. [DOI] [PubMed] [Google Scholar]