Abstract
Information mapping using pattern classifiers has become increasingly popular in recent years, although without a clear consensus on which classifier(s) ought to be used or how results should be tested. This paper addresses each of these questions, both analytically and through comparative analyses on five empirical datasets. We also describe how information maps in multiple class situations can provide information concerning the content of neural representations. Finally, we introduce a publically available software toolbox designed specifically for information mapping.
1 Introduction
The traditional analysis of fMRI data using a General Linear Model [8] (GLM) approach aims to find voxels whose activation time series is well reconstructed by the combination of several regressor time series. These time series reflect alternations between conditions of interest – periods when a task is being performed versus rest periods, for instance – or more complicated contrasts between those conditions, as well as nuisance factors such as volume registration parameters. This analysis is generally performed on a dataset that has undergone both spatial normalization to a reference brain and spatial smoothing. Although the analysis is performed for each voxel separately, the result is usually a set of clusters of voxels with similar time series that reflect a contrast of interest (and are deemed to be active with respect to that contrast). The reference brain is used to reduce that set of clusters to a list of cluster centroids and their anatomical location, together with a measure of statistical significance of their activation.
Over the last few years, an alternative approach to neuroimaging analysis has emerged, which uses machine learning classifiers (see [23] [16] [28] for reviews of a large part of this work). The analysis of fMRI data with classifiers differs from the traditional GLM-based analysis by reversing the question asked. Instead of finding voxels whose time series is explained by a contrast of interest, it asks whether it is possible to predict the value of a regressor based on the pattern of activation over a set of voxels. Although it is possible to consider the question of which anatomical locations are used by a classifier, the type of conclusion usually drawn is about whether information about the variable of interest is present within the overall volume.
The GLM approach is justified by two key assumptions. The first is that the information present in the data is described by the regressors provided, in isolation or combined. Beyond that, it is assumed that the voxels in a cluster become active as a whole and carry the same signal; spatial smoothing will thus not destroy information. In [19] the authors question these assumptions, in particular the notions that information is only present in voxels that strongly reflect a regressor or that adjacent voxels affected by the task necessarily have similar time courses. They introduce the idea of information mapping using a “searchlight” statistic; this combines signal from all voxels in a small spatial region without averaging them, by considering their covariance structure. Intuitively, this means shifting from asking the question of whether a voxel does something different in two conditions – by being active in one and inactive in the other, say – to asking whether the pattern of activity in each region carries enough information to distinguish between the two conditions the subject is in. The statistic introduced would still detect voxels with very clear alternations between conditions, but also detect weaker alternations occurring together in several voxels in the region. The authors argue that their use of this statistic is a way of boosting sensitivity relative to traditional univariate testing.
The idea of combining information mapping and decoding by training classifiers in small voxel neighbourhoods is natural and has been used in several papers for two main purposes (see [25] for a recent overview). The first is information mapping, by producing an image where each voxel is assigned the accuracy of a classifier trained using it and its searchlight neighbours. The second is voxel selection, using those accuracy values as scores with which to rank voxels; we will not be concerned with this purpose, but see [30] for an overview of this and other approaches to selecting voxels.
One should note that there are other ways to localize information through the use of classifiers. This generally entails dissecting a trained classifier using a large number of voxels to identify those that contribute the most to its classification performance, an approach known as sensitivity analysis or importance mapping (see [13] or [17] for examples of use). A different way of localizing information is representational similarity analysis [20], which considers the similarity relationships between the activation patterns for different stimuli (or stimulus classes), and how these relationships change across the brain. This is related to nearest-neighbour classifiers, which also resort to similarity relationships or distance measures between stimuli and whose performance can be examined by considering those relationships and seeing which stimuli are distinguishable.
Regardless of purpose, there are two important methodological questions in the production of information maps with classifiers: which classifier to use and how to test whether information is present in a given searchlight. This paper seeks to address both of these questions, analytically if possible or resorting to empirical evidence obtained by using many different classifiers in five datasets with varying numbers of classes.
In choosing among classifiers, an important consideration is the fact that different classifiers have different inductive biases, i.e. when learning from a training set each classifier assumes a particular relationship between voxels and the variable being predicted, which is then taken to hold for future predictions. If a classifier cannot decode information from a particular neighbourhood it is not necessarily the case that that information is not present; it could also mean that the relationship between the voxels is not one the classifier can capture, given its inductive bias. We will make these notions more precise in Section 4, by giving examples of relationships various types of classifier can capture.
To give one example of why this choice matters, though, consider the two-class problem accuracy maps produced with two different classifiers (each voxel shows the accuracy of a classifier trained and tested on the searchlight centered at that voxel) in Figure 1.
Figure 1.
Maps of accuracy in a two-class problem produced for the same subject by two different classifiers.
Listed with each slice is the number of voxels where accuracy is deemed to be significantly different from chance, after testing each map in the same way and thresholding for the same false discovery rate. Even though the maps are similar in some locations, the numbers of such voxels are rather different between the two classifiers; the less successful classifier happens to be one of the most popular choices (when default parameters are used, as is often the case in the literature).
Turning to the question of how to test for statistical significance, there are two different approaches to testing: analytical p-values, where the null hypothesis is that a searchlight classifier performs at chance, and permutation test p-values, where the null hypothesis is that examples in various classes came from the same distribution. We will describe the rationales for using one or the other approach in Section 2.3 and compare them empirically in Section 3.3.
Beyond addressing the questions above, we will introduce various approaches for identifying different types of information present in a dataset with more than two classes. This is necessary because the more classes there are the easier it is for a voxel to be deemed significant, even if it only distinguishes a few of those classes from others, as we will show happens in Section 4.3.
Finally we introduce a publically available MATLAB toolbox for information mapping, which implements efficient versions of all the classifiers used and evaluation procedures described in the text.
2 Methods
2.1 Terminology
For the datasets used in this paper and described in Section 3.2, an example is a vector of feature values, which correspond to the voxels in some part of a 3D image, e.g. those containing cortex, and which can be assigned a class label, such as which of two classes, tools or buildings, a subject was seeing at the time (Figure 2, left). In these datasets that image is generally the average of several images around the peak of the haemodynamic response in a trial or most of the images in a block. There are as many examples as trials or blocks and they divide naturally into groups, which can be the various runs or epochs in an experiments (Figure 2, right).
Figure 2.
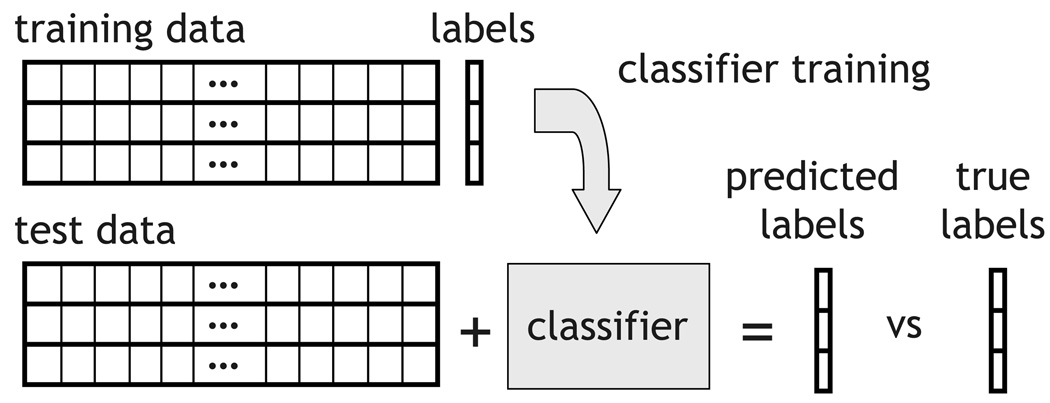
A classifier is learned from the training set, examples and their labels, and used to predict labels for a test set, examples whose labels it cannot see.
A classifier is a mechanism for predicting the label of an example. It is learned from a training set, consisting of examples and their labels, and evaluated on a test set, where it predicts the labels for other examples, as shown on Figure 3. The classifier accuracy on a given test set is the fraction of examples for which it predicted the correct label. A good basic introduction to these and other machine learning concepts is [22] (and [30] and [25], in the specific context of using classifiers with fMRI data)
Figure 3.
A classifier is learned from the training set, examples and their labels, and used to predict labels for a test set, examples whose labels it cannot see.
Whereas one could divide any set of examples into training and test sets, some form of cross-validation is typically used in practice. This consists of making that division repeatedly (e.g. half of the examples are training, half are testing, then this is reversed), training and testing a classifier for each division and averaging the accuracy scores across divisions. This allows every example to be used once for testing, ensuring a better estimation of the classifier’s true accuracy, as described in Section 2.3. In most of the experiments in this paper we will use leave-one-example-group-out cross-validation (see Figure 2, one group is test, all others are train) as that will maximize the amount of data available for training.
The searchlights described in [20] had a spherical shape, with various possible radii. In this paper we will focus on the simplest searchlight case: a 3 × 3 × 3-voxel cube containing a voxel and its adjacent neighbours. A searchlight example will be the subset of an example containing solely the values of voxels in that searchlight, with the same label as that of the entire image.
2.2 Classifiers
We will train three broad types of searchlight classifier (see [14] for extensive descriptions of all of them):
Generative Model
These classifiers rely on modelling the joint distribution of activation of the voxels in each searchlight and using it with Bayes’ Rule to make a prediction about the class of an example. In more detail, the classifier learns the distribution of an example x belonging to each of k classes, P(x|classk), the class conditional distribution. Given a new example xtest, Bayes’ rule yields the probability of each class
and one can classify by picking the class k for which this is highest. One could assume P(x|classk) to belong to any family distribution, or even estimate it non-parametrically; the most common choice – and the one we will use – is to assume that distribution is a multivariate gaussian [14]. In that situation, what is learned for each class is a vector µ̂k of mean values taken by the voxels in examples of class k and also their covariance matrix Σ̂k. Even then, there are several possibilities:
single voxel gaussian classifier (same as a t-test, for comparison)
GNB (“gaussian naive bayes”, diagonal covariance matrix, shared between classes)
LDA (“linear discriminant analysis”, full covariance matrix, shared between classes)
QDA (“quadratic discriminant analysis”, full covariance matrix, different for each class)
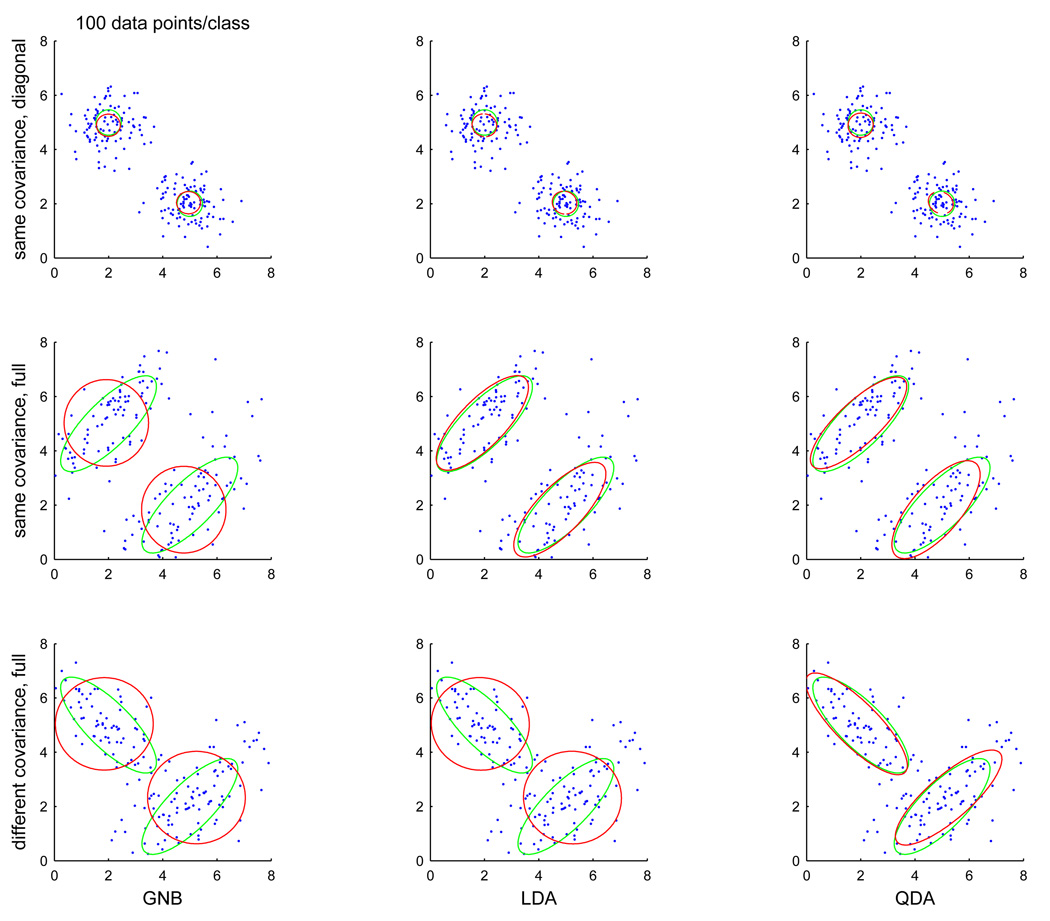
Figure 14 provides a depiction of what these assumptions mean geometrically. There are also various options for estimating the covariance matrix in LDA or QDA, of which we will consider two. The first is the usual maximum likelihood estimator; this may yield a matrix that is not invertible – this inversion is a step that both LDA and QDA use – if there are more variables than data points and sometimes even when there are more. The classifiers are often modified to add a zero matrix with a very small nonzero value in the diagonal, which will allow the matrix inversion to take place. The second is to use a shrinkage estimator, which combines diagonal and full covariance matrix estimates using the data to decide on the extent of the trade-off [31]). This type of estimator is often used to address the problem the first estimate can suffer from; in the experiments described later we will use both kinds of estimate.
Figure 14.
Probability contours for class conditional distributions in 3 scenarios (rows) estimated using 3 different covariance matrix estimators (columns), with 100 data points per class (true contours are green, estimated ones red).
Discriminative Model
These classifiers model the decision of which class to predict directly from the voxel activation values, rather than modelling the joint voxel activation P(xtest|classk) and then using Bayes’ Rule. This model could be probabilistic in nature, in which case P(classk|x) is what is being learned, or instead a function f mapping x to the prediction, i.e. ŷ = f(x). Logistic regression is an example of the former and support vector machines (SVMs) of the latter. For example, a linear classifier in a two class situation would predict by considering a linear combination of voxels
with each voxel v weighted by wv and w0 being a bias term.
Given the close correspondence between logistic regression and some of the gaussian generative models described above[26], and the fact that SVMs have been frequently used for information mapping and voxel selection, the analyses that follow focus on the latter.
The decision function that is learned by a SVM is a linear combination of feature values in a particular feature space. What changes between the different types of SVM is the relationship between that feature space and the original features (voxels, in our case); a given choice of kernel function will determine an (implicit) feature space in which the decision takes place. For a linear kernel, this is the same as the original space, hence one would be learning a linear discriminant on voxels. For a quadratic kernel the feature space also contains features that correspond to the product of the activation of every pair of voxels, something analogous to interaction terms in a linear regression model. For kernels such as radial basis function (RBF) or sigmoid, the implicit feature space is more complicated than we have space to discuss. Suffice to say that, for anything other than a linear kernel, the linear decision function in the implicit feature space corresponds to a nonlinear decision in the original space.
When applying SVMs to classification problems involving more than two classes the classification problem generally has to be converted into several binary problems, each of each yields one SVM classifier. These classifiers are each applied to a test example and their outputs combined in order to make a prediction. The method implemented in the SVM software package we will use [3] is an all versus all encoding, in which one classifier is trained for each of all possible binary problems involving a pair of classes. A test example label is predicted by applying each binary classifier, recording a ‘vote’ for the winning class for that pair and, after doing this for all pairs, picking the class with the most votes. There are alternative schemes for doing this, though they are not directly supported by the SVM software we used. For thorough descriptions and comparisons of those methods, see [6] and [1].
Nearest-neighbour
This is the simplest type of classifier, in that no parameters are learned. Classification of a test example xtest is done by reference to neighbours, other examples in the training set that are closest to it by some measure (e.g. euclidean distance or correlation similarity of the voxel vectors) and using their respective labels as votes in a prediction decision. There are two different choices to make here. The first is what similarity or distance measure to use. This decision is combined with the need to downplay the influence of irrelevant or noisy voxels in the measure computation [22]. We will consider correlation similarity, as these is commonly used with fMRI data (a trend started in [15]) and the number of voxels per searchlight is small. The second choice has to do with what neigbours are considered:
nearest neighbour - this will assign the label y of example x in the training set that is closest to xtest. It’s conceptually simple but also susceptible to noise, as it only takes one example of the wrong class to be close to yield an incorrect prediction.
nearest class mean - this is a variant of nearest neighbour where what is considered is distance to the mean activation vectors for examples of each class.
k-nearest-neighbours - instead of considering just the nearest neighbour, consider an odd number of neighbours and pick the class to which most neighbours belong.
2.3 Statistical testing of accuracy
The person training a classifier on fMRI data is concerned with establishing that a variable of interest can be decoded from it, i.e. a classifier can be trained whose true accuracy is better than that of a classifier deciding at random. Formally, the true accuracy is the probability that the classifier will correctly label a new example drawn from the same distribution that the training examples came from; it can also be viewed as the accuracy one would get if one had an infinite number of examples in the test set. The accuracy on the test set is thus an estimate of the true accuracy of the classifier trained. It is an unbiased estimate because the test examples have not been seen by the classifier during training. How precise an estimate it is depends on the size of the test set; the fewer examples used the greater the variability of the estimator, as we shall see below. One could take this further and consider that the training set is also drawn from an example distribution, if what was desired was a result about all classifiers trained on a dataset of a given size rather than the specific training data we have; this is beyond the scope of this paper, but see [7] for a discussion of this topic.
A statistically significant classification result is one where we can reject the null hypothesis that there is no information about the variable of interest in the data. Establishing statistical significance is generally done by determining how improbable the observed classification accuracy would be were the null hypothesis to be true. This p-value can be obtained in two ways: through an analytical model that provides a distribution of accuracy under the null hypothesis and through a permutation test. The next two sections describe each of these approaches in more detail as well as guidelines and caveats of their use, and they are compared across datasets in Section 3.3.
2.3.1 Analytical test
Suppose we have a problem in which the classifier predict one of two classes that are equally frequent in the data, and that the classifier succeeds in correctly classifying k of the n test examples it is given. To determine whether this experimentally observed accuracy is statistically significant we must determine how likely it is that we would observe at least k successes out of n test trials if the classifier were in fact operating at chance (i.e., if the null hypothesis were satisfied). If this were the case, and if the test examples were drawn independently, then we would expect an accuracy of k/n = 0.50 on average; the actual observed accuracy might vary above or below 0.5 due to variations in the sample of test data we happen to be using. It’s to ward off against this that we need to determine the probability that this experimentally observed accuracy might vary to a value at least as high as k/n even when the null hypothesis is satisfied. Note that the observed accuracy might also reach values substantially below 0.5 under the null hypothesis, but we are not interested in the chance of coincidental deviations below the expected 0.5 because we would not try to claim our classifier was succeeding in that case.
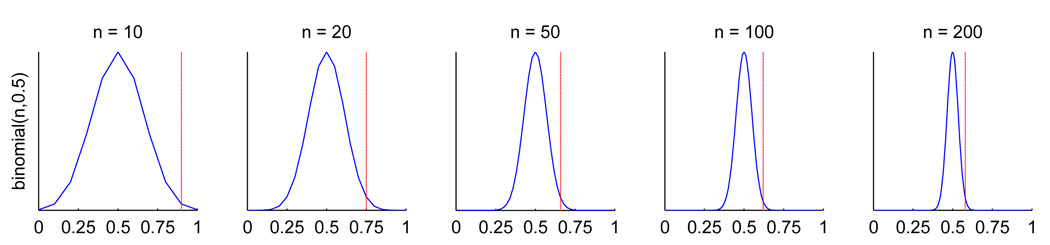
The probability of obtaining a given classification result under the null hypothesis can be viewed as the outcome of tossing a coin for each of the test examples to be classified, with the coin’s bias reflecting the probability of labelling an example correctly by chance (50% in a two class problem, 25% in a four class problem, etc). More formally, each coin toss can be modelled as a Bernoulli trial with probability q of success. The probability of achieving k successes out of n independent trials is given by the binomial distribution. If we define k to be the number of correctly labeled test set examples out of n, the p-value under the null hypothesis is simply P(X ≥ k), where X is a random variable with a binomial distribution with n trials and probability of success 0.5 (two class), 0.25 (four class), etc. If the p-value is below a certain threshold (typically 0.05 or 0.01) the result will be declared significant. Figure 4 shows what this distribution looks like for n ranging from 10 to 200 with q = 0.5, over the range of possible accuracies. As n increases the distribution becomes narrower and lower values of accuracy above 0.5 would be declared significant. This is indicated by the position of the vertical red line in each plot, which is the accuracy value that would be significant at the 0.01 level.
Figure 4.
Distribution of accuracy under the null hypothesis that the classifier performs at chance (p = 0.5, two class problem), for test set sizes n from 10 (leftmost plot) to 200 (rightmost plot). The vertical red line indicates the accuracy value above which a result would be deemed significant at the 0.01 level using the binomial test described in the text.
Note also that, thus far, we have been talking about a single classifier being applied to a test set. The accuracy estimate obtained through cross-validation is a combination of results produced by classifiers trained on mostly overlapping training sets, hence we will treat that estimate as if it came from a single classifier, following common practice [18], which then allows us to test it in exactly the same way.
2.3.2 Permutation test
The analytical test described above is based on a null hypothesis about classifier performance in the face of there being no information about the class label in the data. One can, instead, have a null hypothesis about that absence of information by using a permutation test. Assuming there is no class information in the data, the labels can be permuted without altering the expected accuracy (chance level). In practice, this entails shuffling the labels within each training set, training a classifier and applying it to the test set. The procedure is then repeated many times, with a different shuffling each time. Over many repetitions, this yields a sample of accuracy results under the null hypothesis.
The p-value in this case is the fraction of the sample that is greater than or equal to the accuracy actually observed when using the correct labels. Note, also, that the true labeling is one of the possible labelings and should be included; a consequence of this is is that the smallest possible p-value is , where P is the number of permutations tried [27]. A good review of permutation tests in classification (with one functional neuroimaging application) is [10].
2.3.3 Test choice and caveats
Multiple comparisons
When extending these points to information mapping, the first issue that arises, regardless of which test is used, is that the procedures described are for testing a single classification result. When computing accuracy over the searchlight centered around each voxel in the brain, we would have as many results as voxels and thus a multiple comparison correction would be required. Given that searchlights overlap, this will ensure correlation between test results and thus should be taken into account when selecting a correction criterion. In this paper we will use False Discovery Rate [9] (FDR), which controls the average fraction of false positives out of the set of all positive test results. We chose it both because it caters for the case where the test results can be correlated and also because we only expect a small fraction of the total number of voxels to be deemed informative.
Conservatism of permutation tests
The binomial test is exact if the assumption about test example independence holds and hence preferrable to the permutation test if considering computational expense; a large number of permutations may be required to get possible p-values in a range that would survive multiple comparison correction. By virtue of inclusion of the correct labelling along all other shufflings of labels, the permutation test will be conservative.
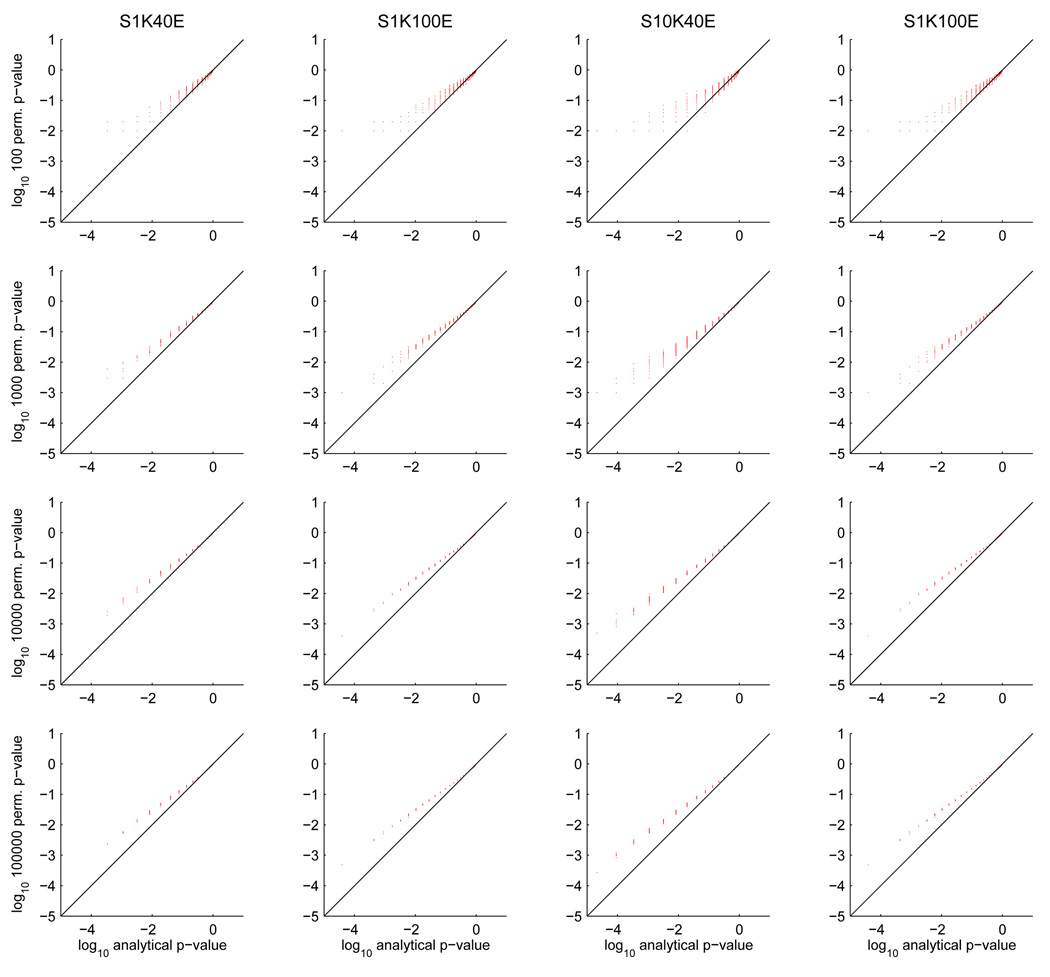
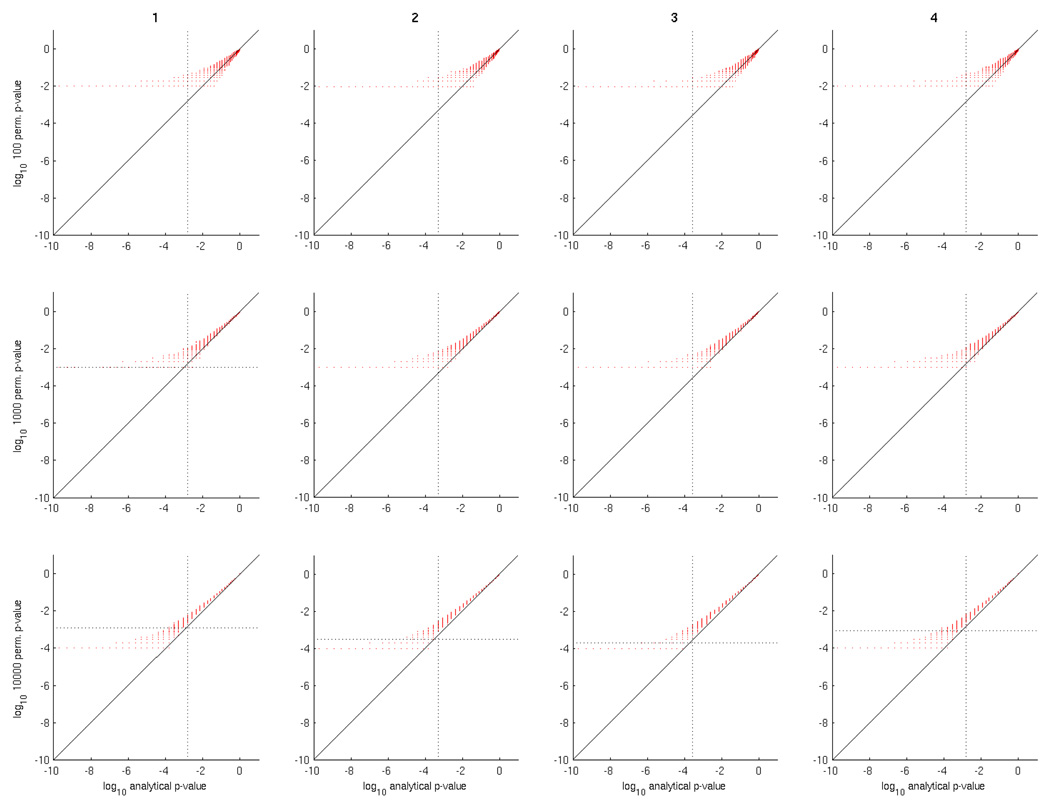
In order to ascertain whether this is an issue in practice, with the numbers of examples or permutations typically used, we generated various datasets containing independent, normally distributed noise examples in which each voxel was generated independently, structured as a 3D volume. We then trained/tested Gaussian Naive Bayes searchlight classifiers to produce analytical p-values, and ran a permutation test using them as well. Figure 5 shows the results of this, by contrasting analytical and permutation test p-values, at various numbers of permutations and voxels. As expected, the lower permutation test p-values get smaller as the number of permutations increases, getting closer to the lower analytical p-values; the distribution of points still lies above the diagonal line regardless of the number of permutations. The effect of increasing the number of permutations is to narrow the spread of permutation p-values. This makes sense if we consider that each permutation p-value is an estimate of the value we would get with an infinite number of test examples, with a distribution centered around this value where the variance depends on the number of permutations [11].
Figure 5.
Comparison of analytical versus permutation test p-values for 4 noise datasets (columns): 1000 voxels, 40 examples (S1K40E), 100 examples (S1K100E), 10000 voxels 40 examples (S10K40E) and 10000 voxels 100 examples (S10K100E). The rows correspond to number of permutations, 100, 1000, 10000 and 100000. In each scatter plot, the x-axis is the analytical p-value and the y-axis the permutation p-value. For visual convenience, the scales in each scatter plot are logarithmic (base 10), hence the p-values close to 0 are on the left and those close to 1 on the right.
Example independence assumption
If the assumption of independence does not hold the binomial test would be assuming the count of correctly labeled examples came from a larger number of trials than was effectively the case, thus yielding lower p-values than it otherwise should. To see why this is the case, consider a situation where trials are well separated – more than 30 seconds, say – and the two consecutive images at the peak of the trial response are taken as examples. Given the properties of the hemodynamic response [21], the values of any voxel would be similar between these two examples. Let’s assume, further, that we are training a classifier on the examples from all other trials and testing on those from this one. Because of the similarity between the two examples, it is likely that the label predicted for one would also be the label predicted for the other; the prediction would hence be correct for both or wrong for both. In this situation, the number of independent decisions would be roughly of the number of test examples, and thus the correct n to use in the binomial distribution for the analytical p-value. The accuracy estimate would still be unbiased but its true variance would be higher than what one would expect. This is a particularly extreme illustration of example dependence, but it can happen in more subtle ways. So how does one determine whether it is happening and, if so, how it should be addressed?
Consider a situation where there is one event per trial, and an example is the image collected at the peak of the BOLD response in that trial. If trials are very clearly separated, i.e. the BOLD response to one trial does not overlap with that of the subsequent trial, then it is reasonable to assume the corresponding examples are independent. The duration of the BOLD response is a good starting point for considering the dependence between consecutive examples. Following [4] (Figure 2), the BOLD response in primary visual cortex to a 1 second flashing checkerboard stimulus lasts roughly 12 seconds; we will not be overly concerned with the weaker fluctuations beyond that, which might extend a few seconds longer. In [2], similar stimuli (checkerboards interleaved with vertical gray bars) with durations of 3, 6, 12 and 24 seconds lead to responses lasting roughtly 12, 16, 24 and 36 seconds. Given that the BOLD response is stronger in visual cortex than in most other locations, we take these as reasonable upper bounds on how long a response would last given those stimulus durations, assuming it would be less intense and perhaps a bit shorter elsewhere.
We could also approach this issue from a statistical angle and say that consecutive examples x and y are independent if p(y|x) = p(y) (assuming examples are images and thus high-dimensional vectors where voxels are the vector entries). Estimating these probabilities and whether they are close is not practical, as we would need to estimate the joint distribution of activity of all voxels xi in an example x. If we are willing to assume voxels are independent it would be feasible, though it would still require specifying a distribution for the activity of each voxel.
A more practical approach would be to invert the implication between independence and lack of correlation and look for correlation as an indicator of lack of independence. To do this we need to examine the autocorrelation of each voxel at lag 1 and higher, with the lag corresponding to how many preceeding examples could influence each example. In the lag 1 case, this is simply the correlation between voxels xi and yi over all pairs of consecutive examples x and y. The first way of using this is simply to plot a histogram of the correlation values for all voxels at a given lag and see if deviates substantially from a symmetric distribution with a median around 0; if it does, it means that most voxels in an example depend to some extent on the previous example. If one wanted to be more stringent, the second way of using this would be to convert the correlation ri in each voxel xi into a z score, using the Fisher transformation (where n is the number of values used to compute the correlation, i.e. the number of examples minus the lag). Using the standard normal distribution, the z score for each voxel can be converted into a p-value under the null hypothesis that the true correlation is 0 and the entire set can be thresholded (using FDR, for instance). This latter approach is more useful if one wants to look at the time series of voxels that exhibit dependence, to see if responses to different trials overlap enough that the images used to create an example in a trial are still influenced by those used to create the example in the preceeding one. We will illustrate the use of autocorrelation for some of our datasets later, in Section 3.3.
What if it is known that there is a dependence that cannot be eliminated, e.g. a fast event-related design where the responses to trials are certainly overlapping? In that particular situation, one could resort to deconvolution to obtain images of beta coefficients (one per trial, or one per condition, keeping in mind that deconvolution would have to be performed separately for each cross-validation leave-one-out unit, e.g. a run, otherwise there would be circularity [20]). A different possibility is to use a permutation test to obtain p-values, as the permutation distribution incorporates the dependence between examples in the test set, i.e. the variance of the result is higher than it would be if the examples were independent. To see if this is warranted, one could simply compute the p-values both analytically and using a permutation test for a classifier where this can be done quickly (e.g. the GNB provided in the toolbox we will describe in Section 4.5), and see if the significance results are very different. If so, it would be worthwhile to run a permutation test for whatever classifier produced the best results. Yet another possibility is the following heuristic: reasoning either from BOLD response first principles or the autocorrelation statistics described above, determine how many preceeding examples an example is likely correlated with and divide the number of test examples n by that; in the example given above, n was divided by 2. While this will almost certainly be conservative, as the dependent examples will likely not be perfectly correlated, it’s a simple way of checking whether the significance results are robust in face of the dependence and that may all that is required.
Circularity
A second reason for using permutation tests arises in a situation where there is a suspicion that a classification procedure is optimistic due to circularity; this is situation where data that is used for testing also influences the training of the classifier or selection of the features it sees (see [20] for an excellent description of many possible scenarios where this could happen). Another subtle way of biasing results is to report the highest classification result out of several, testing it as if it were the only one. Even if all classifiers being compared performed at chance, it would be possible for one of them to show better performance than the others. In such situations, running a permutation test of the entire procedure (e.g. train all the classifiers from which you will pick the best and then do so) would yield results with the same positive bias and thus would make it harder for the result to be declared significant erroneously (see the second chapter of [29] for a lengthy discussion and experiments on this topic).
Exchangeability
If combining permutation tests with cross-validation, one needs to keep track of the fold structure when permuting example labels, as it is possible to have training sets where a given class is not represented and others where it is overrepresented. The effect of this would be to artificially lower performance, as the classifier would have to deal not just with the labels having been permuted but also with an imbalance the real classifier did not face. A practical solution is to do a stratified test, and permute within the partitions of the dataset used for cross-validation, e.g. runs or epochs.
In general, one should be satisfied that the examples in set that can be permuted are exchangeable under the permutation distribution. Intuitively, this means that any order of examples could have arisen out of the process generating them; if using successive TRs as examples, for instance, this would certainly not be the case. To see how this could be a problem, consider a situation where there are 10 examples which are consecutive TRs, all with the same label. The labels are permuted and, in this permutation, 5 of those examples have one class label and 5 have another. When the classifier is trained on these examples, it will see very similar examples with opposite labels. This could produce a worse classifier than what would be possible if training with independent examples labelled at random, where chance could lead to some coherent structure in voxel activation being identified over examples with the same label. This would, in turn, lead to the results under the permutation distribution being negatively biased and p-values thus lower than they should be. A way of addressing this would be to ensure that the permutation distribution assigned the same label to all 10 examples (which could be different for different permutations, of course).
A second situation where exchangeability could be violated is if examples from one part of the dataset were somewhat different from examples from another part, regardless of label. An example of this would be data from various runs having a different characteristic, such as mean activation or variability in each voxel, or coming from multiple sessions. Whereas there is no obstacle to cross-validating while mixing from both parts, it is common to simply equate the parts with the folds in cross-validation in order not to have to worry about exchangeability. For a discussion of the exchangeability property see [27] in the imaging context or [11] in general.
Equating cross-validation folds with example groups is also often done to make sure that the examples in the training and test sets are definitely well separated. Note, though, that differences between folds could violate a more important assumption than exchangeability; that the training and test examples come from the same distribution. This is the basis for claims about a classifier being able to generalize to unseen data, and one of the things to consider examining in face of poor results.
3 Experiments comparing accuracy maps
The main purpose of the experiments in this section is to understand which factors determine whether a classifier will be better than another for the purpose of identifying informative voxel searchlights. In order to test this we will produce classifier maps for several datasets, with varying numbers of classes and examples per class. Beyond this, we will address the question of whether the analytical test of accuracy described in Section 2.3 is more powerful than a permutation test, at various numbers of permutations.
3.1 Classifiers
The basic details about all the various types of classifier considered are provided in Section 2.2, the following is a key for the designations used in all figures (all classifiers operate on searchlights unless otherwise mentioned):
voxelGNB - single voxel gaussian naive bayes
voxelGNB_smooth - single voxel gaussian naive bayes over spatially smoothed data (using a 3 × 3 × 3 uniform smoothing box around each voxel)
GNB - gaussian naive bayes
LDA - linear discriminant analysis (using the trick of adding a small value to the diagonal of the covariance matrix)
LDAshrinkage - linear discriminant analysis (with a shrinkage estimator for the covariance matrix)
QDAshrinkage - quadratic discriminant analysis (with a shrinkage estimator for the covariance matrix)
SVMlinear - linear support vector machine (LIBSVM [3] implementation, default parameter C = 1)
SVMlinearxv - same as SVMlinear, training set cross-validation to set C parameter
SVMquadratic - quadratic support vector machine (LIBSVM implementation, default parameters)
SVMrbf - RBF kernel support vector machine (LIBSVM implementation, default parameters C = 1 and )
nearest_neighbour - nearest neighbour classifier using correlation over all voxels in the searchlight as the similarity measure
nearest_mean - same as nearest neighbour, but computing distance to all class mean patterns
3.2 Datasets
We considered five different datasets 1 with similar tasks but rather different numbers of classes and examples. Datasets D1, D2, D4 and D5 shared the same experimental paradigm. In each trial, a subject sees a word or picture for a given concept for three seconds, during which she needs to consider its properties, visualize its use, etc. This is followed by eight seconds of blank screen, until the beginning of the following trial. In datasets D1 and D2 the stimuli (words/pictures) belong to one of two categories, tools or dwelling types, and those are the two classes a classifier will have to distinguish. Dataset D4 is similar to D2 but we will consider ten classes (which exemplars of tools or dwellings) for classification purposes. D5 contains stimuli belonging to twelve categories and is described in more detail in [24]. Dataset D3 has a block design, with all the photo stimuli in one block belonging to the same category, one of eight possibilities; for more details see [15].
In order to create examples for classification in datasets D1, D2, D4 and D5, the images around the haemodynamic peak of each trial were averaged into a single one, which becomes the example. The label of that example has to do with the stimulus shown in the trial, and is one of two categories (tools/dwellings) for D1 and D2 (2 classes, 48 examples per class), ten exemplars for D4 (10 classes, 6 examples per class) and twelve categories (12 classes, 30 examples per class) for D5. For dataset D3 we averaged the images in one block (minus the first two) into an example, labelled with the category of the stimuli in that block (12 examples per class). The voxel sizes were 3 × 3 × 5 mm for datasets D1, D2, D4 and D5 and 3.5 × 3.75 × 3.75 mm for dataset D3. Numbers of voxels in cortex varied between 14K-20K for D1, D2, D4, 23K-24K for D3 and 20K-21K for D5.
We selected 4 subjects from each dataset, both for practical computational reasons but also to facilitate the presentation of figures; the number should also suffice to show that any trends identified are consistent across subjects within each dataset. Throughout the paper, subjects are numbered 1–4 in each dataset, corresponding to original subject identifiers 01481B, 01482B, 01897B and 02062B (dataset D1), 02553B, 02607B, 02714B and 02745B (dataset D2), subj1_ii, subj2_ss, subj4_jj and subj6_wp (dataset D3), 02553B, 02607B, 02714B and 02745B (dataset D4) and P1, P2, P3 and P4 (dataset D5).
3.3 Generation and testing of accuracy maps
All the accuracy maps are produced by cross-validating a classifier on the data for the voxels inside each searchlight and assigning the resulting accuracy value to the voxel at the center of the searchlight. Note that this procedure is an unbiased estimator of the true accuracy of the classifier over that particular searchlight and thus there is no need for separate test data. Each accuracy value is then converted into a p-value for the null hypothesis that the true accuracy of that classifier over that searchlight is chance level, using the analytical test procedure described in Section 2.3 (this takes into account the variability of the accuracy estimate). Each map is then thresholded using FDR, q = 0.01, to yield the significant voxels for that map.
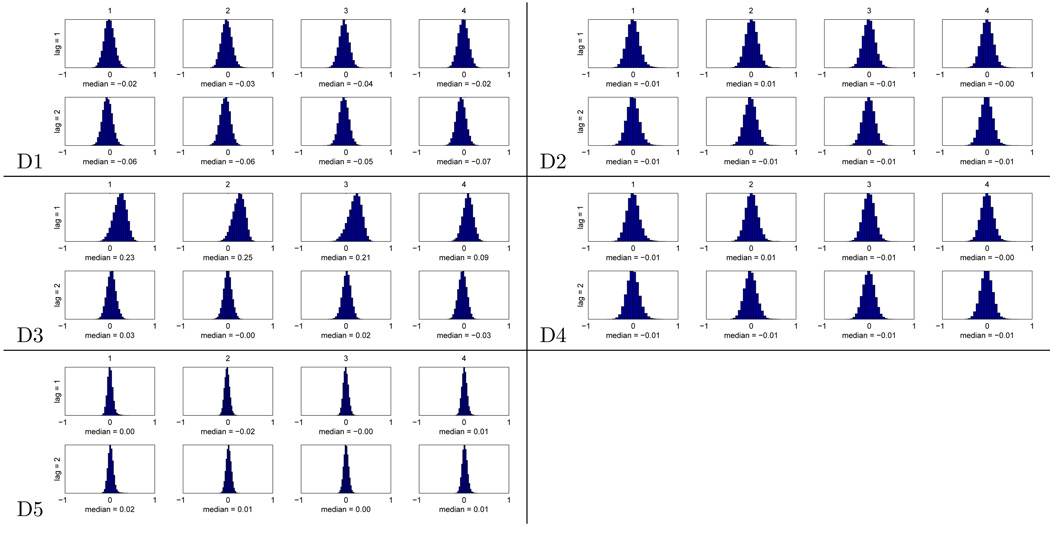
The alternative way of obtaining a p-value for each voxel is to resort to a permutation test. The criteria for whether this is desirable or necessary were discussed in Section 2.3.3. In order to judge that we computed the autocorrelation at each voxel between consecutive examples (lag 1) and, for comparison, between examples with one example between them (lag 2). The comparison of these two lags seems reasonable, since for all the studies examples with another example between them are well separated as far as the respective trial BOLD responses are concerned. The results are displayed in Figure 6, as histograms with the distribution of autocorrelation values across voxels for each subject and lag. For datasets D1, D2, D4 and D5 the distributions at the two lags are very similar, symmetric and their median is close to 0. For dataset D3, however, the distributions at lag 1 clearly differ from those at lag 2, and they have medians well above 0. This indicates that there is dependence between consecutive examples, even though the separation between stimuli going into the two examples is almost 18 seconds (7 TRs). The practical consequence of this is that the analytical p-values for D3 are lower than they should be and thus optimistically biased, whereas this appears not to be the case for the other datasets.
Figure 6.
For each of 4 subjects (columns) in the 5 datasets, histograms of voxel autocorrelation between consecutive examples (lag = 1) and examples separated by another example (lag = 2). The median of the distribution is shown below each histogram.
This allows us to revisit the question of whether permutation p-values are conservative relative to analytical p-values, discussed earlier in Section 2.3.3, with real datasets instead of one consisting entirely of noise. This comparison is subject to two different kinds of practical consideration: computational expense (each permutation requires the production of an entire accuracy map) and power (the smallest p-value possible is , which might be much larger than the FDR threshold for significance).
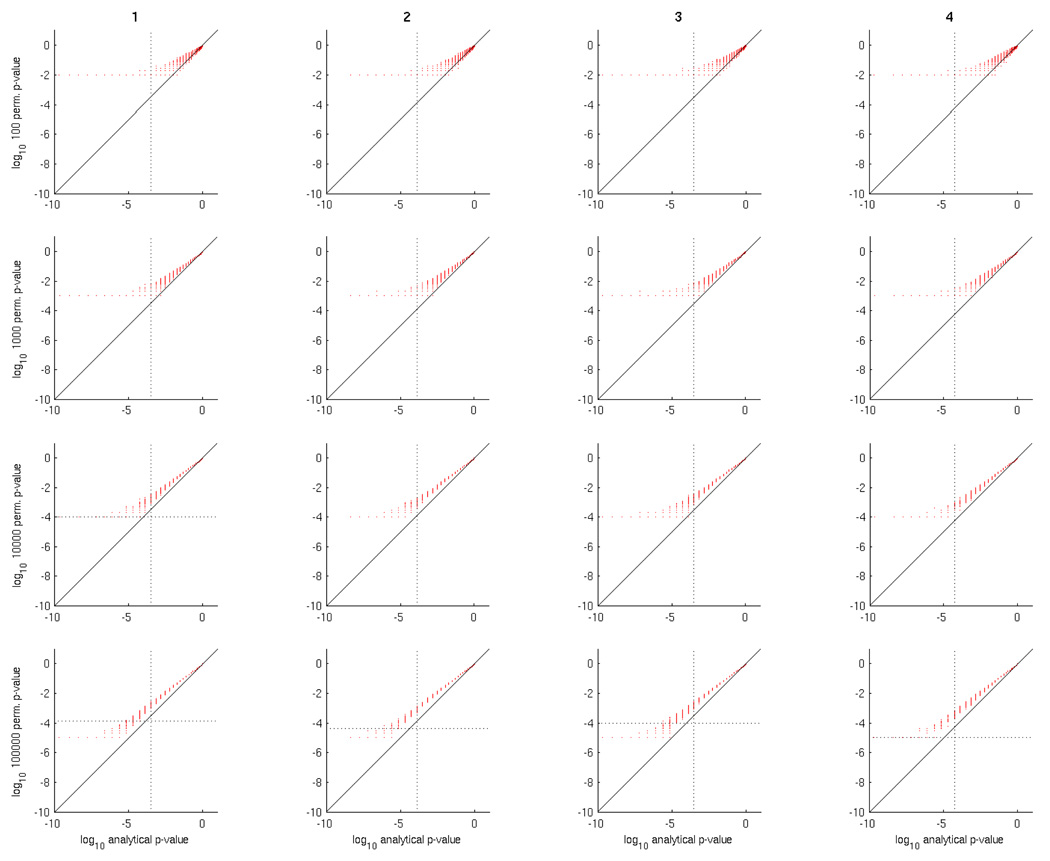
In order to examine this question empirically we considered datasets D1, D3 and D5, in order to have both two and multi-class problems. Using a special-purpose implementation of GNB capable of producing a whole-brain accuracy map in seconds (more details in Section 4.5), we computed permutation p-values for each searchlight using various numbers of permutations, which we then compared with analytical p-values for the same searchlight. The results are shown in Figure 7 (dataset D1) and Figure 8 (dataset D3).
Figure 7.
Comparison of analytical versus permutation test p-values for 4 subjects (columns) in dataset D1, using 100, 1000, 10000 and 100000 permutations (rows). In each scatter plot each red point has analytical and permutation p-values as the x and y axes, respectively. For visual convenience, the scales of each axis are logarithmic (base 10), hence the p-values close to 0 are on the left and those close to 1 on the right. The vertical dotted line is the FDR q = 0.01 significance threshold for the map of analytical p-values, and the horizontal (if it exists) for the map of permutation test p-values.
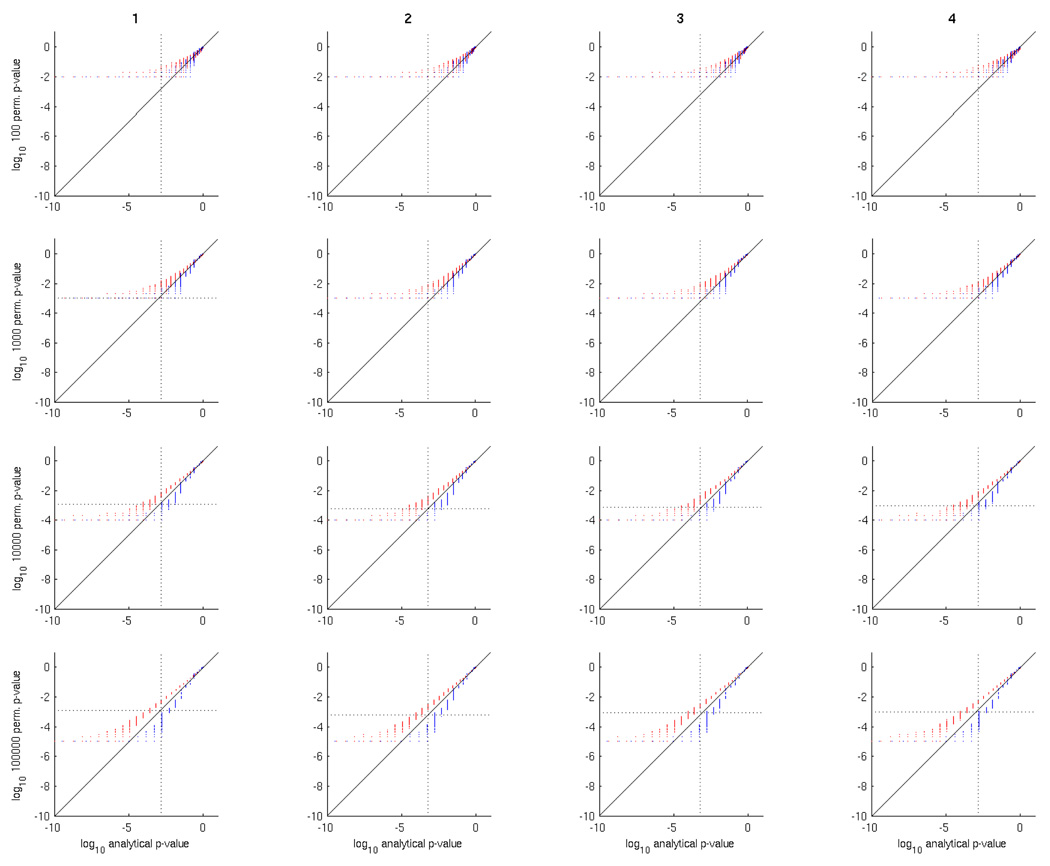
Figure 8.
Same as Figure 7, for dataset D3. Each scatter plot has a second set of points (in blue) overlaid on the main one (in red). This depicts analytical versus permutation p-values, as before, but the analytical p-values are with respect to half the number of examples actually used for testing, as a heuristic lower bound on what they should be.
Considering Figure 7 for dataset D1, the first thing to note is that permutation test p-values are higher than analytical ones; so much so that it would take 10000 or 100000 permutations for any searchlight classification accuracies to be deemed significant under FDR. In addition, as the number of permutations increases, the permutation test p-values approach the analytical ones, by narrowing the distribution of the former for a given value of the latter. This suggests that, for a given searchlight classifier accuracy, and corresponding analytical p-value, the permutation p-values converge towards a value that is higher than that analytical p-value.
Considering Figure 8 for dataset D3 we have the added complication that consecutive examples are dependent, rendering the analytical p-values likely optimistic. In order to examine the effect of this, we overlaid a second scatter plot (in blue) on top of the original one (in red), contrasting the lower bound analytical p-values obtained by considering half the number of testing examples (as discussed in Section 2.3.3) with the permutation test p-values. This shows that permutation p-values are a viable choice in a situation where examples are dependent, and not as conservative as the lower bound.
Also considering Figure 9, it takes fewer permutations for p-values to be significant in D3 or D5, even though the number of voxels considered is similar to D1. Our conjecture is that this happens because many of the permutations in D1, which has two classes, leave many of the examples with similar labels to those they had originally; this is far less likely in D3, as each example can have one of eight labels and even less so in D5, where it can have one of twelve.
Figure 9.
Same as Figure 7, for dataset D5.
Figure 8 also suggests a possible heuristic for finding a reasonable compensation for optimistic bias in analytical p-values: use GNB to produce permutation test p-values and then reduce the number of test examples for analytical p-values until the cloud of points in each scatter plot is spread around the diagonal, both above and below. This reduction factor could then be used on analytical tests for results from other classifiers, if running permutation tests is unfeasible.
We think these results justify the use of analytical p-values to determine classification result significance in datasets D1, D2, D4 and D5, and will use them in the rest of the paper. We will be more cautious with dataset D3 and use the heuristic of halving the number of test examples when determining significance. While this lowers the number of voxels deemed significant, the various plots that depend on this look qualitatively similar with and without the heuristic, which suggests the findings are robust.
3.4 Methodology for comparing accuracy maps
For each dataset, we will consider maps produced with several classifiers, using the notation a = [a1,…,av] for the map produced by classifier a (and similarly b, c, etc). We would like to be able to say whether, for a given dataset, a classifier is better than another. But how should this be defined? If we knew precisely which voxels were informative, we could compare the accuracies of the two maps over those; an experiment with synthetic data would allow it, at the cost of having to specify exactly how information would be encoded in the data. Given this, one possibility would be to compare the respective accuracy maps voxel by voxel and see whether one map is higher than the other for the majority of voxels. The issue with this approach is that we would be considering tens of thousands of accuracy results, most of which would likely be around chance.
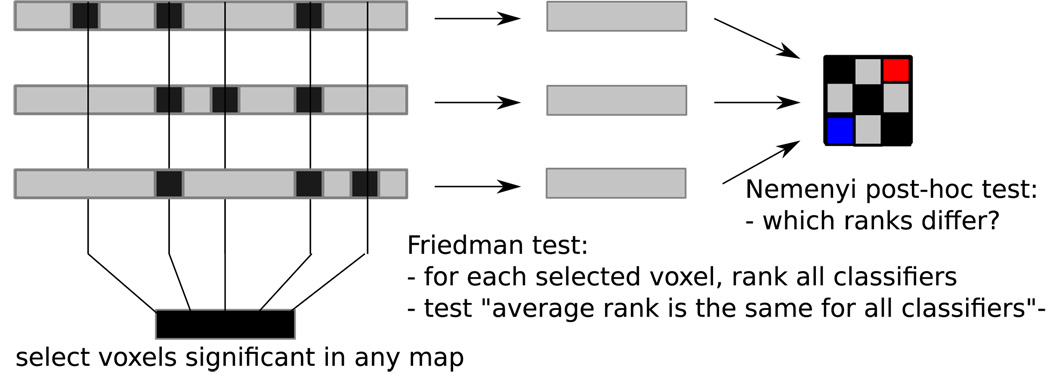
The approach we will take tries to combine the two ideas above by comparing over the set of voxels that are deemed informative by any classifier; this can be obtained by thresholding the accuracy map for each classifier using the analytical test in Section 2.3 to transform it into a p-value map and FDR to correct for multiple comparisons (q = 0.01). The main idea is that, not knowing a priori which voxels are informative (or how much), we will at least be using a subset of those. After this process accuracy map a is reduced to just this set of voxels, a* (see the left of Figure 10).
Figure 10.
In order to compare multiple accuracy maps, their maps of p-values are thresholded with FDR (q = 0.01 and the set of voxels significant in any map is identified (left). Each pair of accuracy maps is compared across that set of voxels, using a Friedman test (center). If the test rejects the null hypothesis that no pairs are different, a post-hoc Nemenyi test is conducted to identify which pairs are (right).
In order to compare the reduced maps of all the classifiers we will use a combination of a Friedman test and a Nemenyi post-hoc test, following the procedure described in [5]. The Friedman test consists of the following steps:
for each selected voxel, rank all classifiers (the ranks for classifier a are ra)
compute the average rank across selected voxels for each classifier
null hypothesis: any two classifiers a and b are equally good and their average ranks r̂a and r̂b are the same
If the null hypothesis is rejected, we then use a Nemenyi post-hoc test (0.05 level). This test considers the magnitude of the difference in average ranks (r̂a − r̂b) for each pair of classifiers and also controls the family wise error rate for comparing all the pairs. This difference is deemed significant if it is greater than a certain critical value (see [5] for more details). The end result is a #classifiers × #classifiers matrix that summarizes these results and will be discussed and illustrated in the next section.
3.5 Comparison of accuracy maps
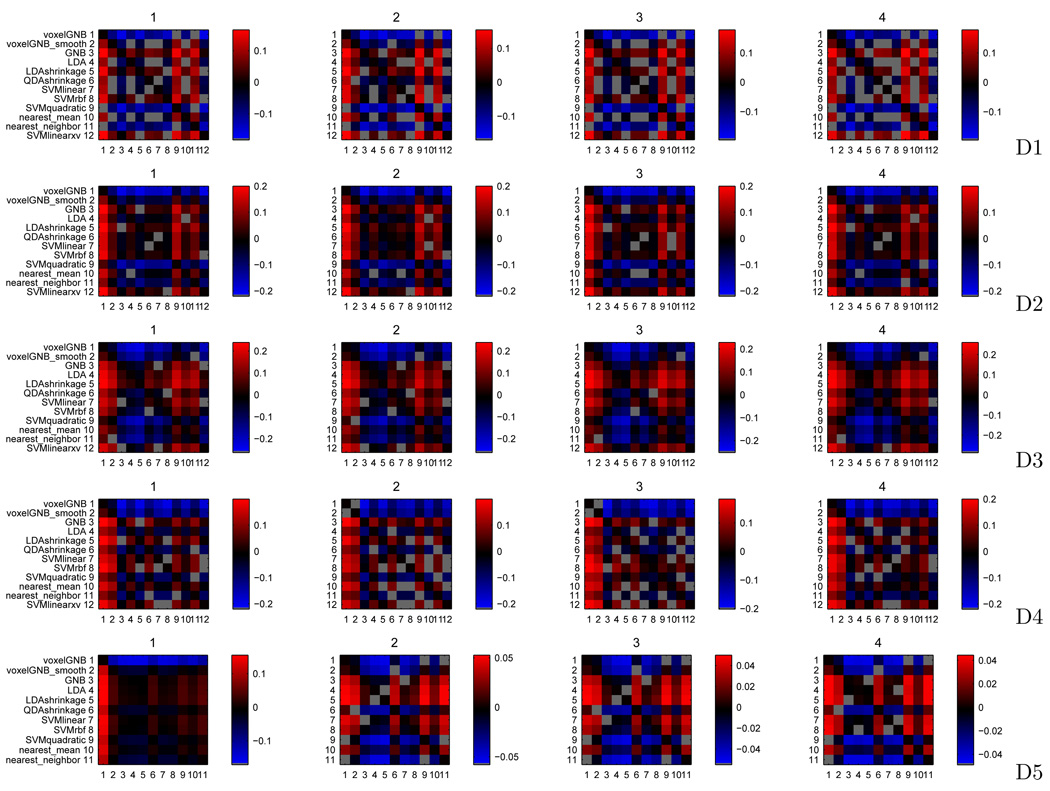
Figure 11 depicts a comparison of each classifier against each other, for each of 4 subjects in 5 datasets. For each subject, the result of the comparison procedure is a #classifiers × #classifiers binary matrix, where entry (a, b) is 1 if the difference r̂a − r̂b is significant and 0 otherwise. In order to provide a visualization of the significant differences in an informative scale, we created a new matrix from this one where each entry (a, b) shows either dab, the median of the sample of values a* − b* (more informative than rank difference, as the scale is in the units of accuracy), or gray if the difference r̂a − r̂b was not deemed significant. In practical terms, (a, b) is positive if the paired accuracy of classifier a is larger than that of classifier b across the voxel searchlights considered (those that were deemed significant in any classifier accuracy map), negative if the reverse is true and gray if the difference is not statistically significant under the Nemenyi test performed.
Much as [19] points out, there is a benefit to using a searchlight (almost all searchlight classifiers do better than a single voxel classifier) and most of that gain does not come from a spatial smoothing effect (as the voxelwise classifier on smoothed data is still outperformed by almost all searchlight classifiers, even as it outperforms the basic voxelwise classifier).
For gaussian classifiers, GNB and shrinkage LDA show better performance than LDA and shrinkage QDA. In a two class situation (D1 and D2), GNB and LDA with shrinkage are roughly equivalent in terms of performance. With more than two classes (D3,D4,D5), LDA shrinkage is better (D3,D5) unless there are relatively few examples per class (6 in D4 versus 12 in D3 and 30 in D5). Overall, this suggests there is covariance structure to exploit in multiple class situations, even though it may not be different between classes.
For SVM classifiers using default parameters, quadratic kernel SVMs are uniformly worse than either linear or RBF kernel SVMs across all datasets. RBF kernel SVMs are slightly better than linear kernel SVMs for D1 and D2, but the reverse is true for the multi-class datasets. Finally, cross-validating the C parameter in linear SVMs makes them comparable to RBF kernel SVMs in D1 and D2. This, together with the accuracy maps in the Appendix, could indicate that there may be no nonlinear voxel interactions to exploit. Exploring this further would require either an exhaustive two parameter search for RBF kernel SVMs or training of another nonlinear classifier such as a neural network.
For nearest-neighbour classifiers, nearest-mean is better than nearest-neighbour across all datasets. This may indicate that individual examples are just too noisy for reliable classification, but also that the class mean examples are good enough (in that results are not much worse than for methods that use class means and voxel variance/covariance inside the searchlight).
Figure 11.
Comparison of each classifier against each other, for 4 subjects (columns) in 5 datasets (rows). In each plot, entry a, b is positive (red) if the paired accuracy of classifier a is larger than that of classifier b across the voxel searchlights considered, negative (blue) if the reverse is true and gray if the difference is not statistically significant under the Nemenyi test performed.
Whereas Figure 11 provides a measure of how classifiers compare across all the voxels that are significant in at least one of them, we can also consider more condensed measures: the number of such significant voxels for each classifier or the median accuracy across all significant voxels, as shown in the left and right, respectively, of Table 1. These corroborate the results above and indicate that, in terms of numbers of voxels detected, GNB and shrinkage LDA are the best methods but comparable to cross-validated parameter linear SVM.
Table 1.
One table for each of the 5 datasets, counts of number of voxel searchlights deemed significant using each classifier (4 subjects are left 4 columns) and 50 and 95 percentiles of accuracy across those (4 subjects are middle and right 4 columns, respectively).
| dataset D1 | #searchlights significant | median accuracy | 95 percentile accuracy | |||||||||
| classifiers—subjects | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| voxelGNB | 1 | 0 | 2 | 0 | 0.57 | 0.57 | 0.56 | 0.58 | 0.72 | 0.71 | 0.70 | 0.73 |
| voxelGNB_smooth | 36 | 0 | 24 | 0 | 0.68 | 0.64 | 0.67 | 0.68 | 0.77 | 0.75 | 0.76 | 0.76 |
| GNB | 170 | 79 | 229 | 43 | 0.74 | 0.74 | 0.74 | 0.76 | 0.80 | 0.79 | 0.80 | 0.80 |
| LDA | 13 | 19 | 6 | 0 | 0.68 | 0.69 | 0.67 | 0.68 | 0.75 | 0.77 | 0.75 | 0.74 |
| LDAshrinkage | 126 | 86 | 100 | 16 | 0.71 | 0.74 | 0.71 | 0.73 | 0.79 | 0.79 | 0.77 | 0.80 |
| QDAshrinkage | 22 | 4 | 6 | 2 | 0.67 | 0.67 | 0.68 | 0.67 | 0.76 | 0.74 | 0.75 | 0.75 |
| SVMlinear | 21 | 21 | 19 | 2 | 0.69 | 0.70 | 0.68 | 0.68 | 0.76 | 0.77 | 0.76 | 0.76 |
| SVMrbf | 106 | 44 | 84 | 7 | 0.71 | 0.71 | 0.73 | 0.71 | 0.78 | 0.77 | 0.79 | 0.78 |
| SVMquadratic | 0 | 0 | 0 | 0 | 0.58 | 0.58 | 0.57 | 0.57 | 0.68 | 0.68 | 0.68 | 0.69 |
| nearest_mean | 21 | 47 | 24 | 3 | 0.67 | 0.70 | 0.69 | 0.68 | 0.76 | 0.77 | 0.76 | 0.78 |
| nearest_neighbor | 1 | 0 | 0 | 0 | 0.61 | 0.60 | 0.58 | 0.60 | 0.70 | 0.70 | 0.68 | 0.65 |
| SVMlinearxv | 149 | 72 | 170 | 29 | 0.74 | 0.74 | 0.74 | 0.76 | 0.80 | 0.80 | 0.79 | 0.79 |
| dataset D2 | #searchlights significant | median accuracy | 95 percentile accuracy | |||||||||
| classifiers—subjects | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| voxelGNB | 40 | 18 | 11 | 8 | 0.58 | 0.57 | 0.57 | 0.58 | 0.75 | 0.75 | 0.75 | 0.73 |
| voxelGNB_smooth | 447 | 174 | 85 | 74 | 0.70 | 0.67 | 0.65 | 0.67 | 0.85 | 0.83 | 0.83 | 0.82 |
| GNB | 1057 | 683 | 453 | 617 | 0.78 | 0.78 | 0.77 | 0.77 | 0.88 | 0.90 | 0.90 | 0.87 |
| LDA | 594 | 219 | 158 | 203 | 0.73 | 0.72 | 0.72 | 0.72 | 0.85 | 0.85 | 0.83 | 0.83 |
| LDAshrinkage | 1043 | 630 | 458 | 612 | 0.78 | 0.77 | 0.77 | 0.77 | 0.90 | 0.90 | 0.90 | 0.88 |
| QDAshrinkage | 734 | 510 | 229 | 286 | 0.75 | 0.75 | 0.73 | 0.73 | 0.88 | 0.88 | 0.87 | 0.85 |
| SVMlinear | 720 | 291 | 198 | 277 | 0.75 | 0.73 | 0.73 | 0.73 | 0.87 | 0.88 | 0.87 | 0.87 |
| SVMrbf | 891 | 580 | 284 | 433 | 0.77 | 0.77 | 0.75 | 0.75 | 0.88 | 0.87 | 0.88 | 0.83 |
| SVMquadratic | 15 | 12 | 0 | 12 | 0.63 | 0.62 | 0.62 | 0.63 | 0.77 | 0.75 | 0.75 | 0.75 |
| nearest_ mean | 614 | 267 | 236 | 231 | 0.73 | 0.73 | 0.73 | 0.72 | 0.87 | 0.85 | 0.85 | 0.83 |
| nearest_neighbor | 256 | 122 | 57 | 65 | 0.67 | 0.67 | 0.66 | 0.65 | 0.83 | 0.82 | 0.80 | 0.80 |
| SVMlinearxv | 962 | 624 | 442 | 539 | 0.78 | 0.77 | 0.77 | 0.77 | 0.90 | 0.90 | 0.88 | 0.87 |
| dataset D3 | #searchlights significant | median accuracy | 95 percentile accuracy | |||||||||
| classifiers—subjects | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| voxelGNB | 0 | 0 | 0 | 0 | 0.17 | 0.17 | 0.16 | 0.17 | 0.27 | 0.25 | 0.26 | 0.28 |
| voxelGNB_smooth | 15 | 0 | 0 | 75 | 0.23 | 0.21 | 0.21 | 0.23 | 0.34 | 0.30 | 0.31 | 0.36 |
| GNB | 1216 | 418 | 283 | 1097 | 0.34 | 0.34 | 0.30 | 0.33 | 0.52 | 0.46 | 0.41 | 0.49 |
| LDA | 1652 | 630 | 1297 | 1895 | 0.38 | 0.36 | 0.36 | 0.41 | 0.56 | 0.49 | 0.49 | 0.59 |
| LDAshrinkage | 1978 | 1014 | 1577 | 2073 | 0.40 | 0.40 | 0.39 | 0.43 | 0.59 | 0.52 | 0.51 | 0.61 |
| QDAshrinkage | 646 | 277 | 99 | 774 | 0.31 | 0.31 | 0.28 | 0.32 | 0.48 | 0.44 | 0.39 | 0.50 |
| SVMlinear | 1373 | 524 | 653 | 1580 | 0.35 | 0.35 | 0.34 | 0.39 | 0.53 | 0.48 | 0.46 | 0.55 |
| SVMrbf | 640 | 265 | 108 | 615 | 0.31 | 0.31 | 0.28 | 0.31 | 0.48 | 0.43 | 0.39 | 0.46 |
| SVMquadratic | 11 | 0 | 0 | 0 | 0.21 | 0.21 | 0.19 | 0.21 | 0.32 | 0.29 | 0.27 | 0.31 |
| nearest_mean | 327 | 77 | 22 | 317 | 0.27 | 0.29 | 0.26 | 0.28 | 0.43 | 0.40 | 0.36 | 0.41 |
| nearest_neighbor | 83 | 5 | 3 | 97 | 0.24 | 0.25 | 0.23 | 0.25 | 0.36 | 0.35 | 0.32 | 0.38 |
| SVMlinearxv | 1402 | 564 | 642 | 1571 | 0.35 | 0.36 | 0.34 | 0.38 | 0.54 | 0.49 | 0.46 | 0.55 |
| dataset D4 | #searchlights significant | median accuracy | 95 percentile accuracy | |||||||||
| classifiers—subjects | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| voxelGNB | 0 | 0 | 0 | 0 | 0.13 | 0.13 | 0.13 | 0.13 | 0.23 | 0.23 | 0.23 | 0.23 |
| voxelGNB_smooth | 24 | 0 | 1 | 1 | 0.18 | 0.18 | 0.17 | 0.18 | 0.30 | 0.27 | 0.27 | 0.28 |
| GNB | 489 | 312 | 136 | 300 | 0.33 | 0.33 | 0.32 | 0.33 | 0.53 | 0.47 | 0.45 | 0.50 |
| LDA | 220 | 86 | 30 | 119 | 0.25 | 0.25 | 0.23 | 0.27 | 0.42 | 0.38 | 0.36 | 0.45 |
| LDAshrinkage | 468 | 219 | 89 | 283 | 0.33 | 0.32 | 0.28 | 0.33 | 0.53 | 0.48 | 0.40 | 0.50 |
| QDAshrinkage | 181 | 78 | 19 | 105 | 0.25 | 0.23 | 0.23 | 0.25 | 0.42 | 0.37 | 0.35 | 0.38 |
| SVMlinear | 423 | 191 | 102 | 205 | 0.30 | 0.30 | 0.30 | 0.32 | 0.52 | 0.45 | 0.42 | 0.50 |
| SVMrbf | 469 | 212 | 144 | 229 | 0.32 | 0.32 | 0.32 | 0.32 | 0.52 | 0.45 | 0.43 | 0.48 |
| SVMquadratic | 134 | 21 | 73 | 134 | 0.23 | 0.22 | 0.27 | 0.27 | 0.37 | 0.33 | 0.38 | 0.42 |
| nearest_mean | 366 | 201 | 105 | 179 | 0.30 | 0.30 | 0.30 | 0.30 | 0.50 | 0.47 | 0.45 | 0.50 |
| Nearest_neighbor | 166 | 78 | 45 | 94 | 0.23 | 0.23 | 0.25 | 0.23 | 0.42 | 0.39 | 0.39 | 0.43 |
| SVMlinearxv | 431 | 205 | 121 | 222 | 0.32 | 0.32 | 0.32 | 0.32 | 0.50 | 0.46 | 0.44 | 0.50 |
| dataset D5 | #searchlights significant | median accuracy | 95 percentile accuracy | |||||||||
| classifiers—subjects | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| voxelGNB | 0 | 0 | 0 | 5 | 0.00 | 0.10 | 0.10 | 0.10 | 0.00 | 0.13 | 0.14 | 0.14 |
| voxelGNB_smooth | 303 | 9 | 1 | 78 | 0.12 | 0.11 | 0.11 | 0.11 | 0.16 | 0.15 | 0.14 | 0.15 |
| GNB | 2282 | 545 | 353 | 1336 | 0.15 | 0.14 | 0.14 | 0.15 | 0.20 | 0.18 | 0.18 | 0.18 |
| LDA | 2494 | 719 | 496 | 1225 | 0.15 | 0.15 | 0.15 | 0.14 | 0.21 | 0.20 | 0.18 | 0.18 |
| LDAshrinkage | 2624 | 775 | 562 | 1338 | 0.16 | 0.15 | 0.15 | 0.15 | 0.22 | 0.20 | 0.18 | 0.18 |
| QDAshrinkage | 594 | 90 | 32 | 152 | 0.12 | 0.11 | 0.11 | 0.12 | 0.17 | 0.16 | 0.15 | 0.16 |
| SVMlinear | 2234 | 564 | 341 | 1058 | 0.15 | 0.14 | 0.14 | 0.14 | 0.20 | 0.19 | 0.18 | 0.18 |
| SVMrbf | 2019 | 369 | 252 | 1156 | 0.14 | 0.14 | 0.14 | 0.14 | 0.20 | 0.18 | 0.17 | 0.18 |
| SVMquadratic | 275 | 12 | 0 | 0 | 0.12 | 0.10 | 0.10 | 0.11 | 0.16 | 0.14 | 0.14 | 0.14 |
| nearest_mean | 1117 | 256 | 134 | 515 | 0.13 | 0.13 | 0.13 | 0.13 | 0.18 | 0.18 | 0.17 | 0.16 |
| nearest_neighbor | 146 | 7 | 6 | 9 | 0.11 | 0.10 | 0.10 | 0.10 | 0.15 | 0.14 | 0.14 | 0.14 |
But how different are the maps produced by the various classifiers? In the Appendix we provide pictures of the maps for one subject in each of the studies, in Figure 23, Figure 24, Figure 25, Figure 26 and Figure 27. Comparing these with the naked eye shows relatively few differences across maps for the various datasets.
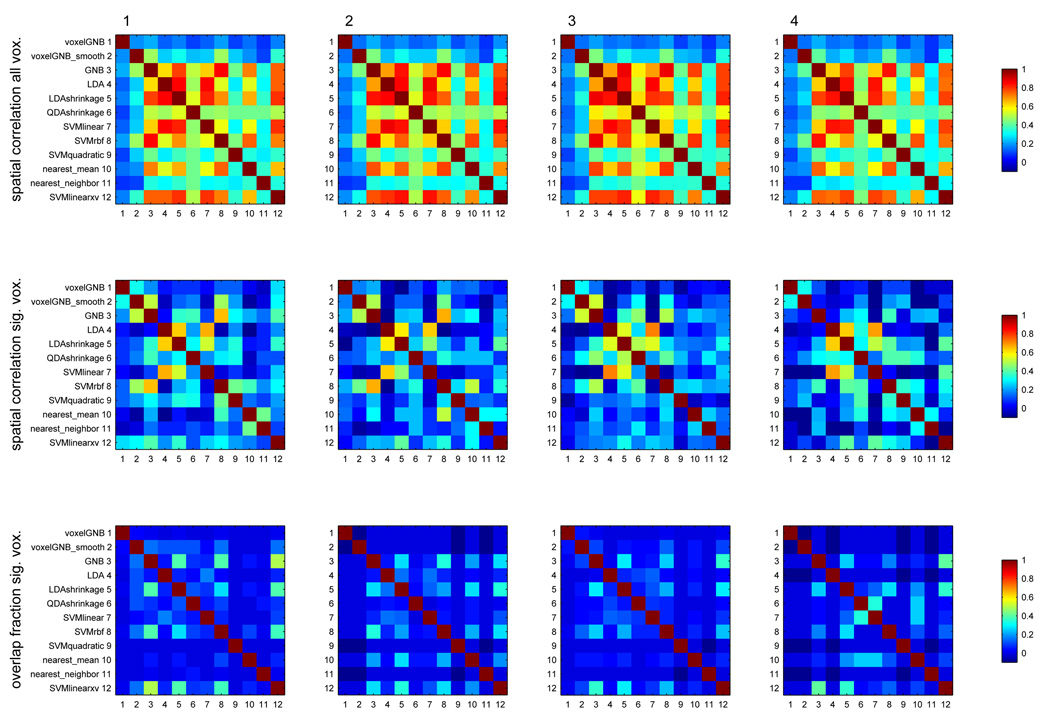
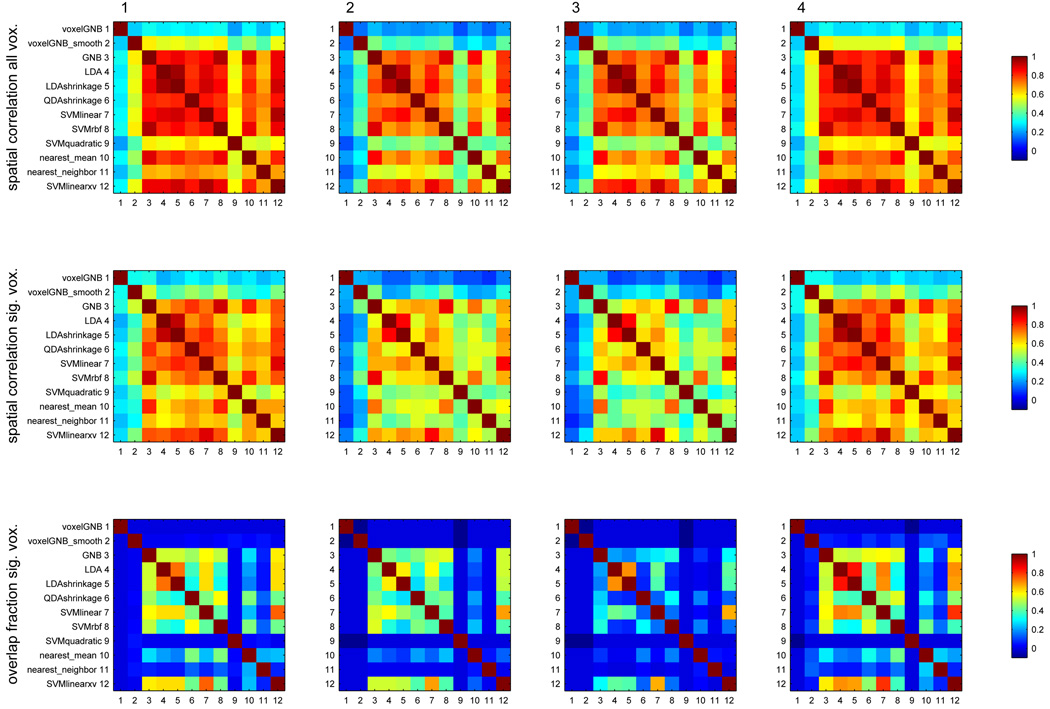
A more revealing approach is to consider the similarity of the maps. Figure 12 examines the similarity of the accuracy maps produced by the various classifiers, via their correlation across voxels in the entire brain, and the same computed just across voxels significant in any map, for dataset D1. The figure also quantifies the extent to which two maps a and b have the same significant voxels by their overlap fraction, . A few examples will make the overlap fraction plots more tangible: for two classifiers sharing approximately half of their significant voxels, the overlap fraction would be around , sharing 60%, around , sharing 80%, around and sharing 90%, around . Figure 13 shows the same for dataset D3 (and Figure 20, Figure 21 and Figure 22 for datasets D2, D4 and D5 in the Appendix) show the same for datasets D2, D3, D4 and D5. From these figures, and the pictures of maps in the Appendix, we can conclude that the better classifiers identified above share most of the voxels they identify as significant, especially in the multiclass problems.
Figure 12.
For 4 subjects (columns) in dataset D1, correlation of all pairs of accuracy maps across voxels in the entire brain (top row), same just across voxels significant in any map (middle row) and overlap fraction between sets deemed significant by any two maps (overlap fraction is ) (bottom row).
Figure 13.
Same as Figure 12, for dataset D3.
4 Experiments on exploratory data analysis with accuracy maps
4.1 What can classifiers learn?
Although it is feasible to compare various classifiers on several datasets, as we did in the previous section, it is helpful to consider their capabilities in ideal circumstances to guide our choice or aid in interpretation of results. The ability of a classifier to learn complex relationships between features and the class label comes together with more sensitivity to the amount of training data available. If this is not enough, a classifier can base the prediction mechanism on details that are idiosyncratic to the training set and would not be present in the test set; this phenomenon is called overfitting. This can also be viewed as a bias-variance tradeoff: a classifier that is simple has high bias, whereas one that is too complex may be very different from training set to training set, thus having high variance. If there are more features than examples, it is generally possible to learn to predict the training set perfectly even if there is no information about the class label.
In the following sections we will consider several scenarios for relationships between features and connect that to what classifiers can or cannot learn. As, in practice, we usually do not have the luxury of large datasets or few features, we will compare classifiers in ideal circumstances; to do this we will use synthetic data generated from a “searchlight” with just a few voxels, allowing us to have large training and test sets. The former allows each classifier to learn all it can learn and the latter to reduce the uncertainty of the accuracy estimate until it is close to the true accuracy.
4.1.1 Learning the covariance structure of searchlight voxels
All of the gaussian classifiers described earlier rely on estimating the mean and covariance matrix of the class conditional distribution of the values of the voxels in a searchlight; they vary in what they assume about the structure of that covariance matrix. The view of activation under this model is that each voxel will take a particular mean value in each class (e.g. active or inactive) and that that value is corrupted by noise, whose structure is described by the covariance matrix. A diagonal matrix shared between classes means noise at each voxel is independent from the others but at the same level for both classes, a full matrix will allow for voxels to have correlated noise (e.g. adjacent voxels) and a different full matrix for each class means that the noise structure changes between classes. In order to understand the impact of these assumptions, we considered the output of the estimators used by the various classifiers in those three scenarios. We generated synthetic data for a two-voxel searchlight and estimated the class conditional covariance matrices using GNB, LDA and QDA (which make the assumptions in each of the three scenarios, respectively).
Figure 14 shows scatterplots of a sample of 100 points for each class (x axis is voxel 1, y axis voxel 2) in each of the three scenarios (rows), repeated for three estimators (columns). Overlaid on each scatterplot are probability density estimate contours (an ellipse of constant probability density, which is a graphical depiction of the point spread implied by the covariance matrix), green for the true covariance matrices used to generate the data and red for the ones estimated from that data. In this situation there is enough data to estimate covariance matrices using any of the methods, so we can focus on the mismatch between the scenario and the assumptions of each method. In the first row, all methods retrieve the correct spherical covariance shared between classes. In the second row, GNB cannot retrieve the correct matrix because it is forced to assume that both axes of its ellipse are parallel to the graph axes (it does not require the length of the axes to be the same, which would happen if one further constrained the covariance matrix to have the same value in all entries of the diagonal). In the third row, GNB and both LDA versions fail to retrieve the correct matrices because they assume that they have to be the same for both classes.
4.1.2 Learning the relationship between voxels and the target label
In the previous section we considered classifiers that learned the covariance structure of voxels in a searchlight, and their mean activation patterns in each class. As we saw before in Section 2.2, the covariance and class mean patterns can then be used to make classification decisions via Bayes’ Rule. We could, instead, examine how the values taken by the voxels relate to the class label, in particular in the case where that relationship can be expressed as a linear discriminant with one weight per voxel. This is the case for a linear SVM, for instance, where this discriminant is learned directly, but also for GNB and LDA, where the classification decision with Bayes’ Rule is equivalent to that of a particular linear discriminant.
We consider six synthetic data scenarios with 1000 examples for each of two classes, in a searchlight with 5 or 6 voxels. The activation of a voxel in one class is generated from a gaussian distribution with a mean that reflects the voxel’s response to that condition. For simplicity, we assume all voxels have the same level of noise (standard deviation of the gaussian) in each condition. In each scenario, half the voxels are uninformative (mean activity is the same for both classes) and half are informative in a scenario-specific way:
3 voxels are equally informative (same distance between class means)
3 voxels are informative, one more than the others (larger distance between class means)
3 voxels are equally informative, but the noise in the 3rd correlates with noise in the 2nd
2 voxels are informative and the class is the logical AND of their being active (e.g. a conjunction detector)
2 voxels are informative and the class is the logical OR of their activations (e.g. either voxels is on for the desired class, but both are on together only for some stimuli)
2 voxels are informative and the class is the logical XOR of their activations (a control case)
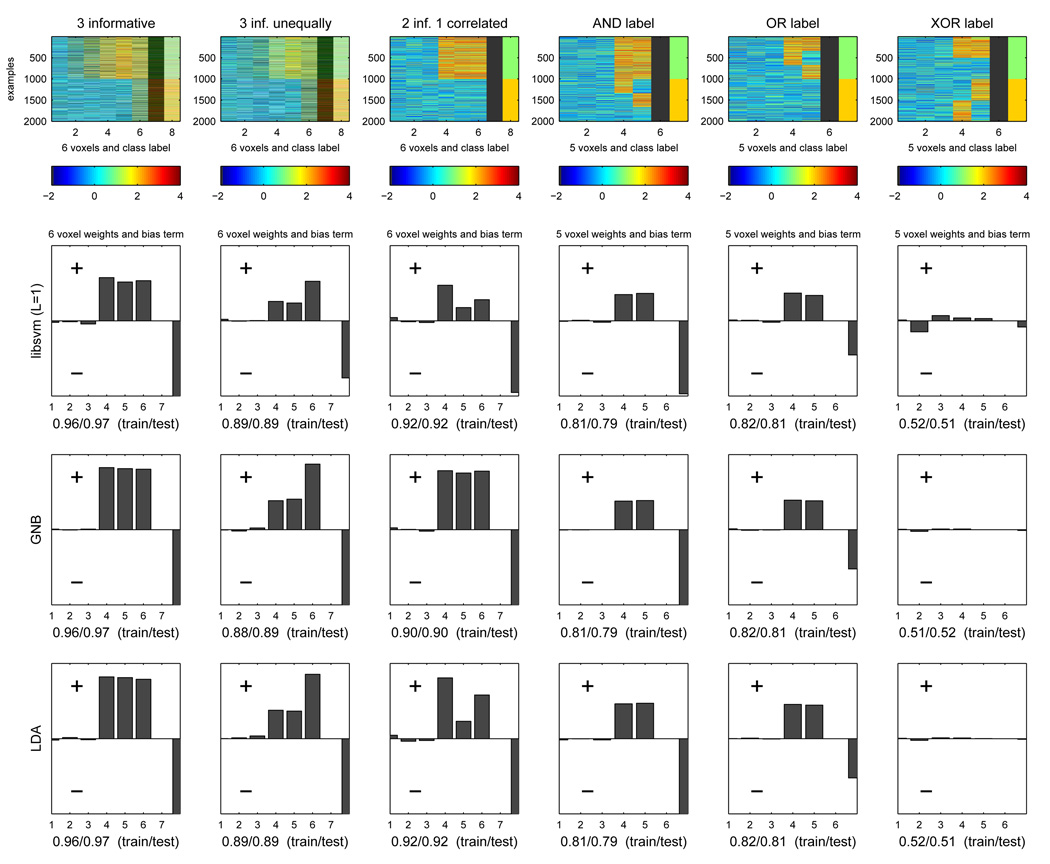
The first row of Figure 15 depicts a sample of 2000 examples generated from each of the six scenarios (columns). For each sample plot, the first 1000 examples belong to one class and the following 1000 to the other (as indicated by the class label in the rightmost column). A higher value of a voxel (yellow/red) corresponds to activation.
Figure 15.
Top row: samples of 2000 examples generated from each of the six scenarios in the text (columns), 1000 from one class and 1000 from the other (red is activation, blue/green is lack thereof) Bottom three rows: weights on each voxel of the linear discriminants learned by each of the three classifiers we consider. Each plot shows the weights first (1 to 5/6 weights), followed by the bias term to the right and the train/test accuracy below.
We trained and tested three classifiers - linear SVM, GNB and LDA - on data generated from each of the six scenarios, yielding one linear discriminant per classifier. The linear discriminant weights w1,…,w#voxels and bias w0 for each (see Section 2.2) are plotted in the remaining rows of Figure 15. Under each discriminant weight plot are the train and test set accuracies of that classifier on the datasets from the corresponding scenario.
For linear SVM, all informative voxels are weighted equally in scenario 1, as one would expect. In scenario 2, the voxel that is more informative gets more weight than the other ones. In scenario 3, even though voxels 1 and 2 are equally informative, the fact that voxel 3 is correlated with voxel 2 means a weight equivalent to that of voxel 1 gets split between them. In scenarios 4 and 5 the two informative voxels get weighted equally, as they contribute the same amount to the decision. What changes between the two scenarios is the bias of the discriminant; in scenario 5, it is high enough that either voxel being active by itself is enough to get the decision past the threshold to predict class 1. In scenario 4, the bias has a lower value and hence it takes both voxels being active for this to happen. Scenario 6 is included to show how, in a situation where there are more examples than voxels, a linear classifier cannot learn this particular relationship between voxels and class label.
GNB displays a very similar pattern of weights for all scenarios except 3, where it weighs each of the two correlated voxels the same as the other voxel. Whereas this is one reason the classifier is sometimes overconfident (it overcounts evidence that appears repeatedly), it can also be used to counter the dilution of weight seen with linear SVM if its test set accuracy is comparable. This should also demonstrate that care needs to be applied when interpreting the relative magnitudes of weights assigned by a classifier to different voxels.
LDA weights are very similar to those produced with linear SVM, in this setting. In practice, the former positions the linear discriminant taking into account the entire sample of points of each class (and assuming, furthermore, that each sample has a certain class of parametric shape). The SVM considers only support vectors, the examples at the edges of the margin around the discriminant. This can be relevant in that considering the differences between those examples may be more informative - they are crucial differences - than the differences between the two class mean examples.
4.2 Why learn multiple classifiers?
The synthetic data examples in the previous sections show the component parts – class mean patterns, voxel covariances, voxel weights – of the simpler classifiers, and how those reflect the relationships between voxels and between those voxels and the class label in several common situations. This knowledge is necessary in order to interpret why a classifier can (or fail to) capture information in a searchlight. But how would we know that a more complex classifier was required?
In order to compare classifiers of increasing complexity, at least within the same type (generative or discriminative, say), we can apply the following kind of reasoning:
If complex does better than simple, we know there is a complicated relationship between the features and the class label that can be identified.
If simple does better, we know there is overfitting and hence not enough data to say that anything beyond the simple relationship exists.
If they do equally well and models learned look similar (if they can be visually or numerically compared) or make exactly the same predictions in the same examples, it would be reasonable to assume that nothing more than the simple relationship is present.
If no classifier does well, one cannot say that information about the class label is not present. Whereas that may be the case, it’s also possible that there is too much noise, not enough data to learn even a simple relationship or that the relationship present is entirely out of the scope that the type of classifier used can learn.
The interpretation of what a non-linear or non-parametric classifier captured is more dependent on the type of classifier than in the case of the linear classifiers in the previous sections. A RBF-kernel SVM would require comparison of the support vectors for one and the other class, whereas a QDA classifier would still allow for a decision function to be considered, though it would be quadratic and thus involve not just voxels but also their interactions (via products of voxel values).
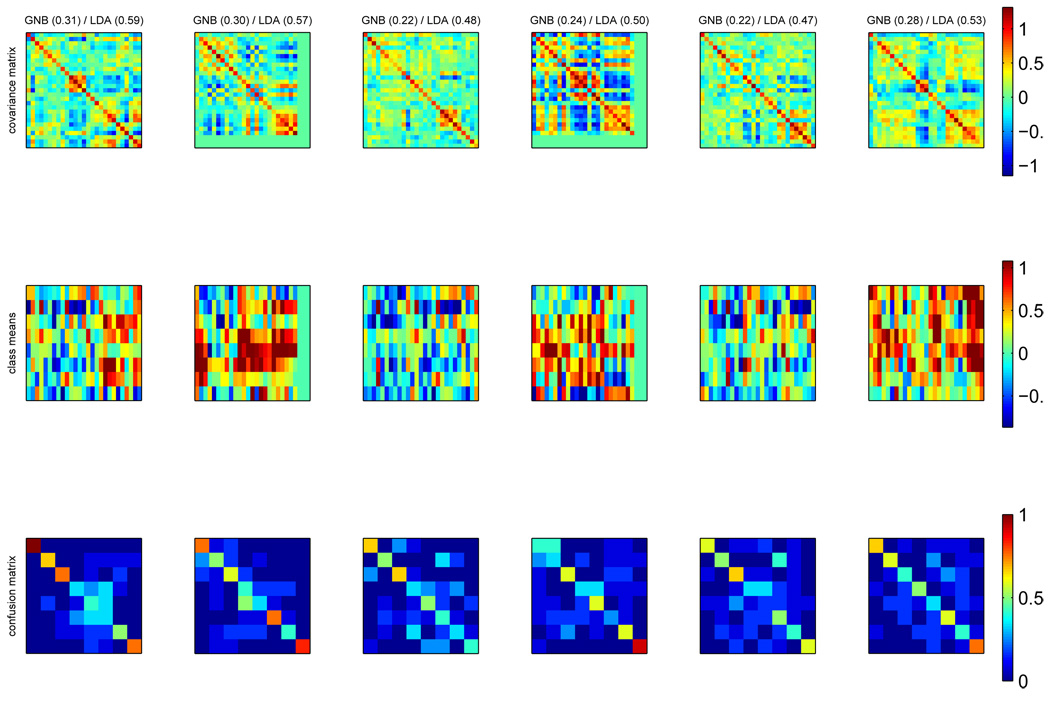
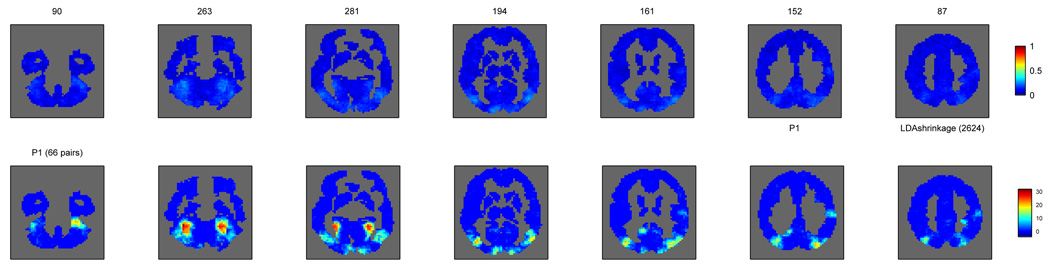
To provide a more concrete example of how this type of reasoning could be used, we could use a GNB and shrinkage LDA map to identify locations where it was advantageous to capture covariance structure, as determined by the accuracy being larger for shrinkage LDA. In Figure 16, we consider the top 6 such searchlights for one of the subjects from dataset D3, via their respective covariance matrices, mean activation patterns in each class (both averaged across cross-validation grops) and confusion matrices between the classes. In this case, we can see which searchlights “specialize” on one class (e.g. 1) or contain information about multiple classes and a covariance structure where groups of voxels are correlated or anti-correlated (e.g. 4).
Figure 16.
For subject subj1_ii in dataset D3, in 6 searchlights (columns) where accuracy is larger for shrinkage LDA than GNB, top: covariance matrices, dimensions are #voxels × #voxels middle: mean pattern across the voxels in the searchlight for each of 8 classes (in each plot rows are faces, houses, cats, chairs, scissors, bottles, shoes and scrambled objects, columns are voxels), bottom: confusion matrices between 8 classes (in row i, fraction of examples of class i that gets labelled by the classifier as each of the 8 classes). Above each column is the accuracy of the GNB and LDA classifier trained on the corresponding searchlight.
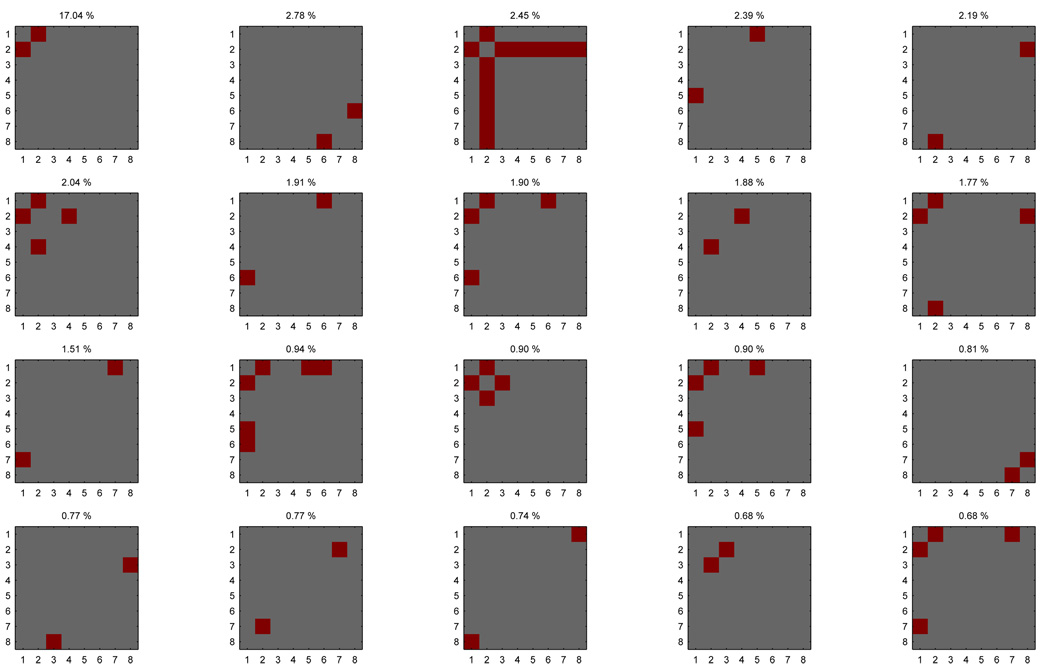
4.3 Extracting different kinds of information from a multiple class dataset
The previous section focused on how one might find interesting structure in the data that was related to the prediction task of interest through the comparison of various classifiers. One can, instead, turn to a different question: identifying how many different kinds of information are present in a multiple class dataset. This is more exploratory in nature than the analyses in the previous section, and hence the emphasis will be on providing examples of what can be done rather than exhaustively try every approach on all subjects in every dataset.
Thus far we considered accuracy maps where classifiers performed multi-way discrimination. In that setting, the more classes there are, the lower ”chance” level is and the easier it is for any voxels to have significant accuracy, as seen for datasets D3, D4 and D5 in Table 1. It is not likely that a voxel will distinguish every class from every other class, and hence accuracy values can be relatively low and yet significant. But what does it mean to say that a voxel with 20% accuracy contains information when 10% is chance, for instance? One possibility is that the classifier labels 20% of the examples of each class correctly. More plausible is that, in a given searchlight, a classifier can distinguish a few of the classes from a few of the others, doing no better than chance on the rest (as seen in confusion matrices in the third row of Figure 16, say). Taking this further, one could also ask if those distinguishable categories would be the same for all voxels; the answer is clearly no, and one need only consider voxels preferentially responsive to faces, houses or body parts, for instance. The question in a multiple class situation should therefore be not only whether there are searchlights with significant accuracy but also how many different confusion matrices there are among such searchlights and what those matrices look like.
One possible approach to this question would be to compute the confusion matrices for all searchlights and then cluster them and, hopefully, have a few groups emerge. This would require specifying an appropriate distance measure between confusion matrices, as well as dealing with the more standard practical issues that arise while clustering.
Given that we are interested in confusion matrices as indicators of whether pairs of classes can be distinguished, there is a simpler alternative:
produce a searchlight accuracy map for every pair of classes (for a total of #pairs) using a versatile classifier (given the results in previous sections, shrinkage LDA is a good choice)
threshold all the pairwise maps into binary maps of significance using FDR with q = 0.01
this produces a matrix with #pairs rows and #voxels columns, where each row is a binary map
the column for each voxel is a binary vector encoding all the pairwise distinctions its searchlight makes, which can be reshaped into what is essentially a binarized confusion matrix
Prior to examining the binary confusion matrices produced, one can simply count the number of class pairs that can be distinguished within the searchlight for a voxel, and contrast that with the accuracy map obtained with the same classifier. In Figure 17 and Figure 18 we can see this contrast for one subject in datasets D3 and D5. Although this still does not tell us whether two voxels with the same counts distinguish the same classes, it provides a more detailed image than the accuracy map, especially as the number of classes (and pairs) increases; this is especially evident for D5.
Figure 17.
For subject subj1_wp in dataset D3, accuracy map (top row) and count map (bottom row), both obtained with a shrinkage LDA classifier. Note that the scale for the count map ranges from 0 to the maximum number of pairwise tasks a voxel searchlight is deemed significant on.
Figure 18.
For subject P1 in dataset D5, accuracy map (top row) and count map (bottom row), both obtained with a shrinkage LDA classifier.
Finally, one can simply look at the various binary vectors/binarized confusion matrices that occur. Whereas one could have up to 228 different ones in dataset D3 (as there are 28 pairs of classes), only 1388 actually occur and, at that, most are very infrequent. Figure 19 shows the 20 most frequent. In dataset D5 there are 266 possible different matrices, and only 2770 actually occur.
Figure 19.
The 20 most frequent binarized confusion matrices appearing in the pairwise maps for subject subj1_wp in dataset D3. Some correspond to distinctions between faces (1), houses (2) or scrambled objects (8) against other categories.
4.4 Group level analysis
Thus far we have not touched on the topic of group level analyses, except to look for coherence of conclusions across subjects. While there is no canonical approach, we can suggest a few possibilities. The most basic is to report per-subject results in the manner of Table 1 and summarize across subjects; one example would be to do a sign test on whether one result is better than another in each subject, for instance. Beyond that, one can look for commonalities in the various reports described in this part of the paper, e.g. qualitatively similar confusion matrices across subjects.
If the datasets for various subjects have been normalized to a common space (e.g. MNI or Talairach), one can combine the binary significance maps obtained by thresholding accuracy maps by stacking and adding them, yielding a count map that depicts how many subjects a voxel (searchlight) is significant in. In each significance map, a voxel that is significant is a false discovery with a certain probability, and one could use this fact to attach probabilities to values in the count map under various null hypotheses. If one cannot expect a neat superposition of significant voxels across subjects, even with the intrinsic smoothing that comes from the fact that searchlights overlap, one could still report counts of significance within regions of interest defined anatomically or via separate localizers.
4.5 The Searchmight toolbox
Until now we refrained from any discussion on how the various classifiers and tests used in the paper were implemented. There are two excellent general purpose toolboxes for MVPA, namely the Princeton MVPA toolbox (in MATLAB, http://www.pni.princeton.edu/mvpa) and PyMVPA (in Python, http://www.pymvpa.org, [12]), which have been used in several publications and have mailing lists with vibrant user communities. We opted not to use either of them for this paper, as we felt there were advantages to focusing on a single, specific workflow: information mapping of the same data with as many classifiers as possible, uniform statistical testing and making subsequent interpretation easier. For that aim we introduce the Searchmight toolbox, which is available as standalone code via the Resources section of the website for the Botvinick lab (http://www.princeton.edu/~matthewb) or with Princeton MVPA toolbox wrapper functions at their web site.
Concretely, this consisted of producing either custom implementations of classifiers optimized to cross-validate while caching computation for each searchlight or efficient wrappers for existing classifiers. An example of the former is a version of GNB that can be run for the whole brain in 1 second, in dataset D1; an example of the latter is LIBSVM, where we altered the code not to output any messages during training, which speeds it up substantially given that the process happens for each of tens of thousands of searchlights.
We also implemented a single API that can be used to call all the different classifiers (with a few specific parameters, if using something other than default settings) and returns not just an accuracy map but also a p-value map, produced with either of the approaches described in the text. The goal of this is to lower the barrier to doing this kind of analysis, such that conclusions are not biased by the use of a single classifier (all of them can be tried with the same amount of effort) or by misguided statistical testing of accuracy results. Finally, the toolbox directly supports the creation of the pairwise classification maps described in Section 4.3 for exploratory analysis of multiple class datasets; it also returns various classifier specific information (such as searchlight covariance or confusion matrices, or linear classifier weights) directly, instead of requiring that the users know about the specific way in which these are stored for the various wrapped classifiers. Beyond this, the toolbox also includes the functions implementing the statistical tests used to compare multiple classifiers against each other and example autocorrelation which were described in Section 3.3 and Section 3.4.
5 Conclusions
With respect to choice of classifier, we have shown there are differences between classifiers in terms of how many searchlights they can be trained on with significant accuracy; that said, the better classifiers identify many of the same voxels. This suggests that, at least at the scale of tens of cubic millimeters per voxel and for this type of experimental paradigm, there seems to be no advantage to training a nonlinear classifier; that said, it is definitely worth trying to exploit the covariance structure between voxels in a searchlight, at the very least. Hence, if processing time is a scarce resource, a GNB classifier is a reasonable choice for quick mapping or for voxel selection. Given more time, shrinkage LDA is likely preferrable. A linear SVM can achieve the same level of performance, but we have found that training set cross-validation for setting the sole classifier parameter was required in order to get it.
The conclusion regarding testing of the significance of accuracy results is that analytical result significance tests are less conservative and computationally much cheaper than permutation tests. Whether they can be deployed depend on the verification of a number of assumptions described in the test, and this should precede the choice of either testing approach
These conclusions must be considered provisional, since they are based on the analyses of empirical data. Nevertheless, we used different datasets and tasks with varying degrees of difficulty and obtained consistent results across multiple subjects, suggesting that our conclusions may hold a reasonable degree of generality.
Finally, showing that there are different kinds of informative voxels in a multiple class dataset requires reasoning from several accuracy maps and careful scrutiny of the classifiers learned for each searchlight. Given that this is a more ad-hoc process, we opted to provide details about the nuts and bolts of each classifier and the interactions between those and possible voxel behaviours in the data, where this could be visualized, as well as the general principles for reasoning about differences between maps. Furthermore, we provided various examples of how to use accuracy maps for all possible two-class problems in a dataset, in order to identify various types of informative voxel behaviour present in the data.
Supplementary Material
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Datasets D1, D2, D4,D5 were shared by Rob Mason and Marcel Just, of the Center for Cognitive Brain Imaging and Tom Mitchell of the Machine Learning Department, both at Carnegie Mellon University. Dataset D3 was shared by James Haxby of Dartmouth College.
References
- 1.Allwein Erin L, Schapire Robert E, Singer Yoram. Reducing Multiclass to Binary: A Unifying Approach for Margin Classifiers. Journal of Machine Learning Research. 2001 April;1(2):113–141. [Google Scholar]
- 2.Boynton GM, Engel Sa, Glover GH, Heeger DJ. Linear systems analysis of functional magnetic resonance imaging in human V1. The Journal of neuroscience : the official journal of the Society for Neuroscience. 1996 July;16(13):4207–4221. doi: 10.1523/JNEUROSCI.16-13-04207.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chang CC, Lin CJ. LIBSVM: a library for support vector machines. 2001 [Google Scholar]
- 4.Dale Anders M, Buckner Randy L. Selective Averaging of Rapidly Presented Individual Trials Using fMRI. Human Brain Mapping. 1997;340:329–340. doi: 10.1002/(SICI)1097-0193(1997)5:5<329::AID-HBM1>3.0.CO;2-5. [DOI] [PubMed] [Google Scholar]
- 5.Demšar J. Statistical comparisons of classifiers over multiple data sets. The Journal of Machine Learning Research. 2006;7:30. [Google Scholar]
- 6.Dietterich TG, Bakiri G. Solving multiclass learning problems via error-correcting output codes. Arxiv preprint cs/9501101. 1995;2:263–286. [Google Scholar]
- 7.Dietterich Thomas G. Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithms. Neural Computation. 1998 October;10(7):1895–1923. doi: 10.1162/089976698300017197. [DOI] [PubMed] [Google Scholar]
- 8.Friston Karl J, Ashburner John, Kiebel Stefan J, Nichols Thomas E, Penny WD. Statistical Parametric Mapping: The Analysis of Functional Brain Images. Academic Press; 2006. [Google Scholar]
- 9.Genovese Christopher R, Lazar Nicole a, Nichols Thomas. Thresholding of statistical maps in functional neuroimaging using the false discovery rate. NeuroImage. 2002;15(4):870–878. doi: 10.1006/nimg.2001.1037. [DOI] [PubMed] [Google Scholar]
- 10.Golland Polina, Fischl Bruce. Permutation tests for classification: towards statistical significance in image-based studies; Information processing in medical imaging : proceedings of the … conference; 2003. Jul, pp. 330–341. [DOI] [PubMed] [Google Scholar]
- 11.Good Phillip. Permutation, Parametric and Bootstrap Tests of Hypotheses. New York, New York, USA: Springer; 2005. [Google Scholar]
- 12.Hanke Michael, Halchenko Yaroslav O, Sederberg Per B, Hanson Stephen José, Haxby James V, Pollmann Stefan. PyMVPA: A python toolbox for multivariate pattern analysis of fMRI data. Neuroinformatics. 2009;7(1):37–53. doi: 10.1007/s12021-008-9041-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hanson SJ, Halchenko YO. Brain reading using full brain support vector machines for object recognition: There is no face identification area. Neural Computation. 2008;20:486–503. doi: 10.1162/neco.2007.09-06-340. [DOI] [PubMed] [Google Scholar]
- 14.Hastie Trevor, Tibshirani Robert, Friedman Jerome. The elements of statistical learning: data mining, inference and prediction. Springer-Verlag; 2001. [Google Scholar]
- 15.Haxby JV, Gobbini MI, Furey ML, Ishai A, Schouten JL, Pietrini P. Distributed and overlapping representations of faces and objects in ventral temporal cortex. Science. 2001;293(5539):2425. doi: 10.1126/science.1063736. [DOI] [PubMed] [Google Scholar]
- 16.Haynes John-Dylan, Rees Geraint. Decoding mental states from brain activity in humans. Nature reviews. Neuroscience. 2006;7(7):523–534. doi: 10.1038/nrn1931. [DOI] [PubMed] [Google Scholar]
- 17.Johnson Jeffrey D, McDuff Susan GR, Rugg Michael D, Norman Kenneth a. Recollection, familiarity, and cortical reinstatement: a multivoxel pattern analysis. Neuron. 2009;63(5):697–708. doi: 10.1016/j.neuron.2009.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kohavi R. A study of cross-validation and bootstrap for accuracy estimation and model selection. International joint Conference on artificial intelligence; Citeseer; 1995. p. 11371145. [Google Scholar]
- 19.Kriegeskorte N, Goebel R, Bandettini P. Information-based functional brain mapping. Proceedings of the National Academy of Sciences. 2006;103(10):3863. doi: 10.1073/pnas.0600244103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kriegeskorte Nikolaus, Simmons W Kyle, Bellgowan Patrick SF, Baker Chris I. Circular analysis in systems neuroscience: the dangers of double dipping. Nature neuroscience. 2009;12(5):535–540. doi: 10.1038/nn.2303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Menon Ravi, Kim Seong-Gi. Spatial and temporal limits in cognitive neuroimaging with fMRI. Trends in cognitive sciences. 1999 June;3(6):207–216. doi: 10.1016/s1364-6613(99)01329-7. [DOI] [PubMed] [Google Scholar]
- 22.Mitchell Tom M. Machine Learning. 1997 [Google Scholar]
- 23.Mitchell Tom M, Hutchinson Rebecca, Niculescu Radu S, Pereira Francisco, Wang Xuerui, Just Marcel, Newman Sharlene. Learning to Decode Cognitive States from Brain Images. Machine Learning. 2004 October;57(1/2):145–175. [Google Scholar]
- 24.Mitchell Tom M, Shinkareva Svetlana V, Carlson Andrew, Chang Kai-Min, Malave Vicente L, Mason Robert a, Just Marcel Adam. Predicting human brain activity associated with the meanings of nouns. Science (New York, N.Y.) 2008;320(5880):1191–1195. doi: 10.1126/science.1152876. [DOI] [PubMed] [Google Scholar]
- 25.Mur Marieke, Bandettini Peter a, Kriegeskorte Nikolaus. Revealing representational content with pattern-information fMRI-an introductory guide. Social cognitive and affective neuroscience. 2009;4(1):101–109. doi: 10.1093/scan/nsn044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ng Andrew Y, Jordan Michael I. Neural Information Processing Systems. 2001. On Discriminative vs. Generative Classifiers: A comparison of logistic regression and Naive Bayes. [Google Scholar]
- 27.Nichols Thomas E, Holmes Andrew P. Nonparametric permutation tests for functional neuroimaging: a primer with examples. Human brain mapping. 2002 January;15(1):1–25. doi: 10.1002/hbm.1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Norman Kenneth A, Polyn Sean M, Detre Greg J, Haxby James V. Beyond mind-reading: multi-voxel pattern analysis of fMRI data. Trends in cognitive sciences. 2006;10(9):424–430. doi: 10.1016/j.tics.2006.07.005. [DOI] [PubMed] [Google Scholar]
- 29.Pereira Francisco. Beyond Brain Blobs: Machine Learning Classifiers as Instruments for Analyzing Functional Magnetic Resonance Imaging Data. Ph. d. Carnegie Mellon University; 2007. [Google Scholar]
- 30.Pereira Francisco, Mitchell Tom, Botvinick Matthew. Machine learning classifiers and fMRI: a tutorial overview. NeuroImage. 2009 March;45(1 Suppl):S199–S209. doi: 10.1016/j.neuroimage.2008.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Schäfer Juliane, Strimmer Korbinian. A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics. Statistical applications in genetics and molecular biology. 2005 January;4 doi: 10.2202/1544-6115.1175. Article32. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.