Evaluation and ranking of enzyme designs

Abstract

In 2008, a successful computational design procedure was reported that yielded active enzyme catalysts for the Kemp elimination. Here, we studied these proteins together with a set of previously unpublished inactive designs to determine the sources of activity or lack thereof, and to predict which of the designed structures are most likely to be catalytic. Methods that range from quantum mechanics (QM) on truncated model systems to the treatment of the full protein with ONIOM QM/MM and AMBER molecular dynamics (MD) were explored. The most effective procedure involved molecular dynamics, and a general MD protocol was established. Substantial deviations from the ideal catalytic geometries were observed for a number of designs. Penetration of water into the catalytic site and insufficient residue-packing around the active site are the main factors that can cause enzyme designs to be inactive. Where in the past, computational evaluations of designed enzymes were too time-extensive for practical considerations, it has now become feasible to rank and refine candidates computationally prior to and in conjunction with experimentation, thus markedly increasing the efficiency of the enzyme design process.

Introduction

Biocatalysts achieve a great variety of difficult chemical transformations under mild conditions with remarkable efficiency and specificity.¹ Harnessing these features to catalyze useful chemistry could be of considerable practical value to biotechnology, pharmacology, and chemical industries, although the design of biological molecules that promote unnatural reactions (any chemical reaction for which no natural enzyme has evolved) is a grand challenge for chemists and biologists. In the 1990s, the successful production of catalytic antibodies^2–4 signified considerable progress towards that goal: antibodies were raised against haptens that mimic the electronic and geometric characteristics of rate-determining transition states and gave up to 10⁶ fold rate accelerations.^5,6

In recent years, computational “Inside-out” approaches have been employed to design novel enzyme catalysts,^7,8 extending the sequence-space beyond that of antibodies to utilize virtually any protein of known structure. Quantum-mechanically computed geometries that predict the ideal arrangement of catalytic sidechains around the transition state of a reaction (theozymes)^9,10 are “matched”¹¹ into protein scaffolds from the Protein Data Bank.¹² The active site is then repacked in an attempt to stabilize the ideal transition state geometry, resulting in sequences that differ by up to 20 amino acids from those of the original template proteins. The approach yielded two series of enzyme catalysts, promoting the Kemp elimination¹³ and a retro-aldol reaction.¹⁴ Both are important examples of the current state of the art in computational and experimental biotechnology. Although this methodology has been shown to work in these cases, much remains to be done to improve the biological economy and overall rate acceleration of future design endeavors. The current design protocol necessitates that hundreds of proteins need to be expressed to obtain a few candidates with activity. These are then carried forward through multiple rounds of mutations in an effort to increase the initial rate enhancement. For the Kemp elimination (Scheme 1), 59 designs from 17 distinct scaffolds were selected for synthesis.¹³ In the end, the procedure yielded eight proteins with measurable Kemp elimination activity. The k_cat/k_uncat rate accelerations of these eight ranged from 10² to 10⁵. Site directed mutagenesis confirmed the importance of critical catalytic residues. Subsequent directed evolution resulted in a 200-fold increase in k_cat/k_M and a k_cat/k_uncat of 10⁶ for one of the Kemp eliminases (KE07). While these numbers slightly exceed those of the most proficient catalytic antibodies, both pale in comparison to natural enzymes, with average k_cat/k_uncat values of ∼10¹¹.¹⁵ The modest rate acceleration and turnout hints at deficiencies even for the most active enzyme designs.

Scheme 1.

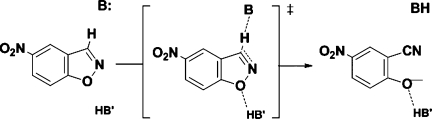
The base-catalyzed Kemp elimination of 5-nitrobenzisoxazole, depicted with hydrogen-bond donor for stabilization of the developing negative charge in the transition state.

In several cases, X-ray structural data provide important insights. Thus far crystallization efforts have resulted in the structural determination of two retro-aldolases,¹⁴ one Kemp eliminase (KE07/1thf),¹³ as well as four evolved variants of KE07,¹⁶ all of which are active. Comparison of the designed models with the crystal structures shows only minor rearrangement of the active site side chains. For instance, in the case of KE07/1thf the root mean square displacement (RMSD) is 0.32 Å for the backbone and 0.95 Å when side chains are included. This further highlights the predictive power of the RosettaMatch and RosettaDesign algorithms. But no structural data have yet become available for any of the inactive designs, so that the reasons for inefficient catalysis remain elusive.

To address this and other issues, we utilized in silico methods for the study of both active and inactive designs. Our goals were twofold: (1) to reveal the shortcomings of these designs and to determine how they could be improved; (2) to devise a method to screen out designs that are likely to be inactive, thus maximizing the chances of successful experiments. Our study focuses on a set of Kemp elimination enzymes, which were designed to promote the conversion of 5-nitrobenzisoxazole to cyanophenoxide. This ring-opening reaction that was initially studied by Kemp and coworkers (Scheme 1) and is a model for the biochemically relevant proton abstraction from carbon centers.^17,18 The reaction follows a classical E2 mechanism in which a proton is transferred from the substrate to the catalytic base (Glu/Asp, or His–Glu/Asp dyad). Hydrogen-bond donors and π-stacking residues have been proposed to stabilize the transition state¹⁹ and were incorporated in most designs.

Catalytic antibodies,³ serum albumins,²⁰ “synzymes”,²¹ micelles,²² and even charcoal²³ have been shown to promote this reaction to some degree. As a result, the source for the rate enhancement of Kemp eliminations has been discussed extensively, and both nonspecific medium effects and the specific positioning of catalytic groups have been shown to be important in achieving catalysis.¹⁹

To develop a better understanding of the energetics, the following considerations are helpful: the background reaction in aqueous buffer solution is characterized by a ΔG^‡_uncat of 23.2 and 25.7 kcal/mol, with measurements of k_uncat = 3 × 10⁻⁵s⁻¹ (Thorn)³ or 1.2 × 10⁻⁶s⁻¹ (Röthlisberger),¹³ respectively. The free energy profile of the auto-ionization of water has a ΔG^‡ of 23.8 kcal/mol and a ΔG_R of 21.4 kcal/mol.^24–26 Formation of OH⁻ and H₃O⁺ can thus be the rate-determining step of base-catalyzed reactions in pure water.

Kemp found that the rate of reaction depends strongly on the medium, when a carboxylate is the base.²⁷ Acetate in the polar aprotic solvent MeCN, for instance, accelerates the Kemp elimination by a factor of 10⁷ compared to acetate in H₂O. Water solvates the carboxylate base much more effectively than it solvates the transition state of the reaction, and hence the rate is slowest in protic environments. But catalysis is not limited to nonspecific medium effects. Kirby demonstrated that rate accelerations of up to 10⁶ can be achieved through precise positioning of donor and acceptor in general acid-base catalyzed reactions.²⁸ The theoretical limit of the Kemp elimination can thus be placed at a rate enhancement of 10¹³. In fact, the maximum k_cat/k_uncat measured for any natural enzyme-catalyzed reaction, and even then by estimates of k_uncat from high temperature experiments, is 10¹⁵–10¹⁷.^29–31 In comparison, Hilvert's³ antibody 34E4 exhibits a k_cat/k_uncat = 10⁴; the Röthlisberger et al. designed enzyme KE59 achieves a k_cat/k_uncat = 10⁵.¹³

Previous studies conclude that the catalytic Kemp elimination antibodies benefit from both nonspecific medium effects and the specific positioning of catalytic groups.^28,19,32 Kirby further argues that while the latter contributes considerably, “the very precise positioning of the general base that we believe is necessary for exceptionally efficient proton transfer catalysis is not achieved.”²⁸ We propose that these conclusions are also valid for the computationally designed Kemp elimination enzymes, and examined their active site structures with QM and classical MD. We find that a dynamic treatment of the systems in the presence of explicitly modeled water molecules is necessary to identify structural flaws and other sources for inactivity. MD-derived geometric descriptors are instrumental for this purpose and can be used to differentiate active from inactive designs. A direct comparison of the reaction profiles is desirable, but the high computational cost of obtaining activation barriers with ab initio or density functional QM limits such high-level approaches to a static treatment of the systems. We further note that even the most active designs appear to have considerable shortcomings, underlining Kirby's conjecture that there is much room for improvement.

Results and Discussion

QM cluster model and QM/MM approaches

DFT ab initio transition state calculations were performed, and the applicability of truncated QM cluster models (CM) and full protein QM/MM were explored for the purpose of a reaction barrier based evaluation. Similar methodologies have been applied successfully for the study of natural enzymes,³³ and the utility of these models should be applicable to non-natural biocatalysts. Two distinct protocols (P1 and P2) were explored: P1 starts QM from the static RosettaDesign geometry of a given final design; P2 relies on short 2 ns MD simulations to generate solvated active sites for subsequent QM that include explicit water molecules. One key aspect of the CM approach is the degree to which the theozyme geometry is constrained: full optimization in the absence of constraints will generally yield the original theozyme geometry that was utilized in the design process; constraining the catalytic residues in their entirety will yield too rigid a model to faithfully describe the protein. We compromised by constraining the backbone heavy atoms of each catalytic residue and allowed the sidechains to relax in response to the presence of the transition state, the substrate, and/or water molecules. CM1 [Fig. 1(a)] consists of the catalytic residues, which were modeled with B3LYP/6-31G(d); CM2 [Fig. 1(b)] extends CM1 and includes surrounding non-catalytic residues within 3 Å of the catalytic unit. These were treated at the semi-empirical PM3MM level of theory. All other residues were omitted. CM1 and CM2 were both tested on the design structures (P1) and after 2 ns of MD (P2).

Figure 1.

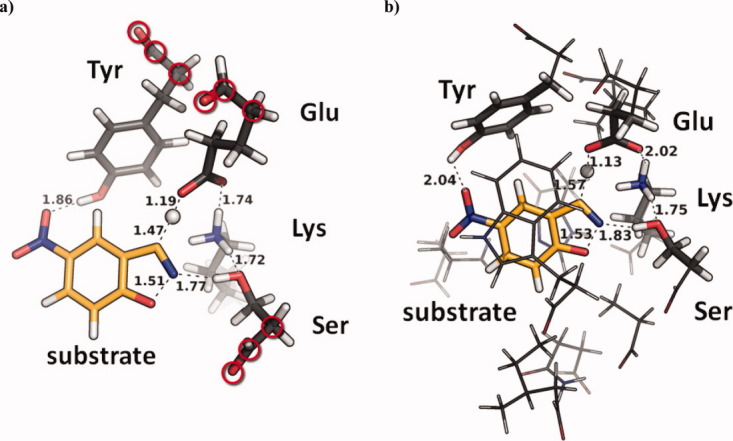
(a) TS in cluster model 1 (CM1). (b) Cluster model 2 (CM2); sticks computed with DFT, lines computed with PM3MM. Both (a) and (b) of KE07. Backbone heavy atoms (circled in CM1) were constrained. An interactive view is available in the electronic version of the article. PRO462 Figure 1

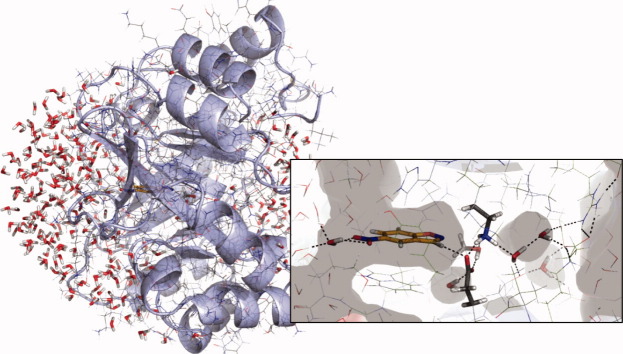
Full protein QM/MM calculations were also performed. Only the MD-relaxed protocol P2 was used for these (Fig. 2). Each system was divided into two overlapping layers that were treated with distinct model chemistries, as implemented in the ONIOM method.³⁴ The QM layer includes the substrate molecule and the theozyme residues and is computed at the B3LYP/6-31+G(d,p)//B3LYP/6-31G(d) level (Fig. 2, inset), while the MM layer contains all atoms of the enzyme and a 10 Å solvent sphere surrounding the substrate. The MM layer is treated with the AMBER force field and the TIP3P model for waters. Solvent molecules that were in direct contact with either the substrate or one of the theozyme residues were included in the higher accuracy layer. A link atom approach was used to treat the QM/MM boundary, and the effect of the MM region was incorporated via a point charge representation that polarizes the QM Hamiltonian (electronic embedding). Reactant and transition states were then obtained by systematically stepping along the reaction coordinate, followed by optimizations towards the respective stationary point.

Figure 2.

Full enzyme QM/MM from 2ns MD (here: KE07); explicit waters within 10 Å of substrate were retained; QM layer (sticks in inset) was treated with DFT; MM layer with the AMBER force field. A movie of the computed reaction path is available as part of the SI. An interactive view is available in the electronic version of the article. PRO462 Figure 2

Table I displays the results from QM-CM1-P1, QM-CM2-P1, QM-CM2-P2, QM/MM-P2 full protein calculations, and the results from Alexandrova et al.,³⁵ where the semiempirical PDDG/PM3 method was used in a QM/MM Monte Carlo study. The designs are ordered according to their experimental activities, with the most active on top. Kinetic data of the active designs was obtained from Ref.13. The inactive designs constitute a set of never before published structures, which were included to put these methods to the test (see Supporting Information Fig. 6 and Supporting Information text). RCSB-PDB IDs of the respective scaffold proteins are provided along with an overview of the catalytic machineries in terms of catalytic base and TS-stabilizing hydrogen-bond donor groups. First-order rate constants (k_cat) and the corresponding derived free energies of activation are given for each functional design. The right hand columns summarize the activation barriers that were computed with the aforementioned model chemistries.

Table I.

QM/CM2–P1, QM/CM2-P2, and QM/MM-P2 Design Evaluation

Design	Scaffold	Base	H-bond	kcat (s−1)	ΔG‡expa (kcal/mol)	ΔE‡CM1-P1b (kcal/mol)	ΔE‡CM2-P1c (kcal/mol)	ΔE‡CM2-P2d (kcal/mol)	ΔE‡QM/MM-P2e (kcal/mol)	ΔG‡PDDG/PM3f (kcal/mol)
KE59	1a53	Glu	None	0.290	18.3	3.7	7.0	17.7	17.8	—
KE70	1jcl	His–Asp	Tyr	0.160	18.7	6.2	9.6	19.0	16.5	—
KE10	1a53	Glu	None	0.029	19.7	7.1	9.3	14.7	13.2	13.5
KE15	1thf	Asp	None	0.022	19.8	3.8	6.1	24.9	25.1	12.3
KE07	1thf	Glu	Lys	0.018	20.0	21.9	25.4	30.2	24.8	8.1
KE16	1thf	Asp	Lys	0.006	20.6	15.3	19.7	20.5	23.9	—
KE54*	1jcl	His–Glu	Ser	Inactive	—	10.5	9.1	18.1	28.4	—
KE60*	1jul	Glu	None	Inactive	—	6.3	7.7	24.7	29.5	—
KE66*	1lbl	His–Glu	Ser	Inactive	—	8.4	9.3	Inactive	Inactive	—
KE38*	1lbm	His–Glu	Trp	Inactive	—	6.7	7.1	Inactive	Inactive	—

^aCalculated from k_cat (Ref.¹³) using the Eyring equation with T = 20°C.

^bQM/CM1-P1: b3lyp/6–31+g(d,p)//b3lyp/6–31g(d).

^cQM/CM2-P1: ONIOM b3lyp/6–31+g(d,p)//b3lyp/6–31g(d):pm3mm.

^dQM/CM2-P2: ONIOM b3lyp/6–31+g(d,p)//b3lyp/6–31g(d):pm3mm with explicit H2O from MD.

^eFull protein QM/MM-P2: ONIOM b3lyp/6–31+g(d,p)//b3lyp/6–31g(d):AMBER with explicit H2O from MD.

^fQM/MM/MC study at PM3:OPLS level of theory (from Ref.35).

^*Indicates inactive designs, see SI for details.

The P1 protocol vastly underestimates the absolute activation barriers in both cluster models, CM1 and CM2. This is also true for the Alexandrova approach. The CM2-P2 and QM/MM-P2 protocols, in which QM is preceded by 2 ns unrestrained MD, give greatly improved absolute activation barriers. The reason is twofold: backbones and sidechains were allowed to deviate from their ideal designed geometries, and explicitly modeled water molecules that come into direct contact with the catalytic machinery during MD are included in the QM calculations. The QM/CM2-P2 barriers do not reflect experimental trends, but the full enzyme QM/MM-P2 approach performs better. Aside from qualitatively high barriers of the inactive designs, QM/MM-P2 shows a weak correlation with the experimental barriers, giving an R² of 0.58 and a slope of 1.5 (Supporting Information Fig. 3). While this appears promising on first sight, the computational demand is too high and the achieved correlation too poor to be of use for the in silico ranking of designs prior to the experimental phase. The P2 protocol, however, seems to provide a significant advantage over P1: Two of the inactive designs (KE66 and KE38) failed to maintain their catalytic geometries—an observation that would have remained inaccessible without an unrestrained dynamics treatment of the entire protein.

Siegbahn and Himo have used cluster models in the past to explore mechanisms of catalysis by natural enzymes.³³ While good results have been obtained in their work, they have also shown that many residues beyond the catalytic groups must be included to obtain reasonable energetics. We have been less successful in using cluster models to predict whether a designed enzyme would be an active catalyst or not. We conclude that the major shortcoming of these QM-based quantitative approaches is due to their static nature. The issue was addressed by employing the P2 protocol: subjecting the full designs to MD simulations, extracting multiple structures from each trajectory and following up with QM-methods. These subsequent relatively high-accuracy calculations are nonetheless static; as such the computed barriers depended greatly on the quality of the extracted geometries, and the environment of the active site. Alternative methods have been reported by Jorgensen^36,37 and Warshel.³⁸ For instance, recent work by Alexandrova et al. describes the use of the semiempirical PDDG/PM3 method in a QM/MM Monte Carlo study of four active Kemp elimination designs KE07/1thf, KE10/1a53, KE15/1thf, and KE16/1thf (far right column of Table I).³⁵ These systems consisted of 200 residue cutaways of the four designs, in which the semiempirical QM part consisted of the substrate and the catalytic base (Glu/Asp). No water molecules were included in the QM region, but turn out to be important for adequately computing absolute barriers, as we found from DFT calculations. The protein backbones were held fixed in the Alexandrova study, and only side-chain motions were sampled. Here too, the attempt to obtain a correlation between computed and experimental barriers was not successful, and the trend of Alexandrova's barriers is opposite to what was found experimentally. This is not a surprise, considering that the absolute error bars of the Alexandrova approach are between 6 and 12 kcal/mol for these systems, where the experimentally determined range is 0.9 kcal/mol for this subset of designs.

We also explored the use of semi-empirical QM/MM umbrella sampling calculations after initial classical equilibration MD, with the hope of more adequately exploring the configuration space along the reaction coordinate. We found that these computationally intense simulations have at best an average error of +/−1.5 kcal/mol, which is inadequate for a quantitative ranking: the experimental rates of the Kemp elimination designs span only a small range of 2 kcal/mol, clearly necessitating the application of high-level model chemistries (such as CCSD(T) with a large basis set) in conjunction with exhaustive sampling, if a sufficiently reliable quantitative treatment is sought.

Molecular dynamics simulations

The quantum mechanical cluster models and full enzyme QM/MM that are described here, as well as PM3/PDDG/MC calculations³⁵ proved to be inadequate to differentiate active from inactive designs, let alone for the attempt of a quantitative ranking. The problem appears to be the failure of these methods to account for changes in the protein structure and in solvent accessibility; both arise from significant motions of the side-chains and the backbone. We explored the use of molecular dynamics to assess the stability of the active sites in designed structures. The enzyme:substrate complexes as well as the apo enzyme structures were subjected to MD. Rather than emphasizing the activation energy expected from a design, we set out to test whether the catalytic arrangement of a putative enzyme would be maintained in a dynamic and aqueous environment.

In the design process, once a match is found for a particular theozyme, the surrounding residues are redesigned and repacked such as to stabilize the catalytic unit with RosettaDesign.¹¹ Multiple mutations are introduced to the native sequence in this process (up to 20 in the case of Kemp designs). In our experience, the new active sites often times jeopardize the structural integrity of the protein scaffold. On the other hand, seven published crystal structures demonstrate that active proteins appear to have folds and side-chain geometries that are nearly identical to the computational designs.^13,14,16 We hypothesize that once a design expresses and is soluble, lack of activity is most likely due to rather subtle geometric deviations from the computational model, such as alternative loop and side-chain conformations in or near the active site. Sidechains of mutated residues would be expected to have a particularly high propensity to adopt alternative configurations. Scheme 2 corresponds to a simplified visualization of this idea. The design process introduces around 20 mutations in and around the active site of the template protein (Step 1). This changes the potential energy landscape of the original protein (grey line to red line) and can cause one or multiple neighboring local minima to dominate over that of the Rosetta design. The solution structure might thus significantly differ from that of the computational geometry (large Δ values). Whether a design is susceptible to such change can be addressed with nanosecond scale molecular dynamics (Step 2).

Scheme 2.

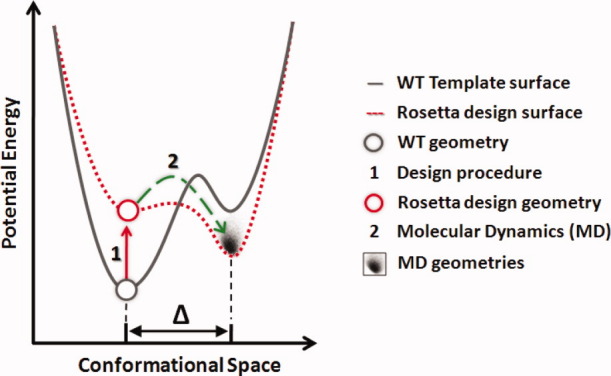
Schematic representation of the enzyme design process in terms of potential energy and conformational space.

We tested the active site structural integrity of 23 Kemp elimination designs, using cathepsin K and catalytic antibody 34E4 as a reference. Each protein structure was immersed in a box of up to 16,600 explicit waters and subjected to 20 ns, constant pressure, periodic-boundary MD simulations. Post-processing of the trajectories yielded data in the form of pair wise distance distributions, hydrogen bond directionalities, solvent accessibility, and root-mean-square displacements (RMSDs) relative to the respective RosettaDesign geometry. Taken together, the data can yield a comprehensive picture of a given design and allows for in-depth analyses. Particularly interesting cases, such as designs KE59/1a53, KE70/1jcl (the two most active Kemp eliminases), design KE07/1thf (active, crystal structure, subsequent directed evolution), and design KE38/1lbm (inactive), are discussed in detail.

MD—structural validation

We first explored whether the MD protocol is capable of reproducing structures that were obtained from X-ray crystallography. The catalytic antibody 34E4 (PDB-ID 1y0l) and the crystal structure of design KE07 in the 1thf scaffold (PDB-ID: 2RKX) were used. Both of these proteins catalyze the Kemp elimination. MD simulations were carried out from the crystallographic geometries with and without the bound substrate. In the case of KE07/1thf an independent set of MD simulations was started from the RosettaDesign geometry. Figure 3 shows an overlay of the respective crystal and MD structures. The active sites maintain their geometries in both cases throughout the 20 ns MDs: the backbone geometries deviate from the crystal structure by root-mean-square values of 0.74 and 0.67 Å with standard deviations (σ) of 0.30 and 0.17 Å; the sidechain geometries show RMSD values of 1.26 and 1.15 Å with σ of 0.25 and 0.15 Å for antibody 34E4 and design KE07/1thf, respectively (Fig. 3). The MD protocol accurately recapitulates both structures. It should perform equally well on computational designs for which no X-ray data are available.

Figure 3.

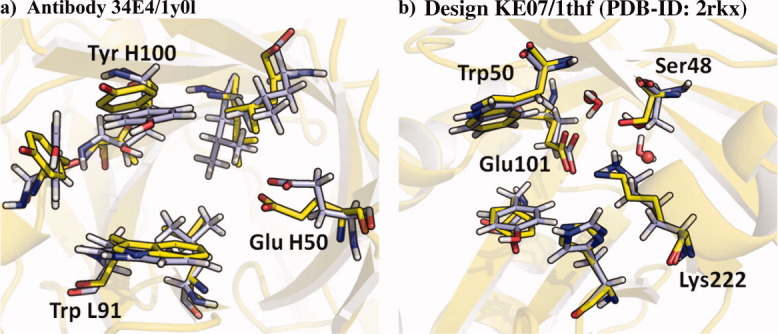
Overlay of representative MD geometry (blue) and crystal structure (yellow). (a) Active site of antibody 34E4 with backbone RMSD of 0.74 Å (σ = 0.30 Å) and all atom RMSD of 1.26 Å (σ = 0.25 Å). (b) Active site of design KE07/1thf with backbone RMSD of 0.67 Å (σ = 0.17 Å) and all atom RMSD of 1.15 Å (σ = 0.16 Å). The positions of two ordered active site water molecules that were co-crystallized in 2RKX (spheres) are also very well reproduced with MD. An interactive view is available in the electronic version of the article. PRO462 Figure 3

MD—hydrogen bond distance and directionality

Hydrogen bonds have a preference for linearity and are related to the transition states of proton-transfer reactions.³⁹ Analyses of crystal structure databases show that the hydrogen bonding angles deviate appreciably from linearity and peak between 160 and 170°.^40,41 The non-linearity is due to the large number of possible hydrogen bond configurations with deviation from 180°.⁴⁰ “The shortest distances occur at relatively linear angles, whereas longer bonds are observed with a larger angular range.”³⁹ While hydrogen bonds clearly exist with a continuum of strengths, due to practical reasons they are generally assigned to one of three categories: strong, moderate or normal, and weak (Table II).^39,42

Table II.

Categories of Hydrogen Bond Strength^39,42

	Strong	Moderate	Weak
Interaction type	Mostly covalent	Mostly electrostatic	Electrostatic/dispersion
Bond lengths (Å) XH···Y	1.2–1.5	1.5–2.2	2.2–3.2
Bond angles (°) X-H···Y	170–180	>130	>90
Bond energies (kcal/mol)	15–40	4–15	<4

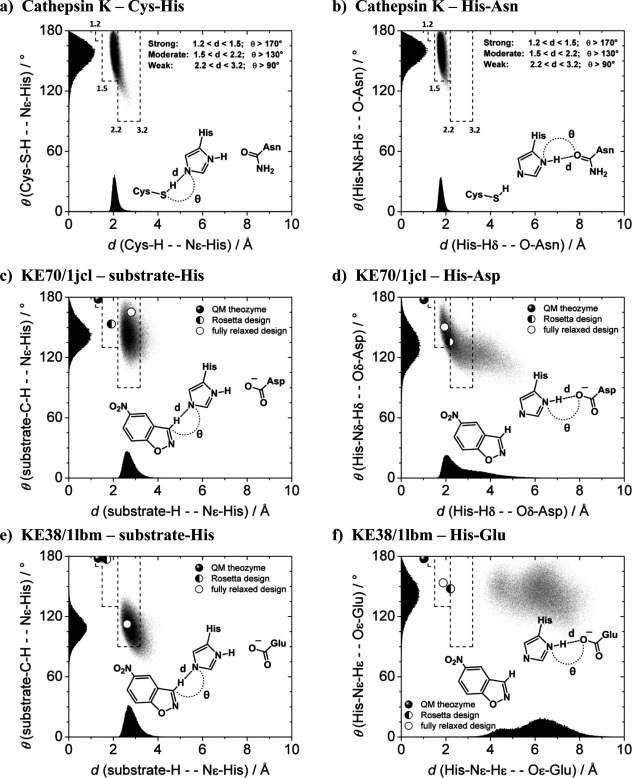
Strengths of hydrogen bonds can be assessed graphically with angle-versus-distance scatter plots.³⁹ Figure 4(a,b) show this representation for the Cys–His–Asn catalytic triad of the naturally evolved cysteine protease cathepsin K. The system is a prime example of well-defined active site hydrogen bonds involved in acid-base catalysis.⁴³ MD simulations were performed for 20 ns starting from the crystal structure 1ayu.⁴⁴ Both, the Cys–His and His–Asn hydrogen bond distances and angles are plotted in Figure 4(a,b), respectively. Densely populated clusters of data points peak at short distances and nearly linear angles. The Cys–His data fall mostly into the region of moderate bond strength, peaking at 2.1 Å and 160° [Fig. 4(a)]. The His–Asn hydrogen bond gives rise to a very dense cluster that falls entirely into the region of moderate bond strength and peaks at 1.8 Å and 161° [Fig. 4(b)]. These tightly maintained angles and distances provide a guide as to the desired catalytic hydrogen bonding that is achieved in fully evolved natural catalysts.

Figure 4.

Angle versus distance scatter plots. (a) Cys–His contact and (b) His–Asn contact of the naturally evolved cathepsin K catalytic triad; (c) substrate-His contact and (d) His–Asp contact of the active design KE70; (e) substrate-His contact and (f) His–Glu contact of the inactive design KE38. Data points are from 20 ns MD. The individual distributions are projected onto the axes. The three hydrogen bond categories of Table II are outlined with dashes.

Figure 4(c–f) compares MD simulations for the active KE70 (4c,d) and the inactive KE38 (4e,f) with the naturally evolved cathepsin K (4a,b). The substrate-to-His and the His-to-Asp/Glu contacts are shown. Three additional data points are plotted: the QM theozyme (filled disk), the final Rosetta design (half-filled disk), and the AMBER optimized substrate complex (empty disk). QM calculations give the ideal arrangement of the catalytic groups that stabilize the transition state (filled disk). Matching of these theozyme sidechains to the protein backbone typically comes with a geometric penalty. As a result, the catalytic contacts of the final computational design (half filled disk) deviate significantly from their ideal (filled disk). Optimization of the design in the presence of substrate (empty disk) was used here as the starting geometry for MD.

Compared to cathepsin K [Fig. 4(a,b)], both KE70/1jcl distributions are broad, but still within the outlined hydrogen bond categories [Fig. 4(c,d)]. The two catalytic contacts of KE70/1jcl are simultaneously established in only 66.3% of the MD frames (distance cutoff = 3.2 Å, angle cutoff = 90°) and the remaining 1/3 of frames correspond to arrangements in which the catalytic dyad is temporarily disrupted by water molecules. This highlights that the distance and angle distributions of the KE70 catalytic contacts are far from the ideal of a naturally evolved enzyme. Yet KE70 is the second most active of the computationally designed Kemp elimination enzymes, showing a k_cat/k_uncat of 1.4 × 10⁵ and a k_cat/k_M of 78 M⁻¹s⁻¹. Improved catalysis is possible, if shortcomings of this nature are addressed as part of the design process.

In terms of the catalytic hydrogen bond geometry, the inactive KE38/1lbm design is more similar to the theozyme than the active KE70/1jcl [compare half-filled disks in Fig. 4(c,d) vs. 4(e,f)]. This is also reflected in Table I: the QM/CM2-P1 barrier of KE38/1lbm is 2.5 kcal/mol lower than that of KE70/1jcl; a clear shortcoming of the static nature of such computations. Optimization in AMBER leaves the catalytic dyad relatively unchanged [half-filled vs. empty disk in Fig. 4(f)] and the two designs (KE70 and KE38) appear indistinguishable in terms of the dyad at this stage [compare empty disks in Fig. 4(d,f)]. MD, on the other hand, illustrates the impact of solvent accessibility and active site dynamics on catalytic hydrogen bonds of KE38/1lbm: the designed His–Glu contact is not maintained and the two catalytic dyad residues are separated by 4–8 Å. No activity is predicted, in agreement with experiment.

MD—structural integrity of the active site

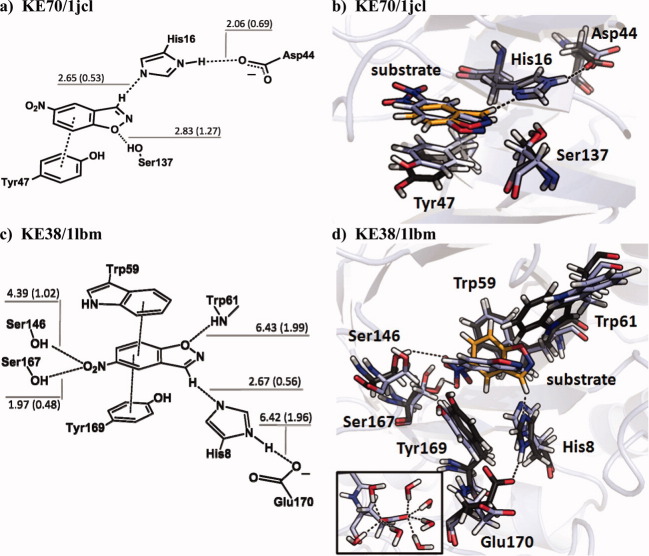
Figure 5 puts the distributions of Figure 4 into geometric context. KE70/1jcl is the second most active Kemp design and employs a His–Asp dyad as the catalytic base. Ser137 was designed to serve as the TS-stabilizing hydrogen-bond contact, and Tyr47 as the π-stacking residue [Fig. 5(a)]. KE38/1lbm is an inactive design. Its binding site consists of a Glu–His dyad (as the base), a Trp residue (as the phenoxy-hydrogen-bond), and a Tyr/Trp π-stacking arrangement [Fig. 5(c)]. 20 ns MD simulations were performed on each of the designs. The distance distributions of all polar contacts are summarized by the hydrogen bond labels in Figure 5(a,c): all values are in Å and correspond to the distances at which the distributions have their maxima; values in parentheses are the full width at half maxima (FWHM).

Figure 5.

Design versus MD. Schematic representation of the catalytic unit (a and c) and representative MD geometry (blue) over Rosetta design geometry (black with orange substrate) (b and d). Bond labels in (a) and (c) are maxima of distance distributions with FWHMs in parentheses. All values in Å. The backbone RMSD of the catalytic unit of KE70 and KE38 is 0.57 and 0.76 Å; the sidechain RMSD is 0.95 and 2.24 Å, respectively. The inset in (d) shows Glu170 in direct contact with seven water molecules. An interactive view is available in the electronic version of the article. PRO462 Figure 5

Figure 5(b,d) show structural comparisons of our simulations with the Rosetta design geometries. The backbone RMSDs are low in both cases: 0.57 Å in KE70 and 0.76 Å in KE38. The sidechain RMSDs, on the other hand, diverge: 0.95 Å in KE70, but 2.24 Å in KE38. This is also evident from visual inspection of Figure 5(b,d): KE70 displays little to no structural differences to the design, while the geometry of the KE38 active site is not maintained. We observe that the solvent-exposed Glu170 is easily enclosed by a shell of water molecules and becomes separated from His8 [Fig. 5(d), inset]. The catalytic dyad is intact in only 0.05% of the MD frames (cutoff-criteria: 3.2 Å) and Glu170 is thus unfit to activate His8 for deprotonation.

Similar instabilities, while less severe, have been proposed to limit the activity of RA22,⁴⁵ a previously published retro aldol design.¹⁴ RA22 uses a His–Asp dyad base to deprotonate one alcohol after formation of the aldol-Lys iminium. Head-Gordon et al. performed MD and found the dyad to be intact in merely ∼25% of the frames (cutoff-criteria: 3 Å).⁴⁵

MD—water accessibility and coordination

It was established by Kemp that the rate of the Kemp elimination depends strongly on the medium, particularly when a carboxylate is the base.^17,18 The observation is relevant to enzymatic processes that involve an aspartate or glutamate as part of the catalytic machinery: proteases, kinases, phosphatases, DNA topoisomerases, cellulases, glucosidases, deaminases, and aminotransferases, to name just a few, utilize Glu or Asp as a general base. Individual water molecules are often involved, but the carboxylate is always well shielded from bulk solvent to achieve large rate accelerations.⁴⁶ Figure 6 (top) illustrates this for the example of the cysteine protease cathepsin K, which is used here as a naturally evolved reference for computationally designed enzymes: the MD analysis shows that no water molecule coordinates to the carbonyl-oxygen of Asn182 in 98% of the frames. The carboxylate oxygen water coordination numbers of catalytic antibody 34E4, the active KE70/1jcl and the inactive KE38/1lbm, on the other hand, follow Gaussian distributions that peak at 3.5, 5, and 7, respectively (Fig. 6). While there appears to be a trend, no significant correlation exists between k_cat and the water coordination number of the catalytic base: the inactive designs average at five waters in direct contact to the catalytic base, while the active designs average at three water molecules.

Figure 6.

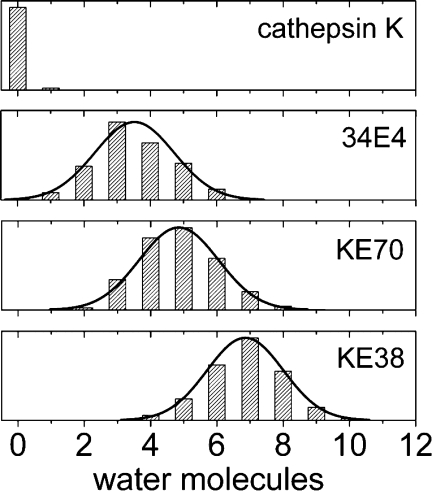
Water coordination numbers from MD at d < 3.2 Å. Asn182 in the naturally evolved cathepsin K, GluH50 in the catalytic antibody 34E4, Asp44 in the active KE70/1jcl, and Glu170 in the inactive KE38/1lbm. Note: histograms are scaled to the same height.

Similar water accessibilities are observed for most other Kemp designs, three of which are addressed as part of the Supporting Information (Supporting Information Figs. 1 and 2), and highlight a clear inadequacy of these catalytic microenvironments. Because future design endeavors will build on the charge-relay of catalytic triads or on acid-base catalysis in general, this observation underscores an area of the enzyme design protocol that requires improvement.

MD—distance distribution-based descriptors

The preceding examples show how MD can be used to rationalize experimental observations and to differentiate active from inactive designs: maintenance of catalytic pre-organization even under aqueous and thermal relaxation conditions is necessary for activity. We explored whether MD could be used as a routine screen for activity of new designs by examining a number of Kemp eliminases, including catalytic antibody 34E4. Catalytic distances and angles, polar contacts, structural integrity, and degree of solvation were monitored throughout the trajectories of substrate-bound and substrate-free designs. Table III provides a summary of the entire dataset. The designs are shown in order of their catalytic rates (k_cat). Active designs from Ref.13 are contrasted to a set of previously unpublished inactive designs (see Supporting Information Fig. 6 and text). Characteristic information, such as scaffold PDB-IDs, catalytic groups, and rate constants are given in the left half. The right hand columns provide the root mean square displacements of the active sites, the water coordination number of the catalytic base, and the distances and angles of the catalytic hydrogen bond contacts. The values correspond to the distribution maxima of the respective measurements. Based on our discussion of hydrogen bond distance and directionality, designs are considered to be active, if the catalytic contact distance distributions peak at d < 3.2 Å; distributions at d > 3.2 Å are regarded as inactive, as denoted with “A” and “I,” respectively. Cathepsin K serves as a reference and is listed at the top of the table.

Table III.

MD-Based Evaluation of Kemp Designs Compared to Antibody 34E4 and Cathepsin K

Design	Scaffold	Base	H-bond	kcat (s−1)	RMSDa	H2Ob	Distancec	Angled	Rankinge
Cathepsin K	1ayu	His–Asn	—	4.200	0.4 (0.6)	0.0	2.1 and 1.8	160 and 161	—
KE07 R7 10/11G	1thf	Glu	Lys	1.370	0.9 (1.9)	3.9	2.5	152	A
KE07 R4 1E/11H	1thf	Glu	Lys	0.699	0.6 (1.4)	2.8	2.4	132	A
34E4 antibody	1y0l	Glu	None	0.660	0.7 (1.3)	3.5	2.5	125	A
KE07 R6 3/7F	1thf	Glu	Lys	0.600	0.6 (1.7)	3.1	2.4	151	A
KE59	1a53	Glu	None	0.290	0.8 (1.6)	3.0	2.5	123	A
KE07 R2 11/10D	1thf	Glu	Lys	0.021	0.9 (1.4)	1.8	2.5	126	A
KE70	1jcl	His–Asp	Tyr	0.160	0.6 (1.0)	5.0	2.7 and 2.1	144 and 132	A
KE113	1jcl	His–Asp	Ser	0.150	0.7 (0.9)	4.0	2.7 and 2.2	143 and 126	A
KE70 D45N	1jcl	His–Asn	Tyr	0.060	1.0 (1.2)	3.1	2.8 and 2.3	128 and 116	A
KE59 G130S	1a53	Glu	Ser	0.032	0.7 (1.7)	3.9	2.5	148	A
KE07 K222A	1thf	Glu	None	0.030	0.5 (1.2)	4.1	2.5	123	A
KE10	1thf	Glu	None	0.029	0.5 (1.8)	0.0	2.5	127	A
KE15	1thf	Asp	None	0.022	0.5 (1.8)	2.9	5.0	147	If
KE07	1thf	Glu	Lys	0.018	0.7 (1.2)	2.0	2.5	128	A
KE16	1thf	Asp	Lys	0.006	0.7 (2.0)	3.0	5.1	143	If
KE38	1lbm	His–Glu	Trp	Inactive	0.8 (2.2)	7.0	2.7 and 6.4	108 and 146	I
KE54	1jcl	His–Glu	Ser	Inactive	0.6 (1.0)	5.6	2.6 and 1.9	150 and 149	Ag
KE60	1jul	Glu	None	Inactive	1.2 (3.1)	4.6	4.7	116	I
KE66	1lbl	His–Glu	Ser	Inactive	0.6 (1.9)	4.7	7.4 and 1.8	37 and 112	I
KE108	1jcl	His–Asp	Thr	Inactive	1.0 (1.6)	5.0	5.4 and 2.0	80 and 143	I
KE111	1jcl	His–Asp	Ser	Inactive	0.5 (0.8)	5.4	2.6 and 3.5	165 and 132	I
KE112	1jcl	His–Asp	Ser	Inactive	0.6 (0.9)	5.9	2.7 and 3.7	161 and 132	I
KE114	1jcl	His–Asp	Ser	Inactive	0.9 (1.2)	5.0	5.5 and 2.0	153 and 144	I
KE116	1jcl	His–Asp	Ser	Inactive	0.7 (1.0)	5.1	4.2 and 1.9	150 and 150	I

KE38 through KE116 are inactive designs (see SI for experimental data).

^aRMSD (Å) of active site back-bone (and sidechains) relative to design or crystal. Active sites are defined as all residues within 3 Å of the theozyme TS.

^bNumber of water molecules at d < 3.2 Å from catalytic base oxygen(s).

^cCatalytic h-bond distances (Å) and angles (°). First/single value: substrate-to-base. Second value: His-to-Asp/Glu/Asn.

^dCatalytic h-bond distances (Å) and angles (°). First/single value: substrate-to-base. Second value: His-to-Asp/Glu/Asn.

^eActive: d < 3.2 Å; inactive: d > 3.2 Å.

^fFalse negative.

^gFalse positive.

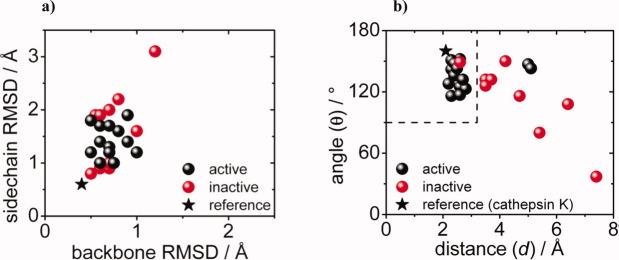
Figure 7(a) plots the sidechain and backbone RMSDs of all active sites from Table III. No correlation is apparent that would set active designs apart from inactive designs in terms of active site rigidity, although the evolved KE07s show an increase in sidechain flexibility in each successive round (Table III). Still, while not predictive in terms of activity, RMSD distributions are often helpful at pinpointing structural inadequacies.

Figure 7.

The entire dataset. (a) Sidechain versus backbone RMSDs of active sites. (b) Angles versus distances of the catalytic H-bond contacts.

Figure 7(b) extends Figure 4(a–f) to the entire dataset. The maxima of the angle and distance distributions from Table III are plotted. Active designs cluster at hydrogen bond distances below 3.2 Å and angles above 90°; inactive designs are scattered at larger distances and random angles. The data suggests that these simple geometric descriptors can be used to qualitatively deduce from MD whether or not a design is active. Presumably a similar scheme could be used for other acid-base catalysts. In our systems the hydrogen bond directionality of both the donor (X-H) and acceptor (A) group is linear. Additional geometric factors that map out the hydrogen bond acceptor directionality might need to be considered when employing MD-based hydrogen bond analysis for other systems, that is, when carbonyl oxygens are involved.

2D distance scatter-plots become instructive in cases in which the catalytic base requires two polar contacts to be formed simultaneously (His–Asp/Glu dyads such as in KE70 and KE38). Here, activity can be deduced when the signal-peak falls within a quadratic area that expands from 1.2 to 3.2 Å on each axis (Supporting Information Fig. 4). 1D distance histograms can be used in cases in which formation of only a single catalytic hydrogen bond is necessary (Supporting Information Fig. 5).

MD evaluation examples

Aside from KE70, KE38, and cathepsin K, three active Kemp elimination designs are described in more detail as part of the supporting information. Supporting Information Figure 1 contrasts the most active KE59 to the surprisingly less active KE59_G131S variant. Supporting Information Figure 2 introduces KE07 and highlights the effect that seven rounds of directed evolution had on the catalytic unit.

Conclusions

In this work, we expand the previously published set of active Kemp eliminases to include nine additional designs with no activity. We analyzed both active and inactive computational designs with QM and QM/QM′ cluster-model-type QM calculations, full-enzyme QM/MM, and classical MD. These and other computational approaches were compared in terms of their ability to evaluate the Kemp eliminases and rank them by activity. We conclude that the active site geometry of a given static computational design can differ substantially from the ensemble of equilibrated structures that one would find in solution. To differentiate active from inactive designs, it appears essential to capture sidechain and backbone dynamics in an explicitly solvated NPT system, allowing the formation of statistically significant distributions. DFT and higher level QM methods are currently far too expensive computationally as to treat such systems dynamically. Focusing on the enzyme:substrate complex with AMBER classical molecular dynamics simulations proved to be a useful approach. We monitor a set of representative descriptors such as active-site-RMSDs, water-coordination-numbers, hydrogen-bond-distances as well as angles, and outline a protocol for the rapid qualitative evaluation and ranking of biocatalyst designs when Bronsted acid-base catalysis is involved.

Activity was deduced from the distribution patterns of polar contacts and their relative orientations to one another. When subjected to explicit-solvent, periodic-boundary MD, active designs were found to have well-defined catalytic contacts and active sites that closely resemble the QM theozyme geometries that they are based on. Inactive proteins showed ill-behaved catalytic contacts that deviated significantly from the designed active site arrangements. RMSD distributions are helpful at pinpointing structural inadequacies, and the average water coordination number of the catalytic base can be viewed as a crude estimate of the microenvironment pKa modulation, a feature that becomes of particular interest in general acid-base catalysis. Both, structural integrity and solvent accessibility are directly linked to the degree to which active site contacts deviate from the ideal QM theozyme geometry. Thus, only cases for which the designed catalytic contacts are maintained at hydrogen bonding geometries pass the MD filter and move on to the experimental stage.

Major design flaws were noticeable early in the simulations, and 20 ns trajectories turned out to suffice for the purpose of distinguishing active from inactive designs in 20 of the 23 cases. Of the 14 active proteins, only two of the least active three were categorized as inactive. This highlights that the MD ranking approach is not failsafe in borderline cases with low activity, but robust otherwise: all of the most active designs as well as eight out of nine inactive designs were identified correctly. Applied to a dataset of 120 designs, the MD-based procedure would produce an approximate enrichment factor (EF) of 4.3 [EF = (a/n)/(A/N), where a = 12 (14 active designs – 2 false negatives), n = 24 (12 active designs + (120-14)*(1/9) false positives), A = 14 (active designs), and N = 120 (total number of designs)]. Put another way, only 24 instead of 120 designs would have needed to be tested experimentally to obtain the same active designs as in the 2008 Roethlisberger study.

Underlying problems in the structure and dynamics that may lead to inactivity (KE38) or limited activity (KE70, but also KE59 and KE07 as part of the SI) were discussed for selected designs and contrasted to the naturally evolved cathepsin K and the catalytic antibody 34E4. MD shows that even the most active Kemp eliminases have considerable geometric deficiencies compared to naturally evolved enzymes, which suggests that there is much room for improvement. These observations are relevant to enzyme design and redesign endeavors that build on the charge-relay of catalytic triads and on acid-base catalysis in general.

The MD-based assessment of final designs has become an integral part of the inside-out protocol. Currently its utility is twofold: (a) MD is being used as a final computational filter to discern active from inactive designs just prior to the experimental stage and (b) MD proved useful for the rational refinement of active designs during the experimental stage. The latter, MD-based refinement approach has been effectively employed in the recent design of enzymes that promote a bimolecular Diels-Alder reaction.⁴⁷ Here, the applicability of the methodology was established after initial blind tests. Similarly, we encourage this practice when applying the MD-based assessment to other reactions.

Methods

Computational details

The computational Kemp elimination designs were generated with RosettaDesign, as discussed in Ref.13 stational Kemp elimination were used as starting structures. The structures of the catalytic antibody 34E4 (1Y0L⁴⁸) and cathepsin K (1AYU⁴⁴) were downloaded from the RCSB. Co-crystallized water molecules and ions were removed. The four evolved variants of KE07 were constructed with RosettaDesign from the KE07 wt, applying the mutations that were published in Ref.13. The substrate molecule was docked into each active site with RosettaDock. QM, QM/QM,′ and QM/MM calculations were used to map out the reaction coordinate of individual designs as is described in the results section.

MD simulations were performed on the enzyme: substrate complexes to assess the viability of the designed active site arrangements. Substrate parameters were generated with the antechamber module of AMBER 10.⁴⁹ Each structure was immersed in a truncated octahedral box of explicit water molecules. The systems were neutralized by addition of explicit counter ions. A two stage geometry optimization approach was utilized, initially minimizing the positions of water molecules and ions, followed by an unrestrained minimization of all atoms. The systems were heated gently from 0 to 300K at constant volume periodic boundary conditions. Each system was then equilibrated for 2 ns at a constant pressure of 1 atm. A 20 ns production MD simulation was performed for each of the systems (with and without the substrate bound to the active site). Post-MD data-extraction and analysis was performed using the ptraj module of AMBER 10 and the statistical analysis software OriginPro8 (Origin, OriginLab, Northampton, MA). A more detailed description of the MD protocol is available as part of the Supporting Information.

Experimental details: Protein expression and purification, initial activity screen, and kinetic measurements

The inactive designs discussed here have not been previously published, but were generated, screened, and characterized through the same protocol as is outlined in Ref.13. A detailed description is available as part of the Supporting Information.

Glossary

Abbreviations:

CM

cluster model

DFT

density functional theory

k_cat

first-order rate constant (s⁻¹) of the catalyzed reaction

k_uncat

first-order rate constant (s⁻¹) of the uncatalyzed reaction

KE#

Kemp elimination design #

MD

molecular dynamics

MM

molecular mechanics

ONIOM

Morokuma's “our own n-layered integrated molecular orbital and molecular mechanics”

QM

quantum mechanics

RMSD

root mean square displacement