The effect of metric selection on the analysis of diffusion tensor MRI data

Abstract

The measurement of the distance between diffusion tensors is the foundation on which any subsequent analysis or processing of these quantities, such as registration, regularization, interpolation, or statistical inference is based. In recent years a family of Riemannian tensor metrics based on geometric considerations has been introduced for this purpose. In this work we examine the properties one would use to select metrics for diffusion tensors, diffusion coefficients, and diffusion weighted MR image data. We show that empirical evidence supports the use of a Euclidean metric for diffusion tensors, based upon Monte Carlo simulations. Our findings suggest that affine-invariance is not a desirable property for a diffusion tensor metric because it leads to substantial biases in tensor data. Rather, the relationship between distribution and distance is suggested as a novel criterion for metric selection.

1. Introduction

The unique microstructural geometric information provided by Diffusion Tensor MRI (DTI) (Basser et al., 1994) has made it a widely used research and clinical tool (Basser and Jones, 2002; Assaf and Pasternak, 2008). At this point in the development of DTI a statistical framework is needed to characterize tensor variability, permitting group comparisons and statistical inferences based on the entire tensor. Such a tensor-variate statistical framework would subsume univariate statistical distributions for scalar (tensor-derived) quantities, such as the fractional anisotropy (FA), Trace, or the apparent diffusion coefficient (ADC), which can only account for a portion of the variability. In addition, tensor processing tools are constantly being developed for tasks such as artifact correction, noise removal, segmentation, and image transformations (Lenglet et al., 2009). The literature of recent years reflects these developments, supplying numerous options for tensor manipulations and analysis (e.g. Weickert and Hagen, 2006, and references therein).

A prerequisite for most, if not all, tensor analysis methods is the ability to compare tensors and, hence, to define the distance between them. The general notion of distance involves a connected Riemannian manifold (Eisenhart, 1940). The manifold includes the set of all points in the space and a metric, G(x) = {g_{i j}(x)}, defines the infinitesimal distance: ds² = dx^T G(x)dx, where x is the coordinate of a point on the manifold for a chosen coordinate system. Any positive-definite and symmetric metric is admissible. The distance function is defined as the geodesic, i.e., the shortest path on the manifold.

To define the geometric distance between tensors, a metric and a local coordinate system for tensor representation are chosen. Therefore, if more than one metric is admissible, selecting among them and determining which coordinate-metric combination would best characterize the distance between tensors, are challenging issues. For these tasks, we need additional information and constraints, derived by empirical observation or physical considerations relating to the system under study.

A tensor-variate statistical framework for diffusion tensors was proposed in Basser and Pajevic (2003), placing diffusion tensors on a Euclidean manifold, with a constant metric, G(x) = I, resulting in ds² = tr((dD)^T dD), where D is the tensor coordinates in the canonical tensor coordinate system, and tr denotes the matrix Trace. The geodesic between any two tensors, D₁ and D₂, with this metric, is simply a straight line, or the Euclidean distance

$${\mathit{Dist}}_{\mathit{Euc}}(D_1,D_2)=\left|\right|D_1-D_2\left|\right|,$$ (1)

where ||·|| denotes the Frobenius norm. The Euclidean metric is defined over the entire space of symmetric matrices and is rotation invariant, which makes it invariant for the selection of orthogonal coordinates, but not for the selection of non orthogonal tensor coordinate systems.

In another framework the distance function is restricted to affine-invariance (which includes rotation, scale, shear, and inversion invariance), and operates only on tensors belonging to the space of positive definite symmetric matrices, S⁺ (Batchelor et al., 2005; Pennec, 2006a; Moakher, 2006; Lenglet et al., 2006; Fletcher and Joshi, 2007; Gur et al., 2009). The Affine-invariant metric (Pennec, 2006a), a Reimannian metric that satisfies these requirements, has an infinitesimal distance ds² = tr((D⁻¹dD)²) (Maaβ, 1971). This distance is affine-invariant and therefore does not depend on the choice of tensor coordinate system (see Appendix A). The corresponding geodesic is found by integration (Maaβ, 1971):

$${\mathit{Dist}}_{\mathit{Aff}}(D_1,D_2)=\sqrt{tr\left({\mathit{log}}^2(D_1^{-1}{D}_2)\right)}.$$ (2)

The matrix logarithm, log(D), is defined in Appendix B. The Affine-invariant metric has led to the development of a family of Reimannian metrics (Pennec, 2006b) and to the development of Reimannian statistical frameworks for tensors (Pennec, 2006a; Lenglet et al., 2006).

The Affine-invariant metric was proposed as the natural metric for diffusion tensors, since, in theory, diffusion tensors are positive semi-definite and should reside on a symmetric space (Terras, 1988). The Euclidean metric was deemed not appropriate for diffusion tensors, specifically since it admits non positive tensors and exhibits the “swelling effect,” where interpolating two tensors yields a tensor with a determinant larger than either of the original tensors (Batchelor et al., 2005; Arsigny et al., 2006). It was shown that the Affine-invariant metric coincides with the Fisher information metric (Lenglet et al., 2006), and with the Kullback-Leibler divergence (Wang and Vemuri, 2005; Lenglet et al., 2006). In addition, the Log-Euclidean metric with its corresponding geodesic (Arsigny et al., 2006),

$${\mathit{Dist}}_{\mathit{LogEuc}}=\left|\right|\mathit{log}(D_1)-\mathit{log}(D_2)\left|\right|,$$ (3)

was proposed as an efficient approximation for the computationally demanding Affine-invariant metric. Some scientists have since begun adopting the use of the new family of metrics for tensor processing applications (Weldeselassie and Hamarneh, 2007; Malcolm et al., 2007; Commowick et al., 2008).

In this paper we identify the Affine-invariant metric as the appropriate metric for positive physical quantities that are log-normally distributed, and the Euclidean metric appropriate for quantities that are normally distributed. We then examine whether diffusion MRI quantities can be classified as normally or log-normally distributed quantities. In order to investigate the physical meaning and consequences of using the affine-invariance constraint we consider the simpler case of isotropic diffusion, which has many of the same properties and features of the 6D diffusion tensor space. We provide a statistical analysis that estimates the distribution of Monte-Carlo simulated ADCs, and compare the results of applying the Euclidean and Affine-invariant metrics. A similar simulation framework is used to examine diffusion tensors utilizing variability maps obtained for the Log-Euclidean and the Euclidean metrics. The results are then validated using diffusion MRI acquisitions.

2. Theory

In order to select a metric for diffusion quantities we classify their asymptotic distribution by analyzing the properties of the quantity. We then test if the asymptotic distribution is in-line with distributions generated by specific sources of variability in the acquisition of diffusion MRI.

2.1. Reduction to a One-Dimensional Problem

The DTI framework is especially important when dealing with an anisotropic medium, when different ADCs are measured along different orientations (Basser et al., 1994). The diffusion equation dictates that (for a Gaussian displacement distribution) the orientational variability of the ADC be fully described by the diffusion tensor (Crank, 1975). Given that a distance function for diffusion tensors must account for this orientational variability and be applicable for all diffusion tensors, we find it useful to first consider a metric for isotropic tensors. An isotropic tensor describes the case where the diffusivity in all directions is equal. In this case the tensor has three equal eigenvalues:

$$D^{\mathit{iso}}=\lambda I.$$ (4)

The eigenvalue λ describes the entire 3D diffusion process and equals the ADC, d (Basser and Jones, 2002). Equation (4) reduces the parametrization of a diffusion tensor to a scalar, thus the metric required for the special case of isotropic tensors is a metric for scalars. Using equations (2) and (4), the Affine-invariant geodesic for isotropic tensors becomes:

$$\begin{array}{l}{\mathit{Dist}}_{\mathit{Aff}}(D_1^{\mathit{iso}},D_2^{\mathit{iso}})=\sqrt{tr(lo{g}^2({({\lambda }_{1}I)}^{-1}{\lambda }_{2}I))}=\\ =\sqrt{3}\mid \mathit{log}(d_2/d_1)\mid =\sqrt{3}\mid \mathit{log}(d_2)-\mathit{log}(d_1)\mid ,\end{array}$$ (5)

where d₁ and d₂ are the ADCs for the isotropic tensors, $D_1^{\mathit{iso}}$ and $D_2^{\mathit{iso}}$, respectively. This geodesic can also be derived from the metric G(d) = 3/d². We note that for isotropic tensors, the Affine-invariant metric is identical to the Log-Euclidean metric. Similarly, the Euclidean distance between isotropic tensors is simply

$${\mathit{Dist}}_{\mathit{Euc}}(D_1^{\mathit{iso}},D_2^{\mathit{iso}})=\sqrt{3}\mid d_2-d_1\mid ,$$ (6)

which means that the metric, G(d) = 3, is constant.

2.2. The Effect of Distribution on Metric Selection

In order to choose between the metrics we match their properties with properties of the measured diffusion quantities. This procedure is common practice in statistical analysis, where, for example, when attempting to estimate a true value of a measured parameter, one has to account for the expected sources of variability (such as noise or sample heterogeneity) that may cause a distribution in the measurements; if the distance function is appropriate for the distribution then the true value is better estimated (Jeffreys, 1939). When a certain distribution is complicated or unknown, a common practice is to approximate it with a simpler distribution. The normal distribution is the favorite candidate since the central limit theorem (CLT) states that the asymptotic distribution of a variable that is the sum of independent factors (each with its own mean and variance) is normal (Mood et al., 1974). Indeed, many measurable quantities are found to be normally distributed. Another popular approximation assumes that the quantities are log-normally distributed, which unlike the normal distribution, is defined only for positive numbers. The approximation is again backed by the CLT that dictates a log-normal distribution for a variable that is the product of independent factors (Benjamin and Cornell, 1970). Accordingly, many measurable quantities are defined as positive, and the log-normal distribution approximates them well (e.g., Koch, 1966).

Selecting to approximate a distribution with a log-normal or a normal distribution determines which distance function and analysis method better suit the quantity. Let x be a normally distributed random variable, then an appropriate distance between x₁ and x₂, two realizations of x, is the Euclidean distance,

$${\mathit{Dist}}_{\mathit{Euc}}(x_1,x_2)=k\mid x_2-x_1\mid ,$$ (7)

Due to the relative simplicity and ubiquitousness of the normal distribution many analytical and statistical tools have been designed for this distribution. For example, the maximum likelihood estimator (MLE) of the expected value, E[x], is the arithmetic mean,

$${\widehat{\mu }}_{\mathit{arithmetic}}=\frac{1}{n}\sum _{i=1}^n{x}_n.$$ (8)

The log-normal distribution has a convenient property that by taking a log transform it becomes a normal distribution: Let y be a log-normal distributed random variable, then

$$x=\mathit{log}(y/y_0),$$ (9)

where y₀ is any fixed value of y, is a normally distributed random variable. This relationship provides a mechanism for adopting all normal distribution related tools to the log-normal distribution. Specifically, the appropriate distance is the Logarithmic distance,

$${\mathit{Dist}}_{\mathit{Log}}(y_1,y_2)=k\mid \mathit{log}(y_2/y_1)=k\mid \mathit{log}(y_2)-\mathit{log}(y_1)\mid ,$$ (10)

and the MLE for E[y] is the geometric mean,

$${\widehat{\mu }}_{\mathit{geometric}}={\left(\prod _{i=1}^n{y}_i\right)}^{1/n}=\mathit{exp}\left(\frac{1}{n}\sum _{i=1}^n\mathit{log}{y}_i\right).$$ (11)

An important property of the logarithmic distance function (Eq. 10) is that for any α ∈ ℛ, Dist_Log (y₁, y₂) = Dist_Log(αy₁, αy₂), i.e., it is scale invariant.

In this paper we use the term “Jeffreys”, coined by Albert Tarantola in honor of Sir Harold Jeffreys (Tarantola, 2006, 2005), for physical measurable quantities that are more likely to be log-normally distributed, and the term “Cartesian” for quantities that are more likely to be normally distributed. The two quantities are related by the log-transformation in Eq. (9). A comparison of Eq. (10) with Eq. (5), and Eq. (7) with Eq. (6) clearly shows that the difference between the distance functions stems from how the ADC quantity is classified: for a Jeffreys quantity, the Affine-invariant metric is appropriate; for a Cartesian quantity, a Euclidean metric is appropriate. There are two criteria that can help identify a potential Jeffreys quantity: the quantity must be arbitrarily scaled, in which case the scale invariant metric accounts for its physical quality, and the quantity must be positive (Tarantola, 2006, 2005).

2.3. Metric Selection for Diffusion Quantities

Studying the properties of the diffusion weighted (DW) signal helps us determine whether the ADC is a Jeffreys or a Cartesian quantity. The DW signal is obtained by a pulsed-field gradient (PFG) MR experiment that makes the MR signal sensitive to the displacement of water molecules along a certain orientation (Stejskal, 1965). The DW signal is the magnitude of a complex quantity so it is always positive, limited by the highest integer value allowed. We expect the signal to carry information regarding diffusion, but the intensity of the signal is known to be proportional to the quantity of molecules (Carr and Purcell, 1954). The exact ratio is determined by various machine and MR-dependent parameters (Hahn, 1950). For instance, a completely homogenous object scanned with a range of voxel sizes, on different MRI scanners (with different static magnetic fields and gradient strengths) and different pulse timings will yield a variety of signal intensities that clearly does not imply any physical qualities of the object itself, and its diffusion properties, which remain the same. The DW signal is therefore positive and scale sensitive, which makes it a Jeffreys quantity.

As a Jeffreys quantity, the DW signal has a related Cartesian quantity, which we can find using Eq. (9): we set the non-DW signal, S₀, as the origin, and compare any other signals obtained, S_i, by taking their logarithms:

$$x=\mathit{log}(S_i/S_0).$$ (12)

Interestingly Eq. (12) is known to be proportional to the ADC (up to the scale factor b) (Stejskal, 1965):

$$d=-b^{-1}\mathit{log}(S_i/S_0).$$ (13)

This means that d, the ADC, is the Cartesian quantity associated with measured DW signals.

The diffusion tensor is a generalization of the ADC to a higher dimensional space (Torrey, 1956): its eigenvalues are the ADCs along the principal axis (Basser et al., 1994). Since the eigenvalues of the diffusion tensor are Cartesian quantities, a scale invariant metric is not appropriate¹ as shown above in the case of isotropic tensors. Hence, affine invariance, which encompasses scale invariance, is not a desirable property either. An appropriate metric for diffusion tensors is the one in Eq. (1), associated with a Euclidean metric.

2.4. The Relationship between MR Variability Sources and Distance

The result above suggests that given the type of measurement, the accumulative effect of sources of variability on the DWIs is expected to be log-normally distributed, while the accumulative effect of the sources of variability of the ADCs is expected to be normally distributed. Therefore, the Euclidean metric is appropriate for ADC and diffusion tensor distance functions. In practice the distribution of the diffusion quantities estimates is affected by a number of variability sources, each with its own statistical distribution. In the next section we cover known sources of variability in diffusion measurements and check whether they are in line with the theoretic prediction of an asymptotic distribution.

2.4.1. Stochastic variability

Self-diffusion is a stochastic process, where molecules are free to move in any direction. While predicting the motion of a single molecule is not possible, statistics can help us predict the motion of an ensemble of molecules that all have the same intrinsic diffusion coefficient. The Einstein equation for free diffusion caused by Brownian motion establishes the fundamental defining relationship between the diffusion coefficient and the mean-squared displacement along an axis (Einstein, 1926)

$${\sigma }^2(t)=\text{E}[{(x_t-x_0)}^2]=2dt.$$ (14)

The position along the axis at time t is x_t; x₀ is the position at the origin. This relationship defines the diffusion coefficient, d, as proportional to the variance of particle displacements, σ²(t), at time t, and arises from the normal distribution of particles expected for Brownian motion, x_t ~ N(x₀, σ²(t)). The stochastic process dictates the distribution of the estimated diffusion coefficient

$$\stackrel{\sim }{d}\sim \frac{{\sigma }^2(t)}{2tn}{\chi }_n^2=\frac{2dt}{2tn}{\chi }_n^2=\frac{d}{n}{\chi }_n^2,$$ (15)

and its variance

$$\mathit{Var}(\widehat{d})=\frac{2d^2}{n},$$

where ${\chi }_k^2$ is the chi-square distribution with k degrees of freedom. The derivation of Eq. (15) is given in Appendix C. The distribution in Eq. (15) suggests that variability in the measurement of diffusion coefficients originates from the stochastic nature of the experiment itself, even when other sources of variability such as measurement errors and artifacts are neglected. The same argument holds for diffusion tensors. In that case the displacement x − x₀ is a vector in ℛ³, and the χ-squared distribution is generalized by the Wishart distribution (Jian et al., 2007).

In the MR diffusion experiment a typical voxel contains a very large number of molecules on the order of n = 10¹⁷². Each molecule follows an identical normal probability distribution, and the displacement of one molecule is assumed independent of the other. This means that for all practical considerations we can assume n → ∞. According to the central limit theorem, the chi-square distribution asymptotically becomes a normal distribution, i.e., ${\chi }_n^2\to N(n,2n)$ and therefore, the distribution of the estimated ADC, given in Eq. (15), can be approximated as

$$\stackrel{\sim }{d}\sim \frac{d}{n}N(n,2n)=N(d,\frac{2d^2}{n}).$$ (16)

As a result, the estimate of the diffusion coefficient from a large number of displacement measurements is normally distributed around the real diffusion coefficient, d, with a variance that is inversely proportionally to n. This distribution exists even in a completely noise-free environment. However the large n in realistic MR experiments dictates that this source of variability vanishes.

2.4.2. Variability caused by Johnson noise

In addition to the stochastic nature of the ADC, its estimation from diffusion NMR is affected by noise and other artifacts. Even assuming a static magnetic field, a static measured object, and no hardware or sequence artifacts, the complex RF measurement contains Johnson noise. This noise is realized as a Rician distribution in the magnitude images (Henkelman, 1985), and the effects on DW signals can be modeled using a Monte Carlo simulation (Pierpaoli and Basser, 1996). It is a common practice in MRI to increase the accuracy of the estimation by performing repetitive measurements, under the assumption of a constant true diffusion coefficient over time. As shown in the previous paragraph, this assumption is reasonable given the large number of molecules in each voxel. As a result, a number of realizations of ADCs are obtained that are expected to differ from each other by the acquisition noise (Pajevic and Basser, 2003). Estimation is usually performed by averaging: if the ADCs are Jeffreys quantities, their proper mean is the geometric mean in Eq. (11) and if the ADCs are Cartesian quantities, their proper mean is the arithmetic mean in Eq. (8). Determining whether the normal or log-normal distributions better approximates the ADC distribution will determine which metric is preferable.

2.4.3. Additional sources of variability

Johnson noise can be easily generated and its effects on MRI measurements have been widely investigated (Henkelman, 1985; Jones and Basser, 2004; Koay and Basser, 2006; Andersson, 2008). But in reality, Johnson noise is just a single component among many other types of noise and artifacts, most of which have not been modeled using a parametric distribution. To name a few, there are eddy currents, which depend on the gradient magnitude and direction and specific acquisition sequence used (Rohde et al., 2004); reconstruction artifacts originating from the use of multiple surface coils (Koay and Basser, 2006); and motion artifacts, due to rigid head motion or non-linear cardiac pulsation effects (Skare and Anderson, 2001; Pierpaoli et al., 2003). These sources of variability affect the accuracy of intra-voxel estimations. When estimating cross-voxel (or inter-voxel) quantities for example, in region of interest (ROI) analysis or for spatial manipulations, biological heterogeneity is also a confound. And when comparing cross-subject quantities, a population variability factor is encountered. Differences in hardware, sequences, and even clinical protocols contribute another source of variability. Since the parameterization of all of these sources is extremely hard, and since so many different and independent sources are involved, it is reasonable to approximate the distribution by either the normal or log-normal distributions.

Although it is hard to parameterize, we can still quantify the total effect of noise as the variability which is found within a population that is supposed to be homogeneous. This can be done using designated statistical frameworks (Basser and Pajevic, 2003; Lenglet et al., 2006; Commowick et al., 2008).

3. Methods

A Monte Carlo simulation of Johnson noise is used to create a distribution of noisy DWI, ADC, and diffusion tensors. For the DWIs and ADCs, the distributions are statistically tested for normality and for log-normality, and the bias in the estimation of the sample mean is calculated for the arithmetic mean and geometric mean. For the diffusion tensor distribution a variance map is produced for a dataset that is influenced by generated Johnson noise alone, and for an acquired MRI dataset, which is subject to additional types of acquisition noise and artifacts. The variability maps for the Euclidean and the Log-Euclidean metrics are then compared.

3.1. Monte Carlo DWI and ADC Simulations

The Monte-Carlo experiment simulates a repeated MRI acquisition affected solely by Johnson noise. The experimental design follows one found in Pajevic and Basser (2003): an initial ADC, d̄, b-value (we use b = 1000 s/mm²), and non diffusion-weighted baseline image, S̄₀, are selected. The noise free DWI, S̄, is calculated as S̄ = S̄₀exp(−bd̄). Noise is simulated as a random variable drawn from a normal distribution with zero mean and variance, ${\sigma }_{\mathit{noise}}^2$, and is aded to both real and imaginary channels of the DWIs. The magnitude of both channels is a Rician distributed random variable S ~ Rice(σ_noise, S̄). Similarly S₀ ~ Rice(σ_noise, S̄₀) is the noisy baseline DWI. A set of n noisy S and S₀ couples is generated for a range of baseline values and noise variances. The ADC distribution is generated by calculating d = −log(S/S₀)/b for each S and S₀ couple. The log-normal distribution does not allow non-positive values and therefore a positive ADC, d₊ = exp(L), is estimated by minimizing |S/S₀ − exp(−bexp(L))|. This minimization is the scalar form of the 3D positive definite tensor estimation proposed in Fillard et al. (2007). The solution for this minimization is d₊ = d if d > 0 and d₊ = ε otherwise, where ε is a small positive value.

3.1.1. Hypothesis tests

As demonstrated above, the Euclidean metric is associated with a normal distribution and the arithmetic mean and the Affine-invariant metric family is associated with a log-normal distribution and the geometric mean. In order to assign an adequate metric we test for normality and for log-normality of the DWI and ADC distributions, using the Anderson-Darling (AD) hypothesis test (Anderson and Darling, 1952). The AD test calculates a statistic which is a distance measure between the sorted samples and a commutative distribution function (CDF) of a chosen distribution. In order to calculate the CDF, the AD test estimates the sample mean and sample variance. The test provides a significance level for rejecting a null hypothesis of the type, “The samples were drawn from the distribution X.” This is done by comparing the statistic against critical values that depend on the selected distribution and the sample size. Critical values for the AD test are available for several distributions, including the normal and log-normal distributions (D’Agostino and Stephens, 1986). We chose to use the AD test since it estimates the sample mean and variance, unlike other tests, such as the KolmogorovSmirnov test, that require a prior knowledge of the mean and variance of the underlying distribution (D’Agostino and Stephens, 1986). A procedure for calculating the AD statistic is given in Appendix D.

In order to check whether a distribution is normally distributed, we apply the AD test with the null hypothesis, H₀, that the distribution is normal. In order to check whether a distribution is log-normally distributed we apply the AD test with the null hypothesis, H₀, that the distribution of the log transformed data is normal. This is equivalent to checking whether the initial data is log-normally distributed. In order to check whether ADC are log-normally distributed we apply the log transform on the d₊ distribution. Like any other statistical tests, the AD test results in a decision to reject or not to reject the null hypothesis for a given significance level, α (here α = 0.05). Each hypothesis test was applied on 100 independent Monte-Carlo generated sample sets. The False Discovery Rate (FDR) method is then applied in order to account for the multiple hypothesis test comparisons (Benjamini and Hochberg, 1995). The FDR method modifies the p-value for the given α and dictates how many of the 100 independent hypothesis tests should be rejected.

The results are visualized as surfaces that represent the hypotheses rejection rate at various noise levels and baseline levels, and each surface is calculated for a different sample size (we used 3², 25², 50² and 100² samples), indicating the simulated repetitions. A high rejection rate indicates that there is enough evidence to reject the null hypothesis (i.e., it was rejected in many independent tests).

3.1.2. Bias estimation

For each distribution d̂ and Ŝ_i are estimated either as the arithmetic mean (using equation 8) or as the geometric mean (using equation 11). The deviation of an estimated parameter, x̂, from its original value, x̄, is obtained from the estimated normalized bias, calculated as bias = (E[x̂] − x̄)/x̄ (Pajevic and Basser, 2003).

3.2. Repeated MRI Acquistion

In the MRI experiment a DTI acquisition of a healthy volunteer was repeated 20 times. A 3T MRI scanner (GE-Signa) with 16 channel phased array head coils was used (image reconstruction using GE’s ASSET technology). The images were acquired using a PGSE-EPI sequence with the following parameters: T R/T E of 12000/86.1ms, matrix size of 128X128, Field of view (FOV) of 20cm and slice thickness of 2.5mm. The images were acquired for 6 non-collinear gradient orientations with b-value of 1000 s/mm², and a single non-diffusion-weighted image (b = 0). All 140 DWIs were corrected for head motion using rigid body transformations (SPM2, UCL) relative to the first DWI volume acquired, and the gradient orientations were compensated for the rotation component of the transformation. A segmentation mask was applied on the aligned images to exclude background noise. In addition, voxels where any of the DWIs provided zero signal (due to digitation artifacts) were excluded to prevent artificial bias in the tensor estimation. Diffusion tensors were estimated using a linear fit (Basser and Pierpaoli, 1998) and where negative tensors were found, the Log-Euclidean non-linear tensor fit (Fillard et al., 2007) that assures positive-definite tensors was applied. This tensor fitting procedure is used in order to allow the use of the Log-Euclidean metric which requires positive definite tensors. As a result 20 tensor maps, one for each repetition, were obtained. The tensors were represented using the canonical tensor representation.

A second dataset, acquired on the same scanner with a second volunteer, included 8 repetitions of a DTI sequence with the following parameters: T R/T E of 8500/80.9ms, matrix size of 128X128 and 1.4mm³ voxels. The images were acquired for 15 non-collinear gradient orientations with a b-value of 1000 s/mm², and a single non-diffusion-weighted image (b = 0). The smaller voxel size and shorter TR, compared with the first dataset, yielded noisier images. The analysis of the data was identical to that of the first dataset, resulting in 8 tensor maps, one for each repetition.

3.2.1. Monte-Carlo DTI simulations

A single repetition of the above-mentioned first MRI acquisition was used in order to simulate the effect of Johnson noise on different types of diffusion tensors that appear in brain imaging. Monte-Carlo simulation was again used. Here the positive definite tensors that were estimated for the MRI acquisition were used as the initial tensors. The appropriate noise-free DWIs for the 6 gradient orientations were then calculated as $S_i=S_0\mathit{exp}(-{bg}_i^{T}D{g}_i)$, where g_i is the i^th applied gradient orientation. Noisy replicates for all images were then synthesized, and each noisy realization was fit with a tensor by the Log-Euclidean tensor fit. This procedure resulted in a distribution of tensors for each voxel that simulates acquisition repetition where only Johnson noise affects the variability. We used 20 simulated repetitions to match the MRI acquisition.

3.2.2. Variability maps

Variability was estimated using the 4th-order tensor estimation as proposed in Basser and Pajevic (2003). We use the 6X6 representation, M, of the 4th-order covariance tensor and tr(M) as a measure of the total diffusion tensor variability. In order to obtain M_Euc, each diffusion tensor, D, was vectorized to a 6 element vector, $[D]=(D_{xx},D_{yy},D_{zz},\sqrt{2}{D}_{xy},\sqrt{2}{D}_{yz},\sqrt{2}{D}_{xz})$ (Koay, 2009). The matrix M was then defined as:

$$M_{\mathit{Euc}}=\frac{{\sum }_{i=1}^n([D_i]-[\overline{D}]]{([D_i]-[\overline{D}])}^T}{n-1}.$$ (17)

The mean tensor, D̄, was replaced by the original tensor in the Monte-Carlo simulation experiment, and was estimated as the arithmetic mean for the MRI experiment. In a similar manner, the Log-Euclidean 6X6 representation of the 4th-order tensor can be calculated (Commowick et al., 2008):

$$M_{\mathit{Log}}=\frac{{\sum }_{i=1}^n\left([\mathit{log}(D_i)]-[\mathit{log}(\overline{D})]\right){\left([\mathit{log}(D_i)]-[\mathit{log}(\overline{D})]\right)}^T}{n-1}$$ (18)

In the MRI experiment, D̄ was estimated as the geometric mean (Fillard et al., 2007). The sample size, n, is n = 100 for the Monte-Carlo experiment, and n = 8 for the MRI experiment. Finally the quantity that summarizes the variability is tr(M), which is calculated for each voxel.

4. Results

4.1. DWI Monte-Carlo Simulations

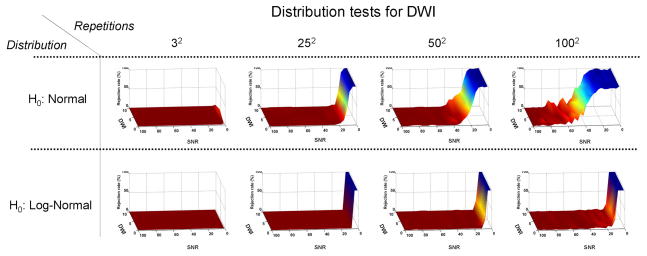
Figure (1) presents the results of the AD tests for normal distribution (top row) and log-normal distribution (bottom row) of the Monte Carlo simulated DWI sample sets. While the DWIs are Rician distributed, the AD test results suggest that their distribution can be safely approximated by both normal and log-normal distributions: for a low number of repetitions there is not enough evidence to reject either the normal or the log-normal distribution hypothesis; as the number of repetitions increases, there is enough evidence to reject both the normal and log-normal hypotheses only for low SNR levels. It seems that the baseline level of S₀ does not affect the tests and that the normal distribution assumption is rejected for a lower number of repetitions than for the log-normal distribution.

Figure 1.

Monte Carlo simulation of noisy DW signal resulting in a distribution of DWI values. The surfaces represent the result of the Anderson-Darling (AD) hypothesis tests for normal (top row) and log-normal (bottom row) distributions, for various numbers of repetitions. As the height of the plane increases, there is more confidence in the rejection of the hypothesis. Both the normal and log-normal distribution hypotheses can only be rejected for a large number of repetitions and low SNR.

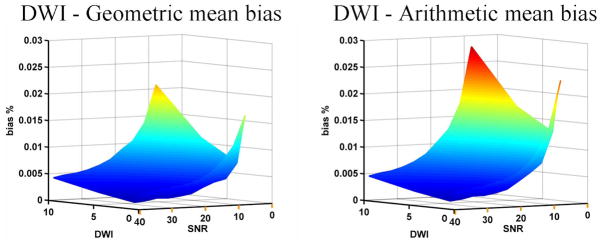
Figure (2) shows the bias of the arithmetic (right) and geometric (left) mean DWI estimation. The two cases show a similar dependence on SNR and baseline value, yet log-normal distribution consistently better approximates the true distribution, yielding slightly less bias in the estimation of the geometric mean relative to the arithmetic mean. This result supports the theoretic finding that the scale invariant metric is more appropriate for DWIs.

Figure 2.

Bias estimation. The surfaces represent the bias in the estimation of the arithmetic (right) and geometric (left) mean DWI, compared with the initial noise-free DWI value. The shape of both surfaces is similar, yet the bias of the geometric mean is consistently lower.

4.2. ADC Monte-Carlo Simulations

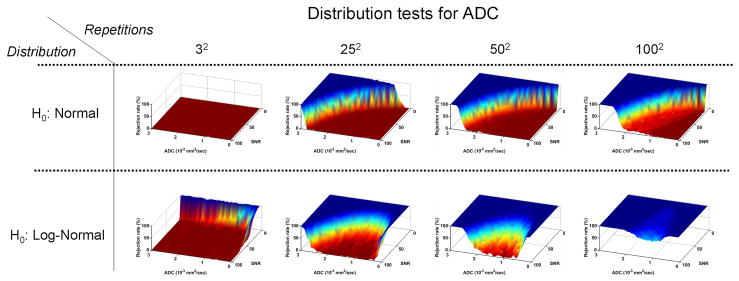
Figure (3) presents the results of the AD tests for normal (top row) and log-normal (bottom row) distributions applied to the ADC sample sets. The results in this figure are in line with the expectation that the ADC will be normally distributed, due to its log relation with the log-normal distributed DWIs: the normal distribution hypothesis cannot be rejected for a small number of repetitions. As the number of repetitions increases, the hypothesis is rejected for increasing ADC values and decreasing SNR. Yet even for a large number of repetitions the normal distribution hypothesis cannot be rejected for a wide range of ADC and SNR values. The log-normal distribution hypothesis is rejected for small values of ADC or for low SNR values, even for a small number of repetitions. Similar to the normal distribution, as the number of repetitions increases, the hypothesis is rejected both for increasing ADC and decreasing SNR, but unlike the normal distribution, the hypothesis is rejected for low ADCs as well. As a result the log-normal distribution is admissible only in a small region around ADC = 1 · 10⁻³mm²/sec and high SNR. In general the rejection rate as a function of the repetition number rises much faster than that of the normal distribution test.

Figure 3.

Monte Carlo simulation of noisy ADCs. The top row presents the results of the AD test for normal distribution. The bottom row shows the results for testing log-normal distribution. The ADC distribution is consistently better approximated by the normal distribution. Distribution around small ADC values are rejected for being log-normal even for a low number of repetitions.

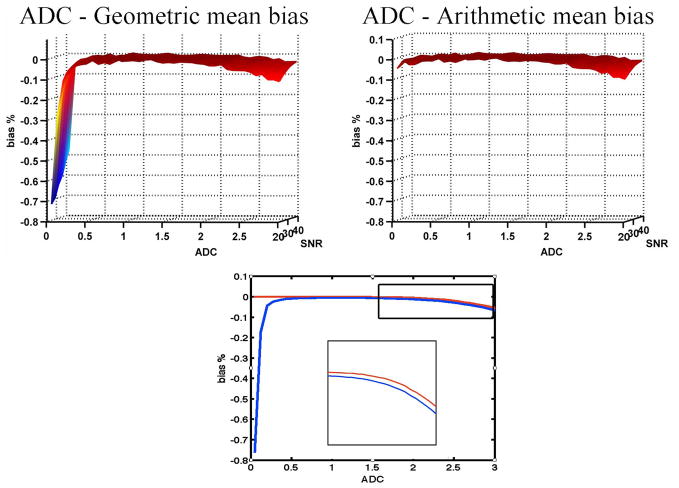
Figure (4) shows the bias of the estimated arithmetic (right) and geometric (left) mean ADC. While the biased behavior seems similar for increasing ADC values, the geometric mean is consistently more biased than the arithmetic mean. In addition the geometric mean is extremely biased for low ADC values, while being very small for the arithmetic mean. This found bias predicts that the most effect of metric selection is in the range of low ADC values.

Figure 4.

The bias estimations for the arithmetic mean (right) and geometric mean (left) of the ADC distributions, compared to the initial noise free ADC value. The geometric mean has an extreme bias for low ADC values. Otherwise, the shapes are similar. The plots for both geometric and arithmetic means for a representative SNR level (SNR=30) (bottom) show that the geometric mean is consistently less biased than the arithmetic mean. The inset shows a rescaled portion of the higher ADC part of the graph.

4.3. DTI Monte Carlo Variability Simulations

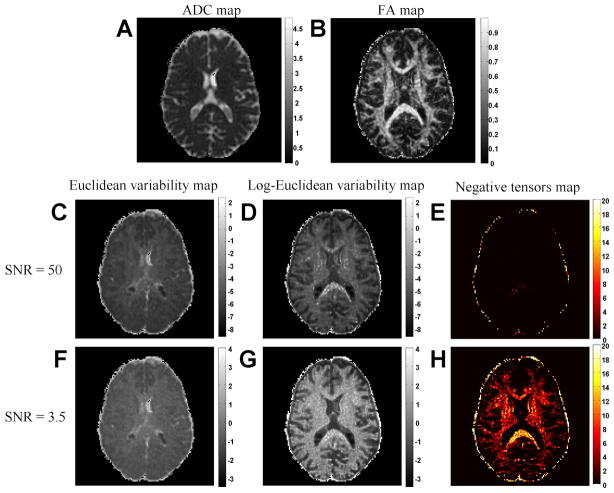
Figures (5A–B) show the ADC and FA maps of a single repetition of the MRI experiment. The tensors are all positive, hence FA is never larger than 1. This set of tensors was used to generate datasets of 20 noisy replicates using the DTI Monte-Carlo simulation described above. There were 5 different datasets, with increasingly higher noise standard deviation (S NR = 50, 20, 15, 7 and 3.5) and Figure (5) presents the Euclidean and Log-Eculidean variability maps for the datasets with S NR = 3.5 and S NR = 50. The variability maps are shown with a logarithmic gray scale value, and each pair of images has the same dynamic range (adapted to minimal and maximal values in the images). The mean intensity and correlation coeffcient with the FA and ADC maps for all of the datasets are given in Table 1.

Figure 5.

Variability maps for Monte Carlo simulation. The ADC and FA maps compared to the Euclidean metric (C,F) and Log-Euclidean metric (D,G) variability maps for two levels of SNR. The variability maps are rendered with a logarithmic dynamic range; the colorbar represents the exponents. The simulation yielded a map similar to the ADC for the Euclidean metric and similar to the FA for the Log-Euclidean metric. Maps of negative tensors (E,H) that were encountered in the linear fit show a drastic increase with noise, yet the overestimation of the Log-Euclidean metric in white matter voxels appears even when a small number of negative tensors is encountered.

Table 1.

Correlation coefficient values for the Euclidean and Log-Euclidean synthetic data variability maps with the ADC and the FA maps for various SNR levels. The correlation is calculated against the log-intensity of the variability maps. The mean log-intensity over the entire image is given as well. As SNR decreases the mean log-intensity for both maps, the correlation of the Euclidean map with ADC, and the correlation of the Log-Euclidean map with FA increase.

	SNR	Correlation - ADC	Correlation - FA	Mean log-intensity
Euclidean map	50	0.4879	0.3515	−5.3346
	20	0.5053	0.3503	−3.6856
	15	0.5146	0.3473	−3.0129
	7	0.5297	0.3269	−1.7651
	3.5	0.5745	0.2723	−0.7016
Log Euclidean map	50	−0.2839	0.7736	−5.2012
	20	−0.3233	0.7986	−3.5278
	15	−0.3466	0.808	−2.8174
	7	−0.4126	0.812	−1.4076
	3.5	−0.4854	0.7653	0.0369

As expected, both the Euclidean (Figures 5C,F) and Log-Euclidean variability maps (Figures 5D,G) show over all higher variability as the noise increases (see Table 1 for the mean intensity values of all datasets). The Euclidean variability map is similar to the ADC map for all repetitions (correlation coefficients can be found in Table 1): the highest variability is observed in the CSF; in brain tissue voxels, the variability is relatively lower and indifferent to tissue type. The level of similarity remains the same through the different noise levels. The dependency of the variability map on ADC values is expected since, although the noise absolute level is homogenous, the baseline signal of a DWI depends on the ADC (lower signal in higher ADC voxels such as CSF voxels). As a result higher ADC voxels are expected to have lower SNR and higher variability. Although the noise added dictates dependency on ADC, the Log-Euclidean variability map is inversely proportional to an ADC map, with decreasing similarity as noise increases (see Table 1 for correlation coefficients). In contrast, the Log-Euclidean maps show higher variability in white matter voxels compared with the Euclidean map and resemble an FA map.

Figures 5(E,H) show the number of negative tensors that were found in the linear tensor fit. Negative tensors appear even for high SNR, and their number increases considerably as SNR decreases. Most of the negative tensors are found in white matter structures or next to the skull.

4.4. Repeated MRI measurements

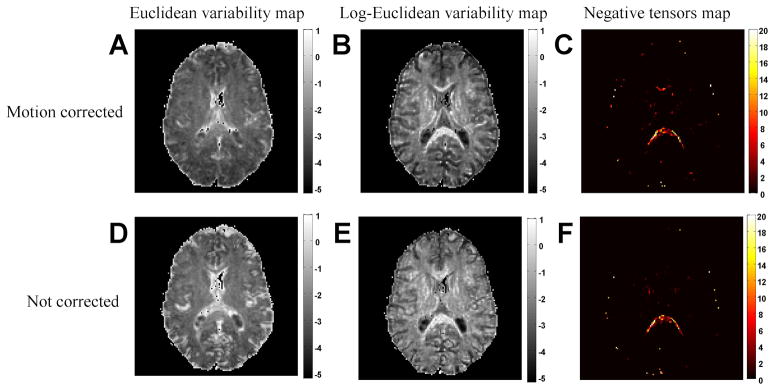
Figure (6A) shows the variability map for the 20 DTI acquisition repetitions that were calculated using the Euclidean metric, and Figure (6B) shows the Log-Euclidean variability map for the same repeated tensor experiment. Overall, the maps are similar to the synthetic maps, suggesting that there were no significant artifacts in this experiment. A small additional high valued variability score can be found, especially around the center of the image. These could be due to pulsation or image reconstruction artifacts. Figures (6D,E) show the variability maps constructed for the same datasets without correcting for motion. Hence, an additional motion related variability is expected to be encountered. Indeed, the maps show increased variability due to motion induced partial volume artifacts. Interestingly, the effect on the Euclidean map is mostly around CSF boundaries, while the effect on the Log-Euclidean map is all around the image, mostly in white matter boundries. There was not a significant change in the number of negative tensors before and after motion correction Figures (6C,F).

Figure 6.

Variability maps for repeated acquisition. The Euclidean metric (A) and Log-Euclidean metric (B) still resemble an ADC and an FA map accordingly. A small additional noise element can be observed. When canceling motion correction the variability increases yet the Euclidean variability (D) is increased mainly around CSF areas, and the Log-Euclidean variability (E) is increased in white matter voxels. The number of negative tensors remains similar (C,F).

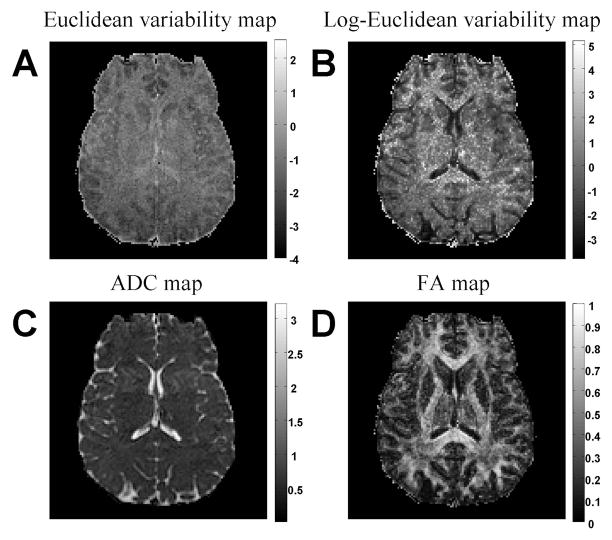
This result presents the utility of the variability maps to explore the effect of various analysis methods or noise sources. Here, comparing the figures before and after motion correction demonstrates that the Log-Euclidean metric is more sensitive than the Euclidean metric to partial volume effects in white matter voxels. An additional comparison is given in Figure (7), which shows the Eulidean and Log-Euclidean maps calculated for a higher resolution, noisier, 8 repetition data. Due to the increased resolution, we expect additional noise components (such as pulsation artifacts) to introduce additional variability. This is indeed the case in the Euclidean map (Figure 7A), where, in addition to the baseline SNR, we can now see increased variability in a space-dependent pattern. The additional noise is mainly in the center of the image, and the image is less similar to the ADC image (Figure 7C). This could be the effect of pulsation, motion, or multiple channel reconstruction, which are all space dependent. The additional noise component is less visible in the Log-Euclidean variability map (Figure 7B), which still resembles an FA map (Figure 7D) suggesting that the overestimation of variability in anisotropic tensors is much bigger than the sources of real variability in the MRI experiment.

Figure 7.

Variability maps for noisier data. The Euclidean metric (A) and Log-Euclidean metric (B) variability maps of a noisy 8 repetition experiment are compared with an ADC (C) and FA (D) maps. The additional noise components are visible in the Euclidean map, but are less visible in the Log-Euclidean map. This suggests that the overestimation of variability in anisotropic tensors is much bigger than the sources of real variability in the MRI experiment.

5. Discussion

Both the theoretic analysis and the experimental results support the claim that a Euclidean metric is more appropriate than an affine-invariant metric for the analysis of diffusion coefficients and tensors.

5.1. The Relationship between Distribution and a Metric

ADCs are found to be Cartesian quantities, which means that they are expected to have a normal distribution that coincides with the Euclidean metric. This expectance is verified by the Monte-Carlo simulations (Figure 3,4) that show ADCs better approximated by normal distribution. In contrast, the log-normal distribution that coincides with a scale invariant metric was found an inappropriate approximation for a wide range of ADCs, and especially for lower values, yielding extreme bias in analysis such as average estimation. Finally, the variability maps that were generated with a Euclidean metric correspond to the type of noise expected, both in the synthetic (Figure 5C,F) and real DTI experiments (Figure 6A, 7A). This is while the Log-Euclidean metric provided variability maps correlated with the tensors shape (ratio between eigenvalues), reflecting the noise properties less.

Finding ADCs to be better approximated by a normal distribution reasserts the empirical findings in Pajevic and Basser (2003) where it was found that the diffusion tensor elements are normally distributed for the SNR range > 2. Given the predicted relationship between the log-normal distributed DWIs and the normal distributed ADCs we can review the connection between the signal and the Trace of the diffusion tensor in Basser and Jones (2002), where it was proved that

$${\left(\prod _{i=1}^n{S}_i\right)}^{1/n}=S_0{e}^{-\beta tr(D)}$$ (19)

for a scaler β. This equation is not restricted to isotropic tensors, and the signal intensities can be obtained using a “balanced” High Angular Resolution Diffusion Imaging (HARDI) acquisition. Taking the logarithm of both sides of Eq. (19) it is clear that the arithmetic average of the log of the DW signals is proportional to tr(D), which is a linear combination of elements of the diffusion tensor (Basser and Pierpaoli, 1998). Based on our findings we can also review Eq. (13), which is by far the most common way diffusion is related to DWIs, and deduce that this is an optimized fitting procedure for DWIs when the distribution of noise is not known. This relationship was originally derived in Stejskal (1965) by fitting a slope acquired in multiple experimental results, without estimating noise distributions. We can also conclude that if the distribution is known, there should be other fitting procedures that account for the exact distribution. We note however, that the Rician distribution may be a good approximation for the distribution only when Johnson noise is the main noise component. Our results (Figures 6D and 7A) suggest that this may not always be the case, especially for in-vivo imaging.

The statistical approach and distribution investigations in the context of metric selection are introduced here as a novel comparison tool. Previous papers (e.g., Arsigny et al., 2006; Fillard et al., 2007) compared the metrics indirectly through the results obtained by a chosen analysis method (e.g., segmentation, interpolation, regularization). An indirect quantitative comparison of the metrics is questionable due to two factors: 1) Usually in tissue samples, there is no ground truth, making the quantification of goodness-of-fit hard. 2) Processing methods usually include inherent factors, which are calibrated for given types of data; metric selection affects the calibration of such factors, and thus, even if synthetic ground truth is available, applying identical frameworks is useless, since each framework may have different inherent factors that optimize its performances. The distribution investigation and variability estimations that we presented here try to circumvent the comparison by applications such as regularization or segmentation. We expect that the tools we introduced here may also be used to investigate the effect of other analysis choices, such as fitting procedures, image correction schemes, and tensor coordinate system selections.

5.2. The Relevancy of an Affine Invariant Metric

The ADC distribution around values of 1 · 10⁻³mm²/sec, which is found to be close to both normal and log-normal distributions (Figure 3), suggests that for many brain tissues, the selection of a metric will have a small effect on any analysis. Indeed, close observation of previous papers that present Affine-invariant or Log-Euclidean approaches versus Euclidean approaches (Arsigny et al., 2006; Fillard et al., 2007) show that most differences are found either in CSF (high ADC) or in very anisotropic white matter (low ADC perpendicular to the fiber).

The simulations predict that using the different metrics mainly affects the analysis of extreme (either low or high) ADC values (Figure 3). The greatest effect of the Affine-invariant metric is predicted near small ADC values. The bias in low ADC values (Figure 4) manifests again in the high FA tensor case, where one of the orientations has a low ADC value. Indeed the Log-Euclidean variability maps consistently estimate extreme variability values in white matter voxels. The overestimation is the consequence of the two constraints imposed by affine-invariant metrics: positiveness and scale invariance, and poses an obstacle in the utility of these metrics to the analysis of brains.

5.2.1. The positiveness constraint

Positiveness is imposed by the Affine-invariant metric. Indeed, the ADC as a physical quantity is non-negative. However, noise, systematic artifacts, or even insufficient experimental designs can result in ADC measurements with negative values, i.e., S_i > S₀. Moreover, the value of a zero ADC, while hard to achieve physically, is still admissible. It means that on average, a particle does not move from its original position during any finite diffusion time. However, an ADC < 0 causes the distance (5) to be undefined and an ADC of zero causes it to diverge. In our experiments here negative eigenvalues appear in all noise levels, their number increases as noise increases, and they appear to be concentrated on specific locations. Within the brain higher FA voxels (white matter) show more tendency to fit negative tensors.

In a single measurement, correcting a negative diffusivity with a small positive value (as recommended by the Log-Euclidean fit) will yield an ADC closer to the real, assumed positive, value. However, when performing repeated measurements or applying a statistical framework we expect that the noise component, which may cause negative values in a single experiment, will cancel out in the averaging. This is indeed the case when the noise is Rician and the Euclidean related arithmetic mean is used. But, using the geometric mean introduces bias (Figure 4), and the ADC as well as the eigenvalues of the diffusion tensor end up being overestimated. A better estimation for diffusion coefficients and tensors may be obtained by incorporating neighborhood information or by outlier analysis that eliminates the measurement that cause negative values (Chang et al., 2005). Such analysis is less affected by metric selection and is beyond the scope of this paper.

The need to correct negative eigenvalues is more a practical need than a mathematical requirement, arising when, for instance, negative eigenvalues cause FA values to be greater than 1 on FA maps. The correction is also useful for tractography methods, which dictate the orientation and size of each step as a function of positive eigenvalues. Positivity may then be considered as a practical requirement and several approaches have been suggested to enforce it (Koay et al., 2006). Positivity may very well be a desired property for ADCs or diffusion tensors, yet, probably not at the cost of assuming affine invariance. The Affine-invariant metric family is the only one that maintains affine invariance, but those are not the only metrics that preserves positiveness. It is interesting to note in this context that due to the maximum principle, the Euclidean metric (a.k.a. Frobenius norm), applied on positive-definite tensors, will remain in the positive-definite domain (Welk et al., 2007) and has been found useful for many tensor processing techniques, including regularization (Weickert and Hagen, 2006).

5.2.2. Affine invariance

Comparing the variability maps with the negative tensors maps (Figures 5, 6) shows that negative tensors increase the variability in Log-Euclidean maps, yet overestimation is also found in voxels where negative tensors were not encountered. The overestimation is the result of the Affine-invariant metric property that maps small ADCs or high FA tensors to infinity, thus artifactually increasing their distance from other tensors. It is interesting to review the way an Affine-invariant metric was derived by Maaβ (Maaβ, 1971). In his study of rotation tensors, Maaβ came up with the metric in Eq. (2) since he wanted the operator for those tensors to be affine-invariant. In order to calculate geodesics with this metric a second assumption of positive definiteness was introduced. This requirement was appropriate since proper rotation tensors are positive. In the application of the Affine-invariant metric to diffusion tensors the motivation was to preserve the positiveness of these tensors and once the metric was chosen, affine-invariance resulted as a consequence. Based on our findings, it is our claim that affine-invariance is not a desirable property for diffusion tensor analysis. Affine-invariance would be desired for a quantity that has an arbitrary scale (such as DWIs), yet ADCs have a physical scale related through the Einstein equation in Eq. (14) to the physical displacement molecules traverse during the experiment (Stejskal, 1965), so preserving their scale is important in a distance measure.

Following the observation that DWIs are better approximated by the log-normal distribution, and since all MRI images have a similar noise model, we predict that affine-invariant (or scale-invariant for the scalar case) metrics will be useful for other MR contrasts analysis, and more so for low SNR modalities (such as fMRI). However, we note that in the noise levels and number of repetitions expected in a realistic DWI experiment, the Monte-Carlo simulation predicts that the normal distribution will be a good approximation as well. A better candidate for a scale invariant metric is the variability measure we proposed here, T race(M), where M is a fourth-order tensor. The variability measure can not be estimated to be negative, and the more informative logarithmic scale dynamic range used here suggests that it is likely to be log-normal distributed. We speculate that a similar statistical analysis to the one performed here could also assert that a proper metric for the forth-order tensor M is indeed affine-invariant. This will put in perspective analysis tools that use Affine-invariant metrics on this kind of tensors (e.g., Ghosh et al., 2008; Barmpoutis et al., 2009).

5.2.3. The effect on statistical inferences

Although statistical frameworks for tensor analysis exist, it is not yet a common practice to use them for statistical inferences in DTI. Whitcher et al. (2007) investigated generalization of scalar statistical tests to tensor statistical tests, and reported on the effect of Euclidean and Log-Euclidean metrics on the statistical tests. The results were consistently in favor of the Euclidean metric, which led the authors to conclude that there is no reason to prefer the Log-Euclidean metric for hypothesis tests. Another application for tensor statistics was suggested by Commowick et al. (2008), where a t-test for tensors was applied. Following the results we show here, we can better understand the consequences of using the Log-Euclidean metric. Most parametric methods are based on the estimation of a variability measure. Here we predict that when using the Log-Euclidean metric the variability will be biased for high FA tensors, i.e., for white matter. As a result, a group which may be initially considered homogeneous (e.g., healthy controls) will show high variability and, as a result, the power and significance of any parametric test will decrease dramatically. Observing the results reported in Commowick et al. (2008), we note that most of the significant results reported are in non-white matter structures, suggesting that the results are partial; considerably more white matter voxels may actually be affected.

To illustrate the effect of the scale invariance constraint on statistical inference we provide the following simple example. Suppose a control experiment where in two given voxels the ADC values obtained were 3 · 10⁻³mm²/sec and 0.2 · 10⁻³mm²/sec. Now suppose that the patient undergoes a treatment followed by a second scan where the same voxels now yield values of 1.5 · 10⁻³mm²/sec and 0.1 · 10⁻³mm²/sec. The first voxel shows a transition from an ADC typical for free water to an ADC typical of white matter, which is most likely to be attributed to the treatment and unlikely to be attributed to Johnson noise. The second voxel originally showed low values, typical of diffusion perpendicular to fibers, and the value was slightly lower following the treatment, a change which could be attributed to noise. We would expect a test to reflect the large change in the first voxel relative to the small change in the second. However, results from tests using a scale-invariant metric would suggest that the same effect caused the changes in both voxels (since the distances are equal).

5.2.4. Swelling effect

Previous studies pointed out that the main effect of selecting the Affine-invariant metric rather than the Euclidean metric is encountered when interpolating or averaging between two anisotropic tensors (Batchelor et al., 2005). The Euclidean metric does not preserve the determinant (which is proportional to the volume of the diffusion ellipsoid described by the tensor) and, as a result, the interpolated tensor may have a determinant larger than the initial tensors, i.e., it may be “swollen.” With the introduction of the Affine-invariant and Log-Euclidean metrics it was shown that the swelling effect is reduced (Arsigny et al., 2006). In practice, the swelling effect is usually obviated by applying piece-wise smoothed operators, or pre-segmentation, that will avoid interpolating initially distant tensors. In theory, it is still interesting to understand why the swelling effect occurs.

The determinant of a tensor represents the volume of an ellipsoid and reflects the shape of the ellipsoid. Elongated ellipsoids have lower determinants than rounded ellipsoids that share the same Trace. We claim that with the absence of prior geometric information (such as the expected anisotropy or orientation), the swelling effect is predicted by the MR measurement, and there is no physical reason to preserve the determinant. Assume two anisotropic tensors, with equal eigenvalues, and orientations that are perpendicular to one another. If we assume that those two tensors were taken in the same experiment (i.e., the same reference frame), then the combined effect of both yields an isotropic displacement profile. Only if we assume that the tensors describe separate experiments and that the variability between the experiments caused the reference frame to rotate, should the interpolation preserve the anisotropy, and hence the determinant of the tensors. This could be the case where we assume that the tensors are taken along the same fiber or across subjects on the same fiber. This additional information is not appropriate for the general case, where we can not assume that the source of variability affects the orientation of the frame of reference, or that the tensors are on the same geometrical structure. In any case, preserving the Trace is desired, since the Trace may be regarded as proportional to the bulk, orientationally-averaged diffusivity. Indeed the Trace is preserved by the Euclidean metric.

5.3. Coordinate Systems for Diffusion Tensors

Once a Euclidean metric is selected, defining the distance function still requires a selection of tensor coordinate system. The Euclidean metric is rotationally invariant, which means that orthogonal basis (such as rotated reference frames) yields the same distance. In our simulations we used the canonical tensor representation, which has a physical significance since it provides estimations of the variance and co-variance of molecule displacement along the image main axis. Other tensor coordinate systems have been proposed for analysis; these include eigen-components (Tschumperlé and Deriche, 2002), rotation angles (Andersson, 2008), Cholesky decomposition (Koay et al., 2006), and Iwasawa decomposition (Gur et al., 2009; Barmpoutis et al., 2009). Some of these choices have clear physical meaning as well. A coordinate system based on DTI measures such as FA and ADC was suggested in Kindlmann et al. (2007). The different coordinate systems are not orthogonal with respect to each other, which means that they yield different distances if using the Euclidean metric. The question of the effect of coordinate system selection on the analysis of diffusion tensor MRI data is reserved for future research.

Common to all metric selections in the Riemannian framework is that they are global, which means that the distance between tensors D₁ and D₂ does not depend on their location in the image or on their association with a certain tissue type or image segment. Our analysis predicts that tissue specific distance functions, where different metrics would apply to different segments, should be useful for DTI analysis because each segment may have its own distribution properties and sources of variation. Analysis methods similar to Isomaps (Verma et al., 2007) may be useful for this cause.

6. Summary

The selection of a distance function is the first step in the analysis of any data, but the selection of a metric cannot be driven by mathematical considerations alone. Practical and physical considerations must be used. In this paper we reexamine the connection between distribution and distance in order to investigate the relevance of the Euclidean and the Affine-invariant metrics for analyzing diffusion MR measurements. Our findings suggest that the Euclidean metric is consistent with the expected statistical properties of tensor distributions and the Affine-invariant metric is not. We show that in most cases the effect of metric selection may be minor, but in certain cases the bias that is introduced by the affine-invariance restriction causes large deviations from the expected values. We therefore do not recommend the use of the Affine-invariant metric or its related metrics for the analysis of diffusion tensors. We predict that the mathematical framework that underpins the use of the Affine-invariant metric should be applied to other types of quantities which are directly related to a measured physical quantity, such as raw MR signal, or for special cases of diffusion measurement, where the sources of variability dictate a log-normal distribution.

A. Affine Invariance

The tangent space at every point on the manifold of symmetric positive definite 3 × 3 matrices, Y ∈ P₃, may be identified with the vector space of 3 × 3 symmetric matrices, SYM₃. Thus, the Riemannian metric at the point Y is defined in terms of the scalar product on SYM₃ as Lang (1999)

$${ds}^2=tr({(Y^{-1}dY)}^2),$$ (20)

This metric is by definition positive-definite (see Lang (1999); Terras (1988)). Define the action of g ∈ GL(3) (any 3 × 3 invertible matrix) on Y ∈ P_n as Y[g] = g^T Yg. The metric is invariant under the action of GL(3): Let W = Y[g] where the differential is given by dW = dY[g]. Then, upon plugging everything in ds² it follows that

$$\begin{array}{l}{ds}^2=tr({(Y^{-1}dY)}^2)=tr({(g{W}^{-1}{g}^T{g}^{-T}dW{g}^{-1})}^2)\\ =tr({(W^{-1}dW)}^2).\end{array}$$ (21)

Being GL(3) invariant, the metric does not depend on the selection of coordinate system. This is since translation between local coordinate systems is linear. Similarly the metric is invariant with respect to the inversion map Y ↦ Y⁻¹, which makes it affine-invariant.

B. The Matrix Logarithm

The matrix logarithm operator, log(D), for a symmetric 3 × 3 matrix, D, is defined as:

$$\mathit{log}(D)=R\left(\begin{array}{ccc}\mathit{log}(a_1)& & \\ & \mathit{log}(a_2)& \\ & & \mathit{log}(a_3)\end{array}\right)R^T.$$ (22)

The entries a_i compose a diagonal matrix, A, that together with a rotation matrix, R, forms the eigen-decomposition, D = RAR^T.

C. The Distribution of Stochastic Estimated ADC

We assume normal distribution of particle displacements, x_t ~ N(x₀, σ²(t)). The probability of measuring a certain displacement R = (x_t − x₀)² is then distributed as $R\sim {\sigma }^2(t){\chi }_1^2$ where ${\chi }_k^2$ is the chi-square distribution with k degrees of freedom. In the case of self diffusion of water molecules, the displacement of all molecules is mutually independent and therefore for n independent experiments we get

$$\sum _{i=1}^n{R}_i\sim {\sigma }^2(t){\chi }_n^2.$$ (23)

The distribution in (23) means that even with a constant and known diffusion coefficient the bulk diffusion measured on different occasions will have a certain variability. However, usually in a diffusion experiment the aim is to estimate an unknown diffusion coefficient. According to Eq. (14), the estimated diffusion coefficient, d̂, is proportional to the estimated variance, σ̂²(t):

$$\widehat{d}=\frac{{\widehat{\sigma }}^2(t)}{2t}.$$ (24)

The variance can be estimated with the maximum likelihood estimator (MLE) as ${\widehat{\sigma }}^2(t)=({\sum }_{i=1}^n{R}_i)/n$. From Eq. (23) we get the distribution of the estimated variance to be

$${\widehat{\sigma }}^2(t)\sim \frac{{\sigma }^2(t)}{n}{\chi }_n^2.$$ (25)

We can then substitute d̂ from Eq. (24) into Eq. (25) to get the distribution of the estimated diffusion coefficient:

$$\stackrel{\sim }{d}\sim \frac{{\sigma }^2(t)}{2tn}{\chi }_n^2=\frac{2dt}{2tn}{\chi }_n^2=\frac{d}{n}{\chi }_n^2.$$ (26)

D. The Anderson-Darling Test

For the normal distribution, the test statistic, A² is

$$\begin{array}{l}{A}^2=\left(1+\frac{0.75}{n}+\frac{2.25}{n^2}\right)\times \\ \times \left(-n-\sum _{i=1}^n\frac{2i-1}{n}[\mathit{log}(w_i)+\mathit{log}(1-w_{n-i+1})]\right),\end{array}$$ (27)

where n is the sample size, and w is the standard normal CDF, with mean and standard deviation that are estimated from the sample. The value of A² is then compared with 0.752 which is the critical values for the normal distribution and α = 0.05 (D’Agostino and Stephens, 1986).