A Fast Algorithm for Calculation of Inhomogeneity Gradient in MRI Data

Abstract

Purpose

To develop and implement a new approach for correcting the intensity inhomogeneity in magnetic resonance imaging (MRI) data.

Material and Methods

The algorithm is based on the assumption that intensity inhomogeneity in MR data is multiplicative and smoothly varying. Using a statistically stable method, the algorithm first calculates the partial derivative of the inhomogeneity gradient across the data. The algorithm then solves for the gradient field and fits it to a parametric surface. It has been tested on both simulated and real human and animal MRI data.

Results

The algorithm is shown to restore the homogeneity in all images that were tested. On real human brain images, the algorithm demonstrated superior or comparable performance relative to some of the commonly used intensity inhomogeneity correction methods such as SPM, BrainSuite, and N3.

Conclusion

The proposed algorithm provides an alternative method for correcting the intensity inhomogeneity in MR images. It is shown to be fast and its performance is superior or comparable to algorithms described in the published literatures. Due to its generality, this algorithm is applicable to MR images from both humans and animals.

INTRODUCTION

Intensity inhomogeneity, or bias field, in magnetic resonance imaging (MRI) generally results in a smooth intensity variation across the image. This intensity non-uniformity is not related to the biology of the imaged subject. Intensity inhomogeneity affects many automatic quantitative image analysis techniques, including segmentation and registration. Therefore, correcting for the intensity inhomogeneity is a necessary pre-processing step in various image analysis tasks.

Prospective inhomogeneity correction methods minimize the intensity corruption by acquiring additional images. For instance, imaging using a combination of volume and surface coils can achieve high uniformity and high signal-to-noise ratio (SNR) (1). The major disadvantage of this method is that it requires additional image acquisition and prolongs the scan time. Furthermore, any inhomogeneity in the image acquired by the volume coil remains uncorrected (2). Thus, prospective methods can be time consuming and may not consistently produce accurate result.

In contrast to the prospective approaches, retrospective approaches are restorative methods that apply the correction based on the bias field in the acquired images. Because retrospective approaches solve for the inhomogeneity field using information from individually acquired images, they can remove patient-dependent inhomogeneities (2). In addition, most retrospective methods do not require a priori knowledge of the inhomogeneity, which increases their generality. Vovk et al. categorized retrospective methods into three groups: histogram based, segmentation based, and surface-fitting (2).

Histogram based methods remove the bias field by operating on the intensity histogram of the image. The information minimization methods parameterize the histogram into information functions (3,4). These methods assume that the inhomogeneity gradient increases the information content in the image. Thus, the restored image can be obtained by evaluating the bias field that produces the minimum information function. Sled et al. introduced the nonparametric nonuniform intensity normalization (N3) algorithm (5). It calculates the bias field by maximizing the frequency content in the uncorrupted image. Other histogram based correction methods include the histogram matching method (6) and the high order intensity coincidence statistics method(7).

Segmentation based methods simultaneously classify tissues and correct the bias field. In one approach, the intensity probability is first assigned to each voxel, followed by an expectation maximization (EM) iterative algorithm to search for the bias field (8,9). Other segmentation based techniques include the fuzzy c-means (FCM) clustering algorithm (10). The inhomogeneity gradient is incorporated into the objective function; the class membership and inhomogeneity estimation are then evaluated iteratively by minimizing the objective function (11–15). A recent study by Zhuge et al. described a method that uses intensity standardization to segment and correct inhomogeneity at the same time (16). Li et al. recently reported a joint segmentation and bias field correction algorithm that employed a new energy minimization approach (17).

Many histogram- and segmentation-based methods (distribution-based methods) require a pre-defined tissue intensity distribution and a fixed number of tissue types; therefore, their application is limited to certain tissue models and anatomical locations (18). Moreover, the aforementioned methods calculate the bias field based primarily on the intensity distribution. Since the intensity inhomogeneity is a function of space, it is unclear that operations in the distribution space would produce accurate representations of the bias field.

Surface-fitting based algorithms are correction methods that fit a parametric surface to the bias field in the input image. Unlike the distribution based methods, surface-fitting methods evaluate the inhomogeneity directly in the image space. Because such algorithms involve calculating the variation between adjacent pixels, they can be considered model-independent and are fast since no extensive iterations are required. Earlier approaches focused on searching for the homogenous regions within the images (19,20). Newer surface-fitting methods have focused on developing techniques to calculate the inhomogeneity gradient from its gradient derivatives. Vokurka et al. integrated the inhomogeneity gradient using a spiral pathway (21), Lai et al. fitted a polynomial to the gradient by minimizing the energy function (22), and Milchenko et al. fitted a polynomial to the gradient derivative directly (18).

A major limitation of the current surface-fitting methods is that they assume all pixels within a homogenous area have the same uncorrupted signal intensity. In reality, due to variation in the biological properties, it is unlikely that a given tissue will have a single intensity value (23). Further, current surface-fitting methods assume that the presence of noise has minimal effects on the calculation of the inhomogeneity. This is true only under the infrequently encountered condition of high SNR and high inhomogeneity wherein the degree of inhomogeneity outweighs the degree of noise. Calculations based on these assumptions may cause spurious results. Most of the above surface-fitting methods attempt to overcome the limitations of this assumption by using averages and applying median filter and different thresholds. However, such corrective attempts may be generally inadequate in reducing the inaccuracy.

We present an algorithm that reduces the effect of inherent intensity variation and noise on the calculation of inhomogeneity gradient derivatives. We also present a novel way to calculate the intensity gradient from the derivatives. The algorithm has been tested on both simulated and real human and animal brain images and the results demonstrate superior or comparable performance relative to some of the commonly used intensity inhomogeneity correction methods.

MATERIALS AND METHODS

All calculations were performed on a personal computer with 3.25 Gb RAM and 3.33 GHz processor. The program is written in IDL 7.0 (ITT Visual Information Solutions, Boulder, CO).

Theory

Here we describe our procedure for calculating the partial derivative of the smoothly varying inhomogeneity gradient, followed by the computation of the inhomogeneity gradient from its partial derivative. The multiplicative inhomogeneity model is used in which the acquired image v(x) at a voxel x is expressed as:

$$v(\mathit{x})=g(\mathit{x})u(\mathit{x})+n(\mathit{x})$$ (1)

where g(x) is the spatially varying inhomogeneity gradient, u(x) is the ideal signal and n(x) is the additive noise.

We first apply this technique to the 2D case. The intensity difference between the pixel at (x, y) and its adjacent pixel along the x-direction is defined as:

$$\begin{array}{l}{\mathrm{\Delta }}_{x}v(x,y)=v(x+1,y)-v(x,y)\\ ={\mathrm{\Delta }}_{x}g(x,y)·u(x,y)+g(x+1,y)·{\mathrm{\Delta }}_{x}u(x,y)+{\mathrm{\Delta }}_{x}n(x,y)\end{array}$$ (2)

where Δ_xf (x, y) ≡ f (x+1, y) − f (x, y) for any function f (x, y). Only the first (gradient) term in Eq (2) provides information for calculating the derivative of g(x, y). However, the second (inherent intensity variation arising from the biological properties of tissues) and the third (noise) terms in Eq (2) are not necessarily small compared to the inhomogeneity term, unless computation is performed on a homogeneous and high SNR region. In order to minimize the effect of the inherent variation and noise terms when calculation is performed in an imperfect environment, we need to use a set of n differences between adjacent pixels along the y direction at the same x₀. The sum of these Δ_xv(x₀, y_j) is:

$$\sum _{j=0}^{n-1}{\mathrm{\Delta }}_{x}v(x_0,y_0+j)=\sum _{j=0}^{n-1}{\mathrm{\Delta }}_{x}g(x_0,y_0+j)·u(x_0,y_0+j)+\sum _{j=0}^{n-1}g(x_0+1,y_0+j)·{\mathrm{\Delta }}_{x}u(x_0,y_0+j)+\sum _{j=0}^{n-1}{\mathrm{\Delta }}_{x}n(x_0,y_0+j)$$ (3)

In the Appendix, it is shown that if n is large enough, we can neglect the second (inherent variation) and third (noise) terms in Eq (3):

$$\sum _{j=0}^{n-1}{\mathrm{\Delta }}_{x}v(x_0,y_0+j)\cong {\mathrm{\Delta }}_{x}g(x_0,y_{av})·\sum _{j=0}^{n-1}u(x_0,y_0+j)$$ (4)

where y_av is an index representing the average of the n samples in the set. Similarly, in order to minimize the effect of inherent variation and noise terms on the sum of adjacent pixels S_xv, the sum of n sums of adjacent pixels, is calculated:

$$\sum _{j=0}^{n-1}{\mathbf{S}}_{x}v(x_0,y_0+j)\cong {\mathbf{S}}_{x}g(x_0,y_{av})·\sum _{j=0}^{n-1}u(x_0,y_0+j)$$ (5)

where S_x f (x, y) ≡ f (x+1, y) + f (x, y). By dividing Eq (4) by Eq (5), we can derive the following partial derivative:

$$\frac{\partial lng}{\partial x}(x_0,y_{av})=2\frac{{\mathrm{\Delta }}_{x}g(x_0,y_{av})}{{\text{S}}_{x}g(x_0,y_{av})}\cong 2\frac{{\sum }_j{\mathrm{\Delta }}_{x}v(x_0,y_0+j)}{{\sum }_j{\text{S}}_{x}v(x_0,y_0+j)}$$ (6)

Eq (6) represents the partial derivative of ln g in the x-direction at (x₀, y_av).

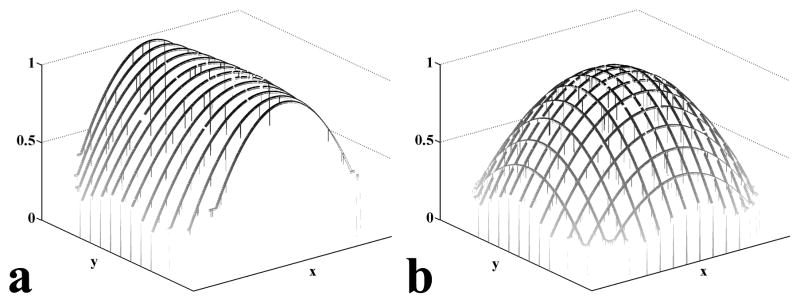
To calculate the gradient line g(x) along y_av, the partial derivatives in the x-direction along y_av is calculated via Eq (6). We use a step-wise integration to calculate the gradient line, g(x). The first point g(x₁) is set to unity, and each subsequent point g(x+1) is calculated from the partial derivative ∂ ln g(x)/∂x and the previous point g(x). The step-wise integration can produce a complete gradient line along y_av, {g(x)}_yav. A parametric curve is fitted to {g(x)}_yav and scaled (maximum = unity). Gradient lines along other y’s and x’s can be obtained in the same way. Figure 1a shows a set of gradient lines along the x-direction obtained from step-wise integrations at various y’s. These gradient lines are not unique solutions of their respective partial derivatives. Any scalar multiple of these gradient lines are also solutions. To bring the gradient lines into scale with one another, each line is multiplied by a scaling factor. The scaling factor is determined by applying the least square requirement on the differences between gradient lines along the x and y directions at their intersections. The result is a mesh of gradient lines that represents the complete 2D inhomogeneity gradient, as shown in Figure 1b. The gradient mesh is scaled so that its maximum is unity and a parametric surface is fitted to the mesh.

Figure 1.

Calculated gradient lines. (a) A set of calculated gradient lines after curve fitting in the x-direction. All of the gradient lines are scaled such that their maximum equals unity. (b) After multiplying by scaling factors, the combination of x- and y-gradient lines form a gradient mesh. The scaling factors are computed by minimizing the least square differences between the x- and y-gradient lines at the intersections.

Methods for 3D correction

The method described in the previous section can be extended to 3D inhomogeneity correction. However, some practical problems may arise if the method is directly applied to the 3D case when multi-slice data are acquired. First, current algorithm using double precision cannot handle common 3D data sets and can cause overflow error during computation; therefore, the algorithm applied directly to the 3D space may result in erroneous coefficients that degrade the result. Furthermore, full 3D calculations involve substantially longer processing time. In order to overcome these limitations, the following simplifications are utilized to compute the 3D inhomogeneity gradients. We first assume that the 3D inhomogeneity is separable in the third dimension, which implies:

$$g(x,y,z)=g_{2D}(x,y)·g_z(z)$$ (7)

This assumption is generally valid for a smoothly varying inhomogeneity gradient in the slice direction. Using the same arguments that lead to Eq (6), we obtain:

$$\frac{\partial ln{g}_z}{\partial z}(z)\cong 2\frac{{\displaystyle \sum _{i=0}^{N_x-1}}{\displaystyle \sum _{j=0}^{N_y-1}}{\mathrm{\Delta }}_{z}v(i,j,z)}{{\displaystyle \sum _{i=0}^{N_x-1}}{\displaystyle \sum _{j=0}^{N_y-1}}{S}_{z}v(i,j,z)}$$ (8)

where N_x and N_y are the image dimensions along the x and y directions. A set of derivatives in the z-direction, {∂ln g_z (z)/∂z}, can then be obtained. The gradient g_z (z) can be solved by step-wise integration, similar to the 2D case. This modification simplifies the computation and reduces the computation time.

Algorithm

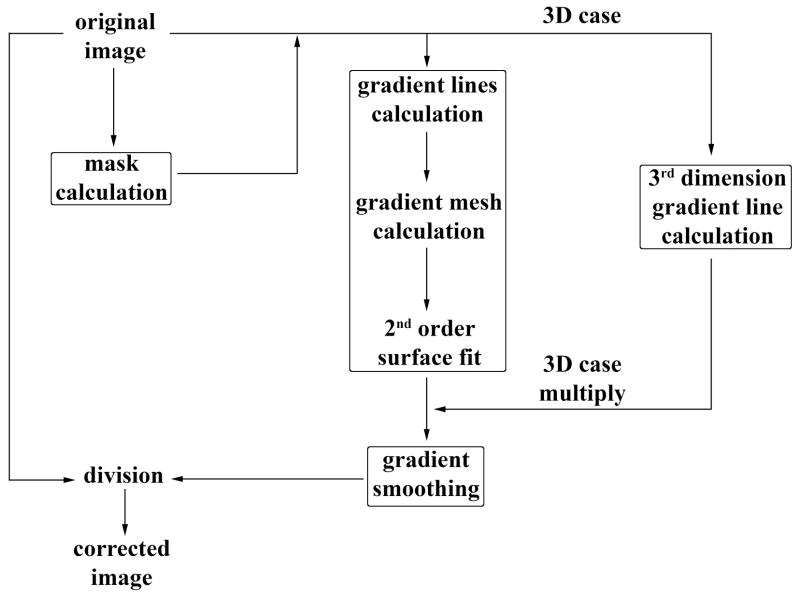
A step-by-step description of the complete procedure of our inhomogeneity gradient correction algorithm is presented here. A flow chart describing the algorithm is shown in Figure 2.

Figure 2.

Flow chart describing the new algorithm. Gradient calculation can be separated into four parts: (1) Mask calculation, (2) 2D gradient calculation on each slice, (3) third dimension gradient calculation, and (4) final smoothing.

Step 1. Mask Calculation

In order to calculate the partial derivatives accurately, the background and edges are excluded from the computation. Four user defined parameters are employed for calculating this mask: the threshold and the Gaussian smoothing radius for the EDGE_DOG edge detection program (IDL 7.0), the background threshold, and the ratio threshold to exclude strong speckle noise. When calculating the difference between adjacent pixels, an edge has a strong inherent variation term that outweighs the gradient term and should be avoided in the calculations. The EDGE_DOG function is based on the Difference of Gaussians approach (24) for detecting grayscale edges in 2D. In the background region, the noise term can outweigh the gradient term. A background intensity threshold is set to exclude the background regions. A ratio threshold is applied to limit the ratio of Δ_xv(x, y) to $\sqrt{{\mathbf{S}}_{x}v(x,y)}$ to reject: 1) edges that are not found by the EDGE_DOG program and 2) strong speckle noise. Calculation of the mask takes approximately 4 seconds for a 180-slice volume. Users can visualize the calculated mask and interactively adjust the parameters to obtain an optimal mask that is free of background and edges. The values of these parameters depend on the image SNR and therefore, once determined, the same parameters can be used for similar imaging protocol.

Step 2. 2D Gradient Calculation

First, the images are smoothed by a 3×3 normalized Gaussian filter. The variance of the filter is equal to square of the Gaussian smoothing radius for the EDGE_DOG program. The user can define the number of in-plane pixels to use, or n in Eq (4–6), to calculate the gradient lines. In addition to the in-plane pixels, the algorithm also allows pixels from n_k adjacent slices in calculating the 2D gradient lines so that Eq (7) becomes:

$$\frac{\partial lng}{\partial x}(x_0,y_{av},z_0)\cong 2\frac{{\displaystyle \sum _{k=0}^{n_k-1}}{\displaystyle \sum _{j=0}^{n-1}}{\mathrm{\Delta }}_{x}v(x_0,y_0+j,z_0+k-(n_k-1)/2)}{{\displaystyle \sum _{k=0}^{n_k-1}}{\displaystyle \sum _{j=0}^{n-1}}{\text{S}}_{x}v(x_0,y_0+j,z_0+k-(n_k-1)/2)}$$ (9)

For ease of calculation, n is restricted to be even and n_k is restricted to be odd. The lines of partial derivatives in each slice are calculated. The partial derivatives are then smoothed by a median filter. Due to the edges and noise, the total number of data used, n_mask, in the derivative calculation is usually smaller than n × n_k. In some cases, n_mask can be too small such that the approximation in Eq (4,5) may no longer be valid. The median filter applied here is weighed by n_mask at each point within the filter to eliminate spurious partial derivatives. Step-wise integration is performed to obtain gradient lines from the partial derivatives. A second order curve is fitted to each gradient line and scaled with its maximum equal to unity. Then, a curve fitting algorithm is employed to adjust the fitted curve so that its partial derivatives match those calculated from the data. After gradient lines are calculated in both directions, they are multiplied by their respective scaling ratios to create a gradient mesh. The scaling ratios are calculated by minimizing the square differences between gradient line intersections. The gradient mesh is fitted to a second order polynomial to smooth the calculated bias field. We used a second order polynomial because it is sufficient to model a smoothly varying inhomogeneity gradient. Moreover, higher order polynomial may not represent the true gradient and variations in the higher order terms can substantially amplify errors. The polynomial is then scaled so that its maximum value is set to unity. For a 256 × 256 image with 16 gradient lines in each dimension, this step takes less than a second.

Step 3. 3D Gradient Correction

If 3D bias correction is desired, the 3D correction methods described in the previous section can be utilized. First, the 2D images are smoothed by a 1D median filter (size = 5% of number of slices) along the third dimension to eliminate some of the abnormal results that sometimes occur at the transition between object and background. The size set here is found to produce favorable smoothing but this value is not critical. The 3D assumption described in Eq (7) is made and the partial derivatives of g_z (z) are calculated using Eq (8). The procedure to calculate g_z (z) is similar to solving an individual gradient line in Step 2. A second order curve is fitted to the gradient line and scaled to a maximum of unity. Since the gradients on different slices are not necessary in scale with each other, a slice-by-slice ratio r_z (z) is used. We start by using the slice where g_z (z) is maximum: r_z (z₀)= g_z (z₀)=1.0. All subsequent r_z are calculated from g_z and the 2D gradients g_2D:

$$r_z(z)=\frac{g_z(z){\sum }_{i,j}{g_{2D}}^{sc}(i,j,z-1)}{g_z(z-1){\sum }_{i,j}{g}_{2D}(i,j,z)}$$ (10)

where g_2D^sc (z) is the updated 2D gradient after multiplying g_2D(z) by r_z(z). The calculated ratios are multiplied with the 2D gradients at each z to obtain a 3D gradient volume. For a volume with 180 slices, this step takes less than 1 second.

Step 4. Smoothing and Final Image Correction

A median filter is applied to the calculated inhomogeneity gradient. For 3D calculation, the slice-by-slice ratios are recalculated after application of a 3D median filter. A 9 × 9 × 5 Gaussian filter (in-plane variance = 16, slice variance = 2.25) is applied to this rescaled gradient. These parameters are set to produce visually smooth gradient field and their values are not critical. The bias-corrected data are computed by dividing the originally acquired data by the gradient volume. We chose to scale the final data so that their 98% scale is equal to the 98% scale of the originally acquired data. This is used so that the restored intensities match those of the original uncorrupted level. We decided to use high intensity scale (98%) to normalize intensity but not maximum intensity (100%) because maximum intensity is likely to arise from high intensity speckle noise. Again, this value is not critical. Step 4 is the most time consuming because it involves 3D convolution. For a 256 × 256 × 170 volume, this step can take up to 1 minute.

Data Acquisition

To evaluate the algorithm on different types of images, we applied it to four different types of images: digital phantom, rat brain, simulated human brain from the BrainWeb database (25), and brain images acquired on healthy human subjects.

Digital Phantom Image

A 256×256 software-generated phantom slice was used to validate the accuracy of the algorithm and its response to noise. The intensity of the image ranged from 0 to 255. This image was multiplied with the following smooth parabolic gradient field:

$$g(x,y)=-\frac{1}{2}+\frac{3}{256}(x+y)-\frac{3}{{256}^2}(x^2+y^2)$$ (11)

In addition to the gradient field, twelve different randomly generated noise fields were added to the image in order to verify the robustness of the algorithm against noise. Each noise field was randomly generated with normal distribution (mean = 0). An absolute value filter was applied to the noise, making it strictly positive. To test the algorithm’s performance against noise, six of the random noise fields had variance of 25 and the other six had variance of 100.

Rat Brain

Four sets of rat brain volumes were acquired on a USR70/30 horizontal bore 7T MR scanner (Bruker Biospin, Karlsruhe, Germany). 2D dual echo (echo times of 22 ms and 65 ms) rapid acquisition with relaxation enhancement (RARE) images were acquired with an echo train length of 4. A 72 mm inner diameter volume coil (Bruker Biospin, Karlsruhe, Germany) was used for transmission. For signal reception, a custom designed 22 mm outer diameter circular surface coil was used (26). As expected, an intensity gradient, with strong signal close to the surface coil and low signal away from the coil, was observed. Two sets of data had an in-plane resolution of 0.137 mm×0.182 mm (matrix size = 256×192), while the other two sets had an in-plane resolution of 0.150 mm×0.150 mm (matrix size = 256×256). All four sets had 20 slices with slice thickness of 1 mm.

Simulated Human Brain (BrainWeb)

Simulated brain images from the BrainWeb MR simulator (25,27) were used. The matrix size of the volumes was 181×217×181 with 1 mm slice thickness. Six sets of volume that included two T1-weighted, two T2-weighted, and two proton density-weighted (PDW) data sets had a noise of 3%. Within each weighting group, one volume represented normal brain and the other represented a brain with multiple sclerosis (MS) lesions. All data had 40% intensity nonuniformity. Two extra sets of PDW volumes with 9% noise were also processed to estimate the effect of noise to the algorithm’s performance.

Real Human Brain

Eight sets of human brain data from normal volunteers were acquired on a 3T Philips Intera Scanner with a T/R head coil (Philips Medical Systems, Best, Netherlands). A magnetization prepared rapid gradient echo (MPRAGE) sequence was employed, with matrix size of 256×256×170 in sagittal view. The resolution was isotropic with 1 mm along each direction. These images were acquired with and without turning on the manufacturer’s inhomogeneity correction for comparison.

Testing Validation

For all images, we used 16 in-plane pixels (n=16) and no adjacent slice (n_k=1). The Gaussian filter standard deviation was set to 1.5 pixels.

Our algorithm calculated the numerical inhomogeneity gradient field from the phantom image. The calculated coefficients are compared to the ones in Eq (11) for accuracy using z-statistics.

In order to quantify homogeneity correction in the rat brain study, we used the coefficient of variation (cv). The coefficient of variation of a class c is the normalized standard deviation that quantifies its nonuniformity (28):

$$cv(c)=\frac{\sigma (c)}{\mu (c)}$$ (12)

where σ (c) and μ(c) are the standard deviation and mean of the calculated values for c, respectively. The region of cerebral cortex was selected in each of the rat brains. We chose this region because it is reasonably large and it covers considerable in-plane area and spans multiple slices.

To evaluate the performance of the new algorithm in the human brain study, we compared it with three other previously published and commonly used algorithms: statistical parametric mapping software (SPM) (29), BrainSuite (BSU) (6,30), and nonparametric nonuniform intensity normalization (N3) (5). SPM does not require any user parameters and for BSU, we used the iterative options after skull stripping to perform the correction. For N3, we used a 1×10⁻⁵ stopping threshold, full width half maximum of 0.05 and 250 maximum iterations. Since different programs scale the results differently, we used the coefficient of joint variation (cjv) proposed by Likar et al. (3) to assess the tissue contrast, which reflects the intensity homogeneity:

$$\mathit{cjv}(c_1,c_2)=\frac{\sigma (c_1)+\sigma (c_2)}{\mid \mu (c_1)-\mu (c_2)\mid }$$ (13)

where μ(c_i) and σ (c_i) are the mean and standard deviation of tissue class i, respectively. The two tissue classes tested were gray matter (GM) and white matter (WM).

To preserve objectivity of the assessment, the images were segmented automatically using SPM. Segmentation masks from each weighting group were created and a common mask for all images was generated by taking the median of the three segmentation masks. For data acquired on the 3T Philips scanner, the scanner software provided a uniform correction program (UNI) to correct for the inhomogeneity. Therefore, in addition to the three previous algorithms, the performance of the new algorithm was also compared with UNI in the real human brain study. In order to test our modified method for 3D correction, we also applied the new algorithm on the real human data in all three orientations. Since the real human data had isotropic resolution, corrections along different orientations are expected to provide similar results.

RESULTS

Phantom Image

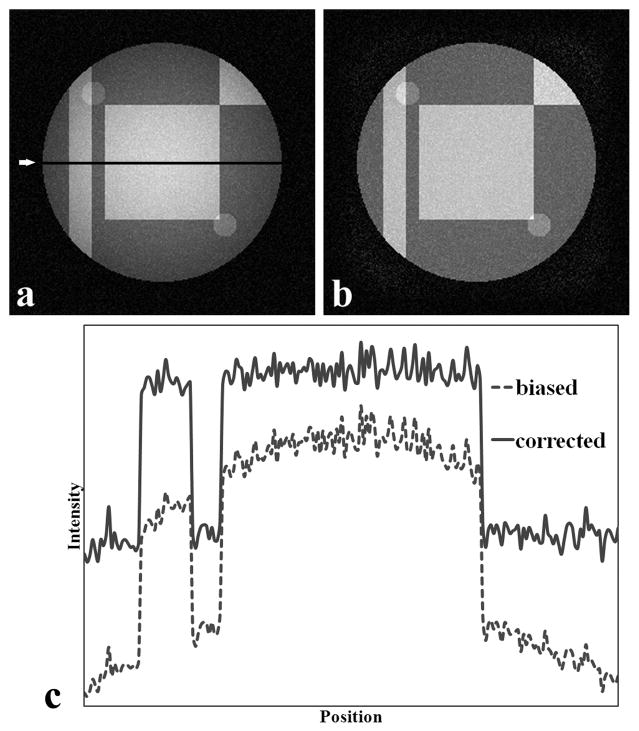
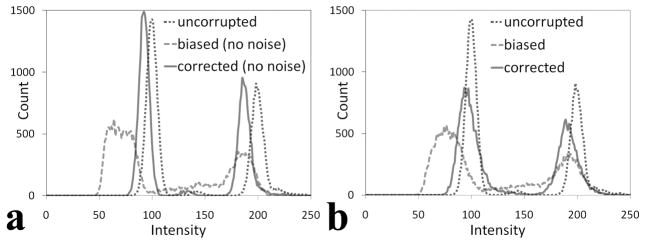
Figure 3a shows an example of the resulting phantom image after multiplication with the gradient and addition of random noise with variance of 100. Figure 3b is the bias-corrected image after applying the inhomogeneity correction algorithm. In Figure 3a, a relatively diffuse and high intensity is present at the image center that fades away towards the sides. After correction, the image appears more homogenous (Figure 3b). This can be better appreciated on the intensity profiles shown in Figure 3c. A comparison of Figs 3a and 3b shows more background noise in the bias-corrected image relative to the uncorrected image. This is because the bias-corrected image is obtained after dividing the original data by the calculated gradient with no noise reduction algorithm applied. Figure 4a shows the histogram of the uncorrupted image, the biased image without additional noise, and its correction. After the inhomogeneity correction, the histogram appears close to the original histogram. Notice that the corrected peaks are all higher than the uncorrupted peaks because the intensity range of the bias-corrected image is smaller than that in the uncorrupted image. Figure 4b shows the intensity distributions of Figure 3a and 3b, along with that of the noiseless uncorrupted image. The histogram distribution of the bias-corrected image appears closer to the uncorrupted image compared to the corrupted image. The corrected histogram peaks are, however, not as sharp as the uncorrupted peaks because of noise.

Figure 3.

Software-generated phantom image with known gradient and additive noise with variance = 100. (a) Biased original image,. (b) image after bias correction with the new algorithm, and (c) one dimensional profiles corresponds to the dark line (indicated by arrow) in (a). The intensities in (c) are offset to allow for easy visualization. Both the image and line profile show visible restoration of homogeneity.

Figure 4.

Intensity distribution of the phantom image. (a) Distribution of the noiseless image with biased field, its corrected image and the uncorrupted image. (b) Histogram of the biased image with additional noise (variance = 100) (Figure 3a), its inhomogeneity corrected (Figure 3b) and the uncorrupted images. After inhomogeneity correction, the histograms of both corrupted images appear closer to the histogram of the uncorrupted image.

Table 1 shows the coefficients of the calculated gradient, along with their respective z-test probability values, obtained from the two noise groups. The zeroth order coefficient is not included in this Table because the inhomogeneity partial derivative does not contain information about it. The zeroth order baseline adjustment, however, does not contribute to the overall contrast of the image. None of the coefficients are significantly different from their corresponding applied values (p > 0.14). On average, increasing the noise variance from 25 to 100 increased cv of the non-zero coefficients by 6.5%.

Table 1.

Coefficients and their corresponding p-values of the gradient used on the computer generated phantom.

Coefficient	Applied Value	Calculated Value (noise σ2 = 25)	p-value (noise σ2 = 25)	Calculated Value (noise σ2 = 100)	p-value (noise σ2 = 100)
c(x)	1.17×10−2	(1.17±0.11)×10−2	0.99	(1.15±0.15)×10−2	0.74
c(y)	1.17×10−2	(1.17±0.07)×10−2	0.91	(1.09±0.16)×10−2	0.18
c(xy)	0	(−0.39±1.56)×10−5	0.54	(−0.55±2.19)×10−5	0.54
c(x2)	−4.58×10−2	(−4.48±0.54)×10−5	0.64	(−4.57±0.76)×10−5	0.98
c(y2)	−4.58×10−2	(−4.45±0.29)×10−5	0.27	(−4.17±0.67)×10−5	0.14
c(x2y)	0	(0.23±7.95)×10−8	0.94	(3.19±9.62)×10−7	0.42
c(xy2)	0	(−0.22±5.19)×10−8	0.92	(0.23±8.00)×10−7	0.94
c(x2y2)	0	(0.58±2.62)×10−10	0.58	(−0.28±2.88)×10−10	0.81

σ² = variance

Rat Brain

Figure 5a shows a representative example from one of the short echo rat brain images and Figure 5b shows the corresponding image after bias correction by the new algorithm. In Figure 5a, an intensity gradient from the top left corner to the bottom right corner is present. After inhomogeneity correction, the bottom region, which was barely seen in Figure 5a, can be clearly seen in Figure 5b. Table 2 shows the summary of the mean intensity, standard deviation and cv in the cortex. The inhomogeneity correction improved the cv value in all of the four data sets. Overall, the inhomogeneity correction algorithm reduced cv by (22 ± 6)%.

Figure 5.

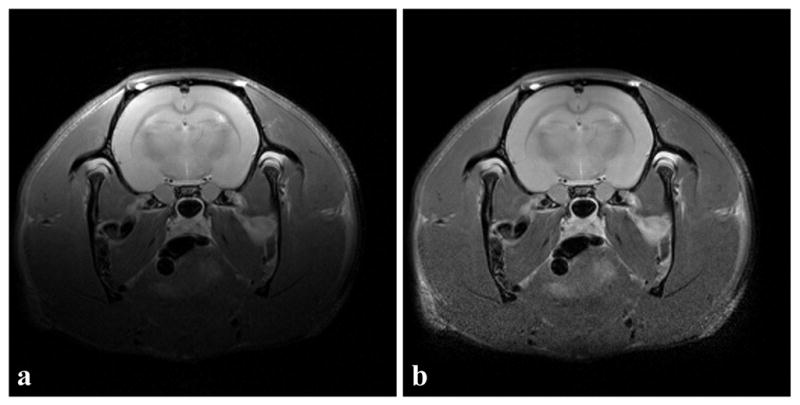
A representative example of a slice from a rat brain (RARE scan, matrix size = 256×256). (a) Original image. (b) Image after inhomogeneity correction with the new algorithm. In the original image, a decreasing intensity gradient starting from top left to bottom right was observed. After inhomogeneity correction, the inhomogeneity was reduced.

Table 2.

Summary of the intensity values within the cortex in rat brain

Set	Image	Intensity (Short TE)	cv (Short TE)	Intensity (Long TE)	cv (Long TE)
1	Original	19730±4153	0.210	8274±1772	0.214
	Corrected	17129±2767	0.162	7180±1179	0.164
2	Original	19931±3935	0.197	8053±1895	0.235
	Corrected	17087±2409	0.141	6904±1237	0.179
3	Original	13405±2851	0.213	5758±1167	0.203
	Corrected	11612±1774	0.153	5007±838	0.167
4	Original	13243±2683	0.203	5436±1140	0.210
	Corrected	11491±1775	0.154	4738±895	0.189

cv = coefficient of variation

Set 1 and set 2 have in-plane resolution of 0.137 mm × 0.182 mm, while set 3 and 4 have in plane resolution of 0.150 mm × 0.150 mm. All sets include two echoes (TE = 22msec and 65msec). The mean ± standard deviation and coefficient of variation are presented here.

Simulated Human Brain (BrainWeb)

For the simulated human brain, there was no visually noticeable difference between the biased and the bias-corrected images. The coefficient of joint variation, however, showed differences between the biased and bias-corrected images. Table 3 shows the cjv(GM,WM) for the eight sets of images. Smaller cjv value implies better separation between the two tissue distributions in the histogram, resulting in improved tissue contrast and smaller intensity inhomogeneity. We used the 0% intensity non-uniformity provided by BrainWeb as the standard. Ideally, the bias-corrected images should have a histogram similar to that of the standard. The intensity inhomogeneity correction should result in a value of cjv that is close to the value in the standard image (with zero bias, referred to as the baseline value). Therefore, as a measure of the performance of the correction, we calculated the reduction of cjv relative to the baseline value (the larger the reduction, the more effective is the inhomogeneity correction).

Table 3.

The coefficient of joint variation (cjv) between gray matter an white matter are presented for eight sets of BrainWeb simulated human brain images. Correct histogram waveforms should have cjv close to that of the standard. A smaller value of cjv implies better tissue contrast. Six sets of volumes had 3% noise level, while two sets of proton density-weighted data had 9% noise level.

Scan Type	Data Set	cjv(GM,WM) (%)
		Standard	Biased	SPM	BSU	N3	New
PDW (3%noise)	Normal	56.4	164.9	59.4	68.5	60.7	83.2
	MS	60.8	201.6	63.6	72.6	65.4	85.8
PDW (9%noise)	Normal	157.1	250.2	153.9*	212.0	154.2*	179.5
	MS	167.3	293.4	162.6*	209.3	162.1*	203.2
T1 (3%noise)	Normal	44.6	67.2	47.4	50.0	47.0	53.7
	MS	44.6	66.0	47.3	50.2	46.9	53.5
T2 (3%noise)	Normal	68.1	100.5	75.2	262.0†	95.7	72.7
	MS	70.2	132.7	77.1	221.8†	76.8	81.4

BSU = BrainSuite, MS = multiple sclerosis, N3 = nonparametric nonuniform intensity normalization, New = the algorithm presented in this study, SPM = statistical parametric mapping,

^*cjv values of processed data smaller than those of the standard unbiased data (over correction),

^†cjv values of processed data larger than those of the original biased data (failed correction)

For the PDW data with 3% noise, our new algorithm reduced relative cjv by 79% and by 74% for 9% noise. The corresponding reductions using BSU were 90% and 54%, respectively. SPM achieved 98% relative reduction in the 3% noise data, but over-reduced cjv by 104% in the 9% noise data. N3 reduced cjv by 96% and 104%, respectively. On average, SPM corrected images had cjv closest to those of the standard sets. For the six 3% noise data sets, SPM reduced relative cjv by 90%. N3 performed well except on the T2 normal data set. On average, N3 improved cjv by 79%. However, both SPM and N3 overcorrected the 9% noise data sets, which may be a result of correcting inherent intensity variation in addition to the inhomogeneity. Our new algorithm consistently brought the corrected cjv closer to the standard values. On average, it reduced their relative cjv by 74%. BSU corrected the bias field in the PDW and T1 data sets; however, it failed to calculate a reasonable inhomogeneity gradient for the T2 data sets. This might be due to the noticeably low SNR in the two T2 data sets.

Real Human Brain

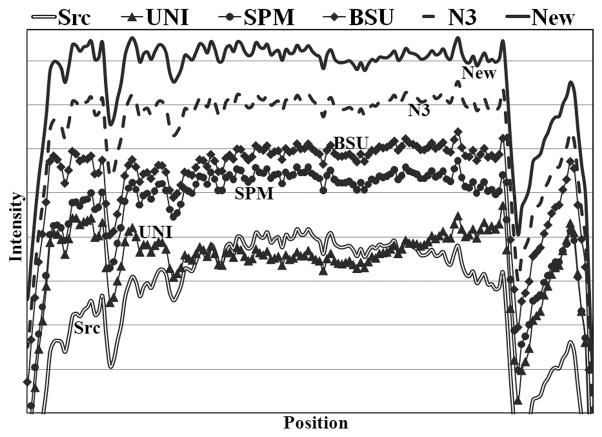
Figure 6a and 6b show examples of an original acquired image with the scanner uniformity correction turned off and the corresponding bias-corrected image by the new algorithm, respectively. Comparison of the two images shows an apparent intensity restoration in the bottom (inferior) area of the image (Figure 6b). A line profile (arrow indicating the line in Figure 6a) through a region of mostly WM is shown in Figure 7. From the line profile, the original source image contained high intensity in the middle that started to fade away from the center. UNI over-corrected the inhomogeneity such that the peripheries had higher intensity than the center. Visually both SPM and BSU flattened the line profile, but N3 and the new algorithm produced the flattest profiles.

Figure 6.

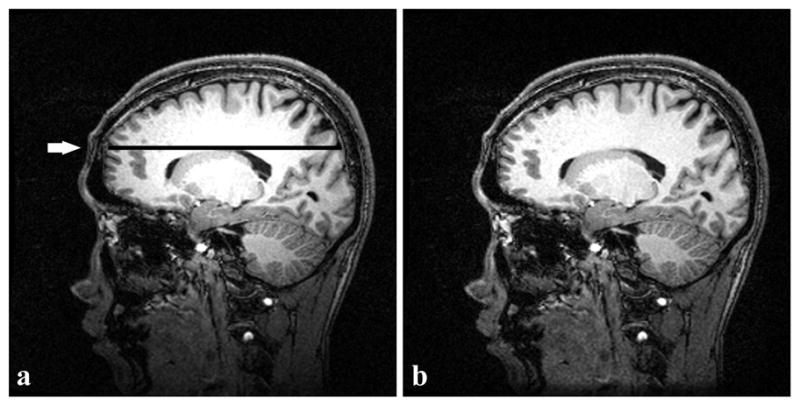
Single slice of an actual human brain volume (MPRAGE scan, matrix size = 256×256). (a) Original image. (b) Image after inhomogeneity correction with the new algorithm. A sharp intensity drop occurs in the inferior part of (a); after correction, intensity is restored in (b). The intensity profile shown in Fig. 7 corresponds to the dark line (pointed out by the arrow) in (a).

Figure 7.

Line profiles without and with bias corrections using different algorithms. The line passes mainly through the white matter (dark line in Fig. 6a) and therefore the profile is expected to be roughly flat. All the profiles were normalized to the same mean, but were offset by the same amount for clear visualization. The original (Src) image had high intensity in the center, while UNI correction produced high intensity in the peripheries. The other four algorithms produced relatively flat line profiles than the original. N3 and our algorithm yielded the flattest profiles.

Table 4 summarizes the cjv(GM,WM) of the source and the different bias-corrected images. In the absence of ground truth, the comparisons among correction schemes were solely based on the absolute cjv reductions. Since the data had isotropic resolution, we expected the cjv values to be comparable in all three orientations if the 3D method operated correctly. The new algorithm reduced the absolute cjv values by 22%, 13% and 12% when correction was performed in the axial, sagittal, and coronal view, respectively. Inhomogeneity corrections in the sagittal and coronal views provided similar results; however, corrections in the axial view significantly outperformed the other two views. The discrepancy could be explained by the rapid intensity drop in the inferior area shown in Figure 6a. This specific field could not be modeled by a second order polynomial designed for the new algorithm. As a result, the calculation of in-plane inhomogeneity was degraded in the sagittal and coronal views. Since the 3D method does not weigh the third dimension in as much detail as it does for the in-plane dimensions, the axial view correction was most effective.

Table 4.

The coefficient of joint variation (cjv) between gray matter (GM) and white matter (WM) of T1-weighted human brain data set. Smaller cjv value represents increased tissue contrast between GM and WM. On average, both our new algorithm and N3 resulted in significantly reduced cjv compared to source data.

Set	cjv(GM,WM) (%)
	Source	UNI	SPM	BSU	N3	New Sagittal	New Axial	New Coronal
1	78.0	76.7	72.1	67.5	60.2	66.0	61.7	67.3
2	80.7	80.0	87.1†	72.3	69.2	71.1	61.9	70.4
3	75.7	75.7	73.5	94.6†	55.8	59.0	52.9	60.6
4	92.3	107.8†	90.8	120.8†	82.3	89.5	81.1	90.3
5	78.2	78.5†	79.3†	90.4†	59.5	64.2	58.1	60.4
6	73.2	83.5†	74.1†	92.3†	61.0	65.9	61.6	66.1
7	71.0	82.7†	75.9†	71.4†	53.4	63.6	58.6	64.7
8	74.6	86.3†	77.1†	118.2†	54.3	63.6	63.2	63.1

BSU = BrainSuite, New = the algorithm presented in this study, N3 = nonparametric nonuniform intensity normalization, SPM = statistical parametric mapping, UNI = uniform correction program,

^†cjv values of bias-corrected data greater than those of source data.

On average, the UNI, SPM and BSU algorithms did not reduce cjv values, implying that these algorithms did not make consistent improvements on the real human data. N3 reduced cjv by 21%, which is similar to the performance of the new algorithm on the axially oriented images. Both N3 and our new algorithm improved consistently the contrast on all four data sets. All other programs failed to improve cjv for at least one data set.

DISCUSSION

We presented a novel retrospective surface-fitting method to correct for the intensity inhomogeneity in MRI. In contrast to the distribution based inhomogeneity correction methods, surface-fitting methods can directly calculate the bias field gradient. However, the results with surface fitting methods are usually not as robust as distribution based algorithms. To overcome some of the problems associated with the general surface fitting methods, our algorithm uses a statistically more stable routine to handle the calculation.

In traditional surface-fitting models, the partial derivative is calculated by averaging the division of difference between adjacent pixels by sum of adjacent pixels (18,19). Our algorithm calculates partial derivative by dividing the sum of n differences between adjacent pixels by the sum of n sums of adjacent pixels, as shown in Eq (6). The mathematical difference between these two is that traditional averaging methods do not take into account the contribution of inherent variation and noise in the sum of adjacent pixels. This would likely produce spurious results in low intensity regions. Using multiple pixels, our new algorithm can reduce the effect of noise and inherent variation, making the derivative calculation more accurate.

We investigated the accuracy of our new algorithm and its response to noise in the phantom study. All the calculated coefficients matched those of the applied values. It was found that quadrupling the noise variance from 25 to 100 increased the cv of the calculated coefficients by 6.5%. Thus, the algorithm does not appear to be very sensitive to noise. To quantify the improvement after inhomogeneity correction, cv or cjv value was calculated in this study. The coefficient of variation cv quantifies the nonuniformity of a single tissue class (reduced cv represents restoration of uniformity within the single class). However, cv does not provide information on overlapping intensity distributions of distinct tissue classes. To quantify the intensity overlap, the coefficient of joint variation cjv between two classes is computed. Reduction of cjv indicates improved ability to separate different tissue classes (i.e. improved contrast). This is especially important in diagnostic imaging because it can enhance segmentation performance, and enables improved lesion identifications and image registration. Many inhomogeneity correction programs are model-specific. A number of inhomogeneity correction programs for human brain images require an extra step of skull stripping to work optimally. Our program works without the need to strip the extrameningeal tissues. In addition it works well on both human and rat brains. On average, our program reduced cv(GM) by 22% in rat study, reduced the absolute cjv(GM,WM) by 34% in stimulated brain study and 22% in real human brain study. Our new algorithm improved the coefficients on every single data set in all three studies.

For comparison, three previously published and commonly used bias correction methods were applied in human brain studies. SPM, N3, and BSU are all readily available online. For the simulated brain, both N3 and SPM performed well in restoring cjv. In fact, in some cases, the reduced cjv after correction was even smaller than the cjv of the original unbiased image. This indicates a possible over-correction by N3 and SPM. It may be a result of mistakenly treating small areas of inherent tissue variation as inhomogeneity gradient. While N3 performed well on all human data, SPM did not improve the GM/WM contrast in the real brain data set. BSU performed well on some data sets but failed on others. We believe that poor skull stripping in BSU could have caused this inconsistency in performance. We also observed that low SNR greatly reduced BSU’s performance. In the real human brain study, the scanner software UNI did not improve cjv after correction. The rat brain data were also processed by SPM and N3 (data not shown). Although some visual improvements were observed with these two algorithms, they did not correct the rat brain data as well as our algorithm did in terms of cv values. This may not be surprising since all the aforementioned algorithms are specifically optimized for human brain studies.

In some instances, the inhomogeneity field is not smooth, such as the steep intensity drop in the inferior region of Figure 4a. In those cases, it is better to correct inhomogeneity in the view where the in-plane bias field appears the smoothest. This was shown in the real brain study, in which the axial correction (in-plane smooth field) outperformed the other two views (in-plane steep drop).

The new algorithm fits the in-plane inhomogeneity field with a second order polynomial. We decided to use second order polynomial because it can model a smooth gradient well in most MR experiments. Second order polynomial fit may not be sufficient to model complicated bias fields that are typically encountered at high fields in human studies. In these cases, higher order polynomials may describe the bias field better. However, it is likely that higher order correction schemes will mistakenly compensate small intrinsic intensity variations and produce incorrect results.

We have implemented simplified 3D method for reduced computational burden. However, it is theoretically possible to extend the bias correction to 3D without any additional simplifying assumptions. Unfortunately, there were two practical difficulties with the direct implementation of 3D correction: 1) the processing time would be very long. As an example, an in-plane gradient fit of 16×16 gradient lines would require the program to solve a group of 32 linear equations. For a volume of 10 slices, 3D calculation of the same gradient lines would require solving a set of 32×10+256 = 576 linear equations, which is not a linear increase. Moreover, the increase in processing time, which is also not linear, would be substantial. Moreover, most of the times, we have of 100+ slices, that means the program calculate the derivatives of 25600+ intersections in each of the 3456+ linear equations. This will further increase the processing time. 2) We have attempted 3D correction and we ran into precision overflow. This perhaps suggests that accurate calculation of the higher order coefficients in true 3D mode requires more than 64bit (double precision) accuracy.

In the real human study, the coronal and sagittal views both had in-plane steep intensity drop. As a result, corrections in these two orientations produce similar outcomes. This suggests that the 3D method worked properly as the third dimension calculation was consistent with the in-plane calculation.

Our new algorithm requires user-defined parameters in order to mask-out edges and background noise. Because the new algorithm utilizes multiple voxels to achieve statistical stability, small changes in these parameters do not produce significant changes in the bias-corrected images. However, we did not explore this in great detail.

The reconstruction of inhomogeneity field from the partial derivatives involves simple step-wise integration along horizontal and vertical lines. The inter-line scales are determined by minimizing the difference of the intersection differences. These processes are fast because they are performed in one-dimension. Under identical computation condition, SPM took approximately 100 seconds (20 iterations) to process a volume of real human data, BSU took approximately 16 minutes, N3 took 120 seconds (250 iterations), and our algorithm took approximately 90 seconds. The processing speed of the new algorithm is comparable to other fast algorithms. Therefore, it can be implemented in a clinical environment to aid in semi real-time assessment and diagnosis.

In conclusion, our new MR inhomogeneity correction algorithm is shown to be stable, fast, and required minimal user intervention. It is independent of acquisition methods and structures being imaged. The results are comparable to those of previously published algorithms.

APPENDIX

Starting from Eq (3):

$$\sum _{j=0}^{n-1}{\mathrm{\Delta }}_{x}v(x_0,y_0+j)=\sum _{j=0}^{n-1}{\mathrm{\Delta }}_{x}g(x_0,y_0+j)·u(x_0,y_0+j)+\sum _{j=0}^{n-1}g(x_0+1,y_0+j)·{\mathrm{\Delta }}_{x}u(x_0,y_0+j)+\sum _{j=0}^{n-1}{\mathrm{\Delta }}_{x}n(x_0,y_0+j)$$

Since g(x, y) is a slow and smoothly varying gradient, we may assume that adjacent Δ_x g(x, y) ’s have similar value. Therefore, Eq (3) becomes:

$$\sum _{j=0}^{n-1}{\mathrm{\Delta }}_{x}v(x_0,y_0+j)\cong {\mathrm{\Delta }}_{x}g(x_0,y_{av})·\sum _{j=0}^{n-1}u(x_0,y_0+j)+g(x_0,y_{av})·\sum _{j=0}^{n-1}{\mathrm{\Delta }}_{x}u(x_0,y_0+j)+\sum _{j=0}^{n-1}{\mathrm{\Delta }}_{x}n(x_0,y_0+j)$$ (A1)

where y_av is an index representing the average of the n samples in the set. In general, it can be expected that the second (inherent variation) term be:

$$\langle g(x_0,y_{av})·\sum _{j=0}^{n-1}{\mathrm{\Delta }}_{x}u(x_0,y_0+j)\rangle \cong 0\pm g·\frac{\sum {\sigma }_u}{\sqrt{n}}$$ (A2)

where σ_u is the standard deviation in pixel intensity from its mean value. Similarly, the expectation value of the third (noise) term is given by:

$$\langle \sum _{j=0}^{n-1}{\mathrm{\Delta }}_{x}n(x_0,y_0+j)\rangle \cong 0\pm \frac{\sum {\sigma }_n}{\sqrt{n}}$$ (A3)

with σ_n being the standard deviation in noise. While the gradient term in Eq (A1) increases by a factor of n, the standard deviations of the inherent variation term and the noise term only increase by a factor of $\sqrt{n}$. If n is large enough, we can neglect the second and third terms in Eq (A1) and obtain Eq (4):

$$\sum _{j=0}^{n-1}{\mathrm{\Delta }}_{x}v(x_0,y_0+j)\cong {\mathrm{\Delta }}_{x}g(x_0,y_{av})·\sum _{j=0}^{n-1}u(x_0,y_0+j)$$

The justification of the above arguments is based only on the statistical properties and do not require the assumptions of homogenous tissue and low noise.