UNDERSTANDING STRUCTURAL EFFECTS OF MULTIPOLE MOMENTS ON AQUEOUS SOLVATION OF IONS USING THE SOFT-STICKY DIPOLE-QUADRUPOLE-OCTUPOLE WATER MODEL

Abstract

The effects of water multipole moments on the aqueous solvation of ions were determined in Monte Carlo simulations using soft-sticky dipole-quadrupole-octupole (SSDQO) water. Water molecules formed linear hydrogen bonds to Cl⁻ using the new SSDQO1 parameters, similar to multi-site models. However, the dipole vector was tilted rather than parallel to the oxygen-Na⁺ internuclear vector as in most multi-site model, while experiment and ab initio molecular dynamics simulations generally indicate a range of values between tilted and parallel. By varying the multipoles in SSDQO, the octupole was found to determine the orientation around Na⁺. Moreover, analysis of the multipoles of more conventional models is predictive of their performance as solvents.

1. Introduction

Ions play crucial roles in the structure, dynamics, and function of biological molecules including the stability and enzymatic activity of proteins [1–3]. In addition, biological macromolecules contain nonpolar, polar, and charged species making their solvation very complex since the water structure around each is very different. Because of the complexity of water structure, computer simulations using explicit water and counterions are powerful techniques for studying biological macromolecules in aqueous solution. A water model must have both good pure water and solvent properties to model the complex solvation but also be computationally efficient since computing the water-water interaction is the most time-consuming process in these simulations.

Currently, non-polarizable atomistic potential energy functions having multiple fixed interaction sites with partial charges for electrostatic interactions are widely used for water, with each water model having strengths and limitations [4]. Popular water models include the three-site SPC/E [5] and TIP3P [6], the four-site TIP4P [7], and the five-site TIP5P [8] models. The three-site models are often used because of their computational efficiency and reasonable pure liquid properties in comparison to experiment: SPC/E reproduces structural and dynamical properties in pure water simulations quite well while TIP3P does less well in structural and dynamical properties but has better dielectric properties than SPC/E [9]. TIP4P also has good structural properties but has not been widely used in simulations of biomolecules in part because of poor dielectric properties [9]. Recent reparameterizations of TIP4P, referred to as TIP4P-Ew [10] and TIP4P/2005 [11], are promising since both have excellent pure water properties. On the other hand, the five-site model TIP5P and the recent extension for Ewald sums referred to as TIP5P-E [12] has excellent structural, dielectric, and dynamical properties but also requires ~55% more computer time than the three- and four-site models [8,13].

The water structure around ions using most multi-site water models is similar. The ion-water radial distribution functions are similar [14–18], with the first peak located within ~0.1 Å of neutron diffraction results [19]. Also, multi-site models generally give a coordination number around Cl⁻ of ~7 with the water molecules in the first hydration shell in a hydrogen bonding orientation, in good agreement with neutron diffraction experiments [20]. However, while multi-site models give a coordination number of ~6 around Na⁺ with the water molecules in a dipolar orientation with the dipole vector parallel to the ion-water internuclear vector, neutron diffraction experiments indicate a coordination number of ~5 [21] and suggest that water has a broad range of orientations between the dipolar orientation to a tilted orientation with a “lone pair” pointing toward the ion [21]. Ab initio quantum mechanics/molecular mechanics molecular dynamics (AI/MM-MD) simulations in which the first hydration sphere is treated by ab initio quantum mechanics while the environment is described by classical pair potentials [22] as well as more recent ab initio molecular dynamics (AIMD) [23–25] predict coordination numbers of ~5 around Na⁺, similar to experiment. Moreover, AI/MM-MD predicts a preference for the tilted orientation and AIMD predicts a broad distribution of orientations of the first shell waters between the tilted and dipolar orientation, also similar to experiment.

In a different direction from the multi-site models, the soft sticky dipole-quadrupole-octupole (SSDQO) model of water [26] was recently developed, which has a single-site with a van der Waals sphere and dipole, quadrupole, and octupole tensors. The dipole and quadrupole can mimic hydrogen bonding [27]; however, at least the octupole is necessary to distinguish between solvation of cations and anions [28,29]. The electrostatic interaction potential in SSDQO is the exact multipole expansion up to order 1/r⁴, contains an approximate 1/r⁵ term, and neglects higher order terms so that only rotations of the molecule and not of the moment tensors are needed. Because of this approximate multipole expansion (AME), SSDQO is about three times faster in Monte Carlo simulations and about two times faster in molecular dynamics simulations than the three-site models. In addition, the multipole electrostatics gives straightforward combining rules with partial charges from atomistic force fields. Remarkably, the SSDQO model reproduces short range of several multi-site models for the pure liquid when the multipole moments of the respective multi-site model are used [26,30] and of SPC/E in aqueous solutions polar and ionic solutes using SPC/E parameters when the ion-water potential includes the linear charge-hexadecapole (1/r⁵) term [31,32]. Moreover, new optimized parameters for SSDQO (referred to as SSDQO1) give excellent pure water properties not only at ambient conditions where the parameters were optimized but also over a wide range of temperatures and pressures [33]. Interestingly, while SSDQO1 gives radial distribution functions around the hydroxyls in sugars that are consistent with SPC/E, TIP4P-Ew, and TIP5P, the orientation of the water in the first shell around the hydroxyls differs and is more consistent with limited experimental data on the hydration of methanol [34]. Because of the limited data for sugars, it is important to investigate the solvation of simpler solutes by SSDQO1 and other water models where more information is available.

The multipole moments of the SSDQO model can be independently varied, thus making the model more flexible than traditional multi-site models, where changing the location and strength of the partial charges affects all higher multipole moments. Given the discrepancies between the multi-site models versus the experimental and AIMD studies, the determination of how the multipole moments affect the solvation structure affords the opportunity of modifying the SSDQO model for solvation without destroying the pure water properties. In particular, the observation that the dipole and quadrupole are sufficient for hydrogen bonding in the pure liquid while the octupole is necessary for distinguishing solvation of cations and anions suggests modifying mainly the octupole. Here, the effects of the multipole moments on the structure of water around Na⁺ and Cl⁻ were studied in radial distribution functions and orientational probabilities of the first shell water from Monte Carlo simulations of SSDQO and other water models. The structure of SSDQO1 water around the ions was compared with SPC/E, TIP4P-Ew, and TIP5P. In addition, the effects of the multipole moments on the structure of water around ions were examined by varying the moments in SSDQO.

2. Methods

Detailed descriptions of the SSDQO water-water and water-ion potentials can be found elsewhere [26,31] so only a brief description is given here. The interaction potential is given by a Lennard-Jones potential and the AME electrostatic potential

$$U_{\mathit{\text{ij}}}(\mathbf{r})=c_m{\epsilon }_{\mathit{\text{ij}}}\left\{{\left(\frac{{\sigma }_{\mathit{\text{ij}}}}{r}\right)}^m-{\left(\frac{{\sigma }_{\mathit{\text{ij}}}}{r}\right)}^6\right\}+\frac{1}{r}\left[q_i{q}_j\right]+\frac{1}{r^2}\left[-q_i\mathbf{(}{\mathit{\mu }}_j·\mathbf{n}\mathbf{)}+\mathbf{(}\mathbf{n}·{\mathit{\mu }}_i\mathbf{)}{q}_j\right]+\frac{1}{r^3}\left[q_i\mathbf{(}{\mathbf{\Theta }}_j:{\mathbf{n}}^{(2)}\mathbf{)}+\mathbf{(}{\mathbf{n}}^{(2)}:{\mathbf{\Theta }}_i\mathbf{)}{q}_j-3\mathbf{(}\mathbf{n}·{\mathit{\mu }}_i\mathbf{)}\mathbf{(}{\mathit{\mu }}_j·\mathbf{n}\mathbf{)}+{\mathit{\mu }}_i·{\mathit{\mu }}_j\right]+\frac{1}{r^4}\left[-q_i\mathbf{(}{\mathbf{\Omega }}_j\therefore {\mathbf{n}}^{(3)}\mathbf{)}+\mathbf{(}{\mathbf{n}}^{(3)}\therefore {\mathbf{\Omega }}_i\mathbf{)}{q}_j+5\mathbf{(}\mathbf{n}·{\mathit{\mu }}_i\mathbf{)}\mathbf{(}{\mathbf{\Theta }}_j·{\mathbf{n}}^{(2)}\mathbf{)}-5\mathbf{(}{\mathbf{n}}^{(2)}:{\mathbf{\Theta }}_i\mathbf{)}\mathbf{(}{\mathit{\mu }}_j·\mathbf{n}\mathbf{)}-2{\mathit{\mu }}_i·{\mathbf{\Theta }}_j·\mathbf{n}+2\mathbf{n}·{\mathbf{\Theta }}_i·{\mathit{\mu }}_j\right]+\frac{1}{r^5}\left[-c_{\text{DO}}\mathbf{(}\mathbf{n}·{\mathit{\mu }}_i\mathbf{)}\mathbf{(}{\mathbf{\Omega }}_j\therefore {\mathbf{n}}^{(3)}\mathbf{)}-c_{\text{DO}}\mathbf{(}{\mathbf{n}}^{(3)}\therefore {\mathrm{\Omega }}_i\mathbf{)}\mathbf{(}{\mathit{\mu }}_j·\mathbf{n}\mathbf{)}+c_{\text{QQ}}\mathbf{(}{\mathbf{n}}^{(2)}:{\mathbf{\Theta }}_i\mathbf{)}\mathbf{(}{\mathbf{\Theta }}_j:{\mathbf{n}}^{(2)}\mathbf{)}\right]$$ (1)

where r = rn is the internuclear vector from particle i to j, ε and σ are Lennard-Jones parameters, m is the power law of the repulsion in the Lennard-Jones interaction, c_m⁻¹ = (6 / m)^6/(m−6) (1 − 6 / m), μ, Θ, and Ω are the dipole, quadrupole, and octupole tensors, respectively, m is a unit vector along the direction of μ, o is a unit vector along the direction of Ω, and c_QQ = 10 and c_DO = 2 are parameters of the SSDQO model. For the water-water interactions, the water molecules i and j interact via the dipole μ, quadrupole Θ, and octupole Ω moments of water, with the monopole q=0. For the ion-water interactions, the charge q_i of the ion interacts with the multipole moments of water molecule j up to the octupole.

For the water molecules, the SSDQO1 parameters are σ = 3.433 Å, ε = 0.089 kcal/mol, m = 9, and the moments are given in Table 1 [33]. The Lennard-Jones sphere and point multipoles as well as the moment of inertia were centered on the water oxygen. The parameters for SPC/E [5], TIP3P [6], TIP4P-Ew [10], and TIP5P [8] and for the ion (σ= 2.583 Å and ε = 0.100 kcal/mol, for Na⁺ and σ = 4.401 Å and ε = 0.100 kcal/mol for Cl⁻) [35] are from the literature. For the ion-water interactions, m = 12 and standard combining rules for Lennard-Jones parameters were used [σ_ij = ½ (σ_ii + σ_jj) and ε_ij = (ε_ii ε_jj)^1/2]; however, for SSDQO1, σ and ε of water are scaled by 2^−1/9 and 16/27, respectively, to account for the different m.

Table 1.

SSDQO1 and multi-site model moments and coordination numbers n (integrated to 3.2 Å for Na⁺ and 3.8 Å for Cl⁻)

Model	μ (D)	Θ (DÅ)	Δ (DÅ)	Ω (DÅ2)	Γ (DÅ2)	Θ/μ (Å)	Ω/μ (Å2)	Γ/Ω	nNa	nCl
SSDQO1	2.12	2.13	0.00	0.67	1.15	1.00	0.32	1.7	6.26	7.35
SPC/E	2.35	2.04	0.00	0.78	1.96	0.87	0.33	2.5	5.85	6.95
TIP3P	2.35	1.72	0.11	0.61	1.68	0.73	0.26	2.8	5.97	7.28
TIP4P	2.18	2.15	0.08	0.76	2.10	0.99	0.35	2.8	6.19	7.11
TIP4P-Ew	2.32	2.16	0.10	0.77	2.11	0.93	0.33	2.7	6.08	6.46
TIP4P/2005	2.31	2.30	0.09	0.82	2.24	1.00	0.35	2.7	6.00	7.00
TIP5P	2.29	1.56	−0.07	0.50	0.59	0.68	0.22	1.2	6.07	7.13
Expa									5.1	7.3

^aRef. [21]

The Monte Carlo (MC) simulations used standard Metropolis sampling [36] in the NVT ensemble at 298 K for a cubic box (box length, b = 24.835 Å) with periodic boundary conditions. In each case, one solute was solvated in a pre-equilibrated box of water created at the experimental density of water (0.033 46 molecules/ų). The simulations consisted of one ion in 511 water molecules. The solute coordinates were fixed. The configurations were equilibrated for 400 000 MC “passes” (one pass equals N attempted translational and rotational moves, where N is the number of water molecules); structural properties were calculated from the subsequent 400 000 MC passes. The structural properties from five successive 400 000 MC passes were indistinguishable from each other. The acceptance ratio in all MC runs was approximately 40%.

Since the focus here was on testing the short-range structure, the long-range interactions are treated using spherical switching functions between (b/2 − 1) Å and b/2 Å. Ewald methods are a more accurate treatment of the electrostatic energies; however, since the longest-range interactions for a solute in SSDQO water are charge-dipole (1/r²) whereas all of the electrostatic interactions in site-model water are charge-charge (1/r), the error here is less than for a completely site-site potential. In our previous molecular dynamics (MD) simulations for pure water using SSDQO, only the long-range dipole-dipole (1/r³) terms were treated by Ewald methods while the higher order (1/r⁴ and 1/r⁵) terms were treated by truncation [30,33]. Ewald methods for charges in SSDQO water will be implemented in our MD simulations of solutes in water along with a more thorough investigation of the treatment of the long-range higher order multipole terms including fast multipole methods [37] and the extension of the isotropic period sum (IPS) method [38] to multipoles.

3. Results and Discussion

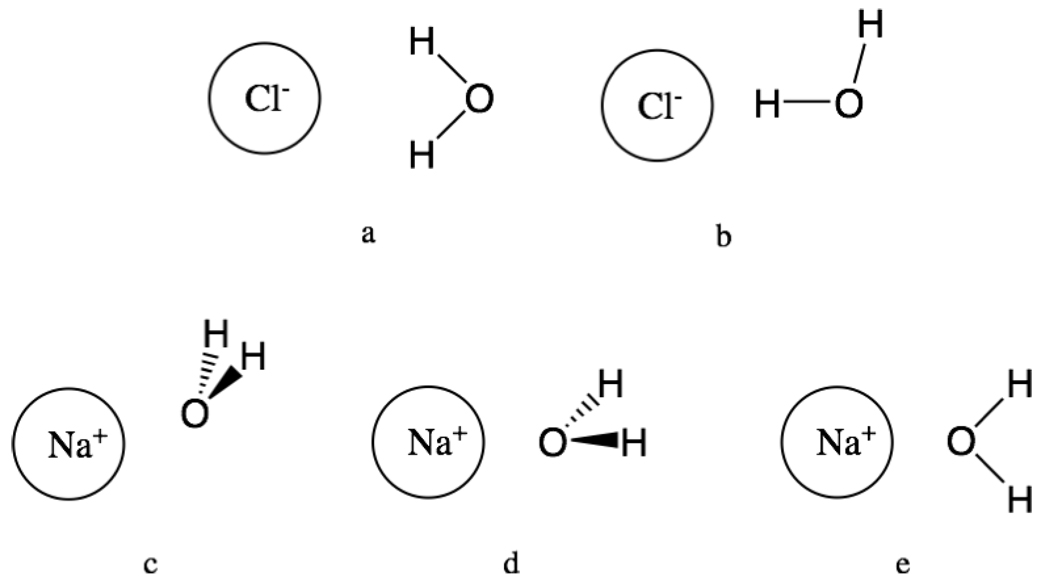
The structure of water around Na⁺ and Cl⁻ in the Monte Carlo simulations was examined. The ion-solvent radial distribution functions g_ij(r) for the solvent atom j (either the water O or H) around the ion i (either Na⁺ or Cl⁻) were calculated. In addition, the orientational probabilities P(cos θ) were calculated for the water molecules in the first shell around the ions, where θ is the angle between the ion-water O internuclear vector and the dipole vector of water. Some possible orientations of a water molecule corresponding to different values of θ are shown in Fig. 1.

Fig. 1.

Orientation of water with respect to ion: a) bifurcated H-bond, cosθ ≈ −1, b) linear H-bond, $\text{cos}\theta \approx -1/\sqrt{3}$, c) tilted, $\text{cos}\theta \approx 1/\sqrt{3}$, d) dipolar, cosθ ≈ 1

3.1. Comparison of SSDQO1 and multi-site water around ions

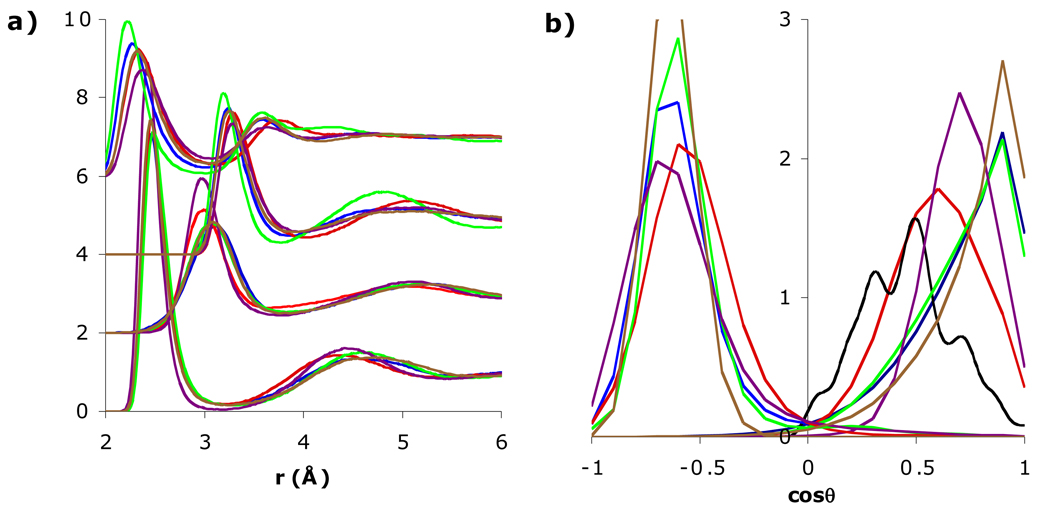
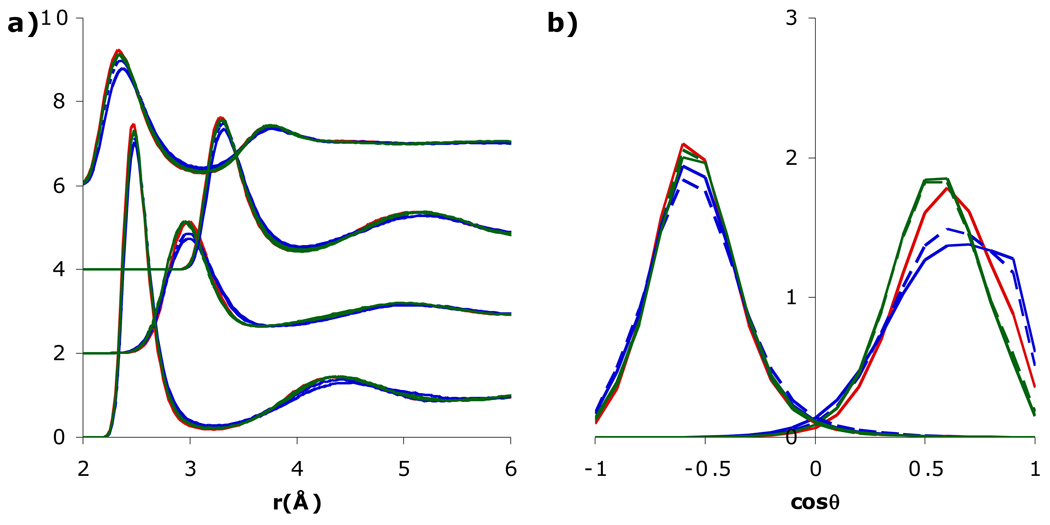
The ionic solution properties of SSDQO1 were first compared with SPC/E, TIP3P, TIP4P-Ew, and TIP5P; moments for each are given in Table 1. The results for TIP4P/2005 (not shown) were similar to TIP4P-Ew. The structural properties around Cl⁻ were similar for SSDQO1 and all of the multi-site water models with minor variations. Specifically, the first peaks in both g_ClO and g_ClH were shifted consistently inward or outward between the models (Fig. 2a). However, the P(cos θ) of the first shell water showed that the molecules have an H-bonded orientation around Cl⁻ in all the models studied (Fig. 2b) although the angular deviation is smaller for both TIP3P and TIP4P-Ew, indicating a somewhat stronger H-bond. On the other hand, for Na⁺, the first peak in g_NaO were at a similar location for all of the models, although it was higher for TIP5P, while the first peak in g_NaH for SSDQO1 and TIP5P was shifted inwards compared to the other water models (Fig. 2a). The P(cos θ) of the first shell water molecules indicated they were oriented with a “lone pair” pointing towards Na⁺ in SSDQO1 and TIP5P (Fig. 2b), consistent with the tilted orientation found in AI/MM-MD simulations [22], while they have an almost dipolar orientation with respect to the Na⁺ in SPC/E, TIP3P, and TIP4P-Ew.

Fig. 2.

Comparison of a) radial distribution functions of Na⁺-O_w, Na⁺-H_w (shifted upwards by 2), Cl⁻-O_w (shifted upwards by 4), and Cl⁻-H_w (shifted upwards by 6) and b) orientational probability of the first shell water around Cl⁻ (left) and Na⁺ (right) for SSDQO1 (red), SPC/E (blue), TIP3P (brown), TIP4P-Ew (green), TIP5P (purple), and AI/MM-MD molecular dynamics [22] (black).

3.2. Effects of the multipole moments on the structure of water around ions

To understand the effects of the multipole moments on the solvation of ions, each multipole moment was varied independently in the SSDQO model while keeping the rest at the values of SSDQO1. The moments were varied to the minimum and/or maximum values found for the multi-site models studied here (Table 1). It is important to note that μ, Θ, and Ω define a tetrahedral quadrupole while Γ creates the asymmetry in which the positive charge is widely separated onto the two hydrogens while the negative charge is more concentrated on the oxygen, even if there is some spread due to the “lone pairs” [26]. Thus, the ratios of these four quantities are important, as discussed below. The water multipoles were first modified only in the ion-water potential while retaining the SSDQO1 multipoles in the water-water potential to examine how the direct interaction between the ion and water is controlled by the strength of the multipole. Next, the water multipoles were modified to be the same in both the water-water and ion-water potentials, which affects the pure water properties so the corresponding pure water radial distribution functions are given in the supplementary materials. Ultimately, the SSDQO moments could be re-optimized for both pure water and solvation or, if necessary, a separate charge-dependent set for charge-water interactions to reflect the average polarization by the charge.

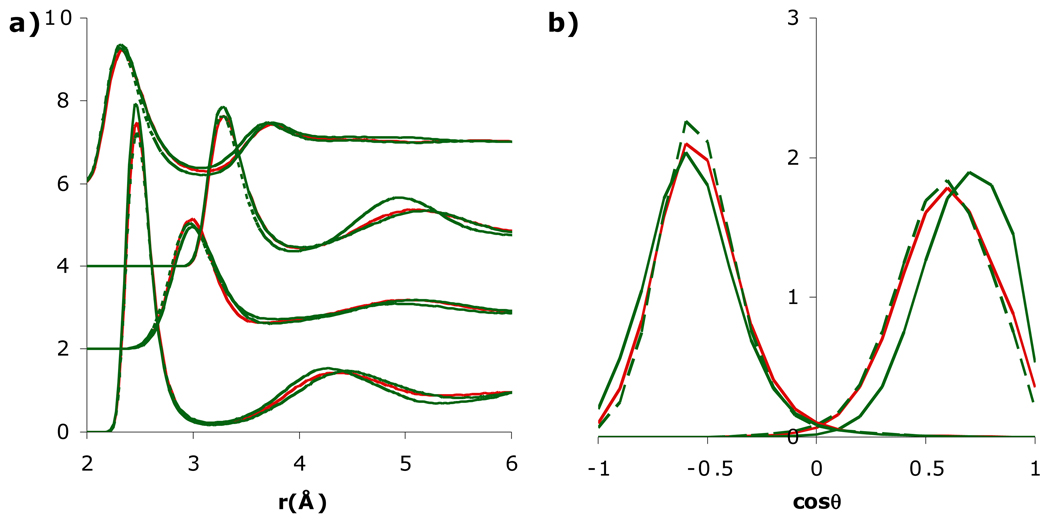
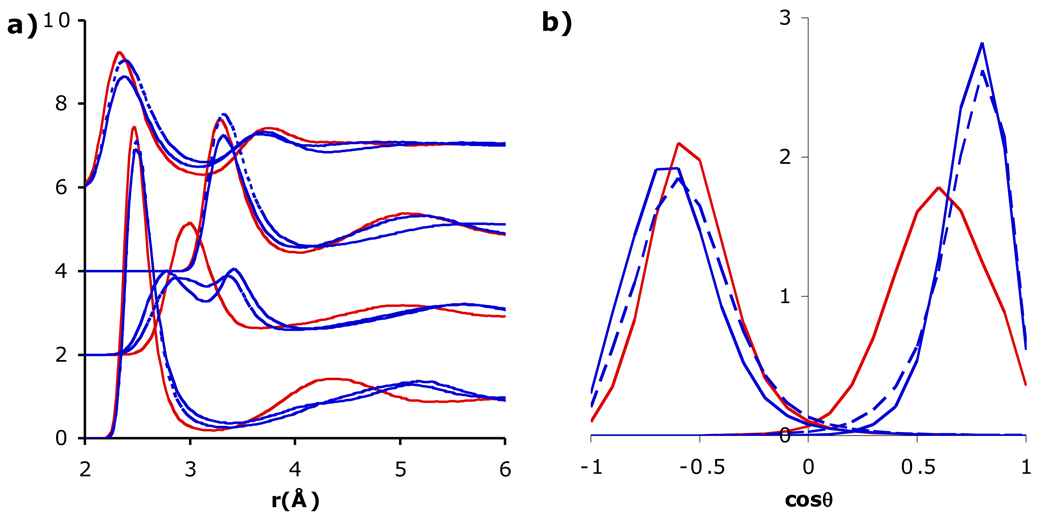
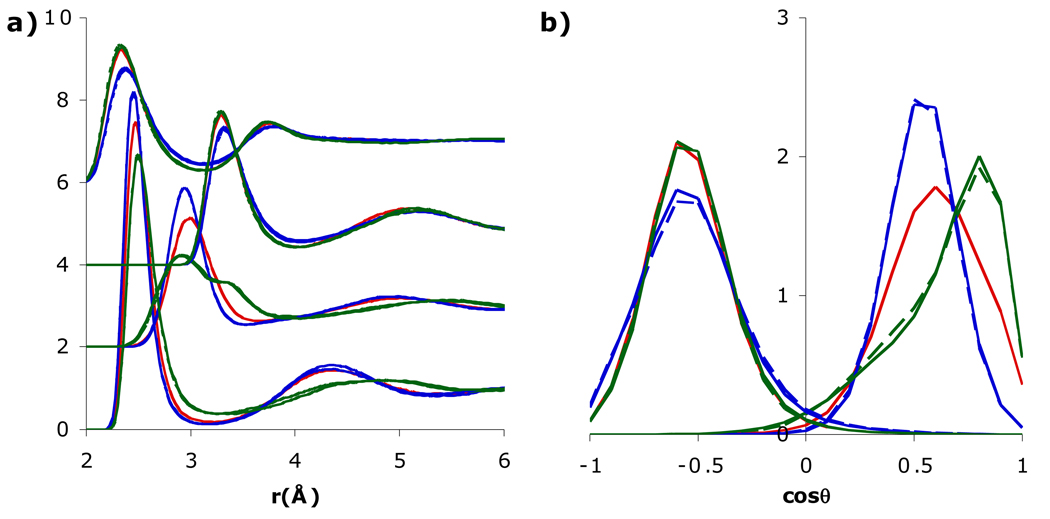
The ratio Θ/μ is heavily influenced by the H-O-H angle (i.e., $\mathrm{\Theta }/\mu =\frac{3}{4}b\text{tan}\frac{1}{2}{\theta }_{\text{HOH}}\text{sin}\frac{1}{2}{\theta }_{\text{HOH}}$ in three-point models [26]), and so varying Θ/μ can potentially change the orientation of water around an ion. Since SSDQO1 has a relatively large quadrupole (Θ/μ = 1 Å), in better agreement with quantum results [33], but a somewhat smaller dipole than most multi-site models, the dipole was first increased to μ = 2.35 D (Θ/μ = 0.91 Å). When the dipole was increased in only the ion-water potential (Fig. 3), the first shell water around Cl⁻ was only slightly affected but that around Na⁺ shifted more towards the dipolar orientation, as might be expected from the increased dipole. Interestingly, when the dipole was increased in the water-water interactions as well, the first shell water around Na⁺ behaved similarly to the original lower dipole (Fig. 3). Since the water-water g(r) indicated stronger hydrogen bonding with increased dipole (Fig. S1), presumably the greater competition by the second shell water led to a preference for the first shell water to be an H-bond acceptor for a second shell water rather than involving both lone pairs with interacting with the Na⁺. On the other hand, decreasing the quadrupole Θ to 1.4 DÅ (Θ/μ = 2/3 Å, close to TIP5P) in only the ion-water potential (Fig. 4) affected the first shell around Cl⁻ slightly more but dramatically affected the first shell around Na⁺ since the orientation shifted more towards the dipole orientation and the g^NaH had a split first peak, similar to SSDQO:SPC/E when the charge-hexadecapole term is neglected [31]. When the quadrupole was also decreased in the water-water interaction, the effects were reduced although not to the extent of the dipole case and the pure water g(r) indicated weaker hydrogen bonding (Fig. S1). Overall, this indicates that a large dipole leads to a more dipolar orientation around Na⁺ while a smaller dipole coupled with a too low Θ/μ ratio can lead to uneven tilted orientation (Fig. 1d).

Fig. 3.

Comparison of a) radial distribution functions of Na⁺-O_w, Na⁺-H_w (shifted upwards by 2), Cl⁻-O_w (shifted upwards by 4), and Cl⁻-H_w (shifted upwards by 6) and b) orientational probability of the first shell water around Cl⁻ (left) and Na⁺ (right) for SSDQO1 (red) and SSDQO1 with all other parameters held constant except μ = 2.35 D (green) for only the ion-water interactions (solid lines) or interactions (dashed lines).

Fig. 4.

Comparison of a) radial distribution functions of Na⁺-O_w, Na⁺-H_w (shifted upwards by 2), Cl⁻-O_w (shifted upwards by 4), and Cl⁻-H_w (shifted upwards by 6) and b) orientational probability of the first shell water around Cl⁻ (left) and Na⁺ (right) for SSDQO1 (red) and SSDQO1 with all other parameters held constant except Θ = 1.40 DŲ (blue) for only the ion-water interactions (solid lines) or interactions (dashed lines).

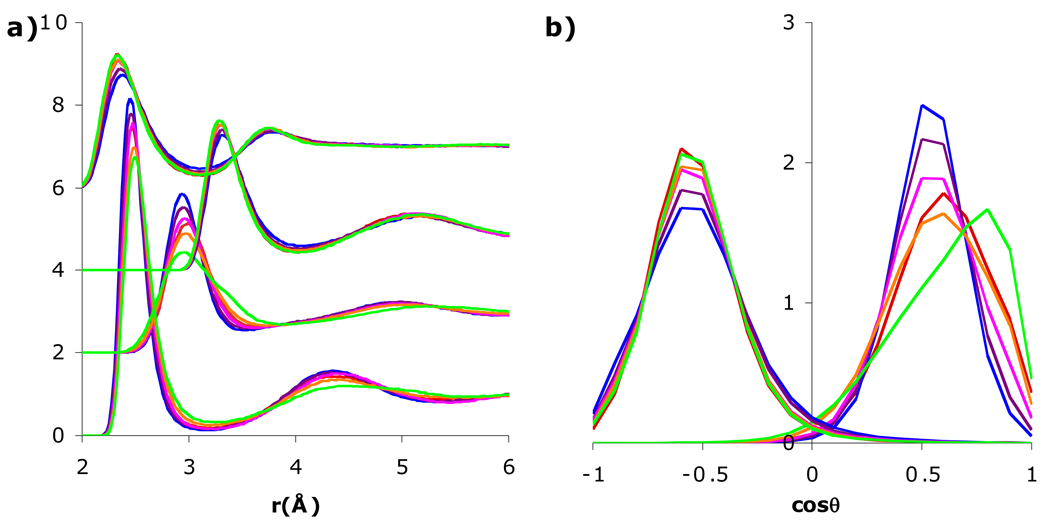
Since the ratio Ω/μ is also heavily influenced by the H-O-H angle (i.e., $\mathrm{\Omega }/\mu =\frac{1}{4}{b}^2[3-5{\text{cos}}^2\frac{1}{2}{\theta }_{\text{HOH}}]$ in three-site models [26]) while the ratio Γ/Ω is controlled by the asymmetry of the positive versus negative charge (i.e., Γ/Ω = 0 for a tetrahedral quadrupole and Γ/Ω = 2.5 for any tetrahedral three-site water model such as SPC/E [26]), the octupole tensor was varied considering these two ratios. Increasing Ω to 0.74 DŲ (Ω/μ = 0.35 Ų) or decreasing it to 0.50 DŲ (Ω/μ = 0.23 Ų), in only the ion-water potential (Fig. 5) again had only a slight effect on the first shell water around Cl⁻ but a higher Ω led to a more tilted orientation while a lower Ω led to a more dipolar orientation. The effect was slightly less pronounced when Ω was modified in also the water-water potential, but the pure water g(r) was not affected (Fig. S1). Moreover, when the octupolar component Γ in only the ion-water potential (Fig. 6) was decreased to 0.50 DŲ, (Γ/Ω ≈ 0.75), the water around both ions was affected slightly but the P(cosθ) became more strongly peaked around Cl⁻ and less strongly peaked around Na⁺. On the other hand, when it was increased to 1.65 DŲ (Γ/Ω ≈ 2.5), the water around the Cl⁻ was less affected but had a more dipolar orientation around Na⁺ and the g_NaO also had a split peak. When Γ was modified in also the water-water potential, the results were essentially identical and the pure water g(r) was not affected (Fig. S1). To further investigate the effect of the Γ/Ω ratio, the octupolar Γ in both the water-ion and water-water potentials was varied from 0.50 DŲ to 1.50 DŲ, in 0.25 DŲ increments (Fig. 7). Interestingly, at Γ = 1.5 Å ≈ 2.2 Ω, the onset of the Na⁺-H_w split peak was observed and the orientational probability shifted drastically to a more dipolar orientation. However, between Γ = 1.15 Å and 1.25 Å, the height of the first peak drops and the coordination number decreases from 6.26 to 6.18. On the other hand, when Ω was increased to 0.74 DŲ or decreased to 0.50 DŲ in both water-water and ion-water potentials while changing Γ so that Γ/Ω = 1.72 as in the original SSDQO1, the solvation around both the Cl⁻ and Na⁺ was relatively unchanged (Fig. S2).

Fig. 5.

Comparison of a) radial distribution functions of Na⁺-O_w, Na⁺-H_w (shifted upwards by 2), Cl⁻-O_w (shifted upwards by 4), and Cl⁻-H_w (shifted upwards by 6) and b) orientational probability of the first shell water around Cl⁻ (left) and Na⁺ (right) for SSDQO1 (red) and SSDQO1 with all other parameters held constant except Ω = 0.50 Dų (blue) or 0.74 Dų (green) for only the ion-water interactions (solid lines) or interactions (dashed lines).

Fig. 6.

Comparison of a) radial distribution functions of Na⁺-O_w, Na⁺-H_w (shifted upwards by 2), Cl⁻-O_w (shifted upwards by 4), and Cl⁻-H_w (shifted upwards by 6) and b) orientational probability of the first shell water around Cl⁻ (left) and Na⁺ (right) for SSDQO1 (red) and SSDQO1 with all other parameters held constant except Γ = 0.50 Dų (blue) or 1.65 Dų (green) for only the ion-water interactions (solid lines) or interactions (dashed lines).

Fig. 7.

Comparison of a) radial distribution functions of Na⁺-O_w, Na⁺-H_w (shifted upwards by 2), Cl⁻-O_w (shifted upwards by 4), and Cl⁻-H_w (shifted upwards by 6) and b) orientational probability of the first shell water around Cl⁻ (left) and Na⁺ (right) for SSDQO1 (red) or SSDQO1 with all other parameters held constant except Γ = 0.50 Dų (blue), 0.75 Dų (purple), 1.00 Dų (magenta), 1.25 Dų (orange), or 1.50 Dų (green).

The SSDQO:SPC/E model needs a linear charge-hexadecapole term in the ion-water potential for Na⁺ to correct the split peak in g_NaH because without it, the ion-water potential with SSDQO:SPC/E has a slightly higher minimum than with SPC/E, which allows a larger number of water molecules with asymmetric orientation in the first hydration shell [31]. However, without a charge-hexadecapole term, SSDQO1 did not show the split peak in g_NaH (Fig. 2) and when either the Θ/μ or the Γ/Ω ratio was reduced while maintaining the rest of the moments (Fig. 4 and 6, respectively), the split peak reappeared. Since radial distribution functions and orientational probabilities with charge-hexadecapoles with the hexadecapole ranging from 0 to 45 Dų were essentially identical (Fig. S3), this term appeared to be unnecessary when the Θ/μ and the Γ/Ω ratios are high enough.

Overall, the octupole moments have the greatest effect on the orientation of the first shell of water around an ion with the least perturbation to the bulk water structure, although they may affect other bulk properties such as the dynamics and dielectrics [33]. Thus, it may be possible to optimize the octupole moments in SSDQO for better ionic solvation properties while maintaining good pure liquid properties. Moreover, since the octupole terms in the energy become negligible beyond the first shell, the induced effects of the ion on the first hydration shell could be included by modifying only the octupole tensor in only the ion-water interaction, while using a different octupole tensor for the water-water interaction optimized for pure liquid properties. However, since the coordination number for SSDQO1 water is similar to multi-site models and thus still too high, it is apparent that further studies are needed and the mixture of dipole and tilted orientations found in experiment [19] and AIMD [23–25] may be important. In particular, the ratios of the populations apparently differ between Li⁺, Na⁺, and K⁺, with increasingly more of the tilted orientation with increasing ionic radius in both experiment [19] and AIMD [24,25], although the experiment indicates almost no dipole orientation for K⁺.

4. Conclusions

The structure of water in the first solvation shell around Cl⁻ and Na⁺ was studied for the SSDQO1, SPC/E, TIP4P-Ew, and TIP5P models in Monte Carlo simulations. While the structure around Cl⁻ was similar, the water favored a dipolar orientation around Na⁺ for SPC/E and TIP4P-Ew and a tilted orientation for SSDQO1 and TIP5P. When the moments in SSDQO were varied, Γ/Ω > ~2 apparently favors the dipolar orientation while Γ/Ω < ~2 apparently favors the tilted orientation, which is also consistent with what was found for the multi-site models. In addition, low Θ/μ ratios favor the dipolar orientation and very low Θ/μ ratios apparently favor an asymmetric packing that leads to a split in the first g_NaH peak as was seen previous for SSDQO parameterized with SPC/E moments [31]. Also, the pure liquid structure is greatly affected by the dipole and quadrupole but relatively unaffected by the octupole tensor. Thus, it may be possible to optimize only the octupole tensor in SSDQO for the orientation of the first shell water around Na⁺, and the short-range nature of the octupole energy terms indicates that the octupole tensor for the ion-water interaction could be made different than the octupole tensor for the water-water interactions to reflect differences due to polarization of the water by the ion. In addition, the relatively small changes in the water around Cl⁻ indicate that the solvation of Cl⁻ is reasonable for the values of the octupole considered here. Moreover, these results show that analyzing more conventional models in terms of their multipole structure is predictive about their performance as solvents.