Solvation of Glucose, Trehalose, and Sucrose by the Soft Sticky Dipole-Quadrupole-Octupole Water Model

Abstract

Water structure around sugars modeled by partial charges is compared for soft-sticky dipole-quadrupole-octupole (SSDQO), a fast single-site multipole model, and commonly used multi-site models in Monte Carlo simulations. Radial distribution functions and coordination numbers of all the models indicate similar hydration by hydrogen-bond donor and acceptor waters. However, the new optimized SSDQO1 parameters as well as TIP4P-Ew and TIP5P predict a “lone-pair” orientation for the water accepting the sugar hydroxyl hydrogen bond that is more consistent with the limited experimental data than the “dipole” orientation in SPC/E, which has important implications for studies of the cryoprotectant properties of sugars.

1. Introduction

Carbohydrates are abundant in nature and are used by organisms for multiple purposes such as energy sources for the cell, components of plant cell walls, and glycosylation of proteins [1]. In addition, sugars such as trehalose have industrial uses as cryoprotectants, possibly by making water structure less ordered and thus protecting against ice formation [2,3]. Of particular interest is why trehalose is a better cryoprotectant than other sugars, which has been attributed to factors such as its ability to alter the structure and dynamics of water [4–8]. Computer simulations of sugars in explicit models of water can be useful in understanding the underlying molecular basis of the aqueous solvation of these molecules, including the hydration sites of sugars and the local water structure around sugars [2]. In computer simulations, trehalose binds a large number of water molecules [9–12], which might cause greater disruption of the structure of the surrounding water, and the lifetime of the trehalose-water hydrogen bond is longer compared to other sugars [13]. Trehalose also reduces the dynamics of the surrounding water, and depending on concentration, diffuses slower in water compared to other sugars [3]. However, there are contradictory results on the conformational flexibility of the molecule [12,13].

Since sugars have three to seven oxygens per ring allowing formation of multiple hydrogen bonds with water, simulations of water structure around sugars require water models that have good pure water structure as well as solvation properties. The most commonly used water models have partial charges on fixed interaction sites for electrostatics. Three-site models such as SPC/E [14] and TIP3P [15] give a reasonable description of water but have problems with dielectric and dynamical properties, respectively [16]. Moreover, these models may be understructured and have poor temperature dependence of densities [17,18]. On the other hand, the four-site TIP4P-Ew [19] and TIP4P/2005 [20] and the five-site TIP5P [21] model have excellent properties for pure water over a wide range of temperatures, although few studies have been performed of their solvation properties and more sites lead to slower computational times.

Unlike the typical multi-site models, our soft-sticky dipole-quadrupole-octupole (SSDQO) model of water [22] has a single-site with a van der Waals sphere and point dipole, quadrupole, and octupole moments. SSDQO is an improvement over the original soft-sticky dipole (SSD) model [23], which has a dipole and an arbitrary “sticky” hydrogen-bond potential. By replacing the arbitrary potential with a moment expansion, not only is the water-water interaction now physics-based, but also solute-water electrostatics can be described by multipoles rather than requiring new arbitrary sticky potentials for each solute. The interaction potential is the exact moment expansion about a single site up to order 1/r⁴, contains an approximate 1/r⁵ term, and neglects the 1/r⁶ term. Since fewer interatomic distances are needed for the single site and slow higher order matrix multiplications are avoided due to the approximations, SSDQO is about two to three times faster than SPC/E and TIP3P in Monte Carlo [22] and molecular dynamics [24] simulations. When the moments and van der Waals parameters of SPC/E, TIP3P, and TIP5P are used, SSDQO reproduces the water dimer potential energy and radial distribution function of the corresponding multipoint model [22]. In particular, SSDQO using SPC/E moments and van der Waals parameters (referred to as SSDQO:SPC/E) has good thermodynamic, dielectric, and dynamic properties [24]. SSDQO:SPC/E also has similar radial distribution functions as SPC/E around simple ions [25] as well as N-methylacetamide, ethanol, and benzene [26]. The similarity of the radial distribution functions, which are sensitive to the short-range interactions [27], demonstrates that the approximate multipole expansion using moments up to the octupole is accurate even at short distances where multipole expansions are least accurate. Besides increasing the speed and accuracy of simulations relative to commonly used three-point models, the decomposition of the energy in SSDQO leads to different ways of analyzing the solvation energetics; i.e., by separating the dipole interactions from the quadrupolar tetrahedral interactions. Furthermore, the moment approach promises to be useful in treating electrostatics for coarse-grained simulations.

Recently, the moments and Lennard Jones parameters of SSDQO have been optimized to reproduce the experimental properties of liquid water. Using the new SSDQO parameters (referred to as SSDQO1), the pure liquid has a dielectric constant of 75 and a density of 0.999 at 298 K and displays excellent structural and dynamical properties over a range of temperatures and pressures [28]. SSDQO1 has moments similar to TIP4P-Ew and TIP4P/2005 and uses a 9-6 Lennard-Jones potential; the large quadrupole moment localizes the hydrogen-bond donating nearest-neighbor waters, resulting in a more ordered tetrahedral structure of the water. Given the good temperature dependence of SSDQO1, it is potentially a good model for studying the cryoprotectant properties of sugars. However, since most force fields for sugars [29–35] use a partial charge description for the electrostatics of the sugar, it is first necessary to assess how the multipole description interacts with a multi-site, partial charge description of a solute. Since a sugar ring has several hydroxyl groups plus the ring oxygen, which can act as hydrogen bond donors and acceptors for water, they are particularly stringent tests for aqueous solvation.

Here, SSDQO is assessed for solvating sugars modeled by the CHARMM potential energy function in Monte Carlo simulations of glucose, trehalose, and sucrose. Both the distance and orientation of the waters around the sugar oxygens will affect not only the solvation energies but also the disruption of the tetrahedral structure of liquid water by a sugar molecule, which may be important in the cryoprotectant properties of sugars. The radial distribution functions and coordination numbers in SSDQO:SPC/E, SSDQO1, and SPC/E are compared to assess how the approximate multipole expansion treats the complex hydration of sugars and to see how different potentials affect the first hydration shell. In addition, a detailed examination of the radial distribution functions, coordination numbers, and angular probabilities for the anomeric oxygen of glucose in SSDQO:SPC/E, SSDQO1, SPCE/E, TIP4P-Ew, and TIP5P is made to compare how the different potentials affect the hydrogen bonding orientation of the first shell water around a sugar hydroxyl.

2. Methods

Detailed descriptions of the SSDQO water-water and water-ion potentials can be found elsewhere [22,25] so only a brief description is given here. The interaction potential is given by a Lennard-Jones potential and an electrostatic potential that is an exact multipole expansion up to order 1/r⁴ with an approximation for the 1/r⁵ term

$$U_{\mathit{\text{ij}}}(\mathbf{r})=c_m{\epsilon }_{\mathit{\text{ij}}}\{{\left(\frac{{\sigma }_{\mathit{\text{ij}}}}{r}\right)}^m-{\left(\frac{{\sigma }_{\mathit{\text{ij}}}}{r}\right)}^6\}+\frac{1}{r}\left[q_i{q}_j\right]+\frac{1}{r^2}[-q_i({\mathit{\mu }}_j·\mathbf{n})+(\mathbf{n}·{\mathit{\mu }}_i\left)q_j\right]+\frac{1}{r^3}\left[q_i\right({\mathbf{\Theta }}_j:{\mathbf{n}}^{\mathbf{(}2\mathbf{)}})+({\mathbf{n}}^{\mathbf{(}2\mathbf{)}}:{\mathbf{\Theta }}_i)q_j-3(\mathbf{n}·{\mathit{\mu }}_i\left)\right({\mathit{\mu }}_j·\mathbf{n})+{\mathit{\mu }}_i·{\mathit{\mu }}_j]+\frac{1}{r^4}[-q_i({\mathbf{\Omega }}_j\therefore {\mathbf{n}}^{\mathbf{(}3\mathbf{)}})+({\mathbf{n}}^{\mathbf{(}3\mathbf{)}}\therefore {\mathbf{\Omega }}_i)q_j+5(\mathbf{n}·{\mathit{\mu }}_i\left)\right({\mathbf{\Theta }}_j:{\mathbf{n}}^{\mathbf{(}2\mathbf{)}})-5({\mathbf{n}}^{\mathbf{(}2\mathbf{)}}:{\mathbf{\Theta }}_i\left)\right({\mathit{\mu }}_j·\mathbf{n})-2{\mathit{\mu }}_i·{\mathbf{\Theta }}_j·\mathbf{n}+2\mathbf{n}·{\mathbf{\Theta }}_i·{\mathit{\mu }}_j]+\frac{1}{r^5}\left[q_i{\mathrm{\Phi }}_j\right({\mathbf{m}}_j·\mathbf{n}\left)\right({\mathbf{o}}_j\therefore {\mathbf{n}}^{\mathbf{(}3\mathbf{)}})+({\mathbf{n}}^{\mathbf{(}3\mathbf{)}}\therefore {\mathbf{o}}_i\left)\right(\mathbf{n}·{\mathbf{m}}_i){\mathrm{\Phi }}_i{q}_j-c_{\text{DO}}(\mathbf{n}·{\mathit{\mu }}_i\left)\right({\mathbf{\Omega }}_j\therefore {\mathbf{n}}^{\mathbf{(}3\mathbf{)}})-c_{\text{DO}}({\mathbf{n}}^{\mathbf{(}3\mathbf{)}}\therefore {\mathbf{\Omega }}_i\left)\right({\mathit{\mu }}_j·\mathbf{n})+c_{\text{QQ}}({\mathbf{n}}^{\mathbf{(}2\mathbf{)}}:{\mathbf{\Theta }}_i\left)\right({\mathbf{\Theta }}_j:{\mathbf{n}}^{\mathbf{(}2\mathbf{)}}\left)\right]$$ (1)

where r = rn is the internuclear vector from particle i to j, ε and σ are Lennard-Jones parameters, m is the power law of the repulsion in the Lennard-Jones interaction, c_m⁻¹ = (6 / m)^6/(m−6)(1 – 6 / m), µ, Θ, and Ω are the dipole, quadrupole, and octupole moment matrices, respectively, and c_QQ = 10 and c_DO = 2 are parameters of the SSDQO model. In the approximate charge-hexadecapole interaction, m is a unit vector along the direction of µ, o is a unit vector along the direction of Ω, and Φ = -H_zzzz/2, where H is the hexadecapole moment matrix. For water-water interactions, the water molecules i and j interact through the dipole µ, quadrupole Θ, and octupole Ω moments of water, with the monopole q=0. For the solute-water interactions, the partial charges q_i of the solute molecule interact with the multipole moments of SSDQO water molecule j up to the hexadecapole Φ. This potential allows straightforward combining rules for interaction with other molecules.

The CHARMM27 potential energy function [29] was used for all solutes. For the water molecules, the SSDQO:SPC/E parameters are σ = 3.1655 Å, ε = 0.1554 kcal/mol, m = 12, µ = 2.3503 D, Θ = 2.0355 × 10⁻²⁶ esu-cm², Δ = 0, Ω = 0.7834 × 10⁻³⁴ esu-cm³, Γ = 1.9585 × 10⁻³⁴ esu-cm³, Φ = 79×10⁻⁴² esu-cm⁴ [22,25]; the SSDQO1 parameters are σ = 3.433 Å, ε = 0.089 kcal/mol, m = 9, µ = 2.12 D, Θ = 2.13 × 10⁻²⁶ esu-cm², Δ = 0, Ω = 0.671 × 10⁻³⁴ esu-cm³, Γ = 1.15 × 10⁻³⁴ esu-cm³ [28], Φ = 45×10⁻⁴² esu-cm⁴; and the SPC/E parameters are from the literature [14]. For the solute-water interactions, m = 12 and standard combining rules for Lennard-Jones parameters were used [σ_ij = ½ (σ_ii + σ_jj) and ε_ij = (ε_ii * ε_jj)^1/2]; however, for SSDQO1, σ and ε of water are scaled by 2^−1/9 and 16/27, respectively, to account for the different m.

The Monte Carlo simulations used standard Metropolis sampling [36] in the NVT ensemble at 298 K for a cubic box (box length, b = 24.835 Å). Periodic boundary conditions and spherical switching functions between (b/2 – 1) Å and b/2 Å were applied. In each case, one solute was solvated in box of water created at the experimental density of water (0.033 46 molecules/ų). The simulations consisted of one glucose molecule in 486 water molecules, one trehalose in 474 waters, and one sucrose in 472 waters. The configurations of all solutes were taken from the Cambridge Structural Database [37]. The solute coordinates were fixed so that the differences in the hydrogen bonding could be compared for the same solute conformation, given the conformational flexibility of the disaccharides [12,13]. The configurations were equilibrated for 400 000 MC “passes” (one pass equals N attempted translational and rotational moves, where N is the number of water molecules); averages and standard deviations were calculated from the subsequent five consecutive 400 000 MC passes except for TIP4P-Ew and TIP5P, which were over 400 000 passes only. The acceptance ratio in all MC runs was approximately 40%.

3. Results and Discussion

Radial distribution functions of glucose, trehalose, and sucrose

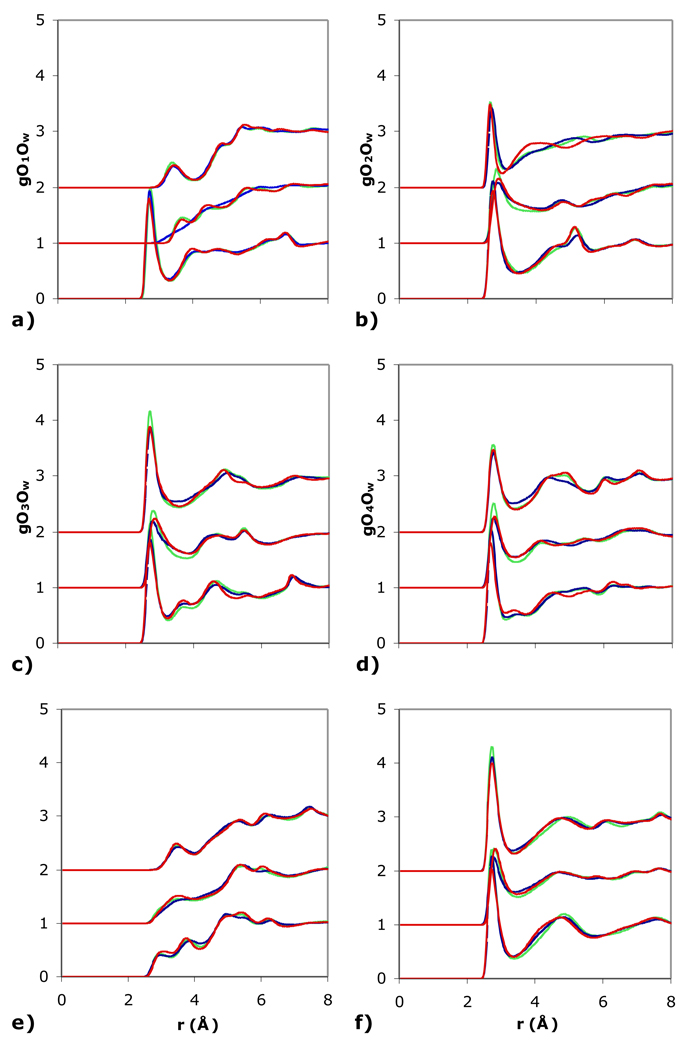
The structuring effects of hydrogen bonding on the solvent as well as the preferred hydration sites [38] were examined in the radial distribution functions of SSDQO and SPC/E water around the oxygens of glucose, trehalose, and sucrose (Fig. 1). Since the trehalose molecule has an α,α-1,1-glycosidic bond between the two α-glucose units while the sucrose molecule has an α-1,2-glycosidic bond between the α-glucose and the fructose, the discussion will focus on the common glucose ring, which for trehalose will refer to the one with the unprimed oxygens. The solute-solvent radial distribution functions g_ij(r) are for the solvent atom j (either the water O or H) around the solute atom i (either the sugar oxygen O_n or the corresponding hydroxyl hydrogen H_n). The number of waters around each sugar are examined by the coordination number of water oxygens around each sugar oxygen (Table 1) and the hydrogen bonding patterns are examined by the coordination numbers of water hydrogens around each sugar oxygen and water oxygens around each sugar hydroxyl hydrogen (Table S1). A coordinating water oxygen found in the O_n-O coordination number will be considered a strong hydrogen bond donor if the corresponding O_n-H coordination number is one and a strong hydrogen bond acceptor if the corresponding H_n-O coordination number is one, with numbers less than one corresponding to weaker hydrogen bonds.

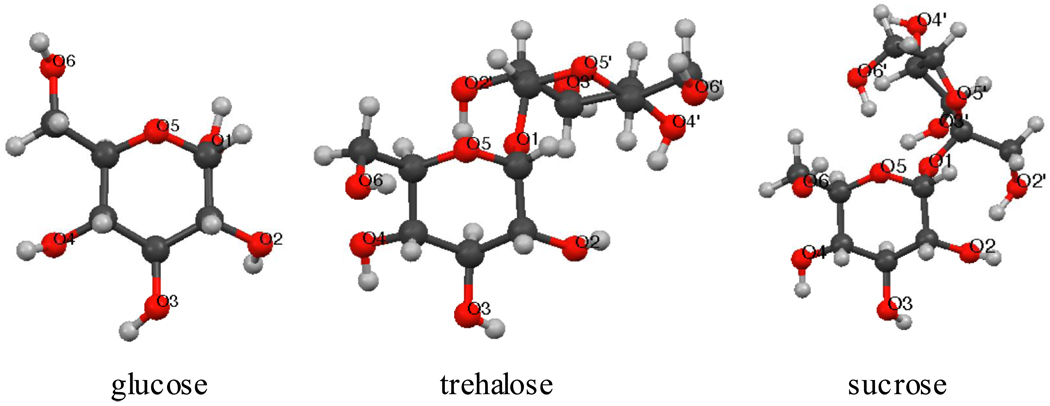
Fig. 1.

Graphical representation of glucose, trehalose, and sucrose and the numbering system.

Table 1.

Number of water molecules in the first shell around the sugar oxygens (O_n) by integrating the O_n-O radial distribution function to 3.4 Å. The average standard deviations of glucose, trehalose, and sucrose respectively were 0.07, 0.08, and 0.09 in SSDQO1, 0.07, 0.08, and 0.07 in SSDQO:SPC/E, and 0.08, 0.08, and 0.06 in SPC/E. Numbers where the last digit is in italics have standard deviations of 0.10 or higher.

Oxygen		Glucose			Trehalose			Sucrose
	SSDQO1	SSDQO: SPC/E	SPC/E	SSDQO1	SSDQO: SPC/E	SPC/E	SSDQO1	SSDQO: SPC/E	SPC/E
1	2.49	2.68	2.55	0.06	0.08	0.06	0.44	0.50	0.38
2	3.20	3.42	3.21	2.68	2.71	2.59	1.83	1.98	1.94
3	2.86	3.04	2.84	2.93	2.90	2.81	3.14	3.17	3.00
4	2.79	2.77	2.79	2.52	2.61	2.48	2.52	2.53	2.53
5	1.19	1.10	1.10	0.91	0.91	0.74	0.53	0.50	0.48
6	3.15	3.25	3.10	2.79	2.70	2.62	2.85	3.08	2.91
2´	-	-	-	2.85	2.98	2.92	2.11	2.16	2.03
3´	-	-	-	2.50	2.70	2.63	3.02	3.12	3.06
4´	-	-	-	2.63	2.78	2.76	2.79	2.89	2.80
5´	-	-	-	0.63	0.59	0.56	0.57	0.43	0.44
6´	-	-	-	3.13	3.29	3.22	1.58	1.65	1.49

For glucose, the oxygens O₁, O₂, O₃, O₄, and O₆ are all free hydroxyl groups while the O₅ is the ring oxygen. The g_O1O for the anomeric oxygen O₁ (Fig. 2a) is consistent with other studies of carbohydrates [2,9,10,13,39–41]. The O₁-O coordination number indicates two to three water molecules around the anomeric oxygen (Table 1), with one water acting as a hydrogen bond acceptor and another as a hydrogen bond donor (Table S1), characteristic of hydrogen bonding of carbohydrates in aqueous solution [42]. The g_OnO of the other hydroxyls are all similar to that of the anomeric oxygen (Figs.2b–2f) except that the distribution around the primary hydroxyl O₆ has a more pronounced second peak (Fig. 2f) since water in the second solvation shell is less perturbed by the solute than around the secondary hydroxyls. The ring oxygen O₅ is less accessible (Fig. 2e) and has about one water molecule that is weakly hydrogen bonded (Tables 1 and S1).

Fig. 2.

Comparison of the radial distribution of the water oxygen of SSDQO1 (red), SSDQO:SPC/E (green), and SPC/E (blue) around the oxygens of glucose, trehalose (shifted upward by 1), and sucrose (shifted upward by 2). (a) O₁, (b) O₂, (c) O₃, (d) O₄, (e) O₅, (f) O₆.

The g_OnO and O_n-O coordination numbers of the glucose ring of the disaccharides trehalose and sucrose are similar to glucose for some oxygens but differ for others. For instance, while the anomeric oxygen O₁ is a free hydroxyl group for glucose, it is less accessible to hydration because it is involved in the glycosidic bond to the second sugar in the disaccharides; thus g_O1O has a very small first peak in the disaccharides compared to glucose (Fig. 2a). Also, the presence of the second ring leads to some differences in the g_OnO (Figs. 2b–2d and 2f) and coordination numbers of the other oxygens (Tables 1 and S1). Moreover, trehalose and sucrose differ in part because two intramolecular hydrogen bonds are formed in sucrose between O_6'H to O₅ (2.85 Å O-O distance, 167° HOH angle) and O_2'H to O₂ (2.78 Å distance, 159° angle) so that in comparison to trehalose, O_2' and O_6' have one less acceptor water hydrogen and O_6' has about a half less hydrogen bond donor water while O₂ and O₅ also have about a half less donor water hydrogen (Tables 1 and S1). Further studies of the effects of intramolecular hydrogen bonds on hydration are warranted.

Overall, SSDQO:SPC/E and SSDQO1 demonstrated similar g_OnO and coordination numbers to SPC/E, although there were some slight differences. For instance, the first peak in g_O1O was located at ~2.8 Å for both SSDQO:SPC/E and SPC/E but was slightly shifted inwards for SSDQO1, while the first minimum was at ~3.3 Å for all three models. In general, the On-O coordination numbers were slightly greater for SSDQO:SPC/E than SPC/E but similar for SSDQO1 and SPC/E. The slightly greater hydration by SSDQO:SPC/E is due to slight more hydrogen-bond donor waters (Table S1) and is consistent with the slightly larger coordination numbers of water around water (4.6 for SSDQO:SPC/E vs. 4.4 for SPC/E) seen in the pure liquid [22].

In addition, the average water-water and solute-water intermolecular energy for the SSDQO and for the multi-site water models were similar (Table S2). Both TIP5P and SSDQO1 have lower water-water potential energy because the self-polarization correction was not included in the parameterization of both models.

The orientation of water around sugar hydroxyls

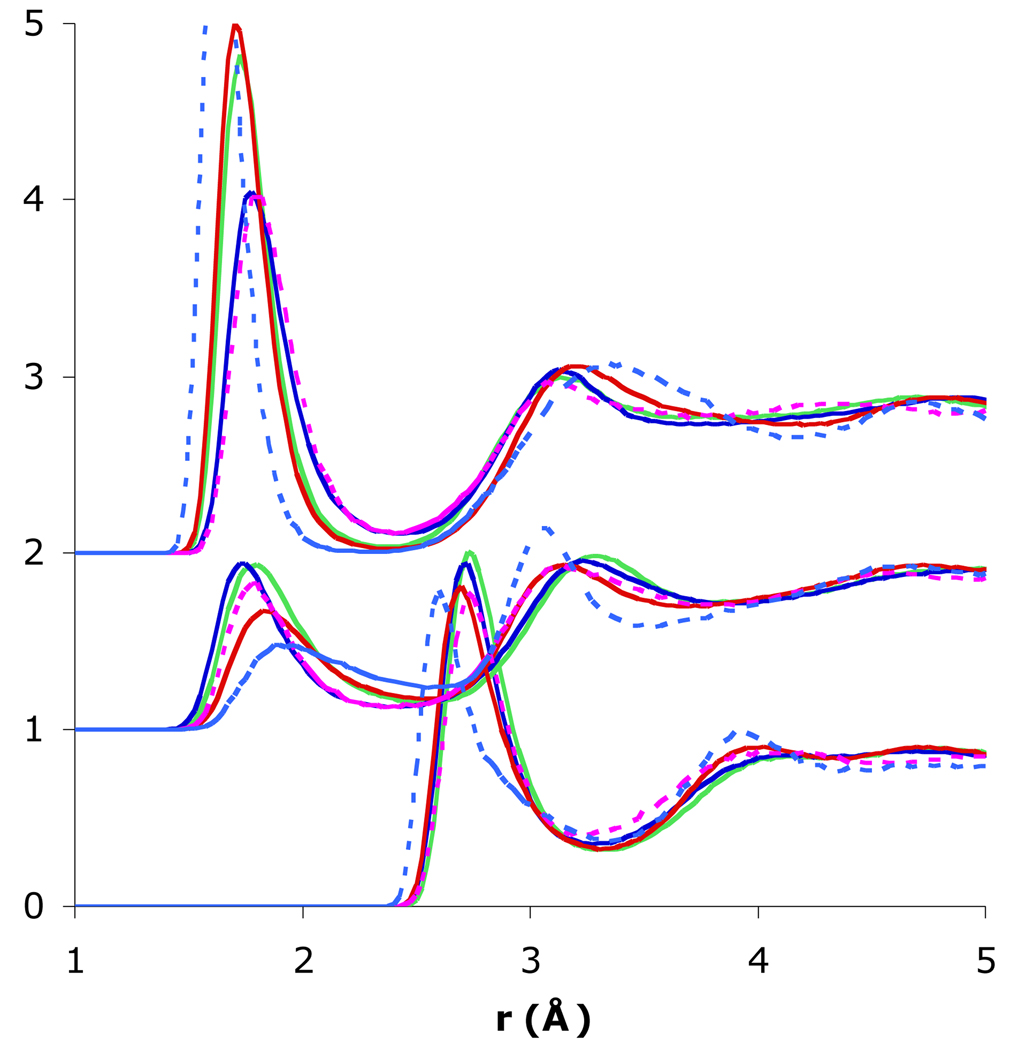
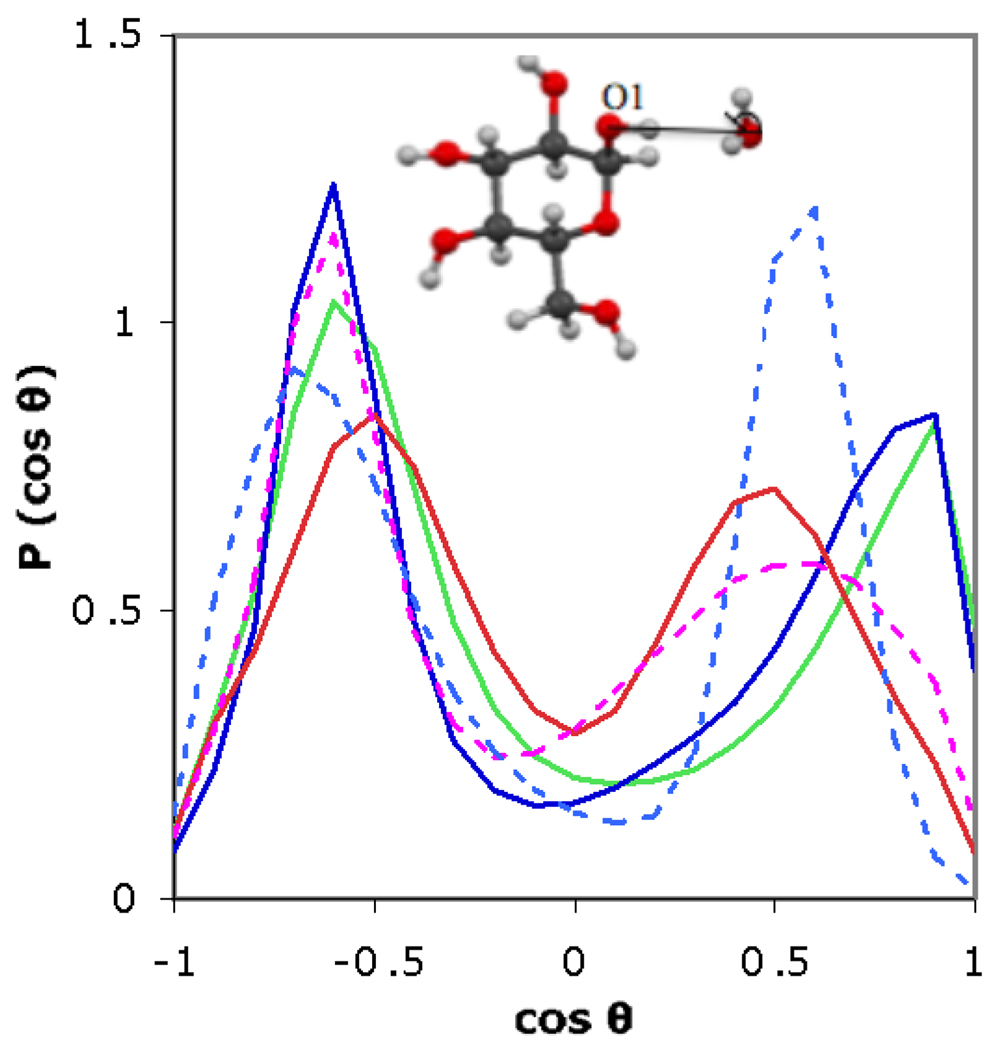
The orientation of water around solute has important implications because it determines the solvation energetics. The orientation of SSDQO:SPC/E, SSDQO1, SPC/E, TIP4P-Ew and TIP5P water around the sugar hydroxyls was examined in the g_O1O, g_O1H, and g_H1O radial distribution functions of glucose (Fig. 3) and coordination numbers (Table 2) and the orientational probability P(cos θ) of the first shell water around the glucose O₁ (Fig. 4), where θ is defined as the angle between the glucose O₁-water O internuclear vector and the dipole vector of the water.

Fig. 3.

Comparison of the radial distributions of glucose O₁- water oxygen (O₁-O_w), glucose O₁-water hydrogen (O₁-H_w, shifted upward by 1), and glucose H₁- water oxygen (H₁-O_w, shifted upward by 2) for SSDQO1 (red), SSDQO:SPC/E (green), SPC/E (blue), TIP4P-Ew (dotted magenta), and TIP5P (dotted light blue).

Table 2.

Coordination numbers of water oxygen (O) and hydrogen (H) around the glucose anomeric oxygen (O₁) and hydroxyl hydrogen (H₁) by integrating the O₁-O radial distribution function to 3.4 Å and from the integration of the O₁-H and H₁-O radial distribution functions to 2.4 Å.

	SSDQO1	SSDQO:SPC/E	SPC/E	TIP4P-Ew	TIP5P
O1O	2.49	2.68	2.55	2.50	2.51
O1H	1.08	1.32	1.11	1.03	0.97
H1O	1.04	1.04	0.99	1.01	1.04

Fig. 4.

Average P(cos θ) as a function of cos θ for the first shell (r = 2.4–3.4 Å) for SSDQO1 (red), SSDQO:SPC/E (green), SPC/E (blue), TIP4P-Ew (dotted magenta), and TIP5P (dotted light blue). The average standard deviation for the SSDQO1, SSDQO:SPC/E, and SPC/E are 0.04, 0.07 and 0.06, respectively. Both TIP4P-Ew and TIP5P results are from single 400 000 steps MC runs.

The g_O1O are quite similar for all of the models (Fig. 3 bottom), and the O₁-O coordination numbers indicate about 2.5 waters in the first shell albeit with some variation in the exact number (Table 2). Also, in all the models, the H₁-O and O₁-H coordination numbers indicate one hydrogen-bond accepting water and one hydrogen-bond donating water in the first shell (Table 2). However, the first peak in g_H1O, which is due to hydrogen-bond accepting waters, is sharper with SSDQO:SPC/E, SSDQO1, and TIP5P than with SPC/E and TIP4P-Ew (Fig. 3 top). Also, the first peak of the g_O1H, which is due to hydrogen-bond donating waters, is progressively shifted further outward in TIP4P-Ew, SSDQO1, and TIP5P relative to SPC/E while the second peak of the g_O1H, which is due to both the other hydrogen of the hydrogen-bond donating waters and the two hydrogens of the hydrogen-bond accepting waters, is shifted slight inward relative to SPC/E (Fig. 3 middle).

Examining the P(cos θ) of the first shell water, the water that donates a linear hydrogen bond to O₁ give rise to the peak at −0.6 in all of the models, with some variation in the peak shape and location (Fig. 4). However, the acceptor water molecule in SPC/E and SSDQO:SPC/E has an almost dipolar orientation with respect to the O₁-O vector with a peak at 0.8 while in TIP4P-Ew, SSDQO1 and TIP5P it has an orientation corresponding to a hydrogen bond with the “lone pair” of the water with a peak at about 0.5. Although to our knowledge there is no experimental information for sugars, this orientation is consistent with X-ray diffraction studies of the orientation of water molecules accepting hydrogen bonds from the methanol hydroxyl in aqueous methanol [43], although further experimental information is necessary. Moreover, the orientation of SSDQO1 around ions is in better agreement with QM/MM simulations than SPC/E (unpublished results).

4. Conclusions

Here, the SSDQO model using SPC/E parameters as well as the new optimized SSDQO1 parameters was shown to solvate sugars described by partial charges in reasonable agreement with solvation by SPC/E, which supports the usage of the single point, multipole moment interaction potential of SSDQO with the multiple point, partial charge interaction potential commonly used in force fields for biological macromolecules. Specifically, the good agreement of SSDQO:SPC/E with SPC/E demonstrates our approximate multipole expansion can mimic a point charge model for the water. In addition, all of the models tested (SSDQO:SPC/E, SSDQO1, SPC/E, TIP4P-Ew, and TIP5P) give similar results for the number of hydrogen bond donor and acceptor waters in the first shell. However, SSDQO1, TIP4P-Ew, and TIP5P, which all demonstrate good temperature dependent properties for the pure liquid, predict a markedly different orientation of the water accepting a hydrogen bond from the sugar hydroxyl than SPC/E and SSDQO:SPC/E; namely a “lone pair” orientation. Although the correct orientation in sugars has not been determined experimentally, the orientation in SSDQO1, TIP4P-Ew, and TIP5P is consistent with experimental studies of methanol in water [43]. Since the orientation of the waters will affect not only the solvation energies but may play a role in the disruption of water structure by a sugar and thus its cryoprotectant properties, further studies of the correct orientation are essential.

Overall, SSDQO1 promises to be a good model for studies of sugars in aqueous solution under cryotemperatures since the pure water density and other properties are excellent over a wide range of temperatures. Moreover, given more information from experiment and quantum calculations about the correct orientation, the parameters of SSDQO model are more flexible for further optimization than multi-site models. More generally, the computational efficiency of SSDQO, which is about two to three times faster in molecular dynamics and Monte Carlo simulations than SPC/E or TIP3P, makes it potentially valuable for computational simulations of large macromolecules in aqueous solution, where the number of water molecules needed is substantial. Finally, the results demonstrate the efficacy of our approximate moment expansion for treating electrostatics in coarse-grained modeling, especially when different parts are treated at various levels of detail, from atomistic to increasingly coarse-grained, in the same simulation. For instance, the current force fields for sugars have not been optimized for “lone pair” effects of the sugar hydroxyl oxygen, which will also affect the orientation of the solvating waters, so the hydroxyl group could be replaced by a multipole expansion.