Abstract
Generalized Born (GB) models provide a computationally efficient means of representing the electrostatic effects of solvent and are widely used, especially in molecular dynamics (MD). A class of particularly fast GB models is based on integration over an interior volume approximated as a pairwise union of atom spheres—effectively, the interior is defined by a van der Waals rather than Lee-Richards molecular surface. The approximation is computationally efficient, but if uncorrected, allows for high dielectric (water) regions smaller than a water molecule between atoms, leading to decreased accuracy. Here, an earlier pairwise GB model is extended by a simple analytic correction term that largely alleviates the problem by correctly describing the solvent-excluded volume of each pair of atoms. The correction term introduces a free energy barrier to the separation of non-bonded atoms. This free energy barrier is seen in explicit solvent and Lee-Richards molecular surface implicit solvent calculations, but has been absent from earlier pairwise GB models. When used in MD, the correction term yields protein hydrogen bond length distributions and polypeptide conformational ensembles that are in better agreement with explicit solvent results than earlier pairwise models. The robustness and simplicity of the correction preserves the efficiency of the pairwise GB models while making them a better approximation to reality.
1 Introduction
The effects of aqueous solvent are critical to the structure and function of biological macromolecules. Commonly, solvent is represented explicitly, by models of multiple water molecules, or implicitly, by a high dielectric region and additional apolar solvation terms. Although explicit solvent is a more physically rigorous representation, implicit solvent models have the advantage of dramatically reducing the degrees of freedom that must be sampled by eliminating those associated with the solvent. Additionally, implicit solvent models are often more computationally efficient than their explicit counterparts.
The solvation effects can be described by ΔGsolv: the free energy of transferring a given configuration of a molecule from vacuum to solvent. To facilitate calculation of ΔGsolv, it is typically decomposed into polar and nonpolar components: ΔGsolv = ΔGpol + ΔGnonpol. Here, ΔGnonpol is the free energy of introducing the solute molecule into solvent while electrostatic interactions between the solute and solvent are turned off, and ΔGpol is the free energy change in the system resulting from turning these electrostatic interactions back on. In this work, the focus is on methods for calculating ΔGpol.
Assuming that the solvent can be faithfully represented by a continuum dielectric region, the Poisson-Boltzmann (PB) equation is the most physically correct method of determining ΔGpol, and has been widely used over the past decade.1–7 Application of PB to molecular geometries requires numerical solution of second order partial differential equations, which is fairly computationally intensive and does not easily yield forces, although recent advances in PB methodology have improved the situation somewhat.1, 8–10 Alternatively, generalized Born (GB) models have become popular as a computationally efficient approximation to numerical solutions of the PB equation,6, 11–23 especially for use in dynamics.24–34
GB models evaluate polar solvation free energy as a sum of pairwise interaction terms between atomic charges. When the solute dielectric is 1 and the solvent dielectric is much greater than that of the solute,35 the interactions can be accurately described by an analytical function first proposed by Still et al.,12 that interpolates between the Coulombic limit at long distances and the Born or Onsager limits at small distances,
| (1) |
where ri j is the distance between atoms i and j, qi and q j are partial charges and εw is the dielectric constant of the solvent. The key parameters in this GB function are the effective radii of the interacting atoms, Ri and Rj, which represent each atom’s degree of burial within the solute. More specifically, the effective radius of an atom is defined as the radius of a corresponding spherical ion having the same ΔGpol as the self energy of this atom in the molecule. The self energy is the polar solvation free energy for the molecule with partial charges set to zero for all atoms except the atom of interest. The effective radius of an atom is larger than the intrinsic radius of its atom sphere because of the descreening effects of surrounding atoms, reducing the extent to which the atom charge is screened by solvent. A computationally inefficient, but theoretically interesting method for determining effective radii is to derive them from self energies calculated using well-converged numerical PB solutions. When these “perfect” effective radii are used, GB results are in close agreement with PB results,36 which serve as a natural point of reference for assessing the accuracy of GB, since current GB models are an approximation to the more fundamental formalism of the PB equation. Although this form of GB is impractical for application, it suggests that in aqueous solution the GB function introduced by Still et al. has so far been a minor source of error compared with the error introduced by non-perfect methods for estimating effective radii. Consequently, considerable effort has been spent on improving the way effective Born radii are computed.
In practice, effective radii for each atom are generally calculated by integration of an approximate electric field density due to the atom of interest over some definition of the molecule’s volume,5, 13, 14, 21, 32, 37, 38 although formulations based on surface integrals have also been proposed.19, 23 Here, we focus on volume-based GB models which have traditionally used a Coulomb field integral,
| (2) |
where the origin is centered on atom i and Ωi represents the volume inside the molecule but outside atom i. The effective radius is then calculated according to
| (3) |
where ρi is the intrinsic radius of atom i. Within the Coulomb field approximation (CFA) embodied by the integral in equation 2, it is assumed that the electric field generated by an atomic point charge is unaffected by the non-homogenous dielectric environment created by the solute, so that the field has the form described by Coulomb’s law. The CFA is exact for a point charge at the center of a spherical solute, but it over estimates effective radii for molecular geometries21 as well as for spherical regions when the charge is off center.39 Some of the success of early GB models on small molecules may be attributed to fortuitous cancellation of errors in effective radius calculations between the over estimates of a CFA based integrand and the under estimates of a van der Waals (VDW) based region of integration.32 Improved approximations based on empirical corrections to the CFA21, 38, 40 or theoretical derivations originating with the Kirkwood formula39, 41 have significantly better agreement with effective radii calculated from PB self energies.
The integration in equation 2 can be performed numerically12, 19, 21, 38, 40 or by an analytical pairwise approximation.13–15, 32, 33, 37 GB methods based on analytically approximated integrals are easily extended to calculate solvation forces and are generally faster than their numerically integrated counterparts,42 so they have traditionally found greater application in dynamics.
Most pairwise approximations estimate the integral over a region formed by the union of atom spheres, which is equivalent to a VDW surface dielectric boundary. In calculating the effective radius for atom i, the contribution of every other atom j ≠ i to the integral is determined as a function of ρj and the distance between atoms i and j. Summation of these terms yields an overestimate of the total integral, due to overlap between descreening atoms. To correct for these overlaps, a multiplicative scaling factor, Sx, is introduced to reduce the intrinsic radius of each descreening atom.
In contrast, PB calculations generally use a Lee-Richards molecular surface dielectric boundary, defined by rolling a solvent sphere over the surface of the molecule.43 Although there is no uniquely correct definition of the dielectric boundary, a van der Waals surface creates regions of interstitial high dielectrics that are smaller than a water molecule, while the molecular surface has the conceptually attractive advantage of excluding high dielectric from regions into which a water molecule is too large to fit. Differences between the molecular and VDW surface definitions are minimal for small molecules, where all atoms are well solvated, but become more substantial for macromolecules, where inclusion of interstitial high dielectrics in VDW-based models leads to overestimation of the solvation of interior atoms, relative to molecular surface results.44 This may partially explain why early GB models that had good results for small molecules were less effective when applied to macromolecules.26, 32, 37 Additionally, implicit solvent models that allow interstitial high dielectrics produce incorrect potentials of mean force between non-bonded atoms.44 However, it may not be practical to use the Lee-Richards molecular surface directly in a GB model as it is fairly computationally intensive and can produce unstable or infinite forces for some molecular configurations.1, 9
Attempts to reduce or eliminate the problems of interstitial high dielectrics in GB models have followed two paths. One approach, embodied by the GBMV2 model developed by Lee et al.,38 has been to use numerical integration with adaptations for calculating forces in combination with an analytic surface definition that closely approximates the properties of a molecular surface. A CFA correction term is also employed in the integration. This GB model yields stable dynamics while providing excellent agreement with PB Lee-Richards molecular surface results. However, both the analytic surface definition and the numerical integration are relatively slow, such that the fastest PB models approach the performance of GBMV2.42 Furthermore, the reliance on numerical integration introduces artifacts, such as a lack of rotational invariance.
A different method (OBC GB), developed by Onufriev, Bashford and Case,32 sought to extend the pairwise integration method (HCT GB) of Hawkins, Cramer, and Truhlar13, 14 to reduce the effect of interstitial high dielectrics. Based on the observation that effective radii for buried atoms are larger than for surface atoms, but still much smaller than PB-derived “perfect” effective radii, this method modifies the radius calculation in equation 3 by rescaling the integral from equation 2 according to
| (4) |
where ρ̃i = ρi − 0.09Å and α, β and γ are tunable parameters. When these parameters are set such that most radii are scaled up, the rescaled radii substantially improve agreement with PB solvation free energies, and the computational expense of the rescaling function is minimal so the efficiency of the Hawkins et al. model is retained. In addition, effective radii calculated with equation 4 are smoothly capped at about 30Å, avoiding problems with numerical instability and negative radii that can be encountered when using equation 3. However, by design, the rescaling function only affects atoms that are sufficiently buried that the interstitial high dielectrics can be accounted for only in an averaged, geometry-independent manner. Uncompensated interstitial high dielectrics between more highly solvated surface atoms still affect solvation energies and potentials of mean force.
In this paper, we attempt to combine the best aspects of both of these efforts in development of a GB model that adds a geometrically-based molecular volume correction term accounting for interstitial high dielectrics to the pairwise approximated integration method. Since the correction term is, itself, a computationally efficient pairwise approximation, the performance and numerical benefits of analytical GB models are retained.
The shortcomings of the CFA are now well known, but rigorously derived non-CFA pairwise approximated GB models have only recently been described41 and their stability and performance have not yet been extensively tested on biomolecules, so the model described here extends the Coulomb field-based HCT GB model.
2 Theory
An ideal volume correction term for a GB model based on VDW volume and the CFA would yield the integral of r−4 over the region inside the Lee-Richards molecular surface and outside the van der Waals surface. This region is designated the correction region.
| (5) |
Since the HCT GB integration scheme calculates the value of the integral within the van der Waals surface, adding this correction term would yield an integral over the region within the molecular surface. In the general case, the correction region cannot be analytically defined. However, in the simple case of two closely spaced or overlapping atoms, the correction region forms an analytically definable “neck” region between the two atoms, as seen in figure 1. The general case of the correction region can be approximated by a union of these neck regions calculated pairwise between atoms. In the simplest form of this approximation, developed here, the integral for each atom includes corrections for only the neck regions in which the atom is directly involved. This simple form is a reasonably good approximation because the value of the integrand (r−4) is much higher in the nearby neck regions with which the atom is directly involved than in the distant portions of the correction region formed by interactions between other pairs of atoms.
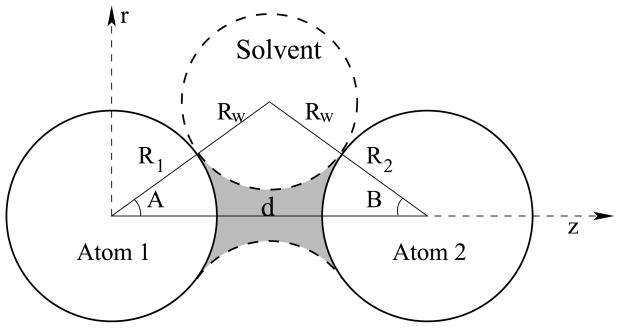
Figure 1.
The neck region (shaded) is defined by the radius of atom 1, R1, the radius of atom 2, R2, the distance that separates them, d, and the radius of the solvent molecule, Rw. The coordinate system used for performing integration is also illustrated (see Appendix I).
Figure 1 illustrates how the geometry of the neck region is defined by four parameters: the radii of the two atoms, R1 and R2; the radius of the solvent molecule, Rw; and the distance between the two atoms, d. Derivations of the expressions for the CFA integrals over the neck region are given in Appendix I. Although the integrands in these expressions are fairly simple, the limits of integration are sufficiently complex to make analytical solution of the integrals impractical. The problem is simplified by considering that in the GB model, parameters R1, R2 and Rw have a relatively small set of discrete values (a single value, in the case of Rw = 1.4 Å), and so d is the only parameter with continuous values. With this view in mind, the function in four variables described by these integrals can be evaluated as a family of single variable functions of d, with each function determined by a particular set of values for R1, R2 and Rw. These functions of d can be plotted by solving the integrals numerically for a range of values of d, producing curves as shown in figure 2.
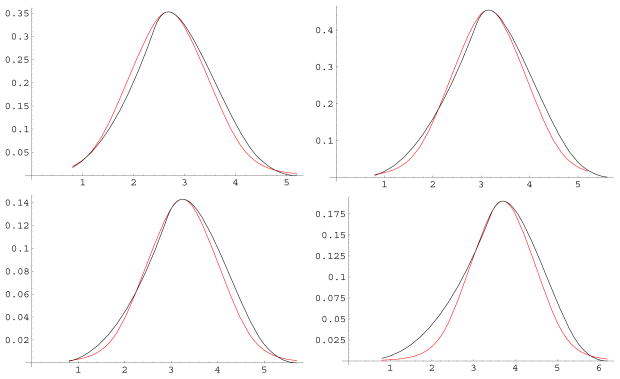
Figure 2.
Values of numerical integration over the neck region (black) and analytical approximation (red) as a function of distance between atoms in angstroms. Left to right, top to bottom, radii (in angstroms) for atoms 1 and 2, respectively are 1.2 and 1.2; 1.2 and 1.7; 1.7 and 1.2; 1.7 and 1.7.
Numerical solution of these integrals is far too computationally costly for application in a GB model. Instead, they are replaced with an empirically determined analytic function shown in equation 6
| (6) |
This function is parameterized by the position (d0) and value (m0) of the maximum, which are determined by numeric optimization (maximization) of the integral of r−4 over the neck region of figure 1. The values of d0 and m0 are dependent on R1, R2 and Rw, but since these variables have a small set of discrete values, tabulating all possible values of d0 and m0 is quite feasible (see Appendix II). As illustrated in figure 2, equation 6 is a very good approximation over the range of atomic radii typically encountered in biomolecules.
Applications of GB solvation models to dynamics require calculation of derivatives with respect to distance. Equation 6 is easily differentiated, yielding equation 7.
| (7) |
Ideally, neck integrals would be calculated only between atoms that are close enough to define a neck region (d < R1 + R2 + 2Rw): beyond this distance the neck integral and its first derivative with respect to d should be zero. However, the analytic approximation used here approaches zero asymptotically, and at d = R1 + R2 + 2Rw its value is on the order of 10−3. Truncating the function at this point would create a discontinuity which could lead to unstable dynamics. A variety of techniques could be employed to smooth this discontinuity; we have taken the simplest approach of continuing to calculate the neck correction for d > R1 + R2 + 2Rw until d is large enough that the value of the function is sufficiently small that the error of truncating it is on the order of rounding error.
The neck correction described by the integrals in Appendix I and approximated by equation 6 is exact for a system of two atoms, but in the usual case of a molecule with more than two atoms, a strict summation of neck integrals calculated pairwise between atoms will tend to over estimate the integral over the correction region. Over estimation of the integral is due to overlap of neck regions with atoms not participating in the neck, as well as overlap with other neck regions, and must be corrected by scaling the contributions to the total integral.
The GBn model (“n” for neck) presented here takes a simple, two step approach to scaling. First, each neck integral value calculated in equation 6 is multiplied by a scaling factor Sneck (Sneck < 1). Second, effective radii are calculated using equation 4 which provides descreening dependent scaling, as well as numerical stabilization for large effective radii. The descreening dependent scaling of the second step helps to compensate for different molecular geometries, as the effective radii of more deeply buried (more de-screened) atoms, which are involved in more necks and thus have more overlaps, can be scaled down to a greater degree than less buried atoms. It appeared likely that a more complex scaling procedure, such as one that employed multiple atom-type dependent values of Sneck, would yield a somewhat more accurate estimate of the molecular volume. However, our tests of such scaling procedures yielded insufficient improvements to justify addition of more free parameters to the model (results not shown); we believe this is because the quality of the current model is most severely constrained by the limitations of the CFA, rather than the simple scaling process described above.
The two step scaling involves four parameters which must be optimized, Sneck, α, β and γ. Since the neck correction alone is expected to bring the integration volume closer to molecular volume, the optimal parameters of equation 4 are different from those used by the OBC model. The key difference between GBn and OBC GB can be best illustrated by a diatomic system such as that in figure 1: the OBC model will produce correct effective radii for only one value of atom-atom separation distance (hence its “geometry-independence”), while the GBn model should calculate accurate radii for this simple system across the entire range of interatomic distances.
Additionally, it is necessary to refit the intrinsic radius scaling factors, Sx. Although formally the Sx scaling factors merely correct overlaps, in practice they have been used as free parameters to optimize GB results for agreement with PB and experimental results.14, 26 As a result, the sets of Sx values used in the HCT and OBC GB models not only correct for atomic overlaps, but also correct for some of the effects of the CFA and interstitial high dielectrics (to the extent that this is possible on an averaged, geometry independent basis). Since the GBn model already accounts for interstitial high dielectrics with the neck term and has a different degree of CFA error due to the altered region of integration, it would clearly be inappropriate to use Sx sets that were fit for VDW regions of integration with the GBn model.
3 Results and Discussion
The ultimate goal of an implicit solvent model is to accurately and efficiently approximate the results of computationally expensive explicit solvent molecular simulations. While agreement with explicit solvent provides a rigorous test of an implicit model, it is often difficult to identify the source of discrepancies due to the dramatic differences between the explicit and implicit solvent formalisms. Therefore the performance of GBn is compared to the earlier OBC GB32 model using multiple levels of less approximate solvation models as standards. Comparison to PB is instructive in identifying the source of shortcomings of the current model, while comparison to explicit solvent provides a more useful assessment of the ultimate quality of the model. The OBC GB model is selected as a reference for comparison because it is among the most recent and most accurate42 pair-wise GB models that do not have a molecular volume correction beyond the “average” rescaling provided by equation 4.
Once the parameters have been optimized, the GBn model achieves approximately a 25% improvement over OBC GB in accuracy of effective radii relative to PB results. The minimal native-state bias and stable dynamics achieved by OBC GB are maintained in this model. A major qualitative improvement of GBn is that it reproduces the free energy barrier to separation of hydrogen bonds that is seen in molecular surface PB results but absent in non-molecular surface implicit solvent models. Although quantitative improvement in agreement of GBn solvation energies with PB solvation energies is fairly small, substantial improvements are seen in agreement between GBn and TIP3P explicit solvent dynamics. Specifically, hydrogen bond length distributions are significantly more similar, there is improved agreement with the TIP3P φ/ψ potential and a dramatic improvement in the conformational ensemble of deca-alanine. The results that have been summarized here are examined in detail in the following.
3.1 Parameterization
Parameters of the GBn model (Sneck, α, β, γ and the Sx parameters for atom types C, H, N and O) were optimized using the Nelder-Mead simplex algorithm.45 The objective function that was minimized measured agreement between PB and GB solvation free energies over a training set consisting of structures from denaturation trajectories of apo myoglobin and protein L and structures representing potentials of mean force (PMF) for two hydrogen bonds and a salt bridge (see Methods for details of the objective function). The objective function has multiple local minima, so 100 minimizations were performed starting from random initial points. Optimized parameter values producing the best overall performance are given in table 1. Treatment of the Sx values as free parameters to optimize GB performance beyond their formal purpose of correcting overlap is made obvious by the values of SO and SH, which exceed 1. This represents a continuation of previous practice, although it may at first appear to be a divergence because previous sets of Sx values where all Sx < 1 may have been incorrectly interpreted as merely correcting overlaps.
Table 1.
Optimized scaling parameters
| Parameter | Value |
|---|---|
| α | 1.095 |
| β | 1.908 |
| γ | 2.508 |
| Sneck | 0.362 |
| SH | 1.091 |
| SC | 0.484 |
| SN | 0.700 |
| SO | 1.066 |
3.2 Comparison with PB effective Born radii and solvation energies
A common first test of a GB model is comparison of effective radii with “perfect” radii derived from PB calculations. Agreement at this level is generally correlated with the overall quality of a GB model. While use of perfect radii in the GB formalism has been shown to guarantee a very good agreement between the GB and PB solvation free energies,36 small improvements in agreement of the effective radii may or may not translate into significantly improved overall performance of the GB model. Nevertheless, radius comparisons are instructive as rough quality measures and in identifying sources of error that may not be readily apparent when molecular solvation free energies are compared. It is most useful to compare inverse radii, as these more faithfully represent the contribution of the effective radii to the energy in equation 1. Such a comparison for a set four structures that includes native and partially unfolded proteins and peptides is presented in table 2. For all structures, the F-test shows a highly significant improvement in the accuracy of effective radii calculated by the GBn model compared to the OBC GB model.
Table 2.
RMS deviation (in units of inverse Å) between inverse effective radii, computed by the GBn and OBC GB models relative to the PB reference with significance of improvement measured by F-test. The β-hairpin and thioredoxin structures are in their native states, while apomyoglobin is represented by two partially unfolded states along an acid denaturation trajectory.46 Both models perform more poorly on thioredoxin than other structures due to a higher number of large effective radius atoms in thioredoxin. The much larger p-value for β-hairpin is due to the small number of atoms in the molecule, resulting in fewer degrees of freedom in the F-test.
| thioredoxin | apomyoglobin-I | apomyoglobin-II | β–hairpin | |
|---|---|---|---|---|
| OBC GB | 0.128 | 0.067 | 0.046 | 0.055 |
| GBn | 0.092 | 0.050 | 0.033 | 0.045 |
| p-value | 10−40 | 10−47 | 10−60 | 10−3 |
A more detailed analysis of effective radii is illustrated in figure 3, showing improvement across the whole range of effective radii. This includes an improvement in the accuracy of large effective radii (left portion of the figure), although these radii continue to have the largest errors. Errors seem to be largest for atoms near crevices that are slightly too small for a water molecule; presumably the pairwise approximation is poorest here.
Figure 3.
Scatter plot comparison of inverse effective radii calculated by the current GB neck model (red +) and earlier OBC GB model (black X) to inverse “perfect” PB radii for thioredoxin (PDB code 2TRX). Diagonal line indicates perfect agreement.
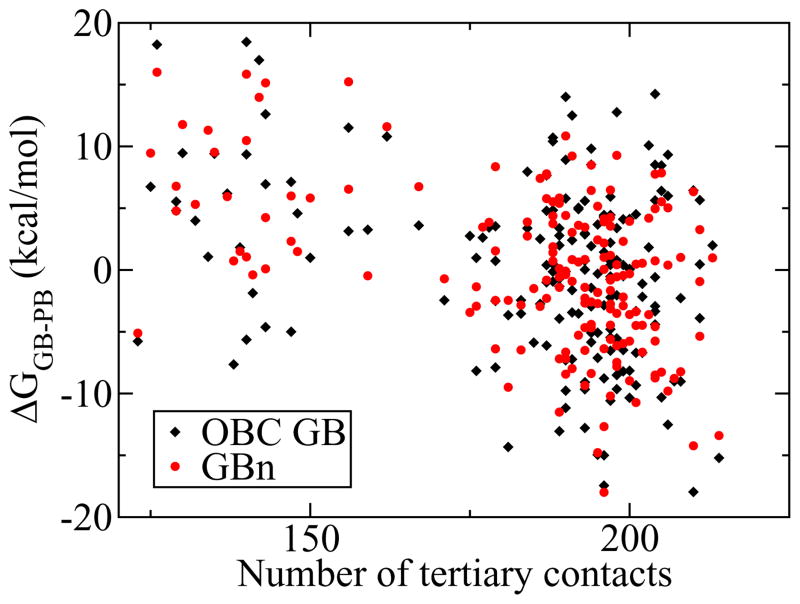
A more direct test of GB model performance is comparison of GB solvation free energies with those calculated by PB methods. Minimizing error across multiple conformations of the same system is of particular interest for GB methods that will be used in dynamics, as conformation-dependent errors will bias sampling. Figure 4 plots the difference between GB and PB solvation free energies for a series of conformations obtained from a thermal denaturation molecular dynamics trajectory of protein A. Error is reduced for the GBn model (standard deviation 6.4 kcal/mol) relative to the OBC GB model (standard deviation 7.2 kcal/mol). The F-statistic for this improvement approaches the accepted theshold of significance with p ≈ 0.06. Solvation free energy errors are plotted as a function of the number of native tertiary contacts for the corresponding conformation to elucidate trends in error with respect to degree of denaturation. The GB model of Hawkins et al.14 has significantly more negative errors for near-native conformations than for denatured conformations, but this native state bias is almost entirely corrected by the rescaling function in equation 4 employed by the OBC GB model.32 As seen in figure 4, the GBn model has a very small native state bias, similar to OBC GB. Similar, slightly better results are obtained for conformations of protein L and apo-myoglobin along their respective denaturation trajectories; these results are not shown because they were used as part of the objective function in the optimization process and as such are likely to be less indicative of performance on other systems.
Figure 4.
Relative deviation from PB solvation energy for GBn and OBC GB for a series of snapshots from a denaturation trajectory of protein A. GBn has a tighter clustering of points, indicating less random error than OBC GB (stdev 6.4 vs 7.2 kcal/mol), while maintaining a similar native state bias (trend of points across the plot). Average errors of −9.2 (OBC GB) and 68.9 (GBn) kcal/mol removed to facilitate comparison.
3.3 Comparison with PB PMFs
The improvements in effective radius and solvation free energy calculations described above represent useful but still fairly incremental improvement over the existing OBC GB model. Indeed, the OBC GB model’s performance is already quite good on low free energy conformations, such as those found in crystal structures or sampled from molecular dynamics trajectories, making dramatic improvements on these structures unlikely. However, performance on higher free energy conformations is also important for common applications like dynamics and docking; here there is ample room for improvement on OBC GB. One common high free energy conformation is encountered in the free energy curve for separating a salt bridge or hydrogen bond, referred to here as a PMF to reflect the averaging of solvent degrees of freedom by the implicit solvent model. It has been shown that implicit solvent models that employ a molecular surface dielectric boundary have a free energy barrier to separation of the bond,44 in qualitative agreement with explicit solvent results,47 but models based on traditional pairwise integration, even with average molecular volume corrections such as OBC GB, fail to reproduce this behavior.
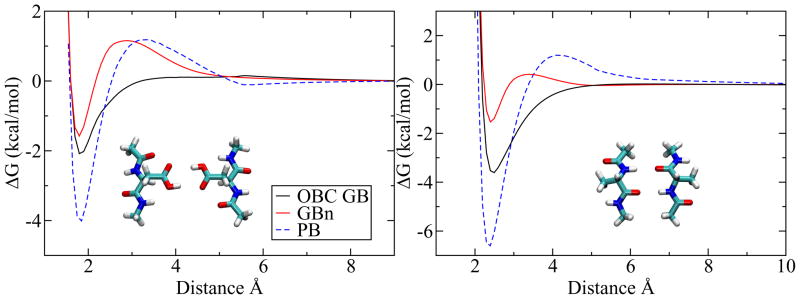
Since the GBn model attempts to approximate a molecular surface dielectric boundary it should be capable of reproducing the barrier in the PMF. As shown in figures 5 and 6 this result is seen in most cases, a distinct departure from implicit solvent models that allow interstitial high dielectrics.44 In general, the GBn minima are less deep and the maxima are less high than the PB PMFs. This is probably a consequence of the CFA. The CFA underestimates the descreening contribution of nearby regions relative to more distant regions, because r−4 diminishes less rapidly than the higher order integrands of more accurate expressions.21, 39 Since the neck region is very close to the atom of interest, it seems likely that its effect is underestimated by the CFA, leading to a smaller difference between minimum and maximum. The shallow minima exhibited by the GBn model, most notable in the β-sheet model of figure 5, raise concerns that secondary structure may not be stable, possibly leading to denaturation. However, this has not been observed in molecular dynamics trajectories (see following), perhaps because the extent of destabilization is less in the protein environment than for these highly solvated model systems, or because the time scales of the simulations conducted here are not sufficient to observe these problems.
Figure 5.
Potentials of mean force for hydrogen bonding systems not included in the objective function, calculated with three implicit solvent methods. Two protonated aspartic acids and two alanines (β-sheet model) are used as examples. Potential includes electrostatic and van der Waals energies.
Figure 6.
Potentials of mean force for hydrogen bonding and salt bridge systems included in the objective function, calculated with three implicit solvent methods. The hydrogen bonding systems are asparagine and asparagine; aspartate and serine; arginine and aspartate. Potential includes electrostatic and van der Waals energies.
3.4 Molecular dynamics
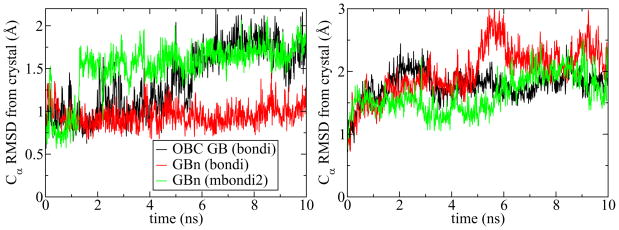
The primary purpose for the development of computationally efficient pairwise approximated GB is application in dynamics; the GBn model, implemented in AMBER, was tested by conducting 10 ns molecular dynamics trajectories of ubiquitin and thioredoxin. As expected, the GBn model retains the computational efficiency of the OBC GB model running only 8–10% more slowly. Conformational stability of trajectories is commonly assessed by computing the RMSD of alpha carbons from their crystal coordinates; plots of the RMSD for thioredoxin and ubiquitin trajectories conducted using the GBn and OBC GB models are shown in figure 7. The GBn model maintains approximately the same high level of stability as OBC GB, with slightly higher RMSD in the thioredoxin trajectory and lower RMSD in the ubiquitin trajectory.
Figure 7.
RMSD of alpha carbons from crystal structure over the course of 10 ns of molecular dynamics of ubiquitin (left) and thioredoxin (right).
Performance of a GB model is affected by the set of atomic intrinsic radii used to define the dielectric boundary. Previous work has shown that for simulations conducted under the HCT or OBC GB models, structural stability is slightly increased and results are somewhat improved by increasing the intrinsic radius of hydrogens bound to nitrogen, H(N), from their Bondi radii48 of 1.2 Å to 1.3 Å (forming the mbondi2 radius set).26, 32 As seen in figure 7, little benefit is realized by this change when using the GBn model.
The GBn model presented here was parameterized for peptides and proteins. This parameterization of GBn is not recommended for use with nucleic acids, since they require different degrees of correction for overlap and CFA error than amino acids. In some of our MD simulations of DNA 10 bp duplexes at room temperature conducted under this GBn parameterization we observed breaking of a substantial number of Watson-Crick bonds after a few nanoseconds (results not shown), in contrast to the corresponding explicit water simulations.
3.5 Comparison with explicit solvent ensembles
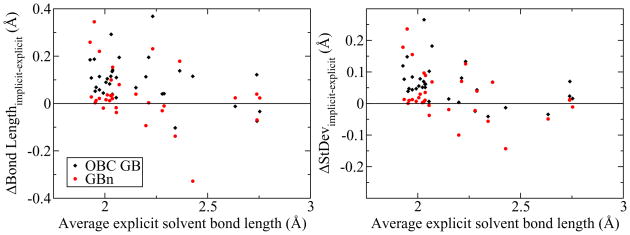
To examine whether the improved PMFs seen in figures 5 and 6 translate into improvements in the ensemble of macromolecular conformations sampled during MD, distributions of hydrogen bond lengths were compared between 10 ns ubiquitin trajectories conducted under OBC GB, GBn and TIP3P explicit solvation models. Figure 8 illustrates the differences in mean and standard deviation of hydrogen bond length for native backbone hydrogen bonds under the three solvation models. In nearly all cases, the OBC GB model yields hydrogen bonds with a higher mean length and standard deviation than in explicit solvent. As a consequence of the narrower potential wells seen in the PMFs, hydrogen bonds under the GBn model are generally shorter and their length distributions usually have lower standard deviations than under OBC GB. The GBn average hydrogen bond lengths are in better agreement with explicit solvent results than OBC GB in 24 of 32 cases, while the length distribution standard deviations are in better agreement in 23 of 32 cases. Based on these results, the null hypothesis that there is no impovement of GBn over OBC GB in reproducing the explicit solvent ensemble of hydrogen bond lengths can be rejected with p < 0.01 and p ≈ 0.01, respectively. The differences between GBn and OBC GB are particularly noticeable for the shorter, more stable hydrogen bonds (left portions of the plots in figure 8), where length distributions are presumably mostly determined by the potential between bonding partners, while distributions for longer hydrogen bonds may be more affected by tertiary structural forces. The data in figure 8 suggest that the free energy barrier introduced by the neck correction affects not only dynamics and kinetic properties, but also average properties of the ensemble sampled by MD.
Figure 8.
Ubiquitin backbone hydrogen bond length data collected over 10 ns of MD for TIP3P explicit solvent, OBC GB and GBn. Plots represent difference between implicit and explicit solvent bond length distribution mean (left) and standard deviation (right) as a function of mean explicit solvent bond length. The zero line represents an exact match between the explicit and implicit solvent results. Hydrogen bond lengths under the GBn model are generally in better agreement with explicit solvent results.
Further exploration of the effects of GBn on conformational ensembles were conducted using a small polypeptide system where converged sampling of the ensemble is feasible. Simmerling and coworkers49 recently used replica exchange molecular dynamics (REMD) simulations50, 51 to show that the OBC GB and HCT GB models performed poorly for short polyalanine sequences. Both of these GB models demonstrated a strong bias favoring α-helical conformations as compared to simulations with TIP3P explicit solvent. These calculations (100 ns REMD) were repeated with GBn. Figure 9 illustrates the φ/ψ free energy surface for Ala5 of deca-alanine. This residue does not adopt a preferred conformation in explicit solvent, with the basins corresponding to the major secondary structure types (right- and left-handed α-helix, β-sheet and polyproline II) nearly equal in free energy. At the same time, OBC GB favors right-handed α-helix by 1–1.5 kcal/mol relative to the other basins; for example, the ratio of the total α-helix to β-sheet populations is 8.67, in noticeable disagreement with the corresponding explicit solvent value of just 1.7. In the GBn model, this α-helical bias is no longer present and the landscape is in much better agreement with the explicit solvent data: the same ratio of α to β populations is 1.64, in very close agreement with the explicit solvent result. Both the OBC GB and GBn models show somewhat too shallow minima for the left-handed α-helix basin with positive φ values as compared to explicit solvent simulations.
Figure 9.
Free energy surfaces at 300K for the backbone conformation of Ala5 in the Ala10 peptide calculated from 100ns of REMD. Energies are in kcal/mol, with the lowest free energy assigned a value of 0. TIP3P and GBn result in similar free energies for the α, β and polyproline II basins, while OBC GB shows a strong preference for α-helix.
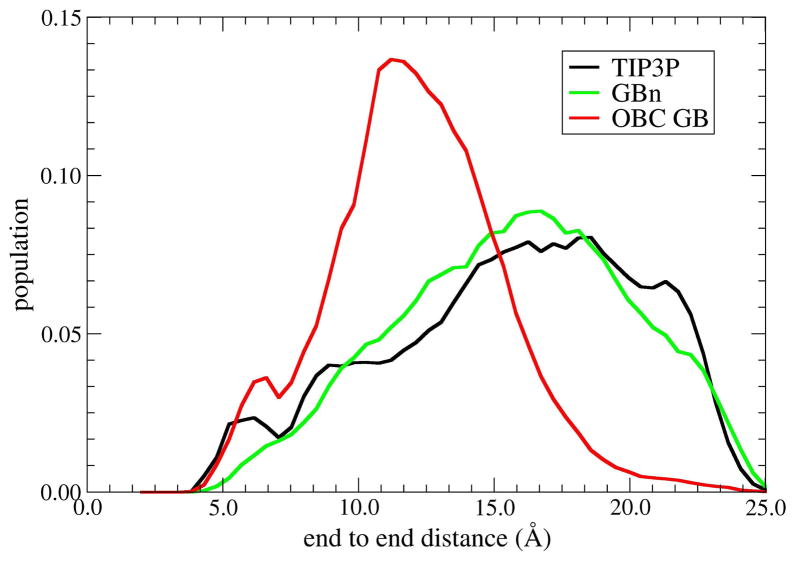
Since the free energy surfaces as in figure 9 give insight primarily into local conformational preferences, more global properties of the chain were examined by calculating end-to-end distance distributions for the ensembles obtained with the different solvent models (figure 10). As previously described,49 the distribution is broad in explicit solvent, in concordance with the lack of specific structural preferences seen in figure 9. At the same time, OBC GB yields a shifted distribution that is distinctly peaked near 10Å due to a high population of fully α-helical conformations that are not observed in explicit solvent. In contrast, the distribution obtained using the GBn model is in good agreement with the explicit solvent data, providing further evidence that the neck model represents a significant improvement over the previous OBC GB model. These improvements suggest that the correction term introduced by the GBn is a move in the right direction with respect to development of fast analytical GB models. However, due to the computational costs associated with generating explicit solvent PMFs, we have been able to provide direct comparisons for only a few systems, and therefore due caution is recommended when applying the GBn model to systems dissimilar to those described above.
Figure 10.
End to end distance distributions of deca-alanine at 300K for 3 solvent models. Profiles from GBn and TIP3P explicit water are in good agreement, with a relatively broad distribution slightly peaked near 15–20 Å. However, OBC GB significantly differs from the other models, with a strong peak at 10 Å.
4 Methods
PB solvation energies and “perfect” radii were calculated using a modified version of APBS 0.3.2. The linearized PB model was employed along with the multiple Debye-Huckel boundary condition. Charge was discretized using the cubic B-spline method (spl2). Dielectric values were 1.0 for solute and 80.0 for solvent regions, except for “perfect” radii calculations, where solvent had dielectric 1000.35 A Lee-Richards type dielectric boundary (mol) was used. APBS versions 0.3.2 and earlier have a flawed molecular surface algorithm that overestimates solute volume; this flaw was fixed in the APBS version used here. All calculations were performed initially on a coarse grid and then on a smaller, finer grid using the coarse grid potential as boundary conditions. Grid spacings were 0.5/0.25 Å (coarse/fine) for protein solvation and perfect radii calculations and 0.2/0.1 Å for PMF calculations.
GB effective radius, solvation energy and MD trajectories were calculated using a pre-release version of AMBER 9.52 MD was carried out using the AMBER ff99 force field.53, 54 Backbone torsional potentials for thioredoxin and ubiquitin were modified by frcmod.mod_phipsi.1;29 a newer version of these modifications55 was employed for the Ala10 simulations. The timestep was 2 fs. Explicit solvent MD employed the TIP3 water model.56 Implicit solvent MD, GB effective radius and GB solvation energy calculations used the OBC GB or GBn models with no cut off. Non-polar solvation effects were represented using a surface area term of 0.005 kcal/mol·Å2. Bonds involving hydrogen were constrained using SHAKE.57 Temperature was maintained at 300K using the Berendsen weak coupling method and a time constant of 2 ps for the thioredoxin trajectory and using Langevin dynamics with a collision frequency of 1.0 ps−1 for the ubiquitin trajectory. The crystal structures (2TRX and UBQ) were prepared for dynamics with 100 steps of steepest descent minimization during which all atoms were harmonically restrained with a weight of 1.0 kcal/mol·Å2, followed by a 20 ps period of equilibration during which all atoms were harmonically restrained with a weight of 0.1 kcal/mol·Å2. The enesemble of protein-A structures was generated by temperature unfolding as previously described.32
Ensembles of Ala10, with acetylated and amidated N- and C-termini, respectively, were generated using replica exchange molecular dynamics (REMD)50, 51 as implemented in AMBER 8.52 Data for the TIP3P and OBC GB models were previously described.49 Parameters for REMD simulations were identical to those used for MD (described above), except eight replicas were used to cover the temperature range of 270K–570K (as with the previously described OBC GB simulations). Exchanges were attempted every 1 ps, with the REMD simulation running for 100,000 exchange attempts (100 ns). The first 5 ns were discarded. Data convergence was monitored by calculating populations of φ/ψ basins corresponding to secondary structure types, which were essentially unchanged after 30ns. Free energy surfaces were calculated using 2-dimensional histograms for backbone φ and ψ dihedrals, with a bin size of 5 degrees. Free energies for bin i relative to the most populated bin were calculated using ΔG = −RT ln(Ni/N0) where Ni and N0 are the populations of bin i and the most populated bin, respectively. End-to-end distances for Ala10 were calculated between Cα atoms of Ala2 and Ala9 (omitting terminal residues) using the ptraj module of AMBER.
Illustrations of molecular geometry in figures 5 and 6 were produced with VMD.58
The Sneck, α, β, γ and Sx parameters were optimized using the Nelder-Mead simplex algorithm45 implemented by the SciPy library.59 The objective function that was minimized measured agreement between PB and GB solvation free energies over a training set consisting of structures from denaturation trajectories of apo-myoglobin46 and protein L21 and structures representing varying degrees of separation of a salt bridge between aspartate and arginine and hydrogen bonds between two asparagine side chains and between serine and aspartate. The total value of the objective function was the sum of each system’s contribution. For the structures from the denaturation trajectories, the difference between PB and GB solvation free energy was calculated for each structure and a linear regression was performed on these data points using the structure’s time value (for apo myoglobin) or number of native tertiary contacts (for protein L) as the independent variable, yielding a regression line slope, m, and intercept, b. Additionally, the root mean square deviation (RMSD) between PB and GB solvation free energies for each structure was calculated. Each system’s contribution to the objective function was defined as . This term is designed to emphasize minimizing native state bias (represented by m) and random error while not overly penalizing systematic error for a particular system. Salt bridge and hydrogen bond systems consisted of 80 configurations where the bonding partners were separated by 1 Å in the first configuration and are moved 0.1 Å further apart in each subsequent configuration (see figure 6 for picture of orientations). PB and GB solvation free energies were calculated for each configuration, and the PB and GB solvation free energies were set to be equal at maximum separation by subtracting the energy calculated for maximal separation from that calculated for every other configuration. The objective function term for these systems was the RMSD of the adjusted errors multiplied by 10. The RMSD was increased by a factor of 10 to prevent the objective function from being dominated by the larger errors of the larger protein systems. Since the objective function has multiple local minima, 100 minimizations were performed starting from random initial points. Initial points were chosen from the following intervals of a uniform random distribution: Sneck ∈ [0.2, 0.5], α ∈ [0.5,1.5], β,γ ∈ [0.5,3.0], and S{C,H,N,O} ∈ [0.6, 0.95].
5 Conclusion
The GBn model, presented here, extends current pairwise GB models with an intuitively attractive property: geometry-dependent exclusion of high dielectric (representing water) from regions into which a water molecule is too large to fit. This extension is computationally efficient, slowing MD simulations by only about 10%. Implementation of the neck correction is simple, requiring only two lookup tables and (in the present implementation) approximately 30 lines of code. The GBn model is available in both the sander and pmemd modules of version 9 of the AMBER suite, and given its simplicity it should be straightforward to add the neck correction to any pairwise volumetric integration-based GB method. Although the correction is a pairwise approximation, it yields non-bonded PMFs with a free energy barrier to separation, a property unique to molecular surface-like dielectric boundaries. The improved agreement between explicit and implicit solvent ensembles sampled by proteins and polypeptides under GBn underscores the importance of calculating accurate solvation energies for high free energy configurations as well as the more stable configurations that have traditionally received more attention.
The neck GB model is the fastest model that reproduces the essential characteristics of molecular surface dielectric boundaries, but it does not correlate as well with PB results as the slower GBMV2 model of Lee et al.38, 44 One potential source of error is the fairly simplistic treatment of neck region overlaps in the current model. Some improvement might be realized by a higher order approach to overlaps, but the largest source of error appears to be the use of the Coulomb field approximation (CFA) to define the integral used to calculate effective radii. Even with a perfect region of integration, errors due to the CFA are large, with effective radii overestimated by a factor of two in the worst case.39 Despite the limitations imposed by the CFA, the current model serves as a proof of principle that a simple pairwise correction can produce an accurate approximation of molecular surface-like solvation properties. We anticipate that a pairwise GB model based on the neck correction and a non-CFA integral, currently under development, will yield substantially improved accuracy.
Table 3.
Distance between atoms at which integral of r−4 over the neck region (defined in equations 13–15) has the maximum value, tabulated for a range of radii for atoms 1 and 2, assuming a solvent molecule (Rw) radius of 1.4 Å. These are the values used for d0 in equations 6 and 7. Distances and atom radii in angstroms.
| Atom 1 Atom 2 |
1.20 | 1.25 | 1.30 | 1.35 | 1.40 | 1.45 | 1.50 |
|---|---|---|---|---|---|---|---|
| 1.20 | 2.6797 | 2.7250 | 2.7719 | 2.8188 | 2.8656 | 2.9125 | 2.9609 |
| 1.25 | 2.7359 | 2.7813 | 2.8281 | 2.8750 | 2.9219 | 2.9688 | 3.0156 |
| 1.30 | 2.7922 | 2.8375 | 2.8844 | 2.9297 | 2.9766 | 3.0234 | 3.0719 |
| 1.35 | 2.8500 | 2.8953 | 2.9406 | 2.9859 | 3.0328 | 3.0797 | 3.1266 |
| 1.40 | 2.9062 | 2.9516 | 2.9969 | 3.0422 | 3.0891 | 3.1359 | 3.1828 |
| 1.45 | 2.9625 | 3.0078 | 3.0531 | 3.0984 | 3.1437 | 3.1906 | 3.2375 |
| 1.50 | 3.0188 | 3.0641 | 3.1078 | 3.1547 | 3.2000 | 3.2469 | 3.2922 |
| 1.55 | 3.0750 | 3.1203 | 3.1641 | 3.2094 | 3.2563 | 3.3016 | 3.3484 |
| 1.60 | 3.1313 | 3.1750 | 3.2203 | 3.2656 | 3.3109 | 3.3563 | 3.4031 |
| 1.65 | 3.1875 | 3.2313 | 3.2766 | 3.3203 | 3.3656 | 3.4125 | 3.4578 |
| 1.70 | 3.2437 | 3.2875 | 3.3313 | 3.3766 | 3.4219 | 3.4672 | 3.5125 |
| 1.75 | 3.3000 | 3.3422 | 3.3875 | 3.4312 | 3.4766 | 3.5219 | 3.5688 |
| 1.80 | 3.3547 | 3.3984 | 3.4422 | 3.4875 | 3.5313 | 3.5766 | 3.6234 |
| Atom 1 Atom 2 |
1.55 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
|---|---|---|---|---|---|---|
| 1.20 | 3.0078 | 3.0562 | 3.1047 | 3.1531 | 3.2016 | 3.2500 |
| 1.25 | 3.0641 | 3.1109 | 3.1594 | 3.2078 | 3.2563 | 3.3047 |
| 1.30 | 3.1188 | 3.1672 | 3.2141 | 3.2625 | 3.3109 | 3.3594 |
| 1.35 | 3.1750 | 3.2219 | 3.2703 | 3.3172 | 3.3656 | 3.4141 |
| 1.40 | 3.2297 | 3.2766 | 3.3250 | 3.3719 | 3.4203 | 3.4688 |
| 1.45 | 3.2844 | 3.3313 | 3.3797 | 3.4266 | 3.4750 | 3.5234 |
| 1.50 | 3.3391 | 3.3875 | 3.4344 | 3.4813 | 3.5297 | 3.5781 |
| 1.55 | 3.3953 | 3.4422 | 3.4891 | 3.5359 | 3.5844 | 3.6313 |
| 1.60 | 3.4500 | 3.4969 | 3.5438 | 3.5906 | 3.6391 | 3.6859 |
| 1.65 | 3.5047 | 3.5516 | 3.5984 | 3.6453 | 3.6922 | 3.7406 |
| 1.70 | 3.5594 | 3.6063 | 3.6531 | 3.7000 | 3.7469 | 3.7953 |
| 1.75 | 3.6141 | 3.6609 | 3.7078 | 3.7547 | 3.8016 | 3.8484 |
| 1.80 | 3.6688 | 3.7156 | 3.7625 | 3.8094 | 3.8563 | 3.9031 |
Table 4.
Maximum value of integral of r−4 over the neck region (defined in equations 13–15), tabulated for a range of radii for atoms 1 and 2, assuming a solvent molecule (Rw) radius of 1.4 Å. These are the values used for m0 in equations 6 and 7. Distances and atom radii in angstroms.
| Atom 1 Atom 2 |
1.20 | 1.25 | 1.30 | 1.35 | 1.40 | 1.45 | 1.50 |
|---|---|---|---|---|---|---|---|
| 1.20 | 0.35281 | 0.36412 | 0.37516 | 0.38594 | 0.39645 | 0.40670 | 0.41670 |
| 1.25 | 0.31853 | 0.32889 | 0.33902 | 0.34890 | 0.35855 | 0.36797 | 0.37717 |
| 1.30 | 0.28847 | 0.29798 | 0.30728 | 0.31637 | 0.32525 | 0.33392 | 0.34240 |
| 1.35 | 0.26199 | 0.27074 | 0.27930 | 0.28768 | 0.29587 | 0.30387 | 0.31170 |
| 1.40 | 0.23859 | 0.24666 | 0.25455 | 0.26228 | 0.26985 | 0.27725 | 0.28449 |
| 1.45 | 0.21783 | 0.22528 | 0.23258 | 0.23972 | 0.24673 | 0.25358 | 0.26029 |
| 1.50 | 0.19935 | 0.20624 | 0.21300 | 0.21962 | 0.22611 | 0.23247 | 0.23870 |
| 1.55 | 0.18285 | 0.18923 | 0.19550 | 0.20165 | 0.20767 | 0.21358 | 0.21938 |
| 1.60 | 0.16807 | 0.17400 | 0.17982 | 0.18553 | 0.19114 | 0.19664 | 0.20203 |
| 1.65 | 0.15480 | 0.16031 | 0.16573 | 0.17104 | 0.17626 | 0.18139 | 0.18642 |
| 1.70 | 0.14285 | 0.14798 | 0.15303 | 0.15798 | 0.16285 | 0.16764 | 0.17233 |
| 1.75 | 0.13207 | 0.13685 | 0.14155 | 0.14618 | 0.15073 | 0.15520 | 0.15959 |
| 1.80 | 0.12231 | 0.12677 | 0.13117 | 0.13549 | 0.13975 | 0.14393 | 0.14804 |
| Atom 1Atom 2 |
1.55 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
|---|---|---|---|---|---|---|
| 1.20 | 0.42646 | 0.43598 | 0.44527 | 0.45434 | 0.46319 | 0.47183 |
| 1.25 | 0.38615 | 0.39492 | 0.40348 | 0.41185 | 0.42001 | 0.42799 |
| 1.30 | 0.35069 | 0.35878 | 0.36669 | 0.37441 | 0.38196 | 0.38934 |
| 1.35 | 0.31936 | 0.32684 | 0.33416 | 0.34131 | 0.3483 | 0.35514 |
| 1.40 | 0.29158 | 0.29851 | 0.30529 | 0.31193 | 0.31842 | 0.32477 |
| 1.45 | 0.26686 | 0.27330 | 0.27959 | 0.28575 | 0.29179 | 0.29769 |
| 1.50 | 0.24480 | 0.25078 | 0.25664 | 0.26237 | 0.26799 | 0.27349 |
| 1.55 | 0.22505 | 0.23062 | 0.23607 | 0.24141 | 0.24665 | 0.25178 |
| 1.60 | 0.20732 | 0.21251 | 0.21759 | 0.22258 | 0.22747 | 0.23226 |
| 1.65 | 0.19135 | 0.19620 | 0.20095 | 0.20561 | 0.21018 | 0.21466 |
| 1.70 | 0.17694 | 0.18147 | 0.18591 | 0.19027 | 0.19455 | 0.19875 |
| 1.75 | 0.16390 | 0.16814 | 0.17230 | 0.17638 | 0.18039 | 0.18433 |
| 1.80 | 0.15208 | 0.15605 | 0.15995 | 0.16378 | 0.16754 | 0.17124 |
Acknowledgments
JM is supported by Burroughs Wellcome through La Jolla Interfaces in Science. CS is supported in part by NIH grant GM6167803 and NCSA allocation MCA02N028 for computer time. DAC is supported in part by NIH grant GM57513. AO is supported in part by NIH grant GM076121. This investigation was conducted in part in a facility constructed with support from Research Facilities Improvement Program Grant Number C06 RR-017588-01 from the NCRR, NIH. This work has been supported in part by grants from NSF, NIH, the NSF Center for Theoretical Biological Physics, the National Biomedical Computing Resource, and Accelrys, Inc.
7 Appendix I
The neck region can be analytically defined using only basic trigonometry, but as the derivation is somewhat tedious, the details are provided here. As shown in figure 1, a triangle is formed by the centers of the atoms and the solvent molecule; the angles of the vertices centered at atoms 1 and 2 are defined as angle A and angle B, and their cosines can be expressed in terms of the four parameters d, R1, R2 and Rw, using the law of cosines, as shown in equation 8.
| (8) |
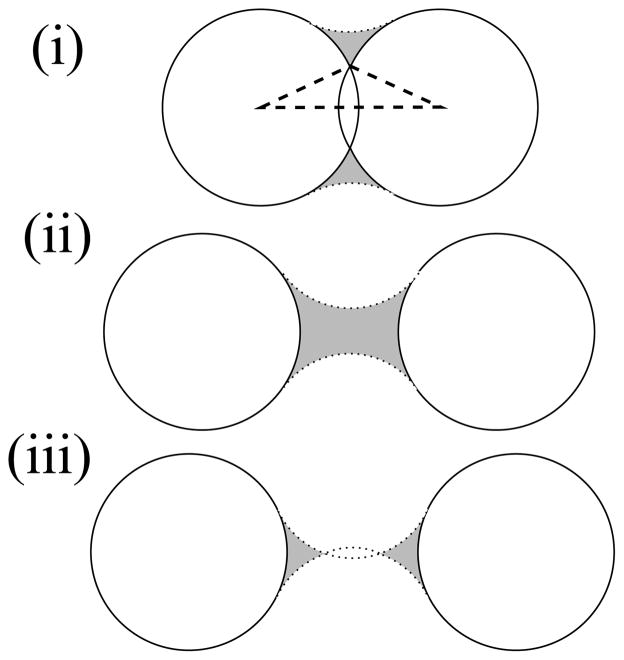
The system is cylindrically symmetric about an axis connecting the centers of the two atoms, so it is most naturally analyzed in cylindrical coordinates. The origin is placed at the center of atom 1 with the positive z axis extending toward the center of atom 2. There are three geometric cases for the neck region, illustrated in figure 11: (i) the atoms overlap and the neck region is ring shaped; (ii) the atoms are moderately separated forming a contiguous region; (iii) the atoms are widely separated such that the surface of the solvent molecule intersects the z axis, forming two noncontiguous spike regions. When d ≥ R1 + R2 + 2Rw a solvent molecule can pass between the atoms and there is no neck region.
Figure 11.
Three cases of neck regions (shaded) formed by atoms (solid circles) at varying separations. Dotted lines represent the surface of the solvent sphere. The leftmost vertex of the dashed triangle in (i) describes the angle A′ referenced in equation 9. Although this figure shows two atoms with the same radius, neck regions may also be formed between atoms with unequal radii.
For case (i), a second triangle can be formed between the centers of the two atoms and a point at which the surfaces of the atoms intersect. The angle formed by the vertex of this triangle that is located at the center of atom 1 is designated A′ and its cosine is defined in equation 9.
| (9) |
Computation of a CFA term based on the neck region requires an expression for the integral of r−4 over the neck region. In the cylindrical coordinate system used here, so when the volume element is included, the integrand becomes r (r2 +z2)−2. Because of the cylindrical symmetry, the limits of integration over θ are always 0 to 2π. The upper limit of the integration over r is formed by the surface of the solvent molecule (dotted line in figures 1 and 11). Since the expression defining the r coordinate of the solvent surface as a function of z (that is, the perpendicular distance from the z axis to the dashed line in figure 1 for a given z) is somewhat complex, the notation is clarified by defining a function, solv, representing this expression:
| (10) |
The lower limit of integration for r is defined by the surface of atom 1, the z axis (r = 0), or the surface of atom 2, depending on the value of the z coordinate. In addition to defining the geometric extents of the neck region, the limits of integration over z are used to break the overall integral into pieces at the points where the r lower limit of integration changes. Thus in case (i) the integral has two contiguous pieces defined by three z limits: the coordinate at which the solvent molecule touches atom 1, the coordinate for the intersection of the two atoms and the coordinate where atom 2 touches the solvent molecule. Case (ii) has three contiguous pieces, with the extreme upper and lower limits defined by the locations that the solvent molecule touches the atoms, as in (i) and the two intermediate limits occurring where the lower r limit changes at the edges of atoms 1 and 2. Finally, case (iii) has two noncontiguous spike regions, each of which is composed of two parts, where the z limits are the intersection of the atom and solvent molecule, the edge of the atom and the tip of the spike. The tips of the spikes are located at the two points where the solvent sphere intersects the z axis (see figure 11). The z coordinate of these intersections can be obtained by setting the function in equation 10 equal to zero and solving for z, yielding
| (11) |
| (12) |
Using the preceding definitions, the integrals of r−4 over the neck region for cases (i), (ii) and (iii) are presented in equations 13, 14 and 15.
| (13) |
| (14) |
| (15) |
References
- 1.Gilson MK, Davis ME, Luty BA, McCammon JA. J Phys Chem. 1993;97:3591–3600. [Google Scholar]
- 2.Honig BH, Nicholls A. Science. 1995;268:1144–1149. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 3.Madura JD, Briggs JM, Wade RC, Davis ME, Luty BA, Ilin A, Antosiewicz JM, Gilson MK, Bagheri B, Scott LR, McCammon JA. Comput Phys Commun. 1995;91:57–95. [Google Scholar]
- 4.Beroza P, Case DA. Energetics Biol Macromol B. 1998;295:170–189. doi: 10.1016/s0076-6879(98)95040-6. [DOI] [PubMed] [Google Scholar]
- 5.Scarsi M, Apostolakis J, Caflisch A. J Phys Chem A. 1997;101:8098–8106. [Google Scholar]
- 6.Cramer CJ, Truhlar DG. Chem Rev. 1999;99:2161–2200. doi: 10.1021/cr960149m. [DOI] [PubMed] [Google Scholar]
- 7.Baker NA. Curr Opin Struct Biol. 2005;15:137–143. doi: 10.1016/j.sbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 8.Im W, Beglov D, Roux B. Comput Phys Commun. 1998;111:59–75. [Google Scholar]
- 9.Luo R, David L, Gilson MK. J Comput Chem. 2002;23:1244–1253. doi: 10.1002/jcc.10120. [DOI] [PubMed] [Google Scholar]
- 10.Lu Q, Luo R. J Chem Phys. 2003;119:11035–11047. [Google Scholar]
- 11.Feig M, Brooks CL. Curr Opin Struct Biol. 2004;14:217–24. doi: 10.1016/j.sbi.2004.03.009. [DOI] [PubMed] [Google Scholar]
- 12.Still WC, Tempczyk A, Hawley RC, Hendrickson T. J Am Chem Soc. 1990;112:6127–6129. [Google Scholar]
- 13.Hawkins GD, Cramer CJ, Truhlar DG. Chem Phys Lett. 1995;246:122–129. [Google Scholar]
- 14.Hawkins GD, Cramer CJ, Truhlar DG. J Phys Chem. 1996;100:19824–19839. [Google Scholar]
- 15.Schaefer M, Karplus M. J Phys Chem. 1996;100:1578–1599. [Google Scholar]
- 16.Qiu D, Shenkin PS, Hollinger FP, Still WC. J Phys Chem A. 1997;101:3005–3014. [Google Scholar]
- 17.Edinger SR, Cortis C, Shenkin PS, Friesner RA. J Phys Chem B. 1997;101:1190–1197. [Google Scholar]
- 18.Jayaram B, Liu Y, Beveridge DL. J Chem Phys. 1998;109:1465–1471. [Google Scholar]
- 19.Ghosh A, Rapp CS, Friesner RA. J Phys Chem B. 1998;102:10983–10990. [Google Scholar]
- 20.Bashford D, Case DA. Annu Rev Phys Chem. 2000;51:129–52. doi: 10.1146/annurev.physchem.51.1.129. [DOI] [PubMed] [Google Scholar]
- 21.Lee MS, Salsbury FR, Brooks CL. J Chem Phys. 2002;116:10606–10614. [Google Scholar]
- 22.Felts AK, Harano Y, Gallicchio E, Levy RM. Proteins. 2004;56:310–321. doi: 10.1002/prot.20104. [DOI] [PubMed] [Google Scholar]
- 23.Romanov AN, Jabin SN, Martynov YB, Sulimov AV, Grigoriev FV, Sulimov VB. J Phys Chem A. 2004;108:9323–9327. [Google Scholar]
- 24.Dominy BN, Brooks CL. J Phys Chem B. 1999;103:3765–3773. [Google Scholar]
- 25.David L, Luo R, Gilson MK. J Comput Chem. 2000;21:295–309. doi: 10.1002/jcc.10120. [DOI] [PubMed] [Google Scholar]
- 26.Tsui V, Case DA. J Am Chem Soc. 2000;122:2489–2498. [Google Scholar]
- 27.Calimet N, Schaefer M, Simonson T. Proteins. 2001;45:144–158. doi: 10.1002/prot.1134. [DOI] [PubMed] [Google Scholar]
- 28.Spassov VZ, Yan L, Szalma S. J Phys Chem B. 2002;106:8726–8738. [Google Scholar]
- 29.Simmerling C, Strockbine B, Roitberg AE. J Am Chem Soc. 2002;124:11258–11259. doi: 10.1021/ja0273851. [DOI] [PubMed] [Google Scholar]
- 30.Wang T, Wade RC. Proteins. 2003;50:158–169. doi: 10.1002/prot.10248. [DOI] [PubMed] [Google Scholar]
- 31.Nymeyer H, Garcia AE. Proc Natl Acad Sci U S A. 2003;100:13934–13939. doi: 10.1073/pnas.2232868100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Onufriev A, Bashford D, Case DA. Proteins. 2004;55:383–94. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- 33.Gallicchio E, Levy RM. J Comput Chem. 2004;25:479–499. doi: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- 34.Lee MC, Duan Y. Proteins. 2004;55:620–34. doi: 10.1002/prot.10470. [DOI] [PubMed] [Google Scholar]
- 35.Sigalov G, Scheffel P, Onufriev A. J Chem Phys. 2005;122:094511. doi: 10.1063/1.1857811. [DOI] [PubMed] [Google Scholar]
- 36.Onufriev A, Case DA, Bashford D. J Comput Chem. 2002;23:1297–304. doi: 10.1002/jcc.10126. [DOI] [PubMed] [Google Scholar]
- 37.Onufriev A, Bashford D, Case DA. J Phys Chem B. 2000;104:3712–3720. [Google Scholar]
- 38.Lee MS, Feig M, Salsbury FR, Brooks CL. J Comput Chem. 2003;24:1348–56. doi: 10.1002/jcc.10272. [DOI] [PubMed] [Google Scholar]
- 39.Grycuk T. J Chem Phys. 2003;119:4817–4826. [Google Scholar]
- 40.Im W, Lee MS, Brooks CL. J Comput Chem. 2003;24:1691–702. doi: 10.1002/jcc.10321. [DOI] [PubMed] [Google Scholar]
- 41.Wojciechowski M, Lesyng B. J Phys Chem B. 2004;108:18368–18376. [Google Scholar]
- 42.Feig M, Onufriev A, Lee MS, Im W, Case DA, Brooks CL. J Comput Chem. 2004;25:265–84. doi: 10.1002/jcc.10378. [DOI] [PubMed] [Google Scholar]
- 43.Lee B, Richards FM. J Mol Biol. 1971;55:379. doi: 10.1016/0022-2836(71)90324-x. [DOI] [PubMed] [Google Scholar]
- 44.Swanson JMJ, Mongan J, McCammon JA. J Phys Chem B. 2005;109:14769–14772. doi: 10.1021/jp052883s. [DOI] [PubMed] [Google Scholar]
- 45.Nelder JA, Mead R. Computer Journal. 1965;7:308–15. [Google Scholar]
- 46.Onufriev A, Case DA, Bashford D. J Mol Biol. 2003;325:555–67. doi: 10.1016/s0022-2836(02)01207-x. [DOI] [PubMed] [Google Scholar]
- 47.Masunov A, Lazaridis T. J Am Chem Soc. 2003;125:1722–30. doi: 10.1021/ja025521w. [DOI] [PubMed] [Google Scholar]
- 48.Bondi A. J Phys Chem. 1964;68:441–451. [Google Scholar]
- 49.Okur A, Wickstrom L, Layten M, Geney R, Song K, Hornak V, Simmerling C. J Chem Theory Comput. 2006;2:420–433. doi: 10.1021/ct050196z. [DOI] [PubMed] [Google Scholar]
- 50.Hansmann UHE. Chem Phys Lett. 1997;281:140–150. [Google Scholar]
- 51.Sugita Y, Okamoto Y. Chem Phys Lett. 1999;314:141–151. [Google Scholar]
- 52.Case DA, Darden T, III, TEC, Simmerling C, Wang J, Merz KM, Wang B, Pearlman DA, Duke RE, Crowley M, Brozell S, Luo R, Tsui V, Gohlke H, Mongan J, Hornak V, Caldwell JW, Ross WS, Kollman PA. AMBER 9. University of California; San Francisco: 2006. [Google Scholar]
- 53.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. J Am Chem Soc. 1995;117:5179–5197. [Google Scholar]
- 54.Wang JM, Cieplak P, Kollman PA. J Comput Chem. 2000;21:1049–1074. [Google Scholar]
- 55.Hornak V, Abel R, Okur A, Strockbine B, Roitberg A, Simmerling C. Proteins. 2006 doi: 10.1002/prot.21123. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 57.Ryckaert JP, Ciccotti G, Berendsen HJC. J Comput Phys. 1977;23:327–341. [Google Scholar]
- 58.Humphrey W, Dalke A, Schulten K. J Mol Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 59.Jones E, Oliphant T, Peterson P. SciPy: Open source scientific tools for Python. 2001–2006 SciPy.Org.