Cerebral dynamics and metabolism of hyperpolarized [1-¹³C]pyruvate using time-resolved MR spectroscopic imaging

Abstract

Dynamic hyperpolarized [1-¹³C]pyruvate metabolic imaging in the normal anesthetized rat brain is demonstrated on a clinical 3-T magnetic resonance imaging scanner. A 12-second bolus injection of hyperpolarized [1-¹³C]pyruvate is imaged at a 3-second temporal resolution. The observed dynamics are evaluated with regard to cerebral blood volume (CBV), flow, transport, and metabolic exchange with the cerebral lactate pool. A model for brain [1-¹³C]lactate, based on blood–brain transport kinetics, CBV, and the observed pyruvate dynamics is described.

Introduction

Magnetic resonance (MR) metabolic imaging of hyperpolarized [1-¹³C]pyruvate is a useful tool in the study of oncology and cardiology (Golman et al, 2006, 2008). Dynamic and tissue level changes in [1-¹³C]pyruvate and its metabolic products, [1-¹³C]lactate, [1-¹³C] alanine, and [¹³C] bicarbonate, have been shown to correlate with metabolic states of interest, including disease progression (Albers et al, 2008; Chen et al, 2007) and response to therapy (Day et al, 2007; Chen et al, 2008a, 2008b). However, because of the very limited 1- to 2- minute lifetime of hyperpolarized signal in vivo, brain metabolism has been largely ignored as an application. Although the kinetics of blood–brain transport of pyruvate (Cremer et al, 1979; Pardridge, 1983; Miller and Oldendorf, 1986) are 30- to 100-fold slower than the typical rates of [1-¹³C]pyruvate to [1-¹³C]lactate conversion (Day et al, 2007; Zierhut et al, 2010), single time point images have been reported, showing significant levels of both [1-¹³C]pyruvate and [1-¹³C]lactate in the normal anesthetized rat brain (Hurd et al, 2010). From these single time point studies, the distribution of C13 metabolites between the blood and brain tissues is not possible, nor is it possible to distinguish [1-¹³C]lactate produced in the brain relative to inflow. To overcome these limitations, fast 125 milliseconds dynamic spiral chemical shift imaging (Mayer et al, 2009) and transport modeling are combined in this study to better characterize the bolus, transport, and metabolic effects, separating the metabolites in the cerebral blood volume (CBV) from the metabolites in the brain tissue.

Materials and methods

Animal Preparation

The experiments were performed on 5 healthy male Wistar rats, weighing 197 to 257 g, anesthetized with 1% to 3% isoflurane in oxygen (∼1.5 L/min). Respiration, rectal temperature, heart rate, and oxygen saturation were monitored throughout the experiment. Rectal temperature was kept at 37°C by placing the animal on top of a temperature-controlled warm water blanket. Hyperpolarized solution was injected through the tail vein catheter. Each rat was injected 2 to 3 times at a 1.5-hour interval, and images were collected after each injection. Preparation and physiologic monitoring of animals in the ¹³C experiment followed the protocol approved by the local Institutional Animal Care and Use Committees.

Hyperpolarized [1-¹³C]Pyruvate

A solution of hyperpolarized, iso-osmolar, 80 mmol/L sodium [1-¹³C]pyruvate was prepared using a HyperSense polarizer (Oxford Instruments, Abingdon, UK). A 24-μL aliquot of [1-¹³C]pyruvic acid, containing 15 mmol/L trityl radical (OX63) and 1 mmol/L Dotarem gadolinium chelate, was polarized to near equilibrium (∼1 hour at 3.35 T and 1.4 K), followed by rapid dissolution and neutralization using a heated solvent containing 40 mmol/L Tris, 80 mmol/L NaOH, 100 mg/L disodium EDTA, and 58 mmol/L NaCl. The level of liquid-state polarization was estimated from solid-state dynamic nuclear polarization, DNP, build-up levels. A calibration of the solid-state DNP level with liquid-state polarization was made on the 3-T scanner using the pyruvate thermal equilibrium signal and the thermal equilibrium signal of an 8 mol/L ¹³C-urea standard. Liquid-state polarization levels ranged from 20% to 25%. The pyruvate T₁ at 3 T, and apparent T₁ during the low-field transfer process, were also determined to help estimate losses between dissolution and injection. The time delay between dissolution to injection into the animal ranged from 23 to 25 seconds. Depending on the size of the rat, 2.4 to 3.0 mL of the 80 mmol/L hyperpolarized [1-¹³C]pyruvate was injected, preceded by a 0.5-mL saline volume and followed, after a 1- to 2-second delay, by a saline flush, all at 0.25 mL/s.

Magnetic Resonance Hardware and Methods

All measurements were performed on a clinical 3-T MR scanner (GE Healthcare, Waukesha, WI, USA) with a high-performance insert gradient coil (500 mT/m, 1,800 mT/m per ms, 160-mm inner diameter) (Chronik et al, 2000). A custom-built dual-tuned (¹H/¹³C) quadrature coil (Ø=50 mm), operating at 127.7 MHz for proton and 32.1 MHz for carbon, was used for both radio frequency (RF) excitation and signal reception.

¹³C Spiral Spectroscopic Imaging

Dynamic metabolic imaging was performed using spectrally undersampled, spiral chemical shift imaging (Mayer et al, 2009) with a nominal in-plane resolution of 2.7 × 2.7 mm² (field of view=43.5 × 43.5 mm², 16 × 16 matrix, T_acq=125 milliseconds, spectral width (SW)=280 Hz). A 10-mm axial (animal coronal) slice through the front and middle of the rat brain was selected. In all, 16 images were collected, 1 every 3 seconds, starting at 9 seconds from the start of injection (7 seconds after the leading edge of pyruvate enters the tail vein). A variable flip angle scheme (Zhao et al, 1996) was used to avoid the signal attenuation of brain metabolites at later time points.

Urea Reference

A reference phantom was constructed using 8 mol/L ¹³C-urea in 80:20 w/w water:glycerol and 3 μL/mL (1.5 mmol/L) Gd-chelate, (OmniScan, GE Healthcare, Oslo, Norway), with a T₁ of 1 second. The signal intensity at 3 T is 2.1 mmol/L%, where mmol/L% is concentration × polarization. For reference images, an 800 μL sample in a sealed 1 mL plastic syringe barrel was inserted in the RF coil, next to the head, and within the observed field of view. A full preinjection imaging time series was collected. The final 90 excitation was used for intensity reference, and all of the variable flip angles were validated by relative image intensity. The reference was removed before injection to avoid overlap with pyruvate signal in the spectrally undersampled spiral chemical shift imaging acquisition.

Estimate of [pyruvate] and [lactate] from Hyperpolarized Signal Level

Pyruvate was determined as a ratio with the 3-T thermal equilibrium urea reference signal, corrected for initial polarization and T₁ losses:

where t_di is the transfer time from the polarizer to injection and t the time after injection. T_1,pyr,di was 60 seconds and T_1,pyr,vasc was 40 seconds (Leung et al, 2009). β Is the ¹³C-urea concentration divided by polarization enhancement (initial liquid-state polarization/3-T thermal polarization). In this case, β also included a partial volume correction for the small phantom diameter (0.8). The observed [lactate] tissue levels were determined from image signal intensities, substituting S_lac for S_pyr and substituting an average of the in vivo [1-¹³C]lactate and [1-¹³C]pyruvate T₁ values, for the in vivo [1-¹³C]pyruvate T₁ in equation (1). An in vivo T₁ for a lactate of 28 seconds was estimated from the studies by Chen et al (2008a, 2008b). An average T₁ was used because the in vivo residence time is mixed between pyruvate and lactate. Fortunately, the two T₁s are similar.

To investigate the impact of [1-¹³C]lactate produced outside, and then carried into the brain, the dynamic ratio of [1-¹³C]lactate to [1-¹³C]pyruvate was measured in a vascular region of interest (ROI) outside the brain, and then used to determine [1-¹³C]lactate in the brain ROI.

Model for Brain [lactate] Dynamics

In the model presented in this study, blood–brain transport is assumed to be rate limiting relative to conversion of cerebral [1-¹³C]pyruvate into [1-¹³C]lactate. Thus, the observed brain pyruvate signal will be dominated by pyruvate in the CBV, and transported pyruvate will be primarily observed as lactate. The lactate label in the brain can then be modeled as the pyruvate transported from blood to the brain minus the lactate label that exchanges out of the brain:

Thus, with the initial condition [lac] (t=0)=0:

In this model, lactate blood–brain exchange rate, K_tr was set at 0.14 per min (Lear and Kasliwal, 1991). The nonsaturable pyruvate blood–brain transport rate, K_d=34 μL/g per min (Pardridge, 1983) was used in the initial fit. K_d was then treated as a variable, when the fit to equation (3) was optimized. Pyruvate concentration in CBV was calculated as:

The initial condition for this model was CBV=2.7%, which corresponds to the blood volume fraction in the isoflurane anesthetized rat brain (Todd and Weeks, 1996). A correction for variable flip angle θ_i is also included, as pyruvate in the CBV is expected to be largely refreshed by the normal cerebral blood flow for each 3-second time point (Todd and Weeks, 1996). A correction was made for each angle θ:

The saturable transport of pyruvate is described by transport velocity V_o=V_max[pyr]/(K_m+[pyr]). As [Pyr]_CBV in these images greatly exceeds K_m=57 nmol/g, V_o was assumed to be equal to V_max=88 nmol/g per min (Pardridge, 1983) at each of imaged time points, and 0 before that. The pyruvate bolus was not extrapolated to estimate transport before the first time point. Even if pyruvate was available for an additional 3 seconds, a nonsignificant transport, <5 nmol/g, would be added to the total. Goodness of fit was estimated as confidence:

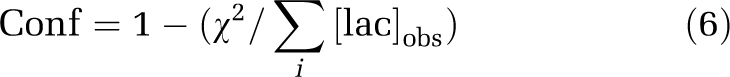Fits were made to each individual run and the average of the images acquired in each rat studied. Fits were also made to data corrected for [1-¹³C]lactate inflow. This includes contributions from [1-¹³C]lactate in the CBV and [1-¹³C]lactate that has been transported from blood to the brain.

Results

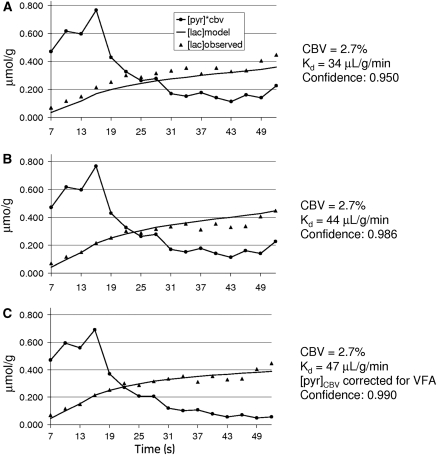
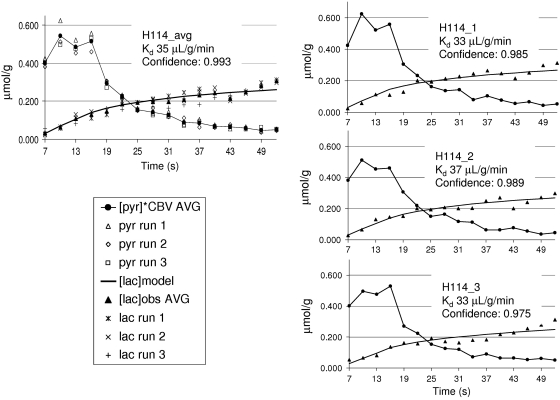
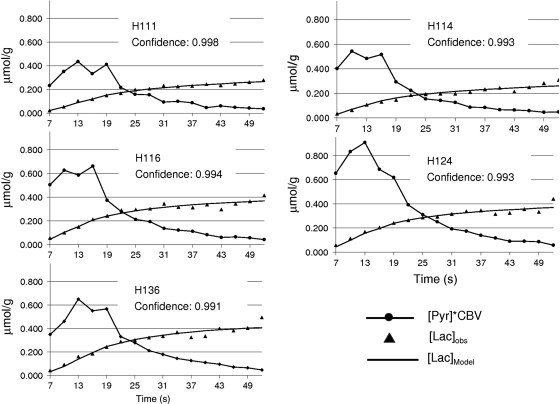
Figure 1 shows an example of the dynamic imaging obtained with this method. The 16 image frames are shown in the top panels; pyruvate (A) and lactate (B). The result shown is the average of three injections in one rat (H116). The times listed on the image are from the start of the injection and include 2 seconds of saline in-line, before pyruvate first enters the tail vein. The bottom left panel (C) in this figure shows an average of frames 5 to 12 of the pyruvate response, superimposed onto a gray-scale proton anatomic MR image. The bottom panel on the far right (D) is the lactate response from the same eight image frames scaled to the pyruvate. The bottom center panel (E) shows the dynamics from [1-¹³C]pyruvate and [1-¹³C]lactate in two ROIs. To reduce partial volume contribution to the brain from the large pyruvate signal in the peripheral vascular structures, the brain ROI for this study was limited to a 2 × 3 voxel region in the center of the brain. There is a small amount of [1-¹³C]lactate in the peripheral vascular structure ROI as well. It is <5% relative to pyruvate at the peak of the bolus, but gradually increases in later time points. This represents a lactate label in blood and a lactate label buildup in the surrounding tissues. As a worst case, [1-¹³C]lactate in this ROI was evaluated entirely as a vascular lactate. The ratio of vascular [1-¹³C]lactate to vascular [1-¹³C]pyruvate was used to estimate the [1-¹³C]lactate to [1-¹³C] pyruvate in the CBV. Figure 2A shows the lactate model result using the observed [pyr]_CBV input function with previously reported values for transport kinetics and CBV. The initial fit is made without correction for variable flip angle. The underestimation of lactate can be reduced by a decrease in the value for CBV, or by an increase in the value of K_d (B). A further improvement in fit is achieved by correcting [pyr]_CBV for variable flip angle (C). Figure 3 shows optimized fits with K_d as a variable from three individual injections into one of the rats (H114), along with a fit to the average of those three runs. Fitting confidence was increased, to 0.993, by averaging the data over the three injections. The average is also plotted with data from each of the individual runs to illustrate injection-to-injection variability. The variability is highest near the peak of the pyruvate bolus. Table 1 shows the results from fits to each of the 14 individual injections and for a fit to the within-animal average images. Maximum ¹³C [pyr]_CBV and ¹³C [lac] levels are also listed. These values are corrected for the cerebrospinal fluid fraction in the ROI. Cerebrospinal fluid fraction in the ROI was measured using a T₂ map calculated from the proton reference scans obtained on each rat. The cerebrospinal fluid in the restricted ROI used in this study ranged from 6.5% to 8.2%. The lactate label reached a maximum that ranged from 0.276 to 0.481 μmol/g, and pyruvate in the CBV peaked in a range from 17 to 42 μmol/g. The within-animal average dynamics and fits for each of the five rats studied are shown in Figure 4. Despite variations in the pyruvate bolus, especially between the individual runs of H124, within-animal variation was relatively small. Table 2 shows the impact of estimating the contribution of [1-¹³C]lactate generated outside the brain. Over the full time course, this fraction can account for ∼30% of the [1-¹³C]lactate that is observed in the brain ROI, and reduces the estimates of K_d and also the quality of fit.

Figure 1.

Time resolved metabolic imaging of rat brain. Dynamic images of (A) pyruvate and (B) lactate are shown for rat H116. Metabolite images of (C) pyruvate and (D) lactate are shown superimposed on a gray-scale proton image. (E) Dynamic curves are given for vascular pyruvate (blue) and vascular lactate (yellow) outside the brain, as well as for pyruvate (green) and lactate (red) in the brain volume of interest.

Figure 2.

Model fits to the first dynamic run for rat H116. (A) using literature value for CBV and transport kinetics, (B) fit after increasing K_d to 44 μL/g per min, and (C) best fit for K_d after correcting CBV pyruvate concentration for variable flip angle, VFA. CBV, cerebral blood volume.

Figure 3.

Model fits to the three individual dynamic runs on rat H114 (right) and on average (left). Confidence of fit improved with averaging as expected for the signal-to-noise ratio (SNR) limit. K_d and CBV are in very good agreement with literature values. CBV, cerebral blood volume.

Table 1. Model fit results for 14 dynamic runs.

Rat ID	Weight (g)	CSF (%)	Dose (mL)	[pyr]max (μmol/g)a	[lac]max (μmol/g)a	Kd (μL/g per min) at 2.7% CBV	CBV (%) at Kd=34 μL/g per min	Fit confidence
H111_1	197	6.17	2.4	17.8	0.276	41	2.2	0.992
H111_2	197	6.17	2.4	16.6	0.302	44	2.1	0.980
H111_avg	197	6.17	2.4	17.2	0.285	43	2.1	0.998
H114_1	257	7.60	3	25.0	0.290	33	2.8	0.985
H114_2	257	7.60	3	20.5	0.291	37	2.5	0.989
H114_3	257	7.60	3	21.2	0.269	33	2.8	0.975
H114_avg	257	7.60	3	21.8	0.282	35	2.6	0.993
H116_1	246	7.59	3	27.7	0.420	47	2.0	0.990
H116_2	246	7.59	3	25.8	0.393	44	2.1	0.989
H116_3	246	7.59	3	27.8	0.394	40	2.3	0.990
H116_avg	246	7.59	3	26.5	0.398	44	2.1	0.994
H124_1	213	7.12	3	39.3	0.418	34	2.7	0.980
H124_2	213	7.12	3	42.3	0.443	30	3.1	0.991
H124_3	213	7.12	3	28.4	0.351	34	2.7	0.984
H124_avg	213	7.12	3	36.2	0.397	31	3.0	0.993
H136_1	200	8.45	2.4	27.1	0.470	48	1.9	0.992
H136_2	200	8.45	2.4	28.0	0.481	49	1.9	0.986
H136_3	200	8.45	2.4	23.9	0.401	46	2.0	0.985
H136_avg	200	8.45	2.4	26.3	0.446	47	2.0	0.991

CBV, cerebral blood volume; CSF, cerebrospinal fluid.

^aCorrected for %CSF.

Figure 4.

Model fits to the averaged data from five individual rats are shown. Fit quality is maintained over range of different [pyr] input functions.

Table 2. Impact of [1-¹³C]lactate produced outside the brain.

Rat ID	Kd (μL/g per min) at 2.7% CBV	Fit confidence	[lac]max (μmol/g)	Lactate fraction from blood	Kd (μL/g per min) after blood fraction correction	Fit confidence (after correction)
H111_avg	43	0.998	0.285	0.329	28	0.978
H114_avg	35	0.993	0.282	0.294	22	0.982
H116_avg	44	0.994	0.398	0.301	32	0.981
H124_avg	31	0.993	0.397	0.356	20	0.977
H136_avg	47	0.991	0.446	0.317	33	0.972

CBV, cerebral blood volume.

Discussion

The method introduced in this paper, hyperpolarized [1-¹³C]pyruvate time resolved metabolic imaging, provides a quantitative measurement of [1-¹³C]pyruvate transport and resulting [1-¹³C]lactate levels in the normal brain. A model, using previously reported cerebral transport kinetics, fits the dynamic data, and is consistent with a blood–brain barrier (BBB) transport limited process. This model is also consistent with the apparent rate constants reported for the [1-¹³C]pyruvate-to-[1-¹³C]lactate flux in other tissues (Day et al, 2007; Zierhut et al, 2010), which range from 30- to 100-fold higher than the rate of BBB transport. These apparent metabolic rate constants include intracellular transport and lactate dehydrogenase activity, the combination of which significantly exceeds the blood-to-brain transport rate. This difference in rates is also the basis of the assumption that any pyruvate transported into the brain is observed as lactate and that nearly all of the pyruvate observed is in the CBV.

The other initial condition selected for this model, nonsignificant [1-¹³C]lactate in blood, is potentially more of a problem. Although [1-¹³C]lactate in the vascular ROI is delayed relative to the pyruvate bolus peak, the accumulated [1-¹³C]lactate generated outside the brain, could account for ≥30% of the observed brain [1-¹³C]lactate (Table 2). Under these conditions and a reported lactate exchange rate of 0.14 per min (Lear and Kasliwal, 1991), [1-¹³C]lactate in the CBV, and inflow of lactate can be estimated, assuming that most of the [1-¹³C]lactate in a vascular ROI is obtained from blood. As shown in Figure 1E, this [1-¹³C]lactate level is small at first but continues to increase throughout the observation window. The case for even lower blood lactate than observed in this study, is supported by an in vitro study of hyperpolarized [1-¹³C]pyruvate in blood under bolus conditions (Leung et al, 2009). The problem with estimating blood [1-¹³C]lactate levels in this study is that the 2.7 × 2.7 × 10 mm³ voxels contain a large amount of nonvascular tissue that also contributes to the [1-¹³C]lactate signal, especially at later time points. The actual [1-¹³C]lactate levels at the later time points do not match well with the all-vascular partial volume assumption. This mismatch is also reflected in reduced confidence of fit shown in Table 2. To avoid this uncertainty, imaging at higher spatial resolution may be required. Higher spatial resolution would also help overcome the limitation of extracerebral partial volume effects from strong vascular [1-¹³C]pyruvate signals, which prevent full brain coverage.

In this study, reproducibility of repeat injections was sufficient to improve fitting by averaging. There was some variation in the shape and size of the pyruvate bolus, due in part to variation in animal weight and dose, but also as a result of hand injections that required a 1- to 2-second switching delay for saline push. A concomitant dip in the pyruvate bolus was observed at the time of this delay. As illustrated in Figure 3, the peak of the pyruvate bolus shows the greatest variability. Fortunately, the model is independent of the input bolus shape, and a good fit to the lactate response is obtained with literature values for transport kinetics and CBV. Lactate alone can account for the predicted value of transported pyruvate based on the observed pyruvate input. In the ∼60-second window of observation, the impact of saturable pyruvate transport and lactate signal loss caused by exchange across the BBB are small. Thus, a change in CBV, and/or a change in the rate of nonsaturable pyruvate blood–brain transport, K_d, is required to optimize the fit of the observed data. At the literature value for K_d=34 μL/g per min, CBV ranges from 2.0% to 3.1%. This is consistent with the ROI used in this study, which contains both the white matter and the striatum, both of which are reported to have a lower CBV (Perles-Barbacaru and Lahrech, 2007). At a fixed CBV of 2.7%, K_d ranges from 30 to 47 μL/g per min (40±7). These values are also well within the ranges previously reported for the transport of pyruvate through the BBB. Using the worst case to account for [1-¹³C]lactate produced outside the brain, K_d estimates decreased to 20 to 33 μL/g per min (27±6). The value of K_d, at fixed CBV, did not vary much within each animal studied, <±5%, despite run-to-run differences in the hand-injected pyruvate bolus. However, it is likely that variations in both K_d and CBV are responsible for the dynamics reported in this study. Thus, an absolute measure of regional CBV in each animal, and for each injection may be desirable. An independent coregistered measurement, such as that described in the study by Perles-Barbacaru and Lahrech (2007) may be sufficient. However, it may be feasible to coadminister a blood-only hyperpolarized agent. This approach would include, and thus compensate for any transient effect that the pyruvate bolus may have on CBV.

Although the results described in this paper are consistent with BBB-limited uptake, the relative [1-¹³C]lactate level may still reflect regional differences in cellular uptake and lactate dehydrogenase-catalyzed flux and/or exchange. The method described in this study is based on hyperpolarized ¹³C signal, and does not detect unlabeled ¹²C-lactate or ¹²C-pyruvate. Therefore, the total lactate and pyruvate pool sizes are not measured and have no impact on the model presented. Furthermore, the method does not distinguish between lactate dehydrogenase catalyzed flux, exchange, or the cellular uptake of pyruvate. There is potential for both flux and exchange, especially during the bolus-dominated observation window. In a previous study, it was shown that a rapid change in pyruvate concentration, typical of hyperpolarized bolus studies, does result in flux, an increase in the total lactate pool size (Moreno et al, 2009). This is not too surprising, because the equilibrium favors lactate. However, it is also well established that lactate and pyruvate are in rapid exchange under equilibrium conditions (Day et al, 2007; Simpson et al, 1982; Xu et al, 2007). Independent of the balance between net flux and exchange, the level of ¹³C-lactate observed in hyperpolarized ¹³C-pyruvate studies, at least in other tissues, has been linked to several important changes in metabolic state, such as correlations of the ¹³C-lactate signal with lactate dehydrogenase activity (Ward et al, 2010), disease progression (Albers et al, 2008), and changes in redox state, NAD/NADH, caused by alcohol consumption (Spielman et al, 2009). However, in the brain, the impact of transport, on the use of [1-¹³C]lactate level as a marker, requires further investigation.

We have introduced in this study, hyperpolarized [1-¹³C]pyruvate metabolic imaging, as a repeatable noninvasive measurement of regional BBB transport kinetics and regional cerebral lactate levels. Hyperpolarized MR metabolic imaging has the potential to measure cerebral dynamic and metabolic changes for both focal and diffuse diseases.

Three of the authors (REH, Y-FY, and JT) are employees of the General Electric Company.