Abstract
Rationale and Objectives
Airway wall dimensions can be determined in vivo using transverse CT images, but the measurement of airway phantoms shows that the wall thickness is consistently over-estimated for small airways. This phantom study was performed to derive and test corrections to the measurements based on consideration of partial volume averaging and tilt effects.
Materials and Methods
We scanned a lung phantom with six polycarbonate tubes embedded in foam, and determined the cross-sectional dimensions of the tubes using the full width at half maximum (FWHM), zero crossing (ZC), and phase congruency (PC) edge detection methods. Equations were derived using the reported wall intensity to correct for partial volume averaging. Corrections for the over-estimation of the wall thickness due to the tilt of the tube with respect to the CT z-axis were also derived.
Results
All three methods (FWHM, ZC, and PC) overestimated the wall thickness of the small polycarbonate tubes. We verified that two sources of error were partial volume averaging and tilt that was introduced when the phantom was positioned with tube axes at an angle to the CT z-axis. The corrections were applied to the measured tube wall dimensions, and substantially reduced the deviation of the CT measurements from the true values.
Conclusion
Correcting for partial volume effects and airway tilt greatly increases the accuracy of simulated airway wall measurements in transverse CT images.
Keywords: Airway, airway wall, CT, Phase Congruency
Introduction
Now that the size and lumen area of proximal airways can be measured in vivo using CT images, there is increasing interest in determining the relationship between airway dimensions and clinical indices of chronic obstructive pulmonary disease (COPD). CT studies of patients with a range of smoking history have demonstrated associations between the severity of COPD and airway characteristics1-4. Because most of the resistance to airflow occurs in COPD in the small airways5,6, attention has turned to measuring small airways in CT images. However, technical limitations exist.
While CT images of airways as small as 1.5-2.0 mm in diameter can be obtained and measured with reasonable accuracy7, no airway segmentation method has yet emerged as a widely accepted standard. Most methods are either custom-designed for the sole use of the developers or obtainable from commercial entities for a licensing fee. Moreover, the commonly used full width at half-maximum (FWHM) method of edge detection is known to over-estimate wall thicknesses, especially for airways that are below 2 mm in inner diameter.7-9
Regardless of the edge detection method used to measure small airways, the investigator must contend with the partial volume averaging that results from the resolution limits of the CT scanner. Partial volume averaging occurs when both airway lumen and lung parenchyma are included in the pixels that contain the airway wall10,11, limiting the ability to accurately delineate its inner and outer edges. To our knowledge, data demonstrating accuracy for airways having a wall thickness as small as 0.3 mm has been presented for only one, the integral-based method.10 An additional problem is that accurate airway edge detection on two-dimensional cross-sectional CT images does not always result in an accurate calculation of the airway dimensions. For example, when the airway axis is tilted in transverse images with respect to the CT scanner Z-axis, the airway wall is calculated to be thicker than it is in reality. Similarly, the tilt increases the reported wall cross-sectional area. One study assessed a model-based approach to correct for tilt in simulated airways, but all had wall thickness greater than 1.0 mm.12 The limited ability of most methods to measure wall thickness in small airways accurately is a major disadvantage.
We have derived a set of corrections for reducing the errors that are due to both the limited CT resolution and the airway tilt. The purpose of this study was to test these corrections on a phantom lung using Airway Inspector, a free, open-source airway analysis program developed at Brigham and Women's Hospital, Boston, MA13. This program provides three methods of airway edge detection: full width at half maximum (FWHM), zero crossing (ZC), and Phase Congruency (PC).
Materials and Methods
Phantom
The CTP657 lung phantom (The Phantom Laboratory, Inc., Salem NY) consists of a foam block containing six polycarbonate right circular cylinder tubes, two of which are tilted at an angle of 30°, multiple holes, and several openings for inserts of materials of interest (Fig. 1). A collar around the foam simulates the chest wall, and has a mean value of 15 HU.
Fig. 1.
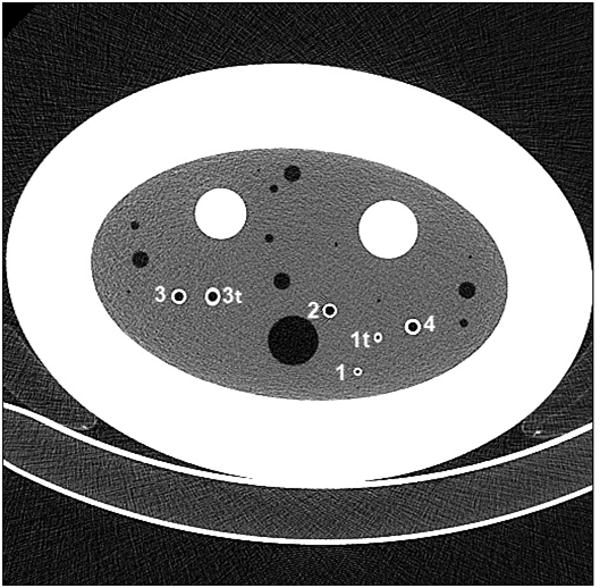
CT image of the CTP657 phantom with tubes numbered for identification. The z-axis of the phantom is parallel to the z-axis of the CT scan, which is perpendicular to the page. The axes of Tubes 1, 2, 3, and 4 are aligned with the phantom z-axis, while Tubes 1t and 3t are tilted 30° with respect to the phantom z-axis. The foam also contains multiple holes, including larger openings for inserts of any materials of interest.
In order to determine the attenuation of the polycarbonate plastic that the tubes are made of, we measured the attenuation of a solid rod of the same material that is 6.25 cm in diameter. The mean attenuation of polycarbonate plastic was determined to be 89 HU, and the foam has an attenuation of -856 HU. The manufacturer-specified inner and outer tube diameters (ID and OD) listed in Table 1 were verified with calipers and drill bits (standard blanks). The inner diameter of the smallest tube is 3 mm, well outside the 2 mm inner diameter limit above which the raw tube measurements are considered to be accurate7. Tube wall thickness uniformity was verified by measurements of the tubes using the Phase Congruency (PC) edge detection method in seven consecutive CT slices of the phantom, which showed little variation as seen by low standard deviation of the measurements (Table 1).
Table 1.
Calculated and measured airway tube cross-sectional dimensions.
| Tube | Tilt* | ID* (mm) | OD* (mm) | Pi (mm) | WT (mm) | WA (mm2) | WA% (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ref. Val.** | Mean | StdDev | Ref. Val.** | Mean | StdDev | Ref. Val.** | Mean | StdDev | Ref. Val.** | ||||
| 1t | 30 | 3.0 | 4.2 | 9.42 | 8.35 | 0.25 | 0.60 | 1.17 | 0.06 | 6.79 | 14.12 | 0.57 | 48.98 |
| 1 | 3.0 | 4.2 | 9.42 | 7.95 | 0.06 | 0.60 | 1.05 | 0.01 | 6.79 | 11.82 | 0.12 | 48.98 | |
| 2 | 6.0 | 7.8 | 18.85 | 18.66 | 0.04 | 0.90 | 1.02 | 0.01 | 19.51 | 22.20 | 0.33 | 40.83 | |
| 3t | 30 | 6.0 | 8.4 | 18.85 | 20.22 | 0.15 | 1.20 | 1.34 | 0.07 | 27.14 | 32.70 | 1.81 | 48.98 |
| 3 | 6.0 | 8.4 | 18.85 | 19.19 | 0.04 | 1.20 | 1.11 | 0.00 | 27.14 | 25.27 | 0.07 | 48.98 | |
| 4 | 6.0 | 9.0 | 18.85 | 19.19 | 0.82 | 1.50 | 1.30 | 0.12 | 35.34 | 29.67 | 1.19 | 55.56 | |
Inner Diameter (ID) and Outer Diameter (OD) were listed in the manufacturer's manual (The Phantom Laboratory, Inc, “CTP657 Lung Phantom Manual”, Salem, NY, 2008.).
Inner Perimeter (Pi) = π ID; wall thickness (WT) = [(OD-ID)/2]; wall area (WA) = [π(OD/2)2 - π(ID/2)2]; wall area percent (WA%) = [WA/π(OD/2)2 × 100%]
Note - Measurements were made using the phase congruency method over seven consecutive slices.
CT Scanning
The phantom was scanned on a Siemens Definition 64-detector row scanner with a peak energy of 120 kVp, X-ray tube current of 90 mA, pitch of 1.5, rotation time of 0.5 sec, and effective tube current of 30 mAs, using 0.6 mm detector collimation. The images were reconstructed at 1 mm thickness with the medium sharp B50f kernel, which provides thinner estimates of wall thickness than smooth kernels (G. Washko, private communication). Measurements were made with four values of the field of view (FOV), ranging from 100 to 350 mm. The wall thickness in pixels of the airway tubes ranges from less than one pixel for Tube 1 at FOV = 350 mm to more than seven pixels for Tube 4 at FOV = 100 mm (Table 2). The effects of changing the field of view on the measured inner perimeter and wall thickness were small (Table 2). A FOV of 350 mm, typical for a medium to large adult, was used for comparing measurements before and after applying the correction methods presented here.
Table 2.
Measured values of Inner Perimeter and Wall Thickness at several fields of view.
| Tube | Reference value (mm) | Measured value, Phase Congruency method | |||
|---|---|---|---|---|---|
| FOV=100 mm | FOV=150 mm | FOV=200 mm | FOV=350 mm | ||
| Inner Perimeter (Pi) in mm | |||||
| 1 | 9.42 | 8.36 | 8.37 | 8.28 | 7.97 |
| 2 | 18.85 | 18.44 | 18.33 | 18.33 | 18.39 |
| 4 | 18.85 | 19.22 | 19.48 | 19.46 | 19.39 |
| Wall Thickness (WT) in mm | |||||
| 1 | 0.60 | 0.99 | 0.98 | 1.01 | 1.05 |
| 2 | 0.90 | 1.15 | 1.14 | 1.14 | 1.12 |
| 4 | 1.50 | 1.41 | 1.42 | 1.42 | 1.33 |
| Reference Wall Thickness in pixels | |||||
| 1 | 3.13 | 2.05 | 1.54 | 0.88 | |
| 2 | 4.69 | 3.07 | 2.30 | 1.32 | |
| 4 | 7.82 | 5.12 | 3.84 | 2.19 | |
The phantom was scanned at several different angles between the CT z-axis and the phantom z-axis to assess the effect on the calculated wall dimensions. The angles between the CT gantry and the phantom were measured using electronic calipers on the topogram at the time of scanning.
Airway Analysis
There are three edge detection methods available in the Airway Inspector component of the open-source software program Slicer (www.slicer.org): full width at half maximum (FWHM), zero crossing (ZC), and phase congruency (PC).8,13-17. Results are reportedly improved by analyzing images using the PC method with multiple kernels13. We tested this option with two kernels and found little difference from the single kernel results. Because it is not common practice to obtain more than two kernel reconstructions of CT scans, we did not test this option with more than two kernels, and used only the single kernel method in this study.
Measurement Correction Assumptions
Because the walls of small airways span at most a few pixels, many of the pixels containing airway wall also include adjacent lumen and parenchyma, which results in overestimation of the wall thickness (Fig. 2). Further, the edge enhancement effects of sharp kernels in large airways, which cause airway walls to have greater measured attenuation than the true value, can result in a calculated wall thickness that is too small. Finally, when the airway axis is tilted with respect to the CT z-axis, the airway wall thickness is overestimated in the direction of the tilt (Fig. 3). The corrections we devised for these problems assume a constant wall thickness over the entire circumference, and also assume that the airways are round or elliptical in cross-section perpendicular to their long axis. These corrections utilize the mean airway wall intensity (attenuation) and the dimensions of the inner and outer ellipses which describe the airway in the cross sectional image, all of which are automatically reported by the Airway Inspector program.
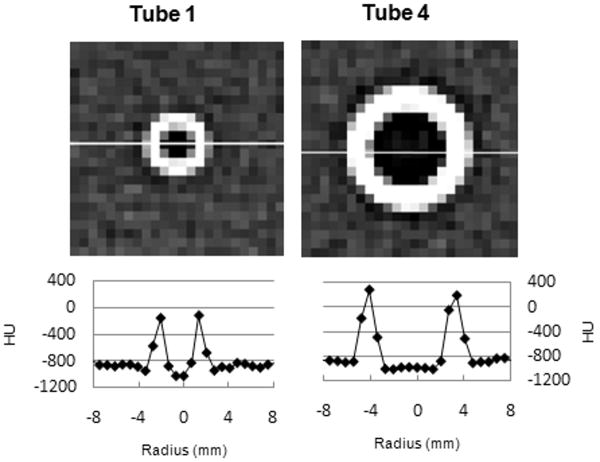
Fig. 2.
The CT images of Tubes 1 and 4 and the graphs below the images were obtained using the public-domain program ImageJ. The graphs show the attenuation (in HU) along the line crossing the tube plotted as a function of distance. The maximum HU value of Tube 1 is much less than the airway tube attenuation, so the half-maximum point is near -700 HU. This will result in a calculated wall thickness that is too large.
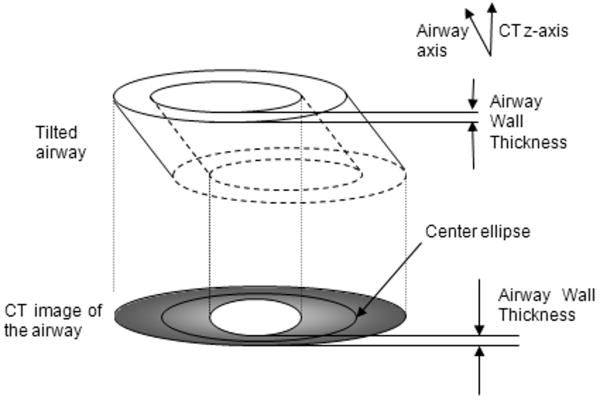
Fig. 3.
Fig. 3a. Side view of an elliptical airway that is tilted with respect to the CT z-axis, which lies along the bore of the CT scanner.
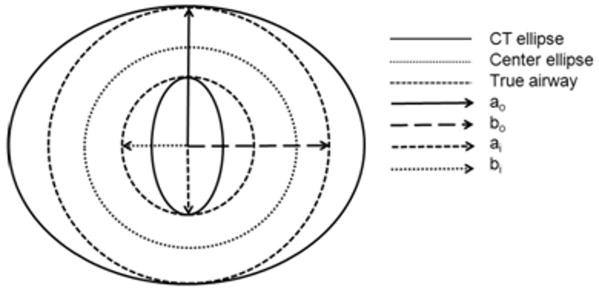
Fig. 3b Top view of an elliptical airway that is tilted with respect to the CT z-axis. The solid inner and outer ellipses are the limits of the airway seen in the CT image (CT ellipses). The Center ellipse, half way between the inner and outer ellipses, is used in finding the airway walls. (ai, bi) are the major and minor axes of the inner edge of the airway. (ao, bo) are the major and minor axes of the outer edge of the airway. Since this airway is circular, the major and minor axes are equal.
Partial Volume Correction
The effect of partial volume averaging on airway wall measurements is illustrated in the HU profiles for the polycarbonate tubes in Figure 2. Because the walls of small airways span at most a few pixels, many of the pixels containing airway wall also include adjacent lumen and parenchyma. The measured maximum attenuation of Tube 1 (internal diameter 3 mm) is roughly -100 HU, much less than 89 HU, which is the known attenuation of the polycarbonate plastic. The smaller maximum attenuation is accompanied by a broadening of the wall attenuation profile, due to pixels that contain both wall and lumen, or both wall and parenchyma (Fig. 2). This effect results in a measured wall thickness that is too large. Thus, the measured wall thickness, WTm, is the sum of the thickness of the true wall, WTw, the lumen, WTl, and the parenchyma, WTp included in the wall profile:
| (2) |
When X-rays travel through a material, the reduction in intensity I of the beam due to the material is related exponentially to the width x and linear attenuation μ of the material: I = I0e−μx. In this case, there are three materials in the volume (airway wall, lumen, and lung parenchyma), with lengths WTw, WTl, and WTp. The final intensity of one pixel is therefore:
| (3) |
where μw, and μl, and μp are the linear attenuation of the tube, lumen, and parenchyma included in the pixel. Then, defining μm as the linear attenuation of the pixel (4a) and converting to Hounsfield units (4b), we have:
| (4a) |
| (4b) |
HUw, HUl, and HUp represent the attenuation of wall, lumen, and parenchyma in Hounsfield units. HUm is the mean attenuation of the airway wall. Since the wall thickness is determined by looking radially outward from the center of the airway, the true wall thickness WTw can be calculated from WTm.
We examined the percent error obtained using values for WTl/WTp ranging from 0 to 2. Because the attenuation of the foam is close to the attenuation of air in the center of the tube, we would expect a nearly equal amount of lumen (WTl) and foam (WTp) to be included in the area identified in the analysis as tube wall. For phantom tubes larger than six pixels in inner diameter, this was found to be correct, and the smallest error was obtained by setting WTl equal to WTp. In other words, for airways larger than six pixels in inner diameter the partial volume effects are seen equally in the lumen and in the parenchyma outside of the airways. For smaller airways, there are not enough pixels in the lumen for an accurate determination of its attenuation since a portion of the wall is included. For instance, the mean attenuation of the lumen of Tube 1 shown in Figure 2 would be calculated to be greater than the correct value of -1000 HU since all but two pixels contain some portion of airway wall. The calculated position of the inner margin of the tube would then encroach on the true lumen by a small amount. For these tubes the most accurate results were obtained by assuming that there is no lumen included in the measured wall, so that WTl / WTp = 0. Therefore we can derive a partial volume correction factor PVC for two ranges of inner diameter (ID):
| (5a) |
The true wall thickness is then
| (5b) |
Details of the derivation are given in Appendix A.
Over- or under- estimation of wall thickness introduces error into other calculated airway dimensions that are derived from the inner and outer ellipse axes. Using the corrected wall thickness, the measurements of wall area and inner perimeter may then also be corrected for partial volume effects. Assuming that the corrected wall thickness is constant, we first find the coordinates of an ellipse that is located at the midpoint between the inner and outer airway walls shown in the CT image, which is defined as “the Center Ellipse” (Fig. 3a and b). The coordinates of the corrected inner and outer airway walls are then determined relative to this demarcation. The corrected inner airway wall will be located at one-half the corrected wall thickness in the luminal direction from the Center Ellipse, and the coordinates of the corrected outer airway wall are found at one-half the corrected wall thickness in the opposite direction from the Center Ellipse. The major and minor axes of the corrected ellipses, (ao, bo) and (ai, bi) are then calculated and used to calculate the partial volume corrected wall area and wall area percent:
| (6a) |
| (6b) |
Since the airway shown in Fig. 3b is circular the major and minor axes are equal, but the principal holds for the more general case of an elliptical airway.
Tilt Correction
When the airway axis is tilted with respect to the CT scanner Z-axis, the scan plane traverses a greater length of some portions of the airway wall, so that the measured airway wall thickness and wall area are overestimated. The tilt correction is illustrated in Fig. 3.
For a given radius extending outward from the center of the airway, the points on the radius marking the inner and outer limits of the wall seen in the CT image are displaced an equal amount but in opposite directions by the tilt of the airway. The most accurate values of wall thickness are obtained in tilted airways by using the smallest distance between the inner and outer ellipses (Airway Wall Thickness in the CT image of the airway in Fig. 3a) which are automatically fitted to the airway by the Airway Inspector program. Since the error in the wall position is equally divided between the inner and outer edges, the true center of the airway wall, or Center Ellipse, is found at a point halfway between the fitted inner and outer ellipses (Fig. 3a), which serve as good approximations of the inner and outer wall edges. Assuming a constant wall thickness, the tilt-corrected inner ellipse (ai, bi in Fig. 3b) is located at one-half the true wall thickness in the luminal direction from the Center Ellipse, and the tilt-corrected outer ellipse (ao, bo in Fig. 3b) is located at half the wall thickness in the opposite direction from the Center Ellipse. The tilt-corrected inner perimeter is the circumference of the tilt-corrected inner ellipse, and the wall area and wall area percent can be calculated from the tilt-corrected ellipses, whose areas are given by πab, where a and b are the major and minor axes:
| (6a) |
| (6b) |
A computer program was written and used to determine the locations of the Center Ellipse and the tilt-corrected inner and outer ellipses, and calculate the tilt-corrected parameters.
Results
Partial Volume Correction
The effects of partial volume averaging were isolated from the error due to airway tilt by examining the four tubes with axis parallel to the phantom z-axis. The measured (uncorrected) and partial partial volume corrected values for each dimension (inner perimeter, wall thickness, wall area, and wall area percent) were compared to the tube reference values for each segmentation method (FWHM, ZC, and PC) (Table 3). There was substantial deviation from the reference values for both tubes having a reference wall thickness < 1 mm with all three uncorrected segmentation methods. The wall thickness reported by the three methods has a much smaller range than the reference wall thickness. In all methods, the thickness of the largest tube is underestimated and the thickness of the smallest tube is overestimated, so the true ratio of largest to smallest tube thickness, 2.5, is measured to be 1.26 by all three methods. For all of the tubes and all of the methods, the inner perimeter Pi is reasonably close to the actual value, though the greatest accuracy is seen with the larger tubes.
Table 3.
Measured and partial volume corrected dimensions of non-tilted airway tubes using each segmentation method (FWHM, Zero Crossing, Phase Congruency).
| Tube | Reference Value | Measured Value, FOV=350 mm | Partial Volume Corrected Value | ||||
|---|---|---|---|---|---|---|---|
| FWHM | Zero Crossing | Phase Congruency | FWHM | Zero Crossing | Phase Congruency | ||
| Inner Perimeter (Pi) in mm | |||||||
| 1 | 9.42 | 7.72 | 8.29 | 7.97 | 7.74 | 8.30 | 8.02 |
| 2 | 18.85 | 18.1 | 18.61 | 18.39 | 19.02 | 19.34 | 19.25 |
| 3 | 18.85 | 18.41 | 19.03 | 19.13 | 18.05 | 19.35 | 19.18 |
| 4 | 18.85 | 18.88 | 19.65 | 19.39 | 19.15 | 19.61 | 19.41 |
| Wall Thickness (WT) in mm | |||||||
| 1 | 0.6 | 1.12 | 0.99 | 1.05 | 0.64 | 0.59 | 0.61 |
| 2 | 0.9 | 1.16 | 1.02 | 1.12 | 0.87 | 0.79 | 0.85 |
| 3 | 1.2 | 1.27 | 1.15 | 1.27 | 1.43 | 1.04 | 1.12 |
| 4 | 1.5 | 1.42 | 1.26 | 1.33 | 1.37 | 1.25 | 1.31 |
| Wall Area (WA) in mm2 | |||||||
| 1 | 7 | 12.56 | 11.26 | 11.79 | 6.33 | 5.63 | 6.19 |
| 2 | 20 | 25.14 | 22.15 | 24.45 | 18.71 | 17.10 | 18.39 |
| 3 | 27 | 28.52 | 26.07 | 29.46 | 32.31 | 23.52 | 25.57 |
| 4 | 35 | 33.24 | 29.61 | 31.28 | 32.18 | 29.48 | 30.71 |
| Wall Area Percent (WA%) in % | |||||||
| 1 | 48.98 | 72.51 | 67.11 | 69.83 | 57.19 | 50.66 | 55.01 |
| 2 | 40.83 | 48.98 | 44.43 | 47.5 | 39.39 | 36.49 | 38.42 |
| 3 | 48.98 | 51.08 | 47.45 | 50.84 | 55.49 | 44.12 | 46.62 |
| 4 | 55.56 | 53.75 | 49.02 | 51.07 | 52.45 | 49.08 | 50.60 |
Note – Reference value based on inner and outer diameter reported by manufacturer
The values of wall thickness, wall area, and wall area percent are greatly improved for the two small tubes (Tubes 1, 2) by the application of the partial volume correction to the results obtained using all three of the analysis methods (Table 3). For example, with the PC method, applying the partial volume correction to the Tube 1 measurement reduced the percent error in wall thickness from 75% to 1.7%. Tube 2 with an inner diameter of 6 mm also had significant improvement in the wall thickness error measured by PC, which reduced the percent error from 24% to -6%. The two large tubes, Tubes 3 and 4, also have inner diameters of 6 mm, but their thicker walls (1.2 mm and 1.5 mm respectively) reduced the effect of partial volume averaging. For Tube 4, the mean wall attenuation is only 14 HU below the attenuation of the tube material, at 75 HU. The partial volume correction factor defined in Equation 5a ranges from 0.62 for Tube 1, which has a wall thickness of 0.6 mm, to 0.98 for Tube 4, which has a wall thickness of 1.5 mm.
To determine the performance of the corrections in the limit of very small wall thickness, we used Airway Inspector to measure three of the holes in the phantom. The measured wall thicknesses of the 2 mm, 5 mm, and 10 mm holes were 1.47 mm, 0.73 mm, and 2.12 mm, respectively. The corrected measured thicknesses of the three holes were 0.06 m, 0.02 mm, and 0.19 mm, respectively.
Tilt Correction
The effects of applying the tilt correction alone are shown in Table 4, where the measured (uncorrected) and tilt-corrected results for Tube 1 obtained using the PC segmentation method are displayed for several angles between the phantom z-axis and the CT z-axis. The accuracy of wall thickness measurements is improved for this small tube at the larger tilt angles, but the measurements are undercorrected at all angles. The wall area is also improved for all angles, though less dramatically than the wall thickness. Results were similar for the other tubes and segmentation methods. The errors are due in part to partial volume effects, which vary at different angles, but are not accounted for in the analysis of Table 4.
Table 4.
The measured Tube 1 wall dimensions compared to the tilt-corrected wall dimensions.
| Angle (degrees) | Pim (Ref.= 9.42 mm) | Picorr | WTm (Ref. = 0.6 mm) | WTcorr | WAm (Ref = 6.79 mm2) | WAcorr | WA%m (Ref. = 48.98 %) | WA%corr |
|---|---|---|---|---|---|---|---|---|
| 0 | 7.97 | 8.59 | 1.05 | 0.85 | 11.79 | 9.62 | 69.83 | 62.11 |
| 6 | 7.86 | 8.50 | 1.08 | 0.88 | 12.09 | 9.87 | 70.95 | 63.20 |
| 17 | 8.01 | 8.57 | 1.08 | 0.90 | 12.29 | 10.32 | 70.49 | 63.89 |
| 22 | 8.16 | 8.48 | 1.13 | 1.03 | 13.20 | 12.15 | 71.17 | 68.12 |
| 27 | 8.58 | 8.81 | 1.12 | 1.05 | 13.50 | 12.73 | 69.57 | 67.52 |
| 43 | 10.03 | 10.81 | 1.05 | 0.92 | 14.15 | 12.67 | 63.38 | 59.44 |
| 60 | 10.97 | 13.56 | 1.31 | 1.05 | 19.97 | 18.44 | 65.22 | 62.46 |
Note: All measurements made using phase congruency method and 350 mm field of view
Pi – inner perimeter (mm); WT – wall thickness (mm); WA – Wall area (mm2); WA% - wall area percent; m – measured value; corr –corrected value; Ref. - reference value based on inner and outer diameter reported by manufacturer
Partial Volume and Tilt Correction
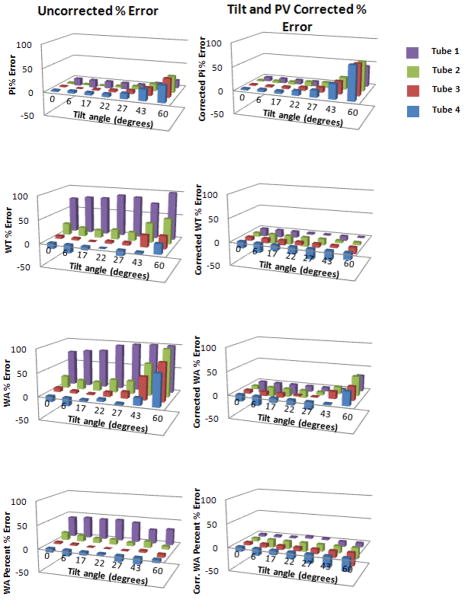
Figure 4 shows the percent error relative to the reference values for each tube over all tilt angles without and with application of both the partial volume and tilt corrections to measurements made using the PC method. Similar results were obtained for using the FWHM and ZC methods. The corrected wall thickness, wall area, and wall area percent of the smaller tubes are much more accurate than the uncorrected results, while the inner perimeter error increases for the tubes tilted 43° and 60°. At large tilt angles the relatively large percent error of the uncorrected wall thickness and inner perimeter combine to give a more accurate value of the uncorrected wall area percent. For instance, at 43 degrees, the inner perimeter of Tube 3 has 16% error and the wall thickness has 24% error. These combine to give a value for wall area percent that has a mere 4% error, and a corrected value that has a -4% error.
Fig. 4.
% Error for the four tubes aligned parallel to the phantom z-axis. The measurements were made using the Phase Congruency method and images reconstructed with the B50f kernel. The graphs on the left show % error values of the uncorrected measurements. On the right are the results with partial volume and tilt corrections applied.
We do not know the smallest airway that can be calculated accurately; the dimensions of the smallest tube have small percent error for tilt angles below 40°. The corrections in general become less effective as the tilt angle increases, particularly for the inner perimeter and the wall area. However, the combined corrections substantially reduce the error in wall area for the smallest tubes (1 and 2) at small to moderate angles.
Discussion
Our study shows that, through consideration of partial volume effects and airway orientation, it is possible to considerably improve the accuracy of dimensions measured on CT images of tubes approaching the size of small airways. Limitations of the measurement accuracy related to airway size and angle of orientation have been previously recognized9-11. These limitations were confirmed by our phantom data, which show overestimation of wall thickness for the smallest tubes and underestimation for the largest tubes, and overestimation with angulation.
The accuracy of measurements obtained from cross-sectional CT images depends on the ability of the CT scanner to resolve the structure of interest, and on the image analysis algorithm used to define the spatial limits of the structure. The use of thin section scans is considered essential for optimizing resolution, to limit partial volume averaging along the z-axis. Although this is not as important in a phantom study using tubes of uniform thickness, the thin sections in our study should have minimized partial volume averaging along the z-axis related to any slight deviations in orientation of the airways from 0° along the z-axis of the scanner bore.
The accuracies of the three airway edge detection algorithms available in the Airway Inspector program were quite similar. The FWHM method has been evaluated in other studies, and found to consistently overestimate airway wall thickness when the inner diameter is less than 2 mm2,9,18. Washko et al.9, who also used the CTP657 lung phantom, reported a wall thickness of 133% for the smallest tube (Tube 1 in our study), 56% for Tube 2, 31% for Tube 3 and 16% for the largest, Tube 4, relative to the true value. These are significantly larger than our results of 87%, 29%, 6%, and -5% error for the same tubes, respectively. These differences may be related to differences in the scanner model (different scan manufacturer in our study), reconstruction kernel (smooth compared to sharp in our study), and slice thickness (2.5 mm compared to 1.0 mm in our study). After correcting our FWHM results for both volume averaging and tilt, the wall thickness of Tubes 1-4 was much more accurate, particularly for the smaller tubes, with errors of -6%, -5%, 18%, and -10%, respectively. All of the tubes are larger than the 2 mm inner diameter considered as the approximate minimum required for reasonable accuracy, indicating that it is also important to consider the wall thickness as limiting the accuracy of airway measurements. To our knowledge, there have been no other assessments of the accuracy of the ZC or the PC methods, though one study reported that correlations between airway measurements and pulmonary function were similar with both the FWHM and the phase congruency methods19.
Others have considered airway tilt and partial volume effects in their development of airway measurement protocols. Wood et al.20 used CT images to reconstruct the airway tree in three dimensions. They were then able to use cross-sections of the airway perpendicular to the airway axis for calculating the inner diameter. This had the effect of correcting for any airway tilt. Using two Plexiglas phantoms, they found that their calculations were quite accurate for tubes of more than 2 mm inner diameter, but the inner diameters calculated for the smaller tubes were too small. They examined their phantom at several angles and found, as we did, that the size of tube was more important than tilt angle in limiting the accuracy of the calculation. A more complex model-based approach that considers the scanner point spread function has also been shown to improve the accuracy of tilted airway measurements on 2D images;12 due to differences in tube sizes and measured parameters, we are unable to compare our results. Other investigators achieved very accurate results with their integral-based method, which corrects for partial volume effects, to measure a phantom with tubes ranging from wall thickness of 0.3 mm to 2.5 mm and inner diameters ranging from 2 mm to 4 mm. At FOV=360 mm, and 512 pixel matrix, the measured thicknesses were 1.00 mm for a 1.00 mm thick airway tube, 0.55 mm for a 0.50 mm tube, and 0.27 mm for a 0.3 mm tube10. We note that while non-orthogonal sections may be reconstructed perpendicular to the airway path to solve the tilt problem more directly if thin-section, isotropic 3D volumetric imaging parameters are used, the partial volume averaging correction may still be applied to improve the results.
Several limitations of this study should be noted. Although we measured only small differences in tube dimensions when the field of view was reduced, the partial volume effects and impact of the corrections may be different at smaller fields of view. The impact of the corrections also may be slightly different if a different reconstruction kernel is used, or when applied to pulmonary airways, which have a lower wall attenuation than the tubes of the phantom used to demonstrate the correction principles. The corrections for partial volume effects and tilt assume a constant wall thickness and elliptical shape, which may not be found in all airways. We note that the attenuation values used in the partial volume correction assume a monochromatic x-ray beam. However, calculations show that the polychromatic nature of CT x-rays has miniscule effect on the correction factor; using the linear attenuation coefficient values for polycarbonate provided by the phantom manufacturer, the correction factor varied by only 0.5% between 70 and 120 keV, and by 2% between 40 and 100 keV.
In summary, our study suggests that correcting for partial volume and tilt effects should make it possible to determine the dimensions of airways on transverse CT images down to a wall thickness of at least 0.6 mm, with greater accuracy than the uncorrected methods previously used in many clinical studies. We do not know the lower limit of accuracy, but the performance of the corrections applied to the measurement of holes with zero wall thickness suggests that the limit may be smaller. To determine the correction factor to use for in vivo scans of real lungs, attenuation values approximating those of airway walls and the surrounding lung would need to be used. The effect of these corrections on associations between in vivo airway wall measurements and pulmonary function parameters remains to be determined.
Acknowledgments
The authors wish to thank Dr. George Washko for many helpful discussions on the use of Airway Inspector and airway analysis methods.
This work has been funded by National Heart, Lung, and Blood Institute grant P50 HL084922, and by the Alan A. and Edith L Wolff Charitable Trust/Barnes-Jewish Hospital Foundation (R. M. Senior)
Appendix A. Partial Volume Corrected Wall Dimensions
The intensity I of a beam of X-rays travelling through an object m of measured thickness WTm and linear attenuation coefficient μm is:
| (A1) |
where μm depends on the X-ray beam energy E and also on the materials that comprise the object. In general, the denser the material, the more the beam is attenuated as it travels through the material, so μ is larger for denser materials. If the object consists of three materials, lumen, wall, and parenchyma, with the beam traveling through them one at a time, the intensity is reduced as it travels through each material. If the beam has an intensity Ip as it leaves the parenchyma, and an intensity Iw as it leaves the wall we have:
| (A2a) |
| (A2b) |
Adding a third material, lumen, we have for the final intensity I:
| (A3a) |
| (A3b) |
The intensity I given in equation A1 is equal to the intensity given in equation A3b, so the linear attenuation coefficient of the entire object is a function of the attenuation coefficients of each material that goes into the object:
| (A4) |
We can convert the attenuation coefficients into Hounsfield units:
| (A5) |
as follows. Dividing both sides of equation A4 by (μwater-μair), we have:
| (A6a) |
Making use of the fact that
| (A6b) |
so that
| (A6c) |
we can subtract equation A6c from equation A6a:
| (A6d) |
Finally, multiplying both sides by 1000, we have the relationship between measured wall thickness and true wall thickness in Hounsfield Units.
| (A7) |
We now have two equations (A6b and A7) and three unknowns (WTp, WTw, and WTl), so in order to find WTw in terms of WTm we must make an assumption about the relative sizes of WTl and WTp. Defining α as WTl / WTp we have
| (A8) |
From Equation A6,
| (A9a) |
| (A9b) |
Substituting (WTw-WTm)/(1+α) for WTp, in equation A8
| (A10a) |
| (A10b) |
| (A10c) |
Finally, we have
| (A11) |
as the value of the true wall thickness in terms of the measured wall thickness WTm and the parameter α. It is possible to determine the best value of α empirically, by calculating WTw with several values of α and using the value that results in the smallest percent error of the corrected wall thickness WTw. For convenience, we will define a partial volume correction factor PVC as:
| (A12a) |
so that
| (A12b) |
For large airways, the smallest percent error results from a value of α equal to 1, or an equal amount of lumen and parenchyma included in our measurement of airway wall. Since the values of HUp and HUl are close (-856 HU and -1000 HU, respectively) compared to the value of the airway wall HUw, this is to be expected. Small airways have do not have enough pixels in the lumen for the mean value HUl to be determined accurately. The small number of pixels in the lumen that contain no airway wall rest in a measured value of HUl that is larger than the true value. This in turn leads to a measured inner diameter that is larger than the true inner diameter. With an inner diameter that is too large, there is no lumen included in the measured wall thickness, so smaller percent error was obtained by setting α equal to 0, corresponding to WTl = 0.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Berger P, Perot V, Desbarats P, Tunon-de-Lara JM, Marthan R, Laurent F. Airway Wall Thickness in Cigarette Smokers: Quantitative Thin-Section CT Assessment. Radiology. 2005;235:1055–1064. doi: 10.1148/radiol.2353040121. [DOI] [PubMed] [Google Scholar]
- 2.Hasegawa M, Nasuhara Y, Onodera Y, Makita H, Nagai K, Fuke S, Ito Y, Betsuyaku T, Nishimura M. Airflow Limitation and Airway Dimensions in Chronic Obstructive Pulmonary Disease. American Journal of Respiratory and Critical Care Medecine. 2006;173:1309–1314. doi: 10.1164/rccm.200601-037OC. [DOI] [PubMed] [Google Scholar]
- 3.Nakano Y, Muro S, Sakai H, Hirai T, Chin K, Tsukino M, Nishimura K, Itoh H, Paré PD, Hogg JC, Mishima M. Computed Tomographic Measurements of Airway Dimensions and Emphysema in Smokers, Correlation with Lung Function. American Journal of Respir Crit Care Med. 2000;162:1102–1108. doi: 10.1164/ajrccm.162.3.9907120. [DOI] [PubMed] [Google Scholar]
- 4.Orlandi I, Moroni C, Camiciottoli G, Bartolucci M, Pistolesi M, Villari N, Mascalchi M. Chronic obstructive pulmonary disease: thin-section CT measurement of airway wall thickness and lung attenuation. Radiology. 2005;234:604–610. doi: 10.1148/radiol.2342040013. [DOI] [PubMed] [Google Scholar]
- 5.Macklem PT, Mead J. Resistance of central and peripheral airways measured by the retrograde catheter. J Appl Physiol. 1967;22:395–401. doi: 10.1152/jappl.1967.22.3.395. [DOI] [PubMed] [Google Scholar]
- 6.Hogg JC, Macklem PT, Thurlbeck WM. Site and nature of airways obstruction in chronic obstructive lung disease. N Engl J Med. 1968;278:1355–60. doi: 10.1056/NEJM196806202782501. [DOI] [PubMed] [Google Scholar]
- 7.King G, Müller NL, Paré PD. Evaluation of Airways in Obstructive Pulmonary Disease Using High-Resolution Computed Tomography. Am J Respir Crit Care Med. 1999;159:998–1004. doi: 10.1164/ajrccm.159.3.9805064. [DOI] [PubMed] [Google Scholar]
- 8.Reinhardt JM, D'Souza ND, Hoffman EA. Accurate Measurement of Intra-thoracic airways. IEEE Trans Medical Imaging. 1997;16:820–827. doi: 10.1109/42.650878. [DOI] [PubMed] [Google Scholar]
- 9.Washko GR, Dransfield MT, Estépar RSJ, Diaz A, Matsouka S, Yamashiro T, Hatabu H, Silverman EK, Bailey WC, Reilly JJ. Airway Wall Attenuation: A Biomarker of Airway Disease in Subjects with COPD. J Appl Physiol. 2009;107:185–191. doi: 10.1152/japplphysiol.00216.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Achenbach T, Weinheimer O, Dueber C, Heussel CP. Influence of Pixel Size on Quantification of Airway Wall Thickness in Computed Tomography. J Comput Assist Tomogr. 2009;33:725–730. doi: 10.1097/RCT.0b013e318190699a. [DOI] [PubMed] [Google Scholar]
- 11.King G, Müller NL, Paré PD. An Analysis Algorithm for Measuring Airway Lumen and Wall Areas from High-Resolution Computed Tomographic Data. Am J Respir Crit Care Med. 2000;161:574–480. doi: 10.1164/ajrccm.161.2.9812073. [DOI] [PubMed] [Google Scholar]
- 12.Saba OI, Hoffman EA, Reinhardt JM. Maximizing quantitative accuracy of lung airway lumen and wall measures obtained from X-ray CT imaging. J Appl Physiol. 2003;95:1063–1075. doi: 10.1152/japplphysiol.00962.2002. [DOI] [PubMed] [Google Scholar]
- 13.Estépar RSJ, Washko GG, Silverman EK, Reilly JJ, Kikinis R, Westin CF. Accurate Airway Wall Estimation Using Phase Congruency. In: Larson R, Nielson M, Sporring J, editors. MICCAI. Vol. 4191. Springer-Verlag; Berlin: 2006. pp. 125–134. LNCS. [DOI] [PubMed] [Google Scholar]
- 14.Estépar RSJ, Washko GG, Silverman EK, Reilly JJ, Kikinis R, Westin CF. Airway Inspector: an Open Source Application for Lung Morphometry. First International Workshop on Pulmonary Image Processing. 2008:293–302. [Google Scholar]
- 15.Marr D, Hildreth E. Theory of Edge Detection. Proc of the Royal Society of London B. 1980;208:187–217. doi: 10.1098/rspb.1980.0020. [DOI] [PubMed] [Google Scholar]
- 16.Kovesi P. Phase Congruency, A Low Level Image Invariant. Psychological Research. 2000;64:136–148. doi: 10.1007/s004260000024. [DOI] [PubMed] [Google Scholar]
- 17.Kovesi P. Edges are Not Just Steps. The 5th Asian Conference on Computer Vision; 2002. [Google Scholar]
- 18.Amirav I, Kramer S, Grunstein M, Hoffman E. Assessment of Methacholine-Induced Airway Constriction with Ultrafast High-Resolution Computed Tomography. J Appl Physiol. 1993;75:2239–2250. doi: 10.1152/jappl.1993.75.5.2239. [DOI] [PubMed] [Google Scholar]
- 19.Kim WJ, Silverman EK, Hoffman E, Criner GJ, Mosenifar Z, Sciurba FC, Make BJ, Carey V, Estépar RSJ, Diaz A, Reilly JJ, Martinez FJ, Washko GR. CT Metrics of Airway Disease and Emphysema in Severe COPD. Chest. 2009;136:396–404. doi: 10.1378/chest.08-2858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wood SA, Zerhouni EA, Hoford JD, Hoffman EA, Mitzner W. Measurement of Three-Dimensional Lung Tree Structures by using Computed Tomography. J Appl Physiol. 1995;79:1687–1697. doi: 10.1152/jappl.1995.79.5.1687. [DOI] [PubMed] [Google Scholar]