A biomechanical analysis of venous tissue in its normal and post-phlebitic conditions

Abstract

Although biomechanical studies of the normal rat vein wall have been reported (Weizsacker, 1988; Plante, 2002), there are no published studies that have investigated the mechanical effects of thrombus formation on murine venous tissue. In response to the lack of knowledge concerning the mechanical consequences of thrombus resolution, distinct thrombus-induced changes in the biomechanical properties of the murine vena cava were measured via biaxial stretch experiments. These data served as input for strain energy function (SEF) fitting and modeling (Gasser et al., 2006). Statistical differences were observed between healthy and diseased tissue with respect to the structural coefficient that represents the response of the non-collagenous, isotropic ground substance. Alterations following thrombus formation were also noted for the SEF coefficient which describes the anisotropic contribution of the fibers. The data indicate ligation of the vena cava leads to structural alterations in the ground substance and collagen fiber network.

1. Introduction

Although the incidence of venous disease is high (Monos et al., 1995), the investigation of the biomechanical properties of venous tissue is limited (Desch et al., 2007). The need for this information is apparent considering that the biomechanical properties of venous tissue can be used as functional indicators of local vessel biology and the development/progression of disease pathology (Hayashi, 1993).

One of the most common venous disorder is post-thrombotic syndrome (PPS), where the resolution of a venous thrombus results in fibrotic loss of compliance of the vein wall (Line, 2001; Dewyer et al., 2007; Alastrue et al., 2008). Despite the clinical significance and disease burden, the thrombus-induced changes in the vein remain unclear. The lack of biomechanical information is disconcerting, considering that complications from acute and chronic deep venous thrombosis (DVT), the precursor to PPS, affect between 1% and 2% of hospitalized patients in the United States (Anderson et al., 1992), making it one of the most important and commonly occurring venous pathologies (Alastrue et al., 2008).

Mouse and rat models of vena cava ligation have demonstrated a strong correlation to human thrombotic predisposition in the deep veins both clinically and histologically (Henke et al., 2004; Deatrick et al., 2005; Dewyer et al., 2007). Although biomechanical studies of the normal rat vein wall have been described (Weizsacker, 1988; Plante, 2002), there are no biomechanical studies of the mechanical effects of thrombus formation in the mouse vein wall. In response to the lack of fundamental knowledge concerning the mechanical consequences of thrombus resolution, distinct thrombus-induced changes in the biomechanical properties of the vein wall were measured via biaxial stretch experimentation on murine healthy and post-phlebitic vena cava. Biaxial experimental data served as the input for strain energy function (SEF) fitting and modeling. Parameterized strain energy function coefficients served to demonstrate the relevant material changes secondary to thrombus formation.

2. Material and methods

2.1. Model of thrombus formation

Creation of post-phlebetic veins involved complete ligation of the murine inferior vena cava (IVC), inducing stasis laminar thrombi as previously described (Singh et al., 2001; Deatrick et al., 2005). Under isofluorane anesthesia, the infrarenal vena cava of adult mice were ligated (100% flow reduction) via suture occlusion immediately below the renal veins after division of all lumbar branches to the iliac bifurcation. Following seven days of thrombus formation, the mice were euthanized and the IVC was surgically removed. This sacrifice time point was chosen because the thrombus becomes surgically inseparable from the vein wall after this time (Henke et al., 2004). Sham specimens underwent identical laparotomy and pericaval dissection, however caval occlusion was omitted. Samples consisted of IVC segments collected caudal to the renal vein junction and cranial to the iliac bifurcation. Samples were transected axially (along the flow direction) through the vascular wall creating a planar open sector, or vascular sheet. Following transection the resultant thrombus was surgically removed from the underlying vein wall. Harvested samples were stored in cool, isotonic saline (0.9% w/v sodium chloride) and tested within 48 h.

Three experimental groups were tested: (1) CD1 non-operated; (2) wild type (WT) sham; and (3) WT ligation. The CD1 non-operated served as the control group for this study. These mice did not experience any surgical intervention prior to terminal vein collection. The wild type (WT) groups consisted of mice which were bred as the precursor to the MMP-9 Knock Out (KO) model, most commonly use to study the expression and effects of matrix metalloproteinase (MMP). This specific WT model was used to establish baseline data for current work being conducted by our lab using an established MMP-9 KO murine model (Humphries et al., 1999; Henke et al., 2004; Deatrick et al., 2005; Phillips et al., 2007) to address the biomechanical affects of MMP-9 gene expression during thrombus formation. Nine samples per group were evaluated.

2.2. Biaxial stretch experiments

A custom-built, biaxial, mechanical testing device was used to perform the stretch experiments, and was similar in design and functionality to apparatuses described in previous studies (Sacks, 1999; Sacks et al., 2003). This design incorporated rotating carriages, symmetrically place pulleys to insured equal line tension, and allowed the sample to freely shear with negligible friction.

Specimens were mounted to the biaxial device in a trampoline-like fashion by passing two thin threads per side (7-0 suture, 0.03 mm diameter, monofilament, Surgipro II, Syneture) through the sample, allowing the edges to expand freely, and a double square knot at the end of the suture was tied (Fig. 1). The axial direction (AD) and circumferential direction (CD) of the specimen where aligned with the x₁ and x₂ stretch axes of the testing device, respectively. The local axial direction of the specimen was designated as being parallel to the luminal blood flow (Vande Geest et al., 2006). Testing was performed with the specimen completely immersed in phosphate-buffered saline at room temperature.

Fig. 1.

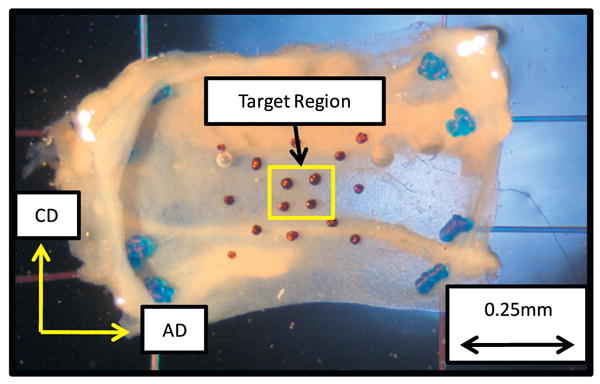
Vein specimen (planar sheet of vein wall) mounted in a trampoline-like fashion for the biaxial stretch experiments. The primary directions of loading, circumferential (CD) and axial (AD), are indicated. Terminal suture knots are visible.

Localized tissue deformations were measured by monitoring the in-plane motion of four indelible ink dots tattooed on the luminal surface of the sample (Fig. 1). Markers outside the target region were also analyzed to insure tissue stretch homogeneity across the entire sample. Permanent set of the markers to the tissue surface was confirmed by applied shear loading to the markers using saline irrigation to insure the markers did not diffuse with or wash off of the underlying tissue. Digital video with a spatial resolution of approximately 2.5 μm per pixel was recorded at 30 Hz to determine the luminal surface deformations throughout biaxial loading.

A true stress-free configuration of the venous wall is nearly impossible to confirm and achieve and, in order to incorporate the effects of residual stress, several approaches are possible. In the current study, it was assumed that this configuration was approximated in a global sense, which was achieved using an ‘opened-up geometry’, by circumferentially and longitudinally transecting the cylindrical vascular specimen (Fung, 1993; Holzapfel et al., 2000; Gasser et al., 2006). After luminal surface marking and mounting of the sample in the testing device, line tension was adjusted such that no load was applied across the sample. The sample was then allowed to freely float for 30 min while completely immersed in saline at room temperature. During this time no measurable external forces were applied at the boundary of the sample. Following this time period the samples were deemed to have naturally conformed to a global stress-free and strain-free configuration (Xie et al., 1991), and this was considered to be the reference state of the specimen.

After the samples had naturally conformed to a stress-free and strain-free preferred configuration during the saline “free-float” phase of the experimental protocol, sample dimensions were determined by taking calibrated length measurements at five equally spaced locations along the vessel (ImageJ 1.38×, National Institutes of Health, Bethesda, MD). Sample width and length were determined from images of the luminal surface, while thickness measurements were calculated from images of the surface created when the intact vessel was transected longitudinally, along the flow direction. This technique resulted in a resolution of 2.5 μm per pixel.

Two pairs of independent, orthogonally positioned, computer-controlled linear actuators (50 mm range, 0.05 μm resolution; Soloist, Aerotech USA and Zaber Technologies, British Columbia, Canada) applied linear displacements to the samples, while two independent in-line load cells (50 g capacity, 0.005g resolution, Sensotec, Ohio) measured the resultant forces along their respective loading directions. Lagrangian stresses were computed along the primary directions of loading. Load data were collected at 30 Hz.

The biaxial stretch protocols consisted of a normal strain component-controlled test, where the ratio of the percent elongation (λ_{Axial direction (AD)} − 1: λ_{Circumferential direction (CD)} − 1) were kept constant (Sacks et al., 1998, 2003; Vande Geest et al., 2004, 2006; Sun et al., 2005). An equal-biaxial preload of 0.1 g was applied quasi-statically to the specimen prior to start of the testing protocols. This load magnitude was determined via pilot testing to be sufficient to flatten the sample prior to biaxial testing and not result in measurable surface strain within the target region.

Each specimen was subjected to four biaxial protocols. Following the conventions established by Sacks et al. (1993) these protocols consisted of tests in which the ratio of the percent elongation along each axis, i.e. (λ_AD − 1):(λ_CD − 1), was kept constant, where λ_AD and λ_CD denotes the stretch ratios along the axial and circumferential direction, respectively. The change in stretch protocols were 1:1, 1:2, 0:1, and 1:0 (Sacks et al., 1993).

Samples were cycled twenty times for each loading protocol, and data from the 20th loading cycle was used for analysis and coefficient parameterization. Equal-biaxial testing (1:1) was repeated throughout the testing procedure to ensure that no structural damage occurred as a result of the biomechanical testing (Vande Geest et al., 2006). The stretch tests (1:1 and 1:2) were used for parameterization of SEF material coefficients. The stretch tests (0:1 and 1:0) were used to check the predictive capability of the material parameters derived from the constitutive model.

The in-plane Green's strain components along the axial and circumferential directions were computed from the luminal markers' displacements (Humphrey et al., 1987). The in-plane deformation gradient tensor F_ij was computed from the optical marker data. The stress–strain field was assumed to be homogenous within the target region, and thus, the components of F_ij were computed directly as the corresponding stretch ratios. Vascular tissue is generally considered to be incompressible. Therefore, the stretch ratio orthogonal to the luminal surface (λ₃) was calculated by setting the determinate of the deformation gradient tensor equal to unity.

2.3. Strain energy function modeling

The main biomechanical constituents of the venous wall are the extra-cellular ground substance, collagen, and elastin fibers. The global mechanical behavior of vascular tissue is primary reflective of the properties of the fibrous components (Apter et al., 1968). Vascular tissues exhibit highly anisotropic and nonlinear elastic behavior due to the functional rearrangement in the microstructure, such as reorientation of the fiber directions with deformation. Therefore, in the current study, the venous tissue was assumed to be a nonlinear, incompressible, anisotropic hyperelastic biomaterial which exhibited behavior according to the theory of pseudoelasticity (Fung, 1981).

The appropriate strain energy function proposed by Gasser et al. (2006) was selected. This form has a micromechanical basis, which takes into account the directions and dispersion of the primary fiber families. Gasser et al.'s form of the strain energy potential was first proposed for modeling arterial layers (Holzapfel et al., 2000; Gasser et al., 2006). For the specific case where there are two families of fibers (as is case for this analysis), the SEF can be expressed in terms of the strain invariants (Gasser et al., 2006)

$$\psi ({\overline{I}}_1,{\overline{I}}_4,{\overline{I}}_6)=C_{10}({\overline{I}}_1-3)+\frac{k_1}{2k_2}\sum _{\alpha =1}^2\left[e^{k_2{[\kappa ({\overline{I}}_1-3)+(1-3\kappa )({\overline{I}}_{\beta }-3)]}^2}\right]\beta =4,6$$ (1)

where C₁₀, k₁, k₂, and κ are the material parameters (k₁ has dimensions of stress; k₂ and κ are the dimensionless structural parameters). The first term in the expression of the strain energy function (ψ) (Eq. (1)) represents the distortional and volumetric contributions of the non-collagenous, isotropic ground substance, where C₁₀ is a material property with dimensions of stress. The second term of the SEF (ψ), represents the contributions from the different fiber families, taking into account fiber dispersion (κ) (Gasser et al., 2006; Holzapfel et al., 2000, 2004, 2007). For the specific case where there are two families of fibers (relevant to this analysis), alpha (α) ranges from 1 to 2.

The SEF model assumes that the fibers within each family are dispersed (with rotational symmetry) about a mean preferred direction. It is assumed that all fibers have the same mechanical properties and the same dispersion, and thus the fourth and sixth strain invariants are equivalent. Under these assumptions and negligible shear stress, the strain invariants are directly calculated from the primary stretch ratios as

$${\overline{I}}_1={\lambda }_{\text{axial}}^2+{\lambda }_{\text{circumferential}}^2+{({\lambda }_{\text{axial}}{\lambda }_{\text{circumferential}})}^{-2}$$ (2)

$${\overline{I}}_4={\overline{I}}_6={\lambda }_{\text{axial}}^2{sin}^2(\gamma )+{\lambda }_{\text{circumferential}}^2{cos}^2(\gamma )$$ (3)

where γ is a structural parameter denoting the angle of fiber orientation between the circumferential and mean orientation of the fiber families. Shear stretch measurements were not included in the calculations of the strain invariants because it was determined that the experimentally measured values for shear stretch were several orders of magnitude below the primary (axial and circumferential) stretch values. Thus, the shear contribution was neglected.

The SEF (ψ), may be regarded as a function of the principle stretches. Consequently, the principle Cauchy stresses (σ_α, where α = 1 for the circumferential direction and, α = 2 for the axial direction) are derived from the SEF:

$${\sigma }_{\alpha }=J^{-1}{\lambda }_{\alpha }\frac{\partial }{\partial {\lambda }_{\alpha }}\psi ({\overline{I}}_1,{\overline{I}}_4,{\overline{I}}_6)={\lambda }_{\alpha }\frac{\partial }{\partial {\lambda }_{\alpha }}\psi ({\overline{I}}_1,{\overline{I}}_4,{\overline{I}}_6)\text{with}\alpha =1,2$$ (4)

The measured stretch data from the (λ_AD − 1): (λ_CD − 1) = 1:1, 1:2 experimental protocols and the corresponding Cauchy stress data for each sample were simultaneously fit to the above constitutive relation using a Levenberg–Marquardt nonlinear curve-fitting algorithm (MATLab, MathWorks, Natick, MA) (Marquardt et al., 1963).

Fiber dispersion, the parameter kappa (κ) (Gasser et al., 2006), and the fiber orientation parameter gamma (γ) (Gasser et al., 2006) were not determined by the least squared fit, rather they were manually varied over a range of discrete values. Kappa was parameterized in the range 0/18 ≤ κ ≤ 6/18 at 1/18 increments and gamma was parameterized in the range 0° ≤ γ ≤45° at 15° increments.

The parameters k₁, k₂, and C₁₀ were determined from the curve-fitting algorithm when the maximum sum of the squares residual value between the experimental and strain energy-based Cauchy stresses matrices was at a minimum over the range of kappa and gamma.

In order to delineate statistical significance of the multi-group parameters, a one-way analysis of variance (ANOVA) was performed. These analyses were performed on the coefficients determined to best fit the strain energy function calculated for each sample in each group (SigmaStat 3.1, Ashburn, VA). A p-value of less than 0.05 was considered to be statistically significant.

3. Results

The parameterized material coefficients, based on the nonlinear curve fit of the strain energy function to the experimental data, are reported in Fig. 2 and Table 1, and a summary of the statistically significant differences between groups are highlighted.

Fig. 2.

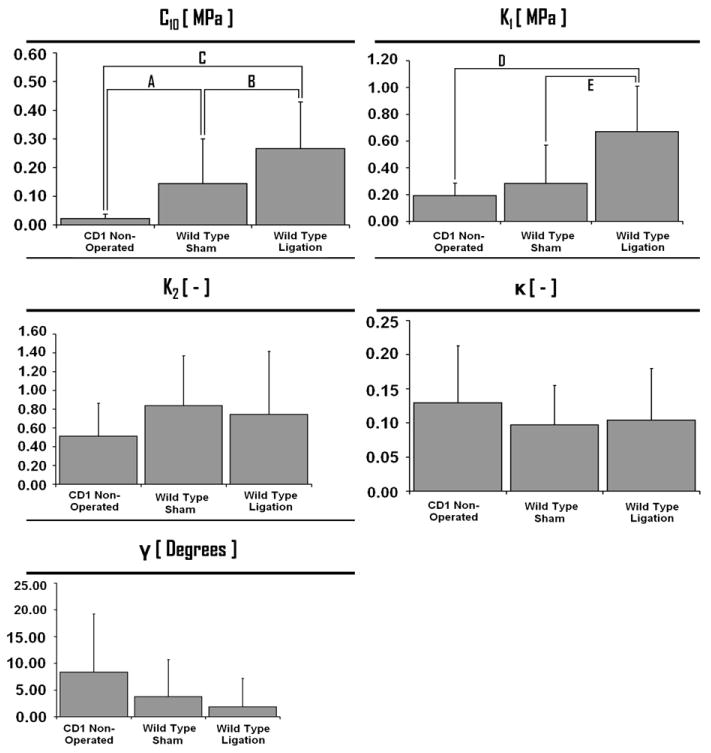
Material parameters (C₁₀, k₁, k₂, γ, and κ) identified from fitting experimental data to the strain energy function shown with means and standard error bars. The coefficients C₁₀ and k₁ have the dimensions of stress (MPa). The coefficients k₂ and κ are dimensionless parameters. The γ coefficient is expressed in degrees. The letters indicate a statistical difference with a p-value less than 0.005: (A) p = 0.002; (B) p = 0.002; (C) p = 0.023; (D) p = 0.008; (E) p = 0.027.

Table 1.

Material parameters (C₁₀, k₁, k₂, γ, and κ) identified from fitting experimental data to the strain energy function shown with means and standard error. Significant statistical differences with a p-value less than 0.005 are listed. The letters indicate the statistical differences highlighted in Fig. 2.

Strain energy function coefficients		Statistically significant findings
Group	C10 [MPa]	Findings	p-Values
CD1 non-operated	0.0217 ± 0.0155	A, B	(A) p = 0.002; (B) p = 0.002; (C) p = 0.023
Wild type sham	0.1443 ± 0.1552	A, C
Wild type ligation	0.2655 ± 0.1640	B, C
Group	k1 [MPa]		p-Values
CD1 non-operated	0.1932 ± 0.0916	D	(D) p = 0.008; (E) p = 0.027
Wild type sham	0.2826 ± 0.2874	E
Wild type ligation	0.6714 ± 0.3396	D, E
Group	k2 [dimensionless]		p-Values
CD1 non-operated	0.5130 ± 0.3505		No statistically significant findings
Wild type sham	0.8388 ± 0.5301
Wild type ligation	0.7431 ± 0.6725
Group	κ [dimensionless]		p-Values
CD1 non-operated	0.1296 ± 0.0833		No statistically significant findings
Wild type sham	0.0972 ± 0.0575
Wild type ligation	0.1042 ± 0.0753
Group	γ [deg.]		p-Values
CD1 non-operated	8.3333 ± 10.8972		No statistically significant findings
Wild type sham	3.7500 ± 6.9437
Wild type ligation	1.8750 ± 5.3033

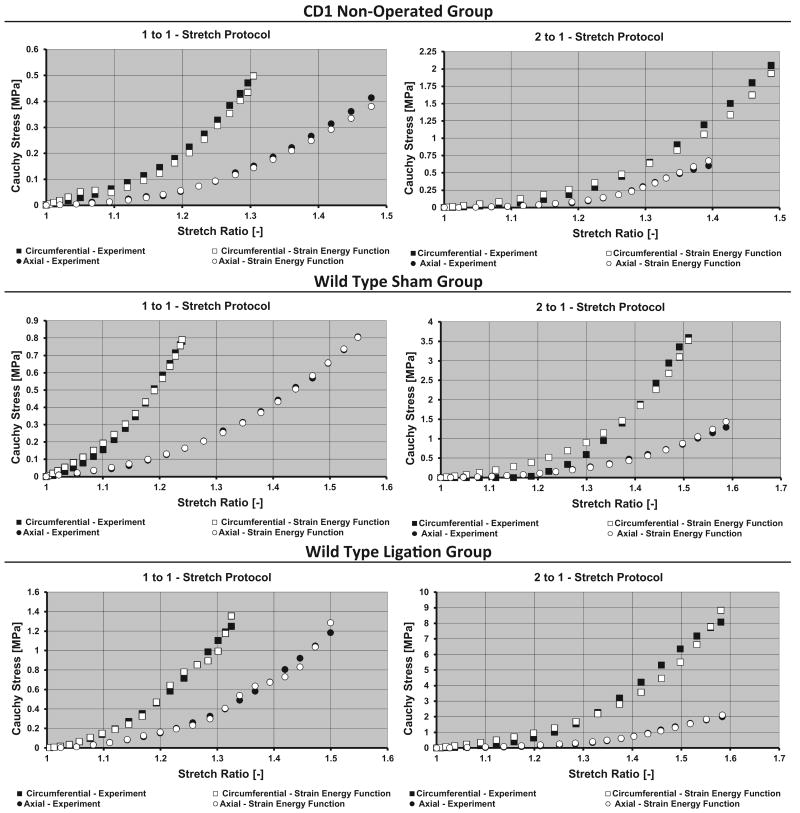
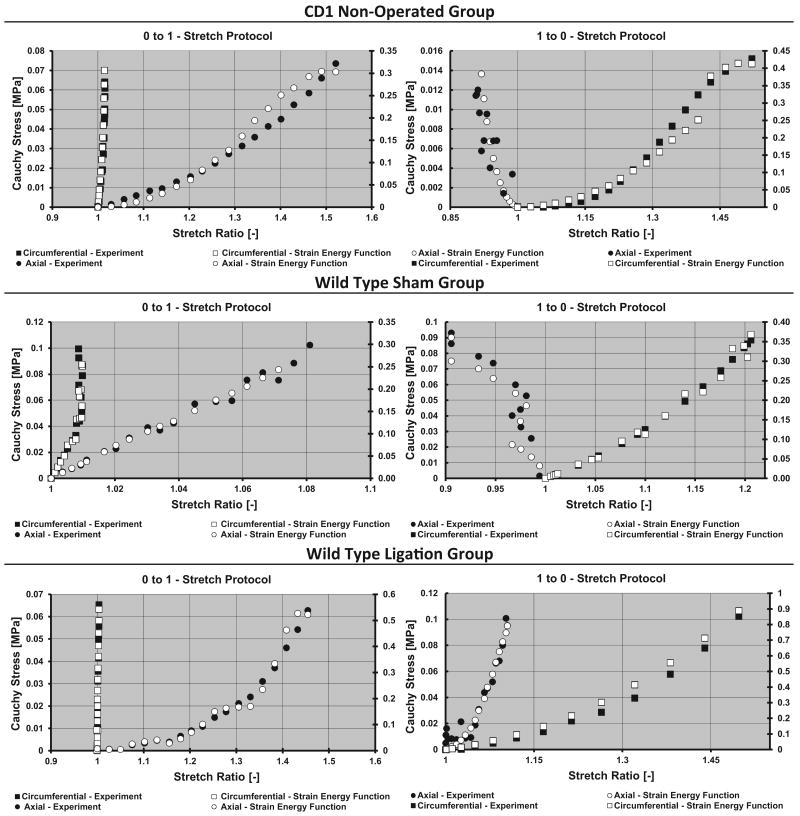
To illustrate the response of the vein wall, plots of the simulated stress–stretch behavior based on the SEF together with the averaged experimental data are depicted for each sample group (Fig. 3). To check the analytic validity and accuracy of the material parameters derived from the strain energy function, the experimentally measured stresses from the 0:1 and 1:0 protocols were compared to the simulated stress data based on the experimentally measured stretch profiles from these protocols. The resultant simulated stress outputs were compared to the experimentally measured stresses for the same stretch protocols (Fig. 4). The fidelity of the agreement between simulated and experimental stress values was observed across all groups, in which the predicted stress values differed from experimental values by no more than 10%. Indicating that the derived material coefficients provide a good model for the material's biomechanical response.

Fig. 3.

Circumferential–experimental (■), circumferential–strain energy (□), axial–experimental (●), axial–strain energy (○). Cauchy stress versus stretch ratio for the 1 to 1 (Left) and 2 to 1 (Right) change in biaxial stretch testing protocols. The stresses based on the strain energy function along with the experimentally measured stresses are plotted against the corresponding primary stretches (axial and circumferential).

Fig. 4.

Circumferential–experimental (■), circumferential–strain energy (□), axial–experimental (●), axial–strain energy (○). Cauchy stress versus stretch ratio for the 0:1 (Left) and 1:0 (Right) biaxial stretch testing protocols. Material parameter coefficients used were derived from the 1:1 and 2:1 biaxial stretch protocols for the sample group. To aid in the strain energy fitting visualization, two vertical axes scales were employed, where curves on the right of the plot area correspond to the axis on the right. Units for all vertical axes are MPa.

4. Discussion

Most research studies investigating the elasticity of the vena cava have been limited to one-dimensional tests (Desch et al., 2007). Thus, the development of specific constitutive relations to describe the mechanical behavior of the vena cava has not been formulated (Desch et al., 2007). The strain energy function used in the current study was capable of accurately fitting the experimental biaxial data over a wide range of physiologically relevant biaxial stretch protocols. Alastrue et al. (2008) demonstrated that the mathematical precursor to the constitutive model used for our analysis (Holzapfel et al., 2000; Gasser et al., 2006) provided an excellent fit to the experimental stress–strain data obtained from ovine caval tissue. Although the strain energy function proposed by Gasser et al. (Holzapfel et al., 2000; Gasser et al., 2006) was originally designed to model arterial behavior, our data indicate that this mathematical form is also capable of producing an excellent concordance to venous stretch behavior (Figs. 3 and 4). This model assumes superposition between the energy stored in the ground substance and the collagen reinforcement. The current study extends the previous work of Alastrue et al. (2008) by including structural parameters associated with the dispersion and orientation of the embedded collagen fibers (Gasser et al., 2006). It was assumed that two families of collagen fibers are embedded in an isotropic, non-collagenous ground substance (Gasser et al., 2006). The aforementioned constitutive and numerical framework allow for the parsing of the individual contributions of the tissue components with respect to the overall mechanical behavior of the venous tissue (Gasser et al., 2002, 2006; Holzapfel et al., 2002).

Following Holzapfel et al. (1998), we modeled the non-collagenous ground substance using an incompressible, isotropic neo-Hookean material definition, where the parameter C₁₀ is generically associated with the non-collagenous, but mechanically relevant, tissue components in the ground substance (Gasser et al., 2002). Statistical differences in the value of the C₁₀ coefficient indicate that there are alterations in the mechanical response of the extra-cellular ground substance between groups. The data demonstrate that both the sham and ligation procedure significantly affect the ground substance as compared to the non-operated CD1 control group. A significant increase of 84% (with respect to the sham group) in the value of C₁₀ following thrombus formation demonstrates that ligation inherently induces changes to the ground substance. Overall, the data indicate that mechanical perturbation to murine venous tissue alters the biomechanical response of the ground substance, which is manifested as an increase in stiffness, and that these increases are further enhanced by thrombus formation (Table 1).

The SED k₁ parameter is associated with the anisotropic contribution of the collagen fibers to the overall response of the material (Gasser et al., 2006). Statistically significant changes between groups were noted for the strain energy coefficient k₁ [MPa]. The mechanisms through which the stiffness of the fibers increase (i.e. an increase in the magnitude of k₁) is unclear, and may be due to changes in the ground substance–fiber interaction, conformation/biochemical alterations within the fiber structure, or modifications in the degree of cross-linking of the fibers is unknown. Future histological studies should be performed to address this question. Regardless, the data indicate that simulated DVT leads to an increase in the stiffness of the fiber constituents in the vessel wall. This finding was found to be independent of the model variant. The statistically significant difference between the sham and ligation group (+123%) in the value of k₁ indicates that thrombus formation, regardless of surgical intervention, causes the fibers embedded in the vein wall to become more stiff. It is theorized that the stiffing of fibers in the vein wall leads to a reduced capacity of the vessel to distend under pressurization while magnifying the fiber stresses. These findings and rationale seem to be congruent with common clinical DVT complications, such as vessel wall rupture. In general, the data indicate that, vessel ligation has a statistically significant and deleterious effect on the stiffness of the embedded collagen fibers as compared to either control values or sham values.

No statistically significant differences where noted between the groups for the parameters k₂, κ, and γ. Physiologically, the k₂ parameter is associated with the anisotropic contribution of the fibers (Holzapfel et al., 2004), however its specific physical meaning has not been explicitly demonstrated. The dispersion (κ) and the preferred spatial orientations (γ) of the fiber families were unaffected by sample type. These data seem to indicate that future histological efforts using these specific murine models should not use fiber dispersion or orientation as resultant outcome parameters. Rather, the current study suggests that collagen type and ground substance constituents, and alterations in these components due to thrombus formation, would provide more meaningful histological data.

The data demonstrate an increased contribution from the neo-Hookean component of the strain energy density equation (Eq. (1)) following both sham and ligation procedures (Table 2). This result is supported by the statistically significant increases observed in the C₁₀ parameter following surgical intervention. For all experimental groups, the axial direction demonstrated an increased contribution from the neo-Hookean component of the stress as compared to the circumferential direction (Table 2). The data further demonstrate that most of the stress generated (as a percent of total stress) in the circumferential direction is dominated by the fiber-related portion of the strain energy function, whereas most of the stress generated in the axial direction is caused by the neo-Hookean (extra-cellular matrix related portion) response of the material. From a mechanobiologic perspective, these findings closely correspond to the vessel microstructural architecture (as determined from histology) wherein the fibers, which constitute the primary load bearing components of the vessel wall, are preferentially aligned in the circumferential direction.

Table 2.

Neo-Hookean stress contribution as a percent (%) of total stress. Contribution of the neo-Hookean component of the strain energy function (Eq. (1)) expressed as a percent of the total stress for each loading protocol in each direction.

Group	1:1 Protocol (%)	2:1 Protocol (%)	Average contribution
CD1 non-operated
Circumferential	23.80 ± 13.40	18.62 ± 15.09	40.07 ± 18.72
Axial	63.50 ± 20.64	54.34 ± 25.76
Wild type sham
Circumferential	28.88 ± 15.01	23.71 ± 13.81	45.39 ± 19.31
Axial	68.23 ± 19.18	60.74 ± 29.25
Wild type ligation
Circumferential	42.54 ± 10.36	29.50 ± 20.67	55.27 ± 13.95
Axial	77.64 ± 2.01	71.38 ± 22.76

It is clear that ligation of the vessel leads to increased stiffness of the ground substance and changes in the anisotropic contribution of the collagen fibers. Yet, despite the clinical importance of investigating these constituents, much of these structure-function interpretations have not been rigorously established (Desch et al., 2007). This is mostly due to significant gaps in the literature base, thereby precluding direct comparisons of known histological data to the present study. In addition, comparisons of the current data set to previously reported investigations involving the mechanical investigation of venous tissue are difficult or impossible to perform because these previous mechanical characterizations have largely involved simple elongation tests. These previous studies fail to accurately detail the boundary conditions used in these investigations, precluding extrapolation to the two-dimensional behavior described in the current study (Desch et al., 2007).

While the current study represents a significant advancement for describe the mechanical alterations associated with DVT, future research is warranted in order to fully understand the biomechanical effects secondary to DVT. Overall, DVT-induced specimens exhibited a marked increase in the overall stiffness of the vessel wall under biaxial loading conditions. It is clear that ligation of the vessel leads to increased stiffness of the ground substance and stiffening in the anisotropic contribution of the fibers. The data provides positive support for the hypothesis that clinical complications following DVT are directly related to increases in the stiffness of the vein wall.