Cognitive Representation in Transitive Inference: A Comparison of Four Corvid Species

Abstract

During operant transitive inference experiments, subjects are trained on adjacent stimulus pairs in an implicit linear hierarchy during which responses to higher-ranked stimuli are rewarded. Two contrasting forms of cognitive representation are often used to explain resulting choice behavior. Associative representation is based on memory for the reward history of each stimulus. Relational representation depends on memory for the context in which stimuli have been presented. Natural history characteristics that require accurate configural memory, such as social complexity or reliance on cached food, should tend to promote greater use of relational representation. To test this hypothesis, four corvid species with contrasting natural histories were trained on the transitive inference task: pinyon jays, Gymnorhinus cyanocephalus; Clark's nutcrackers, Nucifraga columbiana; azure-winged magpies, Cyanopica cyanus; and western scrub jays, Aphelocoma californica. A simplified computer model of associative representation displayed a characteristic pattern of accuracy as a function of position in the hierarchy. Analysis of the deviation of each subject's performance from this predicted pattern yielded an index of reliance on relational representation. Regression of index scores against rankings of social complexity and caching reliance indicated that both traits were significantly and independently associated with greater use of relational representation.

Introduction

Representations are cognitive constructs in which features of the external world are abstracted and mirrored in the nervous system as “functioning isomorphisms” (Spence, 1950; Gallistel, 1990). Operations performed on representations allow extrapolation of implicit properties of real-world systems (Zentall, 2001), so under appropriate conditions, one can infer the “use” of particular representations through controlled behavioral tests. The theoretically simplest form of representation would be generated by a pure conditioning process, in which the perceptual world was considered as an aggregate of distinct elemental events. Representations of each event would be linked only to other events that were “intrinsically associated,” through being similar in appearance, similar in physiological consequences, or sufficiently invariant in sequential occurrence. In the original sense of the British empiricists, these “associative” relationships are thus restricted to correlations that would enable a hypothetical rational observer to make an inference of causality (Boring, 1929).

“Configural” or “relational” representations, in contrast, are those that combine the representations of at least two elemental events that are not otherwise intrinsically associated (Sutherland & Rudy, 1989). So relational representations consist of linkages between events or stimuli that are connected in a non-causal or non-contingent fashion, such as by occurring in particular points in geometric space or by being connected in a social or conceptual network, or by being otherwise unrelated components that occurred simultaneously at some specific time in the past. Relational representations thus encode both the primary attributes of environmental components and the relationships among them (Halford, Wilson, & Phillips, 1998; Godfrey-Smith, 2002). In structurally complex environments with many interlinked components, animals could use relational representations to infer novel, unanticipated connections between stimuli and to update encoded information rapidly and accurately (Tomasello & Call, 1997). The classic example is a “cognitive map,” which postulates a flexible mental representation of spatial relations that would allow an animal to find novel routes between familiar locations (Tolman, 1948; O'Keefe & Nadel, 1978), but similar considerations should also apply to the representation of complex social environments.

Animals that live in large, persisting social groups must maintain a dynamic categorization of group members on several dimensions, including genetic relationship, reproductive status, and dominance ranking (Cheney & Seyfarth, 1990; Seyfarth & Cheney, 2001), requiring a relational representation of the social world that is at least as complex as that demanded by any physical environment (Tomasello & Call, 1997). In fact, social networks have often been compared to cognitive maps, with the social distance between individuals serving as an analog of the physical distance between spatial locations (Boguñá et al., 2004; Liben-Nowell et al., 2005). And as in spatial cognitive maps, experimental subjects can navigate conceptually through a social network by following linkages between adjacent individuals (Watts, Dodds, & Newman, 2002; Kumaran & Maguire, 2005). This implies that even complex social networks can be transitive, where the fact that A dominates B, and B dominates C, allows the inference that A probably dominates C. An ability to make such “social inferences” has been demonstrated in several animal species (Paz-y-Miño C et al., 2004; Grosenick, Clement, & Fernald, 2007), but much of the existing research on non-spatial relational representation has focused on operant transitive inference.

Transitive Inference

In this paradigm, animals are trained to respond differentially in trials of overlapping “premise” pairs from an implicit hierarchical list (such as A>B>C>D>E) of arbitrary stimuli, where only responses to the higher-ranked item in each pair are rewarded. So if the subject is shown B and C, for example, the correct response is to choose B; if it is shown C and D, the correct response is C. Subjects are subsequently tested with trials of novel, more distant stimulus pairs to analyze their ability to make transitive judgments. The primary theoretical focus of the literature has been on models based on “associative strength,” which view an organism's choice between test stimuli to be the result of the difference in their relative reinforcement history, with the ordered series of values constituting the outcome of the training procedure (Lazareva & Wasserman, 2006).

The closest approximation to a purely “associative” interpretation of transitive inference (in the sense we have outlined above) was proposed by Couvillon and Bitterman (1992). The primary assumption of the Bitterman model is that pigeons treat the stimuli in a premise pair independently, making their choice on the basis of the associative strength values assigned to each stimulus. In this model, any process that can produce a monotonic ordering of associative values is sufficient to enable transitive inference (Wynne, von Fersen, & Staddon, 1992). Because there is no assurance that an associative process will produce a truly linear array of strengths, however, choice performance must be a function of the relative associative strength of the two stimuli in a pair, that is, on V_i / (V_i + V_j). The only other aspect of the Couvillon and Bitterman model that is essential is that rewarded responses to a particular stimulus must result in relative increases in associative strength and unrewarded responses to relative decreases. Associative strength thus must depend, not just on the number of rewarded responses, but on the proportion of responses that have been rewarded during the recent past.

The mechanism will produce an “associative representation,” conceptually equivalent to a vector of associative strength. Couvillon and Bitterman (1992) contended that the strength vector would be sufficiently monotonic to enable correct responding to transitive test pairs. Their rationale was luminously simple. Responses to A are always rewarded. It will, therefore, have high strength, so most of the responses to A/B will be given to A. Responses to B will be rewarded when it is presented in B/C, but the few responses to B in A/B will be unrewarded and will ensure that B's strength will always be lower than that of A. Because of B's reduced strength, there will be more erroneous, unrewarded responses to C in B/C than there are to B in A/B. C's strength will, therefore, be lower than B's, even though it is rewarded in C/D trials. Continuing down the hierarchy, by this reasoning, should yield progressively diminishing differential rates of reinforcement, generating a monotonically decreasing gradient of associative strength (Wynne et al. 1992). Transitive choices in this representation would then simply be a matter of choosing the alternative with higher associative strength. To choose between C and E, for example, the animal would reference the strength levels associated with each stimulus and distribute the probability of its response accordingly.

A relational representation, in contrast, must be derived from configural memory of the relationship between both the chosen and the unchosen stimulus. There is no comparably clear rationale for a universal mechanism for relational encoding, but the process has most commonly been expressed in spatial terms, as an analog to a cognitive map (Huttenlocher, 1968; Roberts & Phelps, 1994; Weaver, Steirn, & Zentall, 1997; Lazareva & Wasserman, 2006). Jacobs (2006) has offered a theoretical perspective that can be restated in somewhat simpler terms. When the subject is shown a premise pair, it appears to metaphorically place representations of the two items on a cognitive map in proximity, indicating that they are related by coincident occurrence. If any two items are never seen together, their representations will be shifted progressively further apart. As experience with the premise pairs accumulates, the hierarchical map gradually develops into a linked list, in which the representation of each item converges on a location between the items above and below it in the hierarchy. Based on this structure and knowledge of the identity of the highest-valued stimulus, it is possible to infer the relative rankings of any pair by chaining down from the top of the hierarchy through a succession of spatially adjacent representations (D'Amato, 1991; Terrace, 2005). Most models of relational representation have made use of neural networks (e.g. Delius & Siemann, 1998; Wu & Levy, 2001), though it is by no means clear that simple back-propagation fully captures the complexity of relational learning (De Lillo, Floreano, & Antinucci, 2001; Jacobs, 2006).

Evidence of relational representation in operant studies has come from serial list learning in monkeys, including the “wild card” procedure of D'Amato and Columbo (1988; D'Amato, 1991) and Terrace's (1993, 2005) simultaneous chaining technique. But one of the most compelling demonstrations of non-spatial relational representation in animals is Treichler and Van Tilburg's method of transitive inference across linked lists (Treichler & Van Tilburg, 1996; reviewed in Treichler, 2007). They trained macaques on overlapping premise pairs in two separate, implicit 5-item lists (e.g. A>B>C>D>E and 1>2>3>4>5). Once the lists were learned, they gave the monkeys extensive training on a linking pair that would conceptually place one list above the other in a larger implicit hierarchy (e.g. training on 5>A would place the second list above the first). They then tested novel transitive combinations both within and across the two lists. The monkeys responded with high accuracy to combinations that spanned the two lists, higher even than they displayed on premise pairs within lists. This striking outcome, supported by an extensive analysis of error patterns, is very difficult to explain in terms of pure associative encoding, but it is consistent with a relational representation.

Couvillon and Bitterman's (1992) model proved to be woefully inadequate as a description of the behavior of real animals. If the only outcome of a trial is to increase the relative associative strength of correctly chosen stimuli (and decrease that of erroneously selected ones), choice accuracy will oscillate down the hierarchy in a highly non-monotonic fashion, and the model will only predict performance on transitive test probes under very limited circumstances (Siemann, Delius & Wright, 1996; Delius & Siemann, 1998). Couvillon and Bitterman's model did, however, spark a vigorous program in experimentation and descriptive modeling (reviewed in Wynne, 1998; Lazareva & Wasserman, 2006; Vasconcelos, 2008). The most successful descriptive models have employed variants of Value Transfer Theory (von Fersen et al., 1991), the assumption that by occurring in the same display as a rewarded choice stimulus, a non-rewarded, non-chosen stimulus would also gain associative strength. So in a B/C choice, if B were correctly selected, its associative strength would be incremented, but so would that of C (though to a lesser degree). The strength of C is, thus, dragged up in rewarded B/C trials by this additional, inferential process, stabilizing the oscillatory pattern of pure associative strength. Zentall and his students have found experimental evidence consistent with the existence of this mechanism, which they interpreted to be a form of second-order classical conditioning (Zentall & Sherburne, 1998; Steirn, Weaver & Zentall, 1995; Zentall et al., 1996). This suggests that value transfer may serve as a mechanism for configural encoding in these experiments. It is by no means the only potential mechanism, however. A number of studies have concluded that additional sources of configural information must also be involved (Weaver et al., 1997; Delius & Siemann, 1998; Lazareva & Wasserman, 2006; Vasconcelos, 2008).

In general, stimulus relationships in sequential learning designs are probably multiply encoded (Moyer & Bayer, 1976; D'Amato & Columbo, 1990; Lazareva & Wasserman, 2006), and most species would be expected to make some use of both associative and relational representations in operant transitive inference (Jacobs, 2006). Although either mechanism can potentially enable transitive responding on particular pairs of stimuli, however, they are probably far from equivalent in real-world settings. Because each item links precisely to the next one in the sequence, relational representations should be more accurate than those based only on associative strength (D'Amato, 1991; Terrace, 2005), and they are likely to be much more flexible (O'Keefe & Nadel, 1978; Treichler, 2007). But relational inferences are probably slower than associative ones, since they require chaining down from the top of the hierarchy (Terrace, 2005), and they appear to be unavoidably neurologically complex. From an evolutionary perspective, these considerations suggest that only species with natural histories that demand precise configural memory should make extensive use of relational representation. And this implies that a species comparison grounded in differences in natural history may reveal consistent, predictable differences in the mode of cognitive processing (Kamil, 1988; Riley & Langley, 1993).

Given that there is no generally accepted account of configural encoding, the most robust means of evaluating the level of use of configural or relational information is to compare the performance of each subject to the clear, albeit approximate, standard of the Couvillon and Bitterman (1992) conditioning model. We used a minimal version of this model to predict the pattern of relative accuracy as a function of position in the hierarchy, as it would be displayed by some hypothetical organism that completely lacked configural memory. The virtue of this pared-down model is that it makes unequivocal predictions about the pattern of correct choices in operant transitive inference based exclusively on the past sequence of events and on conditioning processes that have been universally recognized and accepted for well over a century. Each stimulus is valued on the basis of its own reward probability, irrespective of the context provided by the comparison stimulus. It is a conceptually “pure” associative model that can readily serve as a predictive null model for comparing and contrasting the use of relational representations in different species. In this study, we employed this null model to quantify the relative degree of reliance on relational representations during a symbolic transitive inference task, and to compare the use of relational memory across a series of related corvid species that differ in their natural history.

Natural History of Corvids

Corvids present an attractive opportunity for evolutionary comparative research on cognition. The natural history of the family is diverse and well known. Not only are most corvids amenable to operant testing, allowing standardized measures of cognition (Olson et al., 1995; Balda et al., 1997; Bond, Kamil, & Balda, 2007), they are also large-brained and perform very well across a wide range of cognitive tasks (Emery & Clayton, 2004). Pinyon jays (Gymnorhinus cyanocephalus) are among the most social corvids in North America, the peak of what Brown (1987) termed the “colonial” route to sociality in jays. They forage and breed in permanent flocks of 50–100 adults and as many as 200 juveniles and yearlings (Balda, 2002). The flocks are not simple aggregations, but groupings of familial clans, in which foraging, courtship, mating, and parental care are all performed synchronously (Marzluff & Balda, 1992; Balda, 2002). Western scrub jays (Aphelocoma californica), in contrast, show very limited sociality, being found in at most temporary groupings of a mated pair and their young of the year (Curry, Peterson, & Lange, 2002; Carmen, 2004). In our initial study of transitive inference among corvids (Bond, Kamil, & Balda, 2003), we compared the performance of these two species. The results suggested that relational encoding played a much larger role in the responses of pinyon jays while scrub jays appeared to make relatively more use of associative representations. These results were consistent with the hypothesis that relational representation of non-spatial hierarchies is better developed in species that experience greater social complexity (Bond et al., 2003).

The natural histories of even closely related species seldom vary along only a single dimension, however. Pinyon jays and scrub jays differ strongly in their use of spatial memory as well as in sociality. Each summer, pinyon jays bury thousands of pine seeds in unmarked locations across their home ranges, forming food caches that are retrieved and consumed throughout the subsequent winter and spring. They make extensive use of other food resources, as well, but cached seeds are very important for successful reproduction (Marzluff & Balda, 1992). Recovery of food caches is heavily dependent on spatial memory (Vander Wall & Balda, 1981; Balda & Kamil, 1998). Scrub jays cache a variety of food items, but generally only for shorter periods, and they rely far less on subsequent retrieval of caches than pinyon jays (Vander Wall & Balda, 1981; de Kort & Clayton, 2006). Reflecting this ecological distinction, pinyon jays have consistently out-performed scrub jays on a number of spatial memory tasks (Balda & Kamil, 1989; Kamil, Balda, & Olson, 1994; Balda et al., 1997). It is entirely possible, therefore, that the differential use of relational representation in these species is a reflection of their adaptation to differing degrees of spatial, rather than social, complexity. We have explored this possibility by extending our original work to two additional corvids, Clark's nutcrackers (Nucifraga columbiana) and azure-winged magpies (Cyanopica cyanus). Nutcrackers are almost exclusively dependent on cached pine seeds during the winter and display more precise and persistent spatial memory than any other corvid species tested (Balda & Kamil, 1989, 1992; Kamil et al., 1994). They are, however, resolutely and aggressively solitary, perhaps even more so than scrub jays (Tomback, 1998). Azure-winged magpies, in contrast, have a “group territorial” breeding system (Brown, 1987), in which up to 20 related birds defend a common, multipurpose territory (Hosono, 1989; Komeda, Yamagishi, & Fujioka, 1987) and assist one or two breeding pairs in raising their young (de la Cruz et al., 2003). Like scrub jays, however, azure-winged magpies have a broad dietary niche and do not appear to rely heavily on spatial memory, caching only some highly-valued food items for short periods (Turcek & Kelso, 1968; Canário, Boieiro, & Vicente, 2002). Data from these two species, combined with the results of from Bond et al. (2003), would therefore provide information on transitive inference performance from four corvid species with a broad array of social and spatial adaptations.

Although these species are behaviorally distinctive, they are closely related, all members of the same family. Aphelocoma and Gymnorhinus are among the most closely related of the six corvid genera endemic to the New World (Espinosa de los Monteros & Cracraft, 1997). Nucifraga and Cyanopica are Old World genera from an earlier corvid radiation, but they still assort with the North American jays into neighboring clusters in the phylogeny of the family (Ericson et al., 2005). To the degree that there are differences in cognitive capabilities among these species, therefore, a strong case can be made for interpreting these differences as adaptations to the varying sources of environmental complexity that they experience, rather than as the result of taxonomic disparity (Balda, Kamil & Bednekoff, 1996; Healy, 2006).

As the preceding makes clear, our intent in the current experiment was to collect data to be analyzed together with the data from Bond et al. (2003). We therefore used apparatus and procedures that were as similar as possible to those of the earlier study. There were, however, some differences in methods as a result of the interval between the studies. These will be described at the end of the methods section.

Methods

Subjects

Six azure-winged magpies and six Clark's nutcrackers were captured in the field for use in this study. The magpies were obtained from a banded population near Badajoz, Spain, that has been studied for a number of years by Carlos de la Cruz; the nutcrackers were taken with live traps in central Colorado. Birds were housed in individual cages in environmentally controlled rooms (22°C; 14:10 h light:dark). Captive nutcrackers were fed turkey starter, sunflower seeds, parrot pellets, meal worms, and pine nuts; magpies were fed soft-billed avian diet and mealworms. Both were given supplementary vitamins. During experiments, the birds were maintained at 85–90% of their free-feeding weights, with unlimited access to grit and water. They were all initially naïve to operant procedures; but the nutcrackers had previously been used in open room tests of spatial memory.

Apparatus

Stimuli were presented on 15-in ViewSonic LCD monitors embedded in the front panel of a 48×48×48-cm operant chamber. The monitor was framed with an EloTouch Systems infrared touch screen, and a thin sheet of Lexan polycarbonate was placed between the touch screen and the monitor to serve as a resilient pecking surface. A perch was mounted parallel to the front panel of the chamber, re-positioned for each species so that the center of the LCD was approximately at eye level. Rewards of the most preferred food items for each species – pieces of pine nut for nutcrackers and fruit-flavored food pellets for magpies – were delivered by a motorized lazy susan feeder into a food well centered below the touch screen and signaled with a food light. The chambers were diffusely lit, and ambient white noise was provided to mask external sounds. Stimulus presentation, event timing, reward delivery, and data recording were controlled by Pentium computers, using a library of custom-coded C routines.

The circular stimuli were 35 mm in diameter and were uniformly colored in red, green, blue, magenta, yellow, cyan, orange, or white, as defined by the standard VGA palette. Each non-white stimulus was overlaid with a specific alphanumeric character in black at the center. The characters, which had previously been shown to be maximally discriminable for pigeons (Blough, 1985), were X, O, C, E, A, W, and U (Arial font, roughly 13 mm high). White stimuli, which were used for training and for start signals, had a 9-mm black circle overlaid in the center. Stimuli could be displayed at any of three positions, spaced at 6.8 cm intervals across the center of the display.

Training Phase

Birds were first habituated to the operant chamber and autoshaped to peck a central white stimulus. They were then trained to peck the white stimulus in either of the lateral positions. An initial white stimulus in the central position was then added as a start signal, and the birds were conditioned to peck it as a means of initiating the next trial. Finally, the response requirement for the lateral positions was increased to three pecks. When the birds achieved 32 or more correct responses for three consecutive days, they were advanced directly to discriminative training on the full implicit hierarchy, using random trial sequences of the six adjacent premise pairs.

At the beginning of each discrimination trial, the start signal was displayed in the center of the display. If it was not pecked within 15 s, the signal was turned off, and the trial was reinitiated after a 3-s delay. When the start signal was pecked, it was turned off, and a pair of non-white stimuli was displayed in the lateral screen positions. Upon three successive pecks to one of the stimuli (an FR 3), the display was darkened. If the response was correct, a light was illuminated in the food well and a reward was delivered. After 10s, the food light was turned off, and another trial was initiated 20s later. Incorrect responses produced a 30-s delay before the next trial, but no correction procedure was employed. If the bird failed to peck either stimulus three times within 60 s, however, the panel was darkened, and the trial was repeated after a 30-s delay. To control for possible effects of differences in discriminability, the seven colored stimuli were ordered in six distinctive hierarchies. Across the orderings, no stimulus occurred more than twice in the same ordinal position, and no adjacent pairing occurred more than once. Each unique ordering was assigned at random to one individual of each species. Premise pair training was conducted in daily sessions of 36 trials, consisting of equal numbers of all six color pairs in randomized order and counterbalanced with respect to the position of the correct stimulus on the display. Training was continued until each subject was judged to have reached an asymptotic level of performance.

Simulation Methods

We simulated the acquisition of an associative representation with a probabilistic model of the accumulation of associative strength, a simplified version of a pure conditioning account of the acquisition of premise pairs (Luce, 1959; Courvillon & Bitterman, 1992). An implicit linear hierarchy of seven stimuli, S[0] to S[6], was assessed in choices between successive premise pairs, in which the stimulus with the lower index value was always correct. Two seven-element vectors, R and U, tracked the number of rewarded and unrewarded responses, respectively, to each stimulus within a memory window of the previous W trials. For each iteration of the model, these vectors were initialized to zero, and the program was run through a series of 100 sessions of 36 choice trials, including equal numbers of all six premise pairs in random order. To select between a pair of stimulus alternatives, S[i] and S[i+1], corresponding strength values were computed as the proportion of the previous responses to each stimulus that were rewarded (i.e. V[i] = R[i] / (R[i] + U[i])). The probability of choosing S[i] (the correct, higher-ranked stimulus) was then estimated as P = V[i] / (V[i] + V[i+1]), and the choice for the given trial was decided by comparing P to the next (0, 1) pseudo-random number. At the end of each trial, the R and U vectors were shifted down one step (thereby moving W forward in time) and updated with the trial results. R and U were carried over from one session to the next, enabling the program to converge over sessions on a stable distribution of response probabilities.

We used the simplest version of the Couvillon and Bitterman (1992) model: λ (the associative strength increment from a single trial) was assumed to be 1 for correct choices and 0 for incorrect ones, and β (the scaling factor) was 1 for both correct and incorrect choices. As a result, the only free parameter was the size of the memory window. An extensive initial exploration was conducted to determine the effects of differences in W. When W was shorter than a single session, the choice accuracies did not converge on a stable configuration even when hundreds of sessions were run sequentially. However, the results were completely consistent and reliable for any value of W that exceeded the number of trials in two sessions. We decided to use a memory window fixed at 100 trials for our predictive simulation runs, which meant that the final model had no free parameters whose values were arrived at by fitting to the data being analyzed. It was, in effect, an algorithmic re-expression of the primary assumption of a pure associative representation, namely that choice probability was exclusively determined by the relative proportions of rewarded responses.

To assess the characteristic configuration of accuracies resulting from this hypothesis, we programmed the model in Pascal, with pseudo-random numbers provided by a subtract-with-borrow lagged Fibonacci generator with an extraordinarily long period (Marsaglia & Zaman, 1991). The data resulted from 300 iterations of independent runs of 100 successive 36-trial sessions. From the last five sessions of each of the 300 iterations, we calculated and saved the mean probability of responding to each stimulus, the mean proportion of rewarded responses to each stimulus, and the mean accuracy on the six premise pairs. Means of these values across all iterations formed the theoretical basis for comparison to the birds' performance.

Test Phase

Following their attainment of asymptotic performance levels, the birds began transitive inference testing. Test sessions consisted of three probe trials of non-adjacent stimulus pairs imbedded among 33 premise pair trials identical to those used during previous training sessions. In each test session, three of the six types of probe trials were integrated with the premise pair sequence in random order, spaced from one another at variable intervals of between 10 and 14 trials. A complete set of all six probes was given across each two consecutive sessions. Because responses to the highest and lowest stimuli in the implicit ranking were either always or never reinforced, probe tests included all possible novel stimulus pairs that did not involve the first and last items (pairs B/D, B/E, B/F, C/E, C/F, and D/F). Each bird received 40 test sessions for a total of 120 probe trials, with each probe type being presented 20 times. To prevent the birds from learning the test pairs directly, all choices during probe trials were rewarded.

Procedural Differences

The first procedural difference between the current study and the Bond et al. (2003) experiment was that the earlier study used a VGA monitor mounted behind a panel with three pecking keys. The stimuli were the same VGA colors as in the current study, but with slightly smaller circles. We increased the size of the circles and overlaid the alphanumeric characters to offset the tendency of touch screens to produce higher frequencies of off-target pecking than mechanical keys. Both modifications served to improve pecking accuracy.

We also changed the training procedures. In the Bond et al. (2003) study, as well as in many earlier transitive inference experiments (reviewed in Vasconcelos, 2008), training on the premise pairs was conducted in mixtures of gradually increasing complexity, building up to the full design in which all premise pairs were presented in random order within single sessions. Birds were trained first on sessions of a single color pair (A/B, then B/C, then on C/D). When a bird reached a criterion of 32 or more correct responses in each of three successive sessions, it was advanced to the next pair. As each bird completed the last pair (F/G), it was advanced to a second training phase, an equal mixture of trials on two adjacent color pairs (e.g. B/C and C/D). When each bird reached the same training criterion on these triadic sessions, it was switched to a fully intermixed design, in which it was required to track all six color pairs presented in equal numbers and randomized order in each daily session.

Over time, with increased experience with these types of experiments with corvids, we have improved on this training procedure. With the original method, the transition from sessions on one premise pair to sessions on the next pair in the sequence constituted a partial reversal, in which a previously incorrect and heavily trained choice was now rewarded. This insured that accuracy at the beginning of every block of new pair trials would be less than 50%. At least a few birds of both species in the Bond (2003) experiment stopped responding at these transitions and had to be given one or two sessions of non-discriminative re-training on white stimuli to induce them to resume pecking. Treichler and Van Tilburg (1996) encountered similar difficulties with a stepwise introduction of premise pairs in their research with rhesus macaques. They subsequently discovered that operant training that included all premise pairs together from the beginning produced learning that was initially somewhat slower, but that ultimately enabled asymptotic performance in far fewer sessions than any graded introduction. They found that this training did not influence choice performance during the testing phase (Treichler & Van Tilburg, 2002). All corvid research involving transitive designs that we have conducted since 2003, including that on the nutcrackers and magpies in the current study, has used such fully intermixed training from the outset. We have found that performance following intermixed training is fully comparable to that produced by the “sequential” procedure in our 2003 paper. The birds reach comparable levels of accuracy, and perform similarly on premise and probe test pairs.

Results

All of our analyses used data from both the current experiment and the Bond et al. (2003) study. The possible effects of the procedural differences between the experiments on these analyses are discussed below.

Species Differences in Premise Pair Acquisition

During both studies, we trained all birds to an asymptotic level of accuracy on the full set of premise pairs to obtain consistent performance during the test phase. For most subjects, a criterion of three successive four-session blocks at ≥ 80% correct on all trials was sufficient. However, one nutcracker, two magpies, and all of the scrub jays initially failed to attain this level of accuracy. In these cases, we transferred the birds to the test phase when their over-all performance was stable and consistent across at least three successive four-session blocks. For nutcrackers and magpies, completion of the training phase required means of 81 and 77 sessions, respectively (about 3000 trials). Pinyon jays needed an average of only 56 sessions (about 2000 trials) on the full set of premise pairs, though they had previously been given an average of 66 graded training sessions on smaller sets of stimuli. Scrub jays needed an average of 146 training sessions (nearly 5300 trials) on the full task, despite having previously received an additional 133 sessions of graded training. As Treichler and Van Tilburg (2002) found in macaques, gradual introduction of premise pairs does not necessarily improve sequence learning in all species.

To test for species differences in rates of acquisition, we determined a standardized pair of accuracy criteria. The first four-session block during which the bird attained ≥ 60% correct on all premise pairs was chosen as the beginning of a learning assessment interval. The end of the interval was a function of the bird's asymptotic maximum accuracy. We estimated the asymptotic maximum from the bird's performance on the six premise pairs during the last five blocks of the test phase (i.e. the last 20 sessions of the experiment). The lower 95% confidence limit for this presumed maximum was then compared to the upper 95% limits from a running series of five blocks from throughout both phases of the experiment. The first block during which accuracy was statistically indistinguishable from the final asymptotic level was taken as the end of the assessment interval. Species differences in both the asymptotic maximum and the duration of the assessment interval were tested with analysis of variance. There was a significant effect of species on asymptotic performance, F(3,17) = 5.72, p < 0.007, due to the consistently lower accuracy of the scrub jays, F(1,17) ≥ 6.03, p < 0.03. Nutcrackers, pinyon jays, and magpies were all performing at 80% correct or better either by the end of training, or within at most the first two blocks of the test phase. In contrast, only one of the four scrub jays had reached this criterial accuracy even by the end of the experiment. The duration of the assessment interval, however, showed no significant effect of species, F(3,17) < 0.58, p > 0.6. The mean number of acquisition blocks to asymptote was 15 for magpies, 19 for nutcrackers, 17 for pinyon jays, and 21 for scrub jays, and there was a great deal of variation between individuals.

Development of a Relational Index

The results of the simulation runs on the associative model are summarized in Table 1. At first glance, premise pair accuracy appears to fluctuate erratically with distance from the top of the hierarchy. A more careful examination of Table 1, however, reveals that the observed accuracy contour is actually a reliable projection of the complex associative process that takes place in an implicit linear array. Responses to G, for example, are never rewarded, so one might expect that pair F/G would be discriminated with perfect accuracy. The model does very well on F/G, but it never approaches 100% accuracy. This is because on half the trials in which F occurs, it is presented along with E, and responses to F are incorrect in E/F. So the average proportion of rewarded responses to F is about 43%. Because the probability of choosing a particular stimulus is based on the ratio of its associative strength to the sum of the strengths of both stimuli in the display, the probability of choosing F in F/G must, therefore, be less than 1.00. F does derive a significant amount of associative strength from the F/G trials, however, to the degree that it consistently attains about twice the strength of E. So the model incorrectly chooses F about 75% of the time in E/F, making the accuracy for this premise pair lower than for any of the others. In turn, because E is seldom chosen in E/F trials, and because choices of E in D/E are incorrect, the associative strength of E is depressed, which enhances the relative accuracy of D/E choices, and so on up the hierarchy. In essence, the fact that A is always rewarded and G is never rewarded sets up a standing oscillatory wave in the strengths of the intervening items, which is clearly seen in the mean probability of responding to each stimulus (Table 1).

Table 1.

Simulation Results by Stimulus

Stim	Prb Rsp	Prp Rwd	P Pair	PP Acc	T Pair	TP Acc
A	0.9516	1.0000
			A/B	84.0%	B/D	68.4%
B	0.6491	0.7680
			B/C	56.6%	B/E	78.7%
C	0.3580	0.2657
			C/D	37.2%	B/F	64.2%
D	0.6013	0.3549
			D/E	58.1%	C/E	56.2%
E	0.3601	0.2075
			E/F	25.4%	C/F	38.3%
F	0.7584	0.4277
			F/G	77.6%	D/F	45.4%
G	0.2001	0.0000

Note. Simulation consisted of 300 iterations of a 100-session series, with 36 trials per session and a memory window of 100 trials. Columns: Stim = Stimulus identifier; Prb Rsp = Probability of response to given stimulus (irrespective of context); Prp Rwd = Proportion of responses to given stimulus that were rewarded; P Pair = Premise pair; PP Acc = Percent correct responses to given premise pair; T Pair = Transitive probe pair; TP Acc = Percent correct responses to transitive probes. Variables are means over the last five sessions of all 300 iterations.

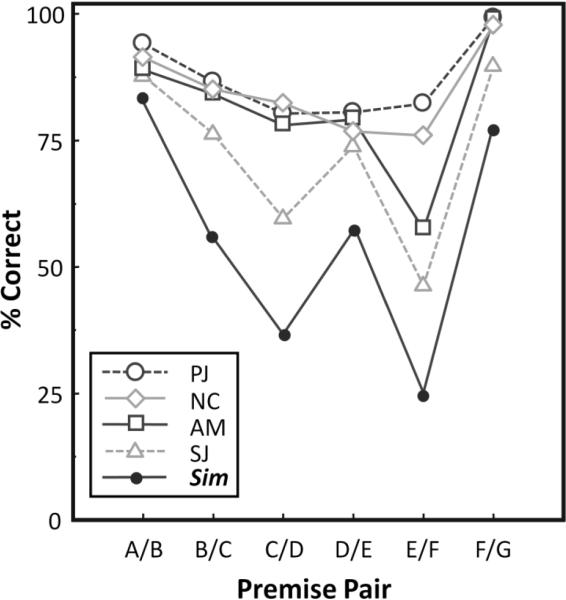
Given the unexpected shape of the predicted function, it is remarkable how closely the mean accuracies for all species on each premise pair from the test phase sessions resembled the contour of simulated accuracies (Figure 1). The scrub jay contour, in particular, followed every fluctuation predicted by the associative model, but the nutcrackers and magpies showed a similarly depressed accuracy on E/F, and all species were more accurate on the terminal pairs than on any of the more central ones. Because the jays all appeared to show some varying degree of correspondence to the model results, we computed a “relational index” for each subject, based on its performance on premise pairs during the test phase. If the mean accuracy on premise pair i of a given bird is B[i], and the predicted accuracy of our model of associative representation is M[i], then the relational index, RI, is calculated as:

$$\mathit{RI}=\frac{{\sum }_i(\mathit{B}\left[i\right]-\mathit{M}\left[i\right])}{{\sum }_i(1-\mathit{M}\left[i\right])}$$

This ratio approaches 1.0 when the bird's performance shows uniformly high accuracy on all pairs, which would be consistent with a purely relational representation (e.g. Terrace, 1993, 2005). It decreases toward 0.0 as the bird's performance approaches that of the associative model. The index thus provides a relatively objective estimate of the extent to which the associative model predicts performance across the premise pairs. Thus if there are two basic processes in use, it also provides a measure of the extent to which relational representations are used. Our next step was to analyze the discrepancies between the Couvillon and Bitterman (1992) model and the behavior of the four corvids to explore the possible relationship between performance in operant transitive inference and natural history.

Figure 1.

Mean accuracy by species of responses to premise pairs during the test phase, compared to the results of simulation of associative representation. PJ = pinyon jays; NC = Clark's nutcrackers; AM = azure-winged magpies; SJ = western scrub jays; Sim = simulation results.

The Influence of Natural History

The four corvid species in these studies differ in their natural histories along two orthogonal dimensions – social complexity and cache reliance. To characterize the species with respect to these dimensions, we employed numeric ranking. Pinyon jays live in persistent groups of hundreds of individuals, so we gave them a sociality rank of 3. Magpies live in groups of related birds that are at least an order of magnitude smaller than those of pinyon jays, so they were assigned a sociality rank of 2. Nutcrackers and scrub jays are basically solitary, so they both received a sociality rank of 1. In the spatial dimension, nutcrackers are wholly dependent on cached pine seeds for survival, so we gave them a rank of 3 for cache reliance. Pinyon jays also make use of cached food, but their niche is broader than that of nutcrackers and they are less dependent on caching, so we gave them a caching rank of 2. Magpies seldom cache, and scrub jays cache much less often than nutcrackers and pinyon jays, so they both were given a caching rank of 1.

To test the effects of the natural history of these species on their cognitive representations, we regressed the relational index from each bird against our rankings of sociality and cache reliance. The regression model was significant, F(2,18) = 7.03, p < 0.006, accounting for 44% of the variance across subjects in the relational index. The squared semi-partial correlation for cache reliance accounted for 30% of the variance, t(1,18) = 3.1, p < 0.007, while that for social complexity accounted for 23%, t(1,18) = 2.69, p < 0.015. Both of our life history variables thus had significant, independent effects on the relational index. Species that make greater use of cached food, as well as those that live in larger, persistent social groupings, showed greater relative deviations from our simulation of associative representation (Figure 2).

Figure 2.

a) Residuals from regressing the relational index on the species ranking for cache reliance, as a function of the ranking of sociality. Results are plotted by subject, again with an adjustment to prevent overlapping symbols. In the multivariate regression, sociality accounted for 23% of the variance in the relational index. b) Residuals from regressing the relational index on the ranking of species sociality, as a function of the ranking of cache reliance. Results are plotted by subject, with some adjustment in the abscissa to prevent overlapping symbols. PJ = pinyon jays; NC = Clark's nutcrackers; AM = azure-winged magpies; SJ = western scrub jays. In the multivariate regression, cache reliance accounted for 30% of the variance in the relational index.

Transitive Inference Testing

Probe trials from the six transitive test pairs were aggregated within subjects according to “symbolic distance” (Moyer & Bayer, 1976), the degree of separation between stimuli along the implicit hierarchy. (Thus, the symbolic distance = 2 for B/D, C/E, and D/F; 3 for B/E and C/F; 4 for B/F.) Repeated measures anova showed a significant main effect of species on accuracy, F(3,18) = 4.76, p < 0.01 (Figure 3). As was the case in the acquisition of premise pairs, scrub jays were less accurate on transitive tests than any of the other three species, F(1,18) ≥ 4.77, p < 0.05. There was also a significant main effect of symbolic distance, F(2,34) = 15.0, p < 0.0001, but there was no significant species × distance interaction, F(6,34) = 1.14, p > 0.3. Although the scrub jays performed less accurately than the other three species, all four species showed similar patterns of transitive inference across different test pairs.

Figure 3.

Mean accuracy by species of responses to selected premise pairs and transitive probes during the test phase, in order of their symbolic distance. These are visually compared to the results of simulation of associative representation. PJ = pinyon jays; NC = Clark's nutcrackers; AM = azure-winged magpies; SJ = western scrub jays; Sim = simulation results. Both the main effect of species and that of symbolic distance were statistically significant.

If the cognitive demands of an animal's environment had selected for an increased reliance on relational representation, we might conceivably see differences in task acquisition as a function of the relational index. This did not prove to be the case. Regression of the duration of the assessment interval on the relational index was not significant, F(1,19) = 1.19, r² < 0.06, p > 0.2, indicating that birds that showed higher reliance on relational representations did not necessarily learn the task faster. We also tested for the possibility that a high relational index was associated with more accurate performance on transitive test pairs. Mean transitive test accuracy was uniformly higher than the model predictions across all species (Figure 3) and in all but one of the subjects, t(5) ≥ 2.73, p ≤ 0.03, by as much as 30 to 40 percentage points. The sole exception was scrub jay #803, which performed almost precisely as predicted by the associative model, t(5) = 0.14, p > 0.8. This bird also exhibited the lowest asymptotic accuracy level and the lowest relational index of any subject in the study. If a bird made inferences entirely on the basis of an associative representation, our model predicted that at a symbolic distance of 2 steps, accuracy on B/D should be higher than that on D/F, and at a distance of 3 steps, accuracy on B/E should be much higher than that on C/F (Table 1 and Figure 3). We tested these hypothetical relationships for differences between species and effects of the relational index. Neither anova showed a significant main effect of species, F(3,17) ≤ 1.32, p > 0.3, and regression of the differences against the relational index was similarly uninformative, F(1,19) ≤ 1.59, r² ≤ 0.08, p > 0.2.

Discussion

Operant transitive inference in an implicit hierarchy is a deceptively simple paradigm. In our simulation of pure associative representation, the probability of responding to a particular stimulus was determined only by its relative associative strength, that is, the relative frequency of rewarded responses to each stimulus. In contrast to predictions in the early conditioning accounts of transitive inference (Couvillon & Bitterman, 1992), the model did not produce a monotonic decrease in associative strength as a function of distance from the top of the hierarchy. Instead, the response probability tended to oscillate regularly along the hierarchy, driven by the disparity between the invariably positive reward for responses to the top-most stimulus and the invariably negative outcome of responses to the bottom one (Table 1).

Without the benefits of a monotonic strength function, a purely associative representation cannot account for transitive responding. Results from shorter, five-item sequences may appear to be open to an associative interpretation (Allen, 2006), but when the design is extended to larger numbers of stimuli, as in our experiments, or to non-linear sequences or more complex reward relationships, it is extremely difficult to explain transitive responding without including some configural or relational component (Weaver et al., 1997; Delius & Siemann, 1998; De Lillo et al., 2001). Virtually all of our birds responded more accurately on transitive probes than would have been expected from a purely associative representation. The difference from expectation was generally largest for probes of C/F, where the model predicted 38% correct responses (Figure 3). The average accuracy for this pair across all subjects and all species was 89%, consistent with the high accuracies that have been reported for symbolically distant transitive probes in many other studies (e.g. von Fersen et al., 1991; Treichler, 2007). Most animals probably develop both associative and relational representations of pairs of stimuli, perhaps acquiring them simultaneously as two different aspects of a single encoding process (Jacobs, 2006; Lazareva & Wasserman, 2006).

If animals do develop both types of representation than the appropriate focus when making species comparisons, is not on whether an animal's performance can be explained exclusively in terms of associative representations. Instead, it is more useful to explore the use each species makes of the two types of representation and the consequences for task performance. In this regard, the strongest finding from this study was that aspects of the characteristic natural history of these four corvids had direct, predictable influences on their apparent degree of reliance on relational representation. Both dependence on cached food and living in large, persistent social groupings proved to be significantly and independently associated with our index of relational representation, a measure that was derived from the birds' average asymptotic performance on adjacent, premise pairs (Figure 2). Such similar outcomes from such apparently distinctive selective factors may reflect a common requirement for accuracy and flexibility in configural memory among species that deal with structurally complex environments.

Our analysis of these four species combined data from two separate experiments with somewhat different procedures, particularly during premise pair training. In our previous study, the pinyon jays and scrub jays were trained on mixtures of trial types that gradually increased complexity, building up to the full design in which all premise pairs were presented in random order within single sessions. There is no apparent correlation, however, between which procedures were used and performance at asymptote on the premise pairs or during testing on the nonadjacent test pairs. In particular, the species that showed the greatest (scrub jays) and least (pinyon jays) agreement with the simulation model were both tested in the first study. The possible effects of the training methodology appear, therefore, to have been conservative relative to the conclusions of the study.

Given that the primary focus in operant studies has generally been on the animals' responses to the novel, nonadjacent stimulus pairs, it is striking that the clearest evidence of species differences in cognitive representation was found in their pattern of accuracy on premise pairs. Effects of relational representation were not displayed in probes of novel associations, but in the pairs of adjacent stimuli on which the birds had previously been trained for thousands of trials. One consistent interpretation is that transitive inference in these relatively short sequences of arbitrary stimuli is not particularly cognitively demanding (Allen, 2006). In this view, nearly any encoding of relational information, no matter how rough and approximate, will suffice to enable accurate responding on distant transitive probes, but only a fairly precise designation of stimulus positions on a relational map would allow for consistently high accuracies on adjacent pairs.

The species contrasts we observed could, therefore, reflect several types of differences in information processing. For example, birds with lower relational indices may simply not attend to configural features, at least in this experimental design. Scrub jays did not attain the same levels of accuracy at asymptote as the other three species, and they showed the clearest resemblance to the accuracy contour of our associative model (Figure 1). However, the rate of task acquisition showed no effects either of species or of relational index. The lower asymptotic accuracy of the scrub jays did not, therefore, appear to reflect insufficient experience: Indeed, they received 100 more acquisition sessions than did the pinyon jays in Bond et al. (2003) with no significant improvement in accuracy. If the relative frequency of reward is the single most salient feature of the implicit hierarchy design for scrub jays, their predominant focus on associative outcomes would have imposed a fixed ceiling on their maximum performance levels.

The comparative data on spatial memory in seed-caching corvids is consistent with the idea that species differences in cognition are often most apparent when more challenging tasks are employed. Olson (1989, 1991) compared nutcrackers and scrub jays in an operant delayed spatial nonmatching–to-sample task. The two species performed at similar levels during training with a minimal delay between sample and choice. When the task was made more difficult, however, either by increasing the number of samples to be remembered or increasing the delay between sample and choice, nutcrackers performed much better than scrub jays.

It is sometimes suggested that the effects of natural selection on cognition result in modularized cognition, abilities that are confined to the context in which the selection has occurred. The data on spatial memory and cache dependence clearly indicates that this need not be the case. There are many experiments that have found a correlation between cache-dependency and performance during noncaching tests of spatial memory among corvids, in operant tests (Olson, 1991; Olson, Balda, Kamil & Nims, 1995) and radial maze analogs (Kamil et al., 1994). Similar results have been obtained in other taxa (e.g., parids: Brodbeck, 1994; Brodbeck & Shettleworth, 1995, Clayton & Krebs, 1994; kangaroo rats: Barkley & Jacobs, 2007). The results of our comparative studies of operant transitive inference suggest that behavior in this laboratory test of cognition may also be related to the natural histories of the species being tested.

At the neurobiological level, the extent of relational representation may be limited by species differences in the encoding mechanism (Riley, Cook, & Lamb, 1981). Scrub jays may attend equally well to the configural information in the displays, but they may not be able to encode it accurately as a consequence of species-specific differences in neuroanatomy. There is a growing literature implicating the hippocampus as a flexible relational engine intrinsic to all configural learning, one that is capable of producing map-like representations of many different types of event association (Wallenstein, Eichenbaum, & Hasselmo, 1998; Driscoll et al., 2005; Zalesak & Heckers, 2009). In this case, both spatial and non-spatial relational representations may derive from a common neural mechanism, and the similar selective influences of social and spatial complexity may be the result of similar effects on the size and structural complexity of the hippocampus. Comparative research on corvid neuroanatomy has mainly been concerned with the relationship between the size of the hippocampal formation and reliance on cached food (e.g. Brodin & Lundborg, 2003; Lucas et al., 2004). Our results suggest that a narrow focus on comparative spatial memory may be unwarranted, however, as both social and spatial complexity can potentially have equivalent selective effects on hippocampal function. Additional neurobiological studies of corvids, comparing the detailed functional anatomy of the hippocampus in species with a suitably broad range of natural history features, could be of significant value.