New approaches to population stratification in genome-wide association studies

Preface

Genome-wide association studies (GWAS) are an effective approach for identifying genetic variants associated to disease risk. GWAS can be confounded by population stratification—systematic ancestry differences between cases and controls—which has previously been addressed by methods that infer genetic ancestry. Those methods perform well in data sets in which population structure is the only kind of structure present, but are inadequate in data sets that also contain family structure or cryptic relatedness. Here, we review recent progress on methods that correct for stratification while accounting for these additional complexities.

GWAS have identified hundreds of common variants associated to disease risk or related traits¹ (see Web Resources). These studies have overcome the dangers of population stratification, which can produce spurious associations if not properly corrected^2–3. However, accounting for population structure is more challenging when family structure or cryptic relatedness is also present, motivating the development of new methods. Because the spurious associations that have been reported primarily occur at markers with unusual allele frequency differences between subpopulations^{2, 4}, it is critical for new methods aiming to correct for stratification to be evaluated by considering unusually differentiated markers.

The prevailing paradigm in recent years has been to use Genomic Control to measure the extent of inflation due to population stratification or other confounders, and to correct for stratification (if necessary) using methods that infer genetic ancestry, such as Structured Association or Principal Components Analysis. A limitation of this strategy is that it fails to account for other types of sample structure, such as family structure or cryptic relatedness^5–6. Modeling family structure is a necessity in studies with family-based sample ascertainment, and there is increasing evidence that cryptic relatedness may occur in a wide range of data sets (see below). Family-Based Association Tests offer one potential solution for dealing with family structure. More recently, approaches using Mixed Models that incorporate the full covariance structure across individuals have been proposed.

Below, we review each of these methods, conduct simulations to evaluate their performance, discuss stratification in the specific context of low-frequency or rare variants, and conclude with guidelines and recommendations.

Detecting Stratification

A widely used approach to evaluate whether confounding due to population stratification exists is to compute the Genomic Control λ (λ_GC), defined as the median χ²(1 dof) association statistic across SNPs divided by its theoretical median under the null distribution^7–9. A value of λ_GC≈1 indicates no stratification, whereas λ_GC>1 indicates stratification or other confounders such as family structure or cryptic relatedness (see below), or differential bias¹⁰. P-P plots are a standard tool for visualization of test statistics (Figure 1). Values of λ_GC<1.05 are generally considered benign, although inflation in λ_GC is proportional to sample size.

Figure 1. P-P plots for visualization of stratification or other confounders.

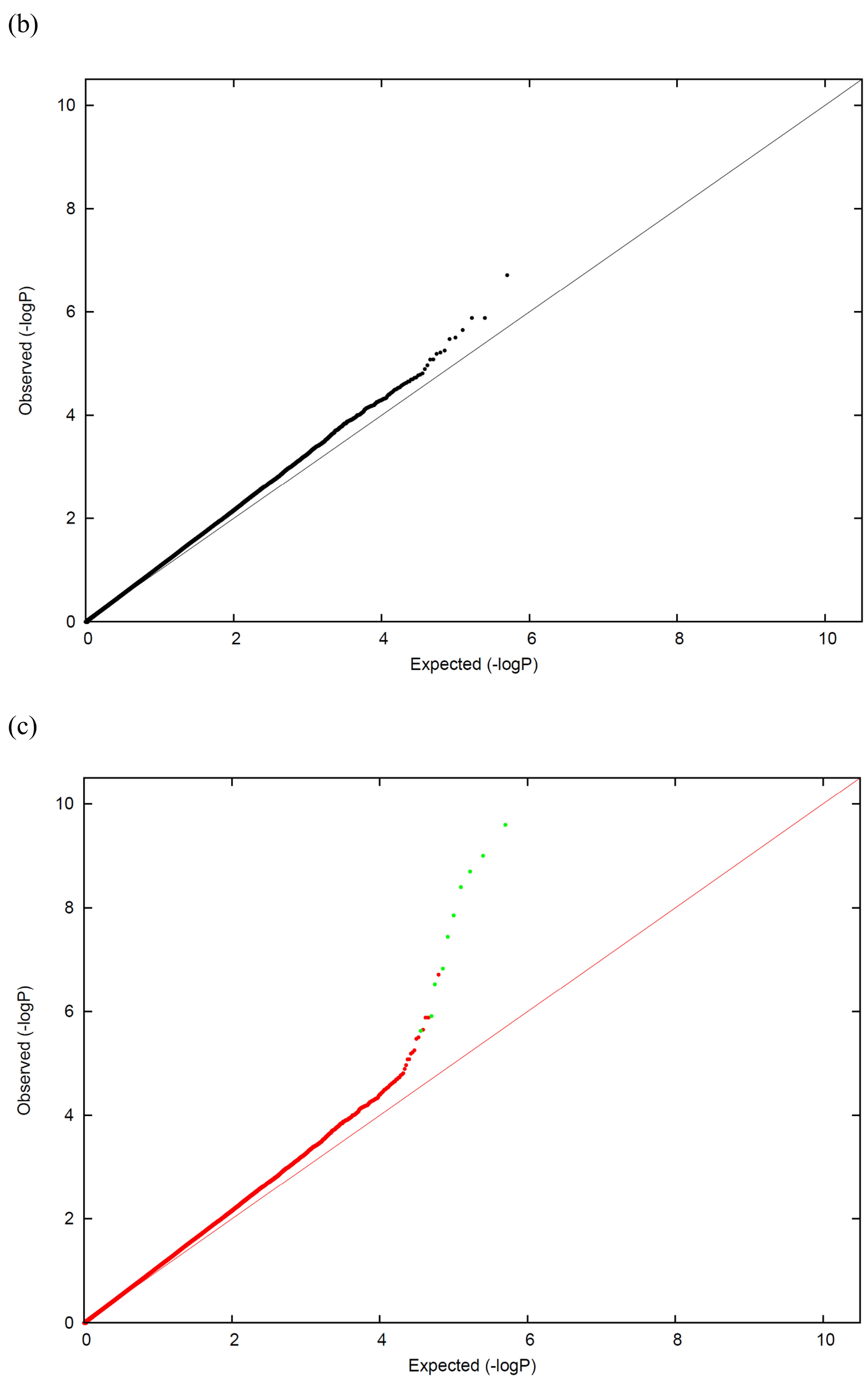
We display simulated P-P plots for genome-wide scans with no causal markers under three scenarios. (a) No stratification: P-values fit the expected distribution. (b) Stratification without unusually differentiated markers: P-values exhibit modest genome-wide inflation. (c) Stratification with unusually differentiated markers: P-value exhibit modest genome-wide inflation, plus severe inflation at a small number of markers.

If population stratification exists, it is important to distinguish between subpopulation differences that are due to very recent genetic drift, and those that arose from more ancient population divergence¹¹. In the case of ancient population divergence, dividing association statistics by λ_GC will provide a sufficient correction for stratification. In the latter case, markers with unusual allele frequency differences that lie outside the expected distribution, which could be caused by natural selection, make stratification a much more severe problem, and dividing association statistics by λ_GC is likely to be inadequate. In the case of family structure or cryptic relatedness, dividing association statistics by λ_GC will generally produce the approximate null distribution, though a refinement to the method may be needed when there is uncertainty in the estimate of λ_GC ¹². However, even if the appropriate null distribution is obtained, in general this approach will not maximize power to detect true associations. Other approaches to correcting for stratification, including approaches that also account for family structure and cryptic relatedness, are described below.

Inferring Genetic Ancestry

Structured Association

Methods that explicitly infer genetic ancestry generally provide an effective correction for population stratification in data sets where population structure is the only type of sample structure. In the Structured Association approach, samples are assigned to subpopulation clusters (possibly allowing fractional cluster membership) using a model-based clustering program such as STRUCTURE^13–14, and association statistics are computed by stratifying by cluster (STRAT; see Web Resources)¹⁵. The applicability of this approach to large genome-wide data sets has historically been limited by its high computational cost when allowing fractional cluster membership, but faster model-based approaches for inferring population structure have recently been developed¹⁶ (ADMIXTURE; see Web Resources). Thus, applying Structured Association to both infer population structure and compute association statistics in genome-wide data sets is likely to become a practical approach.

Principal Components Analysis

Principal Components Analysis (PCA) is a tool that has been used to infer population structure in genetic data for several decades, long before the GWAS era^17–20. It should be noted that top PCs do not always reflect population structure: they may reflect family relatedness¹⁹, long-range LD (for example, due to inversion polymorphisms⁴), or assay artifacts¹⁰; these effects can often be eliminated by removing related samples, regions of long-range LD, or low-quality data, respectively, from the data used to compute PCs. In addition, PCA can highlight effects of differential bias that require additional quality control²¹.

Using top PCs as covariates corrects for stratification in GWAS^21–22 (EIGENSTRAT; see Web Resources). Like Structured Association, PCA will appropriately apply a greater correction to markers with large differences in allele frequency across ancestral populations. Unlike initial implementations of Structured Association, PCA is computationally tractable in large genome-wide data sets. Related approaches such as Multi-Dimensional Scaling (MDS) and Genetic Matching have also proven useful^23–24 (PLINK; see Web Resources). When genome-wide data are not available (for example, in replication studies), Structured Association or PCA can infer genetic ancestry, and hence correct for stratification, using Ancestry-Informative Markers (AIMs)²⁵. A common misconception is that AIMs should be used to infer genetic ancestry even when genome-wide data is available, but in fact the best ancestry estimates are obtained using a very large number of random markers.

A limitation of the above methods is that they do not model family structure or cryptic relatedness. These factors may lead to inflation in test statistics if not explicitly modeled, because samples that are correlated are assumed to be uncorrelated. Although correcting for genetic ancestry and then dividing by the residual λ_GC will restore an appropriate null distribution, association statistics that explicitly account for family structure or cryptic relatedness are likely to achieve higher power, due to improved weighting of the data.

Family-Based Association Tests

Family-based studies, in which individuals are ascertained from family pedigrees, offer a unique solution to population stratification. Family-Based Association Tests that focus on within-family information (generalizing the Transmission Disequilibrium Test²⁶) are immune to stratification, since transmitted and untransmitted alleles have the same genetic ancestry^27–29 (FBAT and QTDT; see Web Resources). However, fully powered statistics for family-based studies will need to incorporate between-family information, which is still susceptible to stratification. A recent suggestion is to transform between-family information into a rank statistic before combining within-family and between-family information, guaranteeing that both sources of information are immune to stratification^30–31. This approach performs favorably compared to previous family-based approaches^30–31, but places an upper bound on the statistical power that can be extracted from the between-family component of the overall signal, because the transformed rank statistic cannot be more statistically significant than one divided by the number of samples.

Mixed Models

Mixed models can model population structure, family structure and cryptic relatedness³². The basic approach is to model phenotypes using a mixture of fixed effects and random effects. Fixed effects include the candidate SNP and optional covariates such as gender or age, while random effects are based on a phenotypic covariance matrix, which is modeled as a sum of heritable and non-heritable random variation (see Box 1 for details). Mixed models have historically been a theoretically appealing but computationally intensive approach; however, very recent computational advances have now made it possible to apply them to GWAS^33–34 (EMMAX and TASSEL; see Web Resources). Methods that explicitly model population structure, family structure and cryptic relatedness are expected to perform better in the presence of these complexities than methods that do not, and this has now been confirmed^33–34. For example, in an analysis of seven Wellcome Trust Case Control Consortium phenotypes, the application of mixed models consistently yielded values of λ_GC that were less than 1.01, in contrast to other approaches³³.

Box 1. Mixed models

Simple linear models

Simple linear models represent the phenotype Y as function of fixed effects X :

$$Y=\mathit{\text{XB}}+\epsilon$$

Here X denotes the genotype at the candidate marker as well as optional covariates such as gender or age, B denotes coefficients of fixed effects, and ε is a normally distributed noise term that accounts for unexplained variation in Y.

PCA addresses the issue of population substructure by including PC covariates in X to explicitly model the ancestry of each individual. If genotype is not causally related to phenotype but genotype and phenotype are both correlated to ancestry, test statistics will be inflated. Using PCA to explicitly model genetic ancestry removes this confounding effect. However, PCA only accounts for fixed effects of genetic ancestry; it does not account for relatedness between individuals, which may also cause inflation in test statistics.

Linear mixed models

Linear mixed models represent the phenotype Y as a function of fixed effects X plus random effects u:

$$\begin{array}{c}Y=\mathit{\text{XB}}+u+\epsilon \hfill \\ \mathit{\text{Var}}(u)={\sigma }_g^{2}K\hfill \end{array}$$

Here u denotes a component of the overall noise variance u + ε that is distributed according to a kinship matrix K. Thus, u represents the heritable component of random variation and ε represents the non-heritable component of random variation.

The kinship matrix K is defined according to the pairwise genotypic similarity of individuals, and so its structure is influenced by population structure, family structure and cryptic relatedness. The parameter ${\sigma }_g^2$ relates this structure to the phenotype Y : σ_g² captures the extent to which genetically similar individuals are phenotypically similar, thus removing confounding effects. The optimal formulation of K, the importance of including PC covariates in fixed effects X, and the effects of these choices have not yet been fully explored.

Population structure: a fixed or random effect?

An important and unanswered question is whether population structure should be modeled as part of the set of random effects together with family structure and cryptic relatedness, or as a separate fixed effect requiring PC covariates and additional model parameters^33–34 (see Box 1). Inclusion in random effects is much simpler, and has been shown to provide a sufficient correction for stratification in Finnish and UK data sets³³.

However, population structure is actually a fixed effect (i.e. its effect as a function of genetic ancestry is the same for all samples), and spurious associations might result if it is modeled as a random effect based on overall covariance, particularly in the case of unusually differentiated markers. Modeling population structure as a fixed effect provides a higher level of certainty in correcting for stratification, but requires running PCA (or a similar method) to infer the genetic ancestry of each sample³⁴. If family structure is present, inferring genetic ancestry via PCA is a challenge, because family relatedness may lead to artifactual PCs¹⁹. A possible solution is to compute PCs using SNP loadings inferred from a set of unrelated samples, either using a different set of samples than those in the disease study or using an unrelated subset of samples from the disease study³⁵. This is likely to be sufficient when the set of unrelated samples used is very large relative to the magnitude of population structure effects. However, unless sample sizes are very large, PCs computed from external SNP loadings will be biased towards zero due to statistical noise in the SNP loadings^{11, 36}. This motivates further work on PCA in related samples.

Modeling phenotypes as fixed

Mixed models view phenotypes as modeled using a fixed set of genotypes. However, as an alternative to mixed models, genotypes can be modeled using a fixed set of phenotypes, a theoretically appealing approach that makes fewer assumptions about phenotypic covariance structure^37–38. Simulations in the absence of unusually differentiated markers have shown that using the genotypic covariance matrix to account for both population and family structure can effectively control spurious associations under a variety of settings³⁷ (ROADTRIPS; see Web Resources). However, in the case of unusually differentiated markers, normality assumptions (about genotype distributions) underlying the test statistics will be violated, and stratification may lead to confounding unless PC covariates are used. The question of whether to model random effects only or to include PC covariates as fixed effects is analogous to the mixed model framework. When viewing phenotypes as fixed, PC covariates may be particularly essential since modeling only random effects leads to a uniform correction factor in the absence of missing data³⁷.

Simulations

To illustrate the properties of the above methods in correcting for stratification at normally differentiated or unusually differentiated markers, in the presence or absence of family structure, we carried out two simulations. We considered a case-control study with two subpopulations POP1 and POP2, with 300 cases and 200 controls from POP1 and 200 cases and 300 controls from POP2. We simulated 99,900 normally differentiated markers based on F_ST(POP1,POP2)=0.01,³⁹ and 100 unusually differentiated markers based on allele frequency difference equal to 0.6 with both minor allele frequencies uniformly distributed on [0.0,0.4]²¹. In simulation 1, all individuals were unrelated. In simulation 2, all individuals from POP1 were unrelated and individuals from POP2 included 80 case-case sibling pairs, 40 case-control sibling pairs and 130 control-control sibling pairs. We computed λ_GC for each of the following methods: uncorrected Armitage trend test, EIGENSTRAT²¹, EMMAX without PC covariates³³, EMMAX with PC covariates³³, and ROADTRIPS³⁷ (see Web Resources). All PC runs used only one PC, but the additional inclusion of random PCs has little effect on results²¹. Power to detect causal variants may vary between methods, but our focus here was on correcting false positive associations. We did not simulate the approach described in ref. 30 as this method is completely immune from stratification, ensuring a value of 1.00 in all entries of the table; this approach has appealing properties, but may have reduced power in some instances (see above). We note that the method of ref. 37 with PC covariates incorporated is an approach of potentially high interest, but not currently implemented in ROADTRIPS software.

The results of the simulations are displayed in Table 1. EIGENSTRAT is effective in correcting for population stratification at both normally and unusually differentiated markers (Simulation 1), but does not control for family structure (Simulation 2). EMMAX corrects for both stratification and population structure except for a modest residual inflation at unusually differentiated markers, which is completely removed by EMMAX with PC covariates; if the number of unusually differentiated markers is small, modest inflation at such markers may not be a major concern. ROADTRIPS corrects for family structure but not for population stratification at unusually differentiated markers, though incorporation of PC covariates could potentially address this. We note that for each method, dividing association statistics by residual λ_GC is guaranteed to produce statistics with λ_GC=1, but this approach may be inadequate for spurious associations at unusually differentiated markers, and/or may not maximize power if family structure (or cryptic relatedness) is not fully modeled.

Table 1. Effectiveness of different approaches in correcting for stratification.

We list the λ_GC (Genomic Control lambda) of each method for normally differentiated (F_ST = 0.01) and unusually differentiated (Δ = 0.6) markers in Simulation 1 and Simulation 2. In each case, λ_GC was computed as the median χ²(1 dof) statistic (restricting to the subclass of markers tested) divided by 0.455. EIGENSTRAT corrects for population structure (Simulation 1), EMMAX and ROADTRIPS correct for family structure and for population structure at normally differentiated markers (F_ST = 0.01), and EMMAX+PCs corrects for family structure and for population structure at normally or highly differentiated markers (F_ST = 0.01 or Δ = 0.6). We note that the approach of ref. 30 is immune to all of these confounders, implying a value of λ_GC=1.00 for each column of the table.

	Simulation 1, FST = 0.01	Simulation 1, Δ = 0.6	Simulation 2, FST = 0.01	Simulation 2, Δ = 0.6
Armitage trend	1.40	48.4	1.57	48.3
EIGENSTRAT	1.00	1.00	1.17	1.14
EMMAX*	1.00	2.05	1.01	1.62
EMMAX* + PCs	1.00	1.02	1.01	1.01
ROADTRIPS	1.00	48.4	1.00	48.3

^*EMMAX can use either the IBS or Balding-Nichols estimate of the kinship matrix³³. Results for IBS are displayed in the table, and results for Balding-Nichols are 1.00, 1.91, 1.00, 1.28 for EMMAX and 1.00, 1.03, 1.00, 0.99 for EMMAX + PCs.

Low-frequency and Rare Variants

GWAS have largely focused on common variants, but because most genetic heritability remains unexplained, future work will increasingly focus on variants of low minor-allele frequency (0.5%<MAF<5%) or rare variants (MAF<0.5%)⁴⁰. First, new low-frequency variants will be identified by the 1000 Genomes Project (see Web Resources) and included in next-generation genotyping arrays. Here, the issues are generally similar to those involving common variants, except that deviation from model specification is more likely, for example if normality assumptions are violated or the genotypic variance of a SNP varies across subpopulations⁴¹. Second, exome resequencing projects will aim to identify genes in which individuals with extreme phenotypes have an aggregate excess or deficiency of rare nonsynonymous variants⁴². Differences in allele frequency spectrum across ancestral populations make stratification a potential concern, but genetic ancestry can be inferred from genotyping array data from the same samples, if available, and included as a covariate. Finally, the advent of whole-exome or whole-genome resequencing raises the question of whether rare variants can be used to infer genetic ancestry with greater precision, perhaps using different methods than the methods currently applied to common variants.

Conclusion

Many different methods of correcting for stratification have been developed, and all of these methods have important advantages. Although mixed models are relatively new and untested, they appear to offer a practical and comprehensive approach for simultaneously addressing confounding due to population stratification, family structure and cryptic relatedness.

In studies where stratification is not a very serious concern, an appealing and simple approach is to use mixed models without including PC covariates. This may include (i) studies in populations of homogeneous ancestry, (ii) studies in structured populations where structure is due to very recent genetic drift, and (iii) studies in any population in which PCA or related methods, applied either to the entire sample or to a subset of unrelated samples, indicate that there is no substantial stratification, i.e. phenotypes are not highly correlated with any of the top PCs.

For studies that do not meet any of the above criteria, an appealing approach is to use mixed models with PC covariates. In family-based studies in which the within-family component contributes much of the overall statistical power, the approach of ref. 30 may also prove useful. In data sets that do not contain family structure or cryptic relatedness, simpler association tests (with or without PC correction, based on above criteria) will probably be sufficient^{21, 23}.

Glossary

Population structure

Sample structure due to differences in genetic ancestry among samples.

Family structure

Sample structure due to familial relatedness among samples.

Cryptic relatedness

Sample structure due to distant relatedness among samples with no known family relationships.

Genomic Control

A method of detecting (or detecting and correcting for) stratification based on the genome-wide inflation of association statistics.

Structured Association

A method of correcting for stratification in which samples are assigned to subpopulation clusters and evidence of association is stratified by cluster.

Principal Components Analysis

A dimensionality reduction technique used to infer continuous axes of variation in genetic data, often representing genetic ancestry.

Family-Based Association Tests

A class of association tests that uses families with one or more affected children as the observations rather than unrelated cases or controls. The analysis treats the allele that is transmitted to (one or more) affected children from each parent as “cases” and the untransmitted alleles as “controls”, to avoid the effects of population structure.

Mixed Models

A class of models in which phenotypes are modeled using both fixed effects (candidate SNP and fixed covariates) and random effects (phenotypic covariance matrix).

Differential bias

Spurious differences in allele frequencies between cases and controls due to differences in sample collection, sample preparation and/or genotyping assay procedures.

Genetic drift

Random fluctuations in allele frequencies over time due to sampling effects, particularly in small populations.

Multi-Dimensional Scaling

A dimensionality reduction technique, similar to PCA, in which points in a high-dimensional space are projected into a lower-dimensional space while approximately preserving the distance between points.

Genetic Matching

A method of association testing in which cases and controls are matched for genetic ancestry, as inferred by PCA or other methods.

Ancestry-Informative Markers

Genetic markers ascertained for large differences in allele frequency between subpopulations that are genotyped to infer genetic ancestry in new samples.

Transmission Disequilibrium Test

A family-based association test involving case–parent trios in which alleles transmitted from parents to child are compared to untransmitted alleles.

Rank statistic

a statistic describing the rank, across markers, of association of each marker. Rank statistics can be transformed into quantiles of a standard normal distribution that can be combined with other statistics.

SNP loadings

The correlations of each SNP to a given PC in PCA. The PC coordinates of each sample are proportional to the sum of normalized genotypes weighted by SNP loadings.

F_ST

A measure of the genetic distance between two populations that describes the proportion of overall genetic variation that is due to differences between populations.

Armitage Trend Test

A standard χ²(1 dof) association test computed as the number of samples times the squared correlation between genotype and phenotype.

Genetic heritability

The proportion of the total phenotypic variation in a given characteristic that can be attributed to additive genetic effects. In the broad sense, heritability involves all additive and non-additive genetic variance, whereas in the narrow sense, it involves only additive genetic variance.

Exome resequencing

A study design in which exon capture technologies are used to obtain resequencing data covering all exonic regions for each individual in the study.

Biographies

Alkes L. Price is an Assistant Professor of Statistical Genetics at the Harvard School of Public Health and a 2010–2012 Alfred P. Sloan Research Fellow. His research interests include disease mapping in admixed populations, deconstructing the heritable components of common disease and gene expression traits, and statistical methods for mapping rare variants.

Noah Zaitlen received his Ph.D. from the University of California San Diego under the supervision of Dr. Eleazar Eskin. He is currently a postdoctoral fellow at the Harvard School of Public Health in the laboratory of Dr. Alkes Price. His research focuses on understanding the genetic basis of complex human phenotypes.

David Reich is an Associate Professor in the Harvard Medical School Department of Genetics and an Associate Member of the Broad Institute of Harvard and MIT. His group focuses on developing methods for understanding human population structure and history, and applying this knowledge to help in the search for disease genes.

Nick Patterson is a senior staff scientist at the Broad Institute in Cambridge, Massachusetts. He received his doctorate in Mathematics from Cambridge University, and has worked both in defense (for the U.K. and U.S. governments) and in finance. His current research interests include the genetics of admixed populations and human genetic history.