Mathematical Modeling To Characterize the Inoculum Effect

Abstract

Killing by beta-lactams is well known to be reduced against a dense bacterial population, commonly known as the inoculum effect. However, the underlying mechanism of this phenomenon is not well understood. We proposed a semimechanistic mathematical model to account for the reduced in vitro killing observed. Time-kill studies were performed with 4 baseline inocula (ranging from approximately 1 × 10⁵ to 1 × 10⁸ CFU/ml) of Escherichia coli ATCC 25922 (MIC, 2 mg/liter). Constant but escalating piperacillin concentrations used ranged from 0.25× to 256× MIC. Serial samples were taken over 24 h to quantify viable bacterial burden, and all the killing profiles were mathematically modeled. The inoculum effect was attributed to a reduction of effective drug concentration available for bacterial killing, which was expressed as a function of the baseline inoculum. Biomasses associated with different inocula were examined using a colorimetric method. Despite identical drug-pathogen combinations, the baseline inoculum had a significant impact on bacterial killing. Our proposed mathematical model was unbiased and reasonable in capturing all 28 killing profiles collectively (r² = 0.88). Biomass was found to be significantly more after 24 h with a baseline inoculum of 1 × 10⁸ CFU/ml, compared to one where the initial inoculum was 1 × 10⁵ CFU/ml (P = 0.002). Our results corroborated previous observations that in vitro killing by piperacillin was significantly reduced against a dense bacterial inoculum. This phenomenon can be reasonably captured by our proposed mathematical model, and it may improve prediction of bacterial response to various drug exposures in future investigations.

Escherichia coli is part of the human gastrointestinal flora and a common pathogen implicated in intra-abdominal infections such as perforated appendicitis and peritonitis. Beta-lactams are often the empirical drug of choice for the management of severe intra-abdominal infections, in view of their spectrum of activity and safety profile. In intra-abdominal infections, a heavy bacterial burden is commonly encountered and the clinical utility of the beta-lactams may be limited by the inoculum effect. This phenomenon is believed to be due to the physiologic state of the bacterial cells, or preferential expression of different penicillin-binding proteins, rendering the bacteria less susceptible to beta-lactams (17). Biofilm production and quorum sensing may also be involved.

We and others have previously developed mathematical models to capture the dynamic relationship between a heterogeneous microbial population and constant drug concentrations (10, 13, 15, 16, 21, 24). Our models were further refined to predict the microbial response to multiple antimicrobial agent dosing regimens (fluctuating drug concentration over time) efficiently (14, 22). Such a modeling approach could be used as a decision-support tool for dosing regimen design, and it may be used at different stages of drug development. It is often observed that killing could be more pronounced against a lower bacterial burden than with a higher bacterial burden (1, 3, 18). Capturing this phenomenon in a mathematical model would require a killing function dependent on bacterial burden. However, one common assumption in most modeling approaches is that the killing function is independent of the bacterial burden (4, 11, 19). This modeling assumption is often restrictive and is useful only when there is not a very significant change in bacterial susceptibility to antimicrobials, as the bacterial burden changes. In other cases, it may be misleading in making accurate predictions about the bacterial behaviors. For example, an experiment with a higher bacterial burden may suggest a dosing exposure requirement to suppress regrowth, but this may overestimate the requirement to suppress regrowth at lower bacterial burdens. In order to capture the overall picture satisfactorily, we need a more robust model the conclusions of which can be extended over a wide range of bacterial burdens.

Therefore, the objective of this study was to extend our mathematical modeling approach proposed previously, to further account for the reduced in vitro killing observed. For illustrative purposes, a standard wild-type E. coli strain with various baseline inocula was used in this investigation.

MATERIALS AND METHODS

Antimicrobial agents.

Piperacillin and tazobactam were purchased from Sigma (St. Louis, MO). A stock solution of each antimicrobial agent in sterile water was prepared, aliquoted, and stored at −70°C. Prior to each susceptibility test, an aliquot of the drug was thawed and diluted to the desired concentrations with cation-adjusted Mueller-Hinton broth (Ca-MHB) (BBL, Sparks, MD).

Microorganisms.

E. coli ATCC 25922 (American Type Culture Collection, Manassas, VA) was used in the study. The bacteria were stored at −70°C in Protect (Key Scientific Products, Round Rock, TX) storage vials. Fresh isolates were subcultured twice on 5% blood agar plates (Hardy Diagnostics, Santa Maria, CA) for 24 h at 35°C prior to each experiment.

Susceptibility studies.

MICs/minimum bactericidal concentrations (MBCs) were determined in Ca-MHB using a modified broth macrodilution method as described by the CLSI (5). The final concentration of bacteria in each broth macrodilution tube was approximately 5 × 10⁵ CFU/ml of Ca-MHB. Serial 2-fold dilutions of drugs were used. The MIC was defined as the lowest concentration of drug that resulted in no visible growth after 24 h of incubation at 35°C in ambient air. Samples (50 μl) from clear tubes and the cloudy tube with the highest drug concentration were plated on Mueller-Hinton agar (MHA) plates (Hardy Diagnostics, Santa Maria, CA). The MBC was defined as the lowest concentration of drug that resulted in ≥99.9% killing of the initial inoculum. Drug carryover effect was assessed by visual inspection of the distribution of colonies on medium plates. The studies were conducted in duplicate and repeated at least once on a separate day.

Time-kill studies.

Time-kill studies were performed using different inocula ranging from approximately 1 × 10⁵ to 1 × 10⁸ CFU/ml at baseline. A clinically achievable unbound concentration range of piperacillin (0 to 512 mg/liter)/tazobactam (4 mg/liter in all investigations to minimize effect of any constitutive beta-lactamase, if present) was used, and the drug concentrations were normalized to multiples of MIC. Serial samples (baseline and 2, 4, 8, 12, and 24 h) were obtained in duplicate over 24 h; viable bacterial burden was determined by quantitative culture. Prior to culturing the bacteria quantitatively, the bacterial samples were centrifuged at 10,000 × g for 15 min and reconstituted with sterile normal saline in order to minimize drug carryover effect. Total bacterial populations were quantified by spiral plating (Spiral Biotech, Bethesda, MD) 10× serial dilutions of the samples (50 μl) onto MHA plates. The medium plates were incubated at 35°C for up to 24 h, and then bacterial density from each sample was enumerated visually. The theoretical reliable lower limit of detection was 400 CFU/ml.

The stability of piperacillin in Ca-MHB was briefly investigated. Three different drug concentrations representing the low, medium, and high concentrations (corresponding to 0.25× MIC, 4× MIC, and 64× MIC used in the time-kill experiments) were chosen. Serial samples (baseline and 2, 4, 8, 12, and 24 h) were obtained in duplicate, and (residual) piperacillin concentrations were determined by a validated liquid chromatography-tandem mass spectroscopy methodology.

Mathematical modeling.

Based on our previous work (15), all time-kill profiles of E. coli over 24 h were modeled collectively. During our investigation, several related mathematical model structures were evaluated. The modified structure of the final growth dynamics model is shown in Fig. 1. Briefly, the rate of change of bacteria over time was expressed as the difference between the intrinsic bacterial growth rate and the (sigmoidal) kill rate provided by the antimicrobial agent. Decline in kill rate over time and regrowth were attributed to adaptation, which was modeled as reduction in the kill function, using a saturable function of antimicrobial agent selective pressure (both piperacillin effective concentration [C_eff] and time [t]). In addition, to account for the inoculum effect, an effective drug concentration was used in all killing and adaptation terms, which was explicitly modeled as a sigmoidal function of the initial inoculum. The effective drug concentration can be conceptualized as the result of a biofilm barrier put up by a dense bacterial population (i.e., the greater the bacterial population, the greater the drug barrier and thus the less effective the drug concentration). The modeling estimation process involved 2 steps. The intrinsic bacterial growth rate (K_g) and maximal bacterial population size (N_max [to account for contact inhibition]) were first determined from placebo (control) experiments. Using these parameter estimates, the parameter values in the killing function were subsequently determined using data from all active treatment experiments simultaneously. The performances of different model candidates were assessed by visual fit to the data and discriminated using the Akaike information criterion. The rule of parsimony was used. All modeling was performed with MATLAB version 7.5 (The MathWorks, Inc., Natick, MA).

FIG. 1.

Bacterial growth dynamics model and various model parameters.

Sensitivity analysis.

After the model fitting, selected parameters were evaluated for sensitivity with respect to their best-fit estimates. This was done by plotting the 95% joint confidence intervals for a selected group of parameters. The joint confidence plots were produced using the Fischer test. If (1 − α) is the confidence level and S(θ) is the residual sum of squares at the point estimate θ̂, the (1 − α) confidence region for P parameters in the vector θ is the region where θ satisfies the inequality:

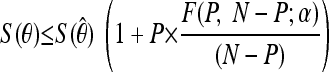Experimental validation.

The association of a bacterial population size with biomass was assessed semiquantitatively using a modified colorimetric assay as described previously (7). Briefly, a late-log-phase growth culture of E. coli was diluted and inoculated into 1/4-strength Ca-MHB (final density of 1 × 10⁵ or 1 × 10⁸ CFU/ml). The bacteria were incubated in an in vitro assay device (Calgary Biofilm device; MBEC, Calgary, AB, Canada) at 37°C on a platform shaker for 24 h. Three pegs were randomly removed from the lid of the assay device. Medium and nonadherent planktonic bacteria were removed by being vortexed briefly in saline, after which they were transferred and fully immersed in 0.1% crystal violet for 15 min. After the excessive dye solution was removed, the attached dye was eluted using 95% ethanol, and the absorbance at 580 nm was determined using a spectrophotometer. Uninoculated growth medium was used as a negative control. Pseudomonas aeruginosa ATCC 700888 (a known biofilm hyperproducer) was used as a positive control.

RESULTS

Susceptibility studies.

The MIC and MBC of the E. coli isolate to piperacillin were found to be 2 and 2 mg/liter, respectively. The susceptibilities to piperacillin did not change in the presence of tazobactam.

Time-kill studies.

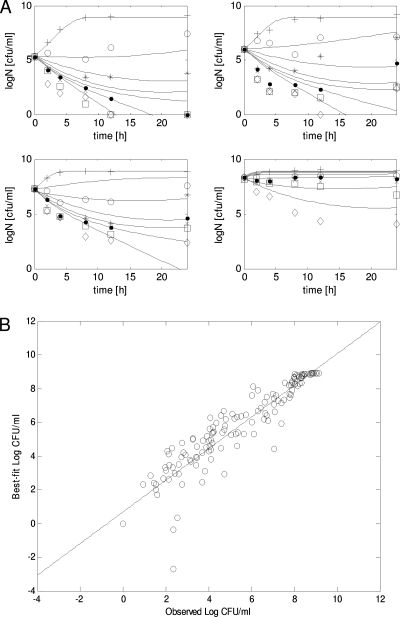
Data from the time-kill studies are as shown in Fig. 2. As anticipated from other previous investigations (1, 3, 6, 9, 12, 20), the killing of piperacillin was considerably reduced as the baseline inoculum increased from 1 × 10⁵ to 1 × 10⁸ CFU/ml. Significant reduction in bacterial burden (>2-log drop at 24 h) was observed with 4× MIC when the baseline inoculum was 1 × 10⁵ CFU/ml (Fig. 2A), compared to 256× MIC when the baseline inoculum was 1 × 10⁸ CFU/ml (Fig. 2A). The average degradation of piperacillin was not significant (<30% in 24 h) relative to the concentration range examined (>1,000-fold).

FIG. 2.

Model fits to the experimental data. (A) Overlay of experimental data with the best-fit model. (B) Correlation between observed and best-fit bacterial burdens. Symbols represent experimental data: +, placebo; ○, 0.25× MIC; *, 1× MIC; •, 4× MIC; ×, 16× MIC; □, 64× MIC; ⋄, 256× MIC. Solid lines depict the best-fit model. R² = 0.88. The best-fit regression line is given as follows: best fit = 0.94 × observed + 0.68.

Mathematical modeling.

The best-fit model fits to the data are as shown in Fig. 2. The estimates of the best-fit model parameters are as shown in Table 1. Taken as a whole, the observations in bacterial burdens over time were reasonably described by the model. Several alternative model candidates were explored (data not shown). Generally, the fits of these alternative models to the experimental data were less satisfactory when (i) the adaptation function was condensed to a single parameter (as expected) and (ii) the actual (instead of effective) drug concentration was used in the killing/adaptation functions. In addition, we attempted to incorporate drug degradation in the model as (i) a zero-order decay with a degradation constant of 0.01 h⁻¹ and (ii) a first-order decay with a degradation rate constant of 0.015 h⁻¹. The final best-fit parameter estimates were not found to be significantly different from the original estimates when drug degradation was not considered (data not shown).

TABLE 1.

Final estimates of the best-fit model parameters^a

Parameter	Point estimate	95% confidence limit
		Upper	Lower
Kg (h−1)	1.3078	1.17	1.47
Nmax (108 CFU/ml)	8.3357	6.886	10.715
Kk (h−1)	2.79	2.5	3.05
C50k (mg/liter)	0.51	0.22	0.68
C50b (mg/liter)	40.31	—
H	0.5	0.3	0.62
C50a (mg/liter)	962.19	367.2	2615
Ha	0.592	0.542	0.662
Log N50 (CFU/ml)	6.55	—
Q	0.8	—

^aK_g, growth rate constant for bacterial population; N_max, maximum population size; K_k, maximal kill rate constant for bacterial population; C_50k, concentration to achieve 50% maximal kill rate of the initial population; C_50b, concentration to achieve 50% maximal kill rate of the most resistant population; H, sigmoidicity constant for bacterial population; C_50a, concentration to achieve 50% maximal adaptation rate; Ha, sigmoidicity constant for bacterial adaptation; N₅₀, bacterial population in which 50% drug concentration is in effect; Q, sigmoidicity constant for effective drug concentration; —, unable to determine. The nonlinear confidence region plotting method was found to be inadequate. The sum of squares flattened off in the case of these parameters.

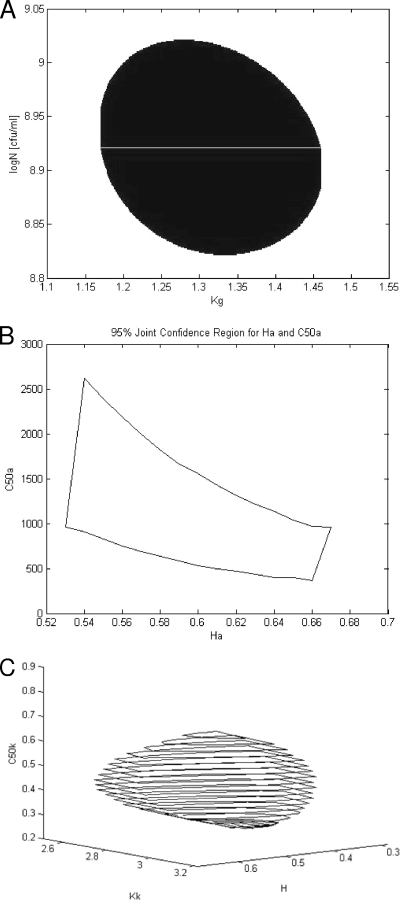
Sensitivity analysis.

The 95% confidence intervals are shown in Table 1, and the corresponding confidence regions for selected parameter groups are shown in Fig. 3. The lower and upper confidence limits have been deduced from confidence regions. This was done by examining the plot and finding the maximum variation in each parameter within the plot.

FIG. 3.

Ninety-five percent joint confidence region for K_g and logN_max (A); C_50a and H_a (B); and K_k, C_50k, and H (C).

Experimental validation.

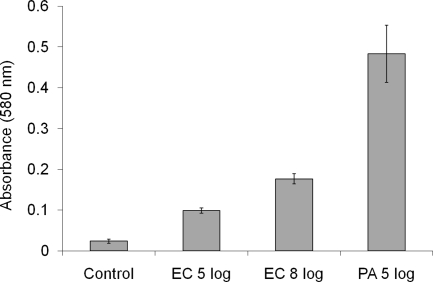
The results of the colorimetric assay are shown in Fig. 4. There was a significant difference in biomass formation as the initial bacterial density was increased from 1 × 10⁵ CFU/ml to 1 × 10⁸ CFU/ml (P = 0.002, Student's t test).

FIG. 4.

Comparison of absorbance values in biofilm assay. Each condition was examined in triplicate. Control, bacterium-free medium (negative control); EC, E. coli ATCC 25922; PA, P. aeruginosa ATCC 700888 (a known biofilm hyperproducer; positive control).

DISCUSSION

Inoculum effect has been the subject of study for several recent investigations. Different researchers have attempted to characterize the phenomenon in various ways. Udekwu et al. conducted experiments with a wide variety of antimicrobial agents against a wild-type Staphylococcus aureus strain and witnessed a consistent reduction in antibiotic efficacy at high cell densities (23). Using a series of escalating inocula (ranging from 2 × 10⁴ CFU/ml to 9 × 10⁷ CFU/ml), the investigators reported that the effect on MIC was not linear and the inoculum effect was not noticed until the starting inoculum was on the order of 10⁷. One logical concept was the reduction in the effective concentration of the drug available to the bacteria. Consequently, mechanisms such as decrease in drug molecules per bacterium or denaturing drug at high bacterial densities were proposed to explain the reduced efficacy observed. However, the bacterial burdens were assessed only at specific time points (e.g., 3 and 18 h) and the mathematical models were not fitted to actual experimental data over time to substantiate these theoretical concepts.

These experimental observations reported previously were similar to our experience. The functional forms of the relationship between the bacterial density and efficacy of an antimicrobial agent were also consistent in the two studies, as reflected by the model parameter estimate of log N₅₀ (6.55) in this study. Our work further extended their conceptual framework and expressed the specific density (inoculum) effect as the effective antimicrobial agent concentration available for bacterial killing. Specifically, the killing function was assumed to be inversely dependent on initial bacterial burden in a nonlinear fashion (i.e., bacterial killing was expected to increase with decreasing initial burden). In addition, we also included a model fit to serial bacterial burden data over time.

On the other hand, Bulitta et al. explained the inoculum effect with the help of mechanistically based models (2). The proposed modeling approach was shown to be useful in predicting the growth of resistant P. aeruginosa in external data sets, which could facilitate effective design of dosing regimens. However, the proposed model was of moderate to high complexity: a total of 17 parameters were involved, and some parts of the model had several interconnected steps. Furthermore, no experimental evidence was put forth to support some of the underlying mechanistic modeling assumptions. In contrast, our model structure was much less complex, and the functional relationship between initial inoculum and effective drug concentration proposed in our model was more straightforward. As a result, the estimability of the model and the confidence interval of the parameter estimates would likely be improved. Also, some experimental evidence was provided to support the key conceptual framework.

There are several limitations with this study. Modeling was performed in only one drug-pathogen combination in this study. We have previously performed similar time-kill studies with several beta-lactams against a variety of E. coli isolates expressing different beta-lactamases (18), and the drug-pathogen combination reported in this study was the most dramatic in illustrating the inoculum effect. As a result, we expect that the same mathematical model would be relevant to other drug-pathogen combinations as well.

From the mechanistic perspective, the inoculum effect was attributed solely to the reduced effective drug exposure. In addition to previous research (8), we provided some experimental data to substantiate the validity of our postulation. However, we recognized that this might still be an oversimplification of the complex interaction between an antimicrobial agent and a bacterial population. Individual bacterial cells in a dense population could be in a different physiological state (e.g., slower growth or metabolism or in an inactive state), in addition to being encased in a biofilm barrier. Despite that, in search of a useful mathematical model to predict bacterial response to an antimicrobial exposure, it is not always necessary to capture all the physiological processes comprehensively in the model. The role of quorum sensing was not investigated. From the modeling perspective, the inoculum effect was attributed to the baseline inoculum only. In reality, the effective drug concentration may be dependent on an additional variable(s) other than the baseline inoculum. For example, it might also be a function of evolving bacterial burden. Although we are not describing effective concentration as a function of instantaneous population in this study, the modeling framework is one step toward this direction. Investigations are in progress to explore if effective drug concentration should be expressed as a function of instantaneous bacterial burden.

In conclusion, using limited data from time-kill studies over 24 h, our modified mathematical model was reasonable in capturing microbial response to piperacillin with various baseline inocula. Our approach appears promising and may be used to improve prediction of bacterial response to various drug exposures in future investigations.