Biological Approach to Modeling of Staphylococcus aureus High-Hydrostatic-Pressure Inactivation Kinetics

Abstract

Graphs for survival under high hydrostatic pressure (450 MPa; 25°C; citrate-phosphate buffer, pH 7.0) of stationary-growth-phase cells of eight Staphylococcus aureus strains were found to be nonlinear. The strains could be classified into two groups on the basis of the shoulder length. Some of them showed long shoulders of up to 20 min at 450 MPa, while others had shoulders of <3.5 min. All strains showed tails. No significant differences in the inactivation rate were found during the log-linear death phase among the eight strains. The entry into stationary growth phase resulted both in an increase in shoulder length and in a decrease in the inactivation rate. However, whereas shoulder length proved to depend on sigma B factor activity, the inactivation rate did not. Recovery in anaerobiosis decreased the inactivation rate but did not affect the shoulder length. Addition of the minimum noninhibitory concentration of sodium chloride to the recovery medium resulted in a decrease in shoulder length and in an increase in the inactivation rate for stationary-growth-phase cells. In the tail region, up to 90% of the population remained sensitive to sodium chloride.

The development of nonthermal methods for food preservation has been a matter of extensive study in the last 25 years. High hydrostatic pressure (HHP) is one of these proposed alternative processes that are being used commercially for the nonthermal pasteurization of different food products (17, 22). This technology consists of the application of pressures in the range of from 100 to 1,000 MPa in order to inactivate pathogenic and spoilage microorganisms without affecting the quality of foods (40).

A prerequisite for the definitive implementation of a new technology is reasonably detailed knowledge of its inactivation kinetics, which will allow calculation and adjustment of the intensity of the treatments (process criterion) and a certain number of log₁₀ cycles of bacterial inactivation to be secured (performance criterion). In addition, to define the performance criteria, it is also necessary to determine the microbial species that represents the main risk in a particular food because of its frequent appearance, its concentration, its low infectious dose, and/or its high level of resistance.

The data accumulated over the last 25 years indicate that microbial inactivation by HHP typically does not follow exponential kinetics. Most of the published survival graphs show pronounced tails (14, 23, 28, 35, 41) and sometimes also shoulders (21, 25). Occasionally, both phenomena occur simultaneously, giving rise to graphs with sigmoid profiles (11, 20, 43). The occurrence of shoulders and tails complicates the comparison of the resistance of different bacteria and also makes it difficult to determine process criteria reliably. In order to solve both problems, diverse mathematical models, initially developed for other aims, have been applied to fit experimental survival data. The most widely used are the models based on the Weibull distribution, the log-logistic model, the model of Gompertz, and the model of Baranyi (10, 13, 39, 43, 51). Unfortunately, none of them has a solid biological basis, and thus, although they are useful for curve fitting, they have a limited utility for predictive purposes. Furthermore, although most authors indicate that providing the models with a biological basis is desirable, attempts to coordinate the recent knowledge on damage and inactivation mechanisms with the existing models are scarce.

Many aspects, including the HHP inactivation mechanism(s), as well as cellular damage and its recovery, should be studied by a multidisciplinary approach in order to develop models more adequate than those that are currently being used. For this purpose it will also be necessary to determine if the different phases of the survival curves (shoulder, log-linear phase of inactivation, and tail) reflect the occurrence of different events and if these events are interrelated or not. Also important is the question of whether the appearance of shoulders and tails is a characteristic of the species, the strain, the physiological state of the cells, or the treatment conditions. Finally, it would be of interest to study bacterial damage during the shoulder and tail phases, to investigate the relationship between the evolution of the damage and the rate of inactivation. Within this context, this investigation tries to provide data to help answer some of these questions.

The safety of a preservation process depends on the reliability to deliver an adequate kill of the key problematic microorganisms (18). Staphylococcus aureus is considered one of the most HHP-resistant nonsporulated food-borne pathogens (4, 36, 44, 47, 49), and it could represent a significant problem for the practical application of pressure technology in food preservation (30). The importance of S. aureus is due not only to its ability to produce enterotoxins responsible for gastroenteric disease with symptoms including nausea, vomiting, abdominal cramps, and diarrhea but also to its frequent occurrence in food products and the existence of asymptomatic human carriers (6).

In a previous study, we have observed that S. aureus sometimes shows HHP survival graphs with a sigmoid profile (11). Thus, the aim of this work was to study in detail the HHP inactivation kinetics of eight strains of S. aureus by analyzing separately the different phases of inactivation: shoulders, log-linear phases of inactivation, and tails. We also explored the causes of deviations of the first-order kinetics, with special emphasis in the appearance of sublethal damage.

MATERIALS AND METHODS

Bacterial culture and media.

The bacterial strains used in this study are included in Table 1. Bacteria were grown by inoculating tubes of tryptone soy broth supplemented with 0.6% yeast extract (TSB-YE; Oxoid, Cambridge, United Kingdom) with a loopful of growth from tryptone soy agar supplemented with 0.6% yeast extract (TSA-YE, Oxoid). Cultures in stationary growth phase were obtained after incubation at 37°C for 24 to 30 h in a shaking incubator (150 rpm). For exponential phase, cultures were incubated under the same conditions until their optical density at 600 nm reached a value of 0.8 (approximately 2.5 to 3 h).

TABLE 1.

Bacterial strains used in this study

S. aureus strain	Origin	Characteristic	Reference
CECT 976	Food	Produces enterotoxin A
CECT 4459	Not specified	Produces enterotoxin B
CECT 4465	Clinical	Produces enterotoxin C
CECT 4466	Food	Produces enterotoxin D
CECT 4630	Clinical	Natural mutation in rsbU gene	Giachino et al. (16)
CECT 435	Clinical	Test, control, and bioassay strain
Newman	Clinical	High level of clumping factor
IK184	Laboratory	S. aureus Newman ΔrsbUVW-sigB	Kullik et al. (24)

Resistance determinations.

Before HHP treatments, cell suspensions were centrifuged (for 5 min at 6,000 × g) and resuspended in the same volume of McIlvaine citrate-phosphate buffer (pH 7.0). Subsequently, 1-ml samples were sealed in a polyethylene bag, after exclusion of air bubbles, and pressurized at pressures of between 350 and 600 MPa for different holding times (up to 60 min) in an eight-vessel (each with a volume of 8 ml) system driven by an automatic pump and held at 25°C with an external water circuit (HPIU-10000, 95/1994; Resato, Roden, Netherlands). A glycol-oil mixture (TR-15; Resato) was used as pressure transmission fluid. The compression rate was approximately 100 MPa/min, while decompression was immediate. Due to adiabatic heating during pressure buildup, the temperature in the chamber inevitably increased but never exceeded 35°C; hence, heat shock effects could be excluded. Resistance determinations were performed at least in triplicate with independent cultures and in separate pressurization runs.

Incubation of treated samples.

After exposure to HHP, appropriate serial dilutions were prepared, plated on TSA-YE, and incubated aerobically at 37°C for 24 h. The extent of sublethal damage was estimated by differential plating on TSA-YE and TSA-YE supplemented with the maximum noninhibitory concentration of sodium chloride (TSA-YE-NaCl) previously determined for each strain. This concentration ranged from 10% for S. aureus Newman ΔsigB to 13% for S. aureus CECT 4459. In those experiments in which an anaerobic recovery was performed, the TSA-YE plates, supplemented with 0.1 M sodium pyruvate (12), were incubated in a sealed anaerobic jar with a sachet of the AnaeroGen system (Oxoid). Sodium pyruvate was added as a reactive oxygen species (ROS) quencher (26).

Resistance parameters.

Survival curves for HHP treatments were obtained by plotting the logarithm of the fraction of survivors versus the treatment time. Inactivation curves were fitted by a special case of the model of Baranyi and Roberts (8), considering an inactivation curve to be a mirror image of a growth curve, as described by Baranyi et al. (7). The Office Excel 2002 program (Microsoft Co., Redmond, WA) with the special package DMFit (http://www.ifr.ac.uk/safety/DMFit; IFR, Norwich, United Kingdom) was used to fit the data. The same software was used to calculate determination coefficients (r² values) and standard deviations. Statistical analyses (analysis of variance, t test, and one-sample t test) (P = 0.05) were performed with an appropriate statistical package (Prism; GraphPad Software, Inc., San Diego, CA).

RESULTS

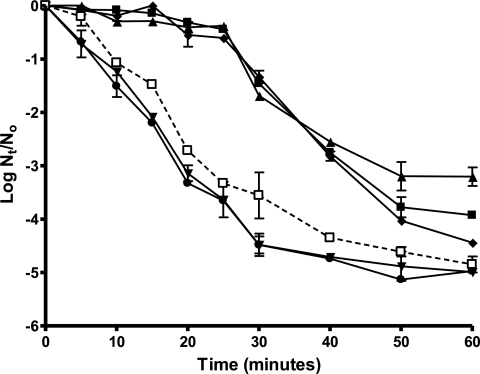
The survival curves for S. aureus showed deviations from linearity in all cases. As an example, Fig. 1 shows the survival curves under HHP (450 MPa) for 6 S. aureus strains under the standard conditions (stationary growth phase, recovery in nonselective medium, aerobiosis). These deviations varied with the strain, the physiological state of the cells, and the recovery conditions. The description and quantification of these deviations required the application of nonlinear inactivation models. For this investigation it was decided to use for survival curve fitting a special case of the Baranyi model (7).

FIG. 1.

Survival curves for HHP (450 MPa) of stationary-phase cells of S. aureus CECT 976 (▴), CECT 4459 (▪), CECT 4465 (•), CECT 4466 (⧫), CECT 435 (▾), and CECT 4630 (□). The initial temperature was 25°C, the treatment medium was citrate-phosphate buffer, pH 7.0, the initial cell concentration was 2 × 10⁸ to 6 × 10⁸ cells/ml, the recovery medium was TSA-YE, and the recovery atmosphere condition was aerobiosis. N_t/N₀, number of surviving cells/total number of cells at time zero.

Table 2 shows the averages of the parameters calculated after fitting of the model to all the survival curves under HHP (450 MPa) obtained in this investigation. Table 2 includes the coefficients of correlation of the fitting, the maximum specific inactivation rate (μ), the time before exponential inactivation begins (lag), and the level of inactivation reached before tailing (Y_f/Y₀; Y_f and Y₀ are the log₁₀ of the minimum cell concentration remaining in the tailing phase and the log₁₀ of the initial cell concentration, respectively). The standard deviations of these parameters have also been included. Table 2 includes the resistance data for eight strains of S. aureus, including strain Newman and its isogenic sigB deletion mutant (S. aureus IK184). Resistance in stationary and exponential growth phase was studied in McIlvaine buffer of pH 7.0, and the recovery of the survivors was carried out in nonselective medium (TSA-YE). In order to explore the mechanisms responsible for the deviations of the linearity, the evolution of the cellular damage in a resistant and a sensitive strain (CECT 4459 and CECT 4465, respectively) and in strain Newman and its isogenic ΔsigB mutant was also studied. For the quantification of damaged cells, survivor recovery was carried out in nonselective medium (TSA-YE) and selective medium (TSA-YE-NaCl) and under conditions of anaerobiosis. These data are also included in Table 2.

TABLE 2.

Resistance parameters corresponding to survival curves under HHP for the eight strains studied^a

Growth conditions and strain	μ (min−1)	S for μ (min−1)	lag (min)	S for lag (min)	Yf/Yo (log CFU)	S for Yf/Yo (log CFU)	r2
Stationary GP, nonselective RM, aerobic RA
CECT 976	0.117a	0.023	17.45A	3.583	−3.133α	0.333	0.97
CECT 4459	0.151a	0.013	21.89A	1.420	−3.833β	0.113	0.99
CECT 4465	0.158a	0.015	0.790B*	1.360	−4.905γ	0.032	0.99
CECT 4466	0.143a	0.008	21.12A	0.970	−4.355δ	0.134	0.98
CECT 435	0.158a	0.011	1.319B	0.525	−4.889γ	0.230	0.98
CECT 4630	0.144a	0.017	3.184B*	1.473	−4.677δ,γ	0.122	0.99
Newman	0.120a	0.013	21.36A	2.317	−3.482α,β	0.315	0.99
Newman ΔsigB	0.113a	0.026	5.975B,C*	3.529	−3.605α,β	0.039	0.97
Exponential GP, nonselective RM, aerobic RA
CECT 976	0.254b	0.034	2.771B*	1.274	—	—	0.97
CECT 4459	0.338b	0.058	4.526B,C*	1.899	—	—	0.97
CECT 4465	0.296b	0.017	<0.001B*	<0.001	—	—	0.98
CECT 4466	0.292b	0.057	3.241B,C*	2.819	—	—	0.99
CECT 435	0.288b	0.005	0.317B*	0.390	—	—	0.97
CECT 4630	0.246b	0.048	1.192B*	2.065	—	—	0.97
Newman	0.360b	0.050	4.513B,C*	3.924	—	—	0.95
Newman ΔsigB	0.335b	0.064	3.327B,C*	2.912	—	—	0.99
Stationary GP, selective RM, aerobic RA
CECT 4459	0.254b	0.091	6.757C	1.064	−4.503δ	0.072	0.99
CECT 4465	0.462c	0.016	<0.001B*	<0.001	−5.487ɛ	0.130	0.98
Newman	0.252b	0.091	6.735C	1.057	−4.517δ	0.053	0.99
Newman ΔsigB	0.316b	0.056	0.603B*	0.889	−4.445δ	0.120	0.98
Stationary GP, nonselective RM, anaerobic RA
CECT 4459	0.065d	0.013	19.14A	4.743	—	—	0.95
CECT 4465	0.073d	0.003	2.243B*	2.176	—	—	0.94
Newman	0.057d	0.021	17.48A	2.374	—	—	0.98
Newman ΔsigB	0.073d	0.001	9.630C	2.874	—	—	0.96

^aThe table also includes the standard deviations (S) of the values and the coefficients of determination of the fittings (r²). Conditions were as follows: treatment pressure, 450 MPa; initial temperature, 25°C; treatment medium, citrate-phosphate buffer pH 7.0; initial cell concentrations, 2 × 10⁸ to 6 × 10⁸ cells/ml for stationary-growth-phase cells and 8 ×10⁷ cells/ml for exponential-growth-phase cells. GP, growth phase; RM, recovery medium; RA, recovery atmosphere. Values with the same superscripts did not show statistically significant differences (P > 0.05). *, the values were not significantly different (P < 0.05) from 0 (one-sample t test); —, parameter could not be calculated.

As can be deduced from the data in Table 2, the main differences in the survival curves of the different strains under standard conditions (stationary growth phase, nonselective medium, aerobiosis) were shoulder duration and, to a lesser extent, the number of cycles of inactivation before the appearance of tails. According to this and following criteria of statistical significance (P < 0.05), the studied strains could be classified into two groups. Strains CECT 976, CECT 4459, CECT 4466, and Newman displayed a clear shoulder with an average duration of 20 min. On the contrary, strains CECT 4465, CECT 435 CECT 4630, and Newman ΔsigB displayed shoulders of very small durations (most of them were not statistically different from 0). Surprisingly, the inactivation rate in the log-linear section of the survival curves did not differ significantly (P > 0.05) between the two groups.

The statistical analysis of the number of log₁₀ reductions reached before the appearance of tails shows that strains could not be divided into the two previously established groups; i.e., there was no significant relationship (P > 0.05) between the level of inactivation reached before the appearance of tails and the length of the shoulders. Nevertheless, it is noticeable that the strains with prolonged shoulders produced tails at higher count levels (always <4.5 logarithmic cycles of inactivation). It is also remarkable that under our standard experimental conditions (pH 7.0, nonselective recovery medium, 450 MPa) it was not possible to obtain more than 5 logarithmic cycles of inactivation of S. aureus with this technology.

Survival curves for exponential-growth-phase cells (Table 2) showed important differences compared to those for stationary-phase cells. Exponential inactivation rates (μ values) did not differ significantly among the strains (P > 0.05) but were between 2 and 3 times higher than those calculated for stationary-growth-phase cells. Shoulders almost completely disappeared and were not significantly different among strains (P > 0.05). Under our experimental conditions, it was not possible to establish the level at which tailing took place.

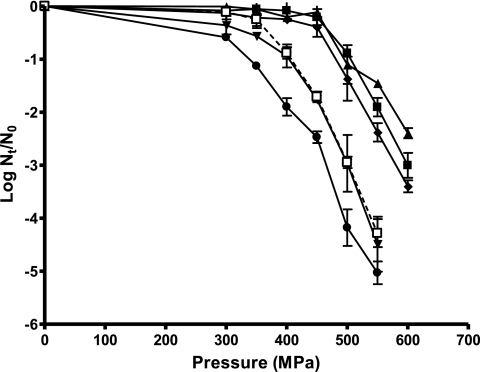
Figure 2 illustrates the relationship between the log₁₀ cycles of inactivation reached after 15 min of treatment at different pressures ranging from 300 to 600 MPa for six S. aureus strains in stationary phase. The values of the parameters (pressure dependence rate [μ_P] and threshold pressure [lag_P]) obtained after fitting of the curves in Fig. 2 with Baranyi's model are shown in Table 3. As can be observed in Table 3, a threshold pressure value below which no lethal effects were observed could be estimated. This phenomenon could be attributed to sublethal pressure levels and/or to the existence of shoulders longer than 15 min. Two clearly differentiated groups were observed: one included strains CECT 976, CECT 4459, CECT 4466, and Newman, for which inactivation began at pressures close to 500 MPa, and the second group included strains CECT 4465, CECT 435, CECT 4630, and Newman ΔsigB, for which inactivation began at pressures below 350 to 400 MPa. These groups were in agreement with those established earlier according to shoulder length (Table 2). This would indicate that the pressure threshold observed in Fig. 2 is probably related to the shoulder phenomenon. No statistically significant differences (P > 0.05) between the μ_P values were found, which indicated that the barodependence of the reactions that led to the inactivation was the same for all the strains.

FIG. 2.

Influence of pressure on HHP resistance (log cycles of inactivation achieved after 15 min) of stationary-phase cells of S. aureus CECT 976 (▴), CECT 4459 (▪), CECT 4465 (•), CECT 4466 (⧫), CECT 435 (▾), and CECT 4630 (□). The initial temperature was 25°C, the treatment medium was citrate-phosphate buffer, pH 7.0, the initial cell concentration was 2 × 10⁸ to 6 × 10⁸ cells/ml, the recovery medium was TSA-YE, and the recovery atmosphere condition was aerobiosis. N_t/N₀, number of surviving cells/total number of cells at time zero.

TABLE 3.

Resistance parameters corresponding to curves representing the fraction of survivors after HHP treatments at pressures between 300 and 600 MPa for the eight strains in stationary growth phase^a

Strain	μP (MPa−1)	S for μP (MPa−1)	lagP (MPa)	S for lagP (MPa)	r2
CECT 976	0.024a	0.002	499.8A	15.44	0.98
CECT 4459	0.031a	0.004	509.8A	10.24	0.99
CECT 4465	0.023a	0.003	332.7B	14.90	0.96
CECT 4466	0.026a	0.004	471.1A	27.49	0.97
CECT 435	0.030a	0.007	408.6C	12.63	0.98
CECT 4630	0.028a	0.002	396.2C	9.395	0.99
Newman	0.028a	0.003	498.5A	32.52	0.99
Newman ΔsigB	0.023a	0.003	399.6C	34.12	0.98

^aThe table also includes the standard deviations (S) of the values and the coefficients of determination of the fittings (r²). Y_f /Y₀ and its standard deviation could not be calculated. Conditions were as follows: treatment duration, 15 min; initial temperature, 25°C; treatment medium, citrate-phosphate buffer, pH 7.0; initial cell concentration, 2 × 10⁸ to 6 × 10⁸ cells/ml. Values with the same superscripts did not show statistically significant differences (P > 0.05).

Inactivation by high pressures is not regarded as an all-or-nothing event (27). Before death, cells incur damage in several structures that can be repaired if the conditions of recovery are adequate (27, 33). In order to determine the number of cells with damaged membrane function, the counts obtained in selective medium (with NaCl added) and nonselective medium were compared. For this purpose we used strain CECT 4459, which showed the longest shoulder; strain CECT 4465, which was included in the HHP-sensitive group and showed the tail at the lowest level; and strains Newman and its ΔsigB mutant.

In the recovery medium with NaCl added, the survival curves for S. aureus CECT 4459 and S. aureus Newman showed a drastic reduction of the duration of the shoulders, and those for CECT 4465 and Newman ΔsigB did not show shoulders (Table 2). μ values were between 2.1 and 2.9 times higher than those obtained in nonselective medium, and the increase was slightly higher for strains CECT 4465 and Newman ΔsigB (approximately 2.85 times) than for strains CECT 4459 and Newman (approximately 2.15 times). The number of log₁₀ reductions before the appearance of the tails varied between 4.5 and 5.5 and was between 0.6 and 1.0 log cycles higher than the number in nonselective medium for each strain. Thus, the results obtained demonstrate that baroresistant strains (CECT 4459 and Newman) were also more HHP resistant than barosensitive ones (CECT 4465 and Newman ΔsigB) when they were recovered in medium with added NaCl.

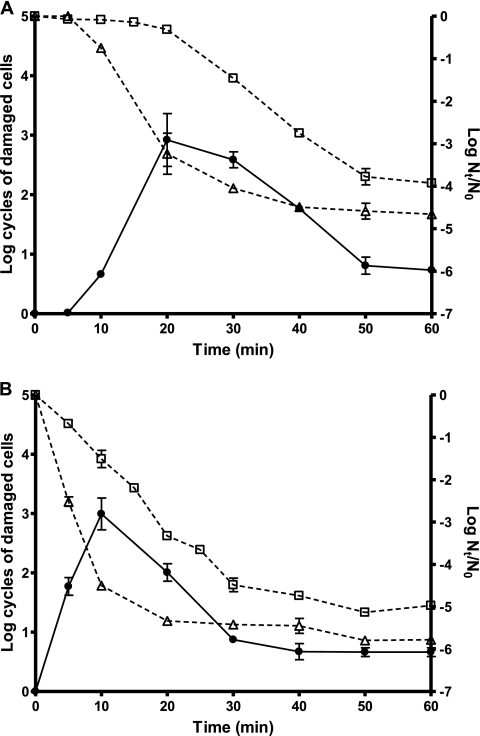
Figure 3 shows the evolution of the percentage of damaged cells of strains CECT 4459 and CECT 4465 throughout a 450-MPa treatment. As shown in Fig. 3A, during the first 5 min of treatment no sublethally damaged or inactivated cells were detected in strain CECT 4459. Then, the percentage of damaged cells increased almost exponentially until it reached 99.9% of the surviving population, after 20 min of treatment. From 30 to 50 min of treatment, the number of nondamaged cells (counts in TSA-YE-NaCl) decreased very slowly, whereas the counts in TSA-YE dropped exponentially, resulting in an overall decrease in the percentage of damaged cells. Between 50 and 60 min of treatment, the percentage of damaged cells remained constant (approximately 90% of the surviving population) and no additional inactivation took place. It is remarkable that approximately 1 out of 10⁵ cells of the initial population remained able to outgrow in the presence of sodium chloride after 60 min of treatment at 450 MPa. Barosensitive strain CECT 4465 shows a behavior similar to that described for the barotolerant strain; however, in this case the counts on both the nonselective medium and the selective medium began to decrease earlier. After 10 min of treatment, 95% of the initial population had been inactivated and the proportion of damaged cells had reached 99.9% of the survivors. Beyond this time the percentage of damaged cells dropped until it became stabilized at about 90% of the surviving population. As for the other strain, after 30 min of treatment the inactivation rate fell abruptly and the percentage of damaged cells remained constant. One out of 10⁶ cells of the initial population of strain CECT 4465 was insensitive to the presence of sodium chloride in the recovery medium after 1 h of treatment at 450 MPa (Fig. 3B).

FIG. 3.

Evolution of the number of sublethally damaged cells (closed circles, continuous lines) during an HHP treatment (450 MPa, 60 min) of stationary-phase cultures of S. aureus CECT 4459 (A) and CECT 4465 (B). Also included are the survival curves (open symbols, discontinuous lines) when HHP-treated cultures were plated on nonselective medium (□) and selective medium (▵). The initial temperature was 25°C, the treatment medium was citrate-phosphate buffer, pH 7.0, the initial cell concentration was 2 × 10⁸ to 6 × 10⁸ cells/ml, the recovery medium was TSA-YE (nonselective medium) or TSA-YE-NaCl (selective medium), and the recovery atmosphere condition was aerobiosis.

Besides membrane damage, cellular damage leading to sensitivity to oxidative stress has also been reported after HHP treatment (1). In order to determine the occurrence of cells sensitized to aerobic recovery conditions, samples were recovered under aerobic and anaerobic conditions, as described in the Materials and Methods. The results obtained demonstrate that incubation under anaerobic conditions barely affected the length of the shoulder for strain CECT 4459, but it decreased its μ value (P < 0.05) (Table 2). For barosensitive strain CECT 4465, recovery under conditions of anaerobiosis notably decreased the μ value but did not induce the appearance of a shoulder. Similar results were obtained when the findings for strain Newman and its isogenic ΔsigB mutant were compared, although the survival curves for the sigB-knockout mutant displayed a small shoulder under both aerobic and anaerobic recovery conditions (Table 2).

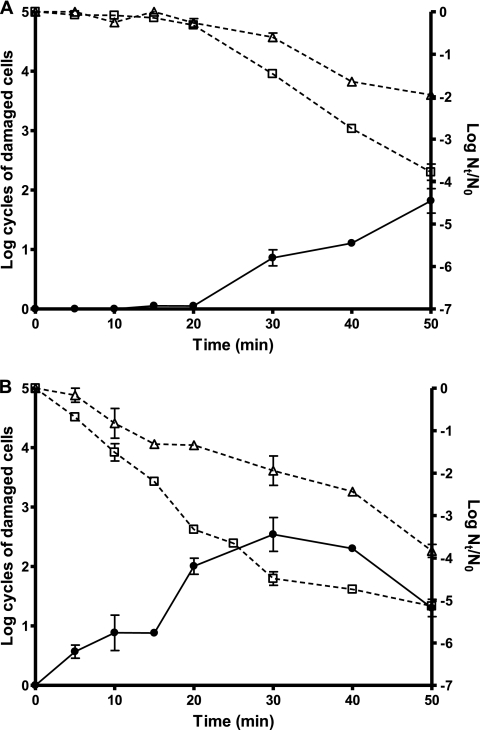
Figure 4 shows the evolution of the percentage of cells of strains CECT 4459 (Fig. 4A) and CECT 4465 (Fig. 4B) sensitized to oxygen throughout a 450-MPa treatment. As can be observed in Fig. 4A for strain CECT 4459 cells, as the inactivation began after 20 min of treatment, cells were sensitized to the presence of oxygen in the recovery environment at a percentage that increased with treatment time, reaching 99% of the surviving cells after 50 min. For strain CECT 4465, a similar behavior was observed and the inactivation proceeded in parallel to the occurrence of oxygen sensitivity (Fig. 4B). Similarly, for S. aureus Newman and S. aureus Newman ΔsigB, oxygen-sensitive cells were detected in the log-linear inactivation phase (Table 2).

FIG. 4.

Evolution of the number of cells sensitized to aerobic recovery conditions (closed circles, continuous lines) during an HHP treatment (450 MPa, 50 min) of stationary-phase cultures of S. aureus CECT 4459 (A) and CECT 4465 (B). Also included are the survival curves (open symbols, discontinuous lines) when HHP-treated cultures were recovered under aerobic (□) and anaerobic (▵) conditions. The initial temperature was 25°C, the treatment medium was citrate-phosphate buffer, pH 7.0, the initial cell concentration was 2 × 10⁸ to 6 × 10⁸ cells/ml, the recovery medium was TSA-YE (aerobiosis) or TSA-YE-sodium pyruvate (anaerobiosis), and the recovery atmosphere condition was aerobiosis or anaerobiosis.

DISCUSSION

The sensitivity of S. aureus to HHP under different experimental conditions reported by different authors varies widely (4, 5, 32, 36, 46, 47, 49, 51). Our results would fall within the range of most published data: a treatment at 450 MPa for 15 min led to 0.10 and 2.45 log₁₀ cycles of inactivation for strains CECT 976 and CECT 4465, respectively (Fig. 2); however, it should be remarked that this comparison can be misleading because inactivation did not follow first-order kinetics.

In this investigation, concave upward as well as sigmoid survival curves have been observed. Deviations in survival curves under HHP are quite commonly reported in the literature, but the appearance of shoulders is rare (11, 21, 25); however, to the best of our knowledge, neither the different phases of the inactivation curve nor the events taking place in each phase have been studied separately. For this purpose, data should be fitted using an adequate model. The advantages of Baranyi's model have been discussed in detail by other investigators (43, 50). For our aims, the main advantage of Baranyi's model is that it allowed us to describe accurately and independently the shoulders, the log-linear course of inactivation, and the tails and, therefore, to separately correlate each phenomenon with the mechanisms of inactivation.

S. aureus strains could be divided into two groups according to their resistance to HHP in stationary phase. It is remarkable that the major differences between strains were due to the different durations of the shoulder. In previously published work, we reported a relationship between heat resistance and pigmentation of several strains of S. aureus (12, 42). According to the pigment content data previously reported and the HHP resistance data obtained here, we also found a relationship between a higher level of HHP resistance and a higher carotenoid content. The pigmentation of S. aureus cells is mainly due to the presence of the pigment staphyloxantin (37), whose concentration is dependent on the expression of the sigma B (σ^B) factor (16, 37). Sigma factors are the recognition units of the RNA polymerase, and the set of genes that is expressed in the cell depends on which sigma factor is bound to the core enzyme. General stress sigma factors include sigma S, also known as rpoS, in some Gram-negative bacteria and σ^B in some Gram-positive bacteria and are considered by many researchers to be functionally homologous (15). The Staphylococcus aureus σ^B factor controls at least 251 genes in this species (9), and its implication in S. aureus resistance to various stresses, including HHP, has been demonstrated (11). It has also been observed that σ^B is mainly expressed at the beginning of the stationary phase of growth. In order to explore the implication of this general stress factor in the appearance of shoulders, the survival curves for the eight strains in exponential phase of growth were also obtained. As can be observed in Table 2, shoulder duration drastically decreased when cultures were pressurized in exponential growth phase, suggesting that σ^B expression might be responsible for the increase in shoulder duration in S. aureus cultures after the entry into stationary growth phase. Given the importance of this observation, the same experiment was carried out with S. aureus strain Newman and its isogenic mutant without the sigB operon. From this experiment we can conclude that σ^B expression effectively leads to an increase in the duration of shoulder; i.e., cells expressing the σ^B factor show long shoulders (approximately 20 min; Table 2); however, there were also other mechanisms accountable for the appearance of small duration shoulders (up to approximately 6 min; Table 2).

The shoulder has been attributed to different phenomena directly related to the mechanism of inactivation, such as the need to damage multiple targets or to surpass a certain threshold of damage to a specific structure before cells become irreversibly and lethally damaged. Although HHP has been proven to affect many cellular structures, the relationship with inactivation has not been clearly established; however, most of the authors point out that the cell membrane is an important target in HHP bacterial inactivation since membrane-related damage, including loss of solutes, loss of osmotic responsiveness, and increased permeabilization to nonpermeant dyes, has been observed in pressurized cells (33, 45). It can be hypothesized that the shoulder might represent the time during which the membrane maintains its integrity and functionality. Thus, the differences in resistance to HHP between barosensitive and barotolerant strains would rely on the retention of a functional membrane, which, according to our results, would depend to a great extent on σ^B expression. This dependence might be explained because σ^B expression induces the synthesis of diverse components that take part in mechanical resistance and/or the functionality of cell envelopes (9, 24, 34, 37).

On the other hand, several authors have suggested that permeabilization of the cell membrane could be an indirect cause of the inactivation, without the need for a drastic decrease in its integrity (21, 29, 38), since it would facilitate the interchange of components between the cytoplasm and the treatment medium. Therefore, the shoulder could represent the time needed to attain a sufficient (lethal) level of component interchange. After treatment, some cells would have been permeabilized but remain viable and would appear as damaged cells. Thus, in the nonselective medium, these cells would restore the functionality of their membranes and would resume their normal physiology. On the contrary, in the selective medium damaged cells would not be able to repair the damage and would die. This would explain why shoulders became shorter in the selective medium. This mechanism could also explain the different HHP resistance of strains, since the implication of σ^B in the effectiveness of the cellular repair systems has been demonstrated (11, 34).

From our results it can be concluded that those injuries responsible for the sensitization to sodium chloride would not be directly responsible for microbial inactivation, since sensitization to the sodium chloride in the recovery medium took place in the shoulder phase, before microbial death began (Fig. 3A); however, under our experimental conditions, in every experiment in which an increase in the rate of sensitization to sodium chloride was observed (for instance, for strain CECT 4465 in comparison to that for strain CECT 4459) a reduction in the duration of shoulders was also detected. This suggests that both phenomena might somehow be related (Table 2).

Besides the damage and permeabilization of the cell membrane, oxidation sensitivity has also been detected in Escherichia coli after HHP treatments (1). The comparison of survival under aerobic and anaerobic conditions (Fig. 4A and B) demonstrated the existence of cells sensitized to the presence of oxygen in the recovery medium in both the baroresistant (Fig. 4A) and the barosensitive (Fig. 4B) strains of S. aureus. Our results also demonstrate that recovery under conditions of anaerobiosis resulted in a decreased apparent inactivation rate in the log-linear section of the survival curve but did not influence the appearance or duration of the shoulder.

A mechanism has been proposed by Aldsworth et al. (2), stating that, upon disturbing cellular homeostasis, inimical processes can result in the uncoupling of growth and the metabolic rate. As a consequence of this imbalance, a burst of ROS production occurs and is responsible for cell death. Aertsen et al. (1) observed that endogenous oxidative stress was indeed generated upon HHP treatment, that the amount of oxidative stress generated was related to bacterial HHP resistance, and that mutants affected in oxidative-stress management (katE, katF, oxyR, sodAB, and soxS mutations) were less HHP resistant than their parental strains. These results led them to hypothesize that, in line with the concept formulated by Aldsworth et al. (2) for other stressing agents, (i) HHP might affect cytoplasmic or membrane enzymes, thereby disturbing cellular metabolism and induce endogenous ROS, (ii) cytoplasmic proteins denatured by pressure or oxidized by HHP induce a heat shock response, and (iii) accumulation of oxidative damage leads to cell death. The hypothesis of Aertsen et al. (1) was based on data generated by the end-point method at different pressures. Our results provide through kinetic data another convincing indication that endogenous oxidative stress is a possible cause of bacterial death after HHP treatments. Also, our data show that membrane damage, measured through the acquisition of sensitivity to NaCl in the recovery medium, occurs prior to sensitization to aerobiosis. Whether membrane damage or a secondary cellular event depending on membrane integrity is the trigger that initiates an endogenous oxidative burst remains to be investigated.

According to the theory of Aertsen et al. (1), the time between the establishment of membrane damage and the onset of death could correspond either to the time required for the induction of damage capable of triggering the production of ROS or to the time required for the accumulation of sufficient oxidative damage to overwhelm the detoxification capability of cells. On the basis of this hypothesis, HHP-resistant strains would display longer shoulders because they would present a higher ability to withstand and/or repair those damages. Our results demonstrate that (i) pigmented strains display longer shoulders than nonpigmented strains, (ii) stationary-phase cells display longer shoulders than exponential-phase cells, and (iii) deletion of σ^B significantly decreases the shoulder length. In summary, all these effects indicate that shoulders are related to the expression of the σ^B factor. With regard to the possible role of σ^B in this increased ability to prevent, withstand, or repair oxidative damage, it should be noted that a number of products with detoxifying and/or antioxidant function, such as catalases and carotenoids, are known to be under σ^B control in S. aureus (24, 34, 37).

Most published data demonstrate that HHP survival curves always show a phase of quasiexponential inactivation. Similarly, all our survival curves show long log-linear sections. One of the main advantages of the Baranyi model is that it produces a practically straight line in the log-linear phase (50). Moreover, the first-order kinetics model can be derived from Baranyi's model. Comparison of μ values from stationary-growth-phase cultures of S. aureus Newman and its isogenic ΔsigB mutant allow us to state that, as opposed to the shoulder, the inactivation rate was independent of σ^B expression. Nevertheless, all the strains, including the ΔsigB mutant strain, showed μ values between 2 and 3 times higher in exponential phase than in stationary growth phase (Table 2). This would indicate that there are structural and compositional changes taking place along growth which are not related to σ^B expression and that modify HHP resistance, as observed previously (11). On the other hand, our results demonstrate that the apparent inactivation rate was lower when cells were recovered under conditions of anaerobiosis. Therefore, increasing the ability to withstand and/or repair oxidative damage leads to a decrease in the inactivation rate. Several authors have observed that stationary-phase cells are more resistant to oxidative chemicals after the entry into the stationary phase (19, 48), which is in agreement with our observations. Furthermore, Aldsworth et al. (3) suggested that the intrinsic suicide mechanism that they proposed could also explain in part the higher resistance to inimical processes of stationary-phase cells than exponential-phase cells by assuming that this oxidative burst is more prominent, and thus destructive, in actively respiring cells (2).

Appearance of tails in HHP survival curves is the most frequently observed deviation from linearity; however, the physiology and the characteristics of cells responsible for their appearance remain almost unknown. This is probably due to the difficulties inherent to working with fractions of the populations that usually represent less than 0.001% of the whole population. All strains used in this investigation showed tails when they were treated at 450 MPa in stationary growth phase, and the proportion of bacteria responsible for their appearance represented 1 of each 10³ to 10⁶ cells of the initial population; however, these values must be taken with caution since the inactivation level at which tails appear may change with the treatment pressure (23). This is an aspect that should also be studied in detail.

Tails can possibly be attributed to the existence of a continuous distribution of resistance within the population or to the existence of two differentiated subpopulations. As observed in Fig. 3B, during the first 30 min of treatment, more than 4.5 logarithmic cycles of the CECT 4465 population were inactivated, whereas in the following 30 min, the counts barely decreased 0.5 additional log cycle. With strain CECT 4459, no statistically significant differences (P > 0.05) were found between counts corresponding to those at 50 and 60 min of treatment (Fig. 3A). On the other hand, differences in the counts of the tails of strain Newman and its isogenic ΔsigB mutant were not detected, therefore indicating that neither the appearance of tails nor the level of inactivation achieved before tailing depended on σ^B activity.

Tails were even more marked when recovery was carried out in the medium supplemented with sodium chloride. Our results indicate that the percentage of cells sensitized to sodium chloride increased with time until a certain value and then decreased before finally reaching a constant value (Fig. 3A and B); however, it remains unclear if over this threshold value the severity of the damage inflicted to each cell increased with the treatment time because neither the number of alive (nondamaged) cells decreased nor the percentage of damaged cells increased with time. To the best of our knowledge, there are no data in the literature dealing with this aspect. As shown in Fig. 3B, whereas in the first 20 min of treatment 99.9999% of the cells died or were damaged, in the following 40 min the counts on selective medium did not change significantly. Furthermore the analysis of the tails in Fig. 3 showed that at between 50 and 60 min of treatment for strain CECT 4459 and 30 and 60 min of treatment for strain CECT 4465, 10% of the surviving population was insensitive to sodium chloride. Noma et al. (31) demonstrated that the addition of nonionic surfactants, such as 0.5 μl/ml polyoxyethylene p-t-octylphenyl ester (Triton X-100) and 0.53 mg/ml lauric sugar ester, significantly reduced the level of tailing. Triton X-100 has been widely used to solubilize the cytoplasmic membrane. This leads to the hypothesis that pressure treatment in the presence of the nonionic surfactant destabilizes the cytoplasmic membrane of the cells, therefore reducing the tailing effect. The results reported here are in agreement with the hypothesis that the tails are generated by cells with more robust cellular membranes, since in the tail region the number of viable cells remained almost constant and the percentage of damaged cells either remained constant or even decreased (Fig. 3A and B).

In summary and regarding the biological basis of the kinetics of inactivation observed for S. aureus strains, we can hypothesize that the increased resistance of pigmented cells might be due to an increased resilience of their membranes together with an increased ability either to withstand the production of ROS or to detoxify them. The higher barotolerance of their membranes would be responsible for their higher tail levels compared with those for nonpigmented cells and, at least partly, for the increased shoulder length. A remarkable finding is that for stationary-growth-phase cells, once a particular threshold of damage has been surpassed, the rate of inactivation would be the same regardless of the strain. In contrast, this rate of inactivation has been proven to be higher for exponential-growth-phase cells. Comparison of the kinetics of inactivation and damage of S. aureus Newman and its isogenic ΔsigB mutant indicate that shoulder length, but not the rate of inactivation in the log-linear phase or the microbial counts in the tail region, depends on σ^B expression.

Concluding remarks.

In conclusion, whatever mechanistic model is finally developed to describe the inactivation kinetics of S. aureus by HHP, it should consider that the survival curves may include shoulders, log-linear inactivation phases, and tails. Furthermore, the three different phases must be analyzed separately because their kinetics might be related to different physiological phenomena. Regarding its biological basis, our results indicate that the model should, at least for S. aureus, consider the involvement of the general stress factor σ^B in shoulder length but not on the rate of inactivation during the log-linear phase. On the other hand, the inactivation during this log-linear phase could be linked to the occurrence of oxidative damage. It is also important to emphasize that in the tail region a fixed percentage of the surviving population remained insensitive to sodium chloride.