THE IMPACT OF FALLIBLE ITEM PARAMETER ESTIMATES ON LATENT TRAIT RECOVERY

Abstract

In this paper we propose an upward correction to the standard error (SE) estimation of θ̂_ML, the maximum likelihood (ML) estimate of the latent trait in item response theory (IRT). More specifically, the upward correction is provided for the SE of θ̂_ML when item parameter estimates obtained from an independent pretest sample are used in IRT scoring. When item parameter estimates are employed, the resulting latent trait estimate is called pseudo maximum likelihood (PML) estimate. Traditionally the SE of θ̂_ML is obtained on the basis of test information only, as if the item parameters are known. The upward correction takes into account the error that is carried over from the estimation of item parameters, in addition to the error in latent trait recovery itself. Our simulation study shows that both types of SE estimates are very good when θ is in the middle range of the latent trait distribution, but the upward-corrected SEs are more accurate than the traditional ones when θ takes more extreme values.

Introduction

Item response theory (IRT) scoring offers various advantages. For example, the examinees can be placed on the same scale as the items. IRT also offers conditional standard errors (SE) of latent trait estimates. In IRT scoring, usually the item parameter values are considered known (see Baker & Kim, 2004; Embretson & Reise, 2000), unless the joint maximum likelihood (JML) method (Birnbaum, 1968) is used, which can produce estimates of the item and latent trait parameters simultaneously. JML estimation used to be a standard practice for item parameter estimation as implemented in LOGIST (Wingersky, Barton, & Lord, 1982). However, using JML estimation for tests of finite length may result in estimates that are not statistically consistent (Harwell & Baker, 1991).

Nowadays, it is a common practice in psychological and educational testing to first estimate item parameters from a pretest sample, and then treat the item parameter estimates as true values when estimating the latent trait in the scoring sample. However, the item parameter estimates are “fallible” in the sense that they do not equal the true parameter values, and they have their own standard errors. When item parameter estimates are treated as true values in scoring, the errors will affect the precision of resulting latent trait estimates.

It is important to obtain good estimates of the standard errors (SE) for the latent trait estimates. For instance, the SE can serve as the termination criterion in variable-length computerized adaptive testing. The test stops for an examinee when his or her ability estimate is sufficiently precise, i.e., when the SE of the final latent trait estimate is small enough. If the SE is underestimated, the test may end prematurely.

Researchers have long been aware of the issue that, when item parameter estimates are used instead of the true values, the standard error of final ability estimates can be underestimated. In the context of Bayes estimation with the three-parameter logistic (3PL) model (Hambleton & Swaminathan, 1985), Tsutakawa & Johnson (1990) discussed two sources of error in latent trait estimation, one being the scoring process itself, and the other being the error carried over from item calibration. They proposed approximations of the posterior mean and variance of latent trait and found that the uncertainty in latent trait estimation may be seriously underestimated when the pretest sample is small or moderately large. A remedy is to use posterior standard deviations from the Markov chain Monte Carlo (MCMC) output as standard errors. Specifically, one can obtain the latent trait estimates along with the standard errors by marginalizing over other dimensions of the joint posterior of item and person parameters (Patz & Junker, 1999).

Instead of adopting the Bayes framework, we will study the effect of fallible item parameter estimates on the precision of latent trait estimates in the context of maximum likehood (ML) estimation, which is widely used in IRT applications (see chapter 3 of Baker & Kim, 2004; chapter 7 of Embretson & Reise, 2000). In the ML approach with known item parameters, the SE of the estimated latent trait is obtained from the test information. When the item parameters are estimated rather than known, the true SE of the estimated latent trait will be inflated. Therefore the theory of ML has to take into account the extra errors. The procedure is called pseudo ML (PML) (Gong & Samaniego, 1981; Parke, 1986) estimation, which leads to an asymptotic quantification of how the errors in item parameter estimates affect the estimation of latent trait. The development allows us to obtain a correction to the information-based SE. It can also be shown that, as long as the item parameter estimates are consistent, the ML estimates (MLE) of latent traits are also consistent. We will use Monte Carlo methods to compare the corrected SE and the original SE against the empirical SE, with calibration sample of different sizes. The simulation study shows that the commonly used formula for SE underestimates the amount of variability in the final latent trait estimates for examinees with high or low latent trait levels.

Methodology

Dichotomous IRT models relate the probability of correct responses to the person parameter, θ. A widely used IRT model is the two-parameter logistic model (2PL, Birnbaum, 1968), which includes two item parameters, item discrimination α and item difficulty β:

$$P(U_{\mathit{\text{ij}}}=1|{\theta }_i,{\alpha }_j,{\beta }_j)={\{1+\text{exp}[-{\alpha }_j({\theta }_i-{\beta }_j)]\}}^{-1},$$ (1)

where U_ij = 1 represents a correct answer of subject i to item j, and U_ij = 0 otherwise.

Without loss of generality, the 2PL model can be re-parameterized as follows:

$$P(U_{\mathit{\text{ij}}}=1|{\theta }_i,{\gamma }_{j0},{\gamma }_{j1})={\{1+\text{exp}[-({\gamma }_{j0}+{\gamma }_{j1}{\theta }_i)]\}}^{-1}.$$ (2)

Naturally, γ_j0 = −α_jβ_j and γ_j1 = α_j.

The Fisher information measures the amount of information that an observable random variable X carries about an unknown parameter θ (Cover & Thomas, 1991), given a model. In the context of 2PL, the Fisher information of item j can be expressed as:

$$I_j(\theta ;{\gamma }_j)={\gamma }_{j1}^{2}P(\theta ,{\gamma }_{j0},{\gamma }_{j1})(1-P(\theta ,{\gamma }_{j0},{\gamma }_{j1})),$$ (3)

where P (θ, γ_j0, γ_j1) is a shorthand expression of P(U_j = 1|θ, γ_j0, γ_j1), and γ_j = (γ_j0, γ_j1)′. Assuming local independence, the test information is the sum of item information:

$$I_T(\theta ;\gamma )={\displaystyle \sum _{j=1}^m{I}_j(\theta ;{\gamma }_j),}$$ (4)

where m is test length, and γ is a 2m × 1 vector containing all the γ_j0 and γ_j1, j = 1, 2,…, m.

The square root of the inverse of test information evaluated at θ′,

$$\sqrt{I_T^{-1}\left(\widehat{\theta };\gamma \right)},$$ (5)

provides a consistent estimate of the SE of θ̂. In reality, however, γ is never known with certainty. They are often replaced with estimates from a pretest sample. In other words, the standard error of θ̂ is usually approximated by (see Embretson & Reise, 2000):

$$\sqrt{I_T^{-1}\left(\widehat{\theta };\widehat{\gamma }\right)}.$$ (6)

However, Eq. 6 may underestimate the standard error of θ̂. Let’s denote the realization of U_ij as u_ij. The log likelihood function, under the assumption of local independence, is given by:

$$l(\mathit{\theta },\gamma )={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^m\{u_{\mathit{\text{ij}}}\text{log}[P({\theta }_i,{\gamma }_{j0},{\gamma }_{j1})]+(1-}}{u}_{\mathit{\text{ij}}})\text{log}[Q({\theta }_i,{\gamma }_{j0},{\gamma }_{j1})]\},$$

where n is the size of the scoring sample, Q(θ_i, γ_j0, γ_j1) = 1 − P(θ_i, γ_j0, γ_j1), θ = (θ₁, θ₂, …, θ_n)′, $\gamma ={({\gamma }_1^{\prime },{\gamma }_2^{\prime },\dots ,{\gamma }_m^{\prime })}^{\prime }$ with γ_j = (γ_j0, γ_j1)′.

Suppose that a consistent estimator γ̂ is available and we treat it as known when using the ML procedure to estimate θ, our objective function is:

$$l(\mathit{\theta },\widehat{\gamma })={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^m\{u_{\mathit{\text{ij}}}\text{log}[P({\theta }_i,{\widehat{\gamma }}_{j0},{\widehat{\gamma }}_{j1})]+(1-}}{u}_{\mathit{\text{ij}}})\text{log}[1-P({\theta }_i,{\widehat{\gamma }}_{j0},{\widehat{\gamma }}_{j1})]\}.$$

When the IRT model defined in Eq. 2 is correct, such an approach to estimation is the aforementioned pseudo maximum likelihood (PML) estimation in the statistics literature (Gong & Samaniego, 1981; Parke, 1986). Under standard regularity conditions the pseudo MLE of θ_i, θ̂_i, satisfies the following estimating equation:

$$g_i({\widehat{\theta }}_i,\widehat{\gamma })=\mathbf{0},i=1,2,\dots ,n,$$ (7)

where

$$\begin{array}{ll}{g}_i({\theta }_i,\widehat{\gamma })\hfill & =\frac{1}{m}{\displaystyle \sum _{j=1}^m\left(\frac{u_{\mathit{\text{ij}}}}{P({\theta }_i,{\widehat{\gamma }}_{j0},{\widehat{\gamma }}_{j1)}}-\frac{1-u_{\mathit{\text{ij}}}}{Q({\theta }_i,{\widehat{\gamma }}_{j0},{\widehat{\gamma }}_{j1})}\right)\frac{\partial P({\theta }_i,{\widehat{\gamma }}_{j0},{\widehat{\gamma }}_{j1})}{\partial {\theta }_i}}\hfill \\ \hfill & =\frac{1}{m}{\displaystyle \sum _{j=1}^m[u_{\mathit{\text{ij}}}-P({\theta }_i,{\widehat{\gamma }}_{j0},{\widehat{\gamma }}_{j1})]{\widehat{\gamma }}_{j1}.}\hfill \end{array}$$

When g_i(θ_i, γ) is unbiased, i.e. when E[g_i(θ_i, γ)] = 0, θ̂_i is consistent (e.g., Godambe & Thompson, 1974).

We can use the Taylor expansion to see how the distribution of θ̂_i is affected by treating γ̂ as non-stochastic. Let ġ_iθ(θ_i, γ) and ġ_iγ(θ_i, γ) denote the partial derivatives of g_i(θ_i, γ̂) with respect to θ_i and γ, respectively. Then

$${\dot{g}}_{i\theta }({\theta }_i,\gamma )=-\frac{1}{m}{\displaystyle \sum _{j=1}^{m}P({\theta }_i,{\gamma }_{j0},{\gamma }_{j1})Q({\theta }_i,{\gamma }_{j0},{\gamma }_{j1})}{\gamma }_{j1}^2,$$

$${\dot{g}}_{i\gamma }=(a_{10},a_{11};a_{20},a_{21};\dots ;a_{m0,}{a}_{m1})/m$$

with

$$a_{j0}=-P({\theta }_i,{\gamma }_{j0},{\gamma }_{j1})Q({\theta }_i,{\gamma }_{j0},{\gamma }_{j1}){\gamma }_{j1},$$

and

$$a_{j1}=[u_{\mathit{\text{ij}}}-P({\theta }_i,{\gamma }_{j0},{\gamma }_{j1})]-P({\theta }_i,{\gamma }_{j0},{\gamma }_{j1})Q({\theta }_i,{\gamma }_{j0},{\gamma }_{j1}){\gamma }_{j1}{\theta }_i.$$

Suppose γ̂ is obtained by another sample that is independent from the current sample, with

$$\sqrt{N}(\widehat{\gamma }-\gamma )\stackrel{ℒ}{\to }𝒩(\mathbf{0},\mathbf{\Omega }),$$ (8)

where $\stackrel{ℒ}{\to }$ denotes convergence in distribution, and N the size of the calibration sample. Assuming m ≤ N, the first-order Taylor expansion of g_i(θ̂_i, γ̂) leads to

$$0=g_i({\widehat{\theta }}_i,\widehat{\gamma })=g_i({\theta }_i,\gamma )+{\dot{g}}_{i\theta }({\theta }_i,\gamma )({\widehat{\theta }}_i-{\theta }_i)+{\dot{g}}_{i\gamma }({\theta }_i,\gamma )(\widehat{\gamma }-\gamma )+o_p(1/\sqrt{m}),$$ (9)

where $o_p(1/\sqrt{m})$ denotes a random term r_m such that $\sqrt{m}{r}_m$ converges to 0 in probability when m → ∞ and N → ∞. Notice that

$$\begin{array}{ll}{\dot{g}}_{i\gamma }({\theta }_i,\gamma )(\widehat{\gamma }-\gamma )\hfill & =\frac{1}{m}{\displaystyle \sum _{j=1}^m[a_{j0}({\widehat{\gamma }}_{j0}-{\gamma }_{j0})+a_{j1}({\widehat{\gamma }}_{j1}-{\gamma }_{j1})]}\hfill \\ \hfill & =\frac{1}{m}{\displaystyle \sum _{j=1}^m[a_{j0}({\widehat{\gamma }}_{j0}-{\gamma }_{j0})+E(a_{j1})({\widehat{\gamma }}_{j1}-{\gamma }_{j1})]}\hfill \\ \hfill & +\frac{1}{m}{\displaystyle \sum _{j=1}^m\{[a_{j1}-E(a_{j1})]({\widehat{\gamma }}_{j1}-{\gamma }_{j1})\}.}\hfill \end{array}$$ (10)

Because

$$\frac{1}{\sqrt{m}}{\displaystyle \sum _{j=1}^m[a_{j1}-E(a_{j1})]}$$

converges to a normal distribution according to the central limit theorem, it follows from Eqs. 8 and 10 that

$$\sqrt{m}{\dot{g}}_{i\gamma }({\theta }_i,\gamma )(\widehat{\gamma }-\gamma )=\frac{1}{\sqrt{m}}{\displaystyle \sum _{j=1}^m[a_{j0}({\widehat{\gamma }}_{j0}-{\gamma }_{j0})+E(a_{j1})({\widehat{\gamma }}_{j1}-{\gamma }_{j1})]+o_p(1).}$$ (11)

Let

$$a_{i\theta }=-\underset{m\to \infty }{\text{lim}}{\dot{g}}_{i\theta }({\theta }_i,\gamma ).$$

It follows from Eqs. 9 and 11 that

$$\begin{array}{ll}\sqrt{m}({\widehat{\theta }}_i-{\theta }_i)\hfill & =a_{i\theta }^{-1}[\sqrt{m}{g}_i({\theta }_i,\gamma )+{\dot{g}}_{i\gamma }({\theta }_i,\gamma )\sqrt{m}(\widehat{\gamma }-\gamma )]+o_p(1)\hfill \\ \hfill & =a_{i\theta }^{-1}\{\sqrt{m}{g}_i({\theta }_i,\gamma )+\frac{1}{\sqrt{m}}{\displaystyle \sum _{j=1}^m[a_{j0}({\widehat{\gamma }}_{j0}-{\gamma }_{j0})+E(a_{j1})({\widehat{\gamma }}_{j1}-{\gamma }_{j1})]\}+o_p(1)}\hfill \\ \hfill & =a_{i\theta }^{-1}\sqrt{m}{g}_i({\theta }_i,\gamma )+\frac{{\mathit{a}}_{i\gamma }}{\sqrt{m}}(\widehat{\gamma }-\gamma )o_p(1),\hfill \end{array}$$ (12)

where

$${\mathit{a}}_{i\gamma }={(a_{10},E(a_{11});a_{20},E(a_{21});\dots ;a_{m0},E(a_{m1}))}^{\prime }.$$

Because a_iγ ≠ 0, the distribution and standard error of γ̂ do affect those of θ̂_i. Since a_j0 and E(a_j1) are nonstochastic, the two terms in the braces of Eq. 12 are independent. From Eq. 8 we get

$$\frac{{\mathit{a}}_{i\gamma }}{\sqrt{m}}(\widehat{\gamma }-\gamma )\stackrel{ℒ}{\to }N(0,{\tau }^2),$$

where

$${\tau }^2=\underset{N\to \infty }{\text{lim}}{\mathit{a}}_{i\gamma }^{\prime }\mathbf{\Omega }{\mathit{a}}_{i\gamma }/(mN).$$

It follows from Eq. 12 that

$$\sqrt{m}({\widehat{\theta }}_i-{\theta }_i)\stackrel{ℒ}{\to }N(0,{\omega }_i^2),$$ (13)

where

$${\omega }_i^2=a_{i\theta }^{-2}({\upsilon }_{i11}+{\tau }^2)$$

and

$${\upsilon }_{i11}=\underset{m\to \infty }{\text{lim}}\frac{1}{m}{\displaystyle \sum _{j=1}^m{\gamma }_{j1}^{2}E{[u_{\mathrm{\text{ij}}}-P({\theta }_i,{\gamma }_{j0},{\gamma }_{j1})]}^2.}$$

Consistent estimates of a_iθ, υ_i11 and τ² are obtained using

$${\widehat{a}}_{i\theta }=-\frac{1}{m}{\displaystyle \sum _{j=1}^{m}P({\widehat{\theta }}_i,{\widehat{\gamma }}_{j0},{\widehat{\gamma }}_{j1})Q({\widehat{\theta }}_i,{\widehat{\gamma }}_{j0},{\widehat{\gamma }}_{j1}){\widehat{\gamma }}_{j1}^2,}$$

$${\widehat{\upsilon }}_{i11}=\frac{1}{m}{\displaystyle \sum _{j=1}^m{\widehat{\gamma }}_{j1}^2{[u_{\mathit{\text{ij}}}-P({\widehat{\theta }}_i,{\widehat{\gamma }}_{j0},{\widehat{\gamma }}_{j1})]}^2,}$$

${\widehat{\tau }}^2={\widehat{\mathit{a}}}_{i\gamma }^{\prime }\widehat{\mathbf{\Omega }}{\widehat{\mathit{a}}}_{i\gamma }/(mN)$ with â_iγ being obtained by

$${\widehat{\mathit{a}}}_{i\gamma }=({\widehat{a}}_{10},{\widehat{a}}_{11};{\widehat{a}}_{20},{\widehat{a}}_{21};\dots ;{\widehat{a}}_{m0},{\widehat{a}}_{m1})$$

and

$${\widehat{a}}_{j0}=-P({\widehat{\theta }}_i,{\widehat{\gamma }}_{j0},{\widehat{\gamma }}_{j1})Q({\widehat{\theta }}_i,{\widehat{\gamma }}_{j0},{\widehat{\gamma }}_{j1}){\widehat{\gamma }}_{j1},$$

$${\widehat{a}}_{j1}=[u_{\mathit{\text{ij}}}-P({\widehat{\theta }}_i,{\widehat{\gamma }}_{j0},{\widehat{\gamma }}_{j1})]-P({\widehat{\theta }}_i,{\widehat{\gamma }}_{j0},{\widehat{\gamma }}_{j1})Q({\widehat{\theta }}_i,{\widehat{\gamma }}_{j0},{\widehat{\gamma }}_{j1}){\widehat{\gamma }}_{j1}{\widehat{\theta }}_i.$$

In summary, the standard error of θ̂_i is given by:

$$\sqrt{\frac{{\omega }_i^2}{m}}=\sqrt{\frac{a_{i\theta }^{-2}{\upsilon }_{i11}}{m}+\frac{a_{i\theta }^{-2}{\tau }^2}{m}}.$$ (14)

A consistent estimate of Ω̂ depends on the method and sample that are used when estimating γ. When the model is correct (i.e. when Eq. 1 is the true distribution of U_ij) and the local independence assumption holds, $a_{i\theta }={\upsilon }_{i11}\text{and}{a}_{i\theta }^{-2}{\upsilon }_{i11}/m$ is just the inverse of test information. Eq. 14 therefore implies that, when γ̂ instead of γ is used, the standard error of θ̂_i will be positively affected by that of γ̂. The effect depends on the magnitude of ${\mathit{a}}_{i\gamma }\mathbf{\Omega }{\mathit{a}}_{i\gamma }^{\prime }/m$ and N.

In the following section, we will give a detailed description of a simulation study, which shows how the upward-corrected SE offered by Eq. 14 better reflects the reality.

Simulation and Results

The simulation study consists of three parts: item calibration, subject scoring, and the computation of Ω̂:

1. A calibration sample of size N is first generated following a certain distribution (in this study 𝒩(0, 1)), and their responses to m items are simulated following Eq. 1. Calibration samples of two different sizes are simulated: N = 2, 000 and N = 200. The m items are 40 retired items from a national math test, whose parameter estimates are available from previous large-scale calibration. These estimates are used as true parameter values. Descriptive statistics for these item parameters are summarized in Table 3. In the end, an N × m matrix of 0’s and 1’s is generated.

   BILOG-MG 3 (Zimowski, Muraki, Mislevy, & Bock, 2003) is used for item calibration. The output from this step is the calibrated item parameters for the m = 40 items. Note that the 2PL model is used, so in total we have 80 item parameter estimates.

2. A scoring sample of size n = 1, 800 is generated by having 200 subjects at each of the nine, equally-spaced θ points (step-size = 0.5) from −2.0 to 2.0. Their responses to the m = 40 items are simulated following Eq. 1 as well. The item parameter estimates from Step 1 are adopted to score the 1,800 subjects using maximum likelihood estimation. The ceiling and floor cases (those whose response sequence is either all 1 or all 0’s) are assigned scores of +4.0 or −4.0, respectively. Empirical conditional SEs are obtained within each local θ group of 200 subjects. Note that the empirical SEs are based on θ̂_is that are “contaminated” by the imprecise item parameter estimates from Step 1.

3. It is clear from the derivation that the corrective procedure requires the estimate of Ω, where Ω/N is the asymptotic covariance matrix associated with the maximum marginal likelihood estimation (MMLE) of item parameters. To obtain Ω̂, we use Ω = A⁻¹BA⁻¹, where A is the negative expected second derivative of the MMLE for a single case, and B is the expected cross-product of the first derivative of the MMLE for a single case. Note that when the model is correct, A = B, and consequently, Ω = B⁻¹. In practice, A is estimated by the negative average second derivative of the MMLE, and B by the average cross-product of the first derivative of the MMLE.

TABLE 3.

Summary Statistics of Item Parameters

	α	β
Mean	0.952	−0.252
SD	0.243	0.646

In our simulation study, the numerical differences between the two estimates, Â and B̂, only appear at the second decimal places. Therefore B̂⁻¹ is used in subsequent computation in place of Ω̂ for easier implementation. Cai (2008) discussed a supplemented expectation-maximization (EM) algorithm to compute the information matrix of the item parameter estimates, which could be used as well. Another possibility to come up with Ω̂ is to use a parametric bootstrap.

Table 1 contains the conditional SE of θ̂_is when the calibration sample size is N = 2, 000. The second column represents the empirical SE obtained in Step 2. The third column gives the average SE computed using test information among the 2,000 subjects in the same local θ group. The test information is calculated by plugging the item parameter estimates from Step 1 and θ̂_is in Step 2 into Eq. 4. The fourth column provides the average upward corrected SE in each local θ group, following Eq. 14. The fifth column is the ratio of the information-based SE estimates over the empirical ones. The last column is the ratio of the upward corrected SE estimates over the empirical ones. Clearly, the information-based SE estimates are quite precise when θ ∈ [−1.5, 0.5], where their ratios to the empirical SE estimates are around 1. There are some cases showing overestimation of the SE, but the magnitude is very small (in second decimal places). However, there is serious underestimation of SE when θ is not in the middle range of the ability continuum. For example, when θ = −2, SE_uncorrected/SE_empirical = 0.79, suggesting an error of about 21%; when θ = 2, SE_uncorrected/SE_empirical = 0.64, suggesting an error of about 36%. By contrast, the upward-corrected SE estimates fare much better at these extreme locales: the errors in the corresponding cases are 13% and 6%, respectively. When θ ∈ [−1.5, 0:5], the upward correction also tends to overestimate the SE, but also just slightly (in second decimal places).

TABLE 1.

Comparison of Uncorrected and Upward-corrected SE of θ̂, N = 2,000

θ	SE	Information-based SE	ω-based SE	Ratiouncorrected	Ratiocorrected
	Empirical	Uncorrected	Corrected	SEuncorrected/SEempirical	SEcorrected/SEempirical
−2.0	0.49	0.39	0.43	0.79	0.87
−1.5	0.31	0.32	0.33	1.04	1.07
−1.0	0.25	0.26	0.26	1.03	1.05
−0.5	0.21	0.22	0.22	1.05	1.06
0	0.21	0.21	0.21	1.02	1.03
0.5	0.24	0.23	0.23	0.95	0.96
1.0	0.33	0.29	0.31	0.88	0.93
1.5	0.61	0.39	0.48	0.64	0.79
2.0	0.86	0.55	0.81	0.64	0.94

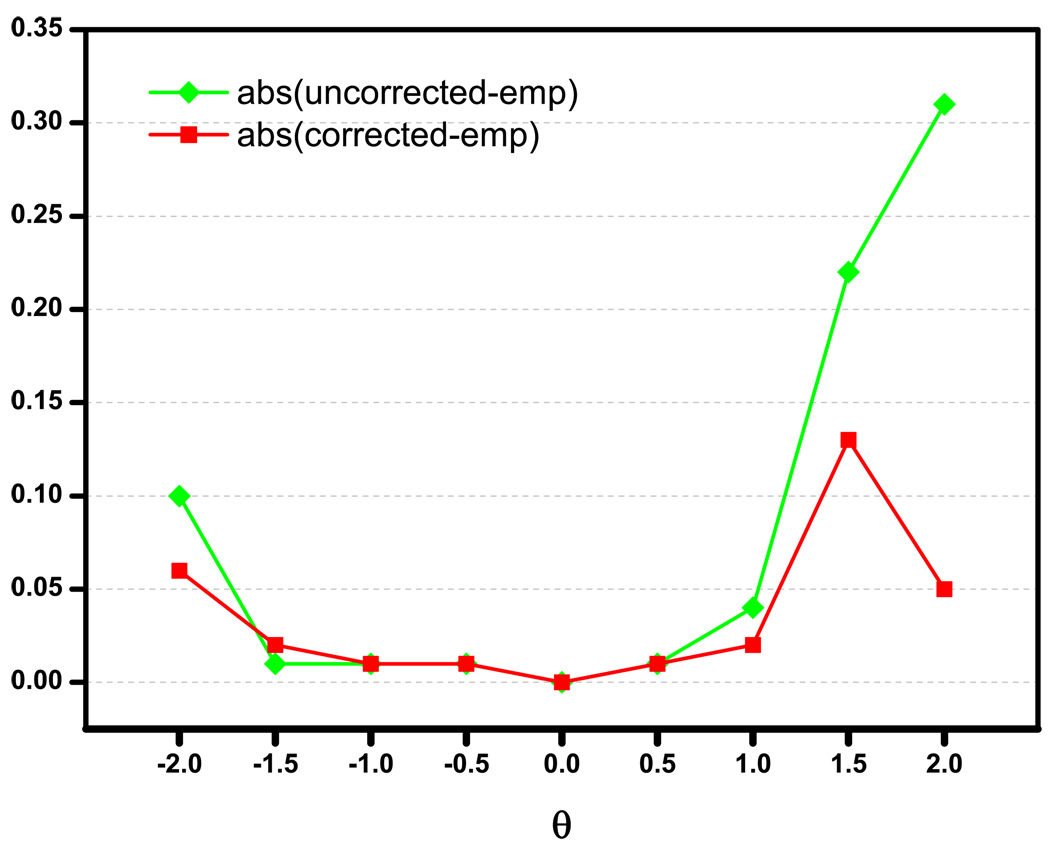
Figure 1 shows how |SE_uncorrected − SE_empirical| and |SE_corrected − SE_empirical| change with θ when θ ∈ [−2, 2]. Again, it is clear that the SE estimates are more accurate in the middle range of latent trait distribution, regardless of whether the SE estimates are corrected or not. Second, the advantage of using the upward-corrected SE estimate, i.e., the one based on ω, diminishes when θ gets in the vicinity of 0, and is larger when θ deviates from the middle range of the ability distribution.

FIGURE 1.

|SE_empirical − SE_uncorrected| vs. |SE_empirical − SE_corrected|, N = 2000

Table 2 is a replica of Table 1, except that the calibration sample size is N = 200. We expect to see a larger SE associated with item parameter estimates when the calibration sample size gets smaller, and consequently the SE estimates of θ̂_ML will be further inflated compared to what is shown in Table 1. This is confirmed by our data. Across all θ levels, the empirical SEs in Table 2 are larger than, or at least equal to, those in Table 1. On the other hand, the inflation in SE estimates of θ is rather small, which suggests that θ recovery in a sense is fairly robust to the size of the calibration sample. This may be due to the fact that we are looking at the 2PL model, which is known to have less stringent requirement on calibration sample size than the 3PL model. Another possible reason is that the simulation study adopts a 40-item test, which is fairly long. The resulting SEs are therefore small.

TABLE 2.

Comparison of Uncorrected and Upward-corrected SE of θ̂, N = 200

θ	SE	Information-based SE	ω-based SE	Ratiouncorrected	Ratiocorrected
	Empirical	Uncorrected	Corrected	SEuncorrected/SEempirical	SEcorrected/SEempirical
−2.0	0.51	0.39	0.45	0.77	0.89
−1.5	0.31	0.32	0.34	1.04	1.12
−1.0	0.25	0.26	0.28	1.02	1.09
−0.5	0.22	0.23	0.24	1.03	1.09
0	0.21	0.22	0.23	1.03	1.08
0.5	0.25	0.24	0.25	0.96	1.01
1.0	0.38	0.30	0.33	0.78	0.86
1.5	0.67	0.40	0.51	0.60	0.76
2.0	0.86	0.57	0.81	0.64	0.91

Again, our focus is on comparing the uncorrected SE estimates with the corrected SE estimates. The last two columns of Table 2 demonstrate the same pattern as Table 1: the ω-based SE more closely matches the empirical SE. In the middle range of θ, both the pure information-based SE estimates and the upward-corrected ones are quite precise. In fact, they both tend to overestimate the SEs when θ is close to 0, but only very slightly. The advantage of upward correction is pronounced when θ moves away from the middle range. Therefore, when the goal is to identify remedial or advanced students, it is important to recognize that the traditional, purely information-based SE estimates are too liberal.

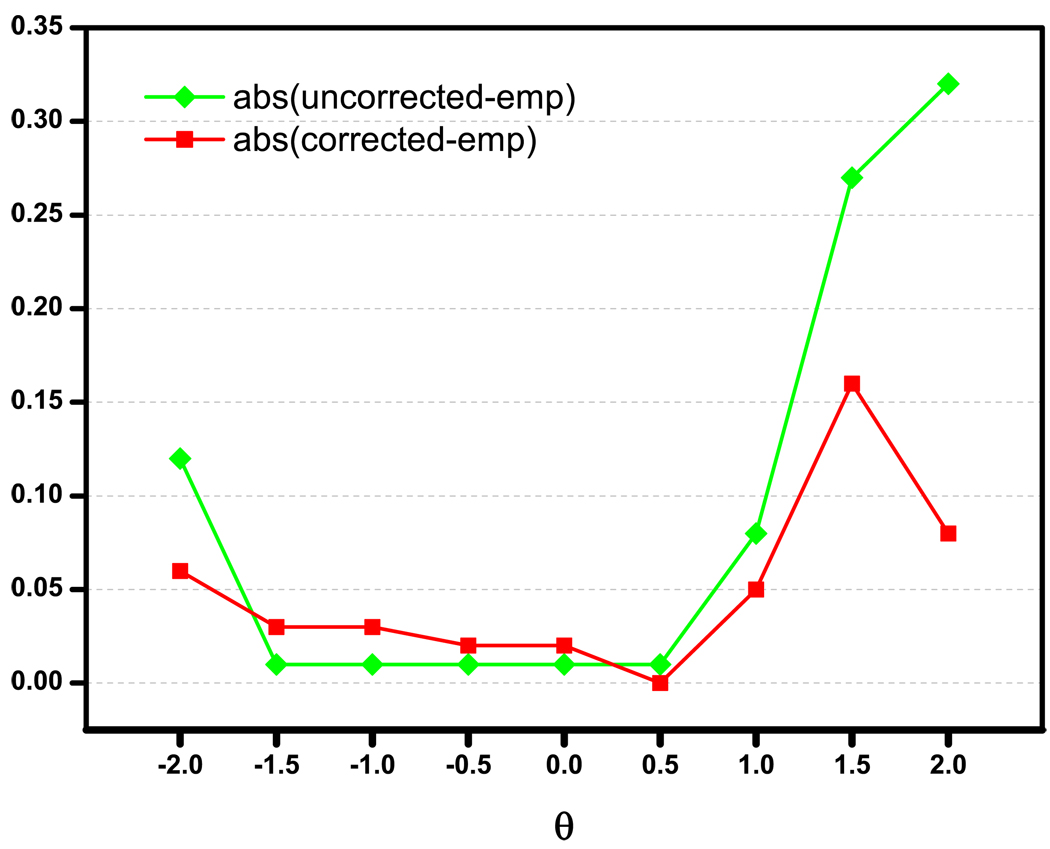
Figure 2 also shows a similar pattern to Figure 1: upward-corrected SE estimates are more accurate when the θ is not in the middle range of the ability distribution. In addition, no matter which SE estimate is adopted, it is safer to use it when θ are in the middle range, where most of the items measure the best. This, again, resonates with what has been shown repeatedly in the literature, i.e., the floor and ceiling effect.

FIGURE 2.

|SE_empirical − SE_uncorrected| vs. |SE_empirical − SE_corrected|, N = 200

In Figure 1 and Figure 2, one may notice a “dip” at θ = 2.0. The “dip” represents an increase in $a_{i\theta }^{-2}{\upsilon }_{i11}/m$, the value added to the test information (see Eq. 14). As a matter of fact, moving towards extreme θ levels, the $a_{i\theta }^{-2}{\upsilon }_{i11}/m$ keeps increasing, as reflected by the difference between the 2nd and 3rd columns in Table 1 and Table 2. The “dip” therefore shows actually the pronounced effect of correction at these θ levels.

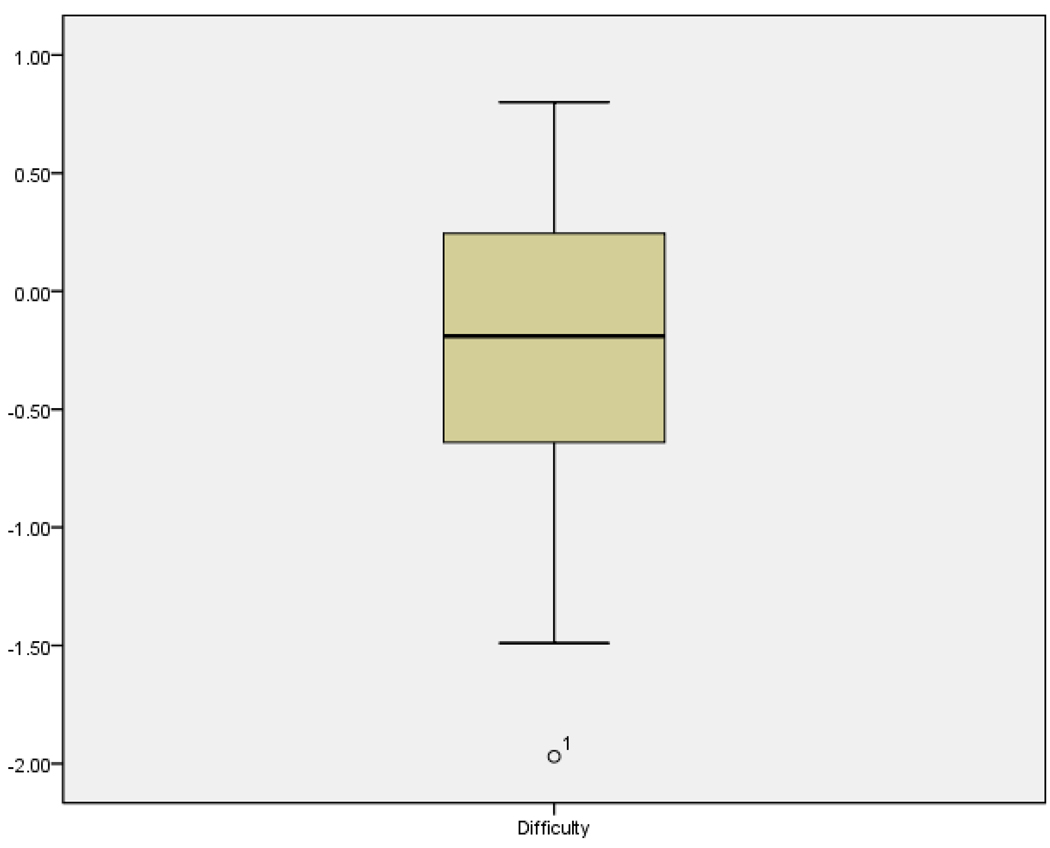
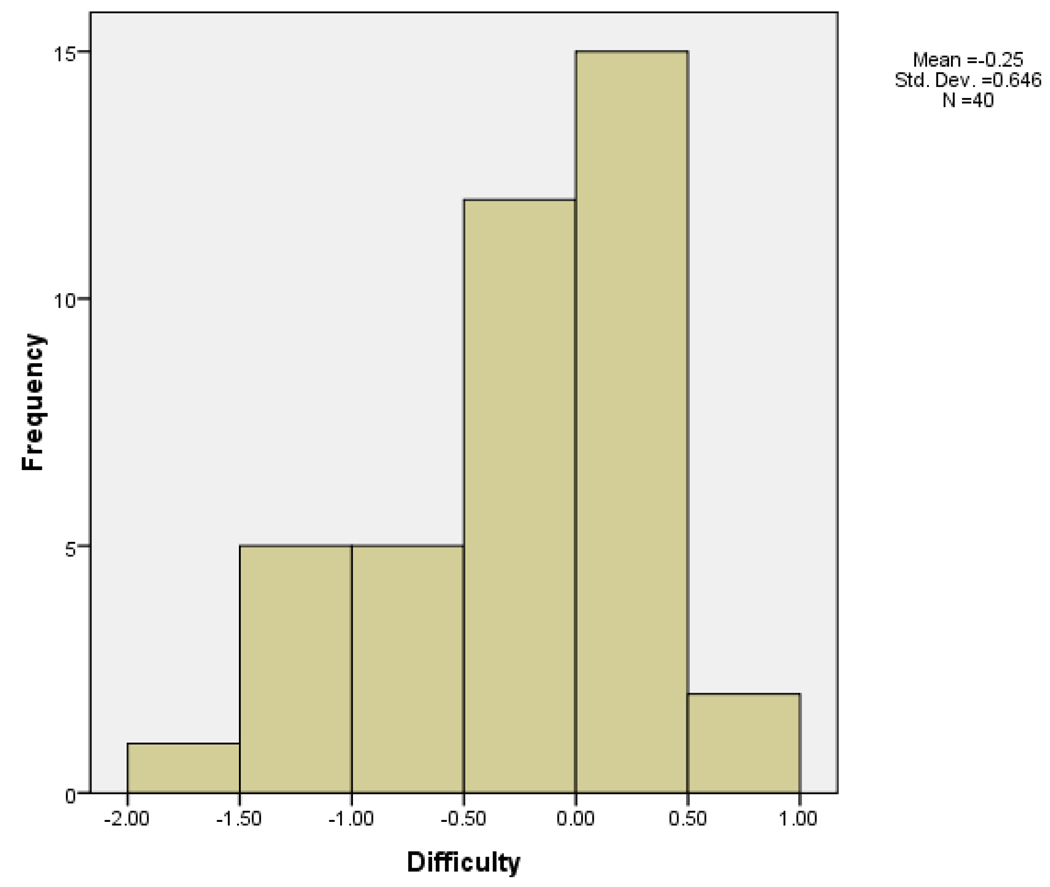
It may be worth mentioning that both Table 1 and Table 2 indicate that the empirical SE estimates are not symmetric around 0: they are clearly lower with examinees from lower ability groups (i.e., θ < 0), which suggests that the test measures these examinees better than the higher-achieving students. This phenomenon can be explained by the particular test used in our simulation study. Table 3 presents the summary statistics of the test. The average item difficulty is −0.25. The boxplot and histogram (Figure 3 and Figure 4) for the difficulty parameter further reveal that the test is in general on the easy side for the scoring sample, whose average θ is 0. The maximum item difficulty level is merely 0.8, while the minimum reaches down to −2.0. Therefore it is not surprising that the test measures low-ability groups better.

FIGURE 3.

The Boxplot of the Difficulty Parameters of the 40 Items

FIGURE 4.

The Histogram of the Difficulty Parameters of the 40 Items

Summary and Discussion

In this study we propose an upward correction to the standard error estimate of θ̂, the latent trait estimate in item response theory. More specifically, the upward correction is provided for θ̂_ML, and it takes into account the error that is carried over from the estimation of item parameters. Our simulation study shows that the upward correction leads to better SE estimates towards the two ends of the latent trait distribution.

It is not uncommon to use item parameter estimates from pretest in scoring, and SE estimates of the final θ̂_ML are used for high-stakes decisions such as terminating a variable-length computerized adaptive test. Hence it is important to understand that the SE estimate based on test information alone might be too small. Findings from this study suggest using the upward-corrected SE estimate for θ̂_ML, especially when the item parameter estimates are obtained from a small sample.

On the other hand, to use the corrective procedure, not only the item parameter estimates, but also their variances and covariances need to be available. Therefore we would encourage reporting variances and covariances terms along with the item parameter estimates themselves, unless the calibration sample size is very large. Intra-item variance and covariance terms are available from BILOG-MG, but not inter-item ones. We would like to investigate further if the corrective procedure still works with a reduced covariance structure, i.e., using only the intra-item terms.

In addition, we feel that the study can be extended in at least the following aspects. In this paper, we have focused on the 2PL model, an extensively used model in psychological and educational measurement. The development can be easily extended to other IRT models, such as the 3PL model or the normal ogive models. Moreover, we have assumed that the probability density function in Eq. 1 or 2 is correctly specified in this study. In case this assumption is violated, consistent SEs for θ̂_ML can still be obtained by replacing the inverse of the information in Eq. 14 by the sandwich-type variance (see Yuan & Jennrich, 2000). In addition, the derivation and simulation study in this paper assume that the calibration sample and the scoring sample are independent. When the same sample is used for calibration first and then the item parameter estimates are employed to score the sample, the rationale of the corrective procedure offered in this paper is still valid. Only one change needs to be made to Eq. 14, which consists of only two components right now: test information, and the error from γ. When the same sample is used for both calibration and scoring, a third term, which represents the covariance of the g_i(θ_i, γ) and γ̂ − γ (see Eq. 12), needs to be incorporated into Eq. 13. Finally, as pointed out by one referee, Bayesian latent trait estimates such as expected a posteriori (EAP) or modal a posterior (MAP) are also used frequently in IRT applications. The technique presented in this paper can be applied in the same fashion to Bayesian posterior probabilities, and can offer similar adjustment to, for example, the SE estimate of θ̂_MAP with a 𝒩(0, 1) prior.