Abstract
We present a method for discovering patterns of selectivity in fMRI data for experiments with multiple stimuli/tasks. We introduce a representation of the data as profiles of selectivity using linear regression estimates, and employ mixture model density estimation to identify functional systems with distinct types of selectivity. The method characterizes these systems by their selectivity patterns and spatial maps, both estimated simultaneously via the EM algorithm. We demonstrate a corresponding method for group analysis that avoids the need for spatial correspondence among subjects. Consistency of the selectivity profiles across subjects provides a way to assess the validity of the discovered systems. We validate this model in the context of category selectivity in visual cortex, demonstrating good agreement with the findings based on prior hypothesis-driven methods.
Keywords: fMRI, clustering, high level vision, category selectivity
1 Introduction
Standard fMRI experiments investigate the functional organization of the brain by contrasting the response to two or more sets of stimuli or tasks that are hypothesized to be treated differently by the brain. An activation map is generated by statistically comparing the fMRI response of each voxel to one set of tasks or stimuli versus another. The consistency of these activation maps across subjects is commonly evaluated by aligning the brain data across multiple subjects in a common anatomical space using spatial normalization. Using such voxel-wise correspondence across subjects, statistical analyses can test whether each voxel produces a higher response in one condition than another, consistently across subjects. In an alternative region of interest (ROI) method, discrete activation foci are functionally identified within each individual subject, and the responses of a given ROI to new conditions are then statistically compared across subjects.
These standard practices have generated a wealth of knowledge about the functional organization of the human brain, most of it unknown just 20 years ago. However the standard methods are also subject to two important limitations: (i) they can only test hypotheses generated by the experimenter; they cannot discover new structure in the fMRI response, and (ii) they assume some consistency across subjects in the spatial pattern of activation across the brain. Here, we introduce a new method that avoids both of these limitations, enabling us to discover patterns of functional response that are found robustly across subjects. These patterns do not have to be hypothesized a priori and do not have to correspond to voxels that exhibit spatial contiguity or spatial consistency across subjects.
Our exploratory approach introduces the concept of a selectivity profile, which is a simple characterization of the function of a voxel in terms of its response to each of the different experimental conditions. The experimental conditions in this approach can number in the tens or even hundreds, instead of the two to eight conditions used in most imaging studies. We aim to discover selectivity profiles that best explain the entire data set.
In the conventional univariate approach, the response of the entire population of voxels is not considered as a whole; tests are performed separately on single voxels to examine the significance of a priori hypothesized activations. In contrast, we devise a model that explains the selectivity profiles of all voxels by grouping them into a number of systems (clusters), each with a distinct, representative selectivity profile across the stimuli/tasks in the experiment. Once a small set of robust systems is discovered, we can map the location of the voxels that correspond to each system to find out where they are in the brain, if they are spatially contiguous, and if they are in similar locations across subjects. With our new method, the answers to these questions are now genuine discoveries, not assumptions built into the method.
Our method offers an additional advantage for group analysis. In the conventional hypothesis-driven analysis, in order to analyze a cohort of subjects, we need to first normalize different subjects into a common anatomical space. Since brain structure is highly variable across subjects, establishing accurate correspondences among anatomical images of different subjects is intrinsically challenging (Gee et al., 1997; Thirion et al., 2006, 2007a,b). In addition to this anatomical variability, functional properties of the same anatomical structures are likely to vary somewhat across subjects (Brett et al., 2002). This variability presents a fundamental obstacle for anatomically-constrained characterization of functional systems.
Since we are primarily interested in the systems with selectivity profiles that are shared across subjects, the space of these profiles for a certain experimental setup can act as a common space for representing data from different subjects. Hence, our model does not require spatial information, and we can analyze group data from different runs and subjects without a need for spatial normalization. Furthermore, rather than relying on spatial consistency to establish the validity of selectivity patterns, we employ functional consistency defined as the robustness of the estimated profiles across subjects. Because our representation of the data relies solely on the functional response, and the basic analysis knows nothing about the location of each voxel, the resulting systems we discover are not constrained to be spatially clustered together or in similar locations across subjects.
Several exploratory, unsupervised learning methods have been previously applied to the analysis of fMRI data. Some methods consider the spatial patterns of response across many voxels; for instance, they may apply an algorithm such as agglomerative clustering to these spatial patterns to infer the hierarchical grouping of stimuli (Kriegeskorte et al., 2008). In contrast, we seek groups of voxels that respond similarly across a large set of images and to characterize the nature of their response.
Most exploratory methods that attempt to partition the set of voxels consider raw fMRI time courses and use clustering (e.g., Baumgartner et al., 1997, 1998; Moser et al., 1997; Golay et al., 1998; Filzmoser et al., 1999; Fadili et al., 2000; Golland et al., 2007) or Independent Component Analysis (ICA) (McKeown et al., 1998; Beckmann and Smith, 2004, 2005; Calhoun et al., 2001a,b) to estimate a decomposition of the data into a set of distinct time courses of interest and their localization maps. However, these methods do not readily express the relationship between the discovered time courses and the functional response of voxels to the experimental conditions. Some variants employ information from the experimental setup to define a measure of similarity between voxels, effectively projecting the original high-dimensional time courses onto a low dimensional feature space, followed by clustering in the new space (Goutte et al., 1999, 2001; Thirion and Faugeras, 2003). Nevertheless, these methods mainly focus on the spatial maps of the clusters corresponding to the activation of interest as the main result of the analysis. Few exploratory or multivariate methods systematically address the issue of group analysis (Calhoun et al., 2001b).
In this paper, we employ the studies of category selectivity in the visual pathway as a concrete example for the applications of our method in fMRI studies with a rich space of experimental conditions. Functional MRI studies of vision have provided a great example for the success of fMRI in revealing structure in brain's functional organization (Grill-Spector and Malach, 2004). Using the conventional hypothesis-driven approach, fMRI data has identified a handful of regions with specific category selectivity in the visual cortex (Kanwisher, 2003). For instance, the fusiform face area and occipital face area (FFA and OFA) are associated with face selectivity (McCarthy et al., 1997; Kanwisher et al., 1997; Kanwisher and Yovel, 2006; Rossion et al., 2003) while the parahippocampal place area (PPA) (Epstein and Kanwisher, 1998; Burgess et al., 1999; Aguirre et al., 1998) and the extrastriate body area (EBA) (Downing et al., 2001; Schwarzlose et al., 2005; Peelen and Downing, 2007) exhibit high selectivity for places and body parts, respectively. In addition, an object-selective region in the lateral occipital complex (Malach et al., 1995) and a small area in the left fusiform gyrus with selectivity to letter strings and visually-presented words (Baker et al., 2007) have been identified and further characterized. However, the collection of all currently known category selective areas constitutes a small part of the visual pathway and accounts for a limited set of categories in the visual world. Further studies to find other selective areas have generally failed, leaving many questions unanswered (Downing et al., 2006).
We face several methodological challenges in proceeding with the present hypothesis-driven approach. With the increasing number of image categories included in the experiments, it becomes more challenging to explore the entire set of possible patterns of selectivity by only comparing voxel responses to two conditions at a time. In principle, for any candidate category, we have to search for a brain region that shows significant activation in pairwise contrasts with all the other categories in the experiment. Moreover, we should also consider possible meta-categories (categories comprised of multiple other categories) in the experiment that might form natural classes of selectivity for a brain system. For instance, if we have images of both human faces and human bodies in the experiment, we can also consider the set of all these images as one candidate category. Finally, the conventional approach uses spatial contiguity of the regions and their spatial consistency across subjects as the only method to evaluate whether a system is truly selective (Kanwisher et al., 1997; Spiridon et al., 2006). Hence, anatomical variability of functional systems in the brain fundamentally restricts the power of this method.
As an illustration of how our method can address the basic limitations of the conventional hypothesis-driven method, we apply it to the data from an experiment investigating category selectivity in the visual cortex. Our results replicate prior findings obtained via numerous hypothesis-driven fMRI studies. We robustly discover the known selectivity patterns, further opening up the possibility of studies on richer sets of stimuli.
2 Methods
In this section, we define the main elements of our approach in three steps. First, we introduce the space of selectivity profiles and explain how this representation enables discovery of the patterns of selectivity in the brain systems of interest. Second, we formulate our model for the analysis of the data, represented in the space of selectivity profiles, and derive an algorithm for estimating the model parameters from fMRI data. Third, we present our approach to validating the results based on our definition of cross-subject and within-subject consistency measures. In the last part, we discuss alternative validation procedures.
2.1 Space of Selectivity Profiles
The goal of our method is to discover the types of response specificity that appear across multiple voxels in our data. Hence, we choose to represent an fMRI time course by a profile that characterizes the selectivity of the voxel response to the set of all experimental conditions. The notion of selectivity focuses on the relative response; for instance, the rough definition of a selective system in high level vision states that a selective voxel's response to the preferred stimulus is at least twice as high as its response to other stimuli (Op de Beeck et al., 2008). This definition involves only a ratio of the responses and is independent of their overall magnitude. Our profile representation, therefore, aims to capture this relative response of the voxels based on their observed BOLD time course.
It is customary to use regression to estimate the contributions of different experimental conditions to the BOLD signal. In this set up, we can represent the BOLD response xv ∈ IRT of voxel v at the T time points as:
| (1) |
where the columns of matrices H and G are the temporal regressors corresponding to the protocol-independent nuisance factors and the D experimental conditions, respectively. Assuming white temporal noise, , the least square solution yields the estimates of the regression coefficients β̂v and α̂v:
| (2) |
where A = [H G]. Component i of the estimated vector β̂v is commonly interpreted as a measure of the response of voxel v to stimulus i. The above model is usually used for assessing the statistical significance of different hypotheses about the response in the framework of the General Linear Models (GLM) (Friston et al., 1994). More accurate models of fMRI signal also account for autocorrelations present in the covariance structure of the temporal noise εv (see, e.g., Aguirre et al., 1997; Woolrich et al., 2001), but the above simple model is adequate for the demonstration of our method.
We define the voxel selectivity profile to be a vector containing the estimated regression coefficients for the experimental conditions, normalized to unit magnitude, that is,
| (3) |
where with 〈·, ·〉 denoting the inner product. Selectivity profiles lie on a hyper-sphere SD−1 and imply a pattern of selectivity to the D experimental conditions defined by a direction in the corresponding D-dimensional space. Normalization removes the contribution of the overall magnitude of response and presents the estimated response as a ratio with respect to this overall response. Furthermore, it is well-known that the magnitude of overall BOLD response of the voxel is mainly a byproduct of irrelevant variables such as distance from major vessels or general response to the type of stimuli used in the experiment (Friston et al., 2007). This provides another justification for the normalization of response vectors, in addition to our interest in representing selectivity as a relative measure of response.
Figure 1(A) illustrates the population of unnormalized estimated vectors of regression coefficients β̂v for all the voxels identified by the conventional hypothesis-driven analysis as selective for one of three different conditions. The differences between voxels with different types of selectivity are not well expressed in this representation; there is no apparent separation between different groups of voxels. We also note that there is an evident overlap between the sets of voxels assigned to these different patterns of selectivity. The standard analysis in this case uses a contrast comparing each of the three conditions of interest with a fourth experimental condition; therefore, it is possible for a voxel to appear selective for all three of these contrasts. In order to explain the selectivity of such a voxel, we can define a novel type of selectivity towards a meta-category which is composed of the three categories represented by these contrasts. The same argument can be applied to any combinations of the categories presented in the experiment to form various, new candidates as possible types of selectivity.
Fig. 1.
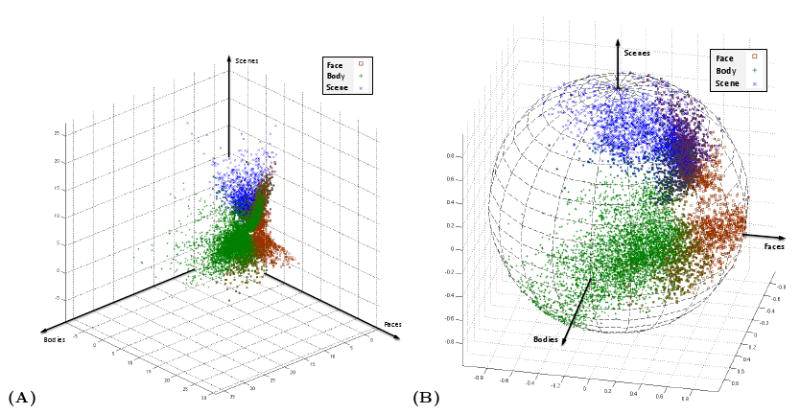
An example of voxel selectivity profiles in the context of a study of visual category selectivity. The block design experiment included several categories of visual stimuli such as faces, bodies, scenes, and objects, defined as different experimental conditions. (A) Vectors of estimated regression coefficients β̂ = [βFaces, βBodies, βScenes]t for the voxels detected as selective to bodies, faces, and scenes in one subject. As is common in the field, the conventional method detects these voxels by performing significance tests comparing voxel's response to the category of interest and its response to objects. (B) The corresponding selectivity profiles y formed for the same group of voxels.
Figure 1(B) shows the selectivity profiles yv formed for the same data set. We observe that the voxels associated with different types of activation become more separated, exhibiting an arrangement that is similar to a clustering structure. Furthermore, it is easy to see that the set of voxels shared among all three patterns of selectivity has a distinct structure of its own, mainly concentrated around a direction close to on the sphere. We interpret the center of a cluster of selectivity profiles as a representative for the type of selectivity shared among the neighboring profiles on the sphere.
Although the clusters of the profiles are not well-separated, the arrangement of concentrations of profiles on the sphere can carry important information about the types of selectivity more heavily represented in the data. This information becomes more interesting as the number of dimensions (experimental conditions) grows and the overall density of profiles on the sphere decreases. This motivates us to consider application of mixture model density estimation, the probabilistic modeling formulation of clustering (McLachlan and Peel, 2000), to the set of selectivity profiles. Each component in the mixture model represents a cluster of voxels, i.e., a functional system, concentrated around a central direction on the sphere. The corresponding cluster center, which we call system selectivity profile, specifies that system's type of selectivity.
2.2 Model
Let be a set of selectivity profiles of V brain voxels. We assume the vectors are generated i.i.d. by a mixture distribution
| (4) |
where are the weights of K components and f(·, m, λ) is the likelihood of the data parametrized by m and λ. We assume that the likelihood model describes simple directional distribution on the hyper-sphere and choose the von Mises-Fisher distribution (Mardia, 1975) for the mixture components:
| (5) |
where inner product corresponds to the correlation of the two vectors on the sphere. Note that this model is in agreement with the notion that on a hypersphere, correlation is the natural measure of similarity between two vectors. The distribution is an exponential function of the correlation between the vector y (voxel selectivity profile) and the mean direction m (system selectivity profile). The normalizing constant CD(λ) is defined in terms of the γ-th order modified Bessel function of the first kind Iγ:
| (6) |
The concentration parameter λ controls the concentration of the distribution around the mean direction m similar to the reciprocal of variance for Gaussian models. In general, mixture components can have distinct concentration parameters but in this work, we use the same parameter for all the clusters to ensure a more robust estimation. This model has been previously employed in the context of clustering text data (Banerjee et al., 2006).
We formulate our problem as a maximum likelihood estimation:
| (7) |
Employing the Expectation-Maximization (EM) algorithm (Dempster et al., 1977) to solve the problem involves adding membership variables p(k∣yv), for k = 1, …, K, that describe the posterior probability that voxel v is associated with the mixture component k. The details of the EM derivation are presented in Appendix A.
Starting with initial values and λ(0) for the model parameters, we iteratively compute the posterior assignment probabilities p(k∣yv) and then update the parameters and λ. In the E-step, we fix the model parameters and update the system memberships:
| (8) |
In the M-step, we update the model parameters:
| (9) |
| (10) |
After computing the updated cluster centers , the new concentration parameter λ(t+1) is found by solving the nonlinear equation
| (11) |
for positive values of λ(t+1), where
| (12) |
and the function AD(·) is defined as
| (13) |
Our algorithm for solving this equation is presented in Appendix B. Iterating the set of E-step and M-step updates until convergence, we find K system selectivity profiles mk and a set of soft assignments p(k∣yv) for k = 1, …, K. The assignments p(k∣yv), when projected to the anatomical locations of voxels, define the spatial maps of the discovered systems.
Figure 2 illustrates 5 systems and the corresponding profiles of selectivity found by this algorithm for the population of voxels shown in Figure 1(B). As expected, the analysis identifies clusters of voxels exclusively selective for one of the three conditions, but also finds a cluster selective for all three conditions along with a group of body selective voxels that show inhibition towards other categories. More complex profiles of selectivity such as the two latter cases cannot be easily detected with the conventional method.
Fig. 2.
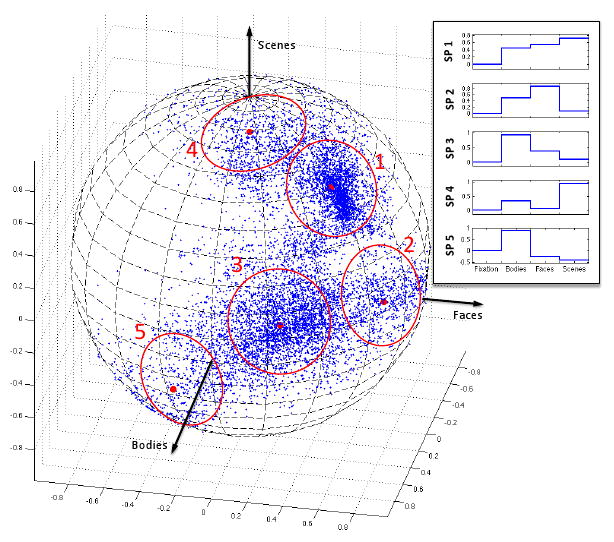
The results of mixture model density estimation with 5 components for the set of selectivity profiles in Figure 1(B). The resulting system selectivity profiles (cluster centers) are denoted by the red dots; circles around them indicate the size of the corresponding clusters. The box shows an alternative presentation of the selectivity profiles where the values of their components are shown along with zero for fixation. Since this format allows presentation of the selectivity profiles in general cases with D > 3, we adopt this way of illustration throughout the paper. The first selectivity profile, whose cluster includes most of the voxels in the overlapping region, does not show a differential response to our three categories of interest. Selectivity profiles 2, 3, and 4 correspond to the three original types of activation preferring faces, bodies, and scenes, respectively. Selectivity profile 5 shows exclusive selectivity for bodies along with a slightly negative response to other categories.
2.3 Cross-subject Consistency Analysis
Consider a group study where a group of subjects take part in an fMRI experiment. We denote a voxel in an experiment with S subjects by , where s ∈ {1, …, S} is the subject index, and v is the voxel index as before. We aim to discover the brain systems with distinct profiles of selectivity that are shared among all subjects. Let us assume that two selectivity profiles and , corresponding to voxel v of subject s and voxel v′ of subject s′, belong to the same selective system in the two brains. The overall magnitude of response of these two voxels can be different but the two profile vectors have to still reflect the corresponding type of selectivity. Therefore, they should resemble each other as well as the selectivity profile of the corresponding system. This suggests that we can fuse data from different subjects and cluster them all together in order to improve the estimates of system selectivity profiles. This approach can be thought of as a simple model that ignores possible small variability in subject-specific selectivity profiles of the same system, similar to the way that fixed effect analysis simplifies the more elaborate hierarchical model of random effect analysis in the hypothesis-driven framework (Penny and Holmes, 2003). At this stage, we choose to work with this simpler model and defer the development of a corresponding hierarchical model to future work.
Based on the above argument, if the set of vectors describes all relevant selectivity profiles in the brain system of interest, each voxel can be thought of as an independent sample from the distribution in Equation (4). Thus, we combine the data from several subjects to form the group data, i.e., , to perform our analysis across subjects. Applying our algorithm to the group data, the resulting set of assignments defines the spatial map of system k in subject s.
In conventional group data analysis, spatial consistency of the activation maps across subjects provides a measure for the evaluation of the results. In our method, we focus on the functional consistency of the discovered system selectivity profiles. To quantify this consistency, we define a consistency score (cs) for each selectivity profile found in a group analysis. Let be the group data including voxel profiles from S different subjects, K be the number of desired systems, and be the final set of system selectivity profiles found by the algorithm in the group data. We also apply the algorithm to the S individual subject data sets separately to find their corresponding S sets of subject-specific systems . We can then match the selectivity profile of each group system to its most similar system profile in each of the S individual data sets.
2.3.1 Matching Selectivity Profiles Across Subjects
The matching between the group and individual selectivity profiles is equivalent to finding S one-to-one functions ωs : {1, …, K} → {1, …, K} which assign system profile in subject s to the group system profile . We select the function ωs such that it maximizes the overall similarity between the matched selectivity profiles:
| (14) |
Here, ρ(·, ·) denotes the correlation coefficient between two vectors:
where 1 is the D-dimensional vector of unit components. The maximization in Equation (14) is performed over all possible one-to-one functions ω. Finding this matching is an instance of graph matching problems for a bipartite graph (Diestel, 2005). The graph is composed of two sets of nodes, corresponding to the group and the individual system profiles, and the weights of the edges between the nodes are defined by the correlation coefficients. We employ the well-known Hungarian algorithm (Kuhn, 1955) to solve this problem for each subject.1
Having matched each group system with a distinct system within each individual subject result, we compute the consistency score csk for group system k as the average correlation of its selectivity profile with the corresponding subject-specific system profiles:
| (15) |
Consistency score values measure how closely a particular type of selectivity repeats across subjects. Clearly, cs = 1 is the most consistent case where the corresponding profile identically appears in all subjects. Because of the similarity-maximizing matching performed in the process of computing the scores, even a random data set would yield non-zero consistency score values. We employ permutation testing to establish the null hypothesis distribution for the consistency score.
2.3.2 Permutation Test for the Consistency Scores
To construct the baseline distribution for the consistency scores under the null hypothesis, we make random modifications to the data in such a way that the correspondence between the components of the selectivity profiles and the experimental conditions is removed. Specifically, we randomize the condition labels before the regression step so that the individual regression coefficients do not correspond to any non-random distinctions in the task. More formally, we implement such a randomization in the linear analysis stage in Equation (1). Each temporal block in the experiment has a category label that determines its corresponding regressor in the design matrix G. We randomly shuffle these labels and, as a result, the regressors in the design matrix include blocks of images from random categories. The resulting estimated regression coefficients do not correspond to any coherent set of stimuli. Applying our analysis to this modified data set still yields a set of group and individual system selectivity profiles and corresponding cs values. Since there is no real structure in the data, all cs values obtained in this manner can serve as samples from the desired null hypothesis.
We estimate the null distribution of the cs values by generating randomly shuffled data sets, finding selectivity profiles of the group systems, and treating the resulting consistency scores for the K selectivity profiles as samples from our null distribution. We evaluate statistical significance of the cs value of each system selectivity profile based on this null distribution. In practice, for up to 10,000 shuffled data sets, the consistency scores of most system selectivity profiles in the real data exceed all the cs values estimated from the shuffled data, implying the same empirical significance of p = 10−4. To distinguish the significance of these different profiles through our p-value, we fit a Beta distribution to the null-hypothesis samples and compute the significance from the fitted distribution. Using a linear transformation to match the range [−1, 1] of cs values to the support [0, 1] of the Beta distribution, we obtain the pdf of the null distribution
| (16) |
where B(a, b) is the beta function. We find the maximum-likelihood pair (a, b) for the observed samples in the shuffled data set. We then characterize the significance of a selectivity profile with consistency score cs via its p-value, as inferred from the parametric fit to our simulated null-hypothesis distribution: .
2.4 Other Validation Procedures
In the previous section, we presented our procedure for assessment of the cross-subject consistency of the discovered selectivity profiles. An alternative way to assess the resulting system selectivity profiles is to examine their consistency across repetitions of the same category in different blocks. If we define two groups of blocks that present stimuli from the same category as two distinct experimental conditions, we expect the corresponding components of a consistent system selectivity profile to be similar. We will employ this method for a qualitative study of consistency.
While our analysis is completely independent of the spatial locations associated with the selectivity profiles, we can still examine the spatial extent of the discovered systems as a way to validate the results. If the selectivity profile of a system matches a certain type of activation, i.e., demonstrates exclusive selectivity for an experimental condition, we can compare the map of its assignments with the localization map detected for that activation by the conventional method. We use this comparison to ensure that our method yields systems with spatial extents that correspond to the perviously characterized selective areas in the brain.
Once we identify a system to be associated with a certain activation, we quantify the similarity between the spatial maps estimated by our method and that obtained via the standard hypothesis-driven method. We employ an asymmetric overlap measure between the spatial maps, equal to the ratio of the number of voxels in the overlapping region to the number of all voxels assigned to the system in our model. The asymmetry is included since, as we saw in the example in Section 2.1, being functionally more specific, our discovered systems are usually subsets of the localization maps found via the standard statistical test.
3 Results
We demonstrate our method on the data from a block design fMRI study of high level vision with 6 subjects. The images were acquired using a Siemens 3T scanner and a custom 32-channel coil (EPI, flip angle = 90°, TR = 2 seconds, in-plane resolution = 1.5 mm, slice thickness = 2 mm, 28 axial slices). The experimental protocol included 8 categories of images: Animals, Bodies, Cars, Faces, Scenes, Shoes, Trees, and Vases. For each image category, two different sets of images were presented in separate blocks. We used this setup to test that our algorithm successfully yields profiles with similar components for different images from the same category. Each block lasted 16 seconds and contained 16 images from one image set of one category. The blocks corresponding to different categories were presented in permuted fashion so that their order and temporal spacing was counter-balanced. With this design, the temporal noise structure is shared between the real data and the random permutations constructed by the procedure of Section 2.3.2. For each subject, there were 16 to 29 runs of the experiment where each run contained one block from each category and three fixation blocks. We perform motion correction, spike detection, intensity normalization, and Gaussian smoothing with a kernel of 3-mm width using the standard package FsFast.2
By modifying the condition-related part of the design matrix G in Equation (1) and estimating the corresponding regression coefficients β̂, we created three different data sets for each subject:
8-Dimensional Data: All blocks for one category were represented as a single experimental condition by one regressor and, accordingly, one regression coefficient. The selectivity profiles were composed of 8 components each representing one category.
16-Dimensional Data: The blocks associated with different image sets were represented as distinct experimental conditions. Since we had two image sets for each category, the selectivity profiles had two components for each category.
32-Dimensional Data: We split the blocks for each image set into two groups and estimated one coefficient for each split group. In this data set, the selectivity profiles were 32 dimensional and each category was represented by four components.
To discard the voxels with no visual activation, we formed contrasts comparing the response of voxels to each category versus fixation and applied the t-test to detect voxels that show significant levels of activation. The union of the detected voxels serves as the mask of visually responsive voxels used in our experiment. Significance thresholds were chosen to p = 10−2, p = 10−4, and p = 10−6, for 32-Dimensional, 16-Dimensional, and 8-Dimensional data, respectively, so that the visually selective masks for different data sets are of comparable size. An alternative approach for selecting relevant voxels is to use an F-test considering all regressors corresponding to the visual stimuli (columns of matrix G in Equation (1)). We observed empirically that the results presented here are fairly robust to the choice of the mask and other details of preprocessing.
3.1 Selectivity Profiles
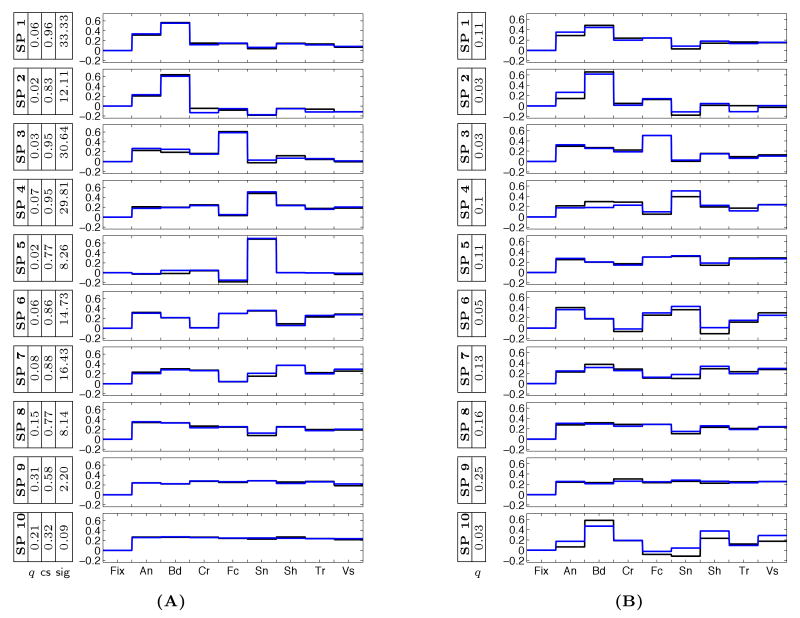
We apply the analysis to all three data sets. Figure 3(A) and Figure 4 show the resulting selectivity profiles of the group systems in the three data sets, where the number of clusters is K = 10. We also report cluster weights qk, consistency scores csk, and their corresponding significance values sig = −log10 p. In all data sets, the most consistent profiles are selective of only one category, similar to the previously characterized selective systems in high level vision. Moreover, their peaks match with these known areas such that in each data set, there are selectivity profiles corresponding to EBA (body-selective), FFA (face-selective), and PPA (scene-selective). For instance, in Figure 3(A), selectivity profiles 1 and 2 show body selectivity, selectivity profile 3 is face selective, and selectivity profiles 4 and 5 are scene selective. Similar profiles appear in the case of 8-Dimensional and 32-Dimensional data as well. Comparing the selectivity profiles found for one of the individual 16-Dimensional data sets with those of the group data in Figure 3(A) and (B) shows that the more consistent group profiles resemble their individual counterparts.
Fig. 3.
(A) A set of 10 discovered group system selectivity profiles for the 16-Dimensional group data. The colors (black, blue) represent the two distinct components of the profiles corresponding to the same category. We added zero to each vector to represent Fixation. The weight q for each selectivity profile is also reported along with the consistency scores (cs) and the significance values found in the permutation test, sig = −log10 p. (B) A set of individual system selectivity profiles in one of the 6 subjects ordered based on matching to the group profiles in (A).
Fig. 4.
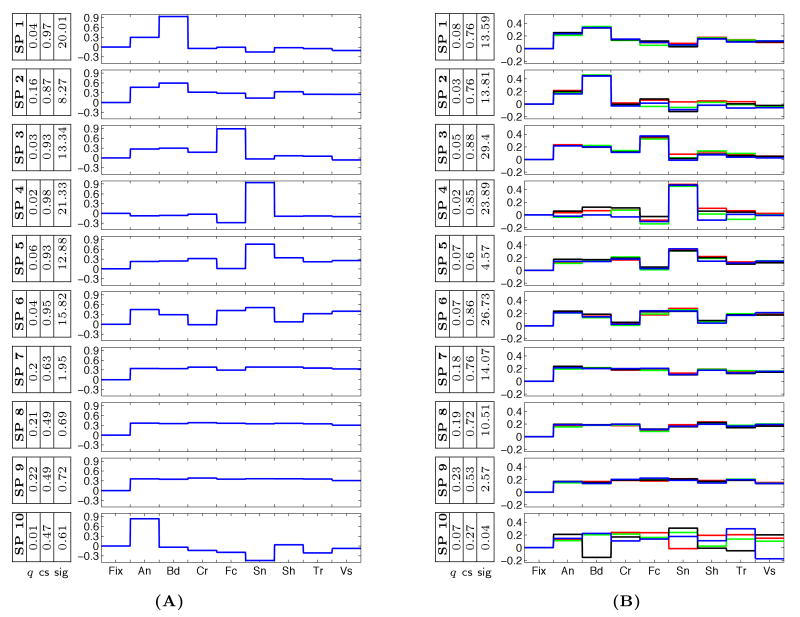
Sets of 10 discovered group system selectivity profiles for (A) 8-Dimensional, and (B) 32-Dimensional data. Different colors (blue, black, green, red) represent different components of the profiles corresponding to the same category. We added zero to each vector to represent Fixation. The weight q for each selectivity profile is also reported along with the consistency score (cs) and the significance value.
In each data set, our method detects systems with rather flat profiles over the entire set of presented categories. These profiles match the functional definition of early areas in the visual cortex, selective to lower level features in the visual field. Not surprisingly, there is a large number of voxels associated with these systems, as suggested by their estimated weights.
The 16-Dimensional and 32-Dimensional data sets allows us to examine the consistency of the discovered profiles across different image sets and different runs. Different components of the selectivity profiles that correspond to the same category of images, illustrated with different colors in Figure 3, have nearly identical values. This demonstrates consistency of the estimated profiles across experimental runs and image sets. The improvement in consistency from the individual data in Figure 3(B) to the group data of Figure 3(A) further justifies our argument for fusing data from different subjects.
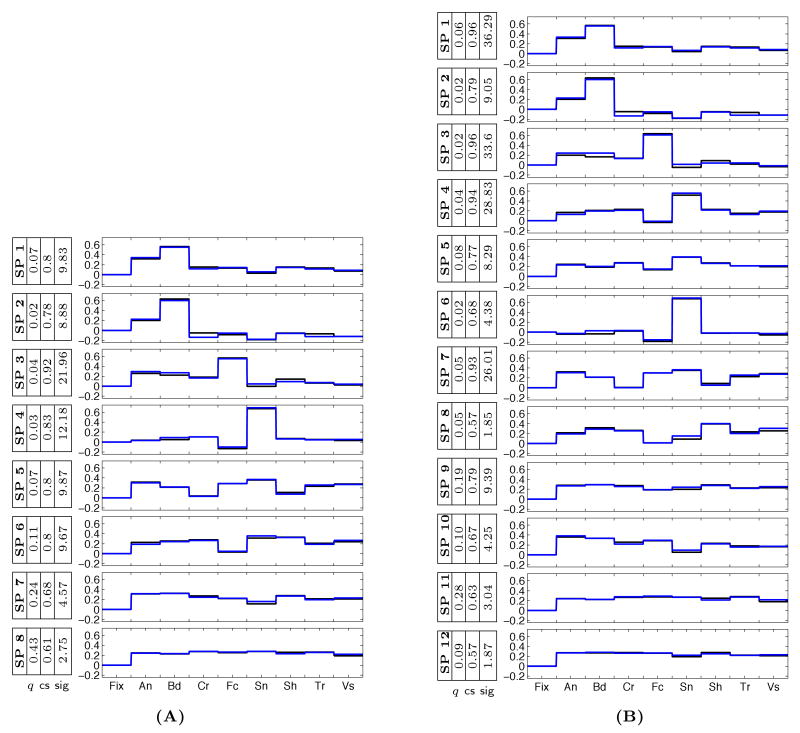
To examine the robustness of the discovered selectivity profiles to the change in the number of clusters, we ran the same analysis on the 16-Dimensional data for 8 and 12 clusters. Comparing the results in Figure 5 with those of Figure 3(A), we conclude that selectivity properties of the more consistent selectivity profiles remain relatively stable. In general, running the algorithm for many different values of K, we observed that increasing the number of clusters usually results in the split of some of the clusters but does not significantly alter the pattern of discovered profiles and their maps.
Fig. 5.
Group system selectivity profiles in the 16-Dimensional data for (A) 8, and (B) 12 clusters. The colors (blue, black) represent the two distinct components of the profiles corresponding to the same category, and the weight q for each system is also indicated along with the consistency score (cs) and its significance value found in the permutation test.
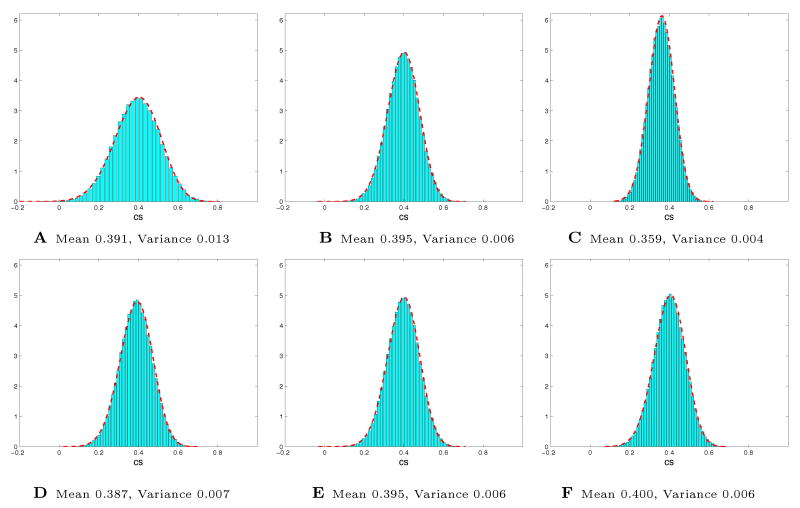
In order to find the significance of consistency scores achieved by each of these selectivity profiles, we performed a permutation test as described in Section 2.3. For each data set, we generated 10,000 permuted data sets by randomly shuffling labels of different experimental blocks. The resulting null hypothesis distributions are shown in Figure 6 for different data sets. Using these distributions, we compute the statistical significance of the consistency scores presented for the selectivity profiles in Figures 3, 4, and 5.
Fig. 6.
Null hypothesis distributions for the consistency score values, computed from 10,000 random permutations of the data. Histograms A, B and C show the results for 8, 16, and 32-Dimensional data with 10 clusters, respectively. Histograms D, E, and F correspond to 8, 10, and 12 clusters in 16-Dimensional data (B and E are identical). We normalized the counts by the product of bin size and the overall number of samples so that they could be compared with the estimated Beta distribution, indicated by the dashed red line.
3.2 Spatial Maps
We also examine the spatial maps associated with each system. Figure 7 shows the standard localization map for the face selective areas FFA and OFA in blue. This map is found by applying the t-test to identify voxels with higher response to faces when compared to objects, with a threshold p = 10−4, in one of the subjects. For comparison, Figure 7 also shows the voxels in the same slices assigned by our method to the system with the selectivity profile 3 in Figure 4(A) that exhibits face selectivity (red). The assignments found by our method represent probabilities over cluster labels. To generate the map, we assign each voxel to its corresponding maximum a posteriori (MAP) cluster label. We have identified on these maps the approximate locations of the two known face-selective regions, FFA and OFA, based on the result of the significance map, as it is common in the field. Figure 7 illustrates that, although the two maps are derived with very different assumptions, they mostly agree, especially in the more interesting areas where we expect to find face selectivity. As mentioned in Section 2.1, the conventional method identifies a much larger region as face selective, including parts in the higher slices of Figure 7 which we expect to be in the non-selective V1 area. Our map, on the contrary, does not include these voxels.
Fig. 7.
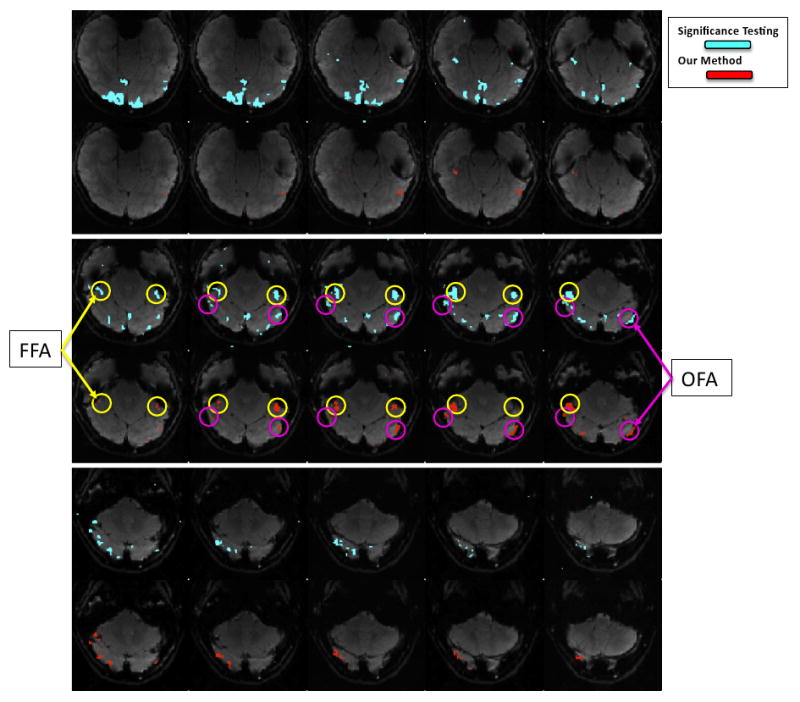
Spatial maps of the face selective regions found by the significance test (light blue) and the mixture model (red). Slices from the each map are presented in alternating rows for comparison. The approximate locations of the two face-selective regions FFA and OFA are shown with yellow and purple circles, respectively.
We compute three localization maps for face, scene, and body selective regions by applying statistical tests comparing response of each voxel to faces, scenes, and bodies, respectively, with objects, and thresholding them at p = 10−4. To define selective systems in our results, we employ the conventional definition requiring the response to the preferred category to be at least twice the value of the response to other stimuli. We observe that the largest cluster always has a flat profile with no selectivity, e.g., Figure 4 (A) and (B). We form the map associated with the largest system as another case for comparison and call it the non-selective profile. Table 1 shows the resulting values of our overlap measure averaged across all subjects for K = 8, 10, and 12. We first note that the overlap between the functionally related regions is significantly higher than that of the unrelated pairs. Moreover, these results are qualitatively stable with changes in the number of clusters.
Table 1.
Asymmetric overlap measures between the spatial maps corresponding to our method and the conventional hypothesis-driven approach. The exclusively selective systems for the three categories of Bodies, Faces, and Scenes, and the non-selective system (rows) are compared with the localization maps detected via traditional contrasts (columns). Values are averaged across all 6 subjects in the experiment.
| Gr. K = 10 | Face | Body | Place | Indiv. K = 10 | Face | Body | Place |
|---|---|---|---|---|---|---|---|
| Face | 0.78 ± 0.08 | 0.14 ± 0.11 | 0 | Face | 0.28 ± 0.44 | 0.05 ± 0.11 | 0.0 ± 0.01 |
| Body | 0.07 ± 0.06 | 0.94 ± 0.1 | 0.01 ± 0.02 | Body | 0.1 ± 0.09 | 0.65 ± 0.51 | 0.01 ± 0.02 |
| Scene | 0.01 ± 0.01 | 0.04 ± 0.04 | 0.57 ± 0.19 | Scene | 0.01 ± 0.01 | 0.05 ± 0.08 | 0.61 ± 0.47 |
| Non-selective | 0.06 ± 0.03 | 0.02 ± 0.02 | 0.1 ± 0.05 | Non-selective | 0.09 ± 0.09 | 0.09 ± 0.08 | 0.13 ± 0.13 |
| Gr. K = 8 | Face | Body | Place | Gr. K = 12 | Face | Body | Place |
| Face | 0.72 ± 0.08 | 0.16 ± 0.11 | 0 | Face | 0.83 ± 0.06 | 0.15 ± 0.12 | 0.0 ± 0.01 |
| Body | 0.07 ± 0.06 | 0.94 ± 0.1 | 0.01 ± 0.02 | Body | 0.07 ± 0.06 | 0.94 ± 0.09 | 0.01 ± 0.02 |
| Scene | 0.02 ± 0.03 | 0.04 ± 0.06 | 0.79 ± 0.19 | Scene | 0.01 ± 0.01 | 0.05 ± 0.05 | 0.66 ± 0.19 |
| Non-selective | 0.05 ± 0.02 | 0.02 ± 0.02 | 0.09 ± 0.04 | Non-selective | 0.08 ± 0.04 | 0.03 ± 0.03 | 0.09 ± 0.05 |
In the table, we also present the results of the algorithm applied to the data of each individual subject separately. We notice higher average overlap measures and lower standard deviations for the group data. This is due to the fact that fusing data from a cohort of subjects improves the accuracy of our estimates of the category selective profiles. As a result, we discover highly selective profiles whose response to the preferred stimuli satisfies the condition for being more than twice the other categories. On the other hand, in the results from the individual data for some noisier subjects, even the selective system does not satisfy this definition. For these subjects, no system is identified as exclusively selective of that category, degrading the average overlap measure. The improved robustness of the selectivity profile estimates in the group data prevents this effect and leads to better agreement in the spatial maps.
4 Discussion
Our new model rediscovers selectivity for faces, places, and bodies, now without assuming spatial contiguity of functionally similar voxels and without even assuming that category selectivity itself is a dominant property of the visual pathway.
Interestingly, we do not detect other possible profiles not known to have a corresponding selective area based on the high level vision literature. Prior work has shown that categories such as cars, shoes, and animals do not correspond to selective regions as robust and consistent as EBA, PPA, and FFA (Downing et al., 2006). Our results clearly agree with these findings but now from a completely data-driven perspective. This finding shows that the method allows us to explore the space of selectivity profiles in a less biased fashion and to search for types of selectivity that have not been hypothesized before. A possible example is the selectivity profile 6 in Figure 3(A) that consistently appears with the same shape in all individual subjects, despite not being exclusively selective of a single category.
The cross-subject consistency scores show qualitative correlation with consistency across runs and different image sets. For example, consider the 10th selectivity profile in Figure 4(B) that has low consistency score and whose components show considerable variability across repetitions of the category. By its definition, cross-subject consistency does not have to necessarily predict consistency of a profile across image sets and experimental runs. But if selectivity profiles are true signatures of the types of category selectivity existing in all subjects, we expect them to exhibit consistent patterns both across subjects and across different samples of the same categories of visual stimuli.
We discussed in Section 3.2 that the spatial maps of our systems have considerable overlap with the corresponding thresholded significance maps found by the conventional method. Note however that we do not expect a perfect overlap between the two methods. The experts commonly identify some subsections of the significance maps as the selective regions based on their prior anatomical knowledge. Therefore, the degree of overlap between our systems and the localization maps does not necessarily yield a quantitative measure of accuracy of our results. Rather, it acts as an argument for relative agreement of these two different definitions of selectivity.
Several dimensions remain for further extension and improvements of the current model. As with many other learning methods, our approach so far does not offer a systematic way to choose the number of clusters (model components, K). Although our results show relative robustness to changes in K, it is more desirable to have a method for automatic selection of the number of systems. By employing nonparametric approaches, such as Dirichlet processes (Teh et al., 2006), that integrate estimation of component number within the modeling framework, we can design appropriate infinite mixture models suited to our application (Rasmussen, 2000). Another possible extension involves introducing an explicit model of inter-subject variability. The model, as it stands now, does not distinguish the individual selectivity profiles from the group profiles, effectively assuming identical structure at the group level and at the individual subject level. We are developing a hierarchical model to address this point.
We also aim to extend the model to include a clustering structure in the space of experimental conditions. In the context of high level vision, for instance, this will enable discovery of the categories of visual stimuli intrinsic to the brain's visual representation. As a result, we can present distinct images to the subjects in the experiment and search for groupings of the images suggested by the data. We are currently performing event-related visual fMRI experiments with richer sets of images than presented here to examine the possibility of discovering novel patterns of selectivity using our new approach to data analysis.
To conclude, we presented an exploratory method that enables automatic discovery of the patterns of selectivity in fMRI experiments with numerous conditions. Our method is based on the idea of selectivity profiles that characterize the specificity of response in a variety of experimental conditions. The mixture model based on the selectivity profiles yields algorithms for discovery of brain systems with coherent patterns of selectivity that robustly appear across subjects. Defining these systems on a purely functional basis opens up the possibility of investigating likely functional systems with significant anatomical variability. The method further allows us to bypass the difficult procedure of spatial normalization for group analysis.
Acknowledgments
This work was supported in part by the McGovern Institute Neurotechnology Program, NIH grants NIBIB NAMIC U54-EB005149 and NCRR NAC P41-RR13218 to PG, NEI grant 13455 to NGK, NSF grant CAREER 0642971 to PG and IIS/CRCNS 0904625 to PG and NGK, in addition to an MIT HST Catalyst grant and an NDSEG fellowship to EV.
A Derivation of the EM Update Rules
We let be the full set of parameters and derive the EM algorithm for maximizing the log-likelihood function
| (A.1) |
for a mixture model . The EM algorithm (Dempster et al., 1977) assumes a hidden random variable k that represents the assignment of each data point to its corresponding component in the model. This suggests a model in the joint space of observed and hidden variables:
| (A.2) |
where k ∈ {1, …, K}, and the likelihood of observed data is simply
| (A.3) |
With a given set of parameters Θ(t) in step t, the E-step involves computing the posterior distribution of the hidden variable given the observed data. Since the data for each voxel is assumed to be an i.i.d. sample from the joint distribution (A.2), the posterior distribution for the assignment of all voxels can also be factored into terms for each voxel:
| (A.4) |
Using this distribution, we can express the target function of the M-step:
| (A.5) |
Taking the derivative of this function along with the appropriate Lagrange multipliers yields the update rules for the model parameters in iteration (t+1). For the cluster centers mk, we have
| (A.6) |
which implies the update rule . The Lagrange multiplier ensures that mk is a unit vector, i.e.,
Similarly, we find the concentration parameter λ:
| (A.7) |
where we have substituted in the first line, used the definition of Equation (12) in the second line, and the last equality follows from the properties of the modified Bessel functions. It follows then that AD(λ(t+1)) = Γ(t+1). Finally, for the cluster weights qk, adding the Lagrange multiplier to guarantee that the weights sum to 1, we find
| (A.8) |
which together with the normalization condition results in the update .
B Estimation of Concentration Parameter
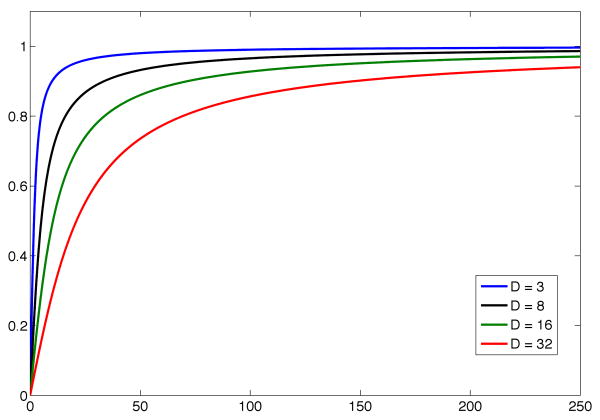
In order to update the concentration parameter in the M-step using (11), we need to solve for λ in the equation
| (B.1) |
Figure B.1 shows the plot of function AD(·) for several values of D. This function is smooth and monotonically increasing, taking values in the interval [0, 1). An approximate solution to (B.1) has been suggested in (Banerjee et al., 2006) but the proposed expression does not yield accurate values in our range of interest for D. Therefore, we derive a different approximation using the inequality
Fig. B.1.
Plot of function AD(·) for different values of D.
| (B.2) |
proved in (Amos, 1974). Defining , it follows from Equation (B.1) and Inequality (B.2) that
| (B.3) |
Due to continuity of as a function of α ≥ 1, this expression equals Γ for at least one value in the interval . For this value of α, we have
| (B.4) |
The expression for u is a monotonically decreasing function of α2 − 1 where ; therefore, we find
| (B.5) |
Now, using the inequality , we find a simpler expression for the lower bound
| (B.6) |
Finally, the parameter can be bounded by
| (B.7) |
Because of the monotonicity of AD(·), starting from the average of the two bounds and taking a few Newton steps towards zero of equation (B.1), we easily reach a good solution. However, when Γ is too close to 1 and, hence, λ is large, evaluation of the function AD(·) becomes challenging due to the exponential behavior of the Bessel functions. In this case, when Γ is large enough such that holds, we can approximate the second term in the upper bound of (B.7) as , reaching the final approximation
| (B.8) |
Footnotes
We used the open source matlab implementation of the Hungarian algorithm available at http://www.mathworks.com/matlabcentral/fileexchange/11609.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Danial Lashkari, Email: danial@mit.edu.
Ed Vul, Email: evul@mit.edu.
Nancy Kanwisher, Email: ngk@mit.edu.
Polina Golland, Email: polina@csail.mit.edu.
References
- Aguirre G, Zarahn E, D'Esposito M. Empirical analyses of BOLD fMRI statistics II. spatially smoothed data collected under null-hypothesis and experimental conditions. NeuroImage. 1997;5(3):199–212. doi: 10.1006/nimg.1997.0264. [DOI] [PubMed] [Google Scholar]
- Aguirre G, Zarahn E, D'Esposito M. An area within human ventral cortex sensitive to “building” stimuli: evidence and implications. Neuron. 1998;21(2):373–383. doi: 10.1016/s0896-6273(00)80546-2. [DOI] [PubMed] [Google Scholar]
- Amos D. Computation of modified Bessel functions and their ratios. Mathematics of Computation. 1974;28:239–251. [Google Scholar]
- Baker C, Liu J, Wald L, Kwong K, Benner T, Kanwisher N. Visual word processing and experiential origins of functional selectivity in human extrastriate cortex. Proceedings of the National Academy of Science. 2007;104(21):9087–9092. doi: 10.1073/pnas.0703300104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banerjee A, Dhillon I, Ghosh J, Sra S. Clustering on the unit hypersphere using von Mises-Fisher distributions. Journal of Machine Learning Research. 2006;6(2):1345–1382. [Google Scholar]
- Baumgartner R, Scarth G, Teichtmeister C, Somorjai R, Moser E. Fuzzy clustering of gradient-echo functional MRI in the human visual cortex. Part I: reproducibility. Journal of Magnetic Resonance Imaging. 1997;7(6):1094–1108. doi: 10.1002/jmri.1880070623. [DOI] [PubMed] [Google Scholar]
- Baumgartner R, Windischberger C, Moser E. Quantification in functional magnetic resonance imaging: fuzzy clustering vs. correlation analysis. Magnetic Resonance Imaging. 1998;16(2):115–125. doi: 10.1016/s0730-725x(97)00277-4. [DOI] [PubMed] [Google Scholar]
- Beckmann C, Smith S. Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE Transactions on Medical Imaging. 2004;23(2):137–152. doi: 10.1109/TMI.2003.822821. [DOI] [PubMed] [Google Scholar]
- Beckmann C, Smith S. Tensorial extensions of independent component analysis for multisubject FMRI analysis. NeuroImage. 2005;25(1):294–311. doi: 10.1016/j.neuroimage.2004.10.043. [DOI] [PubMed] [Google Scholar]
- Brett M, Johnsrude I, Owen A. The problem of functional localization in the human brain. Nature Reviews Neuroscience. 2002;3(3):243–249. doi: 10.1038/nrn756. [DOI] [PubMed] [Google Scholar]
- Burgess N, Maguire E, Spiers H, OKeefe J, Epstein R, Harris A, Stanley D, Kanwisher N. The parahippocampal place area: Recognition, navigation, or encoding. Neuron. 1999;23:115–125. doi: 10.1016/s0896-6273(00)80758-8. [DOI] [PubMed] [Google Scholar]
- Calhoun V, Adali T, McGinty V, Pekar J, Watson T, Pearlson G. fMRI activation in a visual-perception task: network of areas detected using the general linear model and independent components analysis. NeuroImage. 2001a;14(5):1080–1088. doi: 10.1006/nimg.2001.0921. [DOI] [PubMed] [Google Scholar]
- Calhoun V, Adali T, Pearlson G, Pekar J. A method for making group inferences from functional MRI data using independent component analysis. Human Brain Mapping. 2001b;14(3):140–151. doi: 10.1002/hbm.1048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempster A, Laird N, Rubin D. Journal of the Royal Statistical Society. Series B (Methodological) 1977. Maximum likelihood from incomplete data via the em algorithm; pp. 1–38. [Google Scholar]
- Diestel R. Graph Theory. Springer-Verlag; New York: 2005. [Google Scholar]
- Downing P, Chan AY, Peelen M, Dodds C, Kanwisher N. Domain specificity in visual cortex. Cerebral Cortex. 2006;16(10):1453–1461. doi: 10.1093/cercor/bhj086. [DOI] [PubMed] [Google Scholar]
- Downing P, Jiang Y, Shuman M, Kanwisher N. A cortical area selective for visual processing of the human body. Science. 2001;293(5539):2470–2473. doi: 10.1126/science.1063414. [DOI] [PubMed] [Google Scholar]
- Epstein R, Kanwisher N. A cortical representation of the local visual environment. Nature. 1998;392(6676):598–601. doi: 10.1038/33402. [DOI] [PubMed] [Google Scholar]
- Fadili M, Ruan S, Bloyet D, Mazoyer B. A multistep unsupervised fuzzy clustering analysis of fMRI time series. Human Brain Mapping. 2000;10(4):160–178. doi: 10.1002/1097-0193(200008)10:4<160::AID-HBM20>3.0.CO;2-U. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filzmoser P, Baumgartner R, Moser E. A hierarchical clustering method for analyzing functional MR images. Magnetic resonance imaging. 1999;17(6):817–826. doi: 10.1016/s0730-725x(99)00014-4. [DOI] [PubMed] [Google Scholar]
- Friston K, Ashburner J, Kiebel S, Nichols T, Penny W, editors. Statistical parametric mapping: the analysis of functional brain images. Academic Press, Elsevier; 2007. [Google Scholar]
- Friston K, Holmes A, Worsley K, Poline J, Frith C, Frackowiak R, et al. Statistical parametric maps in functional imaging: a general linear approach. Human Brain Mapping. 1994;2(4):189–210. [Google Scholar]
- Gee J, Alsop D, Aguirre G. Effect of spatial normalization on analysis of functional data. Proceedings of SPIE, Medical Imaging. 1997;3034:550–560. [Google Scholar]
- Golay X, Kollias S, Stoll G, Meier D, Valavanis A, Boesiger P. A new correlation-based fuzzy logic clustering algorithm for fMRI. Magnetic Resonance in Medicine. 1998;40(2):249–260. doi: 10.1002/mrm.1910400211. [DOI] [PubMed] [Google Scholar]
- Golland P, Golland Y, Malach R. Proceedings of MICCAI: International Conference on Medical Image Computing and Computer Assisted Intervention. 4791 of LNCS. Springer; 2007. Detection of spatial activation patterns as unsupervised segmentation of fMRI data; pp. 110–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goutte C, Hansen L, Liptrot M, Rostrup E. Feature-space clustering for fMRI meta-analysis. Human Brain Mapping. 2001;13(3):165–183. doi: 10.1002/hbm.1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goutte C, Toft P, Rostrup E, Nielsen F, Hansen L. On clustering fMRI time series. NeuroImage. 1999;9(3):298–310. doi: 10.1006/nimg.1998.0391. [DOI] [PubMed] [Google Scholar]
- Grill-Spector K, Malach R. The human visual cortex. Annual Review of Neuroscience. 2004;27:649–677. doi: 10.1146/annurev.neuro.27.070203.144220. [DOI] [PubMed] [Google Scholar]
- Kanwisher N. The ventral visual object pathway in humans: evidence from fMRI. In: Chalupa L, Wener J, editors. The Visual Neurosciences. MIT Press; 2003. pp. 1179–1189. [Google Scholar]
- Kanwisher N, McDermott J, Chun M. The fusiform face area: a module in human extrastriate cortex specialized for face perception. Journal of Neuroscience. 1997;17(11):4302–4311. doi: 10.1523/JNEUROSCI.17-11-04302.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanwisher N, Yovel G. The fusiform face area: a cortical region specialized for the perception of faces. Philosophical transactions of the Royal Society of London. Series B, Biological Sciences. 2006;361(1476):2109–2128. doi: 10.1098/rstb.2006.1934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N, Mur M, Ruff D, Kiani R, Bodurka J, Esteky H, Tanaka K, Bandettini P. Matching categorical object representations in inferior temporal cortex of man and monkey. Neuron. 2008;60(6):1126–1141. doi: 10.1016/j.neuron.2008.10.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhn H. The Hungarian Method for the assignment problem. Naval Research Logistics Quarterly. 1955;2:83–97. [Google Scholar]
- Malach R, Reppas J, Benson R, Kwong K, Jiang H, Kennedy W, Ledden P, Brady T, Rosen B, Tootell R. Object-related activity revealed by functional magnetic resonance imaging in human occipital cortex. Proceedings of the National Academy of Science. 1995;92(18):8135–8139. doi: 10.1073/pnas.92.18.8135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mardia K. Statistics of directional data. Journal of the Royal Statistical Society. Series B (Methodological) 1975:349–393. [Google Scholar]
- McCarthy G, Puce A, Gore J, Allison T. Face-specific processing in the human fusiform gyrus. Journal of Cognitive Neuroscience. 1997;9(5):605–610. doi: 10.1162/jocn.1997.9.5.605. [DOI] [PubMed] [Google Scholar]
- McKeown M, Makeig S, Brown G, Jung T, Kindermann S, Bell A, Sejnowski T. Analysis of fMRI data by blind separation into independent spatial components. Human Brain Mapping. 1998;6(3):160–188. doi: 10.1002/(SICI)1097-0193(1998)6:3<160::AID-HBM5>3.0.CO;2-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLachlan G, Peel D. Finite Mixture Models. New York: Wiley; 2000. [Google Scholar]
- Moser E, Diemling M, Baumgartner R. Fuzzy clustering of gradient-echo functional MRI in the human visual cortex. Part II: quantification. Journal of Magnetic Resonance Imaging. 1997;7 doi: 10.1002/jmri.1880070624. [DOI] [PubMed] [Google Scholar]
- Op de Beeck H, Haushofer J, Kanwisher N. Interpreting fMRI data: maps, modules and dimensions. Nature Reviews Neuroscience. 2008;9(2):123–135. doi: 10.1038/nrn2314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peelen M, Downing P. The neural basis of visual body perception. Nature Reviews Neuroscience. 2007;8(8):636–648. doi: 10.1038/nrn2195. [DOI] [PubMed] [Google Scholar]
- Penny W, Holmes A. Random effects analysis. In: F RSJ, F KJ, F CD, editors. Human Brain Function II. Elsevier; Oxford: 2003. pp. 843–850. [Google Scholar]
- Rasmussen C. The infinite Gaussian mixture model. Advances in Neural Information Processing Systems. 2000;12:554–560. [Google Scholar]
- Rossion B, Caldara R, Seghier M, Schuller A, Lazeyras F, Mayer E. A network of occipito-temporal face-sensitive areas besides the right middle fusiform gyrus is necessary for normal face processing. Brain. 2003;126(11):2381–2395. doi: 10.1093/brain/awg241. [DOI] [PubMed] [Google Scholar]
- Schwarzlose R, Baker C, Kanwisher N. Separate face and body selectivity on the fusiform gyrus. Journal of Neuroscience. 2005;25(47):11055–11059. doi: 10.1523/JNEUROSCI.2621-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spiridon M, Fischl B, Kanwisher N. Location and spatial profile of category-specific regions in human extrastriate cortex. Human Brain Mapping. 2006;27(1) doi: 10.1002/hbm.20169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teh Y, Jordan M, Beal M, Blei D. Hierarchical dirichlet processes. Journal of the American Statistical Association. 2006;101(476):1566–1581. [Google Scholar]
- Thirion B, Faugeras O. Proceedings of MICCAI: International Conference on Medical Image Computing and Computer Assisted Intervention. 2879 of LNCS. Springer; 2003. Feature detection in fMRI data: the information bottleneck approach; pp. 83–91. [Google Scholar]
- Thirion B, Flandin G, Pinel P, Roche A, Ciuciu P, Poline J. Dealing with the shortcomings of spatial normalization: Multi-subject parcellation of fMRI datasets. Human Brain Mapping. 2006;27(8):678–693. doi: 10.1002/hbm.20210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thirion B, Pinel P, Mériaux S, Roche A, Dehaene S, Poline J. Analysis of a large fMRI cohort: statistical and methodological issues for group analyses. NeuroImage. 2007a;35(1):105–120. doi: 10.1016/j.neuroimage.2006.11.054. [DOI] [PubMed] [Google Scholar]
- Thirion B, Pinel P, Tucholka A, Roche A, Ciuciu P, Mangin J, Poline JB. Structural analysis of fMRI data revisited: Improving the sensitivity and reliability of fMRI group studies. IEEE Transactions on Medical Imaging. 2007b;26(9):1256–1269. doi: 10.1109/TMI.2007.903226. [DOI] [PubMed] [Google Scholar]
- Woolrich M, Ripley B, Brady M, Smith S. Temporal autocorrelation in univariate linear modeling of FMRI data. Neuroimage. 2001;14(6):1370–1386. doi: 10.1006/nimg.2001.0931. [DOI] [PubMed] [Google Scholar]