Pattern Separation in the Dentate Gyrus: A Role for the CA3 Backprojection

Abstract

Many theories of hippocampal function assume that area CA3 of hippocampus is capable of performing rapid pattern storage, as well as pattern completion when a partial version of a familiar pattern is presented, and that the dentate gyrus (DG) is a preprocessor that performs pattern separation, facilitating storage and recall in CA3. The latter assumption derives partly from the anatomical and physiological properties of DG. However, the major output of DG is from a large number of DG granule cells to a smaller number of CA3 pyramidal cells, which potentially negates the pattern separation performed in the DG. Here, we consider a simple CA3 network model, and consider how it might interact with a previously-developed computational model of the DG. The resulting “standard” DG-CA3 model performs pattern storage and completion well, given a small set of sparse, randomly derived patterns representing entorhinal input to the DG and CA3. However, under many circumstances, the pattern separation achieved in the DG is not as robust in CA3, resulting in a low storage capacity for CA3, compared to previous mathematical estimates of the storage capacity for an autoassociative network of this size. We also examine an often-overlooked aspect of hippocampal anatomy that might increase functionality in the combined DG-CA3 model. Specifically, axon collaterals of CA3 pyramidal cells project “back” to the DG (“backprojections”), exerting inhibitory effects on granule cells that could potentially ensure that different subpopulations of granule cells are recruited to respond to similar patterns. In the model, addition of such backprojections improves both pattern separation and storage capacity. We also show that the DG-CA3 model with backprojections provides a better fit to empirical data than a model without backprojections. Therefore, we hypothesize that CA3 backprojections might play an important role in hippocampal function.

Introduction

The mammalian hippocampus, including dentate gyrus (DG) and areas CA3 and CA1, plays an important role in many forms of learning and memory, including the ability to rapidly form memories of unique episodic events (Eichenbaum, 2000; Kesner et al., 2004; Squire, 1987).

Numerous computational models have been constructed to address the role of the hippocampus and associated structures in learning and memory, and many are based upon the work of Marr (1971), who posited that the hippocampus could function as a content-addressable memory or autoassociative network (see also (Willshaw and Buckingham, 1990); autoassociative networks store input “patterns” in the modifiable connections between cells, so that when a partial version of a stored pattern is presented later, activity propagates along the previously-strengthened pathways to reinstate the complete, stored pattern (Kohonen, 1984). This process of reconstructing a complete, stored pattern from a partial version is termed pattern completion. Because such autoassociative networks are reminiscent of the “cell assemblies” proposed by Hebb (1949), they are often called Hebb-Marr networks (McNaughton and Morris, 1987). Within the hippocampus, CA3 is often considered the most plausible site for autoassociation (Kesner, 2007; McNaughton and Morris, 1987; Rolls, 1989a; Rolls, 1989b; Rolls and Treves, 1990; Treves and Rolls, 1994), primarily because there are extensive recurrent collaterals among CA3 pyramidal cells (Figure 1A; Amaral et al., 1990; Anderson et al., 2006).

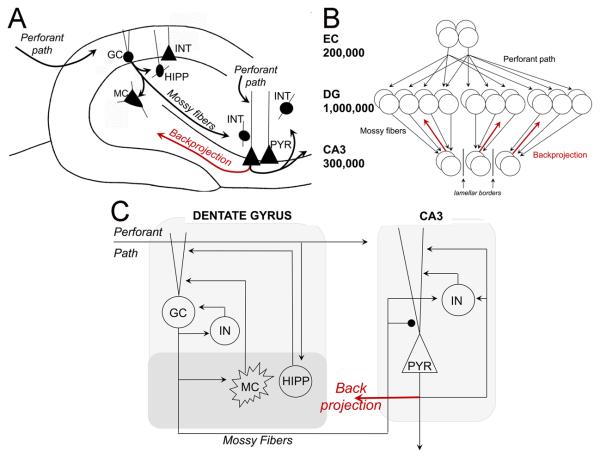
Figure 1.

Characteristics of the standard DG-CA3 model and its modification by addition of backprojections. (A) Simplified schematic of the DG and CA3 circuitry. The perforant path innervates distal dendrites of multiple cell types in the DG and CA3. Granule cell axons (the mossy fibers) project to neurons with dendrites in the hilus (interneurons and mossy cells) and neurons in CA3. Various interneurons exist throughout both areas, and only a subset is shown. Pyramidal cells have a complex projection which targets other CA3 cells via recurrent collaterals, CA1 cells by the Schaffer collaterals, and the contralateral hippocampus. They also send a collateral to the DG via the hilus (backprojection; red). B) In the rat, about 200,000 entorhinal layer II cells project to about 1 million granule cells (Amaral et al., 1990), so that information from entorhinal cortex “diverges” onto a larger number of granule cells; in general, this increases the sparseness of the representation and facilitates pattern separation. But, in the next step, information from the large granule cell layer “converges” onto a smaller number of CA3 pyramidal cells, so that -- in general -- information is re-compressed and some pattern separation would be lost. The mossy fiber pathway from DG to CA3 is predominantly confined within the lamellae of the granule cells of origin (i.e., it is lamellar), further reducing the ability of information from the DG to spread out across a large population of CA3 cells. Thus, anatomical information suggests that there should be some mechanism(s) to allow the pattern separation achieved in DG to be preserved in the transfer to CA3. We suggest that backprojections from CA3 to the DG (red arrows) may be one such mechanism. (C) Schematic of the “standard” DG/CA3 model, incorporating the DG model of Myers & Scharfman (2009) as well as a simple CA3 network that reflects the fundamental characteristics of CA3 circuitry shown in (A). For simplicity, the diagram only shows one of each cell type, and only one lamella. In the “backprojection” model, backprojections from CA3 to the DG (red arrow) are added to the “standard” model, with the simple assumption that pyramidal cells influence the same granule cells that target them, and that these backprojections are sufficient to temporarily silence granule cells. GC=granule cell; INT=interneuron, representing basket cells and other GABAergic neurons; MC=hilar mossy cell; HIPP=hilar interneuron receiving input from the perforant path, PYR=CA3 pyramidal cell. Strong synapses (from mossy fibers onto PYR) are indicated by large black circle; other synapses are indicated by arrowheads.

In order to store new patterns for later retrieval, an autoassociative network generally requires “teaching inputs.” Such teaching inputs are strong enough that, when the presynaptic cell is active, sufficient postsynaptic activity is evoked to trigger synaptic plasticity. The projections from dentate granule cells to CA3 pyramidal cells, called mossy fibers (Figure 1A), form extraordinarily large and strong synapses on the proximal apical dendrites of CA3 pyramidal cells, and spike trains in a single mossy fiber can cause the postsynaptic CA3 pyramidal cell to reach threshold (Henze et al., 2002; Henze et al., 2000; Kobayashi and Poo, 2004; Scharfman et al., 1990; von Kitzing et al., 1994). A second source of input to CA3 is from the entorhinal cortex via the perforant path (Calixto et al., 2008; Do et al., 2002; Wu and Leung, 1998; Yeckel and Berger, 1990), which targets the more distal apical dendrites of CA3 pyramidal cells. These anatomical considerations have led to the view that mossy fibers may function as teaching inputs to an autoassociative network in CA3 (McNaughton and Morris, 1987; McNaughton and Nadel, 1990; O'Reilly and McClelland, 1994; Rolls, 1989a; Rolls, 2007; Treves and Rolls, 1992). According to this view, input from the entorhinal cortex via the perforant path – representing a pattern to be stored – would arrive in CA3 both directly via normal synapses and via an indirect path through the DG (Figure 1A). Mossy fibers would be strong enough to evoke postsynaptic activity in the pyramidal cells they target, allowing synaptic strength to increase between co-active pairs of pyramidal cells and also between co-active pairs of entorhinal inputs and pyramidal cells. Later, when information is to be retrieved, entorhinal activity representing a partial pattern would activate a subset of CA3 pyramidal cells, which would in turn activate other pyramidal cells via the recently-strengthened synapses, until the complete stored pattern is reconstructed. The idea that the mossy fibers are important during learning, but not recall, has been supported recently by empirical data showing that mossy fiber input to CA3 is required for learning of new hippocampal-dependent information, while perforant path input to CA3 is important for recall of previously-stored information (Lee and Kesner, 2004b).

The Dentate Gyrus as a “Preprocessor” for CA3

In addition to its role as a source of teaching inputs to CA3, the DG may also pre-process entorhinal information. One role of preprocessing could be to facilitate storage of this information in CA3. Specifically, the storage capacity of an autoassociative network – meaning the number of distinct patterns it can store and accurately recall – is increased if the input patterns are sparse (containing few active elements) and non-overlapping (such that elements which are active in one pattern are unlikely to be active in other patterns) (Treves and Rolls, 1992; see also Marr, 1971; O'Reilly and McClelland, 1994). The process of changing a set of input patterns to make them sparser and less overlapping is termed pattern separation. Such a pattern separation function seems to be consistent with known features of the DG (e.g., Rolls, 1989a; Rolls, 1989b; Rolls and Treves, 1990; Rolls, 2007; Treves and Rolls, 1994). For example, granule cells tend to fire rarely (Jung and McNaughton, 1993; Scharfman, 1992a; Williamson et al., 1993), which tends to produce DG population firing patterns that are sparser than entorhinal input patterns. In addition, the size of the granule cell layer is large (about 1 million granule cells in rat; Amaral et al., 1990) relative to the entorhinal inputs (about 200,000 layer II entorhinal cells in the rat; Amaral et al., 1990); this “divergence” from a smaller to a larger number of cells means that even relatively similar patterns of entorhinal input should produce relatively non-overlapping patterns of granule cell activation. Moreover, each entorhinal projection cell innervates many granule cells (Tamamaki and Nojyo, 1993; Witter and Wouterlood, 2002), although these inputs may not be sufficient to elicit action potentials in granule cells. Nevertheless, recent empirical data regarding selective DG manipulations support the idea that the DG is involved in pattern separation, particularly in tasks that require very similar stimuli to be distinguished (Clelland et al., 2009; Gilbert et al., 2001; Hunsaker et al., 2008; McHugh et al., 2007).

A major question arises when one considers the DG projections to CA3 (Figure 1B). The divergence from a smaller number of entorhinal cells to a larger number of granule cells is almost immediately reversed in the projection from a large number of granule cells to a smaller number of CA3 pyramidal cells (about 300,000 in rat (Amaral et al., 1990). Even though the mossy fiber projection is extremely sparse, with each CA3 pyramidal receiving input from only about 50 granule cells (Amaral et al., 1990), it has been calculated that if 1% of the granule cells are active, then some 40% of CA3 pyramidal cells will receive input from at least one active mossy fiber input, and some 10% will receive input from two or more (Rolls, 2007). The ultimate effect in area CA3 is complex because one presynaptic mossy fiber does not necessarily cause a postsynaptic CA3 pyramidal cell to reach threshold. However, despite the circuit considerations, the substantial difference in granule cell numbers relative to CA3 pyramidal cells makes it likely that some pattern separation achieved in the DG will be lost as information is transferred to CA3 for storage (see also McNaughton & Nadel, 1990). The issue could be complicated if the primary effect of mossy fiber activity on CA3 pyramidal cells is inhibitory, which has been proposed (Acsady et al., 1998); still, it seems likely some pattern separation will be lost as information is transferred from the large granule cell population to the smaller CA3 pyramidal cell population, potentially counteracting any DG-mediated pattern separation. In fact, it is worth asking if DG preprocessing actually improves pattern storage in CA3, and what benefit is provided by a large granule cell layer, relative to the size of the CA3 pyramidal cell layer (see also McNaughton and Nadel, 1990; Rolls, 2007; Treves et al., 2008).

A large number of computational and analytical models have embodied the basic ideas of autoassociation in CA3 and pattern separation in DG to preprocess information for storage in CA3 (e.g., Becker, 2005; Hasselmo et al., 1995; Hasselmo and Wyble, 1997; Lörincz and Buzsáki, 2000; Lynch and Granger, 1992; O'Reilly and McClelland, 1994; O'Reilly and Rudy, 2001; Rolls, 1989a; Rolls, 1989b; Rolls and Treves, 1990; Rolls, 2007; Rolls et al., 1997; Treves and Rolls, 1992). Nevertheless, it is perhaps surprising that few of these models have specifically investigated the degree to which preprocessing by the DG actually improves pattern storage and retrieval in CA3. In principle, an autoassociative network with sparse connections between cells can perform some pattern separation merely as a result of attractor dynamics in the network (e.g., Marr, 1971; McNaughton, 1989; Treves and Rolls, 1992; etc.), without requiring preprocessing. In fact, many existing computational models of hippocampal autoassociation have made simplifying assumptions, either combining entorhinal cortex and DG or CA3 and DG into a single network, or else by including only as many dentate granule cells as CA3 pyramidal cells, so that the connection from teaching inputs to pyramidal cells is one-to-one (e.g., Burgess and O'Keefe, 1996; Hasselmo et al., 1995; Hasselmo and Wyble, 1997; Hasselmo et al., 1996; Levy, 1989; Levy, 1996; Levy et al., 2005; McNaughton and Smolensky, 1991; etc.). Such models often perform pattern storage and retrieval quite effectively.

Other existing computational models have included a dentate network that is large relative to the CA3 network, and have assumed that such a large DG improves CA3 performance, but most have not explicitly verified this assumption. Among those few modeling studies that have specifically examined the effect of varying DG size, results are surprising: as long as there are about as many granule cells as CA3 pyramidal cells, further increases in the size of the DG do not necessarily improve pattern storage and retrieval in CA3 models (Becker, 2005; Weisz and Argibay, 2009). In fact, under some circumstances, increasing the size of the DG can potentially decrease pattern separation in CA3 models, particularly for inputs that are already very distinct (Weisz and Argibay, 2009). The burden of proof thus shifts to those who construct computational models to verify that a large DG preprocessor indeed improves CA3 functionality. If this is not generally true, then the “standard” view of DG as pattern separator and preprocessor for pattern storage and retrieval in a CA3 autoassociator may be incorrect or, at least, other considerations may need to be invoked, such as additional aspects of the biological circuitry.

One feature of hippocampal anatomy which may be important is the backprojection from CA3 to DG (Figure 1A; Scharfman, 2007). This projection has largely been overlooked by computational models which generally assume a unidirectional flow of information from entorhinal cortex to DG and CA3 and from DG to CA3 (an important exception is Lisman et al. (2005), reviewed further below).

To examine the potential role of backprojections in DG-CA3 function, we develop a simple CA3 network that includes major cell types and anatomical connectivity patterns, and consider how this network might interact with a recently-developed computational model of the DG, which incorporates major cell types and anatomical connectivity patterns (Myers and Scharfman, 2009). This forms the “standard” DG-CA3 model. We also consider a version of the model that includes a simplified backprojection from CA3 pyramidal cells that exert inhibitory effects on granule cells within the same lamella (Scharfman, 2007). Such inhibitory backprojections could potentially help ensure that, once a pattern is stored in CA3, the granule cells that were recently active are silenced, ensuring that different subpopulations of granule cells are recruited to respond to similar patterns in the future, which in turn increases the probability that new subpopulations of CA3 pyramidal cells are targeted, which in turn could improve pattern separation as well as storage capacity in CA3.

A Computational Model of the DG-CA3 Interaction

To model the combined DG-CA3 system, we constructed a simple autoassociative model of CA3 capable of performing pattern storage and recall, and allowed it to interact with a model of the DG, which had been previously shown to be able to replicate several behavioral data sets acquired in vivo (Myers & Scharfman, 2009), including the ability of dentate granule cells to disambiguate small differences in input patterns (Leutgeb et al., 2007) and the effects of ablating hilar mossy cells or interneurons on granule cells activation (Ratzliff et al., 2004). Here, because we wanted a CA3 model containing a few hundred pyramidal cells (discussed further below), and because it is known that there are about three times as many granule cells as pyramidal cells in rats (Amaral et al., 1990), we expanded the previous DG model by increasing it from 500 granule cells to 1000 granule cells, with the numbers of other DG cell types in the model increased proportionally. We also included lamellar organization, as described below. Finally, we allowed the DG and CA3 models to interact, forming a DG-CA3 model. We compare a “standard” DG-CA3 model, in which projections are unidirectional, and a “backprojection” model, in which axon collaterals from CA3 pyramidal cells project back to the DG.

1. DG Network

The dentate gyrus model is a larger version of that presented in Myers & Scharfman (2009), and is illustrated in Figure 1C; full implementation details are provided in Appendix 1. In brief, the DG network includes a layer of 1,000 granule cells; following empirical data (e.g., Morgan and Soltesz, 2008) regarding the lamellar organization of the DG, the DG network is divided into ten non-overlapping lamellae, each containing 100 granule cells. Each lamella in the model contains an interneuron representing somatic or axo-axonic GABAergic inhibition by basket cells and axo-axonic cells. In the model, interneurons are excited by and inhibit granule cells in the same lamella. The DG model also contains 200 entorhinal cells providing perforant path input to the granule cells, 30 hilar mossy cells that are excited by granule cells within the same lamella and provide excitatory input to granule cells outside that lamella, and 12 hilar interneurons with axons that project to the terminal zone of the perforant path (HIPP cells) that are excited by perforant path input and provide inhibition to granule cells. The details of how these cells, numbers and circuitry were chosen are discussed elsewhere (Myers and Scharfman, 2009).

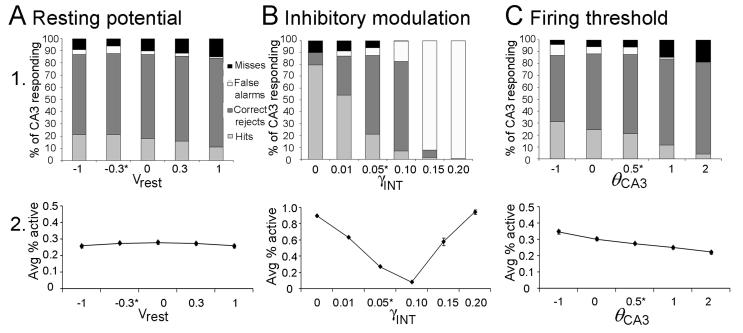
Regarding the perforant path input to granule cell dendrites, it is assumed that each entorhinal input pattern elicits some depolarizations in granule cells that do not reach action potential threshold, and some that do. Furthermore, input patterns are separated sufficiently in time so that granule cells and other DG neurons are not directly influenced by their own previous responses. Regarding granule cell output, subthreshold depolarizations may be influential (Alle and Geiger, 2006), but the model assumes that the most important outputs from the granule cells to CA3 are the action potentials traveling down the granule cell mossy fibers. Therefore, whereas Myers & Scharfman (2009) assessed DG output in terms of continuously-graded granule cell depolarizations, here DG output is assessed in terms of granule cell firing, with each granule cell either producing action potentials (spiking) or remaining silent. Spiking occurs if depolarization passes a threshold Θ_DG (see Appendix 2 for parametric studies that formed the basis for choosing a threshold value).

During each trial, the DG model is presented with a 200-element input pattern specifying whether each entorhinal cell has fired (1) or is silent (0), and produces a 1000-element output pattern specifying whether each granule cell fired (1) or not (0) in response to that input pattern. Simulations with this DG model, including those discussed below, produced pattern separation behavior similar to that described for the previously published version of the DG model (Myers and Scharfman, 2009).

Performance of the DG model is assessed primarily by pattern separation. Specifically, a set of entorhinal input patterns is constructed so that each pattern has a defined level of overlap with the others in the set; each input pattern is presented to the DG model, and the output pattern (whether each granule cell spikes or not in response to that input) is recorded. Pattern separation is defined by output patterns that overlap less than input patterns.

CA3 Network

The CA3 network is a simple autoassociative network, conceptually similar to CA3 models in the literature based on widely-accepted principles of hippocampal anatomy and function (see, e.g., Becker, 2005; Hasselmo et al., 1995; Hasselmo and Wyble, 1997; McNaughton and Morris, 1987; Norman and O'Reilly, 2003; O'Reilly and Rudy, 2001; Rolls, 1989a; Rolls, 1989b; Rolls, 2007; Treves and Rolls, 1992; Treves and Rolls, 1994; etc.), and is illustrated in Figure 1C. Full implementation details are described in Appendix 1.

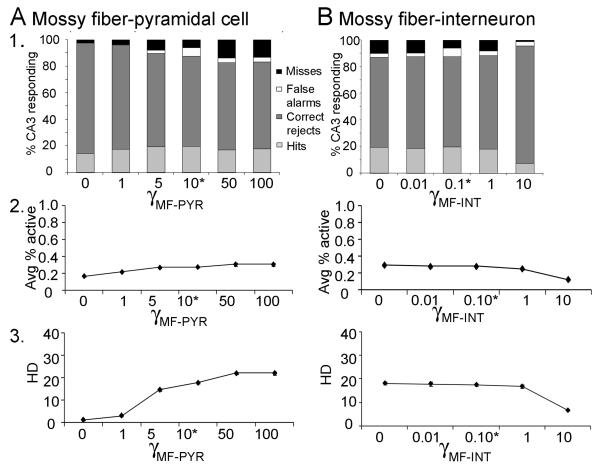
Given 1000 granule cells in the DG model, and following empirical data regarding the ratio of granule cells to CA3 pyramidal cells in rat (e.g., Treves and Rolls, 1994), the CA3 model includes 300 pyramidal cells. Based on empirical data (Lømo, 2009; Witter, 2007), the CA3 model is divided into 10 lamellae, each containing 30 pyramidal cells; each CA3 lamella in the model also contains an interneuron, reflecting the subtypes of interneurons which are excited by pyramidal cells in the same lamella and which inhibit pyramidal cells locally. Connectivity patterns for other cell types follow those observed in the rat (see Treves and Rolls, 1994, for review). Empirical data show that pyramidal cells in CA3 receive diffuse (non-lamellar) excitatory input from about 2% of the entorhinal inputs (Amaral et al., 1990), so the model includes six entorhinal inputs for each CA3 pyramidal cell. Finally, pyramidal cells in CA3 receive diffuse (non-lamellar) excitatory inputs from about 4% of the other CA3 pyramidal cells via recurrent axonal collaterals (Rolls and Treves, 1994; Rolls and Kesner, 2006), so each pyramidal cell in the model receives input from 12 other CA3 pyramidal cells. Pyramidal cells in each lamella of the model also receive mossy fiber input, from granule cells in the corresponding lamella of DG. Similar to other computational models (reviewed above), mossy fiber inputs to CA3 pyramidal cells are presumed to act as “teaching inputs” in the model, meaning that presynaptic action potentials in single mossy fiber axons are sufficient to induce action potentials in a postsynaptic cell. This is consistent with empirical data showing that the quantal size of giant mossy fiber boutons is extremely large, so summation of a few inputs is likely to be sufficient to cause action potential generation (Henze et al., 2000; Scharfman et al., 1990). Because mossy fiber innervation of CA3 pyramidal cells is extremely sparse (Amaral et al., 1990), the model assumes the minimal number of connections, with each mossy fiber targeting one CA3 pyramidal cell. Because granule cells outnumber pyramidal cells, each pyramidal cell therefore receives input from 3-4 granule cells. Because mossy fibers also make numerous contacts onto interneurons that inhibit pyramidal cells (Acsády et al., 1998), mossy fibers from each lamella of the DG model also target CA3 interneurons within the same lamella.

Similar to prior autoassociative models of hippocampus (Hasselmo, 2005; Hasselmo et al., 2002; Hasselmo et al., 1995; McNaughton and Nadel, 1990), we assume that CA3 can operate in a continuum between two modes: a “storage” mode, in which the mossy fibers are active but recurrent collaterals from other CA3 pyramidal cells are selectively suppressed, and a “recall” or “pattern completion” mode, in which mossy fibers are silent but recurrent collaterals are active. This idea of separate “storage” and “recall” modes in the hippocampus is supported by empirical studies of Hasselmo and colleagues (e.g., Hasselmo et al., 1995), who found that cholinergic input to the hippocampus could selectively suppress inputs from other CA3 pyramidal cells more than extrinsic inputs (entorhinal and mossy fiber inputs), just as would be required in “storage” mode; in the absence of cholinergic inputs, recurrent excitatory inputs were active, as would be required in a “recall” mode. Subsequent studies suggested that separate storage and recall phases in hippocampus might also be linked to different phases of the theta rhythm (Hasselmo, 2005; Hasselmo et al., 2002). This basic idea, that mossy fiber activity is important to CA3 acquisition and storage, rather than recall, is further supported by findings that mossy fiber inactivation (or dentate gyrus lesion) impairs new hippocampal-dependent learning but spares recall of previously-acquired information (Lassalle et al., 2000; Lee and Kesner, 2004b).

The model operates in two modes. In “recall mode,” entorhinal input is presented, providing excitatory input to CA3 pyramidal cells, some of which are sufficiently depolarized to fire in response; activity is allowed to reverberate within the CA3 model, including both pyramidal cells and interneurons, until the network settles into a stable attractor, with each CA3 pyramidal cell spiking (1) or not (0). The output of the CA3 model is a 300-element output pattern specifying whether each CA3 pyramidal cell spiked or not. This vector of CA3 outputs is the retrieved pattern.

In “storage mode,” entorhinal input is still present and mossy fiber input arrives in CA3. CA3 pyramidal cells and interneurons respond to the input. Hebbian-like plasticity occurs, increasing synaptic strength between pairs of co-active entorhinal and pyramidal cells, and between pairs of co-active pyramidal cells; synaptic strength decreases in the presence of concurrent postsynaptic activity and presynaptic inactivity. The timing of events in the model, in which CA3 pyramidal cells respond to entorhinal inputs before mossy fiber inputs arrive, is consistent with empirical data showing that CA3 population spikes that are evoked in response to perforant path stimulation occur 0.5-3 ms before the DG population spike that is evoked by the same stimulus (Derrick, 2007; Do et al., 2002).

The performance of the CA3 model is primarily assessed by pattern completion – the accuracy with which a previously-stored pattern is recalled when the entorhinal inputs present a partial version of the original input pattern. Similar to the DG model, pattern separation in CA3 can also be measured in terms of the average overlap in CA3 pyramidal cell spiking to a set of input patterns, compared to the average overlap among the input patterns themselves.

3. CA3 Backprojections

The above describes the “standard” DG-CA3 model, in which information flow is unidirectional (from entorhinal cortex to DG and from entorhinal cortex and DG to CA3).

Anatomical data show that collaterals of CA3 pyramidal cell axons also enter the hilus and project to the granule cell layer/hilar border (Figure 1A; Ishizuka et al., 1990). In the ventral hippocampus, axons from the pyramidal cell axon collaterals enter the granule cell layer and also the inner molecular layer (Li et al., 1994). Physiological studies show that hilar stimulation can evoke antidromic action potentials in CA3 (Scharfman, 2007), and further electrophysiological studies ultimately identified that CA3 pyramidal cells project to hilar mossy cells (Scharfman, 1994a; Scharfman, 1994b; Scharfman, 1994c; Scharfman, 2007) and to DG interneurons with dendrites in the hilus (Kneisler and Dingledine, 1995; Scharfman, 1994a). Under normal conditions in a hippocampal slice, granule cells appear to be inhibited after CA3 pyramidal cell activation, and empirical data suggested that inhibition was mediated by DG interneurons that were activated by CA3 pyramidal cells (Scharfman, 1994a). Therefore, within a given lamella, the net effect of the backprojection appears to be disynaptic inhibition of granule cells. Other characteristics of the backprojection are also important, such as the projection to mossy cells that could activate granule cells in distal lamellae (for review, see Scharfman, 2007).

Here, we hypothesize that one function of such an inhibitory backprojection within a lamella might be to preferentially inhibit those granule cells that projected to the CA3 pyramidal cells where the backprojections originated. In the model, this inhibition lasts for the period from presentation of the next entorhinal input pattern, through its processing by the DG-CA3 system, until the presentation of a subsequent input pattern. This timeframe might correspond to a very brief period (10-20 msec; Scharfman, 1994a) in the substrate. It is intriguing to consider that this timing is similar to a gamma cycle, and that the backprojection may play a role in gamma oscillations. It is also relevant that this inhibitory pathway could allow a different subpopulation of granule cells to respond to the next input pattern from the EC compared to the subset of granule cells activated by the first input pattern. This should improve pattern separation because even highly overlapping patterns occurring in succession would activate different subpopulations of CA3 pyramidal cells.

Therefore, in addition to the “standard” DG-CA3 model described above, we also consider a “backprojection” model which is identical to the “standard” DG-CA3 model except for the inclusion of axon collaterals from CA3 pyramidal cells to the DG (Figure 1C; see Appendix 1 for full implementation details). In the backprojection model, we have modified the DG-CA3 model to include a very simplified backprojection pathway, with each active CA3 pyramidal cell in the model projecting back to the DG within the same lamella to inhibit those granule cells that send mossy fibers to that pyramidal cell. The backprojection has the effect of selectively and temporarily silencing the subpopulation of granule cells that projected to those pyramidal cells that were activated by the first perforant path input pattern – and biases the DG to activate a different subset of granule cells in response to the next input pattern. The new subset of granule cells is likely to activate a different subset of CA3 pyramidal cells than was activated by first subset, and hence the previous input pattern, leading to an increase in pattern separation in CA3.

This “backprojection” model is clearly a simplification, meant primarily to explore the extent to which targeted inhibition to the DG might affect pattern separation in DG and pattern completion in CA3. There is no assumption made in the model that this inhibition is monosynaptic or polysynaptic, although it is likely to be polysynaptic because pyramidal cells are glutamatergic neurons (Scharfman, 2007). Furthermore, no assumptions concerning Hebbian plasticity are made, because empirical information about this issue is currently unavailable.

Pattern Storage and Retrieval in the Model

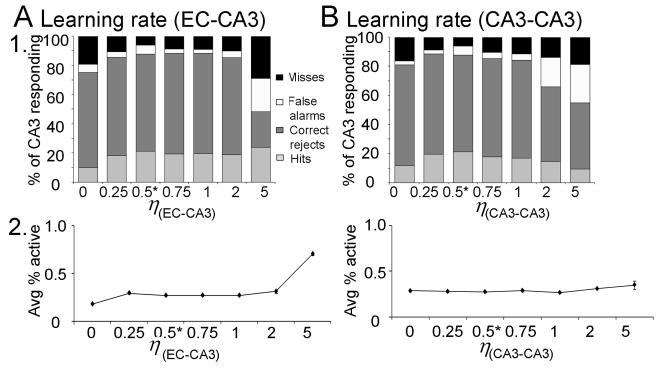
To test the model for its ability to perform pattern storage and recall, a series of simulations were conducted using a small set of randomly-constructed, sparse input patterns. Input patterns I₀, I₁,… were constructed randomly with a fixed input density (d), meaning that d% of the entorhinal inputs were active (set to 1) in each input pattern. Although it is difficult to know what ranges of d might occur in vivo, it has been suggested that granule cells in the rat require input from about 10% of their perforant path synapses in order to become active (McNaughton et al., 1991). As a result, for the current simulations, d was set to a default of 10%, a value also used in other computational models (e.g., Becker, 2005; Myers and Scharfman, 2009; Norman and O'Reilly, 2003; O'Reilly and Rudy, 2001; etc.). Each of the patterns was presented, and trained, 5 times.

Pattern storage and retrieval

To test pattern completion, each of 10 trained patterns I_x was used to construct an incomplete pattern I_x' in which some fixed percentage (p) of the active elements were randomly selected and turned off (set to 0). Ten such incomplete versions were constructed for each trained pattern at each of 10 values of p (p=0%, p=10%, … p=90%), where p=0% means that the test pattern is identical to the original input pattern, and p=90% means that only 10% of the original trained pattern is presented. The performance of the model was evaluated by comparing the output pattern generated in the CA3 model to each test pattern against that generated in response to the corresponding trained pattern. Specifically, CA3 pyramidal cells that were active in response to both the test and training patterns were scored as “hits” and those that were inactive in response to both were scored as “correct rejects”; the sum of “hits” and “correct rejects” together provide a measure of overall accuracy of the reconstructed pattern (and hence, pattern completion). Errors were scored if the response of a pyramidal cell to the test pattern was different than its response to the training pattern, either by incorrect activity in response to the test pattern (“false alarm”) or incorrect silence (“miss”).

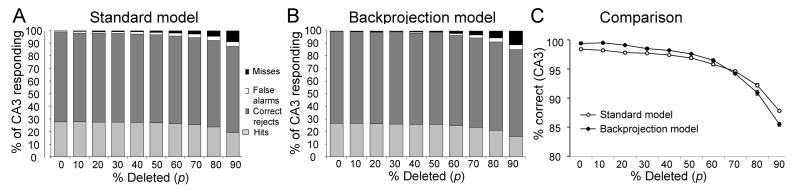
Figures 2A,B show that both the “standard” DG-CA3 model and the “backprojection” model are able to reconstruct the trained patterns almost perfectly for p≤50%, and that retrieval is accurate (few false alarms or misses) even when only a small portion of the original input is presented (p=90%). In terms of percent correct responses (hits + correct rejects, Figure 2C), there is no significant difference in performance between the standard DG-CA3 model and the backprojection model (repeated-measures ANOVA, F(1,18)=1.46, p=0.243). However, as shown in Figure 2C, both models show a significant decrease in pattern completion as the percentage of deleted elements (p) increases (F(9,162)=973.75, p<0.001).

Figure 2.

Pattern completion performance in the standard DG-CA3 model (A) and backprojection model (B), after training on 10 input patterns with input density d=10% (where d is the percent of entorhinal inputs that are active – firing – in each input pattern). Subsequently the model is tested using modified input patterns in which a percentage (p) of active elements is deleted. The performance of the model is evaluated as the percentage of CA3 pyramidal cells showing Hits (gray; active in both stored and retrieved pattern), Correct Rejects (dark gray; active in neither stored nor retrieved pattern), Misses (black; active in stored but not retrieved pattern), or False Alarms (white; active in retrieved but not stored pattern). For p<50%, pattern completion is excellent (mostly Hits and Correct Rejects, with very few Misses or False Alarms). Even at p=90%, more than 85% of the trained patterns are correctly reconstructed. (C) Overall percent correct on the pattern completion task, defined as total Hits plus Correct Rejects, does not differ significantly between the standard and backprojection models. For this figure and following ones, statistical comparisons are presented in the text.

In summary, the DG-CA3 model (with or without backprojections) performed pattern storage and recall well, given a small number of randomly-constructed, relatively sparse (d=10%) input patterns. This result is consistent with the hypotheses discussed above, that the CA3 region performs pattern storage and recall, and is also consistent with many prior models of CA3 and DG-CA3 interactions.

Pattern Separation Tests

The simulations above considered a set of input patterns with a particular input density (d=10% active entorhinal inputs in each pattern). In general, patterns with sparse density (low d) are easier for an autoassociative network to store than patterns with high density, because there is reduced likelihood that elements which are active in one pattern will also be active in others. Rolls (1989b; 2007) has suggested that the very low firing rate of granule cells could help the DG transform high-density input patterns to low-density patterns, facilitating CA3 storage and recall. If so, then one would expect that DG preprocessing might be most important when the input density is high. To test this idea, we tested the DG-CA3 model using sets of input patterns constructed with varying input density (d), and measured pattern separation in both DG and CA3.

One way of assessing pattern separation in this context is by computing the average overlap between pairs of input patterns and comparing this to the average overlap of output to the same pairs of patterns. A convenient metric for quantifying the amount of overlap of two input patterns is the Hamming distance. The Hamming distance between two input patterns, I_x and I_y, is defined as the number of mismatching elements in I_x vs. I_y. For example, if input patterns I_x and I_y are identical, then the Hamming distance between I, and I_y is 0; if they are completely non-overlapping, such that every element set to 0 or 1 in I_x is set to the opposite value in I_y, then the Hamming distance is E, where E is the total number of elements in each pattern. Across an entire set of N input patterns, we can evaluate pattern separation in terms of changes in HD, defined as the average Hamming distance across all pairs of patterns, normalized as a percent of E so that we can compare across pattern sets with differing values for E:

$$\mathit{HD}=\frac{{\displaystyle \underset{x\ne y}{\Sigma }}|I_x-I_y|}{E^{\ast }\left(\frac{N^{\ast }(N-1)}{2}\right)}\ast 100$$

Here, |x| is the absolute value of x. As HD rises, it is more likely that an autoassociative network will be able to store all the input patterns, and more likely that the network will retrieve each stored pattern correctly when presented with a partial or noisy version of the input. Because HD is normalized across patterns of different sizes (E), we can use this metric to assess pattern separation at different stages in the model: pattern separation has occurred if HD measured across the original set of input patterns is significantly less than HD measured in terms of DG output (based on the granule cell responses to each pattern) or CA3 output (based on pyramidal cell responses to each pattern).

For example, if there are 10 input patterns with input density d=10%, then about 20 of the 200 entorhinal inputs are active in each pattern. If no input that is active in one pattern is active in any others, the patterns would all be maximally distinct, and HD=20. If the patterns are randomly constructed, then at least some of the inputs which are active in one pattern are likely to be active in one of the other patterns, leading to a slightly lower HD compared to this theoretical maximum.

When selecting possible values for d, it is worth noting that it is very hard to predict the normal activity of EC cells in vivo from published studies: in particular, it is not clear whether the subset of neurons that comprise the entorhinal cortical input to hippocampus (the perforant path) is fixed (i.e., the number of layer II EC cells that contribute to the perforant path input is always the same). It seems likely that the entorhinal input to the DG would vary as more or less of the layer II population is activated by other pathways, modulated by behavioral state, or silenced by inhibitory inputs. In addition, even if the total number of active layer II entorhinal cells is kept constant, their firing frequencies are likely to vary. As such, while d=10% may be considered a reasonable “standard” estimate for activity in the perforant path inputs to the DG, it is worth considering the effects on model performance when d is allowed to vary within a wide range. As shown in Figure 3A (Inputs), HD (measured across a set of input patterns) generally rises as d is increased.

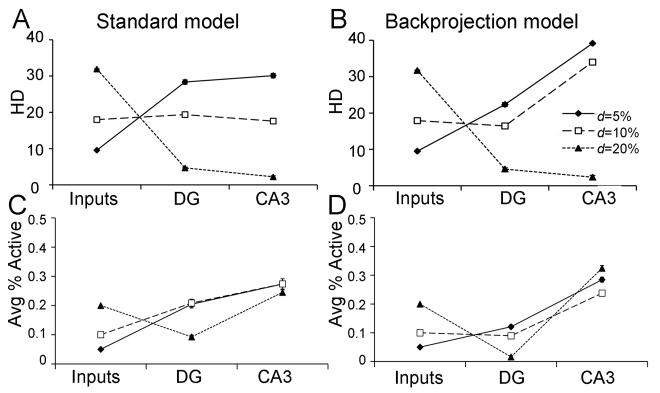
Figure 3.

Pattern separation behavior in the standard DG-CA3 model (A) and the backprojection model (B). For a set of 10 patterns, where d=5%, the DG network performs pattern separation, reflected by increased HD of granule cell output relative to that the EC input; in the standard model, the pattern separation obtained in the DG is maintained in CA3, but in the backprojection model, there is actually an increase in pattern separation in CA3 relative to that obtained in DG. As d increases to 10%, DG preprocessing produces no increase in HD in CA3 of the standard model, but does produce good pattern separation in CA3 of the backprojection model. Only as d increases to 20% does DG preprocessing actually reduce pattern separation in CA3 in both the standard and the backprojection model. (C,D) Activity levels in the DG and CA3 network, as the average percent of granule or pyramidal cells that are active, also varies with d; in general, there is less DG activity in the backprojection model than in the standard model, which could be due to the inhibitory influence of backprojections on granule cells.

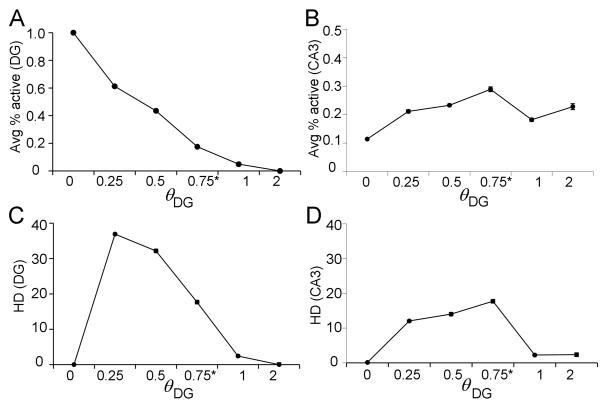
As discussed in Myers & Scharfman (2009), there is a profound effect of input density on pattern separation in the DG model: specifically, pattern separation in the DG is inversely related to input density (Figure 3A, DG). In the DG model, pattern separation is strongly modulated by hilar cells, including mossy cells and hilar interneurons (e.g. HIPP cells). At higher input densities (e.g., d=20%), increased entorhinal activity causes increased activation of hilar HIPP cells, which in turn inhibit granule cells (Figure 3C, DG); when too few granule cells fire in response to any input patterns, HD is low. At lower input densities (e.g., d=5%), HIPP cell activity decreases, disinhibiting granule cells, allowing many granule cells to respond to an individual input pattern, which tends to increase HD.

Pattern separation in the DG affects CA3. In the “standard” DG-CA3 model, where DG outputs (mossy fibers) are used to train the CA3 model, the HD in CA3 generally reflects that observed in the DG (Figure 3A, CA3). Thus, at d=5%, there is good pattern separation (repeated-measures ANOVA, F(2,18)=416.21, p<0.001), meaning significantly greater HD measured at both the DG outputs and the CA3 outputs, compared to the input patterns (post-hoc pairwise comparisons; all p<0.001), but no difference in HD measured at CA3 vs. DG (p=0.138). At d=10%, there is no significant pattern separation (all p>0.0167), and at d=20%, pattern separation fails, with greater HD at the inputs than either at the DG outputs (p<0.001) or the CA3 outputs (p<0.001), and greater HD at the DG outputs than the CA3 outputs (p<0.001).

Yet one would expect that it is precisely when input density is high (which would presumably reflect a time when entorhinal input is very important, such as a time when extensive new information is to be processed) that it would be most useful for DG preprocessing to be robust, i.e., so that input patterns would be sparsified before storage in CA3. Therefore, the simulations with the standard DG-CA3 model raise the possibility that DG preprocessing alone, with unidirectional information flow from DG to CA3, may not always suffice for good pattern separation behavior.

It is also worth nothing that, in the model, about 30% of CA3 pyramidal cells are active in response to an input pattern. It is hard to know how many granule and pyramidal cells are actually active in vivo at any particular moment, because recordings to date have no methods to sample CA3 throughout the septotemporal axis, and most methods have low resolution. However, some arguments have been made that only a fraction of the CA3 pyramidal cell population is active in vivo – possibly about 3%, much less than in the model (e.g., Barnes, 1987, Jung & McNaughton, 1990). The higher rate of activity in the model is a consequence of scaling the model down to 1% of the size of CA3 in rat. Notably, the change in CA3 activity remains relatively constant even if there is a substantial change in input activity (Figure 3C), suggesting that local inhibition is a much more influential variable than the actual number that is chosen to represent the percentage of CA3 pyramidal cells that are active in the model.

In contrast to the standard DG-CA3 model, the backprojection model shows a dramatic improvement in pattern separation (Figure 3B). The backprojection model exhibits significant pattern separation for patterns constructed at d=5% (paired samples t-test, t(9)=125.09, p<0.001) and also at d=10% (t(9)=35.42, p<0.001); this is an improvement over the standard DG-CA3 model, which showed no pattern separation at d=10%. It is only at a very high level of input density, d=20%, that pattern separation fails in the backprojection model (t(9)=64.42, p<0.001). It is also worth nothing that DG activity, in terms of average number of active granule cells, is significantly less in the backprojection than the standard model (Figure 3D; ANOVA, main effect of model F(1,54)=170.63, p<0.001); this occurs because a major effect of the backprojections is to inhibit granule cells. There is also a main effect of d on activity in the DG with the fewest granule cells active when d is smallest (effect of d: F(2,54)=91.19, p<0.001; model-d interaction: F(2,54)=3.40, p=0.041); this occurs because increasing input density d produces increased activity of inhibitory interneurons in the granule cell layer and hilus, which in turn decrease granule cell activity.

Storage Capacity

Although DG preprocessing does not necessarily sparsify dense input patterns in the standard DG-CA3 model, a different way in which DG preprocessing might potentially improve pattern storage and recall in CA3 is by increasing storage capacity in CA3. Specifically, any autoassociative network can only store a limited number of input patterns. If too many patterns are stored, weights can become very strong, so that many of the cells in the network become active whenever any of their neighbors are activated – leading to a population of cells that may become active in response to any input pattern. In such a case, HD plummets, as many of the cells in the autoassociative network respond to many input patterns.

It may be that preprocessing in the DG improves CA3 performance by somehow allowing more input patterns to be stored, even without reduction in HD. To test this premise, the standard DG-CA3 model was trained on sets of N randomly-generated patterns at d=10%. Figure 4A shows that for a set of N=10, 20, or even 50 such patterns, DG preprocessing in the standard DG-CA3 model maintains (although it does not improve) HD relative to the inputs. Figure 4C shows the average activity in the DG and CA3 in the standard DG-CA3 model, as a function of N: DG activity is highest for N=10, but drops as N is increased to 20 or to 50 (one-way ANOVA, F(2,27)=92.65, p<0.001; post-hoc Tukey HSD tests confirm that activity level is higher at N=10 than at N=20 or 50; p<0.05, but that activity at N=20 or 50 does not differ; p>0.05).

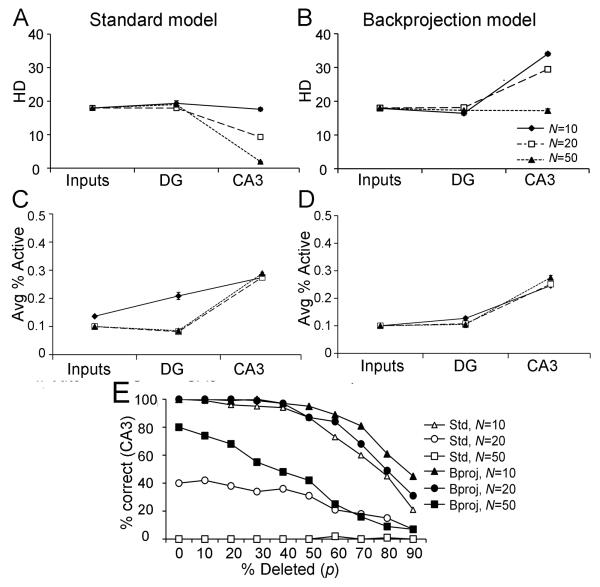
Figure 4.

Effect of the number of patterns stored on pattern separation in the standard (A) and backprojection (B) models, trained on a set of N randomly-constructed patterns where d=10%. (A) When N=10, the degree of pattern separation in the standard model (defined by HD) in DG and in CA3 is comparable to that already present in the entorhinal inputs. As the number of stored patterns increases from N=10 to N=20 or N=50, HD in CA3 of the standard model decreases greatly. (B) In contrast, the backprojection model shows pattern separation at both N=10 and N=20; even at N=50, HD in CA3 is no lower than that of the inputs. (C,D) For both the standard and backprojection models, activity in the DG and CA3 networks, expressed as the average percent of granule or pyramidal cells that are active, is largely constant as N increases, although there is a higher level of DG activity in the standard model for low numbers of patterns (N=10). (E) Effect of N on pattern retrieval and pattern completion in the standard and backprojection models. For N=10, the standard model can reliably retrieve a stored pattern when presented with the complete input pattern (percent deletion p=0%); as increasing percentages of the input pattern are deleted, performance degrades gradually until, at p=90%, CA3 retrieves the correct stored pattern only about 20% of the time. For N=20 stored patterns, the standard model is not always able to retrieve the correct stored pattern even with p=0% deletion, and for N=50, pattern storage and completion fail completely. Thus, the storage capacity of the standard DG-CA3 model for randomly-constructed patterns at d=10% is only between 10 and 20 patterns. In contrast, the backprojection model is able to store and retrieve N=20 patterns, and even for N=50 patterns, it is still able to store and reconstruct some patterns as long as percent deletion p is low.

Despite this pattern separation in the DG, HD in CA3 plummets as the number of patterns trained increases to N=20 or N=50. Paired t-tests show that, when N=10 patterns are trained, HD measured at CA3 is no worse than that of the inputs (t(9)=0.83, p=0.426), but HD at CA3 is much lower than that of the inputs when N=20 patterns are stored (t(9)=27.05, p<0.001) or when N=50 patterns are stored (t(9)=224.73, p<0.001).

Adding CA3 backprojections increases storage capacity in the DG-CA3 model. Whereas the standard DG-CA3 model showed a failure of pattern separation for N>10 trained patterns (compare Figure 4A), the backprojection model (Figure 4B) shows significant pattern separation both for N=10 (t(9)=35.42, p<0.001) and for N=20 (t(9)=39.41, p<0.001). Even at N=50 trained patterns, the backprojection model does not fail completely: HD at the inputs and at the CA3 outputs does not differ (t(9)=1.40, p=0.195); although pattern separation does not occur, at least the output patterns of CA3 are no less similar than the inputs were. Pattern completion can also be assessed using these larger pattern sets. Figure 4E shows that both the standard and backprojection models, after training on a set of N=10 patterns, randomly-constructed with input density d=10%, can perfectly retrieve the trained pattern when it is presented without deletion (p=0%); but as p increases beyond about 40%, there is a gradual decline in performance, with incorrect patterns sometimes retrieved. However, when twice the number of patterns (N=20) are trained, the standard DG-CA3 model does not always retrieve the correct stored pattern even when p=0% (Figure 4E); when there are N=50 trained patterns, retrieval fails completely. In other words, the storage capacity of the standard DG-CA3 model is somewhere between 10 and 20 randomly-constructed patterns. This is not particularly good performance, even for a small model system. By contrast, Treves & Rolls (1992; 1994) used mathematical analyses to calculate that a sparsely connected autoassociative network, based on empirically-derived estimates of cell numbers and connectivity of the rodent CA3, should have a maximum capacity of about 36,000 patterns. Given that there are approximately 300,000 CA3 pyramidal cells in the rat hippocampus (Amaral et al., 1990), compared with 300 in the current model, one might roughly estimate that the current model should be able to store on the order of N=36 sparse, random patterns. Yet this is considerably higher than the number of patterns that the standard DG-CA3 model can successfully store and retrieve.

In contrast, the backprojection model shows good performance at N=20, and even at N=50 its performance degrades gradually as increasing percentages of the stored pattern are deleted at test (Figure 4E). At each value of N, the backprojection model shows significantly better pattern completion (is more likely to retrieve the correct stored pattern) than the standard model (repeated-measures ANOVAs, all p<0.05).

The backprojection model as implemented here makes the assumption that CA3 pyramidal cell axons selectively inhibit those dentate granule cells which target them, creating a kind of inhibitory feedback loop. It is worth considering the performance of the model when alternate assumptions are made. For example, given that the inhibitory effect of the backprojection on granule cells is due to a disynaptic pathway, with CA3 axons targeting GABAergic cells that inhibit granule cells within the same lamella, it is possible that the effect of the backprojection is relatively diffuse, tending to non-selectively inhibit many granule cells within the same lamella as the GABAergic interneuron. The reason for this would be the large divergence of the axons of most dentate gyrus GABAergic interneurons, which is consistent with the strong lamellar inhibition that follows activation of the backprojection (Scharfman 1994a).

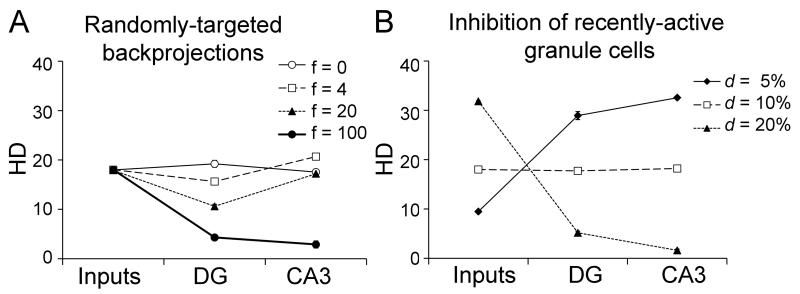
To examine the possibility that interneurons target granule cells randomly rather than selectively, we modified the backprojection model so that each CA3 pyramidal cell produced backprojections that could inhibit f=0, 4, 20, or 100 granule cells – with these granule cells chosen randomly. Note that at f=0, the standard model and backprojection model are the same, while at f=4, each CA3 cell inhibits the same number of granule cells in the standard model and the backprojection model, and there is no assumption that these granule cells targeted the pyramidal cells in question. Figure 5A shows the results after training this “randomly-targeted backprojection” model on a set of N=10 patterns at d=10%. For f=4, there is little effect of randomly-targeted backprojections, in contrast to the strong effects of backprojections that specifically target those granule cells that projected to the CA3 cells in questions (compare Figure 4B). As f rises, pattern separation begins to fall in the DG, and at the extreme (f=100) all granule cells are inhibited and pattern separation fails in both DG and CA3. The results shown in Figure 5A suggest that the mere presence of inhibitory backprojections is not what is responsible for the improved pattern separation in the backprojection model. Instead, the selective targeting of particular granule cells by the backprojections appears more beneficial than the mere presence of diffuse inhibition.

Figure 5.

Alternate implementations of the backprojection. (A) Pattern separation in a model variant where CA3 backprojections provide random inhibition to f randomly-chosen granule cells. If f=0, this is equivalent to the standard model with no backprojections. When f=4 (the same number as in the backprojection model), there is little effect of randomly-targeted backprojections on pattern separation. At higher values of f, widespread inhibition actually decreases pattern separation in the DG and eventually in CA3. (B) If inhibition targets all recently-active granule cells, either by diffusely-targeted backprojections or by other local mechanisms, there is little effect on pattern separation compared to the standard model (compare Figure 3A). Thus, the improved pattern separation seen in the backprojection model reflects not just diffusely or randomly-targeted inhibition, but rather selective inhibition of particular groups of granule cells.

It is also possible that the improved pattern separation performance in the backprojection model relative to the standard model is not due to the inhibition provided by the backprojections per se, but that any type of inhibition of recently-active granule cells would have the same effect of improving pattern separation. In fact, other models of the DG have sometimes invoked the known effects of local inhibitory neurons to inhibit recently-active granule cells, making those granule cells less able than their neighbors in the same lamella to respond to subsequent entorhinal input (e.g. Hasselmo & Wyble, 1997).

To examine this possibility, we investigated a version of the standard DG-CA3 model (no backprojections) in which granule cells that respond to a given entorhinal input pattern are selectively inhibited from responding to the next entorhinal input pattern. This was done by setting the resting potential for currently-active granule cells to −0.6 for the next timestep (instead of the default value of −0.3 as defined in Appendix 1); this inhibition lasted for one timestep. Figure 5B shows the results after training on a set of 10 randomly-constructed patterns at various levels of input density d; the results are similar to those obtained from the standard DG-CA3 model without such inhibition (compare Figure 3A); similarly, there is no difference compared to the standard model as the number of trained patterns rises from 10 to 50 (simulations not shown). In summary, these comparisons suggest that the mere inhibition of recently-active granule cells is not what improves pattern separation in the backprojection model. Instead, what appears to be important is that backprojections from the CA3 neurons that were activated inhibit those granule cells that projected to the CA3 cells in question. Later, in the discussion, we consider how such specificity might arise.

Comparison of the Model to Empirical Data

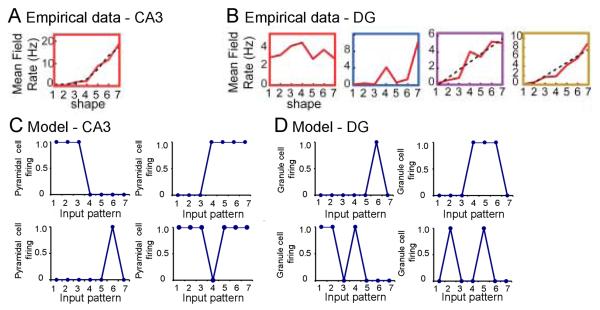
In Myers & Scharfman (2009), we showed that the DG model could be applied to empirical data from Leutgeb et al. (2007), who recorded from single neurons extracellularly (“single units”) in the DG and CA3 as rats explored a series of environments that included a square enclosure (environment 1), a circular enclosure (environment 7), and several intervening enclosures (environments 2-6) that gradually “morphed” between the two extremes. CA3 place cells were identified in environment 1 (or 7) as cells that responded strongly when the rat was in a particular region of the environment (that cell's place field). When the environment was gradually changed from environment 1 through the intervening stages to environment 7 (or vice versa), CA3 place cells showed a progressive change in firing rate. Thus, for example, a CA3 place cell with a high mean firing rate in a particular region of environment 7 showed progressively less firing in the corresponding region of morphed environments 6 through 1 (Figure 6A). In contrast, the majority of DG place cells (presumed granule cells) behaved differently from CA3 place cells, exhibiting greater sensitivity to small changes in the environment. Thus, for example, one DG cell showed a place field in a particular region of environment 7, and fired strongly when the animal was in that region of environment 7 or in the corresponding region of environment 4 – but not in the corresponding region of environments 3, 5, or 6 (Figure 6B-blue). Leutgeb et al. also showed that a single DG cell could exhibit more than one place field, and some of these cells did show gradual changes in response rates when environments were morphed (e.g. Figure 6B-yellow).

Figure 6.

Evaluation of the DG-CA3 computational model relative to empirical data (A). In rodents that were exposed to seven environments that initially resembled a square and gradually changed to a circle (progressively modified or “morphed” environments labeled 1 to 7), CA3 place cells typically showed a single place field, and firing rate gradually changed as the environment morphed. The example shown illustrates that a CA3 cell fired strongly in a particular region of environment 7, less strongly in the corresponding region of environment 6, and progressively more weakly in environments 5 through 1. Adapted from Leutgeb et al. (2007), Figure 2C. (B) In contrast to CA3, place fields in cells of the DG (presumed granule cells) often showed multiple place fields, and there were large differences in firing rate even if there was little difference in the environment. The example shown is from a DG cell that showed four place fields. The first (red) is a place field in a particular region of environment 1, and the cell responded in the corresponding region of all the other environments (2 through 7) also. The cell showed two additional place fields (purple, yellow) in other regions of environment 7, and its responses gradually decreased in environments that were progressively less similar to environment 7. This same cell showed a fourth place field (blue) in a different region of environment 7, and also fired strongly in that same region of environment 4 – but not in the corresponding regions of environments 1, 2, 5, or 6. Adapted from Leutgeb et al. (2007), Figure 2C. (C) CA3 pyramidal cells in the standard DG-CA3 model tended to show similar responses to similar input patterns. Four examples are shown. Top: firing rate of two cells that each responded strongly to several similar input patterns (I₁, I₂, and I₃; or I₄, I₅, I₆, and I₇). Bottom: firing rates of two cells that responded either to a single input pattern, or to all but a single input pattern. Data from the backprojection model (not shown) were similar. (D) Granule cells in the standard DG-CA3 model often showed strong responses to two or more input patterns. Four examples are shown. In some cases (top), cells showed responses only to a single input pattern, or to several similar input patterns. But in other cases, cells responded strongly to distinct input patterns (e.g. I₁, I₂, and I₅; or I₂ and I₅). Such nonmonotonicity of firing patterns is similar to that observed empirically in granule cells (e.g., part B, blue). Data from the backprojection model (not shown) were similar.

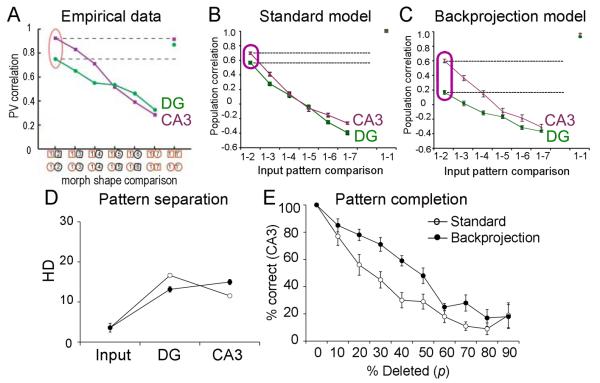
Leutgeb et al. (2007) then computed population correlations for DG and CA3 cells, by dividing each environment into 5 cm × 5cm subregions; they constructed one population vector for each subregion in each environment, where the nth element of each vector represented the firing rate of the nth recorded neuron at that subregion of that environment. Population vector correlations between pairs of environments were then computed by correlating the population vectors for each subregion shared by the two environments. Using this technique, Leutgeb et al. showed that population activity in CA3 was not very sensitive to small changes in the shape of the environment (Figure 7A): population correlation was not significantly less for neighboring shapes (e.g. environment 1 vs. environment 2) than for identical shapes (e.g. environment 1 vs. a re-test in environment 1). In contrast, population activity in the DG was highly sensitive to small changes in the shape of the environment: there was a highly significant decrease in population correlation for neighboring environments (1 vs. 2) compared with identical shapes (1 vs. re-test on 1). As the shapes became more different, the correlations decreased in both CA3 and the DG, and the two subfields did not differ when the shapes were highly distinct (e.g. environment 1 vs. environment 6 or 7).

Figure 7.

The backprojection model a better qualitative fit to empirical data than does the standard DG-CA3 model. (A) In vivo, rodents that were exposed to progressively “morphed” environments 1 to 7, as described in Figure 5, were evaluated with electrodes in CA3 or the DG. CA3 pyramidal neurons showed a smooth decline in population correlation as environments gradually changed. In contrast, there was a much lower population correlation for presumed dentate granule cells for environments that were similar (e.g. 1 vs. 2). Adapted from Leutgeb et al. (2007) Figure 3A. (B) In the standard DG-CA3 model, population correlations in the DG appeared similar to those observed in CA3, which is inconsistent with the empirical data shown in (A). (C) In the backprojection model, the population correlation for similar environments (e.g. I₁ vs. I₂) was lower in DG than in CA3; this is similar to the empirical data shown in (A). (D) On a set of N=10 such highly-correlated patterns, pattern separation defined as decreased HD in CA3 is greater in the backprojection than in the standard model. (E) After training on a set of N=10 highly-correlated patterns, the backprojection model is better than the standard model at retrieving progressively more distorted versions of the trained inputs.

Simulating the Leutgeb et al. Task

To simulate Leutgeb et al.'s (2007) “morphed environments,” Myers & Scharfman (2009) constructed two entorhinal cortical input patterns, I₁ and I₇, each with seven active entorhinal inputs, only one of which was common to both patterns. Five intervening patterns I₂ through I₆ were then constructed to gradually “morph” between these extremes, with each pair of “neighboring” patterns (patterns I₁ and I₂, I₂ and I₃, etc.) sharing six common elements. The DG model was then trained on these patterns, presented in order from I₁ to I₇, for five passes through the set (each pattern presented and trained five times). For each input pattern, a population vector was constructed consisting of the responses of each of the granule cells to that pattern; the correlation between two population vectors was then computed between each pair of elements in the vectors. As in the empirical data, the model showed decreasing population correlation as input patterns became more distinct. However, a CA3 network was not included in the prior model, so the population correlations in the DG model could not be assessed relative to correlations in CA3.

Here, we presented the same morphed environments I₁ through I₇ to the “standard” DG-CA3 model and to the backprojection model, so that the responses of DG and CA3 could be compared.

Results with the “Standard” DG-CA3 and “Backprojection” models

Figure 6D shows examples of responses from individual granule cells in the standard DG-CA3 model; responses of granule cells in the backprojection model were similar (simulations not shown). As illustrated, many granule cells responded in a similar way to pairs of neighboring input patterns (Figure 6D-top); but others showed a non-monotonic response profile, giving distinct responses to non-neighboring input patterns (Figure 6D-bottom). This is reminiscent of the behavior previously observed in the DG model of Myers & Scharfman (2009), and of to the behavior of granule cells in vivo (compare Figure 6B).

Figure 6C shows examples of responses from individual pyramidal cells in the standard DG-CA3 model; results were similar in the backprojection model (simulations not shown). As illustrated, many pyramidal cells that responded to one input pattern also responded to other, neighboring patterns. A few cells responded only to a single pattern. But no pyramidal cells examined in the CA3 model showed such non-monotonic responses. Thus, the model appears to capture this aspect of the empirical data of Leutgeb et al. (2007).

Consistent with the marked differences in the firing of some granule cells to neighboring environments, a finding that was not exhibited by CA3 cells, Leutgeb et al. (2007) showed a decrease in the population correlation of granule cell firing to adjacent environments (e.g., 1 and 2), relative to that of pyramidal cell firing (Figure 7A). Figure 7B shows that the standard DG-CA3 model does not capture this aspect of the behavioral data: comparing the responses to input patterns I₁ and I₂, the population correlation for CA3 pyramidal cells is not significantly lower than that of dentate granule cells (paired t-test, t(9)=81.15, p=0.065). The empirical data are better reproduced by the backprojection model (Figure 7C), which shows a strong decrease in population correlation in the response to I₁ and I₂ in the DG relative to CA3 (p<0.001). Furthermore, when comparing the responses to inputs that differed the most (I₁ vs. I₇), the backprojection model also provided a better fit to the empirical data, because there was a significant difference in population correlation between DG and CA3 in the “standard” DG-CA3 model (p<0.005) but not in the backprojection model (p=0.174). Whereas a mean of 97 granule cells in the backprojection model responded to one and only one input pattern, this mean was only 83 granule cells in the standard DG-CA3 model (independent-samples t-test, t(18)=2.66, p=0.013). The implication is that a single granule cell in the backprojection model would be less likely to respond to two input patterns that were very similar (i.e., “neighboring” patterns), leading to different population responses to the two patterns, producing an improvement in pattern separation relative to the standard DG-CA3 model. Although the increase from 83 to 97 is small numerically, the low firing rate of the granule cells in the DG model (about 10% of 1000 granule cells active at any one time) means that this small numeric increase represents a meaningful fraction (about 10%, on average) of the DG response to a pattern.

The resulting improvement in pattern separation can also be seen on explicit tests of pattern separation and pattern completion. Figure 7D shows that, when trained on a set of N=10 highly-correlated patterns constructed as described above, the backprojection model shows a decrease in HD in the DG relative to the standard model (independent-samples t-test, t(18)=4.08, p=0.001), but an increase in HD in CA3 relative to the standard model (t(18)=2.71, p=0.014). On a pattern completion test, using the same set of N=10 highly-correlated patterns, the backprojection model is significantly better at retrieving stored patterns given progressively more distorted versions (Figure 7E; repeated-measures ANOVA, F(1,18)=14.81, p=0.001). This relative benefit for the backprojection model over the standard model in pattern separation and pattern completion for highly correlated input patterns is similar to that previously shown for randomly-constructed pattern sets.

Discussion

The results show that although a small “standard” DG-CA3 model built to incorporate some known anatomical constraints can perform pattern storage and recall well for a small set of relatively-sparse input patterns, it does not perform very well if the inputs become dense or the number of patterns grows large. In contrast, adding backprojections to the model improves pattern separation and pattern completion, and increases storage capacity in the CA3 model. Further, incorporating backprojections increases the degree to which the DG-CA3 model is capable of accounting for empirical data, specifically by producing population correlations that are qualitatively more similar to empirical observations than those produced by the model without backprojections. Together, the current results suggest that this anatomical feature, which is widely overlooked in existing models of hippocampus, may in fact play an important role in modulating the performance of the hippocampus, and challenge the view of the hippocampus as a linear processing system, with information traveling unidirectionally from entorhinal cortex, to DG, to CA3 and beyond (Scharfman, 2007).

Obviously, the current results do not rule out other possible mechanisms by which pattern separation and pattern storage and completion might also be improved in the hippocampus, for example by considering a possible role for adult neurogenesis in the dentate gyrus (Becker, 2005). In fact, it is interesting to speculate that backprojections may interact with granule cells that are born in postnatal life, because such granule cells may be targets of the backprojection, although this may only occur when new granule cells are slightly ectopic or develop a basal dendrite located in the hilus (Scharfman, 2004; Scharfman et al., 2000; Scharfman and Gray, 2007). The current results do suggest, though, that CA3 backprojections might be one important mechanism contributing to pattern storage and recall in the hippocampus.

The simulation results suggest that the beneficial effects of backprojections on pattern separation depend on inhibition that is specific to certain granule cells; Figure 5 illustrated that when CA3 backprojections inhibit randomly-selected granule cells, or when there is diffuse inhibition of all recently-active granule cells, pattern separation is not improved. Instead, the backprojection model assumes that backprojection-mediated inhibition of granule cells is selective (or most powerful) to those granule cells that targeted the CA3 pyramidal cells that gave rise to the backprojections, which were activated by the granule cells, implementing a negative feedback loop in which a subpopulation of active granule cells sends mossy fibers to CA3 pyramidal cells which in turn backproject to temporarily silence that same subpopulation of granule cells. An important question is thus how such specificity in anatomical connections might arise.

One possibility involves synaptic plasticity. For example, it is possible that synapses from recently-active granule cells would undergo a short-term weakening if the inhibition invoked by the backprojection overlapped the EPSPs evoked by the first input pattern from the EC. This argument is suggested by the findings in area CA1, where hyperpolarization during an afferent train leads to LTD rather than LTP (Stanton and Sejnowski, 1989). However, given that little is known at present about what forms of plasticity might exist within the backprojection pathways, this must remain speculative. Another important factor may be specificity in the existing circuitry of GABAergic projections to granule cells. Although it is not known that GABAergic cells in the DG preferentially silence recently-active granule cells, some neuroanatomical information suggests ways this could occur. For example, the hilar GABAergic neurons which express somatostatin and/or neuropeptide Y are known to innervate the area of the molecular layer (outer 2/3) that is the site where granule cell dendrites are innervated by the perforant path. It has been shown that the hilar NPY GABAergic terminals innervate the afferent synapses in the outer molecular layer (Milner & Veznedaroglu, 1992). Therefore, it is possible that the backprojection inhibits release of glutamate from the perforant path terminals, inhibiting the EPSPs of granule cells that were recently activated by the EC.

It is also important to consider additional ways the backprojection may be important. For example, in very temporal locations along the septotemporal axis, CA3 pyramidal cells may excite dentate granule cells by a monosynaptic projection (Li et al 1994), instead of being inhibitory. It is also interesting to consider the evidence that the entorhinal input evokes CA3 population spikes 0.5-3.0 msec before DG populations spikes in vivo (Do et al 2002, Derrick 2007). Therefore, area CA3 may be activated before the DG by the perforant path, rather than the opposite. If true, then backprojections could provide feed-forward inhibition of granule cells that would make their subsequent activation by the EC more difficult. This feedforward lamellar inhibition might be accompanied by feedforward facilitation in adjacent laminae (cross lamellar facilitation), because the mossy cells that are activated by the backprojection would be likely to excite granule cells in distal lamellae.

Limitations of the Current Model

Like all computational models, our DG-CA3 model is a simplification of the substrate, both in terms of numbers and types of cells, as well as in terms of their physiological properties. As such, the behavior of a model cannot “prove” whether the hippocampus operates in the manner hypothesized. However, a model can still be useful if it illustrates that hypothesized mechanisms can reproduce observed behavior. To the extent that the model fails to reproduce desired behaviors, it is important to consider what features of the biological substrate might, if added to the model, affect behavior. Anatomical and physiological characteristics that are not included in our DG-CA3 model, and that could be examined in future work, include the various subtypes of circuit considerations (e.g., types of interneurons, additional inputs), subthreshold and other modulatory influences (e.g., glia), additional forms of synaptic plasticity (including plasticity of interneurons and mossy fibers as well as within the DG), and use of more realistic timing (axonal conduction, synaptic delays). Addition of some or all of these features might also improve pattern storage and pattern completion behavior in the DG-CA3 model. On the other hand, a strength of this relatively simple and abstract model is that a system with a relatively small number of free parameters (five in the DG model, seven in the CA3 model) is sufficient to produce behavior that simulates some empirical results.

It is also important to note that the backprojection model implements a very simple version of backprojections, in which CA3 axon collaterals directly inhibit DG granule cells. A more realistic implementation of the backprojection would include CA3 axonal collaterals that innervate hilar mossy cells, which in turn would be likely to excite granule cells in distal lamellae (Scharfman, 2007). In this way, activation of a population of CA3 pyramidal cells might produce an elegant pattern of inhibition of granule cells within the same lamella, and excitation of granule cells outside the same lamella. This could result in selective inhibition of recently-active granule cells while depolarizing a different subset of granule cells – making the latter more likely to respond to the next entorhinal input. The idea that the backprojection might directly excite a fraction of granule cells in ventral hippocampus is also interesting to consider, because it may explain some of the differences in function across the septotemporal axis (Kerr et al., 2007; Kesner et al., 2004; Moser and Moser, 1998; Pierce et al., 1999). As more quantitative data become available about the backprojection to interneurons and mossy cells, these ideas could be incorporated into the model.

At present, a great deal remains unknown about the backprojections, both in terms of quantitative anatomy and in terms of their effects on network function. It is our hope that by demonstrating, via a computational model, that these backprojections might play an important role in hippocampal function, more research will be stimulated to understand the backprojections better.

Comparison to Other Models of DG-CA3 Interaction

The current model is similar to many prior models, reviewed above, which assume that the DG acts as a preprocessor, performing pattern separation on inputs from entorhinal cortex, to facilitate pattern storage in CA3 by reducing the overlap among to-be-stored patterns. The current standard DG-CA3 model is no different. The fact that the standard DG-CA3 model showed relatively unimpressive performance when presented with anything but a small number of sparsely-active inputs does not necessarily suggest that there is no real benefit of DG preprocessing, or that the basic assumptions of pattern separation in DG and of pattern storage in CA3 are wrong. The biological substrate includes many additional cell types and characteristics that are not included in this and other simple models, and it is also much larger in terms of cell counts and synapses. What the current results do suggest is that such simple DG-CA3 models, constructed using widely-accepted general principles of unidirectional information flow within the hippocampus, may not suffice to produce the expected behaviors. In specific, the results presented here argue that backprojections from CA3 to DG can greatly improve performance, relative to a model without such backprojections.

Although most prior computational models of the hippocampus have not included a role for backprojections from CA3 to DG, Lisman and colleagues have presented a series of models that do incorporate CA3 backprojections (Lisman, 1999; Lisman and Otmakhova, 2001; Lisman et al., 2005). In these models, projections from CA3 pyramidal cells to granule cells (directly and/or indirectly via hilar mossy cells) are assumed to be excitatory, and allow information to flow reciprocally from DG to CA3 and back again. A recent version of this model (Lisman et al., 2005) assumes that CA3 functions as an autoassociative network, performing pattern completion of its inputs from the DG. The DG is assumed to perform heteroassociation: that is, given an input from CA3, the DG should predict the next inputs which will arrive from entorhinal cortex. Together, the DG-CA3 network is assumed to act as a sequence learner and sequence predictor: given a pattern of entorhinal inputs, the DG predicts the next state, and CA3 performs pattern completion to “flesh out” this prediction, which is then passed back to DG, which can use that information to predict the subsequent state, and so on. Lisman and colleagues have shown that this model exhibits unit activity similar to theta phase precession in vivo, in which hippocampal place cells discharge earlier in the theta cycle as the animal navigates through its place field (Lisman et al., 2005).

The model employed by Lisman and colleagues differs from many other computational models of the DG because it assumes that the DG is a pattern storage device (specifically, a heteroassociative network) rather than “merely” a preprocessor that sparsifies input to optimize CA3 operations. It is not necessarily the case, however, that the two concepts for DG function are mutually exclusive; both a heteroassociative network and an autoassociative network would benefit from pattern separation, and the same features of the DG that could produce pattern separation could also support heteroassociative behavior.

The model of Lisman et al. (2005) also differs from our backprojection model in assuming that the effects of backprojections are primarily excitatory to granule cells. As discussed above, the normal effect of backprojections that have been shown empirically are mainly inhibitory to granule cells in the same lamella where the pyramidal cells of origin are located (Scharfman, 1994a), although these studies were conducted in slices, and therefore it may not be possible to generalize to the in vivo situation. For example, in the ventral extreme of the hippocampus, direct pyramidal cell-granule cell projections have been shown anatomically, and these projections are presumably excitatory to granule cells (Li et al., 1994). Further empirical work will be required to confirm these predictions, and clarify which model simulates the DG-CA3 network best.

Predictions of the Model

Conceptually, the simplest way to verify our prediction that backprojections are important for hippocampal function would be to selectively lesion the backprojections and then examine the effect on hippocampal-dependent tests involving pattern separation. Unfortunately, techniques do not currently exist to selectively ablate axons passing from CA3 to the DG without damage to other branches of the CA3 axons, and other methods to transect the backprojection would also transect additional pathways – such as the mossy fibers traveling from the DG to CA3.

Other predictions of the model are difficult to test given currently available methodology, but experiments might be designed as techniques develop. For example, our model assumes not only that the effect of backprojections on granule cells is inhibitory locally, but further that the backprojection does not inhibit all granule cells equally – even within a lamella; instead, inhibition of some granule cells should be stronger than inhibition of others. Specifically, CA3 activation should strongly decrease the potential of recently-active granule cells to respond to subsequent depolarization by entorhinal input. Interestingly, empirical data suggest that this is true: simultaneous intracellular recordings from CA3 pyramidal cells and granule cells in hippocampal slices have shown that some granule cells are inhibited, and some are depolarized and discharge (Scharfman, unpublished).

Our model also predicts that backprojections should be most active during learning, and least active during recall of previously-learned information. Like other computational models, therefore, our model predicts that the DG inputs to CA3 should be most important during learning, rather than recall, and this is consistent with empirical data showing that mossy fiber input is required for learning of new hippocampal-dependent information, but not for recall of previously-learned information (Lee & Kesner, 2004b). However, because the majority of backprojections appear to pass through the dentate hilus, where they target mossy cells that then project to granule cells, our model also posits an important role for the hilus in learning. Lesioning the hilus, or selectively inactivating hilar cells, should disrupt the backprojection, and strongly impair pattern separation in the dentate gyrus. Therefore, we predict that selective hilar manipulations which do not otherwise damage granule cells or mossy fibers should produce impairments on learning, but not recall, just as larger DG lesions do.

Finally, it is important to note that there is an alternate hypothesis for the role of the backprojections in modulating pattern separation in the DG. Instead of inhibiting recently-active granule cells, backprojections might excite (or release from inhibition) recently-active granule cells. This would imply that backprojections serve not to help increase pattern separation, but to reinforce recently active pathways. In this case, CA3 activation could increase the likelihood that recently-active granule cells will fire, making them more (not less) likely to respond to entorhinal inputs; conversely, CA3 activation could increase inhibition of recently-quiescent granule cells, making them less (not more) likely to respond to entorhinal inputs.

Potential Relevance of the Backprojection to Disease

The current results shed light on subtle aspects of hippocampal circuitry that may be critically important to normal DG-CA3 function. In addition, there are potential implications of the results for disease, because the backprojection is likely to be disrupted in several pathological conditions. For example, in aging, cognitive function declines and there is also a loss of hilar neurons (Azcoitia et al., 2005; Siwak-Tapp et al., 2008). Therefore, cognitive decline may occur – at least in part -- because the backprojection can no longer exert its normal effects. In Alzheimer's disease, hilar cell loss also occurs (West et al., 2004), and may contribute to memory deficits for the same reason, although there is additional pathology besides hilar cell loss that is considered to be very important. In temporal lobe epilepsy (TLE), where memory deficits commonly occur, hilar neurons are also vulnerable (Margerison and Corsellis, 1966; Scharfman, 1999b). One of the reasons that the role of hilar cell vulnerability has never been clarified as causal in these pathological conditions is that it often is accompanied by additional pathology, so hilar loss is hard to study in isolation. Computational models such as those presented here will provide useful tools to evaluate how much a defect in the backprojection from CA3 to DG can cause functional decline in hippocampal-dependent memory and behavior.

Appendix 1: Simulation details

DG Model

The DG model is similar to that previously presented in Myers & Scharfman (2009) except as noted in the main body of the text. In brief, the model contains 1000 granule cells. Based on empirical data suggesting that the DG is split into interacting transverse strips of neuronal assemblies and that the width of these lamellae may be less than 1-1.5 mm in rat (Lømo, 2009), there may be approximately 10 such lamellae in the rat. Accordingly, the granule cells in the model are divided equally across 10 lamellae. Each lamella also contains one local interneuron, meant to simulate the GABAergic neurons which project to the somata and initial axon segment of granule cells (basket cells and axo-axonic cells, respectively); these interneurons receive input from and project back to granule cells within the lamina. The DG network also contains 30 hilar mossy cells and 12 hilar cells with axons that project to the terminal zone of the perforant path (HIPP cells). External input is provided from 200 entorhinal (perforant path) inputs that each contact a random 20% of the granule cells in the network and a random 20% of the HIPP cells; the HIPP cells in turn project to a random 20% of granule cells. Mossy cells receive input from granule cells within the lamella, and project to a random 20% of granule cells outside their lamella.

Each pattern of entorhinal input is a series (vector) of 200 elements representing the action potentials (1=action potential, 0=no action potential) in each entorhinal fiber (input). The cells in the DG model then respond in the following sequence. First, the potential V_j of each granule cell j is calculated as the resting potential V_rest plus the weighted sum of excitatory input from the perforant path, for all entorhinal inputs i that contact j:

$$V_j=V_{\mathit{rest}}+{\displaystyle \underset{i}{\Sigma }}{y}_i{w}_{\mathit{ij}}$$

At the start of each simulation run, the strength or weight w_ij of the connection from each entorhinal cell i to granule cell j is initialized randomly from the uniform distribution [0..1) if i contacts j, and set to 0 otherwise. As in Myers & Scharfman (2009), the resting potential V_rest is set to –0.3 as a default value (see Myers and Scharfman (2009) for parametric explorations of these and other free parameters in the DG model, and justification of the default values for each).

Next, the activity of the GABAergic interneuron (INT) within each lamella is updated as V_INT = β_INT (∀_j V_j) for all granule cells j in that lamella, where max() returns a value equal to the maximum of its arguments. This is the equivalent of a k-winner-take-all computation with k=1. β_INT is a constant governing the strength of somatic and axo-axonic inhibition in the DG model, set to 0.9 as a default value. Once interneuron activity is computed, the granule cell potentials within each lamina are then updated as

$$V_j=V_j-V_{i-\mathit{INT}}.$$

Next, activity for each mossy cell m is computed as y_m = max(∀_j V_j) for all granule cells j in m's lamella. As in Myers & Scharfman (2009), mossy cell inputs to granule cells are conditional: that is, they do not directly excite granule cells but rather increase the activity of granule cells that are already responding to perforant path inputs (for discussion, see Myers and Scharfman, 2009; Scharfman, 1995). Thus, for each mossy cell m and each granule cell j with V_j > 0 that is contacted by m, potential is updated as $V_j=V_j-{\beta }_{\mathit{MC}}{\displaystyle {\Sigma }_m}{y}_m{w}_{\mathit{mj}}$ with V_j clipped at a maximum of 1. At the start of each simulation run, weights w_mj from m to granule cells are set to 1 for all granule cells j that m contacts, set to 0 for all other granule cells (including all granule cells in m's lamella). β_MC is a constant governing the strength of mossy cell input on granule cells in the DG model, set to 5.0 as a default value.

Next, each HIPP cell h computes activity as $y_h={\displaystyle {\Sigma }_i}{y}_i{w}_{\mathit{ih}}$ for all entorhinal inputs i that contact h, and this affects potential in those granule cells j for which V_j>0 and which h innervates: $V_j=V_j-{\beta }_{\mathit{HIPP}}{\displaystyle {\Sigma }_h}{y}_h{w}_{\mathit{hj}}$. At the start of each simulation run, weights from the perforant path to HIPP cells w_ij are initialized from the uniform distribution [0…1); connection weights from HIPP cells to granule cells w_hj are set to 1 if h contacts j and 0 otherwise. β_HIPP is a constant governing the strength of HIPP cell input on granule cells in the DG model, set to 0.1 as a default value.

Finally, those granule cells j with potential V_j greater than a threshold θ_DG generate an action potential; the output of the DG network at timepoint t is computed as a pattern (vector) of binary values y_j:

$$y_j\left(t\right)=1\mathrm{if}{V}_j>\theta$$

$$y_j\left(t\right)=0\mathrm{otherwise}$$

The use of binary outputs is meant to represent the activity – spiking (1) or not spiking (0) of each granule cell. This is a simplification of the biological substrate in which temporal parameters (spiking rates) are a potential means of transmitting information. However, the use of input patterns allows us to at least incorporate some aspects of spiking rates in the approach used here. It is also important to point out another simplification, the use of binary definitions of neural activity compared to analog; we have used binary outputs in the model for several reasons. First, the use of binary ouputs in the model allows a more straightforward computation of pattern separation than would analog output values. Second, implementing an analog approach involves numerous assumptions about the ways in which postsynaptic neurons integrate afferent input, which could introduce error if the assumptions are wrong. Third, conversion to a binary output (spike or no spike) would be required whether an analog output were used or not, so we have emphasized what occurs in relation to spike threshold rather than subthreshold activity per se.

The four free parameters governing DG model behavior are set to the same default values as in Myers & Scharfman (2009), specifically: V_rest=−.30, β_IN=0.9, β_MC=5.0, β_HIPP=0.1. In addition, the current DG model incorporates a firing threshold for granule cells, θ_DG, which is set to 0.75. This value was determined based on parametric simulations, illustrated in Figure 8. When θ_DG approaches zero, many granule cells spike in response to any perforant path input (Figure 8A), which is not biologically realistic and which also produces a loss of pattern separation behavior in the DG model (Figure 8C). There is a corresponding loss of pattern separation in CA3 (Figure 8D). Conversely, when θ_DG is high (e.g. θ_DG≥1), all spiking activity in the granule cells is silenced (Figure 8A), leading again to loss of pattern separation behavior in both the DG (Figure 8C) and CA3 (Figure 8D). The intermediate value of θ_DG=0.75 provides a reasonable balance where only a small percentage of granule cells spike in response to an input pattern, and pattern separation is preserved in both the DG and CA3 models. Note that inhibition in the CA3 model keeps the activity of CA3 pyramidal neurons relatively constant, regardless of the level of activity in the granule cells (Figure 8B).

Figure 8.

Evaluation of free parameters in the DG model: granule cell threshold (θ_DG). θ_DG is a free parameter representing granule cell threshold: the amount of depolarization required for a granule cell to fire an action potential (spike). As θ_DG rises, the number of granule cells responding to entorhinal input falls (A) and pattern separation in the DG is reduced (C). There is little effect of θ_DG on the overall level of CA3 pyramidal cell activity (B), but moderate values of θ_DG produce better pattern separation in CA3 than very low values (0) or very high values (≥1) of θ_DG (D).

CA3 Model

The CA3 model is a simple autoassociative network, similar to several other existing network models, cited above, which assume that extensive recurrent collaterals allow CA3 to perform pattern storage and recall, with input patterns provided by the perforant path and mossy fiber inputs acting as teaching inputs. The current CA3 model was constructed by reviewing empirical data estimates of cell numbers and connectivity in area CA3 of the rodent (e.g., Amaral et al., 1990; Amaral and Witter, 1989; Andersen et al., 2006). Given 1000 granule cells and 10 lamellae in the DG model, the CA3 model was constructed to include 300 pyramidal cells. Although the pyramidal cells in the divisions of CA3 (a, b, and c) differ morphologically and physiologically (Bilkey & Schwartzkroin, 1990; Hemond et al., 2008; Scharfman, 1993), there is no evidence, to our knowledge, that distinctions among CA3 pyramidal cells contribute to pattern separation or completion in vivo; as a result, we make the simplifying assumption in the model that all CA3 pyramidal cells are homogeneous.

As with the DG model, the septotemporal organization of CA3 is represented by including lamellae. Based on the known lamellar and non-lamellar organization of pathways (Amaral et al., 1990; Amaral and Witter, 1989), the following characteristics are applied to the model: 1) the perforant path projection is similar in its input to the DG and CA3 for all lamellae; 2) the mossy fiber pathway is lamellar; 3) the distribution of interneuron innervation is primarily lamellar, reflecting the axons of GABAergic neurons that appear to be most numerous and powerful; 4) recurrent collaterals of CA3 pyramidal cells are non-lamellar (Amaral and Lavenex, 2007; Amaral and Witter, 1989). As with the DG model, the CA3 model is divided into 10 lamellae. Consistent with the sparse mossy fiber innervation of CA3 pyramidal cells observed empirically, each mossy fiber in the model (output from a granule cell in the DG model) innervates one CA3 pyramidal cell within the same lamella; each pyramidal cell thus receives on average 3-4 mossy fiber inputs. Entorhinal cells each contact a random 2% of CA3 pyramidal cells (and thus there are about 4 perforant path inputs to each pyramidal cell in the model). Each pyramidal cell also projects via recurrent collaterals to other CA3 pyramidal cells in a non-lamellar fashion; estimates of the density of this projection vary from about 1.9% (Amaral et al., 1990), to 3.2% (Arbib, 1998), to 4% (Rolls, 2007), and species differences certainly exist. Given the small scale of our CA3 model, we incorporated the upper bound of these estimates, 4%, which means that each of the 300 pyramidal cells in the model targets about 12 other pyramidal cells, and these connections can occur across the extent of the pyramidal cell layer (non-lamellar).

The interneurons of the CA3 subfield are as diverse as other subfields, and difficult to represent in the model with all the anatomical and physiological detail that has been identified empirically. The major classes of interneuron include the basket cell and axo-axonic cells, which innervate the somata and axon hillock respectively, and exert powerful control on pyramidal cell discharge (Buhl et al., 1994). There are many other types of interneurons in area CA3, such as those that innervate pyramidal cell dendrites (Ascoli et al., 2009; Freund and Buzsáki, 1996). In the CA3 model, each lamella contains a single GABAergic interneuron, representing interneurons which receive input both from pyramidal cells within the same lamella and from mossy fibers within the lamella, and which project back to pyramidal cells within the lamella. Importantly, parameters representing the constants associated with the interneurons in the CA3 model can be varied to ask how changes in the interneurons influence the model, including the relative contribution of pyramidal cell and mossy fiber input. Therefore, some of the empirical complexity can be explored even if all types of interneurons are not explicitly distinguished in the model (see Appendix 2).

Each time an entorhinal input pattern is presented, it is presumed to remain present for several timepoints. At each timepoint t, each the potential V_c of CA3 pyramidal cell c is computed as:

$$V_c\left(t\right)=V_{\mathit{rest}}+{\displaystyle \underset{e}{\Sigma }}{y}_e\left(t\right)w_{\mathit{ec}}\left(t\right)+{\displaystyle \underset{x\ne c}{\Sigma }}{y}_x(t-1)w_{\mathit{xc}}\left(t\right)+{\gamma }_{\mathit{MF}\_\mathit{PYR}}{\displaystyle \underset{g}{\Sigma }}{y}_g\left(t\right)$$

where V_rest is the resting potential, y_e(t) is the activity (spiking or not spiking) of entorhinal input e, and w_ec(t) is the weight of the connection between e and c, set to 0 if no such connection exists, and otherwise randomly initialized from the uniform distribution [0..1). Similarly, y_x (t–1) is the activity (spiking or not spiking) at the previous timepoint of a CA3 pyramidal cell x sending recurrent collaterals to c, and w_xc (t) is the weight of that connection, randomly initialized from [0..1) if such a connection exists or 0 if no connection exists; y_g (t) is the activity (spiking or not spiking) of granule cell g sending a mossy fiber connection to c. γ_MF–pyr is a constant representing the strength of the mossy fiber influence on pyramidal cells, set to 10.0 in the simulations reported here (for parametric simulations with this and other network constants, see Appendix 2 below). As in other CA3 models, the network operates in two modes: during “training” mode, mossy fiber inputs are enabled and recurrent collaterals are disabled; during “recall” mode, mossy fiber inputs are disabled and recurrent collaterals are enabled.

Next, the influence of inhibitory interneurons INT in each lamella is calculated as:

$$y_{INT}\left(t\right)={\gamma }_{INT}\underset{c}{\Sigma }{V}_c\left(t\right)+{\gamma }_{\mathit{MF}-\mathit{INT}}\underset{g}{\Sigma }{y}_g\left(t\right)$$

for all pyramidal cells c in the same lamella, and all granule cells g in the same lamella. γ_INT is a constant representing the influence of interneurons in the CA3 model, set to 0.05 in the simulations reported here, and γ_ME-INT is a constant representing the strength of mossy fiber influence on INT, set to 0.1 in the simulations reported here. Again, mossy fiber input is suppressed during the “recall” mode.

This inhibitory influence is then subtracted from the potential of pyramidal cells in each lamella, and those pyramidal cells with net potential exceeding a threshold θ_CA3 are allowed to generate an action potential (spike):

$$y_c\left(t\right)=1\text{if}{V}_c\left(t\right)-y_{\mathit{IN}}\left(t\right)>{\theta }_{\mathit{CA}3}$$

$$y_c\left(t\right)=0\text{otherwise}$$

where γ_IN is a constant modulating the inhibitory influence within a lamella. The threshold for pyramidal cell firing θ_CA3 is set to a default value of 0.5, lower than the threshold for granule cells θ_DG,=0.75, consistent with empirical data (Scharfman, 1992b; Scharfman, 1999a).

Coordinating DG-CA3 Interaction in the Model

Each time an input pattern is presented in “recall” mode, activity is allowed to propagate through the CA3 model for several timepoints, allowing pyramidal cells to provide excitatory input other pyramidal cells via recurrent collaterals. In pilot simulations, the CA3 model was found to usually settle into a stable activity pattern (local minimum) within two or three timepoints; in the simulations reported here, CA3 activity is allowed to propagate for 5 timepoints, to ensure such settling occurs; at the end of this period, the pattern of spiking behavior observed across the CA3 pyramidal cells represents the CA3 output, i.e., the pattern retrieved by the CA3 model in response to the entorhinal input pattern.

Next, the CA3 model is placed into “training” mode, and the DG model computes its own response to the input pattern, and provides mossy fiber input to the CA3 model. The potential of CA3 pyramidal cells and interneurons is updated, according to the above equations, with this new input (and with input from recurrent CA3 collaterals silenced). In general, because of strong excitatory input from mossy fibers, additional CA3 pyramidal cells may now spike, compared to the number that spiked in response to perforant path input alone. As in “recall” mode, activity is allowed to propagate through the network for 5 timepoints, so that the network settles into a stable attractor. Hebbian-like plasticity then occurs at the connections of the perforant path on pyramidal cells and at the connections of recurrent collaterals on pyramidal cells: For any entorhinal input x that projects to pyramidal cell c:

$$w_{\mathit{xc}}(t+1)=w_{\mathit{xc}}\left(t\right)+{\eta }_{\mathit{EC}-\mathit{CA}3}{y}_x\left(t\right)(y_c\left(t\right)-w_{\mathit{xc}}\left(t\right))$$

For any pyramidal cell x that projects to pyramidal cell c:

$$w_{\mathit{xc}}(t+1)=w_{\mathit{xc}}\left(t\right)+{\eta }_{\mathit{CA}3-\mathit{CA}3}{y}_x\left(t\right)(y_c\left(t\right)-w_{\mathit{xc}}\left(t\right))$$

These rules are similar to plasticity rules used in other hippocampal network models (e.g., Treves and Rolls, 1994). Note that the presence of y_x in the equations mean that weight change occurs only in the presence of presynaptic activity (y_x>0); the subtractive term means that weights are strengthened in the presence of strong conjoint postsynaptic activity (y_c=1) and weakened in the absence of conjoint postsynaptic activity (y_c=0). This learning rule approximates many of the aspects of the bidirectional associative synaptic plasticity (associative LTP and homosynaptic LTD) observed between pairs of CA3 pyramidal cells (Debanne et al., 1998). In the simulations reported here, the learning rates η_EC–CA3 and η_CA3–CA3 are set to 0.5 (see Appendix 2 for systematic explorations with a range of values for these parameters).

As in the DG model, behavior of the CA3 model is dominated by a relatively small set of free parameters: three governing pyramidal cell activity (V_rest, γ_INT, and θ_CA3) and two governing learning rate (η_EC–CA3 and η_CA3–CA3); two further parameters govern the interaction between DG and CA3 (γ_MF–pyr and γ_MF–INT). Default values for these parameters, used in the simulations reported here, are summarized in Table 1. Evaluation of the effects of these parameters on model performance is presented in Appendix 2.

Table 1.

Free parameters in the CA3 network model.

Parameter Name	Default Value
Vrest (resting potential)	−0.3
γINT (inhibitory modulation)	0.05
θCA3 (pyramidal cell firing threshold)	0.5
ηEC–CA3 (learning rate for synapses onto CA3 pyramidal cells from entorhinal inputs)	0.5
ηCA3–CA3 (learning rate for synapses onto CA3 pyramidals from other pyramidal cells)	0.5
γMF–pyr (influence of mossy fiber input to CA3 pyramidal cells)	10.0
γMF–IN (influence of mossy fiber input to CA3 interneurons)	0.1

All simulation results reported here are averaged over 10 simulation runs; weights and connectivity matrices are re-initialized at the start of each simulation run. Because of this variation in initial conditions, different simulation runs can produce different results, and the variance across runs is important as a measure of the stability of model performance – just as it is in empirical studies where group means are calculated across a set of individual scores. Accordingly, when simulation results are presented in the figures as averages of results from many simulation runs, the data are expressed as mean ± standard error of the mean. (Note that in some of the figures, the error bars are too small to be visible.) In addition, when comparing performance of the standard vs. backprojection model, we have used statistical tests to assess whether the differences in model performance are statistically significant at the p <0.05 level. When the p criterion is not met, we conclude that the variation is most likely to reflect inherent variation within a model, which would normally occur across simulation runs.

The “Backprojection” Model

The “backprojection” model is identical to the “standard” DG-CA3 model described above, except for the addition of weighted connections from CA3 pyramidal cells back to granule cells (shown in red in Figure 1C). In this simple model, these connections are hardwired to exist between any CA3 pyramidal cell x and any granule cell y that projects to x. Note that although DG-CA3 connections are one-to-one in the DG-CA3 model, each pyramidal cell receives on average 3-4 mossy fiber inputs. Thus, activation of one granule cell y may provide teaching input to a pyramidal cell x, which may in turn become active and produce backprojections that silence about 3-4 granule cells, including y as well as 2-3 other granule cells that may or may not have responded to the previous entorhinal input but which send mossy fiber projections to x. Granule cell inhibition due to CA3 backprojections is presumed to last only for the duration of presentation of the next entorhinal input pattern.

Appendix 2: Parametric Studies

The default values of the free parameters in the CA3 model, shown in Table 1, were chosen after parametric exploration, to produce good pattern completion behavior (maximizing “hits” and “correct rejections” while minimizing “misses” and “false alarms”). These parametric studies are summarized below.

1. V_rest (Resting potential)

V_rest is the resting potential of pyramidal cells in the CA3 model. Figure 9A-1 shows pattern completion behavior for a range of values of V_rest, and Figure 9A-2 shows the average percent of CA3 pyramidal cells that fire in response to each trained pattern, averaged across the set of 10 patterns. Behavior is relatively stable across a wide range of values of V_rest, because of the influence of the interneurons, which ensure that a relatively constant number of pyramidal cells fire at each timepoint. The default value V_rest=−0.3 was chosen to optimize pattern completion behavior (maximize hits and correct rejects; minimize misses and false alarms).

Figure 9.

Evaluation of free parameters in the computational model: resting potential, inhibition, and CA3 firing threshold. (A) Network performance, in terms of pattern completion behavior (1) and average number of CA3 pyramidal cells that spike in response to an input pattern (2), is relatively constant across a range of values of V_rest, the pyramidal cell resting potential. (B) Low values of inhibitory modulation γ_IN produce good pattern completion (1) but allow too many CA3 pyramidal cells to spike at once (2); high values produce chaotic behavior, with all pyramidal cells rhythmically silenced or disinhibited (as shown here). (C) As the firing threshold for CA3 pyramidal cells θ_CA3 increases, both pattern completion (1) and the number of CA3 pyramidal cells spiking in response to an input (2) decline gradually.

2. V_rest (Inhibitory modulation)

γ_INT modulates the strength of inhibition provided by interneurons (INT) to pyramidal cells in the CA3 model. Figure 8B-1 shows that the model performance is very dependent on this parameter. When γ_INT is very low (e.g., 0), too many pyramidal cells are allowed to fire at once (Figure 9B-2). When γ_INT is high (e.g. ≥0.15), network behavior begins to oscillate from timepoint to timepoint during the testing phase: at one timepoint, many pyramidal cells spike, producing a high level of inhibition which silences all pyramidal cells at the next timepoint, resulting in a low level of inhibition, allowing all pyramidal cells to spike during the next timepoint – and so on. Figure 9B-1 shows pattern completion behavior as a function of γ_INT; when γ_INT is low, pattern completion is good – but only because almost all pyramidal cells are active in response to any input (so pattern separation is very poor). When γ_IN is high, chaotic behavior occurs, with alternating timepoints in which most pyramidal cells spike (as in the example shown in Figure 9B-1) or almost none do. The default value of γ_INT=0.05 was chosen to produce a moderate level of pyramidal cell activation (about 20-30% of pyramidal cells spiking in response to an input pattern) while avoiding chaotic behavior.

3. θ_CA3 (Pyramidal cell firing threshold)

θ_CA3 is the firing threshold for CA3 pyramidal cells in the model; pyramidal cells with potentials greater than this threshold (after both excitatory and inhibitory inputs have contributed) are allowed to fire. This parameter has a modest effect on model performance. Figure 9C-2 shows that the number of pyramidal cells spiking in response to each pattern decreases gradually as θ_CA3 increases. Figure 9C-1 shows the effects of θ_CA3 on pattern completion. When θ_CA3 is very low (≤0), many pyramidal cells spike during the pattern completion test, resulting in an increased false alarm rate; when θ_CA3 is high (≥1), too few pyramidal cells spike, resulting in an increased miss rate. The default value of θ_CA3=0.5 was chosen to optimize pattern completion behavior.

4. η_EC–CA3 and η_EC–CA3 (Learning rates)

η_EC–CA3 is the learning rate governing changes in weight of connections from the perforant path to CA3 pyramidal cells. Model performance is relatively stable for a wide range of values for this parameter (Figure 10A). However, if η_EC–CA3 grows very large (e.g. ≥5), network behavior becomes unstable as weights fluctuate dramatically from timepoint to timepoint, leading to chaotic behavior. When η_EC–CA3 is 0, no learning occurs and weights do not change; under these conditions, perforant path inputs alone are insufficient to evoke spiking behavior in most CA3 pyramidal cells. As a result, pattern completion is poor, with no “hits” but many “misses.” (Figure 10A-1).

Figure 10.

Evaluation of free parameters in the computational model: learning rates η_EC–CA3 for connections from perforant path inputs to pyramidal cells and η_CA3–CA3 for connections from CA3 pyramidal cells to other pyramidal cells. (A) Pattern completion behavior (1) is relatively stable across a range of learning rates, within the range 0<η_EC–CA3≤2; activity level in CA3 pyramidal cells (2) is also relatively constant unless η_EC–CA3 is very high, in which case EC-CA3 weights grow strong enough to overcome local inhibition, and most CA3 pyramidals respond to most inputs. (B) Similarly, pattern completion behavior (1) is optimal for an intermediate value of η_CA3–CA3 and there is little effect of this parameter on CA3 activity levels (2).

η_EC–CA3 is the learning rate of recurrent connections between pairs of pyramidal cells. Again, model performance is relatively stable for a wide range of values for this parameter (Figure 10B); when η_EC–CA3 is very low, there are many “misses”; when η_EC–CA3 is very high, weights fluctuate dramatically from timepoint to timepoint, producing chaotic behavior.

The default values of η_EC–CA3=0.5 and η_EC–CA3=0.5 were chosen to maximize pattern completion performance.

5. γ_MF–PYR and γ_MF–PYR (Influence of mossy fibers on CA3 neurons)

γ_MF–PYR and γ_MF–PYR, which are the weights of connections from mossy fibers to CA3 pyramidal cells and interneurons, respectively, determine the effect of mossy fiber input on CA3 function in the model. In terms of pattern completion behavior and pyramidal cell population activity, the effects of modulating γ_MF–PYR and γ_MF–PYR are modest, within a relatively wide range (0≤γ_MF–PYR≤100, Figure 11A-1,2; 0≤γ_MF–INT≤10, Figure 11B-1,2). However, these parameters have a much stronger influence on the degree to which pattern separation achieved in the DG network is successfully transferred to the CA3 network. Figures 11A-3 and 11B-3 show that pattern separation in the CA3 network, defined as HD across a set of 10 patterns constructed at input density d=10%, is high as long as γ_MF–PYR is relatively high (≥5) and γ_MF–INT is relatively low (≤1). The default values of γ_MF–PYR=10 and γ_MF–INT=0.1 are chosen accordingly.

Figure 11.

Evaluation of free parameters in the computational model: mossy fiber input to CA3. (A) The effect of varying the influence of mossy fiber inputs on pyramidal cells, γ_MF–pyr, is modest on pattern completion (1) and on number of spiking pyramidal cells (2), but very low values (3) have a deleterious effect on pattern separation in CA3, calculated as HD across the output to a set of 10 trained patterns. (B) Similarly, the effect of varying the influence of mossy fiber inputs on CA3 interneurons (γ_MF–IN) is modest on pattern completion (1) and on number of spiking pyramidal cells (2), but pattern separation is impaired if γ_MF–IN grows too high (3).