Do Different Types of School Mathematics Development Depend on Different Constellations of Numerical versus General Cognitive Abilities?

Abstract

The purpose of this study was to examine the interplay between basic numerical cognition and domain-general abilities (such as working memory) in explaining school mathematics learning. First graders (n=280; 5.77 years) were assessed on 2 types of basic numerical cognition, 8 domain-general abilities, procedural calculations (PCs), and word problems (WPs) in fall and then reassessed on PCs and WPs in spring. Development was indexed via latent change scores, and the interplay between numerical and domain-general abilities was analyzed via multiple regression. Results suggest that the development of different types of formal school mathematics depends on different constellations of numerical versus general cognitive abilities. When controlling for 8 domain-general abilities, both aspects of basic numerical cognition were uniquely predictive of PC and WP development. Yet, for PC development, the additional amount of variance explained by the set of domain-general abilities was not significant, and only counting span was uniquely predictive. By contrast, for WP development, the set of domain- general abilities did provide additional explanatory value, accounting for about the same amount of variance as the basic numerical cognition variables. Language, attentive behavior, nonverbal problem solving, and listening span were uniquely predictive.

Achieving mathematics competence in its many forms during the elementary school years provides the foundation for learning algebra and other higher forms of mathematics and eventually for success in the labor market and a society that increasingly depends on quantitative skills (National Mathematics Advisory Panel, 2008). Yet, the cognitive mechanisms that support learning of formal mathematics during elementary school are not well understood: specifically, the relative contributions of children’s basic numerical cognition that emerges without formal schooling (e.g., competence in number, counting, and simple arithmetic) as contrasted with their general cognitive abilities, such as working memory (Geary, 2006; Halberda, Mazzocco, & Feigenson, 2008; Spelke, 2000; Swanson, 1993). We examined the relative contributions of two forms of basic numerical cognition tasks, which rely at least in part on children’s informal quantitative competencies, versus eight domain-general abilities to support first graders’ learning of two aspects of formal school mathematics: procedural calculations and word problems.

Theoretical Context

It has been widely documented that individual differences in children’s academic performance can be predicted by mechanisms that influence the rate and depth of learning across many domains. These domain-general mechanisms include, for example, working memory, general fluid intelligence, and speed of information processing (e.g., Ackerman, 1988; Lubinski, 2000; Walberg, 1984). Behavioral genetic studies also identify a core of genes that contributes to learning in both reading and mathematics (Plomin & Kovas, 2005). At the same time, cognitive and behavioral genetics studies reveal important domain-specific competencies that facilitate reading and mathematics learning above and beyond the influence of domain-general mechanisms. For example, young children’s basic pre-reading competencies, such as phonemic awareness and letter naming, predict later reading achievement (Gutman, Sameroff, & Cole, 2003; Stevenson, Parker, Wilkinson, Hegion, & Fish, 1976). Typically achieving children’s general cognitive abilities and domain-specific ones interact in the construction of complex academic competencies, such as fluent reading (Ferrer, Shaywitz, Holahan, Marchione, & Shaywitz, 2010).

Although much is now known about the basic pre-reading competencies that influence ease of learning to read in school, considerably less is known about the informal quantitative competencies that influence ease of learning mathematics in school. Prominent among the proposed informal quantitative competencies are potentially inherent number and magnitude systems that enable the exact representation of quantities of 3 to 4 items and the approximate representation of larger numerical values (Butterworth, 1999; Butterworth, 2005; Dehaene, 1997; Feigenson, Dehaene, & Spelke, 2004; Geary, 2007). von Aster and Shalev (2007) proposed that these number representational systems are the foundation for early aspects of school mathematics learning. Children are hypothesized to map counting words and Arabic numerals onto these representations, and the combination supports the later learning of more complex mathematical competencies, including the base-10 number system and the mathematical number line. The process of moving from inherent representational systems to the mathematical number is dependent on domain-general abilities, such as fluid intelligence and working memory (Geary, Hoard, Nugent, & Byrd-Craven, 2008). As von Aster and Shalev note, however, the developmental course and the contribution of these factors are yet to be clarified.

Interplay between Basic Numerical Cognition, Domain-General Abilities, and Mathematics Learning

Studies on the interplay between children’s basic numerical cognition and domain-general abilities in determining formal school mathematics learning incorporate different types of basic numerical competence tasks, domain-general ability measures, and mathematics achievement outcomes, with varying results. They do not allow for firm conclusions about the relative importance of each domain of competence or determination of whether their relative contributions vary for different forms of formal mathematics learning.

Evidence for the importance of a domain-specific numerical ability for mathematics learning is found in Halberda et al. (2008). They retrospectively examined whether ninth graders’ approximate number system acuity (amount of error in the underlying mental representation of numerosities) was correlated with third-grade performance on a broad mathematics achievement test, while controlling for 16 measures of domain-general abilities also measured at third grade. None of the domain-general abilities were uniquely associated with concurrent third-grade skill whereas ninth-grade numerosity was a uniquely significant correlate of earlier mathematics achievement. This is in keeping with von Aster and Shalev’s (2007) hypothesis regarding the importance of this fundamental representational system. The retrospective design, however, does not eliminate the possibility that poor mathematics achievement helped produce ninth graders’ approximate number system difficulties. Moreover, use of a broad mathematics test does not allow for determination of whether such numerical systems contribute in different ways to learning in different areas of mathematics. Booth and Siegler (2008), by contrast, examined prospective relations over one month of first grade with a highly specified type of mathematics learning: estimating answers to procedural calculations problems. Their measure of basic numerical cognition was a number line task that is thought to be dependent on the approximate magnitude representational system (Siegler & Oper, 2003; von Aster & Shalev). Accuracy in placing numbers on the number line – suggesting a strong mapping between Arabic numerals and the underlying magnitude representations – predicted learning, whereas the domain-general ability (short-term memory) did not. Yet, both the number line predictor and the type of mathematics learning had an estimation component, and short-term memory was the only domain-general ability considered.

By contrast, other studies suggest both informal, basic quantitative competencies and domain-general abilities contribute to formal mathematics learning (Bull, Espy, & Wiebe, 2008). Kroesbergen et al. (2009) assessed whether subitizing, the fast apprehension of up to three or four items, as well as domain-general abilities (fluid intelligence, phonological processing, and executive functions of shifting, updating, and inhibition) account for concurrent counting skill in 5- and 7-year olds. Executive functions and subitizing were uniquely associated with counting skill. Concurrent data collection, however, makes the causal relation from subitizing and executive functions to counting skill unclear; moreover, counting skill, which develops before 5 to 7 years of age, has important connections to the subitizing task. With a prospective design and a broad mathematics achievement test outcome, Krajewski and Schneider (2009) found that quantity-number competencies, assessed 2–6 months before school entry, predicted the mathematics outcome 4 years later, as did preschool number naming speed and nonverbal intelligence. These studies do not, however, lend insight into whether the type of school mathematics learning depends on different constellations of numerical versus general cognitive abilities. To address this issue, Fuchs et al. (in press) found that one basic numerical cognition task, a number sets measure that assesses fluency of accessing and manipulating small quantities, accounted for unique variance in fluency with number combinations (1-digit addition and subtraction), after controlling for domain-general abilities. The combination of this task and the number line task, by contrast, were uniquely associated with word-problem skill. This suggests that learning different aspects of the formal school mathematics curriculum may depend on different constellations of numerical versus general cognitive abilities. However, in this study, the number sets measure was more transparently connected to fluency with number combinations than with word-problem skill, and performance was measured concurrently. There is a need for a prospective study that can speak to the direction of effects, with measures of different types of school learning, basic numerical cognition tasks that do not connect to one form of school learning more transparently than the other, as well as a broad set of domain-general abilities.

Contribution of Present Study

We extended prior work by prospectively examining the interplay between basic numerical cognition and domain-general abilities for two types of mathematics learning that comprise a major portion of the primary-grade school program: procedural calculations (2-digit adding or subtracting, with or without regrouping) and word problems (that involve combine, compare, and difference relationships among numbers). Although these domains of the formal mathematics curriculum both require simple arithmetic (1-digit adding/subtracting), they pose substantially different challenges. A procedural calculations problem is already set up for solution, whereas a word problem requires students to use linguistic information to construct a problem model, identify missing information, and set up a calculation problem for finding the missing information. Further, we relied on two basic numerical cognition tasks, each similarly distal from the two mathematics outcomes, and included a comprehensive battery of eight domain-general abilities in an attempt to define the overlapping and unique contributions of these different cognitive competencies to skill development in formal school learning, while examining development over the course of first grade. In the following sections, we explain the basis for the basic numerical cognition tasks and domain-general mechanisms, and we state our hypotheses.

Domain-Specific Mechanisms

Butterworth (2005) and von Aster and Shalev (2007) proposed that the systems that enable the representation of small, exact quantities and the approximate magnitude of larger ones are core systems for the formal learning of mathematics (also see Geary, 1995; Spelke, 2000). The exact system allows children, and even infants (e.g., Xu & Spelke, 2000; Spelke, 2003), to quickly apprehend the quantity of one to three objects without counting, a process called subitizing. Preschool children easily map Arabic numerals onto these quantities. The approximate representation system represents magnitudes beyond the subitizing range, but not as precisely. The learning of the counting sequence and properties of the sequence (e.g., that each successive count represents an increase of one) contributes to children’s learning the magnitudes of larger numbers and for representing these on a mental number line (Feigenson, Dehaene, & Spelke, 2004). Developmental and neuropsychological studies suggest that individual differences in the precision (e.g., some children may have a subitizing range of only one or two) of these two systems may contribute to individual differences in ease of learning some aspects of mathematics (Geary et al., 2008; Koontz & Berch, 1996).

We chose two basic numerical cognition tasks that are dependent, in part, on the functioning of these systems. Geary, Bailey, and Hoard (2009) developed the Number Sets Test to assess the speed and accuracy with which children understand and manipulate small, exact numerosities within the subitizing range and just beyond this range (<10) while transcoding between quantities and their Arabic numerals. Children combine pairs or triplets of Arabic numerals (e.g., 3 4) or sets of objects (e.g., ♣♣ ◆◆◆) and quickly determine if they match a target numeral (e.g., 5). Subitizing can contribute to fluency if the quantity of small sets of objects is apprehended and then combined (e.g., ♣♣ ◆◆◆ = 5; Geary & Lin, 1998); while it is likely that the task also requires implicit or explicit understanding of addition, fluent performance is aided by subitizing and an understanding of the quantities associated with numerals just beyond this range. First-grade performance predicts mathematics achievement in third grade (Geary et al., 2009).

In terms of approximate representations of large quantities, a systematic program of research relies on Siegler and Booth’s (2004) Number Line Estimation task, in which children locate Arabic numerals on a number line marked only at 0 and 100. The pattern of placements on the number line is thought to reflect the underlying system for representing larger quantities. Placements that conform to the natural logarithm of the numbers suggest dependence on the inherent magnitude representational system, whereas linear placements suggest use of the school-taught system (Feigenson et al., 2004; Siegler & Oper, 2003). The absolute error of the placements correlates with numerical comparison, numerosity estimation, numerical categorization, the linearity of measurement, and broad mathematics achievement test scores and predicts improvement in procedural calculations estimation (Booth & Siegler, 2006, 2008; Laski & Siegler, 2007; Siegler & Booth, 2004).

Although these tasks are not pure measures of precise representation of small number or approximate representation of large quantities, they do map loosely onto these two core systems and are frequently used to tap these forms of numerosity. Moreover, in the present study, they provide a relatively strong test of whether the role of basic competence with numbers and number magnitude differs as a function of type of school learning because procedural calculations and word problems each demands mathematics learning well beyond the transparent demands of either basic numerical cognition task: subtraction for procedural calculations and word problems, columnar addition and subtraction for procedural calculations, and linguistically embedded reasoning about relations between numbers for word problems. Although the Number Sets Test requires combining small quantities and both measures incorporate Arabic numerals, these demands are common across most forms of school learning.

Basis for Domain-General Mechanisms Considered

A body of research also examines domain-general mechanisms that support mathematics learning in school – without considering the role of basic domain-specific numerical competencies. Much of this work has focused on working memory and, as in the present study, most of these studies are based on Baddeley and Hitch’s (1974) multicomponent model (as opposed to a unitary system of working memory primarily involved in attentional control, e.g., Cowan, 1999; Engle, Cantor, & Carullo, 1992). The multicomponent model comprises three systems. The central executive allocates attentional resources and is responsible for planning, sequencing, and maintaining information in the phonological loop and visuospatial sketch pad. The former is specialized for auditory information; the latter for visual and spatial information.

Procedural calculations and the solving of word problems may depend, in part, on one or several of these working memory systems (e.g., Geary & Widaman, 1992; Hitch, 1978; Swanson, 1993). For instance, the central executive may be engaged during translation of word-problem sentences into equations and in executing the sequence of steps (e.g., trading across columns) needed to solve procedural calculations problems. The process of counting, as in the use of counting to solve arithmetic problems, may engage the phonological loop (Logie & Baddeley, 1987), and representing the relation between quantitative sentences in word problems may be aided by visuospatial representations (Johnson, 1984).

The several subcomponents of the central executive that contribute to mathematical competence are not, however, well understood: specifically, those involved in maintaining information in working memory, inhibiting intrusions of irrelevant information into working memory, and switching from one subtask to the next (Bull et al., 2008; DeStefano & LeFevre, 2004). The search for mechanisms underlying mathematics development is further complicated by the relation between working memory and processing speed. Debate exists about whether individual differences in working memory are driven by more fundamental differences in processing speed (Kail, 1991) or whether the attentional focus associated with the central executive speeds information processing (Engle et al., 1999). To further complicate the goal of untangling which domain-general abilities are associated with competence in different mathematics domains, working memory correlates with general fluid intelligence (Embretson, 1995), and with respect to word problems, it is important to consider the role oral language comprehension may play (Jordan, Levine, & Huttenlocher, 1995).

For these reasons, gaining insight into whether and if so which domain-general abilities uniquely contribute to individual differences in procedural calculation versus word-problem development requires simultaneously consideration or control of these many domain-general constructs. Three previous large-scale investigations considered the role of a large battery of domain-general abilities for more than one mathematics outcome but without considering the role of basic numerical cognition. Assessing 353 first through third graders on these dimensions concurrently, Swanson and Beebe-Frankenberger (2004) found that working memory contributed to strong performance across word-problem and number combination skill, but also identified unique abilities: phonological processing for number combinations; fluid intelligence and short-term memory for word problems. Swanson (2006) then followed development of number combination and word-problem skill over one year, identifying controlled attention, vocabulary knowledge, and visuospatial working memory as predictors of number combinations, but the executive control component of working memory for word problems. With 312 third graders, Fuchs et al. (2006) examined the concurrent cognitive correlates of number combinations versus word problems, this time controlling for the role of number combination skill in word problems. Teacher ratings of inattentive behavior correlated with both mathematics domains, but the remaining abilities differed: for number combinations, phonological decoding and processing speed; for word problems, nonverbal problem solving, concept formation, and language. Across studies, some findings recur; others are idiosyncratic. But together, results suggest that different combinations of domain-general abilities underlie the development of different mathematical competencies. This body of research does not, however, consider the role of basic numerical cognition, which may alter understanding about the contribution of domain-general abilities.

Hypotheses

In light of (a) the theoretical model of von Aster and Shalev (2007), (b) empirical work on the interplay between basic numerical cognition and domain-general abilities, (c) evidence on the fundamental role informal, basic numerical cognition may play in development, and (d) findings from large-scale investigation of the relation of domain-general abilities (without consideration of basic numerical cognition), we formulated three hypotheses. (1) Basic numerical cognition contributes substantially to the development of procedural calculations and word-problem skill, even after domain-general abilities have been controlled. (2) For both forms of mathematical development, domain-general abilities contribute a significant amount of variance to the development of procedural calculations and word-problem skill, even after basic numerical cognition is controlled. (3) The domain-general abilities underlying procedural calculations and word-problem development differ, with central executive, attentive behavior, phonological processing, and processing speed predicting procedural calculations and word-problem development; with the visuospatial sketchpad predicting procedural calculations development; and with language and nonverbal reasoning predicting word-problem development. Findings should help advance understanding about the mechanisms that contribute to mathematics development and help inform the identification and treatment of students with risk for mathematics difficulty.

Method

Study Overview

The present data are derived from a larger study with two goals. The first, consistent with the focus of the present paper, is to investigate the contributions of basic numerical cognition and domain-general abilities to mathematics development. The second goal is to assess the efficacy of preventative tutoring for at-risk students where risk is defined as poor mathematics and reading performance at the start of first grade, which is associated with increased odds for developing mathematical learning disabilities. The present data involved students in the first- and second-year samples of this 4-cohort study and centered on only the first goal. Each year, to identify children to enter the study, we screen a large number of students, with the goal of entering only a small subset into the study. (The screening measures are the only data collected on students who do not enter the study.) To assess the efficacy of preventative tutoring, we consider all at-risk students who enter the study (i.e., including the two-thirds randomly assigned to receive tutoring and the one-third randomly assigned to not receive tutoring). However, to examine contributions of basic numerical cognition and domain-general abilities to mathematics development (as in the present paper), we only include students who receive no special mathematics intervention beyond their normal school program: the not-at-risk students who enter the study as well as the one-third of at-risk students who enter the study and are randomly assigned not to receive tutoring. We exclude the tutored at-risk students because we expected tutoring to disrupt the relations between predictors and mathematics development. Also, by excluding two-thirds of the at-risk (i.e., tutored) students, the sample represents the expected distribution of academic development.

Participants

To examine the contributions of basic numerical cognition and domain-general abilities on math development, the study design called for the 312 students who entered the study and received no tutoring. Among these 312 students, 32 students moved to non-study schools during first grade and therefore were lost to the study. So 90% of the 312 students who entered the study (and received no tutoring) were included in this research report.

To select 312 students, we screened students for study entry in 116 classrooms in a southeastern metropolitan school district. Of the 2025 children in these classrooms, parents provided consent on 1416 (70%), 1281 of whom were present for screening on mathematics and reading performance (see Appendix for description of screeners). Because no true cut-point for academic risk has been established, we relied on a latent class approach to identify groups, which combined the four screening scores into a single latent factor. The fit of a single factor model was acceptable (χ² (2) = 35.47, p < .001, CFI = .95, SRMR = .035; Hu & Bentler, 1999).¹ A three-class solution was specified yielding high, average, and at-risk strata.We combined the high and average strata into a “not-at-risk” group.

To select 312 students to enter the study, we excluded (a) 332 students whose mathematics performance was inconsistent with their overall risk status as indexed on the latent variable (this ensured that at-risk students experienced poor incoming performance in both mathematics and reading performance and that not-at-risk students experienced at least average experience in both mathematics and reading); (b) 147 students whose teachers identified them as not speaking English; and (c) 26 students with standard scores below 80 on both subtests of the Wechsler Abbreviated Intelligence Scale (WASI; Wechsler, 1999). (WASI was administered first in the assessment battery to avoid collecting additional data on students who failed this entry criterion.) We then randomly sampled 536 of the remaining 776 students, stratifying by risk status and ensuring that no more than eight students were in the same classroom.

Of these 536 students who entered the study, 190 were not at risk and 346 were at risk. We randomly assigned the at-risk students to three conditions, two of which (n = 232) involved tutoring. These 232 students were not appropriate for the present study because we expected tutoring to disrupt the relations between predictors and mathematics development. This left (a) 190 not-at-risk students, 11 of whom moved during first grade (n = 179), and (b) 114 at-risk students, 13 of whom moved during first grade (n = 101). Mean age for these 280 students was 6.58 (SD=0.37; range 5.77–8.19) at pretest and 7.11 (SD=0.37; range 6.27–8.72) at posttest. See Table 1 for screening and demographic information by risk status. Not-at-risk and at-risk groups were statistically significantly different on all screeners (Fs = 28.87 to 239.12, all ps < .001; effect sizes [not-at-risk mean minus at-risk mean divided by not-at-risk SD] = 1.59–1.89 on math screeners and 0.65–1.02 on reading screeners).

Table 1.

Screening and Demographics Information

	Whole Sample (n=280)			Not-At-Risk (n=179)			At-Risk (n=101)
Variable	M	(SD)	%	M	(SD)	%	M	(SD)	%
1st-Grade Test of
Computation Fluency	12.29	(5.51)		15.10	(4.10)		7.32	(2.80)
Math Concepts/Apps.	18.39	(10.03)		23.46	(8.85)		9.41	(3.86)
Rapid Letter Naming	46.77	(17.59)		50.83	(17.33)		39.62	(15.73)
Word Identification Fluency	26.17	(22.88)		34.67	(23.24)		10.89	(11.49)
Wechsler Abbreviated Scale Intelligence	94.74	(13.75)		100.06	(13.36)		85.42	(8.47)
Sex: Male			54%			55%			54%
Subsidized Lunch			74%			66%			88%
Race: African American			51%			40%			71%
White			33%			41%			18%
Hispanic			8%			8%			8%
Other			8%			11%			3%

Domain-General Abilities Predictors (Also see Table 2 for summary of measures.)

Table 2.

Constructs, Measures, and Timing of Administration

		Administered
Construct	Measure	Fall	Spring
Domain-General Ability
Language	Woodcock Diagnostic Reading Battery-Listening Comprehension	X
Nonverbal Problem Solving	Wechsler Abbreviated Scale of Intelligence-Matrix Reasoning	X
Working Memory	Working Memory Test Battery for Children
Central Executive	Listening Recall	X
	Counting Recall	X
	Backward Digit Recall	X
Phonological Loop	Digit Recall	X
	Word List Recall	X
	Nonword List Recall	X
	Word List Matching	X
Visuospatial Sketchpad	Block Recall	X
	Mazes Memory	X
Attentive Behavior	SWAN	X
Processing Speed	Woodcock-Johnson III Visual Matching	X
Basic Numerical Cognition	Number Sets	X
	Number Line Estimation	X
Mathematics Outcomes
Calculations	Double-Digit Addition Test	X	X
	Double-Digit Subtraction Test	X	X
	Addition Strategy Assessment	X	X
Word Problems	Word Problems Test
	Combine Problems	X	X
	Compare Problems	X	X
	Change Problems	X	X

Language

Woodcock Diagnostic Reading Battery (WDRB) - Listening Comprehension (Woodcock, 1997) measures the ability to understand sentences or passages. With 38 items, students supply the word missing at the end of sentences or passages that progress from simple verbal analogies and associations to discerning implications. Reliability is .80 at ages 5–18; the correlation with the WJ-R is .73.

Nonverbal problem solving

WASI Matrix Reasoning (Wechsler, 1999) measures nonverbal reasoning with pattern completion, classification, analogy, and serial reasoning tasks. Students complete a matrix, from which a section is missing, from five response options. Reliability is .94; the correlation with the WISC-III Full Scale IQ is .66.

Working memory

The Working Memory Test Battery for Children (WMTB-C; Pickering & Gathercole, 2001) comprises nine subtests that assess the central executive, phonological loop, and visuospatial sketchpad. Each subtest has six items at span levels from 1–6 to 1–9. Passing four items at a level moves the child to the next level. At each span level, the number of items to be remembered increases by one. Failing three items terminates the subtest. Subtest order is designed to avoid overtaxing any component area and is generally arranged from easiest to hardest. We used the trials correct score. Because the sample of 280 students in this study is considerably larger than the standardization sample at this age, we used z-scores based on our sample, as has been done elsewhere (e.g., Geary et al., 2007).

Central executive comprises three dual-task items. For Listening Recall, the child determines if a sentence is true; then recalls the last word in a series of sentences. For Counting Recall, the child counts a set of 4, 5, 6, or 7 dots on a card and then recalls the number of counted dots at the end of a series. Backward Digit Recall is a standard format backward digit span.

Phonological loop comprises Digit Recall, Word List Recall, and Nonword List Recall, in which the child repeats stimuli spoken by the tester in the same order. In Word List Matching, the tester speaks two words, adding one word at each level. The same words are presented again, and the child determines if the second list is in the same order as the first.

Visuospatial sketchpad comprises two tasks. Block Recall uses a board with nine raised blocks, each with a number on one side, which only the tester sees. The tester taps a block (or series of blocks); the child duplicates the tapping. For Mazes Memory, the tester presents a maze with more than one solution and a picture of an identical maze with a path showing one solution. The picture is removed, and the child duplicates the path.

Attentive behavior

The SWAN (Swanson et al., 2004) samples items from the Diagnostic and Statistical Manual of Mental Disorders-IV criteria for Attention Deficit Hyperactivity Disorder for inattention (9 items) and hyperactivity-impulsivity (9 items). Teachers rate items on a 1–7 scale. We report data for the inattentive subscale as the average rating across the nine items. The SWAN correlates well with other dimensional assessments of behavior related to attention (www.adhd.net). Coefficient alpha in the present study was .97.

Processing speed

With WJ-III Visual Matching (Woodcock, McGrew, & Mather, 2001), children locate and circle two identical numbers in rows of six numbers; they have 3 min to complete 60 rows. As per the test developer, reliability is .91.

Basic Numerical Cognition Predictors

The Number Sets Test (Geary et al., 2009) assesses the speed and accuracy with which children understand and manipulate small, exact numerosities within the subitizing range and quantities just beyond this range (< 10) while transcoding between those quantities and their Arabic numerals. Two types of stimuli are used: objects (e.g., squares) in a 1/2” square and an Arabic numeral (18 pt font) in a 1/2” square. Stimuli are joined in domino-like rectangles with different combinations of objects and numerals. Dominos are presented in lines of 5 across a page, the last two lines of which show three 3-square dominos. Target sums (5 or 9) are shown in larger font at the top the page. On each page, 18 items match the target; 12 are larger; 6 are smaller; and 6 contain 0 or an empty square.

The tester begins by explaining two items matching a target sum of 4; then, uses the target sum of 3 for practice. The measure is then administered. The child is told to move across each line from left to right without skipping any; to “circle any groups that can be put together to make the top number, 5 (9)”; and to “work as fast as you can without making many mistakes.” The child has 60 sec per page for the target 5; 90 sec per page for the target 9. Time limits were chosen to avoid ceiling effects and to assess fluent recognition and manipulation of quantities. Geary et al. (2007) found that first graders’ performance was consistent across target number and item content (i.e., whether the rectangle included Arabic numerals or shapes) and could thus be combined to create an overall frequency of hits (alpha, α = .88), correct rejections (α = .85), misses (α = .70), and false alarms (α = .90). These data are then converted to the d-prime score, which is derived from ROC analyses to represent the child’s sensitivity to quantities and has been shown to capture variance unique to mathematics achievement (e.g., Geary et al., 2009).

With Number Line Estimation (Siegler & Booth, 2004), 24 number lines containing a blank line with two endpoints (0 and 100) are presented, one at a time, with a target number (e.g., 45) in a large font printed above the line. The child places the target number on the line. As in Siegler and Booth (Experiment 2), the tester shows a number line containing only the endpoints 0 and 100, and the child points to where 50 goes. As per Geary et al. (2007), to explain the task, we permit children to compare their response to a model as the tester says, “the number 50 is half of 100, so we put it halfway in between 0 and 100 on the number line.” Note that these directions produce findings that are comparable (e.g., Geary et al., 2007; Booth & Siegler, 2004) to other work by Siegler and colleagues. After the directions, the measure is administered with numbers lines containing only the endpoints 0 and 100.

Siegler and Opfer (2003) used group-level median placements fitted to linear and log models to make inferences about the modal representation children used to make placements, and they used an accuracy measure for individual difference analyses. Accuracy is defined as the absolute difference between the child’s placement and the correct position of the number.² For 45, placements of 35 and 55 produce difference scores of 10. Other potential individual differences measures include the frequency with which children make placements consistent with a linear representation of the line or placements that conform to the natural log of the numbers, suggesting use of the approximate magnitude representational system. To determine the best measure of children’s understanding of the linear number line, we correlated the following ways of indexing performance, each with procedural calculations (PC) and word problem (WP): absolute number line error, percentage of trials consistent with use of a linear representation and percentage of error for these trials, and percentage of trials consistent with use of a log representation and percentage of error for these trials (i.e., the degree to which the placement differed from the predicted log placement; see Geary et al., 2007, 2008). For PC and WP, the best predictor was absolute number line error, r(280) = .46 to .59, as per Geary, Hoard, and Bailey (2010). Cronbach’s alpha on this sample was .91. In analyses, we multiplied the accuracy scores by −1 so the scores represent accuracy instead of inaccuracy.

Mathematics Outcomes

Procedural calculations

With the Double-Digit Addition Test and the Double-Digit Subtraction Test (Fuchs, Hamlett, & Powell, 2003), students have 5 min to complete 20 2-digit addition problems with and without regrouping and 5 min to complete 20 2-digit subtraction problems with and without regrouping. (Each problem also requires students to answer number combinations for solution.) The score on each test is number of correct answers. Agreement on 100% of protocols by two independent scorers was 99.3% and 99.1%; alpha on this sample was .93 and .95. With Addition Strategy Assessment (Geary et al., 2007), addition problems are presented horizontally at the center of a computer screen. In the present study, we report number correct for complex stimuli (16+7, 3+18, 9+15, 17+4, 6+19, and 14+8, the entire set of complex stimuli).

Word problems

Word Problems (Jordan & Hanich, 2000) comprises 14 word problems requiring simple number combinations for solution, which represent the predominant word-problem types in the primary grades: combine (two quantities are combined to form a total), compare (two quantities are compared to find a difference), or change (an action that triggers an increase or decrease).³ The tester reads each item aloud; students have 30 sec to write an answer and can ask for re-reading(s). The scores are the number of correct answers for each of the three types of relationships. A second scorer independently scored 20% of protocols, with agreement of 99%. Coefficient alpha on this sample for the three scores, respectively, was .60, .66, and .60.

Estimating Development: Latent Change Scores

Latent variable approaches to modeling difference scores successfully address measurement error and restrictive assumptions associated with simple 2-wave difference scores (Little, Bovaird, & Slegers, 2006; McArdle, 2001, 2009; McArdle & Prindle, 2008). In latent change analyses, structural equation models are used to estimate two common factors (i.e., a pretest and a posttest latent factor) and a latent change factor between the two common factor scores. To interpret the latent change factor, equivalent factor structure and loading invariance are required across time (i.e., pretest to posttest). In these models, the common factors do not include error of measurement so individual differences in the latent change score are not confounded by measurement error, eliminating reliability problems.

We calculated a latent change score for each mathematics achievement construct (PCs and WPs) across the measurement occasions (fall to spring of first grade). For each construct, we had three manifest variables at each assessment wave: for PCs, Double-Digit Addition Test, Double-Digit Subtraction Test, and Addition Strategy Assessment; for WPs, Combine WPs, Compare WPs, and Change WPs. Basic measurement models at pretest and posttest confirmed a 1-factor solution for PC and for WPs at each testing occasion, indicating equivalent factor structure across time in the two mathematics domains. Given the sample size, we used bootstrapping procedures (with 1000 draws) to estimate standard errors of the model parameters. For WPs, the overall fit of the latent change model was adequate (see Hu & Bentler, 1999), χ²(13) = 33.56, p=.0014; CFI=.98; TLI=.97; SRMR=.045. For PC, the initial model fit was not adequate, χ²(10) = 113.74, p<.0001; CFI=.89; TLI=.78; SRMR=.100. Suggested modification, allowing the residual variance terms to correlate between posttest Addition Strategy Assessment and Double-Digit Addition Test, pretest Double-Digit Subtraction Test and Double-Digit Addition Test, and posttest Addition Strategy Assessment and Double-Digit Subtraction Test, improved model fit, χ²(7) = 25.00, p=.001; CFI=.97; TLI=.95; SRMR=.06.⁴ The correlation between factors scores generated by the initial PC model and the modified model (e.g., the correlation of f[1] from the initial model with f[1] from the modified model) exceeded .98. See Figure 1, with caption, for the model by which latent change scores are created. These analyses, conducted in MPlus 5.21 (Muthen & Muthen, 1998–2009), were imported into SPSS, where the multiple regression analyses were conducted.

Figure 1.

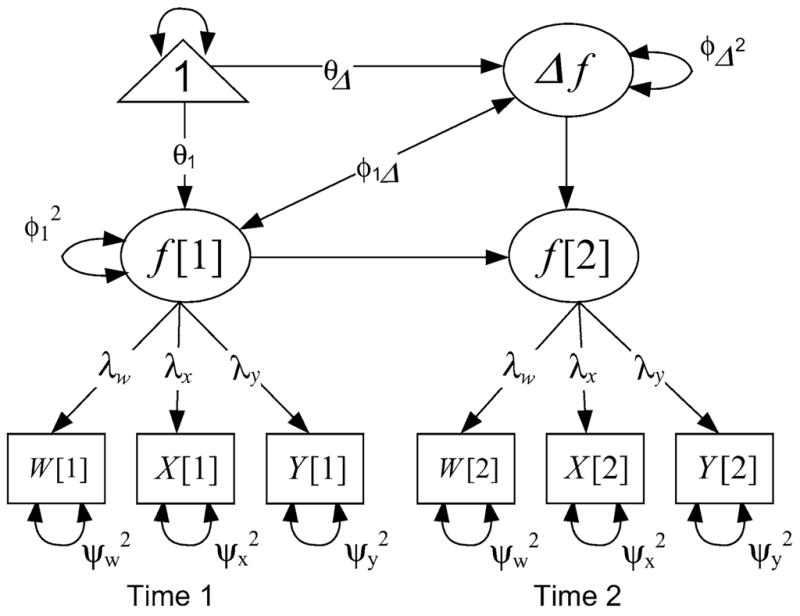
Latent change model. Each of the three observed measures of the construct (procedural calculations or word problems) collected at fall of first grade is entered to create a latent pretest score (f [1]), as is the case at spring of first grade for creating a latent posttest score (f [2]). A third latent score is estimated (Δf) to represent the latent change between the two factor scores (f [1] and f [2]). In SEM, factor scores are not typically estimated, and therefore Δf cannot be calculated directly. Instead, McArdle (2009) described how a fixed unit-valued coefficients (=1) can be included in the model so that the second latent factor (f [2]) is defined as a simple sum of the other two (f [1] + Δf). Because the latent change score (Δf ) now is part of the model, the model parameters include the variation in latent changes across individuals (φΔ 2) as well as covariation of change with the initial common factor (φ1Δ). This allows an estimate of the three factors scores f [1], f [2] and Δf for each individual from the SEM model. This multivariate SEM approach avoids the problems of using unreliable difference scores and the random errors cannot create regression to the mean (McArdle & Nesselroade 1994, Nesselroade et al. 1980).

Procedure

In September of first grade, we screened students for study entry. In September and October, the domain-general ability measures, Number Line Estimation, and Addition Strategy Assessment were administered in three individual sessions, and Number Sets Test and the remaining PC and WP tests were administered in one small-group session. In March, we administered the PC and WP tests in one individual and one small-group session. All individual sessions were audiotaped; 15% of tapes were selected randomly, stratifying by tester, for accuracy checks by an independent scorer, with agreement exceeding 99%. In October, teachers completed the SWAN Rating Scale.

Results

See Table 3 for means, SDs, and correlations among the basic numerical cognition variables, the domain-general ability variables, the PC and WP measures, and the latent change scores. In preliminary analyses, central executive working memory (but not phonological loop or visuospatial sketchpad) uniquely predicted PC and WP development. Because the correlation between Number Sets Test and executive control was relatively high and because two of three executive control subtests involved numerals, we ran correlations among the three executive control subtests. Listening Recall was more highly correlated with Backward Digit Span and Counting Recall than the two subtests involving numbers were correlated with each other (Listening Recall with Counting Recall .46; Listening Recall with Backward Digit Span .34; Counting Recall with Backward Digit Span .22), suggesting that numerical content does not drive results. We then entered the three executive control subtests, without other predictors, into regressions. Listening Recall and Counting Recall, but not Backward Digit Span, were uniquely predictive of PC and WP development. Based on these preliminary analyses, we selected Listening Recall and Counting Recall to represent the central executive. So we entered two basic numerical cognition variables (Number Sets and Number Line Estimation) and eight domain-general abilities (Listening Recall, Counting Recall, language, attentive behavior, nonverbal problem solving, phonological loop, visuospatial sketchpad, and processing speed) into the multiple regression to assess the overall incremental validity of the basic numerical cognition variables when controlling for the domain-general abilities.

Table 3.

Means, Standard Deviations, and Correlations

					Correlations
	Raw Scores		Standard Scores				Working Memory							Numerosity
Variables	Mean	(SD)	Mean	(SD)	L	NP	EF	LR	CR	PL	VS	A	PS	NS	NL
Domain-General Abilities
Language (L)	14.66	(4.83)	89.25	(15.27)
Nonverbal Problem Solving (NP)	9.25	(15.69)	49.71	(9.80)	43
Working Memory (WM)
Executive Function (EF)	42.75	(10.43)	0.01	(1.00)	45	50
Listening Recall (LR)	5.86	(4.86)	0.01	(1.00)	49	41	77
Counting Recall (CR)	11.69	(4.92)	0.01	(1.00)	38	41	70	46
Phonological Loop (PL)	69.64	(16.60)	0.01	(1.00)	40	33	53	43	30
Visuospatial   Sketchpad (VS)	23.37	(7.52)	0.01	(1.00)	31	43	50	36	43	32
Attentive Behavior (A)	40.64	(12.58)	--	--	48	38	48	50	35	40	35
Processing Speed (PS)	474.64	(8.11)	95.87	(17.28)	41	48	44	38	40	33	43	39
Number Sense
Number Sets (NS)	0.45	(1.21)	--	--	48	56	55	50	47	40	48	53	52
Number Line Estimation (NL)	21.28	(7.89)	--	--	47	44	39	39	32	28	34	37	43	52
Procedural Calculations
Fall
Double-Digit Addition (FDA)	3.34	(3.83)	--	--	38	46	37	35	32	29	31	38	33	62	42
Double-Digit Subtraction (FDS)	2.90	(2.68)	--	--	29	35	29	31	26	21	23	29	26	47	35
Addition Strategy (FAS)	1.62	(2.10)	--	--	44	49	43	43	39	32	36	43	38	67	41
Latent Procedural Calculations (FLPC)	−0.07	(2.70)	--	--	40	46	48	46	44	32	40	48	44	74	52
Spring
Double-Digit Addition (SDA)	7.12	(6.53)	--	--	32	35	37	35	35	21	32	36	36	56	37
Double-Digit Subtraction (SDS)	4.75	(4.22)	--	--	23	33	36	30	34	20	30	32	33	48	38
Addition Strategy (SAS)	3.15	(2.83)	--	--	43	38	43	41	40	26	29	44	38	59	52
Latent Procedural Calculations (SLPC)	4.01	(6.00)	--	--	34	36	45	42	42	26	36	45	43	64	50
Latent Change (LCPC)	4.08	(3.71)	--	--	26	25	38	34	37	18	29	37	36	50	44
Word Problems
Fall
Combine Problems (FComb)	0.66	(0.65)	--	--	36	47	43	37	38	31	34	39	39	54	37
Compare Problems (FComp)	1.35	(1.48)	--	--	49	47	45	48	32	30	37	37	38	57	47
Change Problems (FChange)	2.00	(1.54)	--	--	47	48	50	48	43	30	33	44	39	58	40
Latent Word Problems (FLWP)	0.00	(1.09)	--	--	60	62	61	61	47	40	46	58	50	76	58
Spring
Combine Problems (SComb)	0.97	(0.70)	--	--	44	50	43	44	35	30	31	48	39	55	39
Compare Problems (SComp)	2.24	(1.97)	--	--	55	54	50	51	38	30	38	49	43	66	55
Change Problems (SChange)	2.85	(1.87)	--	--	51	52	57	58	38	42	44	62	44	71	52
Latent Word   Problems (SLWP)	0.89	(1.52)	--	--	62	62	61	61	46	41	46	60	50	77	59
Latent Change (CLWP)	0.89	(0.47)	--	--	55	56	54	56	38	37	41	60	45	70	55

	Correlations
	Procedural Calculations
	Fall				Spring
Variables	FDA	FDS	FAS	FLPC	SDA	SDS	SAS	SLP C	LCPC
Procedural Calculations
Fall - Double-Digit Addition (FDA)
Double-Digit Subtraction (FDS)	67
Addition Strategy (FAS)	53	37
Latent Procedural Calculations (FLPC)	77	55	73
Spring - Double-Digit Addition (SDA)	57	43	52	85
Double-Digit Subtraction (SDS)	57	43	40	72	69
Addition Strategy (SAS)	41	28	52	65	41	38
Latent Procedural Calculations (SLPC)	63	43	53	91	90	76	73
Latent Change (LCPC)	41	29	33	75	84	71	71	95
Word Problems
Fall - Combine Problems (FComb)	42	36	45	49	37	29	39	45	37
Compare Problems (FComp)	49	43	51	53	37	33	39	46	37
Change Problems (FChange)	46	37	45	53	39	34	44	50	41
Latent Word Problems (FLWP)	59	48	64	70	51	45	58	65	54
Spring - Combine Problems (SComb)	40	33	42	48	34	31	45	47	40
Compare Problems (SComp)	52	41	60	63	47	42	51	58	49
Change Problems (SChange)	50	36	56	62	45	40	57	60	51
Latent Word Problems (SLWP)	58	46	64	70	51	45	60	66	55
Latent Change (CLWP)	51	38	59	64	47	42	57	61	52

	Correlations
	Word Problems
	Fall				Spring
Variables	FComb	FComp	FChange	FLWP	FComb	FComp	FChange	FLWP
Word Problems
Fall - Combine Problems (FComb)
Compare Problems (FComp)	49
Change Problems (FChange)	54	55
Latent Word Problems (FLWP)	71	81	79
Spring - Combine Problems (SComb)	47	46	49	73
Compare Problems (SComp)	47	67	55	85	61
Change Problems (SChange)	53	57	59	83	62	66
Latent Word Problems (SLWP)	65	76	73	99	77	89	87
Latent Change (CLWP)	46	57	52	86	80	89	87	93

Standard scores are mean=100 (SD=15) except nonverbal problem solving, where mean=50 (SD=10). Multiply correlations by .01. Language is Woodcock Diagnostic Reading Battery-Listening Comprehension. Nonverbal problem solving is Wechsler Abbreviated Scale of Intelligence-Matrix Reasoning. Working Memory is Working Memory Test Battery–Children. Attentive behavior is SWAN. Processing Speed is Woodcock Johnson III Visual Matching. Double-Digit Addition is Double-Digit Addition Test. Double-Digit Subtraction is Double-Digit Subtraction Test. Addition Strategy is Addition Strategy Assessment-Complex Problems. Combine Problems, Compare Problems, and Change Problems are from the Word Problems Test. Latent fall, latent spring, and latent change scores on Procedural Calculations or Word problem measures span run negative to positive values; they are not standard scores.

In the series of regression analyses to assess the predictors of PC development, we first entered the basic numerical cognition variables (R²=.294, SEE = 3.13, F Change [2,277] = 57.64, p < .001) and then added the domain-general ability variables (R²=.332, SEE = 3.09, R²Change = .038, F Change [8,269] = 1.91, p = .06). Next, we reversed the order of entry, with domain-general abilities entered first (R²=.244, SEE = 3.28, F Change (8,271) = 10.94, p < .001) and basic numerical cognition then added (R² = .332, SEE = 3.09, R²Change = .088, F Change (2,269) = 17.61, p < .001). Together, these variables accounted for 33% of the variance in PC development, F(10,269) = 13.35, p < .001. Partitioning this variance revealed that 62.0% of explained variance was shared between basic numerical cognition and domain-general abilities, 26.5% was unique to basic numerical cognition, and 11.4% was unique to domain-general abilities. In Table 4, we show B, SE, Beta, t-value, and p-value for the constant and each predictor. Both basic numerical cognition variables and Counting Span contributed unique variance.

Table 4.

Regression Models Predicting Individual Differences in First-Grade Mathematics Development

Outcome	B	SE	Beta	t	p-value
Procedural Calculations
Constant	−12.13	13.53		−0.90	.371
Number Line Estimation	0.10	0.03	−.22	− 3.49	.001
Number Sets Test	0.90	0.23	.29	4.00	< .001
Language	−0.01	0.05	−.02	−0.28	.781
Attentive Behavior	0.03	0.02	.10	1.61	.109
Central Executive-LR	0.05	0.06	.06	0.86	.393
Central Executive-CR	0.10	0.05	.14	2.22	.027
Phonological Loop	−0.02	0.01	−.09	−1.58	.115
Visuospatial Sketchpad	0.00	0.01	.00	0.03	.980
Nonverbal Problem Solving	−0.06	0.04	−.09	−1.34	.182
Processing Speed	0.04	0.03	.08	1.27	.205
Word Problems
Constant	0.73	1.26		0.58	.564
Number Line Estimation	0.00	0.00	.15	− 3.27	.001
Number Sets Test	0.14	0.02	.36	6.68	< .001
Language	0.00	0.00	.10	2.05	.042
Attentive Behavior	0.01	0.00	.21	4.52	< .001
Central Executive-LR	0.02	0.01	.14	2.84	.005
Central Executive-CR	−0.01	0.00	−.05	−1.11	.269
Phonological Loop	0.00	0.00	−.03	− 0.75	.453
Visuospatial Sketchpad	0.00	0.00	.01	0.15	.880
Nonverbal Problem Solving	0.01	0.00	.15	3.06	.002
Processing Speed	0.00	0.00	−.01	− 0.31	.757

Language is Woodcock Diagnostic Reading Battery-Listening Comprehension. Attentive behavior is SWAN. Central Executive-LR is Working Memory Test Battery–Children (WMTB)-Listening Recall. Central Executive-CR is WMTB-Counting Recall. Phonological Loop is WMTB-Phonological Loop. Visuospatial Sketchpad is WMTB-Visuospatial Sketchpad. Nonverbal problem solving is Wechsler Abbreviated Scale of Intelligence-Matrix Reasoning. Processing Speed is Woodcock Johnson III Visual Matching. Calculations is latent change score from fall to spring of 1^st grade on Double-Digit Addition Test, Double-Digit Subtraction Test, and Addition Strategy Assessment-Complex Problems. Word problems is latent change score from fall to spring of 1^st grade on Combine Problems, Compare Problems, and Change Problems from the Word Problems Test.

We then conducted a parallel set of analyses, this time predicting WP development. We first entered the basic numerical cognition variables (R²=.541, SEE = 0.32, F Change [2,277] = 163.37, p < .001), then adding the domain-general ability variables (R²=.637, SEE = 0.29, R²Change = .096, F Change [8,269] = 8.85, p < .001). Next, we reversed the order of entry, with domain-general abilities entered first (R²=.545, SEE = 0.32, F Change (8,271) = 40.61, p < .001) and basic numerical cognition then added (R² = .637, SEE = 0.29, R²Change = .092, F Change (2,269) = 33.93, p < .001). Together, these variables accounted for 64.7% of the variance in WP development, F(10,269) = 47.17, p < .001. Partitioning this variance revealed that 70.5% of explained variance was shared between basic numerical cognition and domain-general abilities, 14.4% was unique to basic numerical cognition, and 15.1% was unique to domain-general abilities. As shown in Table 4, both basic numerical cognition variables, Listening Span, language, nonverbal problem solving, and attentive behavior contributed unique variance.

Discussion

Findings, which reveal that the development of competence in solving procedural calculation problems and word problems from the beginning to the end of first grade are dependent on a combination of numerical and domain-general abilities, contribute to debate on the relative importance of these classes of ability for formal mathematics learning in school. They demonstrate that different mathematical outcomes may require different constellations of precursor abilities.

We found that the basic numerical abilities tapped by the number line estimation and number sets tasks at the beginning of first grade contributed more to academic-year growth in solving procedural calculation problems than did any of the domain-general abilities assessed in this study. The two basic numerical cognition tasks accounted for 8.8% of the variance in growth or 26.5% of the explained variance, retaining statistical significance after eight domain-general abilities were controlled. By contrast, eight domain-general abilities accounted for only 3.8% of the variance in growth or 11.4% of the explained variance, and this was not a statistically significant contribution after the basic numerical cognition variables were considered. Empirically, this provides evidence for the central role basic numerical cognition plays in the development of procedural calculation skill. However, because the number sets and number line estimation tasks are not pure measures of subitizing or fidelity of approximate magnitude systems, we cannot be certain that these systems are the central foundation for learning in this area of mathematics. Nonetheless, performance on the tasks is very likely dependent to some degree on these inherent numerical systems and thus our results provide support for the predictions of Butterworth (2005) and von Aster and Shalev (2007) and for the empirical findings of Halberda et al. (2008) who retrospectively looked at broad mathematics achievement and Booth and Siegler (2008) who focused on children’s estimation of procedural calculations over several weeks of first grade.

Even so, the relative contribution of these basic numerical abilities and domain-general abilities was notably different for the development of word-problem skill. In this case, the amount of explained variance specifically attributable to the basic numerical cognition and domain-general variables was comparable (32% of the variance in growth for each; 14.14% and 15.1% of the explained variance for basic numerical cognition and domain-general abilities, respectively), with each type of predictor retaining statistical significance in the presence of the other type of predictor. This bolsters the proposition that domain-general abilities are required to help children construct formal mathematical knowledge from their informal foundation (e.g., Geary, 2007), as in Kroesbergen et al. (2009) who focused concurrently on counting skill in 5- and 7-year olds and in Krajewski and Schneider (2009) who found that quantity-number competencies as well as number naming speed and nonverbal intelligence predicted broad mathematics achievement test scores.

The pattern of findings across the procedural calculation and word-problem measures complicates our theoretical understanding of what underlies development of formal mathematics in school. It suggests that such development cannot be conceptualized as a unitary phenomenon; that not all aspects of formal mathematics school learning tap the same underlying abilities. von Aster and Shalev’s (2007) framework, which proposes shared roles for number sense and domain-general abilities, addresses development of early, basic mathematical competencies. It specifies a role for language, working memory, and visual imagery in mastering the verbal number system that links number concepts with words in preschool, in forming associations with the Arabic number system, and in building a representation of the mental number line in elementary school. As demonstrated in the present study, however, this framework needs to be extended to address further development of formal mathematics learning in the primary grades. Toward this end, it is helpful to consider which basic numerical competencies and which domain-general abilities were uniquely predictive of development in the present study.

First, across procedural calculations and word problems, both basic numerical cognition tasks, children’s fluency at processing small numbers and their skill at estimating numerical magnitude, predicted development. The foundational role of the basic numerical competencies assessed by these tasks for school mathematics learning is underscored by the fact that our two measures/conceptualizations of basic numerical competence, which loosely map precise representations of small quantities and approximate spatial representations of large quantities, each uniquely predicted mathematics development, each with a substantial beta weight when competing against each other for variance (Number Line Estimation, .22 for procedural calculations and .15 for word problems; Number Sets, .29 for procedural calculations and .36 for word problems). Moreover, the contributions were similarly large for two transparently different aspects of formal school learning: for procedural calculations that involve multistep addition and subtraction that span ones and tens units of the number system and for word problems that involve linguistically contextualized relations between numbers, requiring students to build problem models and set up calculations problems to derive solutions. In addition, two study features create a stringent test of a domain-specific perspective. First, three measures of domain-general abilities (central executive, phonological loop, and processing speed) involved numerals. As per Landerl et al. (2004), this creates the potential for these domain-general abilities to compete for variance with numerical processing. Second, excluding students whose mathematics performance was inconsistent with reading skill may also bias results toward a domain-general perspective. For these reasons, in an extended model of mathematical development, basic numerical competencies must continue to play the foundational role in formal mathematics learning in school.

Yet, present findings do provide the basis for differentiating which domain-general abilities enable children to construct formal mathematical knowledge from their basic numerical foundations. Procedural calculations seems to require strong executive control for accessing number combination solutions (through retrieval from long-term memory, counting procedures, or decomposition) while executing a series of steps across numerical categories (i.e., ones and tens units), with or without regrouping those units (beta for counting recall = .14). This is in keeping with Hitch’s (1978) findings for adults. However, as DeStefano and LeFevre (2004) noted in their comprehensive review, most research on working memory has focused on number combination solutions (for which the role of the phonological loop and the central executive have been established). A much smaller literature has specifically focused on the solution of multidigit problems (e.g., Fuchs et al., 2006; Geary & Widaman, 1992; Widaman, Geary, Cormier, & Little, 1989), as in the present study. This is unfortunate because, compared to number combinations, procedural calculations may depend more on formal school learning. Based on our results, it appears that although procedural calculations is largely dependent on basic numerical competencies, the one domain-general ability that uniquely accounted for development was a form of executive control that relies on Arabic numerals and their corresponding numbers. We discuss this later. In a general sense, however, this corroborates a role for working memory in procedural calculations.

For word problems, by contrast, a broader range of domain-general abilities, well beyond the fundamental role of basic numerical competencies, appears necessary. First, the central executive component of working memory, this time in the form of listening recall (beta = .14), was uniquely predictive, even when two basic numerical cognition tasks and seven other domain-general abilities competed for variance. Theoretical frameworks posit that word problems involve construction of a problem model, in which individuals sequentially test model features, rejecting some and incorporating new hypotheses along the way. This appears to require working memory (e.g., Kintsch & Greeno, 1985), which is supported by much of the relevant literature (e.g., Fuchs et al., 2005; Swanson & Beebe-Frankenberger, 2004; Swanson & Sachse-Lee, 2001), including present results.

A second potentially important domain-general ability in determining word-problem skill is nonverbal problem solving, which in the present study was uniquely predictive (beta = .15) even when two basic numerical cognition tasks and seven other domain-general abilities were in the statistical model. Nonverbal problem solving requires pattern completion, classification, analogy, and serial reasoning tasks, thereby reflecting the general reasoning transparently required in word problems. Some prior research similarly documents the importance of nonverbal problem solving – but without controlling for basic numerical cognition (Swanson & Sachse-Lee, 2001) as in the present study.

Our findings also suggest the importance of a third domain-general ability: language (beta = .14). Previous studies, which did not simultaneously control for basic numerical cognition variables and only examined concurrent relations, have indicated a role for language. Jordan et al. (1995) showed that kindergarten and first-grade language-impaired children performed lower than unimpaired peers on word problems. Fuchs et al. (2006) showed the relation of language to word-problem skill among third graders, and profile analysis (Fuchs, Fuchs, Stuebing et al., 2008) revealed that poor language ability was the domain-general ability that reliably distinguished third graders with word-problem deficits from those with specific calculation deficits. It makes sense that language supports word-problem learning given the obvious need to process linguistic information when building word-problem models.

A fourth domain-general ability also proved uniquely predictive of word-problem development: teachers’ ratings of attentive behavior (beta = .21). Attention, broadly defined, has been identified as a predictor of mathematics development in previous work. Barnes et al. (2002) showed that children with hydrocephalus (with math difficulties) attempted more problems than they could reasonably solve. Russell and Ginsburg (1984) found that although students with a mathematical learning disability committed algorithm bugs that were similar to those of normal peers, these bugs more closely resembled younger normal children. Although our results provide corroborating evidence for attention as a determining mechanism, the meaning of these teacher ratings is not clear. On the one hand, classroom attention may create the opportunity to persevere with academic tasks and profit from instruction. Alternatively, classroom instruction may fail to address the needs of children with poor mathematical potential, determined by other deficits, and this mismatch creates poor attention. Another possibility is that teacher ratings of attention are clouded by academic performance and therefore serve as a proxy for achievement rather than indexing attention. Our data do not permit us to distinguish among these explanations. Further, the relation between working memory’s attentional control and teacher ratings of attention is unclear. Present findings do, however, provide the basis for hypothesizing that attention plays a critical role in word-problem development and for designing studies to reveal the underlying nature of this relation with varying measures of attention.

In these ways, the present study supports von Aster and Shalev’s (2007) perspective, in which informal number sense provides the foundation for school mathematics learning, but in which domain-general mechanisms are required to help children construct formal mathematical knowledge from that informal foundation. In thinking beyond the earliest forms of school mathematical learning that von Aster and Shalev addressed, we offer the following extensions. First and most generally, the degree and nature of individuals’ reliance on domain-general abilities differs as a function of the type of formal school mathematics learning considered. Second and more specifically, for mathematics learning more closely connected to the whole number representations in the core number systems (such as procedural calculations), basic numerical cognition plays a larger role than for aspects of the school curriculum that are more distal from the core systems of number sense. This is the case for word problems, as revealed in the present study. It may also be true for other components of the school curriculum. For example, fractional arithmetic, which in contrast to whole number arithmetic is a relatively recent cultural artifact that depends on mastering a constructed symbolic notation (Ifrah, 2000), is associated with individual differences in language whereas whole number calculation skill is not (Seethaler, Star, Fuchs, & Bryant, 2010).

Beyond extending understanding of mathematics development, findings have implications for identifying and treating mathematics difficulty. Results suggest the potential for domain-general abilities to serve as predictors of specific types of mathematics difficulty. Future research should explore how screening batteries that incorporate measures of salient domain-general abilities might enhance the accuracy of predicting risk for development of mathematics difficulty, above and beyond what is possible with basic numerical cognition tasks (e.g., Geary et al., 2009). Additionally, the specificity of domain-general deficits for different aspects of the school curriculum provides insights into treatment design. For example, to address the domain-general deficits implicated in word-problem learning, interventions might use motivational strategies to reduce behavioral inattention; explicitly teach students to understand word problems within categories that share similar solution strategies, which is thought to reduce working memory load (Cooper & Sweller, 1987); or teach strategies by which students can decipher the meaning of critical concepts within word problems to address language deficits.

Before closing, we return to the topic of executive control. Although the counting recall subtest predicted procedural calculations, listening recall predicted word problems. This indicates that listening recall taps the verbal demands of word problems whereas procedural calculations derive strength from the specific ability to handle numbers within working memory. It suggests individual differences in working memory for numbers versus words, as had been shown previously (Siegel & Ryan, 1989; Dark & Benbow, 1991). On the other hand, the two tasks involving numerals (backward digit span and counting recall) correlated with each other less well than the listening recall and counting recall tasks correlated with each other (perhaps due to parallel assessment methods). These correlations, which suggest a common working memory mechanism that is not distinct systems for numbers and words, reduce the tenability of a separate working memory system for numbers. It is nevertheless possible that some individuals’ word or number representations are more highly active in working memory. Strong activation of Arabic numerals and corresponding magnitudes in working memory may facilitate execution of procedural calculations, whereas strong activation of verbal information may aid in one or several component processes (e.g., building problem models) involved in solving word problems. Future work examining these possibilities seems warranted.

Appendix

Screening Measures to Constitute the Sample

First-Grade Test of Computational Fluency (Fuchs et al., 1990) is a 25-item test that samples the typical first-grade computation curriculum: adding two single-digit numbers (9 items), subtracting two single-digit numbers (10 items), adding three single-digit numbers (2 items), adding two 2-digit numbers without regrouping (2 items), and subtracting a 1-digit number from a 2-digit number (2 items). Students have 2 min to complete as many items as possible. The score is the number of problems correct. Staff entered responses into a computerized program on an item-by-item basis, with 15% of tests re-entered by an independent scorer. Data-entry agreement was 99.8. Coefficient alpha was .97.

First-Grade Test of Mathematics Concepts and Applications (Fuchs et al., 1990) is a 25-item test sampling the typical first-grade concepts/applications curriculum (i.e., numeration, concepts, geometry, measurement, applied computation, money, charts/graphs, WPs). The tester reads the words in each item aloud. For 20 items, students have 15 sec to respond; for 5 items, 30 sec. The score is the number of correct answers. Staff entered responses into a computerized program on an item-by-item basis, with 15% re-entered by an independent scorer. Data-entry agreement was 98.8%. Coefficient alpha was .93.

Rapid Letter Naming (Fuchs et al., 2001) displays 52 letters (26 letters in upper and lowercase) in random order; students have 1 min to say letter names. The score is the number of correct letters. If the child finishes before 1 min, the score is prorated. Two-week stability is .94.

Word Identification Fluency (Fuchs et al., 2004) provides students with 1 min to read a list of 50 words randomly sampled from 100 high-frequency pre-primer, primer, and first-grade words. If a student finishes before 1 min, the score is prorated. We administered two alternate forms and averaged scores. Alternate-form reliability/stability is .97; correlations with Woodcock Reading Mastery Test-Word Identification (Woodcock, 1998) are .77–.82. WASI (Wechsler, 1999) measures generalized cognitive ability with Vocabulary and Matrix Reasoning (see description below). Subtest scores are combined to yield an Estimated Full Scale IQ score. Reliability exceeds .92.