Use of Drifts and PLS for the Determination of Polymorphs of Piroxicam Alone and in Combination with Pharmaceutical Excipients: A Technical Note

INTRODUCTION

Piroxicam is a nonsteroidal anti-inflammatory drug used to treat arthritis and other inflammatory conditions (1). Crystalline piroxicam is polymorphic and exists in various crystalline forms designated as form I, form II, form III, and monohydrate form. Form I is also named β, cubic form, and form A, meanwhile form II is termed α, α1, α2, needle form, and form B (2,3). Form III is thermally unstable and can be converted to form II and form I, respectively (2). Additionally, the monohydrate form can dehydrate to form I (4).

Generally, the polymorphic form of a drug can transform to a more stable form during storage and manufacturing process, such as drying, milling, and compaction (5,6). The extent of conversion is dependent on the relative stability of the polymorphs and kinetic factors. Moreover, these crystal structures can have different chemical and physical properties (6). Nevertheless, the crucial properties are dissolution, bioavailability and subsequently therapeutic effectiveness of the drugs. Typically, the metastable or thermodynamically instable forms exhibit best solubility and bioavailability (2,6). However, the most stable polymorphic form is often selected for pharmaceutical development based on the minimal potential for conversion to other polymorphic forms and on its greater chemical stability. However, in some cases, such as ranitidine HCl, more than one polymorph are used in commercial formulation (7).

A number of techniques have been used to determine polymorphs including thermal analysis (DSC) (8), X-ray powder diffraction (XRD) (9), near-infrared spectroscopy (NIR) (10), Fourier transform infrared (FTIR) spectroscopy, attenuated total reflectance (ATR) FTIR (11), diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) (9,12,13), and Raman spectroscopy (14), Different techniques are appropriate for analysis of polymorphs of particular drugs. DRIFTS has been commonly used to determine various polymorphs. This method has advantages over conventional FTIR in terms of easier and more rapid sample preparation and no crystal structure changes during sample preparation which can possibly occur in FTIR. Furthermore, these analytical approaches have been effectively used in combination with various chemometric methods including partial least square (PLS)(12,13) and artificial neural network(15) for quantification of polymorphs.

Polymorphic conversion is a major concern of the pharmaceutical industry. Therefore, it is essential to characterize and quantify polymorphic forms of drugs. According to Ghan and Lalla (16), piroxicam form II can transform to form I by compression force. At present, piroxicam forms I and II are commercially available in various countries. However, form I, which is more stable than form II, is more extensively used to manufacture commercial capsules and tablets. The objective of this study is to investigate the use of DRIFTS and PLS to determine piroxicam forms I and II in binary mixtures of these two polymorphs alone and in the presence of pharmaceutical excipients. In addition, this is the first study that quantifies the mixture of piroxicam polymorphs.

MATERIALS AND METHOD

Materials

Forms I and II of piroxicam were obtained from Sigma (Sigma-Aldrich, St. Louis, MO, USA) and Vertex Chemicals (Hong Kong), respectively. The identities of both polymorphic forms were confirmed by comparing their X-ray diffraction (XRD) patterns with those previously reported (2,3). KBr was obtained from Sigma (Sigma-Aldrich, St. Louis, MO, USA). Other materials including Avicel PH-101, lactose, corn starch, and magenesium stearate were obtained from PC Drug Center Co., Ltd. (Thailand).

Sample Preparation

The particle size distribution of all materials including piroxicam and excipients was restricted to the range of 50–250 μm by the use of vibrating sieving. The powder samples with known polymorphic contents of form I and form II were weighed using an electronic analytical balance which is accurate to 0.01 mg (Mettler Toledo XS 205, USA). These two polymorphic forms of piroxicam at various ratios (0, 5, 10, 20, 30, 50, 70, 80, 90, 95 and 100% w/w) were mixed by light grinding in an agate mortar and pestle to avoid polymorphic transition. For the analysis of polymorphic piroxicam in pharmaceutical excipients, the binary mixtures of polymorphs (form I and form II) in 12% w/w were mixed with the common capsule or tablet excipients. These excipients consisted of lactose 25%, corn starch 24%, Avicel 50%, and magnesium stearate 1%. Binary mixtures with 0, 10, 30, 50, 80, 95 and 100% (w/w) of form I were used as a training set and those with 5, 20, 70 and 90% (w/w) of form I were used as a validation set. All samples were diluted as a 10% (w/w) mix in a pure non-absorbing matrix of powdered KBr.

DRIFTS Spectra Collection

The samples were placed in a macro cup for Perkin-Elmer Spectrum One FTIR diffuse reflectance accessory using the supplied sample cup holder. A cover slip was then dragged across the top of the cup to remove excess powder and smooth the sample surface. The FTIR measurements were performed on a Perkin-Elmer Spectrum One and a Perkin-Elmer DRIFTS accessory using KBr as reference material. The spectra were recorded from 4400 to 450 cm⁻¹ by averaging 64 scans at 4 cm⁻¹ resolution. All reflectance spectra were converted to Kubelka–Munk (KM) unit:

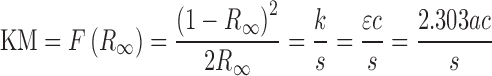1

where 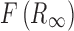is the Kubelka–Munk spectrum, 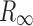is the reflectance spectrum, s is the scattering factor which is dependent on sample preparation, k is the absorption coefficient that is equal to 2.303ac or ɛc, ɛ is the molar extinction coefficient of the analyte, a is the absorptivity related to analyte species, and c is an analyte concentration. Therefore, KM intensity is linearly proportional to the concentration of the analyte if the scattering factor is controlled.

This KM transformation was performed by the use of Perkin-Elmer Spectrum for Windows version 5.02 software package. Triplicate analyses were made for each sample.

Partial Least Square Model

The obtained spectra were further quantitatively analyzed by PLS using Unscrambler 6.1 software package (Computer-Aided Modelling A/S, Trondheim, Norway). PLS or projection to latent structures was first introduced by Wold (17) and has been widely applied in the area of chemometrics. It is a factor analysis method that relates a matrix of independent variables, X, with a matrix of dependent variables, Y. PLS decomposes both X and Y matrices, the spectral data and polymorph concentrations, respectively, into their principal components, i.e. obtaining score and loading matrices. This is similar to the principal component analysis (PCA) except that in PLS both X and Y matrices are decomposed and correlated to each other whereas in PCA only X matrix is decomposed. The principal components in the case of PLS are called latent variables or PLS components. These latent variables are obtained by maximizing the variance of the data. The number of latent variables is much lower than the number of original variables. However, PLS may possibly extract as much of the initial information as possible while acquiring maximum correlation between the latent variables of X and Y.

The number of latent variables for the PLS algorithm is determined using the full cross-validation method. With cross-validation, some samples are kept out of the calibration and used for prediction. This process is repeated so that all samples are kept out once. The value for the left out sample is then predicted and compared with the known value. The prediction error sum of squares (PRESS) obtained in the cross-validation is calculated each time a new latent variable is added to the model. The optimum number of latent variables is concluded as the first local minimum in the PRESS vs. latent variable plot. PRESS is defined as

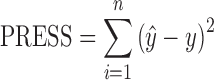2

where 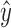is the estimated value of the ith object and y is the corresponding reference value of this object. The goodness of fit is evaluated by root mean squared error (RMSE) which is defined as

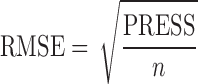3

where n is the number of samples.

All X variables were preprocessed by autoscaling, using weights based on the variables’ standard deviation and the data were mean-centered.

RESULTS AND DISCUSSION

It is well known that one of the important factors affecting the diffuse reflectance measurement of a sample is the particle size. The Kubelka–Munk function has an inverse relationship with particle size, i.e. the KM intensities decrease with increasing particle size (18). Therefore, the particle size distribution of all the materials was restricted to the range of 50–250 μm by a vibrating sieve. In the mixing steps, all samples were gentle grinding to obtain homogeneous samples and to avoid polymorphic transition.

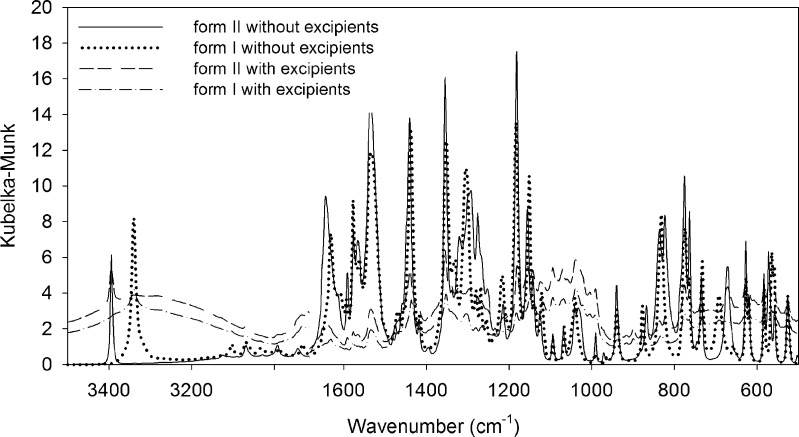
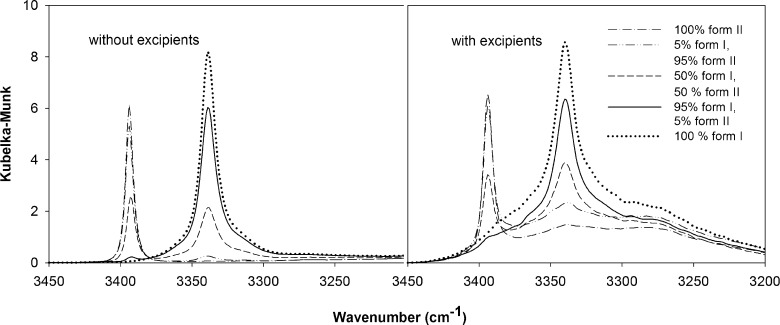
The Perkin-Elmer software was utilized for baseline correction that minimizes the interference between the IR beam and the samples. The DRIFTS spectra of piroxicam form I and form II with and without excipients are presented in Fig. 1. For pure drug, the NH stretching bands (3339 and 3393 cm⁻¹ for form I and form II, respectively) and C = O of amide stretching bands (1630 and 1643 cm⁻¹ for form I and form II, respectively) of both forms appear at different wavenumbers. However, the NH bands of these two polymorphs are more resolved than those of the C = O bands, especially in the presence of excipients. The NH stretching was thus selected for quantifying these polymorphs. Nevertheless, these NH peaks are partially overlapping, especially at a high amount of one form in binary mixtures of polymorphs or in the presence of pharmaceutical excipients (Fig. 2). The quantitative determination using the peak area or peak height of these specific peaks did not yield good results (data not shown). PLS, a widely used chemometric method, is a powerful technique for separating or differentiating samples in the mixtures and obtaining quantitative information from spectral data. Therefore, PLS was employed for the determination of these two polymorphs in the mixtures.

Fig. 1.

Kubelka–Munk spectra of piroxicam form I and form II with and without pharmaceutical excipients

Fig. 2.

Kubelka–Munk spectra of the binary mixtures of piroxicam polymorphs at 100% form II, 5% form I and 95% form II, 50% forms I and II, 95% form I and 5% form II, and 100% form I with and without pharmaceutical excipients

An optimal wavenumber in the region of the characteristic peaks of both polymorphic forms was selected in order to collect a substantial amount of potentially relevant information and to eliminate redundant data. The selection was determined according to the magnitude of the absolute values of regression coefficients and the variable importance on the projection (VIP) obtained by the PLS regression (19). In this study, the optimal spectral region used was from 3450–3200 cm⁻¹.

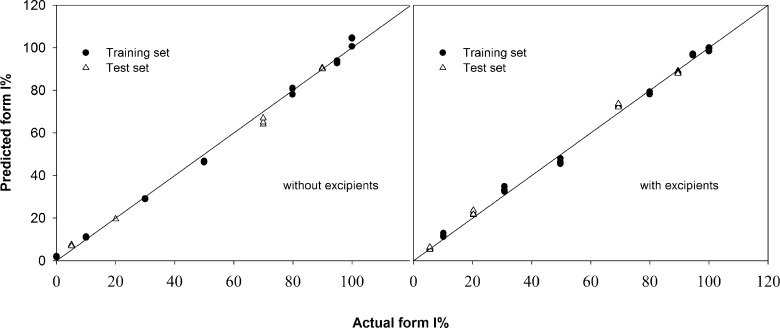
According to the PLS analysis, the best models contain 1 and 2 PLS components for the analysis of polymorphs in binary mixtures alone and in the presence of excipients, respectively. These 1 and 2 PLS components capture 97 and 94% of the variance in the X-variables, respectively, demonstrating that the information contained in the spectral data is effectively used in these calibration models. As shown in Fig. 3, PLS regression yielded a high correlation between the actual and the calculated contents of the individual polymorph for the calibration and cross-validation of the training sets. The squared correlation coefficients (R²) of the experimental and predicted values of polymorph contents in binary mixtures alone and in the presence of pharmaceutical excipients were 0.9964 and 0.9967, respectively (Table I). The cross-validated R² (also termed Q²) were 0.9961 and 0.9955, respectively, for the polymorph contents in binary mixtures with and without excipients. In addition, these PLS models display low values of root mean squared error of calibration (RMSEC), 2.272 and 2.195% for polymorphic mixtures with and without excipients, respectively, and root mean squared error of cross-validation (RMSECV), 2.506 and 2.315% for polymorphic mixtures with and without excipients, respectively (Table I). These values indicate the reliability and predictive ability of the calibration models.

Fig. 3.

Correlation between the actual and predicted contents of piroxicam form I in the binary mixtures of two polymorphs with and without pharmaceutical excipients

Table 1.

Parameters of the Calibrations, Validations, and Limit of Detection (LOD) and Quantification (LOQ) Generated from DRIFTS Data and using PLS Analysis

	Binary Mixtures of Piroxicam Polymorphs
	Without Excipients	With Excipients
R 2	0.9964	0.9967
Q 2	0.9955	0.9961
Number of PLS components	1	2
RMSE of calibration set (%)	2.272	2.195
RMSE for cross-validation of calibration set (%)	2.506	2.351
RMSE for prediction of test set (%)	1.319	2.212
Limit of detection (%)	0.870	0.881
Limit of quantification (%)	2.901	2.935

These calibration models were subsequently validated with the external test sets. As listed in Table I, the values of root mean squared error of prediction (RMSEP) are 1.319 and 2.212% for a mixture of polymorphs alone and in the presence of excipients, respectively. These RMSEP values are in the same magnitude with RMSEC and RMSECV, thus demonstrating that the models are not over-fitted. A plot of the predicted contents against the actual values of these samples is presented in Fig. 3. It shows a high correlation of the predicted and actual values of these validation or test sets and again indicating a good predictive ability of these calibration models.

Additionally, limit of detection (LOD) and limit of quantification (LOQ) were determined from multiple measurements of the spectral response of mixtures containing 5% form II (n = 5) and using Eqs. 4 and 5, respectively, as previously described (9,20)

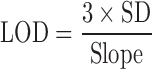4

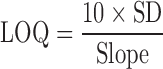5

The slope of the calibration curve represents the analytical sensitivity (21). The slopes for the calibration curves with and without excipients are 0.9967 and 0.9963, respectively. The LOD and LOQ were 0.870 and 2.901%, respectively, for piroxicam in the binary mixtures alone as presented in Table I. Those LOD of 0.881% and LOQ of 2.935% were found for piroxicam in the binary mixtures of two polymorphs with excipients. This suggests that this method can quantify these polymorphs at lower amounts even in the mixtures of pharmaceutical excipients.

SUMMARY AND CONCLUSIONS

The combination of DRIFTS and PLS provides a simple and effective tool for the analysis of piroxicam polymorphs in binary mixtures with and without pharmaceutical excipients. This method is, therefore, applicable for the determination of piroxicam raw materials and is practicable for using in industrial process control. It is also useful to investigate the polymorphic change during the storage of the finished products.