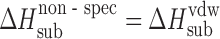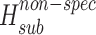Abstract
The objective of the present investigation was to study the influence of size, nature, and topology of substituents on the thermodynamic characteristics of sublimation, fusion, solubility, solvation, and partitioning processes of some drug and druglike molecules. Thermodynamic functions of sublimation process 2-acetaminophen and 3-acetaminophen were obtained on the basis of temperature dependencies of vapor pressure by the transpiration method. Thermodynamic characteristics of solubility processes in water, n-octanol, and n-hexane were calculated from the temperature dependencies of solubility using the solubility saturation method. For evaluation of fusion parameters, differential scanning calorimetry was used. A new approach to distinguishing specific and nonspecific energetic terms in the crystal lattice was developed. Specific and nonspecific solvation terms were distinguished using the transfer from the “inert” n-hexane to the other solvents. For the acetaminophen compounds and for some related drug molecules, the correlation between melting points and a parameter describing the ratio between specific and nonspecific interaction in the crystal lattices was obtained. A diagram enabling analysis of the mechanism of the partitioning process was applied. It was found that for isomers of benzoic acids and for acetaminophens, the position of substituents affects the mechanism of the partitioning process but not the extent of partitioning (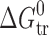 values). In contrast to this, an increased size of substituents (parabens) leads to essential changes in
values). In contrast to this, an increased size of substituents (parabens) leads to essential changes in  values, but the mechanism of the partitioning process stays the same.
values, but the mechanism of the partitioning process stays the same.
Key words: partitioning, solubility, solvation, sublimation, thermodynamics, transfer
INTRODUCTION
Solvation of drug molecules plays an important role in each stage of drug transport and drug delivery, and it may determine important physicochemical and biopharmaceutical properties, such as solubility, passive absorption, distribution, and renal elimination. Until today, the discussed questions have been considered mainly within the terminology of relative Gibbs energy functions in the form of partitioning coefficients (logP). However, to understand the mechanism and driving forces of solvation of the outlined processes from a thermodynamic point of view, it is necessary to analyze the enthalpic and entropic terms separately. Unfortunately, the process of solvation is not directly accessible through experiments. Quantitative information on solvation characteristics depends on knowledge about crystal lattice energies, which so far have not been used widely in the literature for pharmaceutical substances. These solvation functions give us the opportunity to analyze the processes in absolute energy values and to find a correlation between quantitative properties and qualitative terminology, which is commonly described by parameters of lipophilicity and hydrophilicity. To the latter, the quantitative solvation terms can be split into specific and nonspecific contributions.
The present work is a continuation of previous studies on thermodynamics of solvation of drug molecules (1–6). Here, 2-acetaminophen and 3-acetaminophen molecules (Fig. 1) were chosen because, although the compounds are not therapeutically useful (3), their structures are systematically related to those of such druglike compounds as acetanilide, 4-acetaminophen (paracetamol), and phenacetin, which have been described (4). To predict the transport of drug molecules through membranes and their distribution between different compartments, it is common to use n-octanol as a model for the lipophilic phases. Therefore, in the present study, the thermodynamics of sublimation of the solid material, solubility, and solvation processes in pharmaceutically relevant solvents (water, octanol) and specific and nonspecific terms of drug interaction with the medium (by using n-hexane as a standard) were evaluated. Furthermore, the influence of length and position of substituents of phenyl derivatives on the outlined solvation characteristics and partitioning processes was analyzed.
Fig. 1.
Structure formula of 2-acetaminophen a, 3-acetaminophen b, N-(2-methylphenyl)acetamide c, and N-(4-methylphenyl)acetamide d
We believe that these efforts need to be made in order to enable a better understanding of solvation-related processes of pharmaceutical significance. A better understanding of the behavior of drug molecules in different environments includes opportunities for the prediction of their biopharmaceutical properties and for the design of new drug compounds with better performance.
MATERIALS AND METHODS
Materials
The 2-acetaminophen (2-acetamidophenol, C9H9NO2, FW151.16, 97%, lot S27791-095) and 3-acetaminophen (3-acetamidophenol, C9H9NO2, FW 151.16, 97%, lot DO07409HU) were from Sigma-Aldrich (Gillingham, UK).
The 1-octanol (n-octanol, CH3(CH2)7OH, MW 130.2, lot 11K3688) ARG was from Sigma Chemical Co. The n-hexane (C6H14, MW 86.18, lot 07059903C) ARG was from SDS (Peypin, France).
Sublimation Experiments
Sublimation experiments were performed by the transpiration method as previously described (4). A stream of an inert gas passes the sample at a given constant temperature and at a known slow constant flow rate in order to achieve saturation of the carrier gas with the vapor of the substance under investigation. The vapor is condensed at some point downstream, and the sublimate’s mass and purity are determined. The vapor pressure over the sample at this temperature can be calculated from the amount of sublimated material and the volume of the inert gas used. To be convinced that the system is in thermodynamic equilibrium, the dependency P = f(h) and the flow rate (h) of the gas corresponding to the “plateau” on the graph have been chosen. As a rule, h is 1.6 to 1.8 l/h.
The equipment was calibrated using benzoic acid. The standard value of sublimation enthalpy obtained was 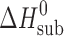 = 90.5 ± 0.3 kJ mol−1. This is in good agreement with the value recommended by IUPAC of
= 90.5 ± 0.3 kJ mol−1. This is in good agreement with the value recommended by IUPAC of 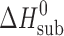 = 89.7 ± 0.5 kJ mol−1 (7). The saturated vapor pressures were measured at least five times at each temperature, with the statistical error being within 3% to 5%. The experimentally determined vapor pressure data are described in (lnP; 1/T) coordinates as follows:
= 89.7 ± 0.5 kJ mol−1 (7). The saturated vapor pressures were measured at least five times at each temperature, with the statistical error being within 3% to 5%. The experimentally determined vapor pressure data are described in (lnP; 1/T) coordinates as follows:
 |
1 |
The value of the enthalpy of sublimation is calculated by the Clausius–Clapeyron equation:
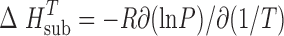 |
2 |
The entropy of sublimation at a given temperature T was calculated from the following relationship:
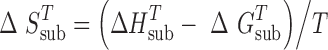 |
3 |
where 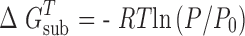 and P0 = 1.013 × 105 Pa.
and P0 = 1.013 × 105 Pa.
Sublimation data were yielded at elevated temperatures for experimental reasons, but these were much lower than the fusion temperature, and the chemical purity of the sublimate was also confirmed. To improve the extrapolation to room conditions, heat capacities of the crystals ( value) were estimated using the heat capacities calculated by the additive scheme
value) were estimated using the heat capacities calculated by the additive scheme 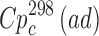 proposed by Chickos et al. (8). Concerning the method, the experimental heat capacity value at 298 K has been estimated by the correlation equation
proposed by Chickos et al. (8). Concerning the method, the experimental heat capacity value at 298 K has been estimated by the correlation equation 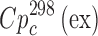 = 0.75 + 0.15
= 0.75 + 0.15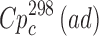 . Heat capacity was introduced as a correction for the recalculation of the sublimation enthalpy
. Heat capacity was introduced as a correction for the recalculation of the sublimation enthalpy 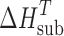 value at 298 K (
value at 298 K ( value), according to Eq. 4, with the assumption that the heat capacity of the gas phase is negligibly small compared with that of the crystal:
value), according to Eq. 4, with the assumption that the heat capacity of the gas phase is negligibly small compared with that of the crystal:
 |
4 |
The heat capacities calculated by the additive scheme for the 2- and 3-acetaminophens are equal, but this fact does not contribute essential errors in ΔHcor, because the outlined value is comparable with the sublimation enthalpy error.
Solubility Experiments
Solubility experiments were performed by the isothermal saturation method at five temperature points: 20, 25, 30, 37, and 42 ± 0.1 °C. The solid phase was removed by both centrifugation and isothermal filtration (Acrodisc CR syringe filter, PTFE 0.2 μm pore size). The experimental results stated are the average of at least five replicated experiments. The molar solubilities of the drugs studied were measured spectrophotometrically with an accuracy of 2% to 2.5% using a protocol described previously (4).
Solvation Parameters Calculations
The solvation of 1 mol of solute molecules in the solvent can be defined as the total change of the standard thermodynamic functions (ΔG0, ΔH0, ΔS0) of the system (gas + solvent) when transferring the compound molecule from the gas phase (ideal gas; single molecules without interaction) into the solvent (9). This transfer process can be presented as the difference between the dissolution and sublimation functions by the following equation:
 |
5 |
where ΔY0 is the standard change of any of the thermodynamic functions (ΔG0, ΔH0, ΔS0) of solvation (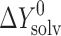 ), dissolution (
), dissolution (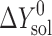 ), or sublimation (
), or sublimation (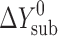 ).
).
Therefore (as follows from the thermodynamic cycle Eq. 5), to study the solvation process, which is not directly experimentally accessible, one needs to investigate the other two processes: sublimation and dissolution.
Differential Scanning Calorimetry Experiments
Differential scanning calorimetry (DSC) was performed using a Perkin–Elmer Pyris 1 DSC differential scanning calorimeter (Perkin–Elmer Analytical Instruments, Norwalk, CT) and Pyris software for Windows NT. DSC runs were performed in an atmosphere of flowing (20 ml min−1) dry nitrogen gas of high purity (99.990%) using standard closed aluminum sample pans. The DSC was calibrated with indium from Perkin–Elmer (P/N 0319-0033). The value of the determined enthalpy of fusion corresponded to 28.48 J g−1 (reference value 28.45 J g−1). The melting point was 429.7 ± 0.1 K (n = 10). All the DSC experiments were performed at a heating rate of 10 K min−1. The accuracy of weight measurements was ±0.0005 mg.
RESULTS AND DISCUSSION
Sublimation Experiments
The experimental results in terms of temperature dependencies of saturation vapor pressures are summarized in Table I. Calculated thermodynamic parameters of sublimation and fusion processes are presented in Table II.
Table I.
Temperature Dependencies of Saturation Vapor Pressure of 2- and 3-Acetaminophens
| 2-Acetaminophena | 3-Acetaminophenb | ||
|---|---|---|---|
| t (°C) | P (Pa) | t (°C) | P (Pa) |
| 57.0 | 6.04 × 10−3 | 71.5 | 5.35 × 10−3 |
| 59.0 | 7.99 × 10−3 | 77.0 | 9.47 × 10−3 |
| 61.0 | 9.37 × 10−3 | 78.5 | 1.19 × 10−2 |
| 64.0 | 1.56 × 10−2 | 82.0 | 1.66 × 10−2 |
| 66.5 | 2.19 × 10−2 | 86.0 | 2.13 × 10−2 |
| 69.0 | 2.93 × 10−2 | 87.0 | 2.45 × 10−2 |
| 72.0 | 4.24 × 10−2 | 91.5 | 3.76 × 10−2 |
| 75.5 | 5.96 × 10−2 | 92.0 | 4.29 × 10−2 |
| 80.5 | 1.18 × 10−1 | 94.0 | 4.83 × 10−2 |
| 86.0 | 2.12 × 10−1 | 96.0 | 6.99 × 10−2 |
| 89.0 | 3.33 × 10−1 | 98.0 | 7.21 × 10−2 |
| 96.0 | 5.92 × 10−1 | 101.5 | 1.08 × 10−1 |
| 99.0 | 9.13 × 10−1 | 103.0 | 1.29 × 10−1 |
| 102.0 | 1.13 | 104.0 | 1.47 × 10−1 |
| 105.5 | 1.73 | 106.5 | 1.59 × 10−1 |
| 110.5 | 2.52 × 10−1 | ||
| 112.0 | 2.81 × 10−1 | ||
| 114.5 | 3.36 × 10−1 | ||
| 117.0 | 4.69 × 10−1 | ||
| 121.0 | 6.21 × 10−1 | ||
| 124.0 | 8.46 × 10−1 | ||
aln(P[Pa]) = (39.0 ± 0.3)–(14 545 ± 113)/T; σ = 5.64 × 10−2; r = 0.9996; F = 16 302; n = 15
bln(P[Pa]) = (33.0 ± 0.4)–(13 188 ± 138)/T; σ = 6.71 × 10−2; r = 0.9990; F = 9161; n = 21
Table II.
Thermodynamic Characteristics of Sublimation and Fusion of Acetaminophens
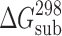 (kJ mol−1) (kJ mol−1) |
 (kJ mol−1) (kJ mol−1) |
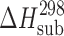 (kJ mol−1) (kJ mol−1) |
 (J mol−1 K−1) (J mol−1 K−1) |
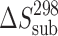 (J mol−1 K−1) (J mol−1 K−1) |
T m a (K) | ΔH fus a (kJ mol−1) | ΔS fus (J mol−1 K−1) | |
|---|---|---|---|---|---|---|---|---|
| 2-Acetaminophen | 52.8 | 120.9 ± 0.9 | 121.8 ± 0.9 | 174.8b | 227 ± 3 | 484.1 ± 0.2 | 37.0 ± 0.8 | 76 ± 2 |
| 3-Acetaminophen | 56.4 | 110 ± 1 | 111 ± 1 | 174.8† | 179 ± 3 | 416.2 ± 0.2 | 24.6 ± 0.3 | 59 ± 2 |
| 4-Acetaminophenc | 60.0 | 116.5 ± 0.7 | 117.9 ± 0.7 | 163 ± 1 | 190 ± 2 | 443.6 ± 0.5 | 27.1 ± 0.2 | 61 ± 2 |
The relationship between specific (hydrogen bonding) and nonspecific (van der Waals) interactions in crystal lattice influences the equilibrium solubility value of molecular crystals (drugs). Therefore, the procedure distinguishing the outlined energetic terms in the crystal lattices has been developed. The sublimation enthalpies for a selection of molecular crystals were taken from the Chickos and Acree (10) database. Van der Waals molecular volumes were calculated by the GEPOL program (11) using Kitaigorodsky’s atomic radii (12). To estimate the energetic level of nonspecific molecular interaction within crystal lattices, we selected crystal structures of molecules that met the following requirements: (1) the crystals have no hydrogen bond networks (ie, molecules have no hydrogen bond centers in the structure); (2) the molecules include groups of compounds with various topological structures [benzene, biphenyl, naphthalene, benzophenone, biphenyl ether, diphenylamine derivatives, and other bicycle substances with a connecting bridge between the cyclic motifs of several atoms (not more than 3)]; (3) the size of substituents does not exceed the size of the t-Bu fragment. Seventy-one molecular crystals were thus selected from the database. For this group the relationship between van der Waals volume and sublimation enthalpy can be described by the following correlation equation (Fig. 2):
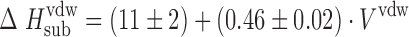 |
6 |
where r = 0.973, σ = 4.1, and n = 71.
Fig. 2.
Relationship between sublimation enthalpies, 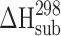 , and van der Waals volumes, V
vdw, of selected molecular crystals. Dashed line corresponds to σ interval
, and van der Waals volumes, V
vdw, of selected molecular crystals. Dashed line corresponds to σ interval
The acetaminophen crystals form the hydrogen bond networks, so to distinguish specific and nonspecific interactions in the crystal lattices, the equation was used the following way. The nonspecific term was estimated by Eq. 6, whereas the specific term was estimated by the difference between the experimental value and the value evaluated for the nonspecific term (Table III).
Table III.
Calculated Values of Nonspecific, 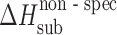 , and Specific,
, and Specific, 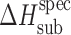 , Sublimation Enthalpy Terms of Acetaminophens
, Sublimation Enthalpy Terms of Acetaminophens
| V vdw (Å3) |
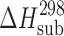 (kJ mol−1) (kJ mol−1) |
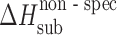 a (kJ mol−1)
a (kJ mol−1) |
 (kJ mol−1) (kJ mol−1) |
ɛ sub b (%) | |
|---|---|---|---|---|---|
| 2-Acetaminophen | 133.1c | 121.8 ± 0.9 | 72.2 | 49.6 | 68.7 |
| 3-Acetaminophen | 133.1d | 111 ± 1 | 72.2 | 38.8 | 53.7 |
| 4-Acetaminophen | 134.4e | 117.9 ± 0.7f | 72.8 | 45.1 | 62.0 |
The discussed compounds can be arranged according to the ratio between specific and nonspecific terms as follows: 2-acetaminophen > 4-acetaminophen > 3-acetaminophen. A rough estimate for hydrogen bond energy, which the OH-group forms with adjacent molecules, may be possible as follows: The sublimation enthalpies of N-(2-methylphenyl)acetamide and N-(4-methylphenyl)acetamide (Fig. 1) are equal to 96.8 ± 0.9 and 99.0 ± 0.9 kJ mol−1, respectively (15). If the sublimation data obtained in the present study are taken into account, the outlined hydrogen bond energy of 2-acetaminophen equals 25 kJ mol−1, whereas for 4-acetaminophen it is 18.9 kJ mol−1. If it is further supposed that the contribution from the specific interactions as presented in Table III correspond to hydrogen bonding energy only, then the hydrogen bond energy of the acetamide group can be estimated as 24 kJ mol−1 for 2-acetaminophen and 26.2 kJ mol−1 for 4-acetaminophen.
If one takes into account the sublimation enthalpy of acetanilide (as a reference compound) obtained in a previous work (99.8 ± 0.8 kJ mol−1), (4) it is possible to analyze the influence of OH-and CH3-groups on the crystal lattice energy. Introducing the CH3-substitute in the ortho-position leads to a slight decrease of the crystal lattice energy, whereas introducing the CH3-substitute in the para-position leads to no change in the discussed energy, within experimental error. Probably, this regularity is connected with the steric hindrances in the crystal, which emerge from the CH3-groups in the ortho-position rather than those in the para-position (where the molecules are more closely packed). Analogous analysis for the acetaminophens shows a complicated picture of influences of OH-group positions on the crystal lattice energy: The minimum value is observed for the meta-position.
For a long time, the relationship between the crystal lattice energetic terms and the melting point has been a matter of discussion (16). Analysis of this problem based on experimental data obtained earlier (1–6) (sublimation enthalpies and melting points) and using the above-outlined approach to distinguish specific and nonspecific terms has been undertaken. The dependence of the melting points on the ratio between specific and nonspecific terms (ɛsub) of several crystal lattices, presented in Fig. 3, can be described by the following correlation equation:
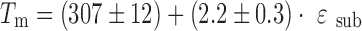 |
7 |
where r = 0.921, σ = 20.3, and n = 16.
Fig. 3.
Dependence of the melting points, T
m, vs the ratio between specific and nonspecific terms, 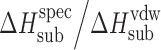 , of the crystal lattices. 2-OH-BA 2-Hydroxybenzoic acid, 3-OH-BA 3-hydroxybenzoic acid, 4-OH-BA 4-hydroxybenzoic acid, AcAN acetanilide, ASA acetylsalicylic acid, BA benzoic acid, BuPB butylparaben, EtPB ethylparaben, IBP ibuprofen, MePB methylparaben, Phenac phenacetin, PrPB propylparaben
, of the crystal lattices. 2-OH-BA 2-Hydroxybenzoic acid, 3-OH-BA 3-hydroxybenzoic acid, 4-OH-BA 4-hydroxybenzoic acid, AcAN acetanilide, ASA acetylsalicylic acid, BA benzoic acid, BuPB butylparaben, EtPB ethylparaben, IBP ibuprofen, MePB methylparaben, Phenac phenacetin, PrPB propylparaben
Thus, if one knows the melting point of the drug belonging to the presented groups of the compounds, then Eq. 7 together with Eq. 6 provides the opportunity to estimate not only the relationship between specific and nonspecific crystal energy terms, but the absolute energetic scale as well. This approach has two advantages over the approach proposed by Li et al. (16) for the ephedrine derivatives: they used direct correlation between the melting point and the Coulumbic energy calculated on the basis of X-ray data. First, our approach predicts the energetic terms (and as a consequence, the crystal lattice energy) on an absolute scale. Second, our approach does not require the use of X-ray data.
Thermodynamics of Solubility, Solvation, and Transfer Processes
The partitioning between water and octanol is the phase transition of the solute molecule across the partition boundary of the two separated phases (water and octanol) because of the thermodynamic driving force, which is defined by the difference of the chemical potentials of solute molecules dissolved in water and in octanol, respectively. However, if it sticks to the thermodynamic formalism, many questions appear about a model to describe the elementary act of the partitioning process. First, it is obvious that the solute molecules in the solution interact with the closest solvent molecules in a stronger way than they do with molecules further out in the bulk. Therefore, a so-called solvation shell is created around the solute molecule. The strength and nature of the drug-solvent interactions within this solvation shell are nonhomogeneous (non-uniform): there are weak van der Waals interactions as well as stronger donor-acceptor interactions, hydrogen bonds (as in the extreme case of a donor-acceptor interaction), and electrostatic interactions. Since most of the drugs are compounds with the ability to create hydrogen bonds, the molecules are solvated in solutions, particularly in aqueous solutions, by strong hydrogen bonds. During the partitioning/distribution process, a molecule solvated in water must rebuild this solvation shell into the octanol solvation shell (resolvation).
To estimate specific and nonspecific solvation terms along an absolute energetic scale and to compare the deduced values with analogous terms for the crystal lattices, temperature dependencies of solubility in pharmaceutically relevant solvents (where water was chosen as well as n-octanol as widely used solvents for the evaluation of lipophilicity and biopharmaceutical properties) were measured. The experimental results are summarized in Table IV. To distinguish the outlined terms, n-hexane was used as a reference solvent; it interacts with the molecules by only nonspecific forces. As a measure of the specific interactions, the respective transfer functions from n-hexane to the other solvents were used. To estimate the contribution of specific interaction in comparison to nonspecific interaction, the ɛH parameter is used (1):
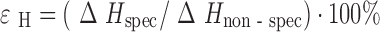 |
8 |
where 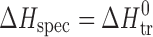 (n-hexane → solvent) and
(n-hexane → solvent) and 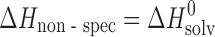 (n-hexane).
(n-hexane).
Table IV.
Temperature Dependencies of 2- and 3-Acetaminophen Solubility, X 2 (mol frac), in n-Hexane, Water, and n-Octanol
| 2-Acetaminophen | 3-Acetaminophen | |||||
|---|---|---|---|---|---|---|
| n-Hexane | Water | n-Octanol | n-Hexane | Water | n-Octanol | |
| t (°C) | X 2 × 106 | X 2 × 104 | X 2 × 103 | X 2 × 106 | X 2 × 103 | X 2 × 102 |
| 20 | 3.69 | 1.20 | 4.70 | 3.73 | 1.18 | 3.47 |
| 25 | 4.98 | 1.34 | 5.63 | 5.13 | 1.58 | 3.88 |
| 30 | 6.14 | 1.58 | 6.41 | 7.14 | 1.99 | 4.42 |
| 37 | 8.46 | 1.90 | 8.31 | 11.8 | 2.71 | 5.18 |
| 42 | 10.8 | 2.14 | 9.47 | 17.4 | 3.31 | 5.84 |
| A a | 2.5 ± 0.4 | −0.5 ± 0.3 | 4.7 ± 0.3 | 9.5 ± 0.7 | 7.9 ± 0.4 | 4.1 ± 0.1 |
| B b | 4401 ± 113 | 2492 ± 81 | 2961 ± 89 | 6455 ± 209 | 4287 ± 117 | 2194 ± 37 |
| R b | 0.999 | 0.998 | 0.999 | 0.998 | 0.999 | 0.999 |
| σc | 2.18 × 10−2 | 1.56 × 10−2 | 1.71 × 10−2 | 4.00 × 10−2 | 2.25 × 10−2 | 7.05 × 10−3 |
aParameters of the correlation equation: ln X 2 = A − B/T
b R is pair correlation coefficient.
c σ is standard deviation.
The thermodynamic functions of dissolution and solvation processes are presented in Table V. As follows from Table V, all dissolution processes in water, in n-octanol, and in n-hexane are endothermic. This is evidence that solvation enthalpies do not overweigh the respective crystal lattice energies.
Table V.
Thermodynamic Functions of Solubility and Solvation Processes of 2-, 3-, and 4-Acetaminophens in Solvents Studied
| Solvent |
 a (mol frac)
a (mol frac) |
 b (kJ mol−1)
b (kJ mol−1) |
 c (kJ mol−1)
c (kJ mol−1) |
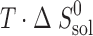 (kJ mol−1) (kJ mol−1) |
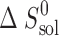 (J K−1 mol−1) (J K−1 mol−1) |
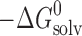 d (kJ mol−1)
d (kJ mol−1) |
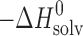 e (kJ mol−1)
e (kJ mol−1) |
 (kJ mol−1) (kJ mol−1) |
 (J K−1 mol−1) (J K−1 mol−1) |
ζHsolv (%) | ζTSsolv (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2-Acetaminophen | |||||||||||
| n-Hexane | 4.98 × 10−6 | 30.3 | 36.6 ± 0.9 | 6.3 | 21 ± 1 | 22.5 | 85.2 | 62.7 | 210 | 57.6 | 42.4 |
| Water | 1.34 × 10−4 | 22.1 | 20.7 ± 0.7 | −1.4 | −4.7 ± 1 | 30.7 | 101.1 | 70.4 | 236 | 59.0 | 41.0 |
| n-Octanol | 5.63 × 10−3 | 12.8 | 24.6 ± 0.7 | 11.8 | 40 ± 1 | 40.0 | 97.2 | 57.2 | 192 | 63.0 | 37.0 |
| 3-Acetaminophen | |||||||||||
| n-Hexane | 5.13 × 10−6 | 30.2 | 53.7 ± 1.7 | 23.5 | 79 ± 1 | 26.2 | 56.3 | 30.1 | 101 | 65.2 | 34.8 |
| Water | 1.58 × 10−3 | 16.0 | 35.6 ± 0.9 | 19.6 | 66 ± 1 | 40.4 | 75.4 | 35.0 | 117 | 68.3 | 31.7 |
| n-Octanol | 3.88 × 10−2 | 8.1 | 18.2 ± 0.3 | 10.1 | 34 ± 1 | 48.3 | 92.8 | 44.5 | 149 | 67.6 | 32.4 |
| 4-Acetaminophene | |||||||||||
| n-Hexane | 4.12 × 10−6 | 30.7 | 41.9 ± 0.7 | 11.2 | 37.6 | 29.3 | 76.0 | 46.7 | 157 | 61.9 | 38.1 |
| Water | 1.72 × 10−3 | 15.8 | 21.8 ± 0.1 | 6.0 | 20.1 | 44.2 | 96.1 | 51.9 | 174 | 64.9 | 35.1 |
| n-Octanol | 2.47 × 10−2 | 6.0f | 11.7 ± 0.2 | 5.7 | 19.1 | 54.0 | 106.2 | 52.2 | 175 | 65.5 | 34.5 |
aThe experimental error within 2%
bCalculated from the temperature dependence of solubility data
c

d
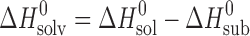
ePerlovich et al. (4)
fTaking into account activity coefficient
To compare enthalpic and entropic terms of solvation, parameters ςH and ςTS are used to describe the relative fraction of enthalpy and entropy of solvation (1):
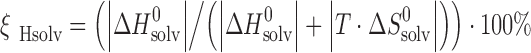 |
9 |
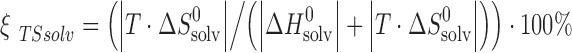 |
10 |
The hydrophobic effect of the compounds depends strongly on the position of the substituents: the biggest entropic contribution to the hydration energy is observed for 2-acetaminophen (ζTSsolv = 41.0%), whereas the smallest one is for 3-acetaminophen (ζTSsolv = 31.7%). According to the solvation energy in n-octanol, the noted substances can be arranged in the following way: 3-acetaminophen < 2-acetaminophen < 4-acetaminophen. However, the regularity of the enthalpic and entropic contributions to the total solvation process in n-octanol is the same as it is in water: ςHsolv(2-acetaminophen) < ςHsolv(4-acetaminophen) < ςHsolv(3-acetaminophen).
The results of the transfer processes from one solvent to another are presented in Table VI. The transfer processes of all the acetaminophen molecules from n-hexane to water (specific solvation) have the same behavior: They are enthalpy driven. However, the ratio between the enthalpic and entropic terms is essentially different: For 2-acetaminophen the enthalpic term exceeds the entropic term by a factor of 2.1; for 3-acetaminophen this factor is 4.6; and for 4-acetaminophen it is 3.9. The transfer process (n-hexane → n-octanol) of the considered compounds is enthalpy driven as well, but for 2-acetaminophen the enthalpic and entropic terms have opposite signs, whereas for 3-acetaminophen and 4-acetaminophen these terms have the same negative signs.
Table VI.
Thermodynamic Parameters of Transfer Processesa for 2-, 3-, and 4-Acetaminophens
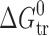 (kJ/mol) (kJ/mol) |
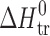 (kJ/mol) (kJ/mol) |
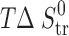 (kJ/mol) (kJ/mol) |
ζHtr b (%) | ζTStr c (%) | ɛH d (%) | |
|---|---|---|---|---|---|---|
| 2-Acetaminophen | ||||||
| n-Hexane → water | −8.2 | −15.9 | −7.7 | −67.4 | −32.6 | 17.8 |
| n-Hexane → n-octanol | −17.5 | −12.0 | 5.5 | −68.6 | 31.4 | 14.1 |
| Water → n-octanol | −9.3 | 3.9 | 13.2 | 22.8 | 77.2 | – |
| 3-Acetaminophen | ||||||
| n-Hexane → water | −14.2 | −18.1 | −3.9 | −82.3 | −17.7 | 32.1 |
| n-Hexane → n-octanol | −22.1 | −35.5 | −13.4 | −72.6 | −27.4 | 63.1 |
| Water → n-octanol | −7.9 | −17.4 | −9.5 | −64.7 | −35.3 | – |
| 4-Acetaminophene | ||||||
| n-Hexane → water | −14.9 | −20.1 | −5.2 | −79.4 | −20.6 | 26.4 |
| n-Hexane → n-octanol | −24.7 | −30.2 | −5.5 | −84.6 | −15.4 | 39.7 |
| Water → n-octanol | −9.8 | −10.1 | −0.3 | −97.1 | −2.9 | – |
a
 (solvent 1 → solvent 2) =
(solvent 1 → solvent 2) = 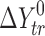 (solvent 2) −
(solvent 2) − 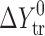 (solvent 1) (where Y = G, H, S)
(solvent 1) (where Y = G, H, S)
bζH
tr = 
cζT
Str= 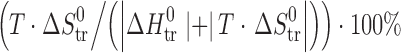
d
ɛ
H = (ΔH
spec/ΔH
non–spec) 100%, where 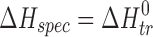 (n-hexane → solvent)/
(n-hexane → solvent)/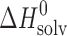 (n-hexane) (experimental error within 6%)
(n-hexane) (experimental error within 6%)
ePerlovich et al. (4)
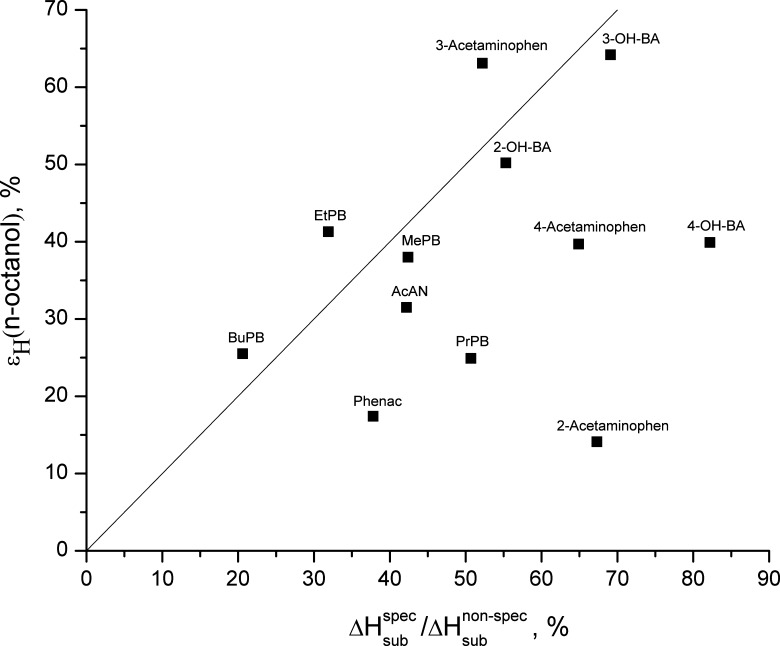
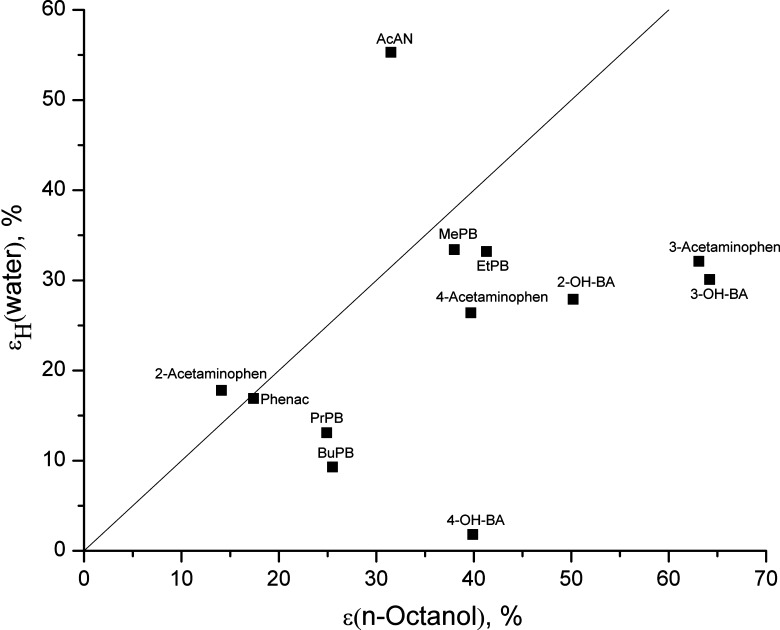
It is interesting to analyze differences in the ratio between specific and nonspecific interactions in the crystals ( ) and in solutions (ɛH) for the compounds studied together with the hydroxybenzoic acid isomers (5) and parabens (2). The experimental data of the ɛH values for water and for n-octanol vs ɛsub values are presented in Figs. 4 and 5, respectively, whereas the ɛH values for water vs ɛH values for n-octanol are shown in Fig. 6. For water, ɛH values do not exceed the analogous characteristics for the crystals for any compounds, except acetanilide (higher value) and ethylparaben (approximately equal). For n-octanol, there are more compounds with ɛH > ɛsub: butylparaben, ethylparaben, and 3-acetaminophen. The ɛH parameter for the water overweighs the analogous one for the n-octanol for only 2-acetaminophen and acetanilide. The analyzed ɛH and ɛsub parameters can be used to characterize the respective compound, showing what role the specific interactions in a solution play in comparison to their role in the solid state.
) and in solutions (ɛH) for the compounds studied together with the hydroxybenzoic acid isomers (5) and parabens (2). The experimental data of the ɛH values for water and for n-octanol vs ɛsub values are presented in Figs. 4 and 5, respectively, whereas the ɛH values for water vs ɛH values for n-octanol are shown in Fig. 6. For water, ɛH values do not exceed the analogous characteristics for the crystals for any compounds, except acetanilide (higher value) and ethylparaben (approximately equal). For n-octanol, there are more compounds with ɛH > ɛsub: butylparaben, ethylparaben, and 3-acetaminophen. The ɛH parameter for the water overweighs the analogous one for the n-octanol for only 2-acetaminophen and acetanilide. The analyzed ɛH and ɛsub parameters can be used to characterize the respective compound, showing what role the specific interactions in a solution play in comparison to their role in the solid state.
Fig. 4.
Relationship between the ɛ H values for water vs the ratio between specific and nonspecific enthalpic terms in crystal lattices. The straight line corresponds to bisector. 2-OH-BA 2-Hydroxybenzoic acid, 3-OH-BA 3-hydroxybenzoic acid, 4-OH-BA 4-hydroxybenzoic acid, AcAN acetanilide, BuPB butylparaben, EtPB ethylparaben, MePB methylparaben, Phenac phenacetin, PrPB propylparaben
Fig. 5.
Relationship between the ɛ H values for n-octanol vs the ratio between specific and nonspecific enthalpic terms in crystal lattices. The straight line corresponds to bisector. 2-OH-BA 2-Hydroxybenzoic acid, 3-OH-BA 3-hydroxybenzoic acid, 4-OH-BA 4-hydroxybenzoic acid, AcAN acetanilide, BuPB butylparaben, EtPB ethylparaben, MePB methylparaben, Phenac phenacetin, PrPB propylparaben
Fig. 6.
Relationship between the ɛ H values for the water vs ɛ H values for the n-octanol. The straight line corresponds to bisector. 2-OH-BA 2-Hydroxybenzoic acid, 3-OH-BA 3-hydroxybenzoic acid, 4-OH-BA 4-hydroxybenzoic acid, AcAN acetanilide, BuPB butylparaben, EtPB ethylparaben, MePB methylparaben, Phenac phenacetin, PrPB propylparaben
Finally, the thermodynamic functions of transfer of the studied compounds from water to n-octanol, being widely discussed as reflecting some biopharmaceutical properties of drugs, were studied (Table VI). The experimental data on the thermodynamic functions of the acetaminophens together with some parabens (2) and hydroxybenzoic acids (5) are collected in Fig. 7. The regions where 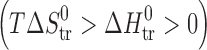 ≡ sector I, and
≡ sector I, and 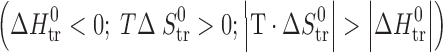 ≡ sector II, correspond to entropy-driven processes. The regions of the diagram where
≡ sector II, correspond to entropy-driven processes. The regions of the diagram where  ≡ sector III, and
≡ sector III, and 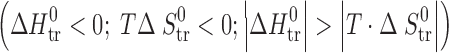 ≡ sector IV, correspond to enthalpy-driven processes. A schematic depiction of these relationships is given in Scheme 1.
≡ sector IV, correspond to enthalpy-driven processes. A schematic depiction of these relationships is given in Scheme 1.
Fig. 7.
Relationship between the enthalpic and entropic terms of transfer functions from the water to n-octanol. The isoenergetic curves of 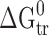 function are marked by dotted lines. 2-OH-BA 2-Hydroxybenzoic acid, 3-OH-BA 3-hydroxybenzoic acid, 4-OH-BA 4-hydroxybenzoic acid, AcAN acetanilide, BuPB butylparaben, EtPB ethylparaben, MePB methylparaben, Phenac phenacetin, PrPB propylparaben
function are marked by dotted lines. 2-OH-BA 2-Hydroxybenzoic acid, 3-OH-BA 3-hydroxybenzoic acid, 4-OH-BA 4-hydroxybenzoic acid, AcAN acetanilide, BuPB butylparaben, EtPB ethylparaben, MePB methylparaben, Phenac phenacetin, PrPB propylparaben
Scheme 1.
A schematic depiction of the relationships of the enthalpic and entropic terms of the transfer processes studied for the various diagram sectors (Fig. 7)
Studying the enthalpic and entropic terms of the transfer process helps one analyze the size of a substructure unit that takes part in a partitioning process. If the transfer enthalpy is positive, then it may be assumed that the drug molecule interacts with the solvate shell more strongly in the water phase than in the octanol phase. Therefore, there is a high probability that the drug molecule and the solvation shell (water molecules) will transfer together. In this case the substructure transferring unit is a drug molecule + solvation shell. At  there is the opposite picture: it occurs the total resolvation of the drug molecule in the water phase at the transferring process. Thus, the substructure transferring unit is just a drug molecule. The entropic term shows a change in the ordering of the system at the transfer of the substructure unit from one phase to the other. Thus, the first sector corresponds to transfer of drug + solvation shell from the water to the octanol phase with essential disordering of the last phase. The second sector corresponds to transfer of an individual drug molecule with essential disordering of the octanol phase. The third sector corresponds to transfer of an individual drug molecule with essential disordering of the octanol phase. Finally, the fourth sector corresponds to transfer of an individual drug molecule with ordering of the octanol phase. This information can be useful to analyze diffusion processes of drug molecules through biological barriers (passive transport), because the size of the substructure unit plays a key role and determines the coefficient diffusion values and mechanism.
there is the opposite picture: it occurs the total resolvation of the drug molecule in the water phase at the transferring process. Thus, the substructure transferring unit is just a drug molecule. The entropic term shows a change in the ordering of the system at the transfer of the substructure unit from one phase to the other. Thus, the first sector corresponds to transfer of drug + solvation shell from the water to the octanol phase with essential disordering of the last phase. The second sector corresponds to transfer of an individual drug molecule with essential disordering of the octanol phase. The third sector corresponds to transfer of an individual drug molecule with essential disordering of the octanol phase. Finally, the fourth sector corresponds to transfer of an individual drug molecule with ordering of the octanol phase. This information can be useful to analyze diffusion processes of drug molecules through biological barriers (passive transport), because the size of the substructure unit plays a key role and determines the coefficient diffusion values and mechanism.
Isoenergetic curves of the 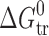 function are marked as dotted lines in Fig. 7. As can be seen from this figure, the partitioning processes of the acetaminophens have approximately the same values of
function are marked as dotted lines in Fig. 7. As can be seen from this figure, the partitioning processes of the acetaminophens have approximately the same values of  as would be expected, but the driving forces and signs of the thermodynamic parameters are essentially different (i.e., the data points appear in different sectors). For example, 2-acetaminophen is situated in sector I, with an entropy-driven mechanism, whereas 3-acetaminophen and 4-acetaminophen are in sector IV, with enthalpy as the driving force. An enthalpy–entropy compensation effect is observed for the outlined compounds. It should also be mentioned that the partitioning process of 4-acetaminophen is enthalpy driven, with an entropy term of almost zero, whereas phenacetin has an enthalpy term of almost zero. Thus, these two substances, which differ in only the position of the substituent in the phenyl motif, have absolutely different mechanisms and components of the driving forces for the partitioning process.
as would be expected, but the driving forces and signs of the thermodynamic parameters are essentially different (i.e., the data points appear in different sectors). For example, 2-acetaminophen is situated in sector I, with an entropy-driven mechanism, whereas 3-acetaminophen and 4-acetaminophen are in sector IV, with enthalpy as the driving force. An enthalpy–entropy compensation effect is observed for the outlined compounds. It should also be mentioned that the partitioning process of 4-acetaminophen is enthalpy driven, with an entropy term of almost zero, whereas phenacetin has an enthalpy term of almost zero. Thus, these two substances, which differ in only the position of the substituent in the phenyl motif, have absolutely different mechanisms and components of the driving forces for the partitioning process.
For the sake of comparison, analogous experimental and previously published data for hydroxybenzoic acids (4) and parabens (2) were added to the same diagram (Fig. 7). The isomers of hydroxybenzoic acid are situated in different sectors of the diagram, as has been found for the isomers of acetaminophens: 2-hydroxybenzoic acid is in sector III (enthalpy driven with opposite signs for the thermodynamic functions), whereas 3-and 4-hydroxybenzoic acid are in sector IV (enthalpy driven as well, but with the same signs for the terms). As is the case for the previously described compounds (acetaminophen isomers), there is an enthalpy-entropy compensation effect with no essential differences in the values, but the present results show that there is a mechanistic difference.
For the parabens, as also plotted in Fig. 7, another picture is observed: the mechanism of the partitioning process is changed from entropy driven for methylparaben to enthalpy driven for ethyl-, propyl-, and butylparabens. Moreover, the enthalpy terms change with increasing size of the substituent, whereas the entropy terms are approximately unchanged and, as a consequence, 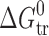 values (in absolute scale) increase. Thus, for the isomers of the benzoic acids and acetaminophens, the position of substituents in the phenyl motif essentially determines the mechanism of the partitioning process but not the Gibbs energy thereof (
values (in absolute scale) increase. Thus, for the isomers of the benzoic acids and acetaminophens, the position of substituents in the phenyl motif essentially determines the mechanism of the partitioning process but not the Gibbs energy thereof ( values). On the other hand, increased length of the substituents (in parabens) leads to essential changes of the partitioning properties (
values). On the other hand, increased length of the substituents (in parabens) leads to essential changes of the partitioning properties (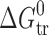 values), while keeping the mechanism of the partitioning process.
values), while keeping the mechanism of the partitioning process.
CONCLUSION
The sublimation and solubility data make it possible to quantify solvation energies in different solvents on an absolute energetic scale. The derived correlation equation for the nonspecific interactions in crystal lattices allows the distinguishing of specific and nonspecific interactions without thorough knowledge of the respective crystal structures. The correlation equation between the melting points of the drugs and the parameter that describes the ratio between specific and nonspecific interaction in the crystal lattices, provides the opportunity to estimate energetic terms of the crystal lattice on the basis of the melting point only. The diagram method applied for the transfer process allows us to characterize the mechanism of the partitioning process.
Acknowledgment
This study was supported by the Russian Foundation of Basic Research no. 06-03-96304.
References
- 1.Perlovich G. L., Bauer-Brandl A. Solvation of drugs as a key for understanding partitioning and passive transport exemplified by NSAIDs. Curr. Drug Deliv. 2004;1:213–226. doi: 10.2174/1567201043334786. [DOI] [PubMed] [Google Scholar]
- 2.Perlovich G. L., Rodionov S. V., Bauer-Brandl A. Thermodynamics of solubility, sublimation and solvation processes of parabens. Eur. J. Pharm. Sci. 2005;24:25–33. doi: 10.1016/j.ejps.2004.09.007. [DOI] [PubMed] [Google Scholar]
- 3.Dikstein S., Grotto M., Zor U., Tamari M., Sulman F. G. Stimulatory effect of paracetamol and its derivatives on growth and the rat tibia test. J. Endocrinol. 1966;36:257–262. doi: 10.1677/joe.0.0360257. [DOI] [PubMed] [Google Scholar]
- 4.Perlovich G. L., Volkova T. V., Bauer-Brandl A. Towards an understanding of the molecular mechanism of solvation of drug molecules: a thermodynamic approach by crystal lattice energy, sublimation and solubility exemplified by paracetamol, acetanilide and phenacetin. J. Pharm. Sci. 2006;95:2158–2169. doi: 10.1002/jps.20674. [DOI] [PubMed] [Google Scholar]
- 5.Perlovich G. L., Volkova T. V., Bauer-Brandl A. Towards an understanding of the molecular mechanism of solvation of drug molecules: a thermodynamic approach by crystal lattice energy, sublimation and solubility exemplified by hydroxybenzoic acids. J. Pharm. Sci. 2006;95:1448–1458. doi: 10.1002/jps.20611. [DOI] [PubMed] [Google Scholar]
- 6.Perlovich G. L., Kurkov S. V., Bauer-Brandl A. The difference between partitioning and distribution from a thermodynamic point of view: NSAIDs as an example. Eur. J. Pharm. Sci. 2006;27:150–157. doi: 10.1016/j.ejps.2005.09.003. [DOI] [PubMed] [Google Scholar]
- 7.Cox J. D., Pilcher G. Thermochemistry of organic and organometallic compounds. London, UK: Academic; 1970. [Google Scholar]
- 8.Chickos J. S., Hosseini S., Hesse D. G., Liebman J. F. A group additivity approach for the estimation of heat capacities of organic liquids and solids at 298 K. Struct. Chem. 1993;4:271–277. doi: 10.1007/BF00673701. [DOI] [Google Scholar]
- 9.Krestov G. A. Thermodynamics of ionic processes in the solution. Leningrad, Russia: Khimiya; 1984. p. 271. [Google Scholar]
- 10.Chickos J. S., Acree Jr W. E. Enthalpies of sublimation of organic and organometallic compounds 1910–2001. J. Phys. Chem. Ref. Data. 1999;31:537–698. doi: 10.1063/1.1475333. [DOI] [Google Scholar]
- 11.Pascual-Ahuir J. L., Silla E. GEPOL: an improved description of molecular surfaces, I: building the spherical surface set. J. Comput. Chem. 1990;11:1047–1060. doi: 10.1002/jcc.540110907. [DOI] [Google Scholar]
- 12.Kitaigorodsky A. I. The molecular crystals. Moskva: Nauka; 1971. [Google Scholar]
- 13.Hansen L. K., Perlovich G. L., Bauer-Brandl A. N-(3-hydroxyphenyl)acetamide. Acta Crystallogr. 2006;62:3627–3628. [Google Scholar]
- 14.Nichols G., Frampton C. S. Physicochemical characterization of the orthorhombic polymorph of paracetamol crystallized from solution. J. Pharm. Sci. 1998;87:684–693. doi: 10.1021/js970483d. [DOI] [PubMed] [Google Scholar]
- 15.Aihara A. Estimation of the energy of hydrogen bonds formed in crystals, III: amides. Bull. Chem. Soc. Jpn. 1960;33:1188–1194. doi: 10.1246/bcsj.33.1188. [DOI] [Google Scholar]
- 16.Li Z. J., Ojala W. H., W Grant D. J. Molecular modeling study of chiral drug crystals: lattice energy calculations. J. Pharm. Sci. 2001;90:1523–1539. doi: 10.1002/jps.1103. [DOI] [PubMed] [Google Scholar]