Solubility Improvement of Drugs using N-Methyl Pyrrolidone

Abstract

The solubilization efficiency of N-methyl pyrrolidone (NMP) has been determined and compared to that of ethanol and propylene glycol for 13 poorly soluble drugs. NMP is found to be a more efficient solubilizer for all the drugs studied. The solubility enhancement as high as about 800-fold is obtained in 20% v/v NMP solution as compared to water. The mechanism of drug solubilization by NMP has also been investigated. It is proposed that NMP enhances drug solubility by simultaneously acting as a cosolvent and a complexing agent. A mathematical model is used to estimate the drug solubility in NMP–water mixture, according to which the total solubility enhancement is a sum of the two effects. This model describes the experimental data well and is more accurate than other models. A large and uniform reduction in the surface tension of water as a function of NMP concentration demonstrates its cosolvent effect. The complexation is supported by the fact that it’s strength is affected by the temperature and the polarity of the medium. A strong correlation exists between log K_ow of the drugs and the cosolvency coefficients. The correlation between log K_ow and the complexation coefficients is weak suggesting that factors such as molecular shape and aromaticity of the drug molecule are significant in determining the complexation strength. This has been confirmed by the absence of a significant complexation between NMP and linear drug-like solutes.

Introduction

The aqueous solubility of a drug is one of its most important physicochemical properties. A low aqueous solubility and slow dissolution can potentially limit a drug’s absorption from the gastrointestinal tract. The aqueous solubility of drug is of prime significance when a direct administration to the blood stream is required. From the drug development standpoint, often a solution of drug is required to conduct pharmacological, toxicological and pharmacokinetic studies. Thus, poor aqueous solubility not only limits a drug’s pharmacological applications but also challenges its pharmaceutical development. As a result, investigation into new solubilizers and techniques for solubility enhancement is important.

N-methyl pyrrolidone (NMP) is a water miscible, aprotic solvent with a log K_ow of −0.54. It has been reported to increase the solubility and permeability of several drugs (1–4). It has low toxicity both orally and parenterally (5). It is thermally stable (boiling point 202 °C) and can be used in formulations that require heat sterilization. These properties make NMP an attractive solubility enhancer in the pharmaceutical field. Some marketed products containing NMP include Atridox® gel (for humans), Nuflor® IV solution and Doxirobe® gel (both for veterinary use).

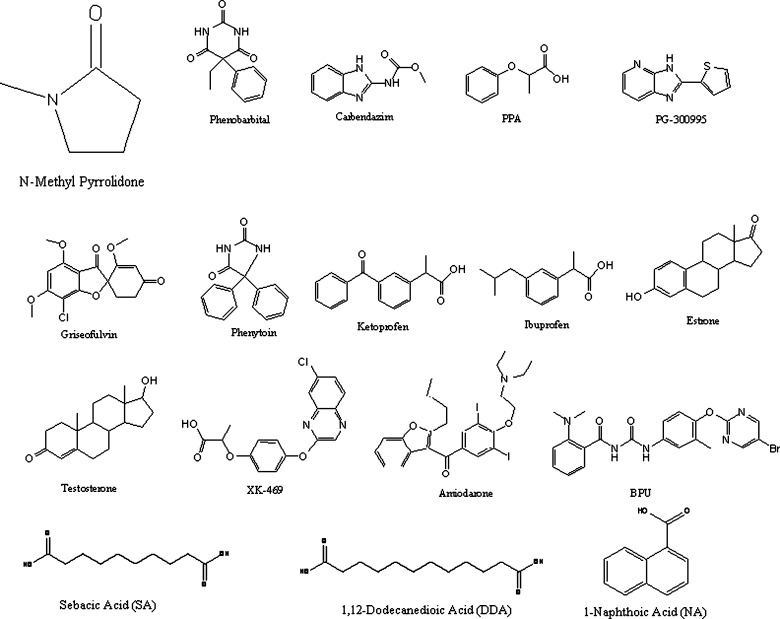
Although, the use of NMP as a solubilizer has been sufficiently reported, its solubilization efficiency has not been directly compared to that of some commonly used solubilizers. Moreover, the mechanism by which NMP enhances drug solubility is not clearly understood. Some researchers believe that it is a cosolvent (1) while others consider it a complexing agent (3, 4). It has been proposed (6) that 2-pyrrolidone which is structurally similar to NMP can simultaneously act as cosolvent and complexing agent. The NMP molecules (Fig. 1) contain a polar disubstituted cyclic amide group, which can interact with water molecules ensuring their complete miscibility. The presence of the non-polar carbons of NMP can weaken the hydrogen-bonded structure of water, thus enabling it to act as a cosolvent. In addition, the presence of a substantially large and nearly planar non-polar region may result in hydrophobic interactions between NMP and drug molecule to form a complex. Such an association will stabilize the drug in dissolved form and further increase its solubility in NMP–water mixture.

Fig. 1.

Structures of N-methyl pyrrolidone, drugs and model compounds used for the study

This study was conducted with two specific aims. First, to determine the solubilization efficiency of NMP and compare that to two commonly used cosolvents: ethanol (EtOH) and propylene glycol (PG). EtOH and PG are chosen on the basis of their greater popularity and better safety profile. The mechanism of drug solubilization by NMP has been investigated as the second aim of the study. It is proposed that besides acting as a cosolvent, NMP can simultaneously stack with the drug molecule in presence of polar aqueous environment. As a result of this dual effect, NMP is expected to be a stronger solubilizer than what would be predicted solely on the basis of either effect. In order to study the mechanism of solubilization by NMP, it is essential to understand the concepts of cosolvency and complexation.

Cosolvency

The addition of a cosolvent reduces the polarity of water by weakening its intermolecular hydrogen-bonding network. This results in a higher solubility of non-polar drugs in cosolvent–water mixture. The solubilization efficiency of a cosolvent depends upon the extent to which it weakens the structure of water. Various models have been proposed to estimate the solubility of drugs in cosolvent–water mixtures (7–16). While it is not possible to compare all these approaches here, a few important ones are discussed:

Parabolic and Regular Solution Theory Based Models

A number of parabolic models have been proposed to estimate the solubility profile in cosolvent–water systems. These models are based on the classical regular solution theory of Hildebrand (9). The general form of these models can be written as (10–12):

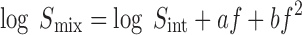1

where S_mix and S_int are the drug solubility in the cosolvent–water mixture and water respectively; f is the volume fraction of the cosolvent in the mixture; and a and b are empirical constants.

Log-Linear Model

Yalkowsky et al. (13–15) proposed that the solubility of a non-electrolyte drug in a cosolvent–water mixture is an exponential function of cosolvent volume fraction:

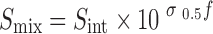2

where σ_0.5 is the end-to-half slope of the solubilization curve.

According to this model, an exponential increase is observed when the solubilities are plotted against the volume fraction of the cosolvent. The value of σ_0.5 is related to the octanol–water partition coefficient (log K_ow) of the drug as (17):

3

where s and t are empirical constants for a particular cosolvent.

Millard et al. (17) also observed that the value for s is a function of the cosolvent polarity. Less polar cosolvents are stronger solubility enhancers and have higher s values.

Recently, Machatha and Yalkowsky (16) have proposed a bilinear model for the estimation of drug solubility in ethanol–water mixtures. This model includes an extra term to cater for the negative deviation from log-linearity at higher cosolvent concentrations. It is applicable to all, polar, semipolar and non-polar compounds. A simplified form of this model is:

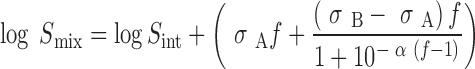4

where σ_A and σ_B are the slopes of the initial and the final asymptotes respectively and σ is an empirical constant for a particular cosolvent.

Complexation

Complexation of a drug molecule with a ligand molecule reduces the exposure of former’s hydrophobic region to water resulting in an increase in its solubility. It is an equilibrium process and the association constant for the formation of a 1:1 complex is given by:

5

where [S_int], [L] and [S_complex] are the equilibrium molar concentrations of the free drug, ligand and the complex, respectively.

The total solubility of a drug in the presence of complexing agent is the sum of its intrinsic solubility and the solubility of the complex (S_complex):

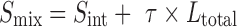6

where:

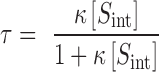7

According to equation 6, the total solubility of a drug undergoing complexation is a linear function of the ligand concentration. The intercept of this line is equal to the solubility of the free drug and its slope is given by τ. The value of κ is a measure of the strength of drug–ligand interactions and is dependent on the properties of the drug and the ligand molecules. For a particular ligand, the size, shape, aromaticity and the non-polarity of the drug molecule play important roles in determining this strength. The properties of the solubilization medium, such as temperature and polarity also influence the strength of these interactions.

Mathematical Model

It is proposed that NMP possess both, cosolvent and complexing properties. The total drug solubility in NMP–water mixture can, therefore, be calculated by simply adding these two effects. Mathematically, this can be stated as:

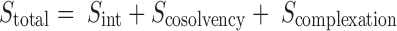8

where S_int is the drug’s intrinsic solubility while S_cosolvency and S_complexation are the solubility obtained as an effect of the cosolvent and the complexing properties of NMP, respectively.

Equation 6 gives the solubility of the solute as a function of the molar concentration of the ligand. A similar equation can be written to calculate the solubility of the drug–NMP complex as a function of the molar concentration of NMP:

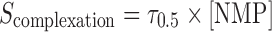9

where τ_0.5 is the slope of the solubilization profile.

The molar concentration of NMP can be converted to its volume fraction f by dividing it by the molarity of pure NMP (10.4 M/l). Thus:

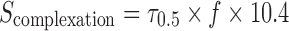10

Equation 2 gives the solubility of the drug in cosolvent–water mixture (S_int + S_cosolvency) as a function of cosolvent concentration. A similar equation can be written for calculating drug solubility in NMP–water mixture:

11

Assuming that the cosolvency and complexation curves are exponential and linear, respectively, up to f = 0.5, Eqs. 10 and 11 may be incorporated into Eq. 8 as:

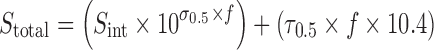12

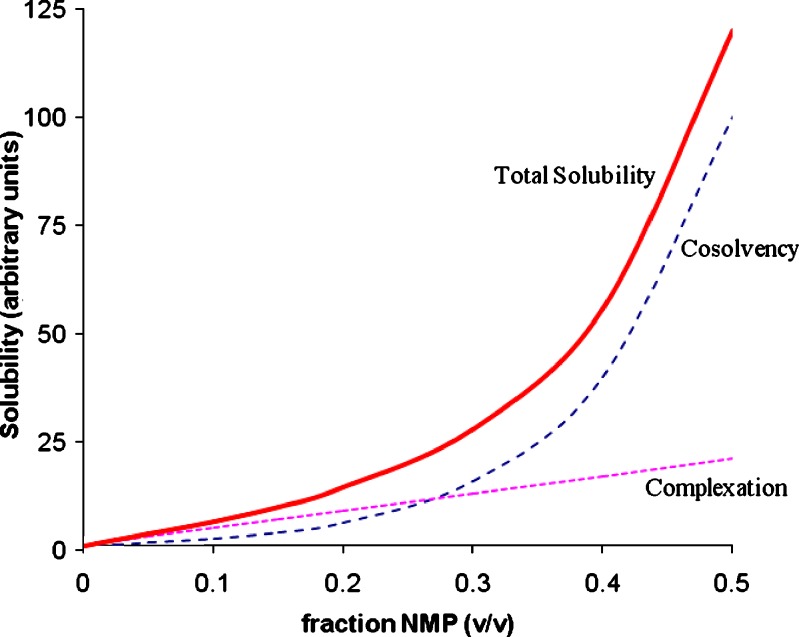
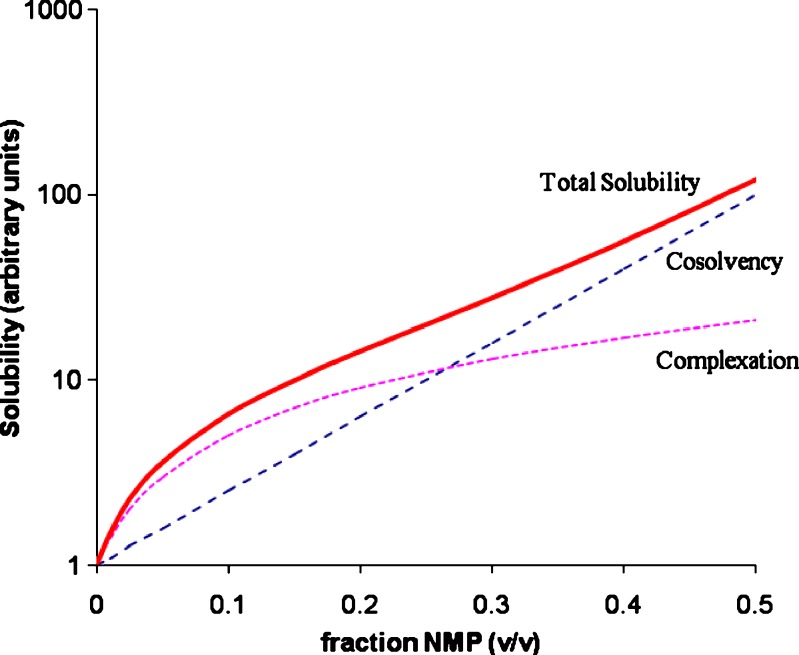
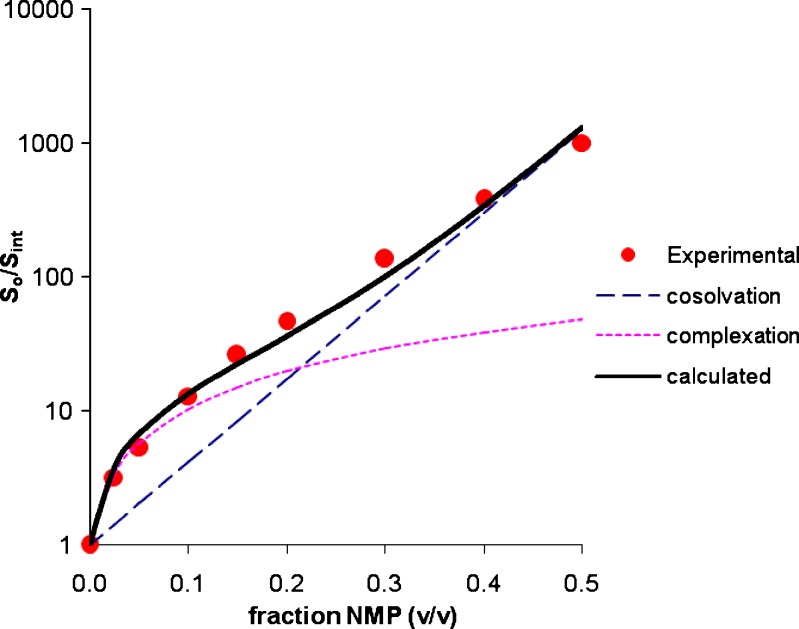
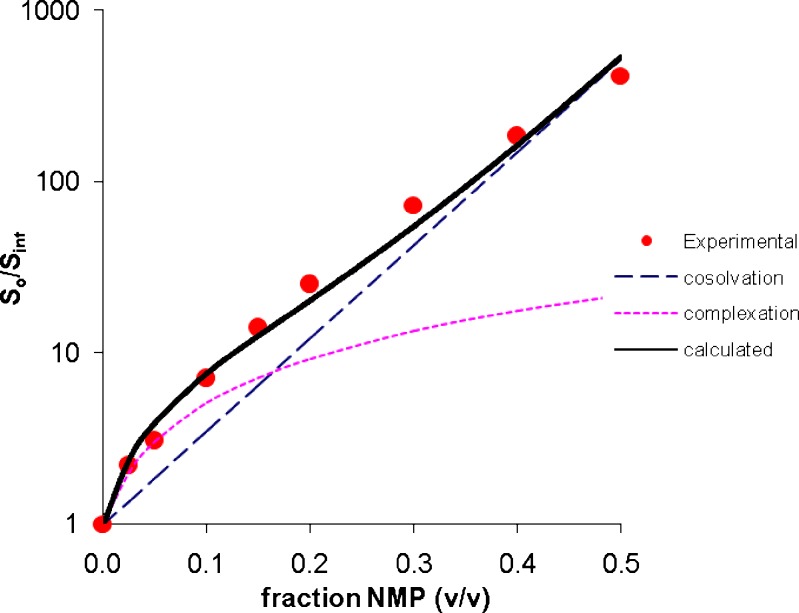
Equation 12 is demonstrated graphically in Figs. 2 and 3, which represents the solubility of a drug as a function of NMP concentration. The dashed line represents the solubility due to cosolvency (described by the first part of Eq. 12) and dotted line represents that due to complexation (described by the second part of Eq. 12). The total solubility is the sum of these two curves and is represented by the solid line. Notice that Fig. 2 is on a normal scale and Fig. 3 is on a semi-log scale.

Fig. 2.

Solubility vs f NMP (normal scale)

Fig. 3.

Solubility vs f NMP (semi-log scale)

The shape of the solid line (total solubility) will depend upon the relative strengths of the two effects. If cosolvency dominates the total solubilization, the solubility profile will be closer to linearity on a semi-log plot. On the other hand, a downward curvature of the solubility profile will be indicative of dominant complexation. The values of σ_0.5 and τ_0.5 can be obtained by deconvoluting the total solubility using Eq. 12. The unit of τ_0.5 in Eq. 12 is (mg/ml)/M. It can be converted to M/M unit by:

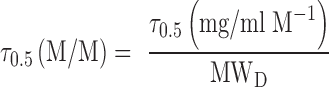13

where MW_D is the molecular weight of the drug. The value of κ can be calculated from τ_0.5 using Eq. 7.

Assumptions

The proposed model is based on the following assumptions:

• The drug solubility due to cosolvency is exponentially related to the concentration of NMP following the log-linear model. This includes the assumption of ideal mixing which is the basis of the log-linear model.

• A 1:1 complex is formed between the drug and NMP; and the concentration of the complex does not exceed its solubility at-least till f = 0.5. The possibility of higher order complexes cannot be ruled out. However, to account for such interactions more variables will have to be added which will result in complicating the model.

• The cosolvency and the complexation phenomena are mutually independent. In other words the drug-NMP interactions do not affect the cosolvent property of NMP. Similarly the complexation strength is not affected by the concentration of NMP in the mixture.

Materials and Methods

Materials

A set of 13 structurally diverse drugs (Fig. 1) with poor aqueous solubility is used for the study: Phenobarbital, Griseofulvin, Phenytoin, Ketoprofen, Estrone, Testosterone, Ibuprofen, Amiodarone (Sigma, St Louis, MO); Carbendazim, 2-Phenoxypropionic acid (PPA) (Aldrich, Milwaukee, WI); XK-469 and Benzoylphenyl urea derivative (BPU) (NCI, Bathesda, MD); PG-300995 (Procter & Gamble, Cincinnati, OH). These drugs vary widely in terms of aqueous solubility (0.028 μg/ml–2820 μg/ml) and the log K_ow (1.5–6.2) calculated using ClogP®. In addition to these drugs, three drug-like solutes are also used: sebacic acid (SA), 1,12-decanedioic acid (DDA) and 1-naphthoic acid (NA) (Sigma, St Louis, MO). N-methyl pyrrolidone and propylene glycol were obtained from Sigma-Aldrich, St Louis, MO while ethanol was obtained from AAPER, Shelbyville, KY. All other excipients were of reagent or HPLC grade and used without further purification.

Methods

Solubility Determination

Aqueous solutions containing increasing volume fractions (0–0.5 v/v) of the three solubilizers (EtOH, PG and NMP) were prepared. For ionizable drugs, buffers were used instead of water to make the solutions. The pH of the buffers was maintained at least 2 units away from the pK_a of the respective drug throughout the equilibration process. This was done to ensure that the drug predominantly exists in its unionized form. For example, pH was maintained at 7.0 in the case of carbendazim which has a basic pK_a of ~4.0. An excess amount of drug was added to the vials containing 1 ml of the aqueous solutions. The vials were placed in an end-over-end rotator at 20-rpm for sufficient length of time (>5 days) under room conditions. The final pH of the samples was measured before filtering them through 0.45-μm filter followed by drug content analysis using HPLC (Agilent 1100 HPLC with G1315B PDA detector, Agilent Technologies Palo Alto, CA with Chemstation software). The degree of adsorption of each drug to the filter membrane was tested by determining the difference between the drug concentration of a solution before and after filtration. The difference in all cases was less than 0.1%. Solubility studies at higher temperatures were performed in temperature chambers. All the experiments were performed in triplicate.

Solubilization Efficiency

The ratio of the drug solubility obtained in the presence of 20% w/v solubilizer (S_0.2) to the intrinsic solubility (S_int) is used as a criterion for comparing the solubility enhancements of NMP to that of EtOH and PG.

Statistical Analysis

WinCurveFit version 1.1.8 for Windows (Kevin Raner Software, Victoria Australia) was used to deconvolute the experimental solubility based on Eq. 12. All the other analyses were performed using Microsoft Excel. The root mean square error (RMSE) was determined using the following relationship:

14

Surface Tension Measurement

The Drop-Number method was used to measure the relative surface tension of solubilizer–water mixtures. A constant flow syringe pump was used at a flow rate of 0.04 ml/minute to create the drops. The first three drops were sacrificed and the time required for the next five drops to form and fall was measured. The densities of the samples were measured using a pycnometer. Water and ethanol were used as the reference liquid. The surface tension was calculated using the following equation:

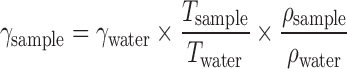15

where γ is the surface tension, T is time required for five drops to form and fall and ρ is the density.

Results and Discussion

Solubilization Efficiency

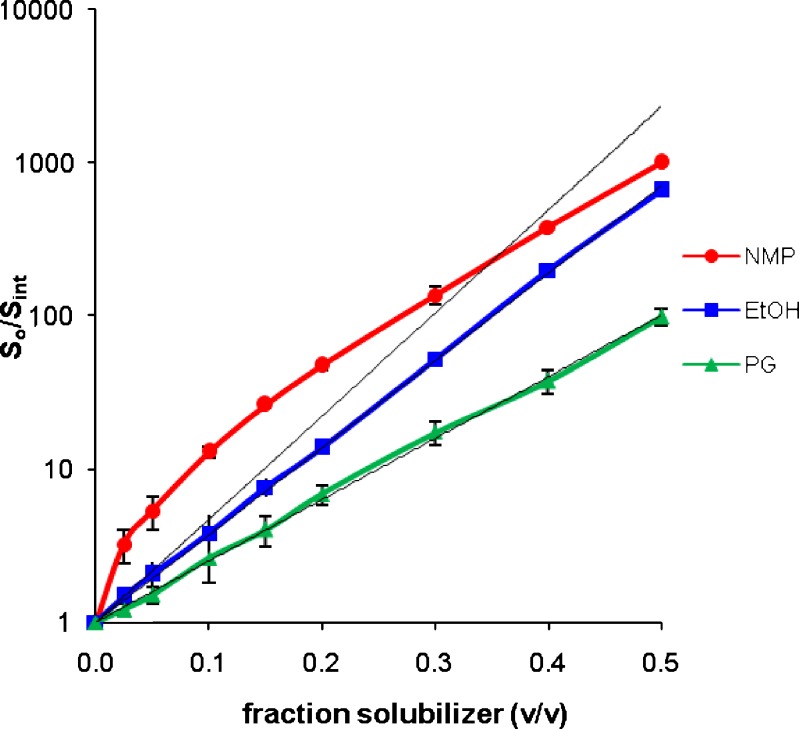
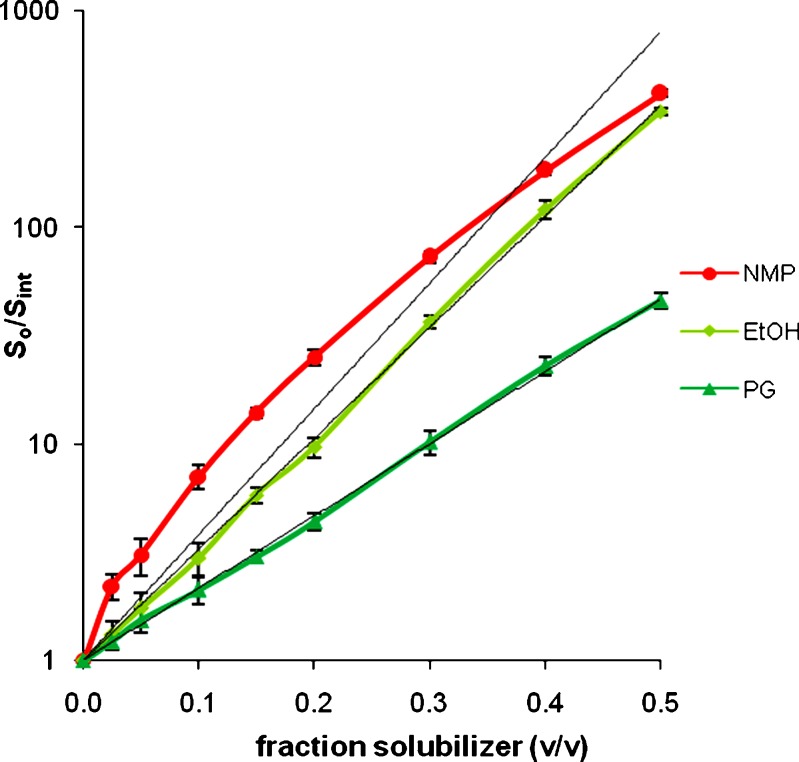
The results presented in Table I demonstrate that NMP results in substantial solubility enhancements for all the 13 drugs. A 20%v/v concentration is chosen arbitrarily but provides a useful way to compare relative solubility enhancements at acceptable levels of the cosolvents. The solubility enhancement as high as about 800-fold is observed in 20%v/v NMP solution. NMP has higher solubilization efficiency (S_0.2/S_int) than EtOH and PG for every drug studied. The solubilities in 20%v/v NMP solutions were nearly two to eight times higher than that in 20%v/v EtOH solutions. This clearly demonstrates that at 20%v/v concentration, NMP is a more powerful solubilizer than EtOH and PG, for the drugs studied.

Table I.

Solubilization Efficiencies of NMP, EtOH and PG

Drug	Log K ow	Log S int (μg/ml)	S 0.2/S int
			NMP	EtOH	PG
Phenobarbital	1.5	2.99	6.2	2.1	1.5
Carbendazim	1.5	0.37	31.7	6.9	5.9
PPA	1.9	3.47	7.4	4.4	4.1
Griseofulvin	2.2	0.91	25.1	9.7	4.4
Phenytoin	2.5	1.03	29.1	6.5	4.5
PG-300995	2.6	1.59	15.3	7.3	3.3
Ketoprofen	3.1	1.89	47.4	6.1	3.2
Estrone	3.1	−0.20	47.0	13.6	6.8
Testosterone	3.3	1.34	14.9	8.6	4.2
Ibuprofen	3.5	1.48	20.6	10.8	6.4
XK-469	3.9	−0.64	50.2	9.1	4.5
Amiodarone	5.9	0.18	389.1	67.5	16.9
BPU	6.2	−1.55	795.8	102.5	145.0

Mechanism of Drugs Solubilization by NMP

In order to investigate the mechanism of drug solubilization by NMP, the complete solubility profiles (0–50%v/v solubilizer) of the drugs were studied. As illustrations, the solubility of estrone and griseofulvin are presented in Table II and their solubility profiles are presented in Figs. 4 and 5. The bold lines represent the solubility profiles while the lighter lines are the best-fit passing through the origin. In cases of EtOH and PG, the profiles are log-linear and follow Eq. 2. However, a distinct downward curvature is noticed in the profiles with NMP along with a positive deviation from the log-linear model, particularly at low NMP concentrations. At higher NMP concentrations the profiles start approaching log-linearity.

Table II.

Solubility of Estrone and Griseofulvin in Cosolvent–Water Mixtures

Solubilizer fraction (v/v)	Solubility (μg/ml)
	Estrone			Griseofulvin
	NMP	EtOH	PG	NMP	EtOH	PG
0.000	0.63	0.63	0.63	8.12	8.12	8.12
0.025	2.01	0.92	0.75	18.48	12.73	11.20
0.050	3.32	1.28	0.94	24.87	14.18	12.47
0.100	8.08	2.38	1.64	57.42	24.15	17.26
0.150	16.43	4.77	2.51	113.15	41.60	24.47
0.200	29.49	8.59	4.27	203.72	78.42	35.55
0.300	84.93	32.60	10.90	591.47	318.15	82.86
0.400	236.76	124.03	23.53	1491.99	1133.23	186.65
0.500	627.16	412.74	61.38	3372.15	2784.44	372.90

Fig. 4.

Solubility profile of estrone

Fig. 5.

Solubility profile of griseofulvin

One of the possible reasons for this deviation can be the non-ideality of NMP–water mixture. The applicability of Eq. 2 is based on the assumption of ideal mixing. If a system behaves in a non-ideal manner, deviation from Eq. 2 may be expected. However, we believe that’s not the case since the solubility profiles with ethanol and propylene glycol are linear even though the aqueous solutions of these cosolvents are non-ideal (18). Moreover, if that’s the case than the deviation from linearity of NMP-water system, should in principle, be related to the deviation from ideality for any physical property of the system. The correlation between the deviation of surface tension from ideality, which is a measure of the system non-ideality, to the deviation in solubility is very weak and insignificant suggesting that the non-ideality of NMP–water mixture is not the reason for this deviation.

In order to explain this deviation, the complexation effect of NMP is considered. As discussed in an earlier section, it is believed that NMP molecule can undergo stacking with the drug molecule in presence of polar aqueous environment. Such an arrangement will stabilize the dissolved drug resulting in an increase in its solubility. Thus, the total solubility will be the sum of the cosolvent effect and the complexation effect of NMP (Eq. 12).

The total solubility has been resolved into cosolvency and complexation components using Eq. 12. Figures 6 and 7 present the deconvoluted solubility profiles for estrone and griseofulvin. The cosolvency, complexation and the calculated total solubility are shown along with the experimental values. In both cases, the calculated solubility values are in good agreement with the experimental values. At low NMP concentration, the profile has a downward curvature due to a dominant complexation effect. As the NMP concentration increases the cosolvency effect (exponential function) starts to dominate making the profile log-linear.

Fig. 6.

Deconvoluted solubility profile of estrone

Fig. 7.

Deconvoluted solubility profile of griseofulvin

The solubility data of all the other drugs were deconvoluted in a similar manner. Table III present the σ_0.5 and κ values.

Table III.

The Cosolvency and the Complexation Coefficients for Various Drugs

Drug	σ 0.5	κ	R 2
Phenobarbital	3.9	1.4	1.00
Carbendazim	4.6	6.2	0.96
PPA	4.1	0.8	1.00
Griseofulvin	5.4	4.0	0.99
Phenytoin	6.1	4.0	1.00
PG-300995	4.8	2.1	1.00
Ketoprofen	6.5	2.4	1.00
Estrone	6.2	9.4	0.99
Testosterone	5.0	2.1	1.00
Ibuprofen	5.8	2.9	0.99
XK-469	6.6	7.6	1.00
Amiodarone	9.3	46.1	1.00
BPU	10.0	26.8	1.00

Comparison of the Studied Model with Some Existing Models

The proposed model has been compared to the parabolic (10–12) (Eq. 1), log-linear (13–15) (Eq. 2), the bilinear (16) (Eq. 4), and the linear (Eq. 6) models. The calculated solubilities from each model were compared to the experimental values. The RMSE were calculated using Eq. 14. The significance of the calculation was tested using a paired two-tailed t-test with α = 0.1. From the results presented in Table IV, it can be seen that the studied model is more accurate than the other models and that the calculated values are not significantly different from the experimental values.

Table IV.

Comparison of Various Models

Model	Equation	No. of parameters	RMSE	p value	Significance
Parabolic (10–12)	1	2	0.13	0.09	No
Log-linear (13–15)	2	1	0.29	0.00	No
Bilinear (16)	4	3	0.13	0.06	No
Linear	6	1	0.66	0.00	No
This study	12	2	0.10	0.54	Yes

Relation of Drug’s Polarity to Cosolvency and Complexation Strength

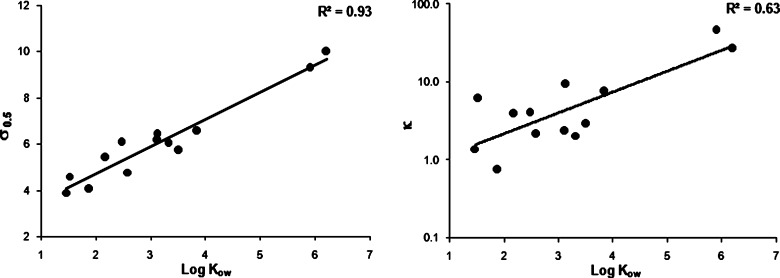
The correlation between the log K_ow of the drugs with σ_0.5 and κ are shown in Fig. 8a and b, respectively. A strong correlation exists between log K_ow of the drug and the corresponding σ_0.5 which is consistent with the observation of Millard et al. (17). The weak correlation between log K_ow and κ may be due to the dependence of κ on factors like molecular shape and aromaticity. In order to test this hypothesis, solubility studies were performed on three model solutes, two linear aliphatic acids: sebacic acid (SA) and 1,12-dodecanedioic acid (DDA); and one aromatic acid: 1-naphthoic acid (NA). Their chemical structures have been presented in Fig. 1.

Fig. 8.

Correlation between log K _ow and σ _0.5 and log K _ow and κ

The results from the deconvolution of the total solubility using equation 12 are presented in Table V. The σ_0.5 values for the solutes follow their log K_ow. However, despite the similarities in their log K_ow, the κ value for NA is much higher than that for DDA. The complexation of NMP with DDA or SA is very weak and almost insignificant. The solubility profiles are nearly log-linear for both, DDA and SA, suggesting that solubilization is a result of cosolvency only. On the other hand a curved profile is obtained for NA due to a strong complexation between NA and NMP. This supports the idea that the presence of planar aromatic region on the drug molecule plays an important role in determining the complexation strength.

Table V.

The Cosolvency and the Complexation Coefficients for the Test Acids

Model Compound	Log K ow	Log S int (μg/ml)	σ 0.5	κ	R 2
Sebacic acid	2.1	2.15	3.7	0.1	1.00
1,12-Decanedioic acid	3.1	0.62	6.2	0.2	0.99
1-Naphthoic acid	3.1	1.77	6.1	5.3	1.00

Based on these results in can be said that whereas the cosolvency strength of NMP is a direct function of the solute’s log K_ow, the complexation strength is related to the size and geometry of solute’s hydrophobic region.

Additional Support for the Proposed Model

In addition to explaining the solubilization from a mathematical stand point, it is essential to obtain experimental support for the proposed mechanism. The existence of the cosolvency and the complexation effects of NMP, is supported by the following results:

Cosolvency Effect

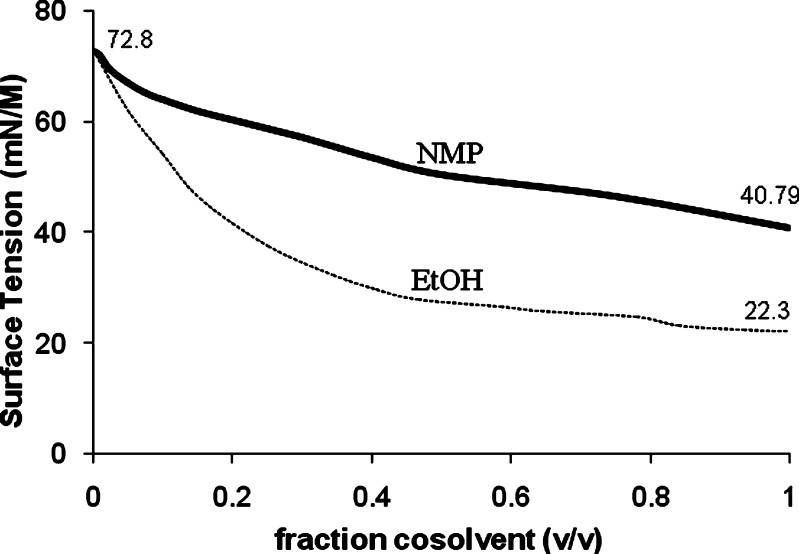
In order to verify the cosolvency effect of NMP, its effect on the surface tension of water has been studied. A cosolvent weakens the self-associated structure of water. Thus, the magnitude of the physical properties such as surface tension that depends on the structure of water reduces with increasing cosolvent concentration. The effect of NMP and EtOH concentration on the surface tension water is presented in Fig. 9. It is evident that NMP reduces the surface tension of water at all volume fractions supporting its cosolvency behavior. The shape of the profile is similar to that of the EtOH–Water mixtures (18). This observation is consistent with the reported lowering of the dielectric constant (reflecting reduction in the polarizability) of water with an increasing concentration of NMP (19).

Fig. 9.

Surface tension of cosolvent–water mixtures (20 °C)

Complexation Effect

The complexation effect of NMP, was studied with the aid of thermodynamics.

The free energy of complexation (ΔG°_comp) is given by:

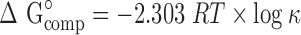16

where R is the gas constant (8.314 J·mol⁻¹ K⁻¹) and T is the absolute temperature in Kelvin.

The enthalpy of complexation (ΔH°_comp) can be calculated from the κ values obtained at several temperatures using the van’t Hoff equation:

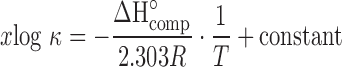17

The entropy of complexation (ΔS°_comp) is related to ΔG°_comp and ΔH°_compcomp by:

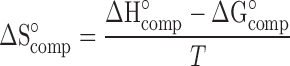18

The ΔH°_comp is a function of the difference between the affinities of drug for water and the ligand. Since a non-polar drug molecule will have a greater affinity for the ligand than for water, ΔH°_comp are typically negative, i.e., enthalpy favors complexation.

Complexation reduces the randomness associated with the solute molecules. Thus, ΔS°_comp is negative and opposes complexation.

For complexation to be thermodynamically feasible, ΔG°_comp must be negative. (20) Thus, ΔH°_comp should be sufficiently large to overcome the effect of the entropy. In other words, the magnitude of −ΔH°_comp must be larger than that of −TΔS°_comp.

The ΔG°_comp is affected by the properties of the medium. Raising the temperature of the medium increases the influence of the entropy term, thereby, reducing the likelihood of complexation. Reducing the polarity of the medium diminishes the enthalpic driving force for complexation. On the other hand increasing the polarity of the medium is expected to strengthen this force.

Effect of Temperature

Increasing the temperature of the system affects the following interactions:

• Water–Water

• Drug–Drug

• Water–Drug

• Water–NMP

• Drug–NMP

The relative strengths of the first three interactions determine the solubility of the drug in water. At higher temperatures, all these three interactions are weakened. The magnitude of the weakening of water–water interactions is generally greater than that of the drug–drug and water–drug interactions. Thus, the water solubility of drugs usually increases with temperature.

The Water–NMP interactions can be expected to weaken at higher temperature due to an increased entropic effect and as a result, the cosolvency effect (σ_0.5) of NMP may increase slightly.

The Drug–NMP interactions will also weaken at higher temperatures. As the temperature increases, the magnitude TΔS°_comp increases making ΔG°_comp less negative. Thus, complexation will be less favored at higher temperatures resulting in lower κ values. Since the NMP–NMP interactions will not occur in presence of water, they have not been considered.

The effect of temperature on the thermodynamics of complexation has been studied using the solubility profiles of estrone and griseofulvin obtained at three temperatures. Table VI presents the values of ΔG°_comp, ΔH°_comp and TΔS°_comp calculated using Eqs. 16, 17 and 18. The ΔH°_comp was determined from the van’t Hoff plot (log κ vs inverse of the temperature). For both drugs, the ΔG°_comp is negative which supports the theory of complex formation. The magnitude and the sign of ΔH°_comp for both drugs suggesting the presence of dispersion interactions between drug and NMP molecules (20).

Table VI.

Effect of Temperature on Solubilization Parameters of NMP–Water Mixture

Temperature (K)	Estrone						Griseofulvin
	Log S int (μg/ml)	σ 0.5	κ	ΔH°comp kJ/mole	TΔS°comp kJ/mole	ΔG°comp kJ/mole	Log S int (μg/ml)	σ 0.5	κ	ΔH°comp kJ/mole	TΔS°com kJ/mole	ΔG°comp kJ/mole
293	−0.20	6.2	9.4	−20.33	−14.86	−5.46	0.91	5.4	4.0	−3.62	−0.25	−3.37
305	−0.07	6.7	6.8	−20.33	−15.45	−4.88	1.03	5.6	3.7	−3.62	−0.26	−3.36
313	0.15	6.9	5.5	−20.33	−15.89	−4.44	1.19	5.7	3.6	−3.62	−0.27	−3.35

Effect of the Polarity of the Medium

A drug undergoes complexation to minimize the exposure of its hydrophobic region to polar aqueous environment. Thus, the complexation strength will naturally be affected by the polarity of the medium. The addition of a chaotrope like ethanol reduces in the polarity of the medium. This should lower the driving force behind the drug–NMP interactions and therefore, is expected to reduce κ. On the other hand, increasing the polarity of the medium by addition of a kosmotrope like sodium chloride (NaCl) is expected to increase κ. It should be noted that modifying the medium also affects the solubility of the drug.

The effect of ethanol concentration on the solubilization parameters of estrone and griseofulvin has been presented in Table VII. As expected, the κ reduced for both the drugs with increase in EtOH concentration. The values of σ_0.5 remained almost unchanged.

Table VII.

Effect of Ethanol and NaCl Concentration on Solubilization Parameters of NMP–Water Mixture

Media (0–50%v/v NMP)	Concentration of additive	Estrone			Griseofulvin
		Log S int (μg/ml)	σ 0.5	κ	Log S int (μg/ml)	σ 0.5	κ
Only NMP	–	−0.20	6.2	9.4	0.91	5.4	4.0
NMP + Ethanol	10%v/v	0.53	6.3	4.6	1.41	5.8	3.0
	20%v/v	0.79	6.1	2.5	1.90	5.3	2.1
NMP + NaCl	0.5M	−0.27	6.5	10.0	0.81	5.5	4.1
	1.0 M	−0.49	7.0	12.6	0.67	5.8	4.2

It must be mentioned that although EtOH does not affect the cosolvency strength of NMP, the overall solubility obtained is a sum of the effect of both cosolvents. Therefore, a combination of EtOH–NMP may be extremely useful for attaining desired solubility enhancement without using too much of any one of these solubilizers.

The effect of addition of NaCl on the solubilization parameters of estrone and griseofulvin has been presented in Table VII. The addition of salt makes water more structured which results in a decrease in drug’s water solubility and a simultaneous increase in the driving force behind complexation. This explains the increase in the κ with NaCl concentration. The cosolvent effect of NMP also increases since it has a greater influence on a more structured water system.

Conclusion

N-methyl pyrrolidone improves drug solubility by simultaneously acting as a cosolvent and a complexing agent. Due to this dual mechanism, it has better solubilization efficiency than both, ethanol and propylene glycol. It offers additional advantage over ethanol by being thermally stable and less volatile. The safety profile for NMP is comparable to that of ethanol. Based on these considerations, NMP can be regarded as a good choice for solubilizer in the pharmaceutical industry.