Modeling Disease Progression in Acute Stroke Using Clinical Assessment Scales

Abstract

This article demonstrates techniques for describing and predicting disease progression in acute stroke by modeling scores measured using clinical assessment scales, accommodating dropout as an additional source of information. Scores assessed using the National Institutes of Health Stroke Scale and the Barthel Index in acute stroke patients were used to model the time course of disease progression. Simultaneous continuous and probabilistic models for describing the nature and magnitude of score changes were developed, and used to model the trajectory of disease progression using scale scores. The models described the observed data well, and exhibited good simulation properties. Applications include longitudinal analysis of stroke scale data, clinical trial simulation, and prognostic forecasting. Based upon experience in other areas, it is likely that application of this modeling methodology will enable reductions in the number of patients needed to carry out clinical studies of treatments for acute stroke.

Electronic supplementary material

The online version of this article (doi:10.1208/s12248-010-9230-0) contains supplementary material, which is available to authorized users.

INTRODUCTION

Annually, 15 million people suffer a stroke where one-third die and one-third are left permanently disabled (1); still, at the time of writing, there are no clinically effective drugs available for shielding the brain from the biochemical and neurological consequences of acute ischemic stroke, and only one agent of any class has been shown to be even modestly effective (2), despite the increasing availability of knowledge on the subject. Clinical trials of new drugs for the treatment of stroke in human subjects have been disappointing (3–16).

Potential explanations for these failures have been discussed at length in the literature, and include differences between preclinical and clinical models, inappropriate inclusion criteria for these studies, lack of sufficient dose–response information prior to study initiation, inappropriate choice of the therapeutic time window for determining effectiveness, and others (17–20). Suboptimal study designs (21) and analytical techniques used in recent trials have been raised as other potential issues, but whatever the reason, the net result has largely been the same: expensive trials that fail to demonstrate any drug effect (22, 23). Assuming that a studied drug is truly effective, given a design and analysis strategy that focuses on a single clinical endpoint, as in stroke, the only way to increase the power of a trial to detect significant differences between treatment and placebo groups is to increase the number of individuals enrolled, and by extension, the costs involved in carrying out the study (24). Conversely, if the drug has no beneficial treatment effect, it does not matter how large the trial is; there will be no treatment effect to detect. Since the sample size, and to some extent, the design of the trials are conditioned on the analysis technique, it seems logical to investigate alternatives to commonly accepted data analysis strategies in areas such as stroke, in which the problem of finding drugs that have statistically demonstrable benefits to patients is notorious.

The current regulatory-approved methodology employed for analyzing the results of Phase III trials in acute ischemic stroke is, essentially, the contrasting of outcomes between treatment and control groups: a statistical comparison of scores on one or more assessment scales for the treatment and placebo groups at a predefined endpoint (25), typically 90 days after study commencement. Almost all failed human stroke trials have relied at least partially or, in most cases, completely on this method of assessing the success or failure of a pharmacological intervention. While the consideration of only the total improvement in score at the endpoint is relatively straightforward and clinically relevant, there are a number of inherent drawbacks in dealing with trial outcomes in this way. The most obvious of these is that information on the time course of disease progression is not considered, and patients who recover more rapidly are indistinguishable from those who do not, since both types of patient may have the same clinical outcome at day 90. Another is seen in the case of protocol deviations, when participants fail to complete follow-up, or ‘drop out’ of the study at some point before its conclusion. A subset of planned measurements in such individuals is therefore missing, representing a challenge to data analysis that is not often addressed adequately.

Scores are recorded using clinical assessment scales, which, in acute stroke, are designed to quantify impairment in neurological and functional disease indicators important for diagnosis and prognosis (26). They are generally comprised of a series of items divided into sections, each of which addresses a different aspect of cerebrovascular disease. The scores from each section are added together to provide cumulative categorical scores, which address particular clinical questions. These questions, in turn, vary from scale to scale.

A model-based analysis addressing the unique characteristics of stroke score data in a small dataset of subjects assessed using the Scandinavian Stroke Scale (SSS) has previously been published (27). We have formalized and reformulated this approach using a larger dataset, comprised of two more commonly used stroke scores—the National Institutes of Health Stroke Scale (NIHSS), which focuses primarily on neurological deficit (28), and is calibrated to have a maximum of 42 points, with 0 representing a state of relative health, and the Barthel activities of daily living index (BI), which is designed to assess motor recovery and functional independence, on a scale of 0 (worst) to 100 (best) and calibrated in five-point steps (29).

A number of key aspects of stroke scale score data inform its analysis. The direction of change in the observed scores may be either positive or negative during longitudinal time course of score measurements in the same individual—the data are non-monotonic, thus preventing their analysis through the use of continuous functions, as might be intuitively appealing given the large range in possible scores. Also, dropout may occur—underlying disease processes may often trigger an event which causes the exit of a subject from the study before the endpoint is reached—with the result that one or more data points for that subject are missing; typically, this is dealt with by using a “last observation carried forward” (LOCF) approach (30).

The challenge, therefore, is twofold. First, analytical methods that allow missing data points to be included as a source of information, based upon the assumption that these missing data are absent due to unobserved disease progress, need to be developed. Longitudinal modeling of the time trajectory of stroke scores as a function of the predicted (but unobserved) score provides us with a method to accomplish this (27). Second, although non-monotonic disease progression has been modeled successfully in cases in which such variation has been cyclic or rhythmic (31), the mathematical functions used in such models cannot be used under conditions in which change in disease state fail to obey such patterns, as is the case in depression, multiple sclerosis and stroke.

In this article we shall demonstrate a method for modeling the typically erratic trajectories of stroke scale measurements while simultaneously addressing the phenomenon of dropout in a statistically rational manner. These models can later be used to inform more efficient and potentially more powerful analyses of these kinds of data in the context of drug development.

METHODS

Patients and Data

Model building was performed using a dataset composed of scores measured on the NIHSS and BI scales, collected from 580 acute stroke patients participating in the placebo arm of a double-blind, multinational, multicenter, placebo-controlled investigation of the effectiveness of a novel acute stroke compound (32). Scores were assessed on the NIHSS at admission, and subsequently at 7, 30, and 90 days. BI assessments were made at 7, 30, and 90 days, as well as by telephone at 60 days. Full informed consent was obtained from each patient before enrolment, and ethical approval for the study design and consent documentation was granted at every study site. Patients eligible for enrollment in the study had stroke onset within 12 h of treatment and the analysis dataset consisted of patients with an average age of 71.7 years (range 26–90) and average baseline NIHSS score of 16.8 (range 4–31).

Modeling Approach

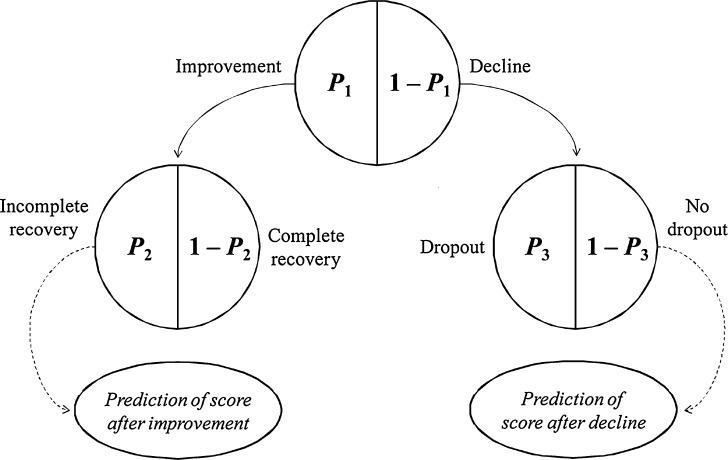
Following on from the work of Jonsson and colleagues (27), score change in each score was described by five submodels, fit simultaneously. Three submodels described the probabilities of three of the four possible score change events at each observation occasion–improvement (I), reaching a maximal score (recovery, R), and dropout (Dr)–while the last, decline, was modeled as 1 − p(I). The key difference we have introduced is a hierarchical structure (conditional independence) to modeling these probabilities, schematically shown in Fig. 1. In the event that a score improvement or decline without dropout or complete recovery took place, the magnitude of score change was assessed through the use of two additional models for improvement and decline in score. Probability of failure to achieve a maximum score was chosen as the basis of the maximum score submodel because it was better supported by the data, and therefore provided the model with more stability overall.

Fig. 1.

A schematic representation of the hierarchical structure of the probabilistic models leading to a linear model for either improvement or decline. Each patient will have records of two probability events and, possibly, one measurement of a relative improvement or a relative decline

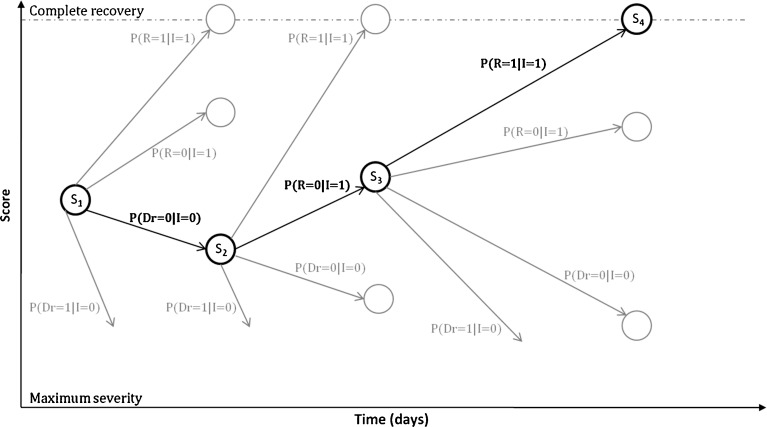
The strategy used to model the process of rehabilitation in acute stroke is summarized in Fig. 2. Consider a scale measurement made at baseline, illustrated here as S₁. The second measurement, S₂, may be a maximum, may be an improvement or a decline relative to S₁, or may not exist, in the event of dropout. Each of these four potential events has a likelihood associated with it, which the modeling approach must quantify. Equally important, the magnitude of score change between S₁ and S₂ must be estimated. To do this, linear functions describing either increase or decrease in score are used, conditioned on the observed improvement or decline event. Similar reasoning applies to subsequent transitions, such as S₂ to S₃.

Fig. 2.

A flowchart illustrating the concept of the core probabilistic model. S ₁, S ₂, S ₃, and S ₄ are observed scores at observations 1, 2, 3, and 4, respectively. Gray circles indicate potential scores after each type of transition (which, in reality, could be any value between the score minimum and the last observation in the event of a score decline, between the last observation and one unit below the score maximum in the event of a score improvement, or the score maximum). Bold lines indicate actual score progression, whereas gray lines represent events that were possible, but did not take place, at every transition. P(R = 1|I = 1), P(R = 0|I =1), P(Dr = 0|I = 0) and P(Dr = 1|I = 0) are the probabilities of reaching maximum score, improvement in score, decline in score, and dropout, respectively; subscripts represent occasion

Scores of the kind recorded in acute stroke are non-monotonic and unpredictable: scores may increase or decrease (a score change of zero was regarded as a decrease, except if complete recovery was reached) at any given measurement occasion, or, in the case of dropout, they may simply cease. The progression of disease (or recovery) may therefore be seen as a series of discrete transitions from one score to another. Each transition has a probability, and in all but dropout, a score change magnitude, associated with it. It is therefore appropriate to consider a model for disease progression using stroke assessment scores to be composed of five key components: three probabilistic submodels, one each for full recovery (reaching a maximum score on the assessment scale), improvement or decline, or dropout, and two continuous, longitudinal submodels, which predict the relative magnitudes of improvement or decline, respectively (27).

Data Preparation

Score data were transformed in order to constrain model predictions to the same (logistic) scale. Given an observation Y_i,j in individual i at measurement occasion j, the observation at the previous occasion (Y_i,j−1) was used to inform its transformation into four input data items, according to the decision tree in Fig. 1. Three dichotomous variables representing complete recovery (R), improvement (I), and dropout (Dr) and a linear variable describing the positive or negative magnitude of score change (C), were created according to the scheme in Table I. Response at admission (Y₀) was not regarded as an observation per se, but was used to determine whether the first observation was an increase or a decline, and as a covariate for predicting individual parameter values. While admission scores on the NIHSS were available, measurements on the BI at admission could not be taken for practical and ethical reasons. A range of baseline values between 0 and 20, both static and randomly imputed from log-normal distributions based on the means and standard deviations of NIHSS baseline scores normalized to the same scale were tested, but these had insufficient predictive power and ultimately the BI score was modeled from day 7.

Table I.

Data Transformation Scheme

Condition	Recovery (R)	Improvement (I)	Dropout (D)	Linear magnitude function (C)
Y i,j−1 < Maximum
Y i,j = Y max	1	1	0	None
Y i,j > Y i,j−1,
Y i,j ≠ Y max	0	1	0	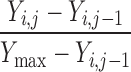a
Y i,j = Y i.j−1	0	0	0
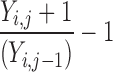
Y i,j < Y i,j−1	0	0	0
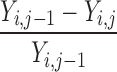
Y i,j missing	None	None	1	None
Y i,j−1 = Maximum
Y i,j = Y max	None	1	0	None
Y i,j < Y j−1	None	0	0
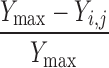
Y i,j missingb	None	None	1	None

Y _i,j score at current occasion in individual i, Y _i,j−1 score at previous occasion in individual i, Y _max score representing complete recovery on modeled scale

^a e.g., a change in score from 20 to 25 on the NIHSS scale, for example, would yield C = (25 − 20)/(42 − 20) = 0.23

^bNo observations of this kind were present in the data

To address the informativeness of dropout, an additional point was imputed in those subjects whose observations ended before the day-90 endpoint. The point was arbitrarily set to be halfway between the last measured observation and the subsequent intended observation appointment. The score value at this time point was predicted during the fitting procedure using the linear model for relative decline and was used to inform the probability of dropout.

Model Development

The general models for relative score change magnitude and event probabilities were similar in that both model classes were linear functions based upon logit-transformed data. Functions describing the effect of Markovian predictors were employed in both scenarios, including previous score, baseline score, and time since previous observation, as well as functions for describing the effect of demographic covariates.

The actual probability (P_i,j) of a given event in individual i at measurement occasion j is obtained by a simple logit transform:

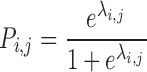where λ_i,j is a linear function which follows the form

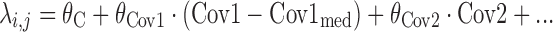where θ_C is a constant, θ_Cov1 is a model parameter describing the influence of continuous covariate descriptor Cov1 on λ_i,j, and θ_Cov2 is a model parameter describing the influence of binary categorical covariate or Markovian predictor Cov2 on λ_i,j. Exponential descriptor terms, as in the example 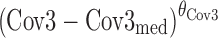(terms defined similarly) were also tested, as were proportional constructs similar to 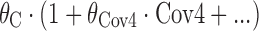(terms defined similarly).

Similarly, relative score change magnitude (Y_ij,rel) is given by

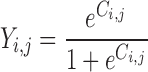with

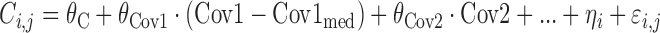where η_i was an interindividual variability (IIV) term, defined as having mean 0 and variance 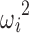, and ε_i,j was a residual error term, defined as having mean 0 and variance σ².

The final modeled score on the original scale, based on the scheme represented in Table I and Fig. 2, is given by

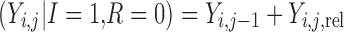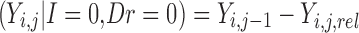or

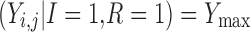for improvement, decline and reaching a maximum score, respectively. Y_max is the score representing normal health, or full recovery, on the modeled scale. 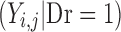, score at dropout, is undefined—no further observations are recorded for this individual.

The models were implemented in the software program NONMEM 7 (33), and the Laplace method was used to fit the models. Model goodness-of-fit was assessed by comparing the objective function value (OFV) provided by NONMEM between nested models, and by visual predictive check. Standard goodness-of-fit plots comparing observations to predictions could not be employed in this scenario, since probabilistic models of this type cannot be used to predict observed scores in individuals, only to simulate new populations. For diagnostic purposes a large sample, of 10,000 individuals, was simulated and the mean and a range of quantiles from the large sample were compared with the same indicators in the observed data to provide a graphical estimate of the appropriateness of each candidate model.

The assessment of potential covariates was made in two parts; first the Markovian predictors were tested and secondly the demographic predictors were tested. In both cases, the criteria for inclusion was based on the OFV (likelihood ratio test, p < 0.05) and the visual predictive check. For a covariate to be included in the model it had to pass the likelihood ratio test and also to improve the graphs in the visual predictive check.

Log-likelihood profiling, as implemented by Perl-speaks-NONMEM (33–35) (PsN), was used to determine confidence intervals for model parameter estimates. Each parameter in each model was fixed to a series of values around the mean, after which the model was re-fit. This procedure generated a 95% confidence interval for the parameter estimates.

RESULTS

The best predictions for the NIHSS score change over time were provided when the probability of improvement was described by a logit function incorporating a constant, and a negative effect of age (the probability of improvement decreased 0.05 units with 10 years, between ages 64 and 74), while the logit for the probability of transition to a score not equal to the maximum score included a baseline term, with a break point at day 45, and increasing probability with previous score and to time since this observation. Finally, the probability of dropout included a baseline term with change points at day 14 and 45, and a proportional effect of predicted NIHSS score (from the NIHSS score change model) at the imputed time of dropout. The effect of the NIHSS score was such that the probability of dropout increased approximately 0.015 units with an increase of 1 score.

The continuous model for relative improvement, measured on the NIHSS scale, consisted of a baseline term, with a break point at day 14, and a negative effect of the baseline NIHSS observation and terms for interindividual variability (IIV) and residual variability. The IIV varied with time elapsed since the initial stroke event; after 14 days, the variance in score magnitude was allowed to take on a new value. Relative decline in score was described similarly, with a positive effect of previous score (i.e. larger decline), however no other changes over time could be supported.

Probability of improvement, for the BI scale, was given by a logit function including a constant term and terms describing the positive influence of previous BI score and negative effect of age. As an example of the age effect, there was a decrease in probability of 0.07 units between two patients of 64 and 74 years, both with a previous BI score of 50. The logit for the probability of transition to a score that is not a maximum at a given sampling occasion included a constant, a positive effect of previous score and a negative effect of time since stroke event. Finally, the logit describing probability of dropout included a constant and a proportional effect of predicted BI score, with the result of a 0.035 unit decrease in the probability of dropout with a five-point increase in BI score.

The continuous model for relative improvement on the BI scale included a constant, a factor describing the positive influence of previous score, a negative effect of age, a negative effect of baseline NIHSS score and terms for interindividual variability and residual variability, respectively. The age effect on the magnitude of improvement was very small, less than a five-point change over 10 years, and was over-shadowed by the effect of baseline NIHSS and previous BI score. The model for relative decline in BI score included a term describing the negative effect of time since last observation, but no baseline observation. Interindividual variability and residual variability terms (the latter shared with the function for improvement) were also included.

A summary of included predictors for the scale-specific models appears as Table II, parameter estimates and final NONMEM control streams are available in supplement A and B, respectively. The results of the simulations of the two scales appear as Fig. 3. The predictive power of the models for the NIHSS scale is good but less good for the BI scale, with 50th and 90th percentiles of simulated scores matching the corresponding observed score percentiles for both scales. Score changes from baseline were similarly well predicted (Fig. 4), except for the 90th percentile in the BI scale which was displaying a larger range of values. The reduced precision at the endpoint for the BI relative to the NIHSS is most likely due to the insensitivity of the BI scale—there is comparatively less information to model, leading to a poorer “fit”.

Table II.

Model Components for the Final Prediction Models

Parameter	NIHSS	BI
Linear model for relative improvement
Constant size of relative score improvement	■	■
Influence of previous score		▲
Influence of baseline NIHSS score	▼	▼
Influence of age		▼
Variability in linear improvement
Interindividual variability in relative score change
Time <14 d	■
Time ≥ 14 d	■
Linear model for relative decline
Constant size of relative score decline	■
Influence of previous score	▲
Influence of time since previous observation		▼
Variability in linear decline
Interindividual variability in relative score change		■
Time <14 d	■
Time ≥ 14 d	■
Residual variability on the logit scale	■	■
Model for probability of improvement
Baseline probability	■	■
Influence of previous score		▲
Influence of age	▼	▼
Model for probability of not reaching maximum score
Baseline probability	■	■
Influence of previous scorea	▲	▼
Influence of time since previous observation	▲
Influence of time since baseline		▲
Model for probability of dropoutb
Baseline probability	■	■
Influence of predicted scorea	▼	▲

filled square included, inverted filled triangle produces decline, upright filled triangle produces increase

^aA low NIHSS score is positive while a low BI score is negative for the patient, which is the reason for the opposite influence of the previous observation in the two models

^bRelationship is proportional, i.e. 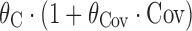, where θ _C is a baseline term, and θ _Cov is a term describing the effect of covariate or Markovian predictor term Cov

Fig. 3.

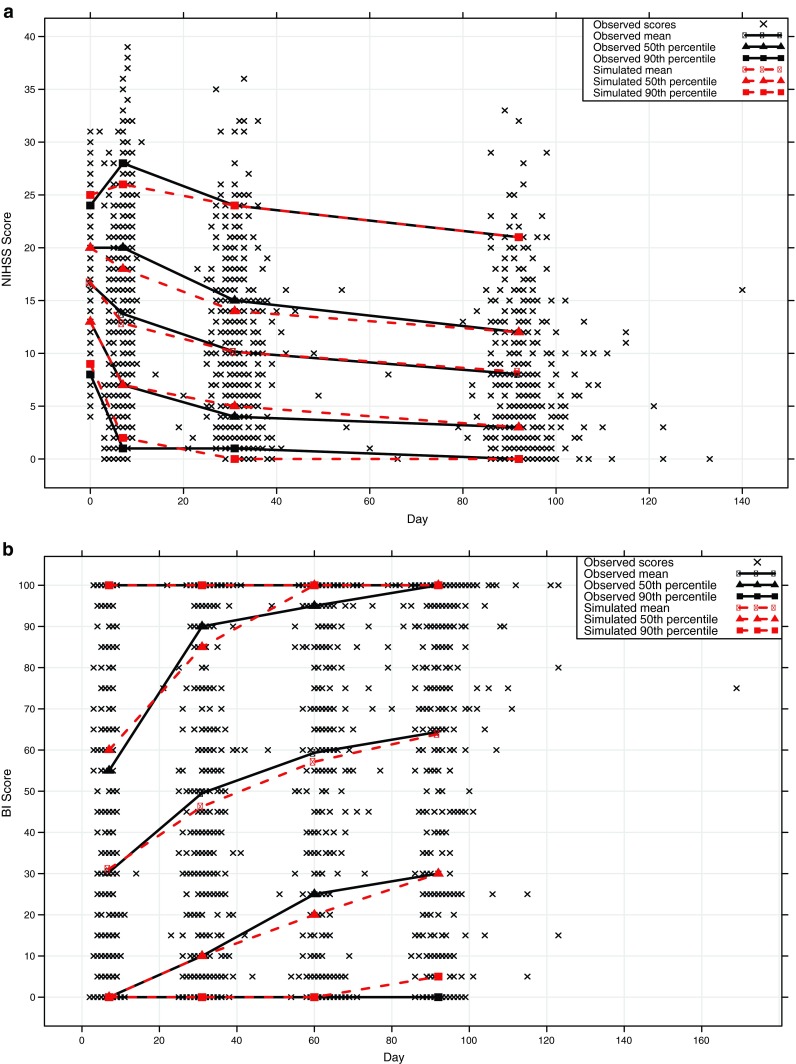
Simulated scores plotted against observed data for the a NIHSS and b BI stroke assessment scales

Fig. 4.

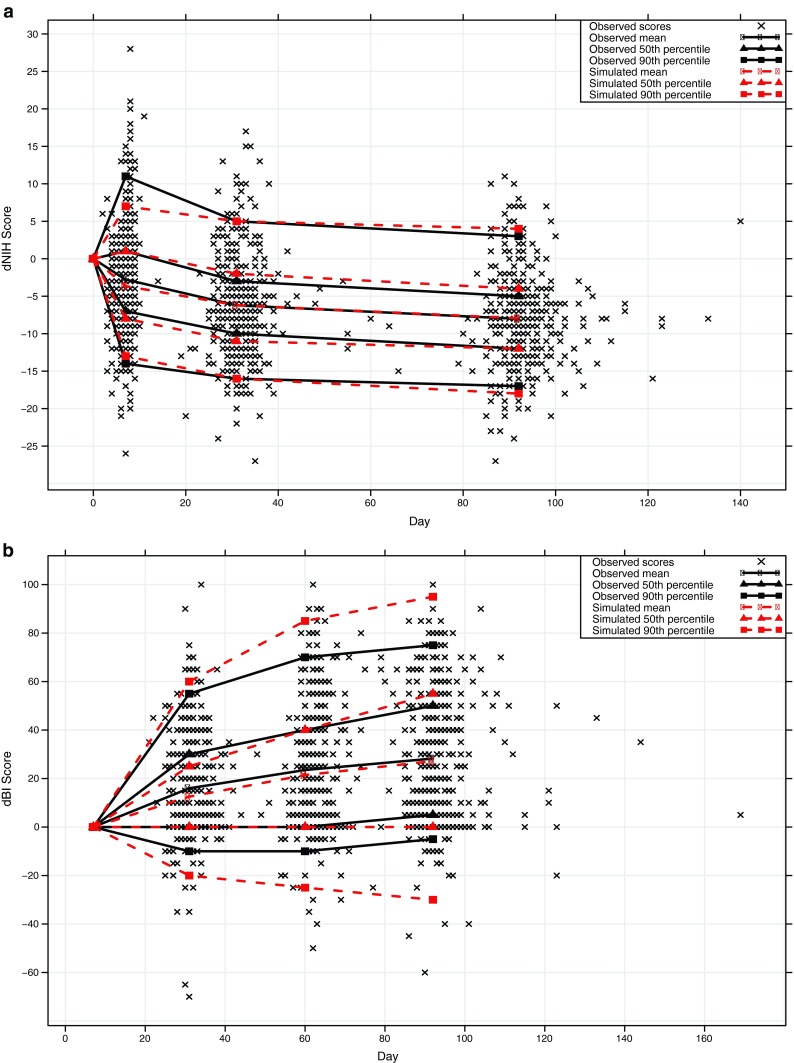
Simulated change from baseline score plotted against observed changed from baseline score for the a NIHSS and b BI stroke assessment scales

DISCUSSION

The non-monotonous nature of stroke data offers a challenge for the modeler. One way to manage this is to use an approach combining categorical and continuous models (36), in which non-monotonicity is accounted for by the former model type in a probabilistic manner. As we have included all observations, even dropout, we believe we have made maximal use of the available information. While a technique for describing recovery in acute stroke has previously been described using the SSS (27), the richness of the data available to us in this paper has enabled the development of a more detailed modeling paradigm with considerably improved probability functions, and we have been able to demonstrate the generality of our approach by applying it to the modeling of two other commonly used scales, the NIHSS and the BI. These models may provide significant advantages over current analytical methodology used in the interpretation of the score data routinely collected during stroke trials, and may allow the identification of clinically relevant benefits that are otherwise routinely neglected.

The models for probability of dropout were based on a proportional relationship with model-predicted score and predicated on the assumption that observed dropout events were informative. A number of different strategies are typically used to handle dropout, including discarding the data accumulated from patients failing to complete the study, analyzing only those observations available at the endpoint, or imputing the missing data values, by using a LOCF approach, for example (30). It is not unreasonable to expect that these approaches are not entirely appropriate for clinical trials in stroke patients, where there is underlying disease progression and the where dropout may depend on the disease state. Patients recovering from an acute ischemic event may indeed drop out for any number of reasons, but it is probable that many of these dropout events may be related to disease progression, and as such, can be explained to a certain extent and are thus not completely random. The majority of available inference techniques designed to deal with dropout have been shown to reduce power, or introduce bias where dropout is not entirely attributable to random processes (37–40). Our approach integrates the “informative missingness” provided by dropout based on these principles.

The model developed for the BI scale was harder to establish than the NIHSS model, and displayed some imprecision in a few of the structural parameters, and supported fewer parameters for relative score change (particularly decline, which was modeled as a linear relationship with time since the previous BI observation on the logit scale). This may be a consequence of the BI scale’s limited range of available scores (20 possible values) as opposed to the NIHSS (42 possible values). The submodels for transition probabilities contained similar numbers of parameters, which supports this hypothesis. However, the model converges, the covariance step is run and the condition number was reasonable.

Drug effects may be built into these models very easily. In the event of a pharmacological intervention being beneficial, it is reasonable to hypothesize that the frequency of dropout, for example, may be influenced by a drug effect. The modeling strategy we suggest will enable investigators to examine this, while at the same time eliminating the bias that results when using imputation methods in data of this kind. In addition, the current regulatory-approved effectiveness endpoint, a discrete improvement in stroke assessment scale score over the placebo group, completely neglects a potential drug effect on the risk of dropout—a drug-related reduction in the dropout rate, for example, is undeniably a clinical benefit if one assumes that dropout is associated with death or decline, as are similar effects on the other probabilistic events we have described in this article. A drug effect might be equally suited to influencing relative score change between occasions, or indeed, probability of improvement or reaching a maximum score, using the same approach we have used for the other covariates we have examined. The choice of which or any of these submodels to target using this approach would probably be suggested by the drug’s mode of action.

These models may also be applied to clinical trial simulation. While it is effectively impossible to simulate non-monotonic categorical data using traditional approaches, our models may be adapted relatively simply for this purpose. Given that stroke trials are particularly prone to expensive failure, performing pre-trial simulation studies using accurate models of disease progression is all the more appropriate.

The models presented here consider the possibility of non-monotonic behavior from one observation to the next. The models cannot, however, account for any unobserved changes between each observation. The NIHSS and BI models are therefore design-dependent, the potential consequences of which may need to be explored using future simulation studies. Use of hidden Markov models (41) may help address this issue, although most mixed-effects modeling software implementations cannot handle models of this kind at the time of writing.

Based upon experience in other areas, it is likely that application of this modeling methodology for both prospective simulation of trial designs and analysis of trial data will enable reductions in the number of volunteers needed to carry out clinical studies of novel therapies for the treatment of acute stroke. This is attributable to a likely increase in statistical power to detect treatment effect (mainly due to the use of repeated measurements), which may in turn reduce the uncertainty with respect to trial outcomes (and hence substantial risk) associated with the development of novel stroke compounds. To verify this idea, future simulation studies will be performed investigating the power to detect a drug effect on top of the disease progression model.

Non-monotonic assessment scales are used in a wide range of clinical applications, including traumatic brain injury, psychiatric illness and geriatric medicine, to name only a few. A combined longitudinal and probabilistic modeling framework is appropriate for any clinical scale in which scores exhibit apparent variation in both positive and negative directions with time. The potential exists to extend this approach still further, by accounting for possible correlations between the probabilistic models, for example. The application of modern methods to the analysis of non-monotonic clinical assessment data may have great promise in improving the ability of industry to conduct stroke trials in a more efficient and cost-effective manner, which can only help improve the chances that an effective drug in the critical area of stroke pharmacotherapy will be found.

Electronic supplementary material

Below is the link to the electronic supplementary material.