Asynchronous Replica Exchange for Molecular Simulations

Abstract

An asynchronous implementation of the replica exchange method that addresses some of the limitations of conventional synchronous replica exchange implementations is presented. In asynchronous replica exchange pairs of processors initiate and perform temperature replica exchanges independently from the other processors, thereby removing the need for processor synchronization found in conventional synchronous implementations. Illustrative calculations on a molecular system are presented that show that asynchronous replica exchange, contrary to the synchronous implementation, is able to utilize at nearly top efficiency loosely coupled pools of processors with heterogeneous speeds, such as those found in computational grids and CPU scavenging environments. It is also shown that employing non nearest-neighbor temperature exchanges, which are straightforward to implement within the asynchronous algorithm, can lead to faster temperature equilibration across processors.

1 Introduction

The temperature replica exchange method^{1, 2} is widely used in biomolecular simulations.^3–8 An important property of replica exchange methods is their ability to enhance conformational sampling preserving canonical distributions at the thermodynamic conditions of each replica.

Current implementations of the replica exchange method in use by the structural biology community are based on a formulation of the algorithm that limits the potential power of the technique. The main limitation is that exchanges occur in a centralized and synchronous manner. After each replica has completed a certain number of MD or MC steps a master process collects information from all the replicas and coordinates the exchanges of parameters. This replica exchange strategy has several implications. (i) Because the master process has to wait for all of the replicas to complete a certain number of MC or MD steps, the periodic synchronization causes the overall simulation to run at the speed of the slowest processor participating in the parallel calculation, (ii) the centralized coordination step is not scalable to many processors especially if these are connected by slow and unreliable network links, (iii) the implementation of exchange schemes other than those involving nearest-neighbor replica pairs can be complex, (iv) loss of one of the replicas due to hardware failure or other causes typically causes the abort of the entire replica exchange simulation. These limitations make it difficult to run replica exchange simulations on heterogeneous and loosely coupled sets of processors, such as in computational grids and CPU scavenging environments, which have proved useful in distributed biomolecular computing applications.^{9, 10}

A modification of the replica exchange algorithm, called serial replica exchange, that eliminates the coupling between processors has been recently proposed.¹¹ Serial replica exchange, analogous to the simulated tempering method,^{12, 13} accomplishes this by employing initial guesses for the potential energy distributions at each temperature, which are then refined as the calculation progresses. Unlike most parallel numerical algorithms, such as parallel molecular dynamics,¹⁴ which require synchronization between the parallel threads, the replica exchange method itself does not impose the restriction that temperature exchange attempts should occur synchronously across all processors. Thus, devising a replica exchange algorithm free of problematic synchronization bottlenecks and suitable for grid computing is, in a sense, more a problem of software implementation design rather than a problem requiring the reformulation of the method.

Following this idea we have developed an asynchronous algorithm for replica exchange based on a distributed communication and match-making framework called Salsa¹⁵ that addresses some of the limitations of synchronous replica exchange implementations. The basic idea is to allow pairs of replicas to contact each other to initiate and perform exchanges independently from the other replicas. Because it does not involve a centralized synchronization step the algorithm is scalable to an arbitrary number of processors and it is not limited by the slowest processor. The asynchronous pair-wise scheduling of exchanges allows the straightforward implementation of arbitrary exchange schemes not limited to nearest-neighbor exchanges. The method is suitable for integration in dynamical simulation environments, such as computational grids, in which processors dynamically join and leave the calculation.

The asynchronous implementation of the replica exchange method we have developed¹⁵ is based on a distributed bulletin board system. According to a given average frequency, periodically each replica posts its temperature (or potentially arbitrary thermodynamic and potential parameters) into this decentralized bulletin board system, expressing its willingness to find an exchange partner. After posting, the replica continues with the MD computation periodically scanning the bulletin board searching for appropriate partners and listening for exchange requests from other replicas. When two replicas are matched for exchange, they attempt the exchange according to the standard replica exchange prescription.

In this work we report the application of the asynchronous replica exchange method to a molecular system to illustrate some of the advantages of asynchronous replica exchange over the standard synchronous implementation. We show that asynchronous replica exchange offers clear advantages in terms of utilization efficiency of heterogeneous sets of processors running at varying speeds, and in terms of scalability with increasing number of replicas both with respect to CPU utilization efficiency as well as temperature diffusion rate. The method is designed to satisfy microscopic reversibility requirements and we show that it returns equivalent thermodynamic results as the standard synchronous implementation.

2 Methods

2.1 Asynchronous Replica Exchange

The replica exchange method is an advanced canonical conformational sampling algorithm designed to help overcome the sampling problem encountered in biomolecular simulations. It consists of running a series of Monte Carlo (MC) or Molecular Dynamics (MD) simulations of the molecular system in parallel over multiple processors under different thermodynamic conditions and potential settings.^16–19 In addition to the frequent MC/MD updates occurring on each replica, occasionally a MC move is attempted aimed at swapping atomic coordinates of one replica with those of another. The acceptance probability expression for the swap move is derived based on the detailed balance condition. Typically one of the replicas corresponds to the physical system of interest whereas the others are set up under conditions that maximize the rate of exploration of conformational space.

The temperature replica exchange method (T-REM)² is the most common version of the replica exchange method. It is implemented in popular computational packages for biomolecular simulations.^20–22 Several replicas of the system are simulated at different specified temperatures. An exchange of conformations between the replicas at temperatures T_m and T_n is attempted periodically and it is accepted according to the Metropolis acceptance probability

$$W(\{T_m,T_n\}\to \{T_n,T_m\})=\text{min}\{1,\text{exp}[-({\beta }_n-{\beta }_m)(U_m-U_n)]\},$$ (1)

where β_m = 1/kT_m and U_m is the current potential energy of the m-th replica. In the case of molecular dynamics temperature replica exchange the exchange move also includes rescaling the velocities of each replica according to the square root of the ratio between the new and old temperatures. Provided that the underlying MC or MD conformational sampling algorithm is canonical, the temperature replica exchange acceptance probability defined by Eq. (1) ensures that a canonical ensemble of conformations is generated at each temperature. In the replica exchange method efficient interconversion between low energy conformations occurs whereby a conformation at low temperature switches to higher temperatures allowing it to overcome potential energy barriers and transition to another conformation. A new low energy conformation is then established when this conformation transfers back to low temperature replicas.

For efficiency considerations, in actual implementations of T-REM, instead of exchanging conformations, processors equivalently exchange temperatures. It is useful in this case to talk about a particular simulation of the system running on an individual processor as a “walker”, reserving the term “replica” for the stream of conformations, produced by different walkers at different times, at a particular temperature. The replicas, while they remain at constant temperature, experience discontinuous jumps in conformation at random intervals when viewed in time sequence. The walkers, on the other hand, follow a continuous path through conformational space, however their temperatures experience random jumps. Since it is more closely connected to the concepts we will use to understand the efficiency of the replica exchange method, we will primarily refer to walkers rather than replicas in the following discussion. In the “walker” view, replica exchange achieves efficient interconversion between low energy conformations by allowing a walker to assume a temperature high enough to rapidly move to a new region of conformational space, and then assumes progressively lower temperatures leading to the formation of new stable conformations.

In standard temperature replica exchange implementations temperatures are exchanged synchronously among walkers using a master/client paradigm. A master node or controlling process periodically collects temperatures from the clients (the walkers), it determines the pattern of exchanges, that is the pairs of walkers scheduled to attempt temperature exchanges, and performs the exchange attempts. It then broadcasts the new temperatures to the walkers. The main drawback of this gather/scatter scheme is that it requires all the walkers to be periodically synchronized. Exchanges are attempted when all the walkers have completed the same number of MC or MD updates, therefore walkers that complete first have to stop computing and wait for all of the other walkers to complete the same computation segment before exchanges can be performed.

Several factors contribute to the differences in speeds at which walkers perform the same computational task. The main factor is heterogeneous hardware characteristics; for example computational grid environments are often composed of processors with a wide range of speeds. Often the aggregate processing power of a pool of processors is divided evenly among a minority of high performance processors and a majority of lower-performance processors, making it necessary to take advantage of both fast and slow processors to achieve efficient utilization of the overall processing power of the processor pool. An additional source of speed heterogeneity is the variability of system complexity; at any one time each walker operates on a different conformation of the molecular system and the calculation of the energy of some conformations, such as extended conformations, can take substantially less CPU time than more compact conformations. Other environmental factors such as variations in processor loads due to temporary interactive usage, and network utilization and operating system functions, can cause substantial processing speed heterogeneity even with dedicated computational clusters composed of homogeneous hardware. These “noise” factors are well known to affect the performance of fine-grained parallel applications on large supercomputers.²³ Although specialized hardware and clock synchronization systems can overcome the effect of speed heterogeneity,²⁴ systems of this kind are not generally available on mainstream computational clusters.

Whatever the source of speed heterogeneity, periodic synchronization has the effect that, at best, the replica exchange simulation will run as fast as the slowest walker in the simulation (which could be a different one for each computational segment in between exchange attempt events). Processors that finish executing a computational segment wait for slower walkers to complete, resulting in wasted cycles of the faster processors. However, unlike many parallel computing applications that require a synchronization step, the replica exchange method itself does not impose this requirement. Only the two walkers which are in the process of exchanging temperatures are required to be synchronized to ensure that they do not resume updating their molecular configurations until the temperature exchange attempt has concluded.

To overcome the limitations of synchronous replica exchange schemes, we developed an asynchronous implementation of the temperature replica exchange method that makes use of a communication and match-making framework called Salsa.¹⁵ In this scheme pairs of walkers initiate and perform temperature replica exchanges independently from the other walkers without the need for a centralized controlling server. Exchange pairs are formed dynamically by letting walkers post their availability to exchange temperature with other walkers within a specified temperature range. The virtual decentralized bulletin board system where walkers post their requests is provided by the Salsa subsystem. Two walkers are matched for temperature exchange if they have posted overlapping temperature interest ranges. A direct communication link between matched walker pairs is then established and temperature exchange is then negotiated independently by the pair as described in the next section.

2.2 Implementation

The Salsa communication framework for asynchronous replica exchange¹⁵ is a specialization of a general asynchronous inter-processor communication architecture layer. It has been interfaced with the IMPACT²² biomolecular simulation software package. Architectural details of the Salsa framework are described in detail elsewhere;¹⁵ in this section we give an overall view of the Salsa framework focusing on the description of the implementation of the IMPACT/Salsa interface. For simplicity we describe the algorithm in the context of temperature replica exchange molecular dynamics. However the method can be based on both MC and MD conformational sampling methods (in this work we use hybrid Monte Carlo sampling,²⁵ which uses both MC and MD), and can support any kind and number of exchange variables (such as temperature, plus potential parameters, etc.)

In our implementation a replica exchange walker exists in one of two states: computing, or posted. While in the computing state a walker performs molecular dynamics to evolve the molecular conformation at constant temperature and does not attempt to contact other walkers nor respond to queries from other walkers. After a certain number of MD steps in the computing state (randomly selected for each computing cycle uniformly between given minimum and maximum values) a walker examines a distributed information system that can be thought of as a shared bulletin board space. If it finds there a posting from a suitable partner, the walker tries to contact it. If the partner answers the request the exchange process is initiated; the two walkers communicate their energies and temperatures, one of them performs the acceptance/rejection test and communicates to the other the outcome of the test. If the test is successful each walker assumes the temperature of the other, otherwise they keep their original temperatures. Regardless of the outcome of the test the two walkers leave the posted state and resume the computing state.

When a walker does not find a suitable partner after having examined the shared bulletin space, it leaves a posting for other walkers to find and resumes the MD computation while still remaining in the posted state. This is the key characteristic of the method that forms the basis of the non-blocking match-making algorithm of the asynchronous replica exchange method. Walkers do not have to stop the MD computation while waiting for suitable exchange partners. To ensure rapid exchange turnaround times, when in the posted state the walker listens for incoming requests with high frequency, typically every MD step. These queries are made efficient by a system of local and remote service daemons as described below.

A walker searches for exchange partners that differ in temperature by no more than a temperature gap parameter ΔT. The ΔT’s are chosen to be proportional to the current temperature to equalize the chance of successful temperature exchanges at each temperature, assuming that the heat capacity of the system is temperature independent.⁴ Specifically, a walker at temperature T employs an exchange temperature range [T − ΔT, T + ΔT] with ΔT = α_gT where α_g is called the fractional temperature gap parameter. An exchange between two walkers, however, is initiated only if the exchange temperature ranges of the two walkers overlap. The latter test is necessary to symmetrize the proposal transition probability matrix of the Monte Carlo temperature exchange move to ensure microscopic reversibility.

In our implementation, the asynchronous replica exchange simulation completes after running for a given amount of wall-clock time, rather than, as in synchronous replica exchange, after all of the walkers complete the same number of MD steps. One of the design goals of the method is to efficiently overcome speed differences between processors. If all of the walkers were expected to execute the same number of MD steps the simulation would fully complete only when the slowest processor completes, leaving idle in the meantime faster processors that have already completed the assigned number of steps. Instead, in asynchronous replica exchange, each walker monitors elapsed wall-clock time and terminates if it exceeds a set maximum value. This ensures that all of the walkers terminate at approximately the same time. This termination scheme implies that each walker performs a different number of steps depending on the speed of the processor and other environmental factors. It can be shown that this does not affect the integrity of the canonical sampling characteristics of the replica exchange method.

The interface between IMPACT and the Salsa asynchronous replica exchange communication framework consists of two functions: put and get. The put function is used to post a temperature in the shared bulletin board system. It takes as arguments the temperature of the walker and the minimum and maximum temperatures of the selected exchange temperature range. The get function performs a temperature exchange if the walker is currently in contact with another walker, otherwise it returns with the original temperature. The get function takes as arguments the current temperature and potential energy of the walker and, in the case of a successful temperature exchange, it returns the new temperature. It also returns a flag that tells IMPACT whether an unsuccessful temperature exchange occurred. The walker leaves the posted state when any exchange attempt occurred, either successful or unsuccessful. The put function is non-blocking, that is after posting the walker immediately resumes computing. The get function instead blocks the computation during the duration of the exchange attempt.

The simple put/get interface purposely hides most of the complexities of the Salsa asynchronous communication framework. Salsa is based on a network of service daemons. In the current implementation each instance of an IMPACT process is accompanied by a service daemon implemented as a light thread spawned by the IMPACT process. The service daemon that resides on the same node as the IMPACT process is called the local service daemon of that process. The service daemons perform the two roles of communication interface between walkers (the communication layer) as well as that of the repositories and maintainers of the shared bulletin board system (the distributed directory layer).¹⁵ All the communications among walkers, and between walkers and the distributed directory layer go through the corresponding local service daemons, which communicate using network sockets.

As part of the distributed directory layer each service daemon is responsible to store and manage the postings in an assigned target temperature bin. A walker wishing to exchange with walkers with temperatures within a given target temperature range leaves a posting with all the service daemons whose temperature bins overlap with the target temperature range. As part of their initialization, the service daemons negotiate the temperature bins assigned to each daemon. In the current implementation the overall temperature range between the minimum and maximum replica exchange temperatures is divided evenly among all the service daemons. The temperature bins serviced by each daemon are distinct from the temperature ranges within which temperature exchanges are allowed. For example in a replica exchange simulation with 25 walkers with temperatures between 200 and 700 K and a fractional temperature gap parameter (see above) α_g = 0.25, a walker at T = 400 K searches for partners with temperatures between 300 K and 500 K, whereas each service daemon is assigned a temperature bin (700−200)/25 = 20 K wide, beginning at 200 K, 220 K, 240 K, and so on. In this example the walker at T = 400 K will post its temperature to as many as 10 of the service daemons whose temperature bins overlap with the [300, 500] K temperature range.

Each service daemon maintains a table of the temperature bins and the network address and port numbers of the service daemons that service them. When the local service daemon receives from IMPACT a request for posting through the put function, the local service daemon examines this table and compiles a list of the service daemons whose temperature bins overlap with the temperature range [T − ΔT, T +ΔT] within which the walker is looking for partners. It then proceeds to query the service daemons in the list in random order. It initiates and conducts an exchange when the first suitable posting is found, otherwise it leaves a posting for other walkers to find. At the same time, each service daemon is responsible to answer queries from other service daemons. There are two types of queries: requests for exchanges directed to the local walker, and requests directed to the local bulletin board. The former are acknowledged only if the local walker is in the posted state and are processed when the IMPACT process calls the get function. Queries for the local bulletin board corresponding to the temperature bin serviced by the daemon are of three kinds, queries to retrieve the available postings, requests to leave a posting, and requests to remove an existing posting.

2.3 Computational details

The T-REM simulations of the capped trialanine peptide [Ace-(Ala)₃-NMA] employed the OPLS-AA force field^{26, 27} with the AGBNP²⁸ implicit solvent model. Calculations were conducted with the IMPACT²² molecular simulation program.

The melting curves of the α conformation of the capped trialanine peptide have been obtained with both the synchronous and asynchronous replica exchange algorithms using similar settings. For both we employed 8 replicas at 200, 239, 286, 342, 409, 489, 585, and 700 K, using the the Hybrid Monte Carlo (HMC)²⁵ method with an outer time-step of 4 fs and 10 MD steps for each HMC cycle. The production phase included 250,000 HMC steps (10ns simulation time) and conformations were saved every 250 HMC steps for analysis. With the synchronous algorithm temperature exchanges were attempted every 25 HMC steps between walkers with nearest neighbor temperatures. With the asynchronous algorithm the number of HMC steps between temperature postings was randomly chosen between 5 and 50 HMC steps, and the fractional temperature exchange gap parameter α_g (see Implementation section) was set to 0.25. α conformations were defined as those in which a hydrogen bond contact exists between the the acetyl and N-methyl amide capping groups. A hydrogen bond was detected based on the OH distance threshold of 4 Å and a hydrogen bond angle threshold of 120 degrees.

The replica exchange tests to measure the utilization efficiency of each replica exchange algorithm on heterogeneous sets of processors were run on four dual-processor Athlon MP 2.2 Ghz nodes (8 processors). The peak performance of these processors for this application was measured as 40.8 HMC steps per second using a serial HMC simulation of alanine tripeptide at 286 K. For the utilization efficiency tests one of the nodes was additionally loaded with zero, 1, 2, 3, or 4 processes running serial HMC simulations of alanine tripeptide to mimic the behavior of a processor set for which the speeds of two of the processors were, respectively, the same, 2/3, 1/2, 2/5, and 1/3 of the speed of the other processors. The tests with the synchronous replica exchange algorithm were performed for 25,000 HMC steps using the same settings as above. The tests with the asynchronous algorithm were performed for 1,000 seconds of wall-clock time. Utilization efficiency was measured as the ratio between the sum over all processors of the number of HMC steps actually executed and the maximum expected number of steps based on the peak processor speed measured above (40.8 HMC steps per second), taking into account the lower speeds of the two processors that were artificially loaded. For example for the test with the synchronous algorithm in which two processors were loaded with one additional simulation each (1/2 speed), overall 200,000 HMC steps (25,000 times 8 processors) were executed in 1, 314 seconds, yielding 152.2 HMC steps per second. This is compared to the maximum aggregate speed of this processor set given by 6 × 40.8 + 0.5 × (2 × 40.8) = 285.6 HMC steps per second, resulting in an utilization efficiency of 152.2/285.6 = 53.3%. In comparison, the corresponding aggregate throughput of the asynchronous algorithm with two processors at half speed was 263.9 HMC steps per second, yielding an utilization efficiency of 263.9/285.6 = 92.4%.

The replica exchange simulations performed to measure the number of temperature crosswalks (see Results and Discussion) employed the same settings as for the melting curve calculation except that the number of walkers was varied from 8 to 64. The temperature of each walker was recorded periodically on disk as the simulation progressed. The temperature trajectory of each walker was then examined to measure the number of temperature crosswalks. A temperature crosswalk event is defined as a transition from a temperature below 250 K to a temperature higher than 650 K and back.

3 Results and Discussion

We evaluated the asynchronous replica exchange molecular dynamics method by simulating the capped alanine tripeptide molecule Ace-(Ala)₃-NMA with the OPLS-AA/AGBNP²⁸ implicit solvent effective potential. We performed three kind of tests. We first computed the melting curve of the intramolecularly hydrogen bonded conformational state and compared it to the corresponding results obtained from the standard synchronous replica exchange algorithm to show that the asynchronous algorithm produces thermodynamic results in agreement with the better established synchronous algorithm. We then compared the relative performance of the asynchronous and synchronous algorithms on a set of processors with heterogeneous speeds to show the superior processor utilization efficiency of the asynchronous algorithm under these conditions. We then illustrate the benefits of performing non-nearest neighbor exchanges by monitoring the rate of temperature diffusion for the capped alanine tripeptide system.

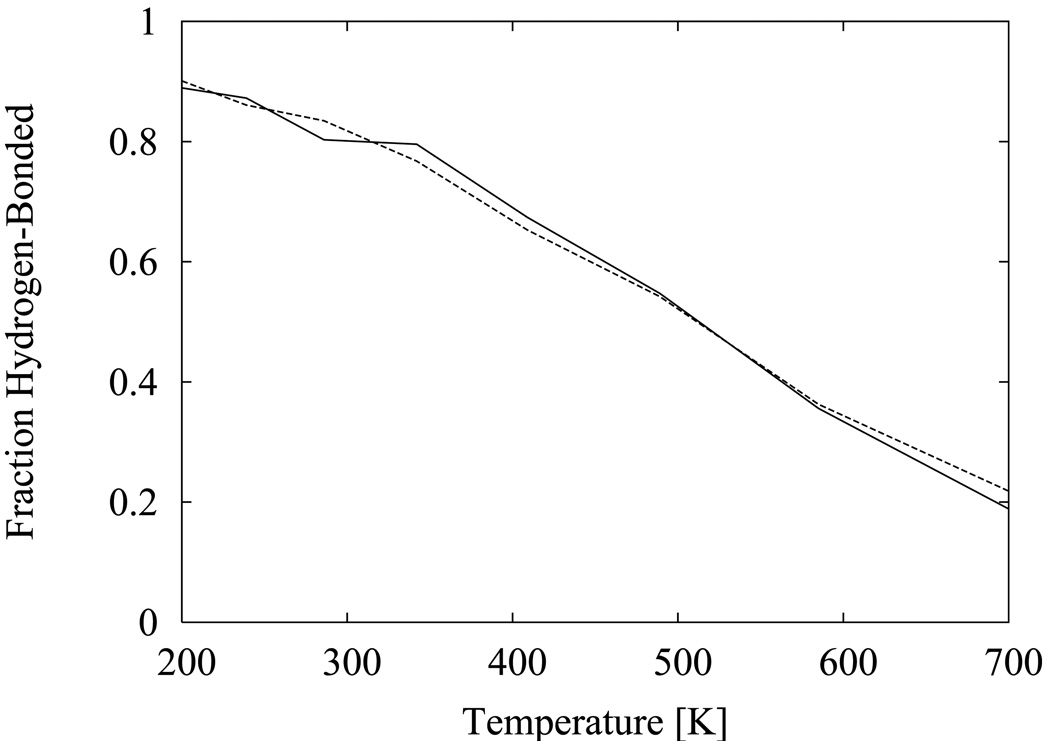
One of the important features of the temperature replica exchange method is that it retains canonical sampling of conformations at each temperature so that, provided that the underlying molecular dynamics or Monte Carlo conformational sampling algorithm is canonical, the method can be used to estimate mechanical thermodynamic quantities comparable to experimental measurements. Under this assumption the estimated values of thermodynamic quantities should depend only on the force field model and thermodynamic conditions, such as the temperature, and not on the details of the conformational sampling algorithm. It follows that, if properly implemented, the asynchronous and synchronous replica exchange algorithms should produce the same estimates of thermodynamic quantities. As an illustration, we show in Fig. 1 the fractional population of the α-helical conformation of the capped alanine tripeptide molecule as a function of temperature, calculated with both the synchronous and asynchronous replica exchange algorithms (see Methods). This property, which in the context of protein unfolding is known as the “melting curve”, is very sensitive to a temperature-dependent ensemble bias, the kind possibly introduced by an incorrectly designed temperature replica exchange scheme. We see that the melting curve calculated with the asynchronous algorithm is in very good quantitative agreement with the one obtained with the synchronous algorithm, indicating that both produce the correct canonical ensemble of conformations.

Figure 1.

Melting curve of the hydrogen-bonded conformational state of the capped alanine tripeptide molecule calculated with the asynchronous (solid line) and synchronous (dashed line) temperature replica exchange algorithms.

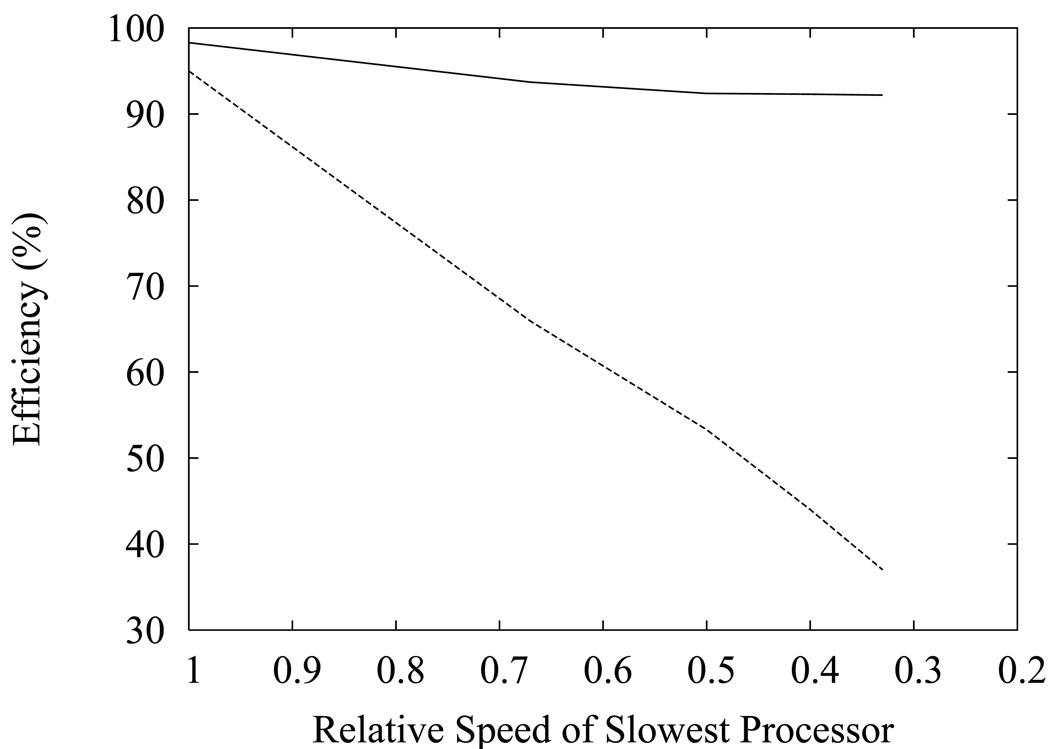
We evaluated the effectiveness of the method on heterogeneous sets of processors. The results of these tests are illustrated in Fig. 2 for the capped alanine tripeptide system. In these calculations 2 of the 8 processors have lower speeds than the others. As Fig. 2 shows, the performance of the synchronous replica exchange algorithm, measured as the total number of HMC updates per unit time, is determined by the speed of the slowest processors. The synchronous algorithm underutilizes faster computers because these are forced to wait for the slower computers to complete a calculation cycle before a new round of temperature exchanges can be attempted. The asynchronous algorithm, instead, is able to take better advantage of the processing power of the faster processors, while still fully utilizing the slower processors. For example for the case in which the speed of the slowest processors is one third the speed of the fastest processors the number of MD steps per second performed with synchronous replica exchange is approximately one third the value obtained when the processors have equal speeds, indicating that for two thirds of the time the fastest processors remain idle waiting for the slowest processors. In contrast, the corresponding efficiency with the asynchronous algorithm is much higher (92%, see Fig. 2), indicating that each processor is utilized at nearly full capacity regardless of the relative processor speeds. The efficiency of the asynchronous algorithm drops slightly as the difference in speed between fast and slow processors increases (see Fig. 2) due to the longer response times of the slower processors which extend the average time required to complete a temperature exchange. However, this effect becomes less pronounced as the rate of exchange attempts is reduced, due to the smaller fraction of time spent in exchange attempts. In contrast, the efficiency of the synchronous algorithm depends mainly on the relative speed of the slowest processor and does not improve significantly upon reduction of the rate of exchange attempts.

Figure 2.

Efficiencies, expressed as the percent ratio of the observed simulation performance relative to the maximum performance, of the asynchronous (solid line) and synchronous (dashed line) temperature replica exchange algorithms on 8 processors as a function of the relative speed of the slowest processor.

In a replica exchange simulation, at equilibrium all the walkers visit each temperature with equal probability. The rate at which this equilibrium condition is approached can be measured by the temperature diffusion rate of each walker, measured as the the number of times walkers traverse the range of temperatures employed in the replica exchange simulation. These quantities can also affect the rate of crossings between stable states separated by energy barriers that can be surmounted only at higher temperatures. If a transition from one low temperature stable state to another occurs exclusively at high temperatures, the transition rate between the two states is bounded by the rate at which a walker, starting at low temperature, assumes higher temperatures and from these goes back to low temperatures.

Standard synchronous replica exchange implementations often allow temperature exchange attempts only between nearest neighbor temperature replicas, that is between walker pairs that have the smallest possible temperature differences. This is done to ensure maximal probability of acceptance of exchange attempts and also to reduce the complexity of temperature swap schemes, which in synchronous implementations are required to occur simultaneously. For example, random selection of pairs of replicas is complicated by the need of ensuring that pairs do not overlap and follow some assigned temperature difference distribution (such as the box function adopted in this work). These complexities are removed when temperature exchanges can occur asynchronously using the algorithm described in this work.

Allowing exchange attempts only between nearest neighbor replicas implies that to traverse a given temperature range walkers have to cross each intervening temperature gap, posing a limit to the rate of temperature diffusion. This is especially noticeable with many replicas when the temperature spacings are small compared to the temperature range to cover. This is illustrated in Table 1 where we list the number of temperature crosswalks per walker (the total number of crosswalks divided by the number of walkers) observed with the asynchronous and synchronous algorithms, where the latter employs a nearest neighbor exchange scheme and the former the non-nearest neighbor exchange scheme, for a 10ns replica exchange simulation of the capped alanine tripeptide with up to 64 replicas. Although a system of this size does not generally warrant these many replicas, it is used here to illustrate the potential benefits of non-nearest neighbor exchange schemes. The number of crosswalks is defined as the number of times any walker, starting at low temperature, progressively assumes the highest temperatures and then returns to lowest temperatures. In this specific test, replica temperatures are distributed exponentially between 200 and 700 K and we define a low temperature as any temperature less than 250 K and a high temperature as any temperature larger than 650 K. A crosswalk event is defined as a transition from a temperature below 250 K to a temperature higher than 650 K and back.

Table 1.

Number of observed temperature crosswalks per walker with the nearest neighbor (synchronous algorithm) and non-nearest neighbor (asynchronous algorithm) schemes as a function of the number of replicas.

Exchange Scheme	Number of Replicas
	8	16	32	64
Nearest neighbor	109	143	104	19
Non-nearest neighbor	79	150	196	190

We see from Table 1 that with increasing number of replicas the number of crosswalks initially increases with both algorithms due to the reduction of the average temperature gap between replicas, leading to greater exchange probabilities. This effect favors the nearest neighbor exchange algorithm since the temperature gaps between neighboring replicas decrease with increasing number of replicas, whereas for non-nearest neighbor exchanges with the asynchronous algorithm the average temperature gap between replicas in a temperature block remains roughly constant. Beyond a certain number of replicas however the increase in the number of temperature exchanges necessary with the synchronous algorithm to traverse the temperature range between highest and lowest temperatures more than offsets the benefit of the decrease of the temperature gaps between neighboring replicas. In contrast, because in the asynchronous algorithm exchanges occur between replicas within a fixed temperature range, the average number of temperature exchanges to achieve a crosswalk does not depend explicitly on the number of replicas. The result is that with increasing number of replicas the number of temperature crosswalks per walker with the asynchronous algorithm remains approximately constant whereas the number of temperature crosswalks per walker with the synchronous algorithm drops significantly. In this specific case (see Table 1) the number of crosswalks with the asynchronous algorithm exceeds that obtained with the synchronous algorithm when the number of replicas is greater than 16. With 64 replicas the number of temperature crosswalks with the asynchronous algorithm is 10 times that obtained with the synchronous algorithm.

4 Conclusions

We presented an asynchronous implementation of the temperature replica exchange method that overcomes some of the limitations of synchronous replica exchange implementations. The method has been implemented in the IMPACT molecular simulation program by interfacing it with a distributed directory layer and communication framework we developed previously. In the asynchronous replica exchange implementation pairs of walkers initiate and perform temperature replica exchanges independently from the other walkers, thereby removing the need for synchronization steps employed in synchronous implementations. A non-blocking protocol, designed so as to interfere as little as possible with the time-consuming MD/MC updates on each processor, is responsible to match likely exchange partners. We performed illustrative calculations that show that asynchronous replica exchange is able to efficiently utilize pools of processors with heterogeneous speeds, whereas the standard synchronous version is limited by the slowest processor in the pool and underutilizes the faster processors. We also show that with the asynchronous algorithm it is straightforward to employ exchange schemes that go beyond simple nearest-neighbor exchanges typically used in standard replica exchange implementations, leading in some circumstances to faster temperature diffusion across the replica exchange walkers.

Ongoing development work is aimed at improving the robustness of the method to make it viable for computational grid environments. We are working on updating the startup procedure so that a single initial replica dynamically spawns new replicas depending on the availability of processors on the grid, and to allow processors to dynamically leave and join the calculation without causing the replica exchange simulation to stop. The aim is to design a redundant and dynamical replica exchange environment that will shrink and expand according to available computing resources and will not abort as long as there is at least one processor that can perform the simulation. The ultimate goal is to make the process of running asynchronous replica exchange simulations as straightforward and robust as distributed computing calculations. We believe that a strategy of this kind will make it possible to run replica exchange simulations on heterogeneous computing clusters and on the ever expanding computing resources available on local and global computational grids.