Abstract
It was found that the variety of function-related conformational changes (“movements”) in proteins is beyond the earlier simple classifications. Here we offer biochemists a more comprehensive, transparent and easy to use approach allowing a detailed and accurate interpretation of such conformational changes. It makes possible a more multifaceted characterization of protein flexibility by identifying rigidly and non-rigidly repositioned fragments, stable and non-stable fragments, domain and non-domain repositioning. “Coordinate uncertainty thresholds” derived from computed differences between independently determined coordinates of the same molecules are used as the criteria for conformational identity. ‘Identical’ rigid substructures are localized in the distance difference matrices (DDMs). A sequence of simple transformations determines whether a structural change occurs by rigid body “movements” of fragments or largely through non-rigid-body deformations. We estimate the stability of protein fragments and compare stable and rigidly moving fragments. The motions computed with the coarse-grained elastic networks are also compared to their DDM analogs. We study and suggest a classification for 17 structural pairs, differing in their functional states. For 5 of the 17 proteins conformational change cannot be accomplished by rigid-body transformations, and require significant non-rigid body deformations. Stable fragments rarely coincide with rigidly moving fragments, and often disagree with the CATH identifications of domains. Almost all monomeric apo-chains, containing stable fragments/domains, indicate instability of the entire molecule, suggesting the importance of fragments and domains motions prior to stabilization by substrate binding or crystallization. Notably kinases exhibit the greatest extent of non-rigidity among the proteins investigated.
The importance of flexibility for protein function is well understood (1). The conformational changes in response to the binding of another molecule are of the utmost importance for protein function. These conformational changes are often referred to as “protein motions,” while usually only a few snapshots can be gleaned from the experimental structures. Such a change can involve only a single side chain or may be as dramatic as long range repositioning (“movement”) of large fragments or domains and even partial folding/refolding. It was suggested earlier that whole folded domains never undergo large distortions at ordinary temperatures (1). However, this last suggestion seems open to question (see below).
Chothia, Lesk, and Gerstein pioneered studies of large-scale protein flexibility from comparisons of two or more structural states of the same protein (2-4). Their studies led to the creation of an important database of significant protein motions (5-8). They suggested a classification of the major types of large protein motions (4,7) characterized by three extents of magnitude - no motion, minor movers, major movers, three sizes - fragment, domain, subunit, and three mechanisms - hinge, shear, other. More recently they found that “The degree of movement in many of the structures that have been examined is striking, particularly in light of the variety of mechanisms involved.” (9). This makes the original classification (8) seem oversimplified and justifies the need for a new scheme for classifying flexibility in proteins (10).
It has often been stated (1,4) that large conformational changes in proteins involve repositioning of rigid loops or preformed rigid domains. This appears to be based on limited analysis and unsettled definitions. There is still no consensus of what constitutes a domain (11-12), making many structural interpretations dubious. The earliest of the two major definitions considered structural domains to be parts of protein structures having more interactions inside individual domains than between them (13-14). A later definition considered a structural domain to be a segment (or several segments) of the polypeptide that forms a compact and stable structure, with a hydrophobic core, and which can fold by itself (12,15-20). Because some papers identified domains with structural “modules” that move relative to each other in protein functioning (21), it raises the question of whether such “modules” are stable and can fold independently.
Furthermore, it has been suggested that “if you know how it moves, you can infer how it works; the knowledge of structural flexibility offers a straight-line connection between structure and function.”(22). In fact one of the central issues in studies of protein flexibility is how much of which observed protein conformational change is actually required for its function (5, 10, 23), especially since many changes can be induced by crystallization (10) or other factors not necessarily directly related to function.
Because a few snapshots of a protein’s conformational change cannot fully reveal all details along the pathways of such change, pathway movies of the motions (morphs) have been constructed as interpolations between two crystal structures (8,24). “Straight Cartesian interpolation” and “Interpolation with restraints,” where energy minimization is applied to interpolated intermediates, can nonetheless yield intermediate structures with rather high energies. Newer methods (25-26) based on elastic models for creation of the motion pathway movies appear to be better in avoiding high energies and more informative about intermediate structures.
Our goal here is to illustrate and provide for biochemists methods (10,16,19, 25-26) allowing a clear, detailed and accurate interpretation of function-related conformational changes in proteins. To move towards this goal here we: 1) use distance difference matrices (DDM) (27) utilizing “coordinate uncertainty thresholds” and a novel, simple and fast algorithm to identify and characterize rigid body movements in proteins (10, 28); 2) verify whether a sequence of rigid body transformations can bring two functionally different protein conformations into coincidence within an “uncertainty threshold” between their coordinates or whether non-rigid-body deformations significantly contribute to function-related motions; 3) determine whether domains and loops involved in function-related conformational changes “move” as rigid bodies or exhibit more complex behaviors; 4) estimate the stability of the protein fragments/domains (16-19) to study whether they behave as rigid bodies in protein functional motions and what other roles stability may play in such motions; 5) propose a more detailed classification of functional motions in proteins; 6) generate pathways of protein functional motions using elastic models of conformational transitions (25-26) and compare them to DDMs of such pathways intermediates.
METHODS
Distance difference matrices (DDM)
For a protein of N residues the distance matrix (DM) is a square N×N matrix, in which element ij represents the distance between residues i and j (or their Cα atoms as used here). Because the distances i to j and j to i are equal, usually only half of the DM matrix is considered (27). For two different conformations of the same protein a distance difference map, DDM, is constructed as a N×N matrix of differences (DDs) between the corresponding elements of the two DMs (10). We follow our previous work (10) representing DDMs in three shades (black, grey and white) based on the ranges of the absolute DD values falling below 0.5Å, between 0.5Å and 1Å, and above 1Å. Each DDM is characterized by the RMS of all its DDs, denoted as RMSDD, and with the percentage of DD values lying outside the range -1Å to 1Å, denoted as Δ.
Contact distance difference matrices (CDDM) and an estimation of the extent of shear
Shear movements (3) can occur at contact interfaces. It has been found (6) that, because of packing restrictions, shearing segments move relative to one another by no more than 2Å. To estimate the amount of restricted motion at contact interfaces we have constructed contact distance difference matrices (CDDM). Contact distance matrices (CDM) for each structure (indexed by k=1,2) contain only |(Cαi)k-(Cαj)k| distances shorter than a ‘contact’ cutoff, chosen here as 8Å, based on tabulated distances between contacting helices and β-strands in proteins (29-30). For each ij, marked as a ‘contact’ on at least one of two CDMs, a distance difference is calculated and marked on the CDDM. All ij positions that were not marked as a ‘contact’ on both CDMs are shown as blank spots on the CDDM. The percentage of contact distance changes within any range can be computed from the CDDM. We calculate such percentages only for j >i+4, to avoid a dominance in our contact statistics of contacts within α-helices and turns. An example of a CDDM is shown in Fig. S2b of the Supporting Information.
We estimate the magnitude of shear in each functional “motion” by evaluating the percentage, δ, of “contact” distances in the corresponding protein’s CDDM that change between 1Å and 2Å. δ < 1.5% includes pairs of structures with only coordinate uncertainty (see the section below). Here we take values of δ < 1.5% as indicating no shear.
Estimation of positional uncertainties
We determined the range of coordinate uncertainties in our previous work (10) by calculating and analyzing the DDMs of 1,014 pairs of structures (at about room temperature) of bovine ribonuclease A, and of whale myoglobin for which the authors did not report any significant conformational changes (“movements”). Each pair was characterized by its DDM, RMSDD and Δ (see above). All of these 1,014 pairs of structures had the RMSDD ≤ 0.44Å and Δ ≤ 4.05%.
Two DDMs (endothiapepsin, 4ape5er2, and thermolysin, 1l3f3tmn) corresponding to functionally significant conformational changes (“motions”) (5,7) have the lowest RMSDDs (0.45Å and 0.46Å) among over 20 DDMs of functional “motions” that we have studied and Δs of 5.2% and 3.4% correspondingly.
The values of the RMSDDs and Δs listed above led us to the criteria that a DDM indicates no significant “motion” but only “coordinate uncertainty” when the RMSDD is below 0.46Å and its Δ is less than 5% (10). These criteria obviously classify DDMs 4ape5er2 and 1l3f3tmn as indicating significant conformational changes (“motions”), while classifying 1,014 DDMs of ribonucleases and myoglobins as indicating the structural identity of the corresponding protein pairs within the “coordinate uncertainty” threshold. Further accumulation and analysis of data might change these criteria somewhat. For further details and discussion see our previous paper (10).
Location of “rigid” fragments and blocks
All DDs within a continuous fragment of the protein form a right triangle along the DDM’s diagonal corresponding to this fragment. If this fragment’s conformations in two molecules differ only within the coordinate uncertainty limits – then the right triangle corresponding to this fragment should be almost entirely black containing minimal white or grey areas. Such a fragment is likely to change its position in a conformational transition as a rigid body.
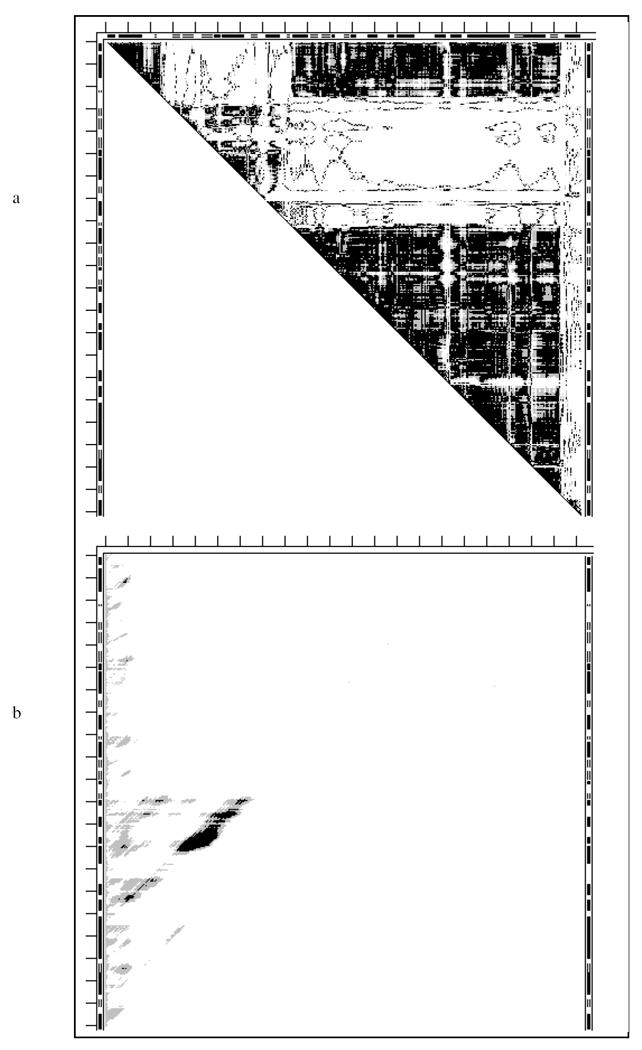
Two such rigid fragments (2-164 and 174-286) with clearly delineated nearly black triangles with straight white borders are exemplified in the DDM 2tbvA2tbvC of chains A and C of Tobacco Bushy Stunt Virus capsid protein (Fig. 1a). Largely white rectangle indicates that most Cα—Cα distances between the two rigid fragments changed by more than 1Å.
Fig. 1.
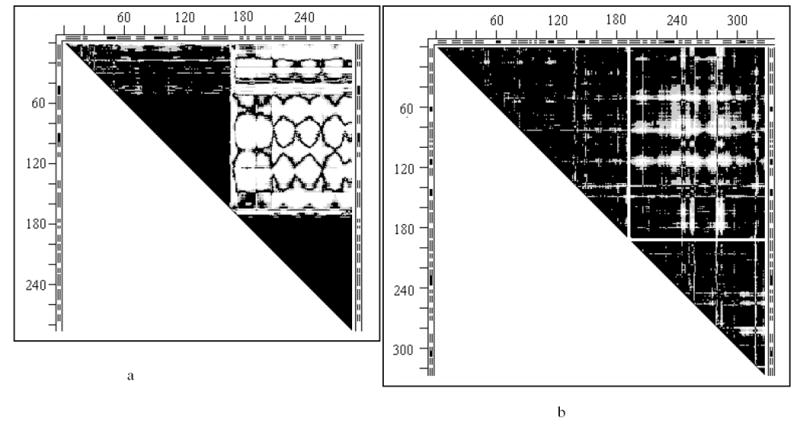
Distance difference matrices (DDMs)
- 2tbvAC for the molecules A and C in the unit cell of the 2tbv virus capsid protein; the mostly white rectangle at the DDM’s top right, providing straight white borders of the “rigid body triangles” of this DDM, indicates that most DDs between the two “rigid bodies” are larger than 1Å, meaning that most Cα-Cα distances between the “rigid bodies” differ in two molecules by more than 1Å.
- 4ape5er2 of the apo-holo structures of endothiapepsin; this DDM has only some white spots and no straight white borders of the black “rigid triangles”; such borders can be provided by drawing white lines encompassing almost all white spots in a rectangle and thus delineating the mostly black “rigid” triangles (see also text on thermolysin below).
No such clearly delineated black triangles with straight white borders are seen in the DDM 4ape5er2 of the apo-holo pair of endothiapepsin structures, which shows only a set of white spots in its top right part. However, we are interested not in straight white borders, but in almost solidly black triangles that likely represent rigid fragments. Two such mostly black triangles can readily be separated (by drawing straight white lines as in Fig. 1b) from the area containing almost all white spots. These white spots do not represent “distributed local distortions” but rather a systematic small amplitude difference between positions of the rigid fragments in two structures, which can be reduced below the uncertainty threshold by a rigid body transformation. (See the Results section.)
Fitting of “rigid” fragments
For the fitting of “rigid” or “nearly rigid” fragments we use the fast and accurate algorithm described in detail in our previous paper (10), which uses a superposition of three non-collinear points of a rigid body to superimpose all points of this body, together with quaternion rotations (31-34, 28). Such a superposition can be represented as an initial superposition of the centers of mass of the fragments (represented by Cα atoms) followed by two rotations around the axes passing through the center of mass and “nearly” (10) superimposing two Cα atoms from each fragment. A few residues at proteins termini or next to crystallographically unresolved fragments are sometimes excluded from the fitting. Fragments of no fewer than three residues were used.
Sequence of fitting steps and evaluation of the result
In the first step the largest rigid fragment of the second molecule is fit to its coordinates in the first (reference) molecule and the resultant transformation is applied to coordinates of the entire second molecule (this does not change the RMSDD; however, parameters of all subsequent rigid body movements depend on the choice of the first transformation). Coordinates corresponding to atoms of bound substrate (or cofactor) are not included in these calculations.
In the following fitting steps the structures of all fragments of the entire sequence of the second molecule should be fit to the structure of the corresponding fragments of the first molecule to verify whether the “functional movement” is a result of a series of rigid body movements of protein fragments. The particular order of fitting steps is arbitrary. For details see our previous paper (10). An example of the transformation sequence and its outputs is provided in the Supporting Information.
If the RMSDD and Δ after rigid body fittings of the entire second structure to the first are outside the uncertainty limits, it means that the functional “movement” involves significant non-rigid deformation of the main chain. It may be useful to look at a DDM to obtain a fast estimate of whether one structure of a protein can be transformed into another by no more than 12 rigid body movements. Here we offer two such simple cues. More might emerge with growing experience.
An idealized L-shaped white band is shown in Fig. 2a. Instead of a half-matrix above the diagonal, which we use throughout the paper, it is convenient here to draw the entire matrix with triangular halves related by a diagonal reflection. Here we consider (in a highly simplified manner) the relationship of the width of the band, measured by the number of residues, and Δ.
Fig. 2.
- Contribution of L-shaped white bands (see text).
- Role of the size of the rigid fragments (see text).
Let N be the number of residues in a protein in Fig. 2a; w - the width of the band given as the number of residues; S - the area of the entire DDM as (number of residues)2; and SLb - the area of the L-band; then S = N2; 2×SLb = 2N×w; if we will ignore double counting where straight bands intersect then 2×SLb/S = 2w/N is the ratio of DDs larger than 1 to the total number of DDs in the DDM; Δ = 100×2w/N; w = N×Δ/(200); if the threshold is Δ = 5(%); then, wthr= 0.025×N. This means that for a protein of 400 residues the critical width of the L-band (wthr) would be 10 residues. For two equalsized L-bands it would be 5 residues each. A total width of L-bands in a DDM larger than this indicates that finding rigid transformations is unlikely. Note that this estimate holds only for L-bands with no black triangles in their corners. Such black triangles can be moved as rigid bodies eliminating the white L-band in the DDM.
Our use of a cutoff of 12 rigid body transformations to label a functional “motion” as “non-rigid” highly “flexible” or “glove” - is somewhat arbitrary. We might instead choose to scale the cutoff number of rigid transformations by the protein length.
Let’s assume, as shown in Fig. 2b, that all rigid blocks (black triangles in the DDM) have an equal width, w, and also assume that m is the allowed number of rigid-body transformations (equal to the number of black triangles). Then w = N/m; if N=204 and m=12, w200 = 17 (residues). This means, that if the white area comes mostly closer than w from the diagonal, one might fail to rigidly transform one structure into another within the required cutoff number, m, of rigid body transformations.
Estimations of stability of protein fragments and blocks
We previously suggested that stable fragments with native-like conformations within proteins can be located based on calculations of buried surface area (15-19). Theoretically predicted stable fragments (18) were successfully found experimentally in thermolysin (35). While this method has its limitations, it nonetheless remains a useful tool for domain identification (11), and can serve as a tested guide in the experimental isolation of stable protein fragments. We use it here to estimate the stability of all protein fragments including rigidly moving “blocks”. Results are also compared to CATH (36) or SCOP (37) domains. Only polypeptide parts of proteins were included in the stability calculations. When PDB (38) files contain alternative side chain conformations, the “A” conformer is always used (a selection of alternative conformers was found (17) to have only a minor effect on the results.)
An estimate of the free energy ΔGDN corresponding to the stability of a protein fragment of molecular weight M can be obtained from the expression below (17) -
| (1) |
where ΔGDN is protein stability; ΔGB is assumed to be proportional to the surface area, B, buried upon fragment’s folding; TΔSconf is the loss of conformational entropy of the chain without disulphide crosslinks upon folding and is a function of its molecular weight; TΔSS-S is the decrease in the absolute value of this entropy caused by disulphide crosslinks. For a protein of N residues, an N×N table of stabilities of all of its contiguous fragments forms a “stability matrix” (SM). Note, that expression 1 should be considered as an empirical formula allowing a reasonable degree of success but leaving aside controversies regarding the mechanism of protein folding (19,39-40). Parameters used here for the stability calculations and some general estimates of the method’s accuracy are provided in Section 1 of the Supporting Information.
Here we show a fragment of SM for the X-ray structure of residues 1-180 of 2tbvA (Fig. 3a) and its ribbon representation (Fig. 3b).
Fig. 3.
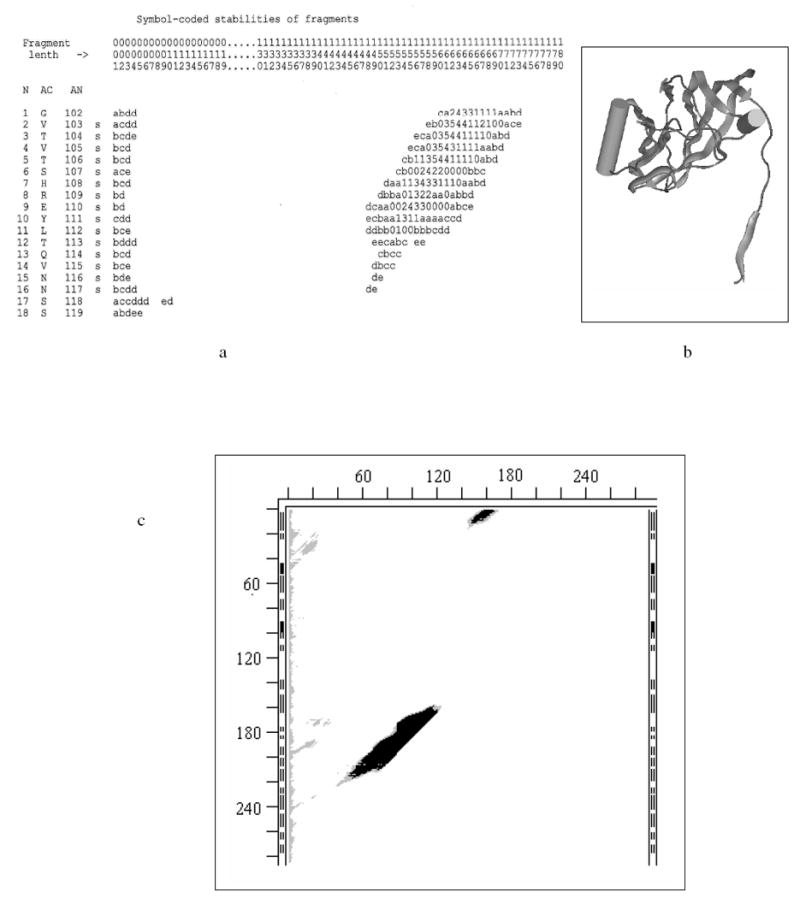
- Stability Map (SM) for 180 N-terminal residues of subunit A of 2tbv (large parts of SM that do not contain stable fragments are omitted for figure’s compactness); location of continuous fragments in the chain are uniquely defined by two perpendicular axes: fragment’s length (L) (horizontal), and position (N) of the fragment’s first residue relative to the N-terminus of the entire chain/molecule (vertical on extreme left); the matrix elements of SM are fragments’ stabilities (rounded to the nearest integer) represented by one character symbols: e.g., 1, 2, … 9, “-” denote ‘stable’ ΔG of -1, -2, …-9, -10 kcal/mol; capital letters A, B, C, D, etc, denote ‘stable’ ΔG of -11, -12, -13, -14, etc. kcal/mol; 0 denotes ΔG of 0 kcal/mol (the fragment spends half time in its x-ray fold and half in an unfolded state); lower case letters a, b, c, d, e, etc, denote positive ΔG of +1, +2, +3, +4, +5, etc kcal/mol; white spaces denote instabilities above the cutoff value (here – above 5 kcal/mol); horizontal coordinate axis “Fragment length” (L) is marked by columns of three numbers (to be read vertically to save on SM sizes); dots in the L-axis markings indicate that a vertical strip of the full SM is omitted (there are no stable fragments of omitted lengths); three columns to the right of the N-axis markings are: AC – one letter residue codes, AN – the residue numbering of the chain accepted in the PDB file, and the last one shows whether the residue in the X-ray structure is in β-strand (s), helix (H) or coil (white space).
- Ribbon diagram of the X-ray structure of the same 180 residues (MOLE CD and manual are available from G.P. Privalov, gpriv@axonx.com – wire molecular images in this paper are also made with MOLE.).
- Bitmap SM for all continuous fragments in 2tbvA; the ticks (distance between them is 20 residues) notations on the left of the SM are the same as in Fig. 1 and mark position of fragment’s beginning (N-terminus) in the entire sequence; ticks on the top of the SM measure the length of the fragment from its N-terminus; black areas in the SM correspond to negative ΔG (stable), grey areas denote marginal stabilities (0 kcal/mol to +5 kcal/mol), white areas indicate instabilities with a cutoff ΔG > +5 kcal/mol (larger cutoffs are sometimes used for more reliable estimates in the text and Table 3.)
For the rest, see Table 1 and the figure legends.
The SM and its cross-sections (15,18-19) closely resemble “free energy landscapes” introduced later. Fig. 3a shows that an unfolded chain has to cross a free energy barrier (white area) to reach a valley with the largest calculated stability of -5 kcal/mol. The longest fragment with this stability includes 162 residues starting from the 2nd residue (fragment 2-163). Except for minor variations in the position of its ends this tightly folded fragment can be easily seen in Fig. 3b. It ends at the tip of the rightmost arrow on a β-strand, and it is obvious that the following coil and β-strand region do not interact with this stable domain. Even in this rather simple case the SM has a large size that can be analyzed on a computer but is inconvenient to print. Therefore in the Results section below we use three-color bitmap SMs with white for fragments with ΔGs above a chosen threshold, T, of instability (we used T=5 or T=10 kcal/mol), grey for ΔGs from 1 to T, and black for 0 and all negative ΔGs. The three color bitmap SM of the entire 2tbvA is shown in Fig. 3c, and the locations of the most stable fragments are listed in Table 3.
Table 3.
Stable Fragments and CATH/SCOP domains in pairs of apo- and holo-protein structures
| # | PROTEIN | #of res. | State | PDB | FRAGMENTS with stabilities (kcal/mol) & CATH Domains |
|---|---|---|---|---|---|
| 1 | Calmodulin | 138 ma | apo | 1cll | (1-138>+10);12-70(-2); 101-138(-1); 120-138(-1) |
| holo | 1ctr | 9-70(-1); 75-138(-1); 119-138(-1) | |||
| CATH | 1-69; 68-138; | ||||
| 2 | Dehydrofolate reductase | 202 m | apo | 4cd2 | 1-202(>+10); 54-81(-3); 48-120(0) |
| holo | 1cd2 | 1-202(>+5); 54-81(0); | |||
| CATH | 1-202 | ||||
| 3 | Adenylate kinase | 214 m | apo | 4ake | 1-214(>+10); 25-102(-3); 1-107(-1); 111-169(-3); 194-214(-1) |
| holo | 1ank | 1-214(>+5); 26-103(-2); 1-109(0); 122-159(0); 196-214(+1) | |||
| CATH | 1-214 | ||||
| 4 | DNA-Uracil glycosylase | 223 m | apo | 1akz | 1-223(-1); 12-33(0); 85-105(0); 185-200(0) |
| holo | 1ssp | 3-223(-9); 23-210(-5); 145-185(0); 88-109(0); 185-200(0) | |||
| CATH | 1-223 | ||||
| 5 | Tobaco Bushi Stant virus | 287 v | Mol. A | 2tbv | 2-162(-5); 171-277(-13) |
| 3 mol. In unit cell | Mol. C | 2tbv | 3-161(-6); 172-278(-15) | ||
| CATH | Not available | ||||
| 6 | Thermolysin | 316 m | apo | 1l3f | 1-316(-18);3-148(-12);76-316(-16);136-316(-17);233-316(-16);255-316(-6) |
| holo | 3tmn | 1-316(-3); 1-148(-3); 76-316(-6); 136-316(-11);234-316(-12);255-316(-2) | |||
| CATH | 6-154; 155-315 | ||||
| 7 | Endothiopepsin | 330 m | apo | 4ape | 1-330(>+10); 1-173(-2);18-125(-12);18-148(-10); 183-330(-2);197-313(-11) |
| holo | 5er2 | 1-330(>+10); 1-173(-5);18-129(-14);18-149(-13); 183-330(-2);197-314(-11) | |||
| CATH | 2-170; 171-326 | ||||
| 8 | Lactate dehydrogenase | 329 | apo | 6ldh | 1-329(>+10); 21-96(-10); 109-162(-5); 21-162(0); 163-236(-3); 255-303(-1) |
| holo | 1ldm | 1-329(>+5); 21-96(-9); 109-162(-5); 165-235(-6); 252-301(-1) | |||
| CATH | 1-162; 163-329 | ||||
| 9 | Glyceraldeh. dehydrogen | 334 | apo | 2gd1 | 1-334(>+5); 1-120(-7); 1-96(-10); 93-150(-2); 236-317(-1) |
| holo | 1gd1 | 1-334(>+5); 1-120(-9); 1-96(-9); 95-145(-3); 236-317(+1) | |||
| CATH | 1-147; 314-332 | ||||
| 10 | Signal regulated kinase | 353 m | apo | 1erk | 1-353(>+10; 1-50(-2); 101-318(-2); 101-233(-3); 172-294(-5) |
| holo | 2erk | 1-353(>+5); 3-50(-4); 101-318(+2); 122-214(-2); 177-295(-4) | |||
| CATH | 1-100; 330-353 | ||||
| 11 | Alcohol dehydrogenase | 374 | apo | 8adh | 6-364(-3); 178-294(-15); 192-293(-15); 172-322(-4) |
| holo | 6adh | 6-364(-3); 178-293(-13); 193-293(-13); 172-322(-4); 261-317(-1) | |||
| CATH | 1-178; 318-374 | ||||
| 12 | Asp aminotransferase | 401 | apo | 9aat | 1-401(>+5); 68-304(-5); 80-102(-2); 321-401(-14) |
| holo | 1ama | 1-401(>+5); 68-304(-9); 80-102(-2); 321-401(-13) | |||
| CATH | 13-46; 47-319; 320-401 | ||||
| 13 | Phospho-glycerate kinase | 415 m | apo | 16pk | 1-415(+3); 3-192(-8); 194-404(-18) |
| holo | 13pk | 2-413(-26); 3-193(-23); 195-414(-21) | |||
| CATH | 5-192; 199-406 | ||||
| 14 | Glukokinase | 424 m | apo | 1v4t | 1-424(>+10); 40-58(-1); 110-130(0); 270-379(-6); 255-341(-10);271-391(0) |
| holo | 1v4s | 1-424(>+10); 270-379(-7); 261-338(-13);338-404(-1) | |||
| SCOPb | 1-181; 182-426 | ||||
| 15 | Citrate synthase (dimer) | 437 | apo | 4cts | 51-417(-5); 275-381(-4) |
| holo | 1cts | 51-417(-2); 277-381(-6) | |||
| CATH | (1-276)+(392-423); 277-391 | ||||
| 16 | Glu dehydrogenase | 449 | apo | 1hrd | 1-449(>+5); 1-53(0); 54-194(-9); 206-376(-17); 227-321(-21); 410-434(-5) |
| holo | 1bgv | 1-449(>+5); 1-53(-2);54-195(-10);206-376(-13);226-321(-18);410-433(-4) | |||
| CATH | 52-187; 207-373; (1-51)+(425-449) | ||||
| 17 | Lactoferrin | 691 m | apo | 1lfh | 37-74(-2);91-256(-14);109-210(-20);376-408(-1);435-594(-9);453-546(-10) |
| holo | 1lfg | 37-74(0);91-256(-13);109-210(-16);376-408(0);435-594(-10);453-546(-11) | |||
| + S-S -9.2 -5.9 -3.4 -9.2 -6.2 | |||||
| CATH | (1-91)+(251-339); 92-250; (340-434)+(595-691); 435-594 |
Monomers are marked with ‘m’ after their length.
CATH unavailable; For the rest see legend to Table 1.
In addition to the general estimates of the method’s accuracy (see Supporting Information) we also obtained a rough estimate of the error in the calculated stabilities due to coordinate uncertainties of all atoms in a set of independently determined structures of the same molecule. We selected from the set of over 30 ribonuclease A structures 7 structures that were classified as “monomeric” by PQS (41) to exclude possible side chain distortions caused by extensive contacts in oligomers. The calorimetrically measured stability of ribonuclease A is 10 kcal/mole (42). Calculated stability values for the selected 7 structures varied from -6 to -12 kcal/mole, with an average of -9.7 kcal/mol and a variance of 2.8 kcal/mole. Calculated differences between the stability of the entire protein and the protein without the S-peptide (residues 1-20) varied between -4 and -6 kcal/mole, with an average of -5.6 kcal/mole and a variance of 0.8 kcal mole. The experimental stability of this shortened ribonuclease decreases by 8.1 kcal/mole, relative to the entire intact protein (43). This gives a measure of reliability of the absolute values of the calculated results and of stability differences within the same molecule. More of the similar statistics will be provided elsewhere.
Functional “motions”, their evaluation and classification
Functional (or protein association induced) “motions” might or might not involve an actual hinge. A significant motion might arise either from a continuous deformation of a flexible fragment of a chain (like a bent spring) or from a series of separate hinges (e.g., rotations around non-neighboring single bonds). The result of either of these can be an accumulated large motion at a distance, and in the present paper we are focusing on such significant accumulated changes at large distances from the local deformations, rather than on the local backbone changes. In particular, these large distant motions can result from a series of smaller motions or main chain deformations that yield a large cumulative remote motion (e.g., as occurs in citrate synthase (3).
We retain the name hinge motion for motions enabled by hinges in the main chain but not involving the grasping of a target, e.g., as in molecules of the viral capsid of 2tbv (6,44). If a motion grabs a target (e.g., substrate) and brings remote protein parts into contact we shall liken it to the closing of the tips of tweezers and call this a tweezers motion. A motion, in which remote protein parts lock onto a target but where their tips do not form a close contact, we shall instead call a pliers motion or, more generally, a chopsticks motion (implying more than one fulcrum position). If transforming one functional conformation into another (within the coordinate uncertainty) cannot be achieved by a large (a dozen) set of rigid body motions of its fragments, we shall call the entire motion a glove tweezers/chopsticks motion. These are the main motion types observed in our Results below.
One can easily imagine a rather large motion of contacting surfaces relative to one another that would not involve shear. An example of such a motion might be the motion of a rocking chair (on a flat floor or on a curved surface), and we call this a rocking motion. If the knobs-into-holes arrangement changes we can liken it instead to a gear motion. Elbow motion had already been introduced in the literature (45).
Here we classify motions using only the characteristics of DDMs and CDDMs (in one case below we also use a SM). More detailed (or alternative) “motion” types can be suggested and used as detailed analysis of the conformational changes (“motions”) in proteins progresses.
The coarse-grained (elastic) modeling of protein dynamics
Existing approaches often elucidate intermediate conformations in protein motions by using an interpolation procedure (8). We found (25-26) that such a procedure often leads to severe atomic overlaps and thus yields partially erroneous descriptions for pathways of motion that are unlikely to provide a clear picture of protein repacking during a motion. The interpolation method for coarse-grained models relying on elastic network representation of dynamics (25-26) appears to avoid most of the severe atomic overlaps exhibited by the coordinate interpolation methods (8) yielding a better understanding of protein motion pathways. Here we represent some from the series of 100 step-wise snapshots of the coarse grained ENM simulations of protein movements, superimposed on the reference wire structure of the pair, along with the corresponding DDMs. Comparisons of these two representations allow us to better identify conformational intermediates for protein functional movements.
RESULTS
1) Rigid and non-rigid movements, their classification and fragments stability
Results of our calculations for 17 function-related protein movements are summarized in Tables 1-3. Four proteins (thermolysin, lactate dehydrogenase, citrate synthase and adenylate kinase) were chosen because there were previous studies on their structures or stabilities. Others were randomly taken from the PDB by searching for apo-holo, apo-tertiary or open-closed pairs of structures with a functional relevance having been suggested in the corresponding publications.
Table 1.
Pairs of protein structures, DDMs, their characteristics and types of movements.
| Pair # | Pair PDB | Resid. includ | Biomol d | Unit cell e | RMSDD Å | Δ % | δ % | Max move | Rigid motions | RMSDD / Δ final (Å / %) | Type |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1cll1ctr | 138c | m | 12.83 | 54.92 | 4.08 | 46.7 | 5 | 0.44 / 2.70 | tweezers | |
| 2 | 4cd21cd2 | 202 | m | 1.25 | 2.62 | 11.7 | 11 | 0.44 / 4.74 | tweezers | ||
| 3 | 4ake1ank | 214 | m | 2 | 6.45 | 59.62 | 16.75 | 24.8 | >12 | glove/tweezers | |
| 4 | 1akz1ssp | 223 | m/tr | 1.14 | 21.89 | 3.19 | 5.5 | 11 | 0.31 / 0.61 | tweezers | |
| 4’ | 7 | 0.45 / 4.07 | |||||||||
| 5 | 2tbv2tbva | 287 | v. shell | 3 | 1.37 | 32.22 | 2.67 | 6.5 | 3 | 0.27 / 1.11 | hinge |
| 5’ | 2 | 0.43 / 3.35 | |||||||||
| 6 | 1l3f3tmn | 316 | m/tetr | 0.46 | 3.35 | 0.38 | 1.8 | 2 | 0.36 / 0.69 | pliers | |
| 7 | 4ape5er2 | 330 | m/d | 0.45 | 5.21 | 0.54 | 2.7 | 2 | 0.40 / 2.47 | pliers | |
| 8 | 6ldh1ldm | 329b | tetr | 1.25 | 15.37 | 4.53 | 12.3 | 10 | 0.41 / 2.86 | tweezers | |
| 8’ | 7 | 0.45 / 4.14 | |||||||||
| 8”g | 8 | 0.43 / 3.70 | |||||||||
| 9 | 2gd11gd1 | 334 | tetr | 0.49 | 6.14 | 0.74 | 3.1 | 2 | 0.36 / 1.89 | pliers | |
| 10 | 1erk2erk | 353 | m | 2.24 | 27.88 | 3.81 | 13.8f | >12 | glove/tweezers | ||
| 11 | 8adh6adh | 374b | d | 1/2 | 1.05 | 21.90 | 2.89 | 5.7 | 12 | 0.45 / 2.61 | tweezers |
| 12 | 9aat1ama | 401 | d | 2/1 | 1.20 | 22.96 | 7.48 | 6.7 | 7 | 0.36 / 2.52 | tweezers |
| 12’ | 3 | 0.43 / 4.12 | |||||||||
| 13 | 16pk13pk | 415b | m/d | 1/4 | 3.07 | 45.61 | 4.39 | 13.3 | >12 | glove/tweezers | |
| 14 | 1v4t1v4s | 424 | m | 6.90 | 49.24 | 5.66 | 38.9 | >12 | glove/tweezers | ||
| 15 | 4cts1cts | 437 | d | 2 | 1.58 | 26.30 | 12.20 | 9.6 | >12 | glove/tweezers | |
| 16 | 1hrd1bgv | 449 | h | 4 | 1.89 | 32.85 | 1.15 | 8.5 | 5 | 0.22 / 0.01 | pliers |
| 16’ | 2 | 0.35 / 1.84 | |||||||||
| 17 | 1lfh1lfg | 691b | m | 4.77 | 41.43 | 1.51 | 24.9 | 11 | 0.37 / 2.00 | tweezers | |
| 17’ | 7 | 0.45 / 3.19 |
there are 3 molecules in the 2tbv unit cell; 2 of them (A and B) do not have 102 residues or Cα atoms on the N-terminus; the 3rd (C) molecule is missing only 66 residues; we used A and C (shortened) molecules with the same number of resolved residues in the calculation.
for #13 3 N-terminal and 2 C-terminal residues, which dramatically change their conformation, were not included in the fitting and RMSDD evaluation; such non-included residues can be denoted by -3N, -2C for #13 and similarly indicate non-included residues in other structures; #17: -4N, -1C; #17’: -4N, -7C; #8 -5C; #11: -4N;
to make molecules comparable residues 1-3 and 148, missing in 1cll, and residues 76-80, missing in 1ctr, are not included in the DDM comparison.
likely but not fully reliable oligomerization state of biologically active molecule, estimates from PQS; notations in the table: m=monomeric, d=dimeric, tr=trimeric, tetr=tetrameric, h=hexameric.
number of molecules in the crystallographic unit cell; not shown – means 1; 1/2 means that 1st PDB entry (e.g., 8adh) has 1 molecule in the unit cell, and the second (e.g., 6adh) has 2 molecules in the unit cell.
9 N-terminal and 3 C-terminal residues move very far in a non-rigid manner; the value is given for the maximum DD closer to the middle of the chain.
characteristics of the transformation identical to 8’ except dividing 96-104 into 96-100 and 101-104 rigid fragments.
Below we represent and comment on the DDMs of some of the motions studied, to demonstrate their (not readily obvious from the Tables) variety and the DDMs’ interpretive power. Additional DDMs are included in the Supporting Information. We describe the pairs of end-structures for each “motion” and the results of the rigid body motions, characterizing the function-related conformational changes, in Table 1. The sequences of these rigid-body motions are listed in Table 2. We also present examples of simplified stability maps (SM), which provide a simple picture of any recurring stability patterns, where details are given in Table 3. Similarly classified conformational changes are grouped together below. In each group focus is concentrated on the most interesting cases with the rest mentioned briefly or relegated to the Supporting Information.
Table 2.
Rigid fragment motions in transformation of holo- to apo-protein structures
| # | Pair PDB | #of res.a | Fragment for initial b molec. superposition | Fragments moved as individual rigid bodies after initial molecular superpositionc,d |
|---|---|---|---|---|
| 1 | 1cll1ctr | 138 m | 24-70 | 74-138; 101-109; 128-138; 3-11 |
| 2 | 4cd21cd2 | 202 m | 190-202 | 17-21; 39-41; 42-44; 45-47; 48-81; 82-85; 86-115; 116-146; 147-151; 152-162. |
| 3 | 4ake1ank | 214 m | More than a dozen: large non-rigid deformation | |
| 4 | 1akz1ssp | 223 m | 174-223 | 3-7; 8-35; 36-48; 49-63, 64-76; 77-121; 122-132; 133-148; 149-170; 171-173. |
| 4’ | 174-223 | 3-7; 8-48; 49-63, 64-76; 122-148; 171-173. | ||
| 5 | 2tbvA2tbvC | 286 v | 174-286 | 2-164; 167-170 |
| 5’ | 174-286 | 2-164 | ||
| 6 | 1l3f3tmn | 316 m | 127-316 | 1-126 |
| 7 | 4ape5er2 | 330 m | 1-194 | 195-330 |
| 8 | 6ldh1ldm | 329 | 3-95 | 96-104; 105-108; 109-121; 122-215; 216-218; 219-223; 224-305; 306-324; 233-236 |
| 8’ | 3-95 | 96-104; 105-108; 109-121; 216-218; 219-223; 306-324 | ||
| 8”e | 96-100; 101-104; 105-108; 109-121; 216-218; 219-223; 306-324 | |||
| 9 | 2gd11gd1 | 334 | 160-334 | 1-159 |
| 10 | 1erk2erk | 353 m | More than a dozen: large non-rigid deformation | |
| 11 | 8adh6adh | 374 | 5-54 | 55-65; 66-96; 97-101; 102-182; 183-292; 293-298; 299-322; 323-354; 355-363; 364-368; 369-374 |
| 12 | 9aat1ama | 401 | 228-319 | 382-401; 350-381; 320-349; 2-13; 14-33; 34-36 (37-227: does not move) |
| 12’ | 47-319 | 320-401; 13-46 | ||
| 13 | 16pk13pk | 415 m | More than a dozen: large non-rigid deformation | |
| 14 | 1v4t1v4s | 424 m | More than a dozen: large non-rigid deformation | |
| 15 | 4cts1cts | 437 | More than a dozen: large non-rigid deformation | |
| 16 | 1hrd1bgv | 449 | 1-203 | 204-372; 373-393; 394-431; 432-449 |
| 16’ | 1-203 | 204-431 | ||
| 17 | 1lfh1lfg | 691 m | 5-86 | 87-92; 93-138; 139-142; 143-250; 251-329; 330-337; 338-417; 418-420; 421-423; 424-690 |
| 17’ | 5-86 | 87-250; 330-337; 338-417; 418-420; 421-423; 424-684 |
Monomers are marked with ‘m’ after their length.
The transformation fitting this fragment is applied to the entire molecule
Each fragment is fit by an individual transformation, not applied to the rest of the molecule;
In some lines the listed fitted fragments do not cover the entire sequence; the gaps indicate fragments that were accurately placed in the initial fitting and no subsequent individual fitting led to a significant improvement.
transformation identical to 8’ except dividing fragment 96-104 into 96-100 and 101-104 rigid fragments.
a) Hinge movement with small shear: viral shell protein, 2tbv, molecules A and C
The DDM of 2tbvA2tbvC (Fig. 1a) from Tomato Bushy Stunt Virus shows two mostly black triangles (2-164 and 174-286), which are likely to be rigid fragments (see Methods). In the 1st step we move the entire structure 2tbvC by fitting its rigid fragment 174-286 to the same fragment in 2tbvA as described in Methods. This 1st move does not change the DDM or RMSDD. After moving 2-164 the RMSDD of structure 2tbvA2tbvC becomes 0.43Å, and Δ=3.35%, which are within the coordinate uncertainty threshold. Thus, it is a true simple hinge with about 3.5Å translation and 22° rotation, agreeing with earlier results (6). An additional rigid body fitting of fragment 167-170 reduces the RMSDD to 0.27Å and Δ to 1.11% (Table 1). However, this additional rigid body movement improves the fit already below the threshold of the coordinate uncertainty and, thus, might be unimportant. The total number of rigid body motions for each protein pair is shown in the column before the last in Table 1. (Entries in Tables 1-3 are arranged in order of increasing protein chain length. Thus 2tbv is entry #5). An example of the output of sequential rigid-body fittings is shown in Section 2 of the Supporting Information.
Stabilities of continuous fragments of 2tbvA (Table 3) are depicted in Fig. 3c. It shows that 2tbv has two stable continuous domains, encompassing most of the chain (the exact locations of the most stable fragments are shown in Table 3). However, these two domains do not join in a single stable structure (that would be indicated by a black patch in the top right corner of the SM), suggesting that in a monomer they move independently, as might be required in a virus shell structural protein.
b) Pliers/chopsticks “movements”, entries 6, 7, 9, 16 in Tables 1-3
The DDM 1l3f3tmn for thermolysin apo- to holo- motion is shown in Fig. 4a. The “movement” is a simple pliers because the substrate is grabbed without the ‘jaws’ of the active site closing upon each other, forming a new contact, and because the δ of the CDDM does not indicate any shear motion.
Fig. 4.
- DDM 1l3f3tmn: for notations see Fig. 1; helices and b-strands are marked in three DDM’s borders; ticks on the left and top are at 20 residue distance, some residue numbers are provided alongside the ticks when helpful.
- A white horizontal line is drawn in the same DDM right under all white spots; intersecting this line at the diagonal a white vertical line is drawn up; These two white lines form borders of two mostly black (no white spots) triangles which might change their position as rigid bodies in function-related conformational transitions.
- Wire superposition of 1l3f (black) and 3tmn(gray) by fragment 127-316.
- SM for 1l3f; for notations see Fig. 3c.
The location of nearly black triangles in the DDM is shown in Fig. 4b. We draw a horizontal white line just below the cluster of white spots in the DDM and then a vertical white line from the intersection of the horizontal line with the DDM’s diagonal. This yields two mostly black triangles behaving as rigid fragments, 1-126 and 127-316 (in agreement with ref. (46)), in the function-related conformational transition (“movement”). We superimpose fragment 127-316 and apply the transformation to the entire holo-structure; then we fit fragment 1-126. After these two transformations the RMSDD falls to 0.36Å and Δ to 0.73%. The translation of the center of mass of 1-126 is 1.3Å and rotation around the axis passing through this center is 6° (almost the same as the 5° reported in Ref. (46)). It is clear from Fig. 4c that the white spots in the DDM represent not local distortions but a systematic, albeit not large, difference between the apo- and holo-structures. We could instead draw a vertical white line to the left of the cluster of white spots in the DDM of Fig. 4a, and then draw the horizontal line. This would lead us to the mostly black triangles for domains comprised of residues 1-148 and 149-316 (not shown). The first fragment also corresponds to the stable domain (Table 3). Using this fragment for the initial fitting followed by the fitting of the second fragment leads to very similar results, possibly indicating a non-uniqueness of the pathway for this functional conformational change.
In contrast to 2tbv, 1l3f has not only stable domains (agreeing reasonably well with the CATH assignment), but a highly stable entire structure including all residues 1-316 (see large black spot in the top right corner of Fig. 4d and Table 3). Interestingly, a comparison of the stabilities of the fragments of apo- and holo-thermolysin (entry #6 in Table 3) suggests that the stabilization from the protein chain alone significantly decreases upon substrate binding, this loss possibly being traded for the stabilization provided by the protein-substrate interactions and perhaps by the accompanying oligomerization suggested by PQS (41).
DDM 4ape5er (endothiopepsin) is shown in Fig. 1a; DDM 1hrd1bgv (glutamate dehydrogenase) and rigid body movements of its fragments were discussed in detail in Ref. (10). The DDM of 1hrd1bgv (Fig. 12a’ below) is similar to that for 2tbv (Fig. 1a), with three vertical white strips added (for details see ref. (10) and Tables 1-3). The DDM for 2gd11gd1 (glyceraldehyde dehydrogenase) can be found in the Supporting Information (Fig. S1).
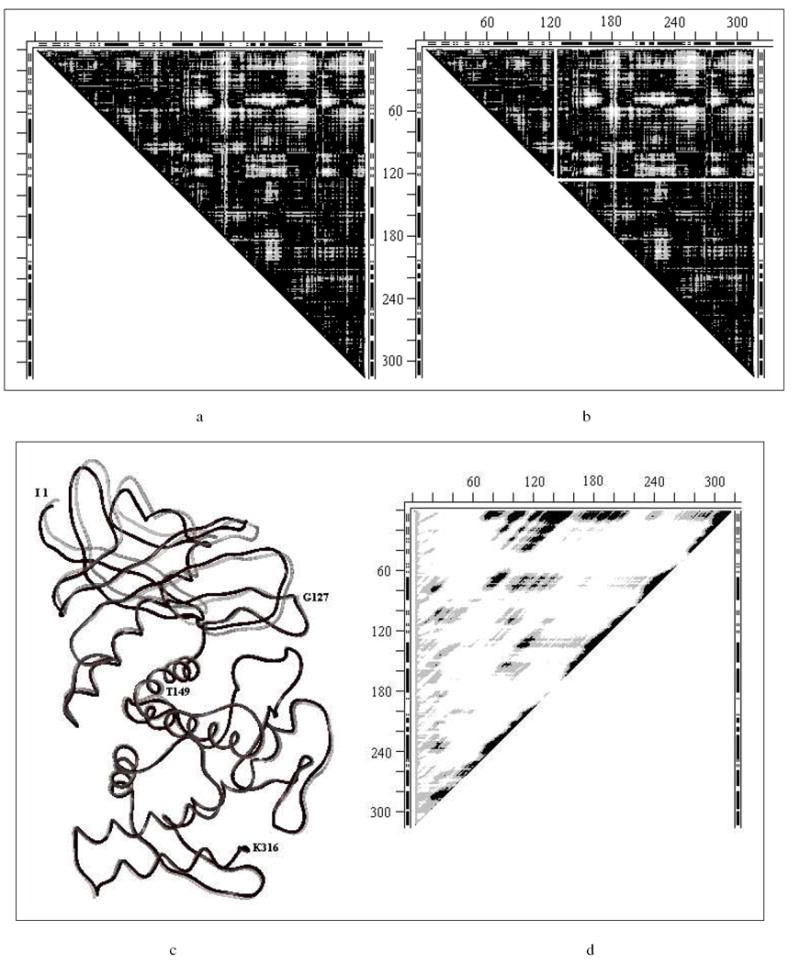
Fig. 12.
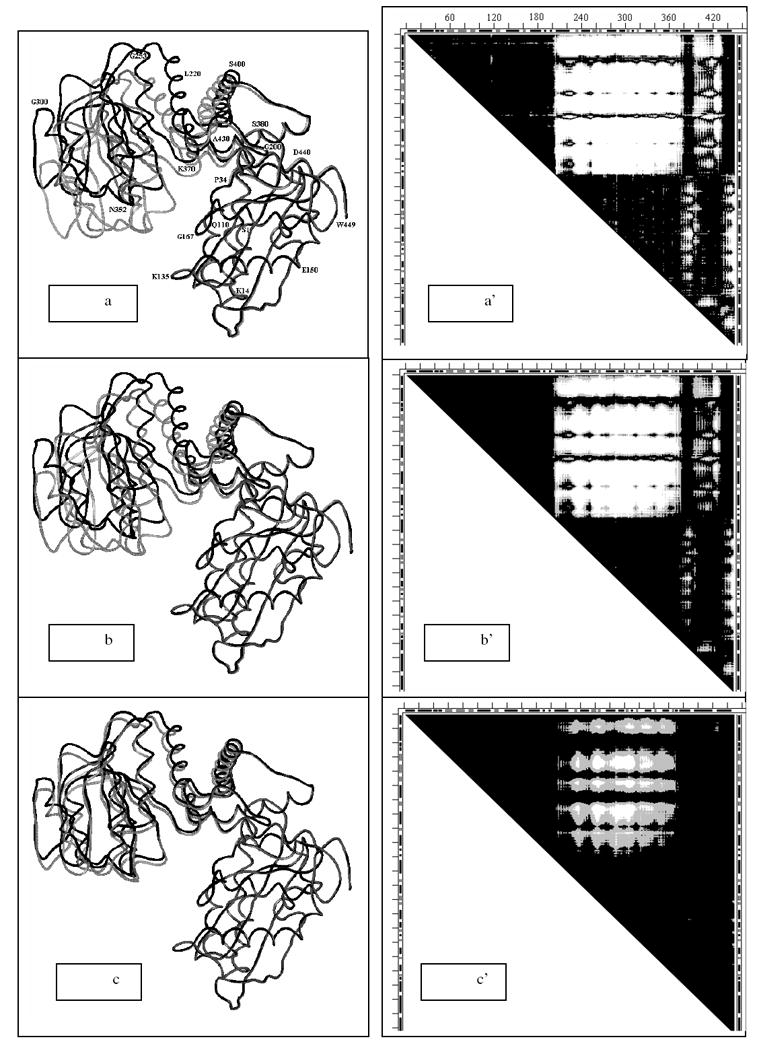
a-c. Three snapshots (#1, #40 and #80 out of 100 total) from elastic coarse grained dynamics movie of the motion pathway of Glu dehydrogenase for each of conformation 1bgv (gray) changing into 1hrd (black) which is completed in snapshot #100). In all snapshots rigid fragments 1-204 are superimposed. Residue numbers (on ‘a’ only) directly refer to the black wire (1hrd) and only approximately to the nearby gray wire (1bgv).
a’-c’. Three DDM-s 1hrd1bgv where conformation of 1bgv is taken to correspond to the three snapshots (#1, #40 and #80) from Fig.14a-c. DDM for snapshot #100 would be completely black because 1aam would completely change its conformation to 1hrd.
These three proteins have stable domains but no stability for the entire molecule. Details of calculated fragment stabilities can be found in Table 3. Locations of predicted stable domains are in a reasonable agreement with CATH. Sequences of rigid fragment movements transforming each holo-structure into the corresponding apo-structure within coordinate uncertainty limits are listed in Table 2.
DDMs of 4ape5er2 (Fig. 1b) and 2gd11gd1 (Fig. S1) are quite similar in their general appearance to DDM 1l3f3tmn (Fig. 3a) and require as simple rigid body transformation. They all have low RMSDDs and Δs (0.46, 3.35; 0.49, 6.16; 0.45, 5.41) just above the coordinate uncertainty thresholds (<0.46 and < 5). PQS suggests that 5er2 undergoes dimerization, 2gd1 and 2gd2 are tetramers, while 1hrd and 1bgv are suggested to be hexamers. There are some differences (10) for 1hrd1bgv between the rigidly moving fragments (Table 2) and domains (Table 3).
c) Tweezers movements, entries 1, 2, 4, 8, 11, 12, 17 in Tables 1-3
The DDM for calmodulin (1cll1ctr) (Fig. S2a) resembles the DDM of 2tbv (Fig. 1a). However, its CDDM (Fig. S2b) shows formation of new long-range contacts (enclosed in small rectangles), which leads us to classify this movement as tweezers, more shear than 2tbv, and the largest RMSDD despite being the smallest structure (Table 1). Stabilities of calmodulin fragments are marginal (as well as of the entire molecule) and their localization is in a reasonable agreement with CATH (see Table 3). After the first two rigid body fittings (Table 2) the RMSDD drops from its initial value of 12.83Å to 1.17Å and after further fittings it drops to 0.85 Å. However, residues 1-2 at the N-terminus, 138 at the C-terminus and residues 71-73, around the fragment without reported structure, move incoherently (they are not parts of any black triangles indicating a rigid block). After their deletion from the structures compared we obtain RMSDD=0.44Å, Δ=2.7%. Note that N- and C-terminal residues often stick out and away from the rest of the monomeric structure and do not contribute to its stability, as well as the visible ends of some loops that are not visible in the crystal. We usually delete these in our comparisons.
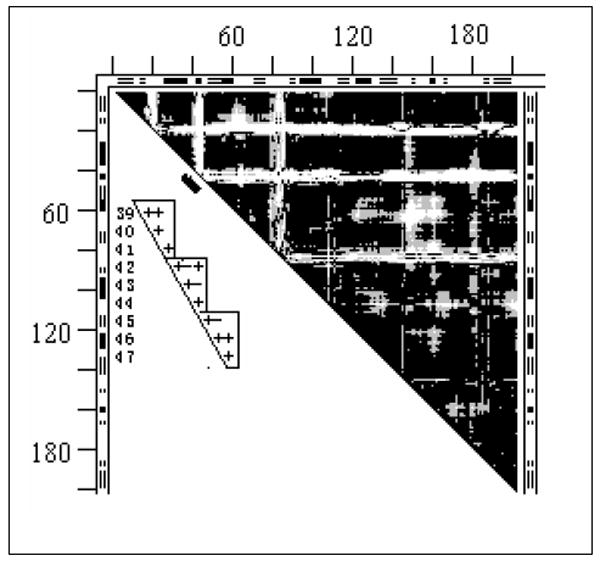
DDM of the tweezers 4cd21cd2 (dehydrofolate reductase, Fig. 5) presents a black-and-white pattern different from all previous DDMs. Instead of large white spots on a black background it shows a series of rather wide (up to 10 residues) L-shaped bands with their right angle bends touching the diagonal. These diagonal-touching areas have twisted borders often requiring more than one small rigid body to be fitted as is shown by three triangles in the insert from a larger DDM (see Fig. 5). Note that there are a few white spaces within these triangles. However, the rigid body fitting of each fragment corresponding to these triangles yields an RMSD of below 0.4Å, suggesting that one should check how bad are effects of a few white DDs in a triangle for the fitting. Except for these L-shaped bands and a few white spots or bulges on the bands’ edges, the DDM is rather black. Results of the series of fittings are listed in Table 1 and their sequence in Table 2. This tweezers motion also has some shear. Its entire structure is not stable but it has a marginally stable fragment. There is no agreement with the CATH domain assignments.
Fig. 5.
DDM 4cd21cd2 (dehydrofolate reductase). For notations see legend to Fig. 1.
The insert shows the 39-47 fragment of the same but larger symbol coded DDM with + for black, - for gray and space for white; this fragment is marked with short thick black line along the part of the diagonal of the bitmap DDM occupied by the corner of the second L-shaped band.
The DDM of tweezers 1akz1ssp (DNA-uracil glycosylase, Fig. S3) appears like an enhanced version of the pliers DDM 2gd11gd1 in Fig. S1. The number of white spots is greater and they are larger in size. There is also one relatively narrow L-shaped band. The pair allows a rigid body fitting within coordinate uncertainty (Tables 1 and 2). The molecule has a marginally stable whole apostructure, with the stability significantly increasing upon the substrate binding. The single stable domain agrees with CATH (Table 3). Binding, according to PQS, is accompanied by trimerization.
The next tweezers DDM represents a milestone in the studies of protein functional motions (4) where it was suggested that a hinge at residues 96-100, another hinge at 105-110 and a kink around residue 119 produce one large motion in lactate dehydrogenase.
The DDM 6ldh1ldm (lactate dehydrogenase, Fig. 6a) transparently translates these suggestions into the terms of our methodology allowing some improvements. This DDM resembles the DDM of 4cd21cd2 (Fig. 5) and is characterized by similar large numbers (7 to 10) of rigid body transformations and the maximum movements magnitudes (Table 1). The five C-terminal residues do not form a rigid fragment (no black triangle at the bottom of the diagonal). If we exclude them from the DDM then its RMSDD drops from 1.35Å (Table 1) to 1.25Å.
Fig. 6.

- DDM 6ldh1ldm (for notations see legend to Fig. 1). The insert shows the 96-121 fragment of the same but larger symbol coded DDM with + for black, - for gray and space for white; this fragment is marked with short thick black line along the part of the diagonal of the bitmap DDM occupied by the corner of the largest L-shaped band.
- SM 6ldh (for notations see legend to Fig. 3c).
- Wire superposition of 6ldh and 1ldm by the fragment 3-95. Residue numbers directly refer to the black wire (6ldh) and only approximately to the nearby gray wire (1ldm).
Three major white areas in Fig. 6a are two L-shaped bands, the top one of them being rather thick, and a ragged vertical band on the right edge of the DDM. The hinges and the kink described by Gerstein and Chothia (4) can be seen as two small overlapping black triangles at the corner of the L-shaped band and one more right under it (the top small triangle has a short intrusive white line, visually interrupting it). The first four rigid motions (including the initial one) reduce the RMSDD to 0.64Å. This constitutes a major part of the decrease in the RMSDD towards the threshold of coordinate uncertainty. The following rigid transformations (Table 2, lines 8, 8’)) yield the RMSDD and Δ for the entire molecule (Table 1, lines 8, 8’) within the coordinate uncertainty threshold. However, the fit of the fragment 96-104 (an important part of the active site “lid”) is rather poor with the RMSD of 0.99Å. The center of mass of this fragment translates 5.7Å and then the fragment rotates by 36°. The insert in Fig. 6a shows details of the DDM for fragment (96-121). It shows that the line for residue 100 contains three white spaces out of five DDs in the triangle 96-104. This suggests dividing it into two triangles: 96-100 and 101-104, which have no white DDs at all. The RMSDs for these two fragments drop to 0.79 and 0.36Å, with centers of mass translations of 2.5 and 9.8Å, and rotations of 21° and 60°, respectively. Analysis of Fig. 6c shows that while the black loop 101-104 is rather flat, its gray counterpart shows a significant upward curvature. Transforming 96-104 as one (the loop assignment in Table 1 of Ref. (4)) or two (96-100 and 101-104) fragments, reflecting this curvature, leads to a 1.2Å difference (out of the total 11.9Å) in change of the position of atom Cα103 in 6ldh to 1ldm conformational transition.
A comparison of the DDM in Fig. 6a and the residue numbering along the wire structure in Fig. 6c reveals that all movements of the fragments indicated in the DDM are coordinated with the “movement” of loop 96-121 through direct interactions of these fragments with this “moving” loop.
6ldh and 1ldm do not possess stability of the whole molecule (Fig. 6b), which might be unimportant if the biological molecule is a tetramer, as suggested by PQS (see also Discussion). However, both structures exhibit four stable fragments (black areas in Fig. 6b). Table 3 lists the locations of only the most stable fragments. Rigidly moving fragments (Table 2) are not stable. This occurs in a majority of proteins. Note, that two CATH domains lump together two stable fragments each (Table 3).
The DDMs of 8adh6adh (Fig. S4) and 9aat1ama (Fig. 11a’) have somewhat similar vertical stripes on their right sides, and Fig. S4 also resembles Fig. 12a’, which has an upper group of white spots coalesced into a solid rectangle. 6adh can be transformed by a series of rigid body movements into 8adh (Tables 1-2). PQS suggests that 8adh and 6adh are dimeric biomolecules (Table 1). 8adh and 6adh are both moderately stable as a whole and also have stable domains. There is no agreement between the locations of the stable fragments and the CATH domain assignments (Table 3).
Fig. 11.

a-c. Three snapshots (#1, #40 and #80 out of 100 total) from elastic coarse grained dynamics movie of the motion pathway of Asp aminotransferase for each of conformations of 1ama (gray) changing into 9aat (black), which is completed in snapshot #100. In all snapshots rigid fragments 228-305 are superimposed. Wire rendering is done with MOLE (G.P. Privalov, gpriv@axonx.com); Residue numbers (on ‘a’ only) directly refer to the black wire (9aat) and only approximately to the nearby gray wire (1ama).
a’-c’. Three DDM-s 9aat1ama where the conformation of 1ama is taken to correspond to the three snapshots (#1, #40 and #80) from panels a-c. DDM for snapshot #100 would be completely black because 1aam would completely change its conformation to 9aat.
The conformational transition 9aat1ama was described in detail in Ref. (10) (see also Tables 1-2). PQS suggests that both 9aat and 1ama are biological dimers (Table 1). Neither 9aat nor 1ama are overall stable folds, but have two stable domains that agree reasonably well with two out of the three CATH domain assignments (Table 3).
The largest structural pair we have studied is 1lfh1lfg, and it also undergoes tweezers motion (Fig. 7). The sequence of moving rigid fragments, fitting structures 1lfh and 1lfg of lactoferrin, are listed in Table 2. Removing the 4 N-terminal and 1 C-terminal residues from the final DDM leads to a DDM having characteristics within coordinate uncertainty threshold (Table 1). A less accurate fitting and the removal of the 7 C-terminal residues lead to fitting within the threshold but close to its limit.
Fig. 7.

DDM 1lfh1lfg (lactoferrin). For notations see legend to Fig. 1.
This large protein does not exhibit stability for the entire folded chain even with the large number of stable fragments additionally stabilized by its 16 S-S bonds (Table 3). Two continuous CATH domains agree well with two of the stable fragments while the two discontinuous CATH domains do not (Table 3). PQS identifies lactoferrin as monomeric.
An important lesson from the DDM 1lfh1lfg fragment 90-250 is that there is no principal difference between L-shaped bands produced by the movements of loops and large fragments in the middle of the chain: the difference is just in the thickness of the band (in 1lfh1lfg the triangular corner of the L-band happens to be rigid, but this is not proven to be a general rule).
d) glove movement, entry 15 in Tables 1-3
The first glove DDM 4cts1cts for citrate synthase, analyzed below, also represents a milestone in the studies of protein functional motions (3) that has been repeatedly described (3, 6, 47-48). It was suggested that the functional movement in citrate synthase involves small shifts and rotations of five packed helices (shear) in the small domain (res. 272-387) accumulating into a 10Å shift and 28° rotation relative to the rest of the protein. It was also suggested that the large interface in the biological dimer precludes having simple hinge motions in this protein.
White areas in the DDM of Fig. 8 indicate significant conformational changes within the small domain as well as its “movement” relative to the rest of the structure. Twelve rigid body movements in the small domain alone do not reduce its RMSDD below 0.54Å or Δ below 6.33% because deformations of helices and loops result in relatively short fragments with poorly retained geometry. The RMSDD of 0.61Å was obtained for the untransformed large domain (with the small domain and the five N-terminal residues excised from the structure). Thus, even the ‘large domain’ undergoes significant conformational changes beyond the coordinate uncertainty. All attempts to fit the entire holo- to the apo-form by rigid body movements do not lead to an RMSDD below 0.67Å, meaning that we have to classify the citrate synthase conformational change as a glove motion with large shear and tweezers closure.
Fig. 8.
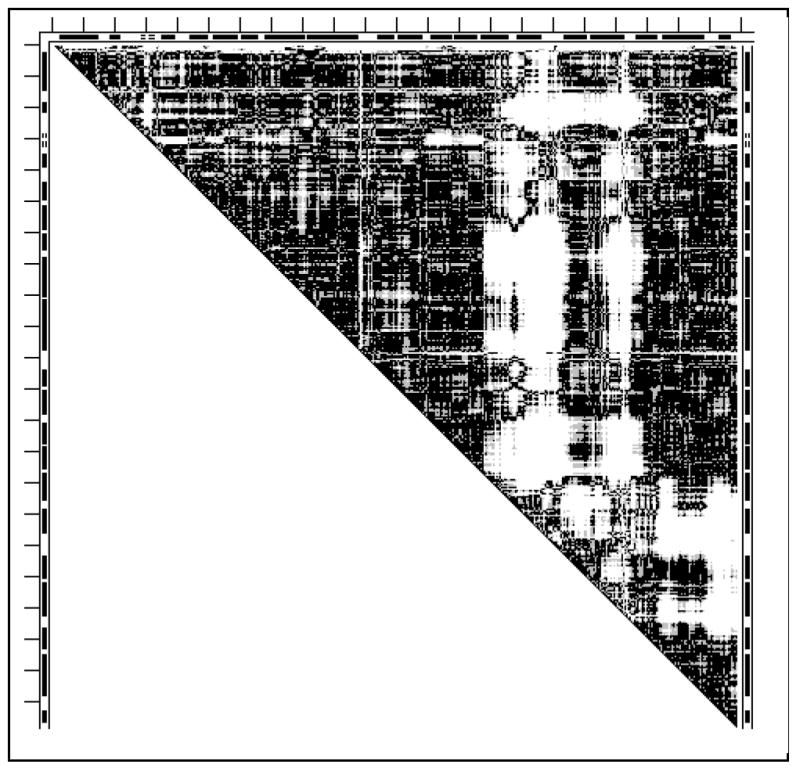
DDM 4cts1cts (citrate synthase). For notations see legend to Fig. 1.
The stabilities of fragments of un-liganded (4cts) and liganded (1cts) citrate synthase are listed in Table 3. Small domains formed by 5 helices (res. 274-386) are stable in both 4cts (-4 kcal/mol) and 1cts (-6 kcal/mol) as well as almost the entire structure including residues 51-415, out of 1-437. Calculated stabilities are 4cts (apo) -5 kcal/mol, 1cts (holo) -2 kcal/mol. Thus the substrate binding is accompanied by the destabilization of the entire (residues 51-405) protein and some stabilization of the small domain. This suggests that the destabilization of the entire protein chain upon this binding can probably be compensated by the binding free energy which has not been included in our calculations. Furthermore, citrate synthase is a biological dimer and dimerization may provide additional stabilization. Thus the stability redistribution is somewhat different in citrate synthase compared to thermolysin. However, in both cases ligand binding seems to destabilize the largest most stable part of the monomer possibly storing energy for throwing out products.
However, in contrast to thermolysin, we cannot say that stable domains move as rigid bodies in the functional conformational change of citrate synthase. A stable small domain of citrate synthase is not rigid but changes significantly through shear, and the other part, usually termed ‘a large domain’, is unstable by itself and also undergoes significant internal deformations (also see Discussion).
e) glove movements in kinases: entries 3, 10, 13, 14 in Tables 1-3
In humans about 1.7% of all genes encode protein kinases (49) and about half of them map to disease loci (49). Thus it is of special interest to look at some typical functional motions in a few kinases (including an example of less numerous nucleotide kinases).
The DDM 1erk2erk (Fig. 9a) of signal regulated kinase resembles the DDM 6ldh1ldm (Fig. 6a) of lactate dehydrogenase and the DDM of 4cd21cd2 of dehydrofolate reductase (Fig. 5) all showing a number of L-shaped bands. The major difference is that the number of such bands is larger in Fig. 9a and the corner of the largest of them at the DDM’s diagonal does not have small overlapping black triangles responsible for the largest group of rigid body moves seen in Fig. 6a for lactate dehydrogenase. In kinase (Fig. 9a) this corner of the white L-band represents a large non-rigid conformational deformation. A similar lack of small black triangles, representing short rigid segments, in other white corners of this DDM adds to the number of parts undergoing non-rigid deformation during the functional movement. This resembles a schematic case in Fig. 2a. As a result, we could not find a series of twelve or fewer rigid body transformations that would convert one functional conformation of this kinase, 2erk, to the other, 1erk (Table 1). Neither 2erk nor 1erk possess stability for the entire structure, but both have three moderately stable fragments. Their positions in the chain do not agree with the CATH domain assignments (Table 3).
Fig. 9.
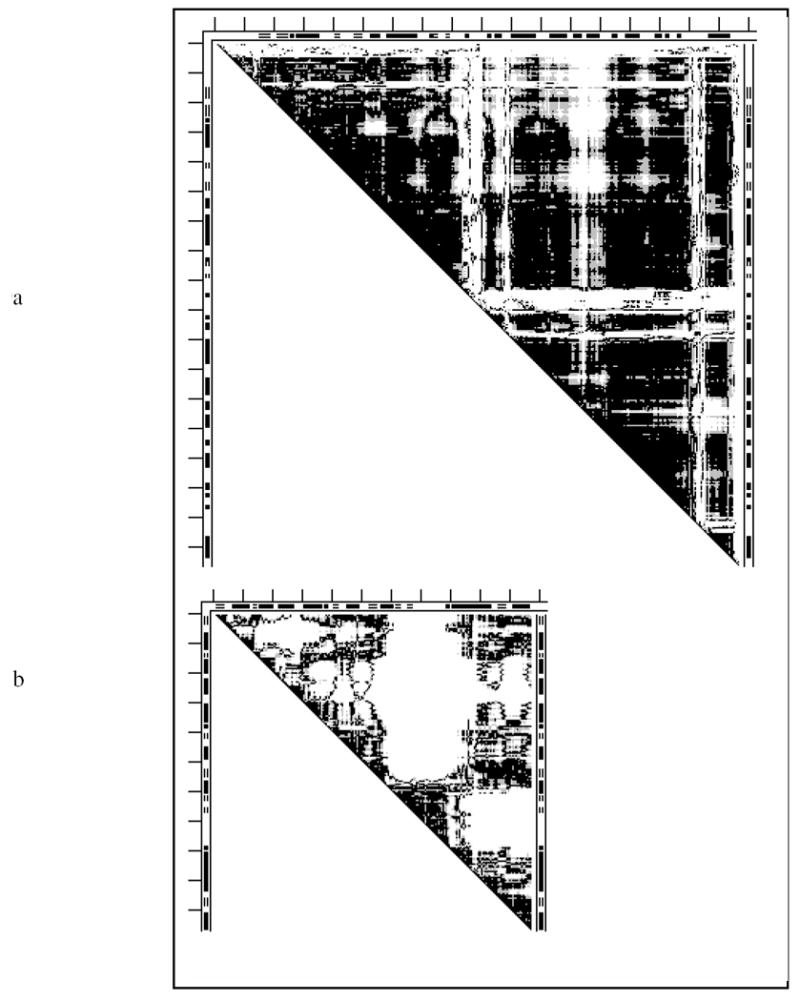
DDMs for two kinases: a) 1erk2erk (signal regulated kinase); b) 4ake1ank (adenylate kinase) For notations see legend to Fig. 1.
The DDM 4ake1ank (Fig. 9b) of adenylate kinase exhibits a complex irregular shape of white patches, with many small and only a few larger black triangles along the diagonal. These predominant small black triangles (short rigid segments) resemble the idealized Fig. 2b. In some places there are white areas along the diagonal, which correspond to non-rigidly deforming chain segments. Both factors make it impossible to transform 1ank into 4ake within the coordinate uncertainty threshold with twelve or fewer rigid body motions.
The apo-structure 4ake shows three marginally stable folding domains (Table 3) that do not include a significant part of the protein chain, and only one of them is present in the holo-form 1ank. The entire folded protein chain is unstable. The stable fragments in 4ake or 1ank do not agree with CATH domains (Table 3).
The DDM 16pk13pk of phospho-glycerate kinase (Fig. S5a) shows two rather solid large black triangles suggesting the presence of large rigid blocks. However, the predominantly white area beyond these black triangles has a rather complex structure with white areas touching the DDM’s diagonal somewhat similar to the DDM in Fig. 9b. Attempts to transform 13pk into 16pk within coordinate uncertainty by over a dozen rigid-body movements failed.
The SM of 13pk (Fig. S5b) shows a very stable entire holo-structure, together with very stable N-terminal and C-terminal folding domains formed by about a half of the protein chain each. However, the stability of the entire bi-substrate 16pk is only marginal (Table 3). PQS suggests that the bi-substrate form is monomeric and the holo-form is tetrameric. No PGK from a particular organism has been crystallized in both the apo- and holo-form. Location of stable fragments is in good agreement with the CATH assignments.
The DDM 1v4t1v4s of glucokinase (Fig. 10a) indicates a highly flexible glove movement as in adenylate kinase. Attempts to transform 1v4s into 1v4t within coordinate uncertainty by over a dozen rigid-body movements failed. The SM of 1v4t (Fig. 10b) shows only a relatively short stably folded fragment (Table 3) in a PQS predicted monomer with the remainder of the structure being unstable and thus mobile. For this protein simple mechanical analogs for a description of the functional “movement” seem to be lacking. A possible fitting analogy might be a ‘boa movement’ (boa is a genus of snakes folding around a target to constrict it). Location of stable fragments does not agree with the SCOP domain assignments.
Fig. 10.
While the four kinases studied above indicate non-rigid functional movements, this may not be the case for all kinases. Our preliminary results for the small protein guanylate kinase (186 residues) indicate that the apo-form 1ex6 can be transformed to the holo-form 1ex7 with 10 rigid body movements.
2) The coarse-grained modeling of protein dynamics and DDMs
It is often quite difficult to clearly identify in a static picture the local differences between two conformations of the same protein even if they are superimposed on the basis of the RMSD fit. Overcoming this difficulty was one of motives for developing “morph” movies of protein motions: human eyes see movements more readily than static differences. However, static pictures are preferable in a print. Therefore, we compare three snapshots from a coarse-grained movie of the motion pathway (25) for each of two protein pairs 9aat1ama and 1hrd1bgv in two forms: a) superpositions of the reference wire apo-structure and the wire structures in the snapshots, and b) the DDMs corresponding to these reference-snapshot structural pairs. The generation of the DDMs and the required (initial) superposition of two conformations of the same protein are performed as described in Methods.
Conformations from snapshots #1, #40 and #80 were chosen for each protein to compare with the reference conformation of the corresponding protein. Because we have fit large rigid fragments of the two structures and have carefully chosen the viewing orientations of the pairs, it is possible to see some differences on the left side of the structure in Figs. 11a-c. They, however, would be difficult to detect in many other projections. Because of the intricacies of the chain fold it may also be difficult to assign these changes to positions along the chain. At the same time the DDMs show easily identifiable changes in the intensity and shape of the non-black areas of Figs. 11a’-c’. These changes can also be easily projected on the sequence and secondary structure marked on the DDMs, and we used this to choose the residue numbers labels for the wire structures. This is also the case for changes noticeable on the left side of the snapshots in Figs. 12a-c and the corresponding DDMs in Figs. 12a’-c’. In 9aat1ama the N-terminal fragment 14-36 folds onto the C-terminal domain and in 1hrd1bgv the C-terminal fragment 432-449 folds on the N-terminal rigid fragment.
It should be noted here that white in the DDMs indicates only that DDs in two structures differ by more than 1Å. Thus many changes within these spots are not visible. A development of the movement can be shown in a single cumulative MDDM (Movie DDM) by painting in different colors those areas that become white at different stages of the simulation. In a movie it might be useful to show the wire structural superpositions and DDMs (like Figs. 11a’-c’ or 12a’-c’) or MDDMs side-by-side for each snapshot with a possibility of pausing both pictures at any frame.
DISCUSSION
Utility of objective thresholds and DDMs
Results presented in this work depend on the values of the coordinate uncertainty thresholds within which we consider two structures to be identical. We derived these values in our previous work (10). Currently this provides us with useful objective thresholds. It is quite remarkable that the range of coordinate uncertainties, derived by using this set, does not overlap but just borders the range of similarly measured coordinate differences for function-induced protein coordinate changes. While these thresholds might change somewhat upon further use, we have shown here that currently they can serve as reasonable guidelines.
One of these two thresholds, RMSDD, is slightly below 0.5Å, which is taken by us as the threshold value for DDs with smaller values to be colored black in the DDMs. The second threshold, Δ, reflects the number of DDs larger than 1Å. We color DDs between 0.5Å and 1Å gray, and above 1Å white in the DDMs. Such DDMs, as shown above, facilitate the easy identification of protein fragments that undergo conformational transformations as rigid bodies. A slightly more careful analysis of the DDM allowed us to easily improve the accuracy of the original (4) description of the conformational change in the functional loop 96-121 of lactate dehydrogenase, resolving four instead of two rigid fragments. This has led to the non-negligible 1.2Å difference in the position of Cα103 near the active site. The more accurate positioning is due to the use of new techniques (10) allowing much easier and transparent identification of rigid fragment “movements” than previous techniques (e.g., compare to Fig. 3 of ref. (4)). Finding that the functionally important loop 96-121 consists of four rigid fragments also challenges a popular perception of a loop usually acting as a solid “lid” (1). In fact, very often loops do not have any rigid sub-structures but “move” in a flexible fashion, rather like wet rags thrown on to cover some part(s) of a protein (e.g., as we have seen in the kinases studied here).
What should be considered “a very flexible structure” or “a major movement”?
The article on movements in adenylate kinase (50) refers to it as “a highly flexible protein”, based on the large amplitude of the domain motion of about 30Å. Maximum DDs agree rather well with higher RMSDD but might lead to some confusion when related to the number of rigid body motions required for transforming one of the structures into another (Table 1). The latter, however, directly shows how many chain fragments move while retaining their internal structure. It is obvious that a cabin with a door swinging on a hinge, even with large amplitude, is less flexible than caterpillar tracks, which in turn are less flexible than a bicycle chain, which is less flexible than a rope. This implies that flexibility increases with the number of rigid fragments and decreases with their size and might require some scaling of the cutoff number of rigid body movements based on protein size. We have used a uniform cutoff of 12 movements, but we tried up to 20 movements for a few large proteins, finding that the transformations were still unable to superimpose two structures within the coordinate uncertainty threshold. The accumulation of more experience and understanding may eventually answer this question and facilitate an automation of the fitting process.
Functional “movements” in proteins are often described in the literature as “mainly hinge” or “mainly shear” (5-6). Classifications into “major” and “minor” movers were also used (4). One might be legitimately interested not in all details but only in a “major” component of a functional movement. However, it is often difficult to unambiguously define what is “major”. Is it a movement of the “rigid” fragment with the largest number of residues or perhaps a movement of a shorter fragment over a longer distance? There could be also various “weighted” combinations of these and other criteria. One question easily answerable with our methodology would be: What movements are required to make all DDs smaller than 2Å? Changing this threshold is easy and might provide useful information. From what we have seen though this would obscure and exclude from a determination the functional “motion” found in thermolysin (46) with the maximum DD of 1.8Å as well as introduce chain breaks of up to 2Å.
Protein stability and compactness of X-ray structures
It is clear that in order for a protein to be compact it must be stable, otherwise it would have many alternative conformations which would require a larger volume to accommodate all of them. Because we ignored interactions with substrates or cofactors and between subunits in oligomers, that can provide important stabilization, we considered compactness only for monomeric apo-proteins. We should also recall the significant simplifications in these calculations, and therefore realize that our estimates of stability may require more validation against available experimental data.
In our set of 17 proteins (Tables 1-3) 10 proteins: 1cll, 4cd2, 4ank, 1akz, 1l3f, 4ape, 1erk, 16pk, 1v4t and 1lfh, do not form oligomers in their apo-form crystals according to PQS.
1l3f (thermolysin) is the most interesting among the other monomeric apo-proteins in our list (Tables 1-3). It has a high calculated stability of the entire protein (-18 kcal/mol) which is very likely to be beyond the inaccuracy of the method. Therefore thermolysin is likely to be compact in solution. However, it is also noted that apo-thermolysin crystallization required Zn ions (46), and it is not clear what their role is in stabilizing the structure. The high B-factors in the apo-thermolysin 1l3f do suggest some residual movement in the crystal (46).
Another interesting feature of the calculations for thermolysin is a 15 kcal/mol drop in the stability of the entire protein chain upon substrate binding (1l3f→3tmn). This is likely to be beyond any possible errors. Calculations for another holo-structure of thermolysin (8tln) yield results within 2kcal/mol. This is suggestive of a mechanism in which substrate binding energy is stored in a strain (destabilization) of the protein that might subsequently be used for the ejection of the reaction product. Certain confidence in our method comes from its use for predictions of stable domain and subdomains in thermolysin (18), which were then successfully isolated and characterized confirming the predictions (35,50).
Of the first four of apo-monomers only one, 1akz, has a marginal stability. The increase in stability by 8 kcal/mol in the holo-form may still lie within the largest possible error bounds of the method, however the sign of the change suggests that the apo-monomer is stable and, thus, compact. The other three monomeric proteins have marginally stable domains, within the method’s error bounds, but instabilities of the entire structures for these are worse than +10 kcal/mole. We can safely infer that it is rather unlikely that these monomers are stable and compact. They might be stabilized by the crystal structures. After the substrate binds they can be stabilized by the binding energy. This suggests that these proteins are either incompletely folded or have domains moving independently in solution before they recognize and then bind substrate. Note that adenylate kinase exhibits three marginally stable substructures in the monomeric apo-form 4ake and only one in the holo-form 1ank. This may suggest that intrachain contributions to protein stability might be traded for stabilization by substrate binding. This “stability trade-off” resembles the hypothesis of “energetic counterweight balancing” for storage of the substrate binding energy in adenylate kinase by shifting the region of higher mobility in the catalytic cycle (52). Mobile sites were located (52) according to the B-factors and cannot be straightforwardly related to the change in domain stabilities. However, it is encouraging that we find a similar effect despite its small magnitude (Table 2). A similar but larger stabilization trade-off was seen above in thermolysin.
Three apo- monomers (4ape, 1erk, 1v4t) do show the instability of the entire protein above +10 kcal/mol, with two (4ape and 1v4t) showing rather stable folded fragments, and one (1erk) – not so stable (-2 to -5 kcal/mol). Thus, they are unlikely to be compactly folded in solution.
Monomeric 16pk has hardly stable (+3 kcal/mol) structure. However, it is not a fully “open” apo-form but some intermediate conformation. A fully “open” apo-form from another organism (1vjd) also shows only marginal stability of -2 kcal/mol. Attempts to crystallize both fully “open” and “closed” structures from the same organism were not successful. Reported experimental domain stability studies indicated that the C-terminal domain is more stable than the N-terminal one (20). While our calculation may overestimate the stabilities of these domains, they show that the C-terminal domain is significantly more stable than the N-terminal one for both 16pk and 1vjd in close agreement with the experiment.
The largest monomeric protein in our set, 1lfh, is strongly stabilized by 16 disulphide crosslinks. However, even accounting for that does not reveal any stability for the entire molecule. As with many other proteins not exhibiting stability of the whole molecule it seems likely that its domains move freely relative to one another until they catch a substrate (and/or cofactor) that stabilizes the entire protein. For oligomeric proteins such stabilization might also be provided by intersubunit interactions. Thus, 9 out of 10 monomeric proteins studied here seem to be either only marginally stable or have folded stable substructures that are mobile in the apo-form. This would enhance substrate access to the active site.
For non-monomeric apo-proteins (2tbv, 6ldh, 2gd1, 8adh, 9aat, 4cts and 1hrd) it is impossible to infer compactness based on stabilities calculated for monomers because of the lack of clarity in treating the thermodynamics of protein binding and association. For small molecules binding and association depend on the concentration and thus on the loss of rotational and translational entropy. It was estimated (53) that dimerization of a protein should cost about 15 kcal/mol in lost entropy, according to classical theory for small molecules. However, it was noted (19) that proteins do refold after being cut into two or three parts. This would supposedly cost 15 to 30 kcal/mol in lost translational and rotational entropy of independent fragments and thus prevent folding into a stable structure, which without cuts usually has stability of less than 15 kcal/mol. This paradox was experimentally supported by calorimetric measurements of the unfolding and dissociation entropy of a homo-dimeric protein and of its mutant with covalently linked monomers (54). The entropies were practically identical in both cases, demonstrating that classical entropic terms do not play any role in protein association.
However, experimental studies of subunits and fragments of lactate dehydrogenase (20) allow some comparisons with our stability calculations for subunits of this tetrameric protein. The dimer-of-dimers structure of this protein is stabilized by the N-terminal decapeptide of each of the subunit polypeptide chains. After cleaving off this decapeptide, a metastable ‘proteolytic dimer’ is obtained, which shows anomalously high flexibility and gains enzymatic activity only in the presence of structure-making salts. The monomer shows a native-like structure, accessible only as a short-lived, proteolytically sensitive kinetic intermediate on the pathway of reconstitution. The separate NAD- and substrate-binding domains are unstable, but still sufficiently structured to recognize one another and to pair correctly. Upon joint reconstitution, they form active, nicked dimers. However, renaturation of the separate domains and subsequent mixing is unsuccessful. Thus, domains may assist each other in advancing to their native structure by mutual stabilization through specific interactions.
Our calculations for 6ldh show four stable fragments which do not include the N-terminal decapeptide. Each of two CATH domains includes two of these four stable fragments. However, the first pair of stable fragments is calculated to form a larger folded fragment with a doubtful stability of 0 kcal/mol, corresponding to a usually assigned lactate dehydrogenase N-terminal domain. The second pair shows no calculated stability better than +10 kcal/mole, very strongly suggesting the lack of any stability for the entire C-terminal domain. Thus, results of our stability calculations agree with experimental instability of individual domains having stable subdomains, possibly sufficient for domain-domain recognition, as well as with instability of the monomers.
All of these correlations and agreements with experimental data strongly indicate that our method for calculating the stability of protein fragments can be rather reliably used for arriving at plausible suggestions deserving of further verifications.
Stable fragments, rigidly moving fragments, continuous, discontinuous and CATH domains
Some recent papers identified domains as structural “modules” that move rigidly relative to one another during protein function (21). The number of rigid body motions required to transform the conformation of one functional state of a protein into that of another state is given in Table 1. Numbers of calculated stable fragments for the same protein can be found in Table 3. For all 4 kinases in our set the number of required rigid body motions exceeds 12 while the calculated number of stable fragments is significantly smaller. The situation is similar for 4cd21cd2, 1akz1ssp, 6ldh1ldm, 8adh6adh and 1lfh1lfg, which require from 5 to 11 rigid body movements and have significantly fewer calculated stable fragments. 9aat1ama (entries #12-12’) has only two non-overlapping stable fragments but requires at least 3 rigid fragments for fitting. For 1cll1ctr there is a partial agreement between the marginally stable fragments (Table 3) and localization of rigidly moved fragments. However, some stable fragments are broken into several rigid fragments and an unstable N-terminal fragment moves as a rigid body. For 2tbv, 1l3f3tmn, 4ape5er2 and 2gd11gd1 the agreement is reasonable – they have two to three non-overlapping stable fragments and a similar number of rigid fragments. For the pair 1hrd1bgv the numbers of rigid and stable fragments are either similar (entry #16) or, in a less accurate fit, there are more stable than rigid fragments (entry #16’).
Thus, only for 5 out of 17 proteins do we find reasonable agreement between the rigid independently moving fragments and the non-overlapping stable fragments. This may mean that, just as in one stable domain of citrate synthase, parts of a stable domain can shift significantly without the loss of stability of the entire domain in contrast to the view of full rigidity for folded domains (1). Generally, our results strongly suggest that rigid and stable fragments do not coincide for a majority of cases.
All earlier publications referred to “small” and “large” domains in citrate synthase (47-48,3,6). Interestingly, we found no fragments of the “large” domain having a stability better than 0 or 1 kcal/mol, and these are usually helical hairpins. We repeated stability calculations, excising the sequence (272-389) of the small domain with 2-3 extra loop residues on each side from its structure (unfolded fragments with fixed ends are entropically very destabilizing, see Eq. S3). This led to appearance of a stability of +2 kcal/mol for the “large domain”. Thus the “large” discontinuous “domain” seems to be unstable without the “small” domain and apparently may assemble on its preformed surface. Of course, stabilization by quaternary structure is also possible.
CATH does not agree with continuous stable domains localization for 8adh (see the previous section of Discussion), poorly agrees for 2gd1, lumps together into one domain two stable fragments separated by an unstable loop in 6ldh, two unstable fragments in citrate synthase, 4cts, and in 1lfh, as well as does not agree for the three kinases (4ake, 1erk, and 1v4t). CATH identifies a discontinuous domain corresponding to two marginally stable fragments in 1hrd-1bgv, which might represent a variation of already discussed above discontinuous domain of 4cts. In 1lfh CATH assigns two discontinuous domains, one of which does not include any stable fragments, and another that overlaps only with one such stable fragment. These discontinuous domains might be a kind of “afterthought” in the folding process, when other stable domains can stabilize them, as in citrate synthase. Thus there are significant disagreements between the CATH domain locations and our computed stable domains for 8 out of 17 proteins.
Do large interfaces in dimers preclude hinge motions?
Our results allow to justifiably challenge the earlier idea (3) that the large interface in a dimer precludes simpler hinge or pliers motions in citrate synthase. According to PQS dimerization buries 4170 Å2 of ASA per 1cts monomer and 4600Å2 of ASA per 4cts monomer. 1hrd buries 3924Å2 of ASA per monomer in the oligomerization and 1bgv buries 3946Å2 according to PQS. The RMSDD for 1hrd1bgv and 4cts1cts are also comparable: 1.89Å and 1.58Å (Table 1). Nevertheless, 1hrd1bgv (Fig. 12) is not constrained to undergo its functional movement through a simple pliers mechanism. Judging from changes in the inter-subunit buried area between 4cts and 1cts, the relative monomer-monomer movement is larger in the 4cts to 1cts conformational change, than in the 1hrd to 1bgv conformational transition, where intersubunit buried area practically does not change. In the dimeric 9aat1ama the inter-subunit buried areas per monomer are slightly lower: 3270Å2 and 3500Å2. However, it has the 3rd highest δ (estimating shear) as shown in Table 1. We concluded that 9aat1ama undergoes a functional conformational transition through a rather simple tweezers motion.
Why do proteins with closely related functions exhibit very different functional motions?
There were some previous efforts to understand this (46). However, most efforts were restricted to protein classification based on their not-so-well-defined domain structures (36-37) or to determining whether a function-driven conformational change involves large “hinge” or “shear” motions (6).
There are two protein groups with similar functions each in our study: dehydrogenases and kinases. In both groups we find examples of movements of rigid or stable fragments or domains (e.g., 2gd11gd1, 1hrd1bgv and 8adh6adh for dehydrogenases; 16pk13pk and less clearly for 4ake1ank in kinases), and of mainly loops movements (e.g., 6ldh1ldm for dehydrogenases and 1erk2erk for kinases). The first type of movement is characterized by large white spots in the DDMs, and the second type is characterized by L-shaped white bands in their DDMs. It is possible that nature uses any working design, as we do.
It was noted earlier (46) that in dehydrogenases NAD-binding domains are similar but might be located in different parts of the chain. Catalytic domains could be quite different because of the sizes and shapes of the substrates. Not much is currently understood about what and how determines particular designs and modes of “motion” in dehydrogenases. Tetrameric lactate and dimeric malate dehydrogenases have similar domain structures with, however, some possibly important variations in the locations of stable fragments. The N-terminal decapeptide, holding together two dimers in the tetramer of lactate dehydrogenase (ldh) (20), folds as a part into the N-terminal stable fragment of dimeric malate dehydrogenase (mdh), a monomer of which may also have some stability. The N-terminal domains are unstable or only marginally stable in both proteins and are comprised of two independently stable fragments. The second domain in ldh is unstable and is formed by two marginally stable fragments. There is only one stable fragment within the second domain of mdh but the entire domain is reasonably stable. Furthermore, the fold without the N-terminal fragment also seems to be stable. Are these differences required for function? A few mutations in lactate dehydrogenase turn it into a catalytically effective malate dehydrogenase (55). A complication is introduced by the fact that crystallized pairs of apo- and tertiary forms of malate dehydrogenases (1b8p1b8u and 2cmd1emd) do not show any motions above the coordinate uncertainty. Is this caused by the choice of improper substrate analogs or does the crystallization itself play a dominant role? A possible answer is provided by mRNA capping enzyme (56) with one molecule in an open and another in a closed conformation in the same unit cell. Running the biochemical reaction in the crystal showed that only the closed form is activated. Thus, closing of the active site might be a necessary step in many reactions, with the binding happening in an open form often preserved by the crystallization.
Can elastic-model dynamics reveal barriers or breaking of “rigid” fragments during the motions?
Some useful insights may be provided by combining elastic network modeling of the functional conformational changes, the location of rigid fragments extracted from the DDM for the end points of the conformational change and from the estimates of fragments stability. The advantage of the sequences of conformational changes, provided by the elastic models compared with earlier interpolation morphs, is the avoidance of significant atomic overlaps during the motions. However, currently the question is not fully resolved of whether transitions follow unique paths and how much the paths depend on elastic model parameters. Another important question is whether such smooth non-overlapping motions require significant distortions at intermediate stages of fragments which seem retaining rigidity in the end-points DDM?
Concluding remark
Methods, results and discussion presented above are likely only a starting point in expanding the studies and interpretations of the vast new information on protein flexibility phenomena. Nevertheless, they can already provide biochemists with a rather comprehensive approach allowing for more transparent, multifaceted, detailed and accurate understanding and interpretation of the function-related conformational changes in proteins than other earlier proposed approaches.
Supplementary Material
Abbreviations
- PDB
Protein Data Bank
- PQS
a protein quaternary structure server
- ASA
accessible surface area
- DM
matrix of Cα-Cα distances in a protein conformation
- DDM
matrix of differences between elements of two DMs
- DD
element of a DDM
- RMSDD
RMS of all elements of a DDM
- CDDM
as DDM but only “contact distances” are considered
- SM
matrix of stabilities of all folded protein fragments
- ENM
elastic network model
Footnotes
This work was supported by NIH grants R01GM072014 and R01GM081680, and NSF grant CNS-0521568.
Additional information, supporting and clarifying methods, results and conclusions of this paper, is placed for the sake of printed space into “Supporting Information” available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Petsko GA, Ringe D. Protein Structure and Function. Blackwell; London: 2004. [Google Scholar]
- 2.Chothia C, Lesk AM, Dodson GG, Hodgkin C. Transmission of conformational change in insulin. Nature. 1983;302:500–505. doi: 10.1038/302500a0. [DOI] [PubMed] [Google Scholar]
- 3.Lesk AM, Chothia C. Mechanisms of domain closure in proteins. J Mol Biol. 1984;174:175–191. doi: 10.1016/0022-2836(84)90371-1. [DOI] [PubMed] [Google Scholar]
- 4.Gerstein M, Chothia C. Analysis of protein loop closure. Two types of hinges produce one motion in lactate dehydrogenase. J Mol Biol. 1991;220:133–149. doi: 10.1016/0022-2836(91)90387-l. [DOI] [PubMed] [Google Scholar]
- 5.Krebs WG, Gerstein M. The morph server: a standardized system for analyzing and visualizing macromolecular motions in a database framework. Nucleic Acids Res. 2000;28:1665–1675. doi: 10.1093/nar/28.8.1665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gerstein M, Lesk A, Chothia C. Structural mechanisms for domain movements in proteins. Biochemistry. 1994;33:6739–6749. doi: 10.1021/bi00188a001. the basis for the original database. [DOI] [PubMed] [Google Scholar]
- 7.Gerstein M, Krebs WG. A database of macromolecular motions. Nucleic Acids Res. 1998;26:4280–4290. doi: 10.1093/nar/26.18.4280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Krebs WG, Tsai J, Alexandrov V, Echols N, Junker J, Jansen R, Gerstein M. Studying protein flexibility in a statistical framework: tools and databases for analyzing structures and approaches for mapping this onto sequences. Methods Enzymol. 2003;374:544–84. doi: 10.1016/S0076-6879(03)74023-3. [DOI] [PubMed] [Google Scholar]
- 9.Gerstein M, Echols N. Exploring the range of protein flexibility, from a structural proteomics perspective. Curr Opin Chem Biol. 2004;8:14–19. doi: 10.1016/j.cbpa.2003.12.006. [DOI] [PubMed] [Google Scholar]
- 10.Rashin AA, Rashin AHL, Jernigan RL. Protein flexibility: coordinate uncertainty and interpretation of structural differences. Acta Cryst. 2009;D65:1140–1161. doi: 10.1107/S090744490903145X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wernisch L, Wodak SJ. Identifying structural domains in proteins. In: Bourne PE, Weissig H, editors. Structural Bioinformatics. Wiley; NY: 2003. pp. 365–385. [PubMed] [Google Scholar]
- 12.Veretnik S, Bourne PE, Alexandrov NN, Shyndialov IN. Toward consistent assignment of domains in proteins. J Mol Biol. 2004;339:647–678. doi: 10.1016/j.jmb.2004.03.053. [DOI] [PubMed] [Google Scholar]
- 13.Wetlaufer DB. Nucleation, rapid folding, and globular intrachain regions in proteins. Proc Natl Acad U S A. 1973;70:697–701. doi: 10.1073/pnas.70.3.697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wodak SJ, Janin J. Location of structural domains in proteins. Biochemistry. 1981;20:6544–6552. doi: 10.1021/bi00526a005. [DOI] [PubMed] [Google Scholar]
- 15.Rashin AA. An approach to calculation of the folding pathway from protein x-ray structure. Studia Biophys. 1979;77:177–184. [Google Scholar]
- 16.Rashin AA. Location of domains in globular proteins. Nature. 1981;291:85–87. doi: 10.1038/291085a0. [DOI] [PubMed] [Google Scholar]
- 17.Rashin AA. Buried area, conformation entropy, and protein stability. Biopolymers. 1984a;23:1605–1620. doi: 10.1002/bip.360230813. [DOI] [PubMed] [Google Scholar]
- 18.Rashin AA. Prediction of stabilities of thermolysin fragments. Biochemistry. 1984b;23:5518–5519. [Google Scholar]
- 19.Rashin AA. Aspects of protein energetics and dynamics. Prog Biophys Mol Biol. 1993;60:73–200. doi: 10.1016/0079-6107(93)90017-e. [DOI] [PubMed] [Google Scholar]
- 20.Jaenicke R. Stability and folding of domain proteins. Prog Biophys Mol Biol. 1999;71:155–241. doi: 10.1016/s0079-6107(98)00032-7. [DOI] [PubMed] [Google Scholar]
- 21.Schneider TS. Domain identification by iterative analysis of error-scaled difference distance matrices. Acta Cryst. 2004;D60:2269–2275. doi: 10.1107/S0907444904023492. [DOI] [PubMed] [Google Scholar]
- 22.Chacyn P. 2006 http://sbg.ci.csic.es/index.html.
- 23.Yang L, Song G, Carriquiry A, Jernigan RL. Close correspondence between the motions from principal component analysis of multiple HIV-1 protease structures and elastic network modes. Structure. 2008;16:321–330. doi: 10.1016/j.str.2007.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Echols N, Milburn D, Gerstein M. MolMovDB: analysis and visualization of conformational change and structural flexibility. Nucleic Acids Res. 2003;31:478–482. doi: 10.1093/nar/gkg104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kim MK, Chirikjian GS, Jernigan RL. Elastic models of conformational transitions in macromolecules. J Molec Graphics and Modelling. 2002;21:151–160. doi: 10.1016/s1093-3263(02)00143-2. [DOI] [PubMed] [Google Scholar]
- 26.Kim MK, Jernigan RL, Chirikjian GS. Efficient generation of feasible pathways for protein conformational transitions. Biophys J. 2002;83:1620–1630. doi: 10.1016/S0006-3495(02)73931-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nishikawa K, Ooi T, Isogai Y, Saito N. Tertiary structure of proteins. I. Representation and computation of the conformations. J Phys Soc Japan. 1972;32:1331–1337. [Google Scholar]
- 28.Kuipers JB. Quaternions and Rotation Sequences. Princeton University Press; 1998. [Google Scholar]
- 29.Chothia C, Janin J. Geometrical principles that determine the three dimensional structure of proteins. Proc FEBS Meeting. 1978;52:117–126. [Google Scholar]
- 30.Chothia C, Levitt M, Richardson D. Helix to helix packing in proteins. J Mol Biol. 1981;145:215–250. doi: 10.1016/0022-2836(81)90341-7. [DOI] [PubMed] [Google Scholar]
- 31.Horn BKP. Closed form solution of absolute orientation using union quaternions. J Opt Soc Am. 1986;4:629–642. [Google Scholar]
- 32.Maiti R, Van Domselaar GH, Zhang H, Wishard DS. Superpose: a simple server for sophisticated structural superpositions. Nucleic Acids Res. 2004;32 doi: 10.1093/nar/gkh477. Web Server issue. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Coutsias EA, Seok C, Dill KA. Using quaternions to calculate RMSD. J Comp Chem. 2004;25:1849–1857. doi: 10.1002/jcc.20110. [DOI] [PubMed] [Google Scholar]
- 34.Kavraki LE. Molecular Distance Measures, Version 1.16. 2006 http://cnx.org/content/m11608.
- 35.Vita C, Dalzoppo D, Fontana A. Independent folding of the carboxyl-terminal fragment 228-316 of thermolysin. Biochemistry. 1984;23:5513–5518. doi: 10.1021/bi00318a020. [DOI] [PubMed] [Google Scholar]
- 36.Orengo CA, Michie AD, Jones S, Jones DT, Swindells MB, Thornton JM. CATH—a hierarchic classification of protein domain structures. Structure. 1997;5:1093–1108. doi: 10.1016/s0969-2126(97)00260-8. [DOI] [PubMed] [Google Scholar]
- 37.Murzin AG, Brenner SE, Hubbard T, Chothia C. SCOP: a structural classification of proteins database for the investigation of sequences and structures. J Mol Biol. 1995;247:536–640. doi: 10.1006/jmbi.1995.0159. [DOI] [PubMed] [Google Scholar]
- 38.Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Privalov GP, Privalov PL. Problems and prospects in the microcalorimetry of biological macromolecules. Methods in Enzymology. 2000;323:31–62. doi: 10.1016/s0076-6879(00)23360-0. [DOI] [PubMed] [Google Scholar]
- 40.Rashin AA, Rashin AHL. Surface hydrophobic groups, stability and flip-flopping in lattice proteins. Proteins. 2007;66:321–341. doi: 10.1002/prot.21169. [DOI] [PubMed] [Google Scholar]
- 41.Henrick K, Thornton JM. PQS: a protein quaternary structure file server. Trends Biol Sci. 1998;23:358–361. doi: 10.1016/s0968-0004(98)01253-5. [DOI] [PubMed] [Google Scholar]
- 42.Privalov PL. Stability of proteins: small globular proteins. Adv Prot Chem. 1979;33:167–241. doi: 10.1016/s0065-3233(08)60460-x. [DOI] [PubMed] [Google Scholar]
- 43.Tsong TY, Hearn RP, Wrathall DP, Sturtevant JM. A calorimetric study of thermally induced conformational transitions of ribonuclease A and certain of its derivatives. Biochemistry. 1970;9:2666–2677. doi: 10.1021/bi00815a015. [DOI] [PubMed] [Google Scholar]
- 44.Harrison SC. Protein interfaces and intersubunit bonding. The case of tomato bushy stunt virus. Biophys J. 1980;32:139–151. doi: 10.1016/S0006-3495(80)84930-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lesk A, Chothia C. Elbow motion in the immunoglobulins involves a molecular ball-and-socket joint. Nature. 1988;335:188–190. doi: 10.1038/335188a0. [DOI] [PubMed] [Google Scholar]
- 46.Hausrath AC, Matthews BW. Thermolysin in the absence of substrate has an open conformation. Acta Cryst. 2002;D58:1002–1007. doi: 10.1107/s090744490200584x. [DOI] [PubMed] [Google Scholar]
- 47.Janin J, Wodak SJ. Structural domains in proteins and their role in the dynamics of protein function. Prog Biophys Mol Biol. 1983;42:21–78. doi: 10.1016/0079-6107(83)90003-2. [DOI] [PubMed] [Google Scholar]
- 48.Remington S, Wiegrand G, Huber R. Crystallographic refinement and atomic models of two different forms of citrate synthase at 2.7 and 1.7 Å resolution. J Mol Biol. 1982;158:111–152. doi: 10.1016/0022-2836(82)90452-1. [DOI] [PubMed] [Google Scholar]
- 49.Manning G, Whyte DB, Martinez R, Hunter T, Sudarsanam S. The protein kinase complement of the human genome. Science. 2002;298:1912–1934. doi: 10.1126/science.1075762. [DOI] [PubMed] [Google Scholar]
- 50.Berry MB, Meador B, Bilderback T, Liang P, Glaser M, Phillips GN., Jr The closed conformation of a highly flexible protein: the structure of E. coli adenylate kinase with bound AMP and AMPPNP. Proteins. 1994;19:193–198. doi: 10.1002/prot.340190304. [DOI] [PubMed] [Google Scholar]
- 51.Jaenicke R. Protein Folding: local structures, domains, subunits, and assemblies. Biochemistry. 1991;30:3147–3161. doi: 10.1021/bi00227a001. [DOI] [PubMed] [Google Scholar]
- 52.Muller CW, Schlauderer GJ, Reinstein J, Schulz GE. Adenylate kinase motions during catalysis: an energetic counterweight balancing substrate binding. Structure. 1996;4:147–156. doi: 10.1016/s0969-2126(96)00018-4. [DOI] [PubMed] [Google Scholar]
- 53.Finkelstein AV, Janin J. The price of lost freedom: entropy of bimolecular complex formation. Protein Eng. 1989;3:1–3. doi: 10.1093/protein/3.1.1. [DOI] [PubMed] [Google Scholar]
- 54.Tamura A, Privalov P. The entropy cost of protein association. J Mol Biol. 1997;273:1048–1060. doi: 10.1006/jmbi.1997.1368. [DOI] [PubMed] [Google Scholar]
- 55.Wilks HM, Hart KW, Feeney R, Dunn CR, Muirhead H, Chia WN, Barstow DA, Atkinson T, Clarke AR, Holbrook JJ. A specific, highly active malate dehydrogenase by redesign of a lactate dehydrogenase framework. Science. 1988;242:1541–1544. doi: 10.1126/science.3201242. [DOI] [PubMed] [Google Scholar]
- 56.Hakansson K, Doherty AJ, Shuman S, Wigley DB. X-ray crystallography reveals a large conformational change during guanyl transfer by mRNA capping enzymes. Cell. 1997;89:545–553. doi: 10.1016/s0092-8674(00)80236-6. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


