Spatially Varying Properties of the Vocal Ligament Contribute to its Eigenfrequency Response

Abstract

The vocal ligament is known to have nonlinear variation in geometry, yet this is rarely considered in empirical or computational studies. This paper investigates the effects of a nonlinear variation of the anterior-to-posterior geometry and the corresponding spatial variation in elastic modulus on the fundamental frequency of vibration for the vocal ligament. Uniaxial tensile tests were performed on a vocal ligament specimen dissected from an excised 60-year-old male larynx. Digital image correlation (DIC) was used to obtain the spatial deformation field for the entire ligament specimen. DIC results revealed that the tensile deformation was very heterogeneous, with the least amount of deformation occurring in the region of smallest cross sectional area. The elastic modulus was calculated locally and was found to be approximately 10 times higher at the mid-point of the vocal ligament than in the anterior and posterior macula flavae regions. Based on the spatially varying material properties obtained, finite element models (isotropic and transversely isotropic) were created to investigate how the effects of varying cross-section, heterogeneous stiffness, and anisotropy could affect the fundamental frequency of vibration. It was found that the spatial cross-section variation and the spatially varying anisotropy (i.e. modulus ratio) are significant to predictions of the vibration characteristics. Fundamental frequencies predicted with a finite element model are discussed in view of rotatory inertia and contribution of transverse shear deformation.

1. Introduction

Phonation is critically determined by the biomechanical properties of the vocal folds. The vocal fold cover and the vocal ligament may both be considered as the vibrating tissue components in the airflow-driven vibration of the vocal folds. In a basic beam model of vibration, the fundamental frequency of the vocal folds in an unstretched state is given as (Zhang et al., 2009)

$$F_0=\frac{\alpha }{L^2}\sqrt{\frac{E{\kappa }^2}{\rho }}$$ (1)

where F₀ is the natural frequency of the lowest mode (under no applied tension), E is the elastic modulus, κ is the radius of gyration for the tissue cross-section, L is the length, ρ is the density of the tissue, and α is a constant equal of the order of unity. In the past, we have considered changes to the fundamental frequency as stretching of the vocal fold occurs (Zhang et al. 2007). Thus, the influence of length L and the current modulus E on F₀ were considered. Here, we hypothesize that spatial variations in cross-section properties, in the tissue modulus, and in the tissue anisotropy could also influence F₀. Such a study would provide more insight into the biomechanical processes of vocal fold vibration and phonatory sound source generation.

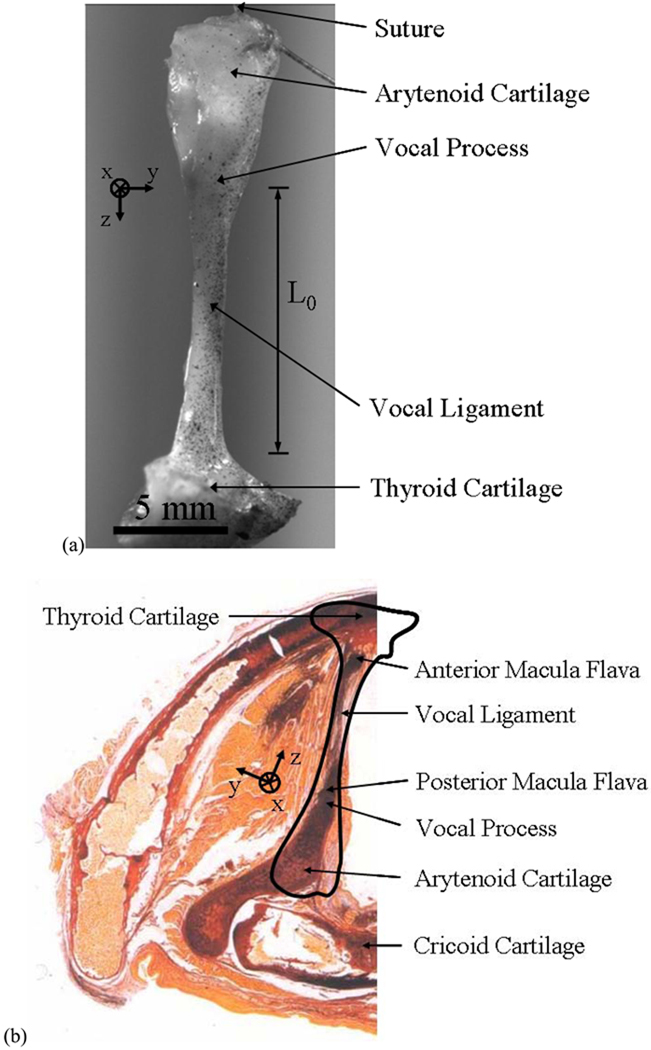
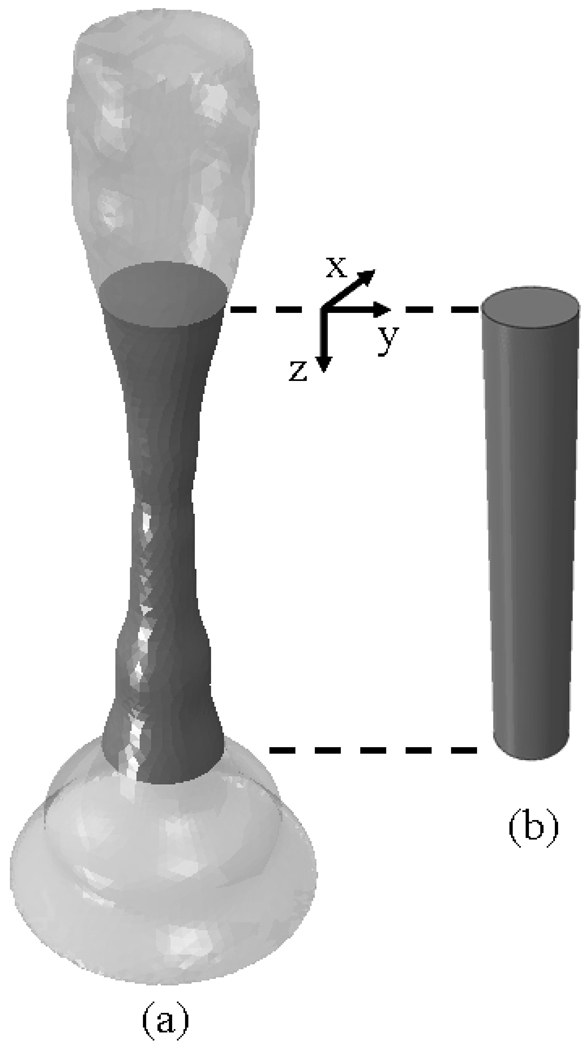
Figure 1 shows the vocal ligament (i.e. intermediate and deep layers of the lamina propria) that is the focus of this study. Figure 1a shows a ligament specimen, extending anteriorly from the anterior commissure to the vocal process of the arytenoid cartilage posteriorly. For the purpose of applying tensile deformation during biomechanical testing, sutures were attached to sections of the thyroid cartilage and arytenoid cartilages naturally attached to the ligament specimen, including the macula flavae. Figure 1b reproduces a horizontal (transverse) section through an adult larynx at the glottal level (Hirano and Sato, 1993). An outline of the specimen in Fig. 1(a) is superimposed onto the anatomical section in Fig. 1(b). It is evident from Fig. 1 that the cross-section of the vocal ligament is not constant, but includes tapering at the macula flavae. Past models for the predictions of fundamental frequencies have assumed the vocal fold cross-section to be constant (Zhang et al. 2009, Zhang et al. 2007). How spatial variations in the cross-sectional geometry could influence the fundamental frequency and vibration characteristics is unknown.

Figure 1.

(a) The vocal ligament specimen used for this study. (b) Horizontal section of the larynx at the glottis of an adult male (from HIRANO. Histological Color Atlas of the Human Larynx, 1E. © 1993 Delmar Learning, a part of Cengage Learning, Inc. Reproduced by permission. www.cengage.com/permissions). An outline of the specimen used in this experiment is superimposed onto the anatomical section.

For biological tissues it has been shown that biomechanical properties can exhibit spatial variations within a single type of tissue. Bones remodel to adapt to mechanical loads, thus causing gradients in the mechanical properties within a single bone (Frost, 1990; Lanyon, 1992; Kishen et al., 2000). Spatial variations in biomechanical properties have also been documented for soft tissues. In the crystalline lens of the human eye, the stiffness was on average 65 times greater in the center than at the periphery for older lenses (Weeber et al., 2007). Additionally, several studies of articular cartilage reported that regional variations occur at the microscopic level, e.g. in cell types, fiber orientation and structure, as well as at the macroscopic level, e.g. the stress-stain response (Tanne et al., 1991; Klein et al., 2009). Recently, a gradation of tissue properties was also reported for vocal fold tissue. Goodyer et al. (2010) report changes in mucosa stiffness with respect to anatomical position for pig larynges. Mucosa stiffness at locations along a line from the midpoint of the vocal fold toward the trachea increased linearly with respect to position, increasing as the measurements are taken further from the vocal fold.

In order to investigate if spatial variation in the biomechanical properties exists in the vocal fold lamina propria, the digital image correlation approach together with a mechanical testing paradigm was employed. Digital image correlation (DIC) is a non-contact, optical measurement technique that tracks the gray scale value pattern in small neighborhoods of the image (“subsets”) of a specimen during deformation, in order to determine displacement fields. Strain fields can then be obtained by spatial differentiation of the displacement field. DIC has demonstrated its usefulness at the macroscopic as well as the microscopic levels (Verhulp et al., 2004), and both in synthetic (Sachtleber et al., 2002) and biological structures (Sachs et al., 2006). Once strain data is combined with stress data any existing spatial distribution in a tissue specimen’s elastic modulus would be revealed. Past models for the predictions of fundamental frequencies have assumed the elastic modulus to be constant throughout the vocal ligament, and it is unknown how spatial variation in the elastic modulus would affect the fundamental frequency and vibration characteristics relevant for phonation.

A macro-scale continuum mechanics approach for the characterization of vocal fold tissue considers tissue biomechanical properties as measured data, but leaves the question of underlying mechanisms leading to such properties unanswered. Alternatively, a micro-mechanics continuum approach considers tissue biomechanical properties as the result of the properties of tissue constituents and their interactions. In a most basic view, the vocal fold lamina propria has shown to be consisting of a network of fibrous proteins (collagen and elastin fibers) enmeshed in “ground substances”, or interstitial proteins such as glycosaminoglycans and proteoglycans. Bundles of the fibrous proteins are aligned in the anterior-posterior (i.e. longitudinal) direction, leading to anisotropy in tissue properties (Gray et al., 2000). Such a microstructural alignment leads to transversely isotropic biomechanical properties (Gray et al., 2000; Hirano et al., 1982). In their study of a vocal fold model in the form of a solid, rectangular parallelepiped, Cook and Mongeau (2007) investigated the level of anisotropy and determined only little impact of anisotropy on the eigenfrequency. We hypothesize that a spatial variation of biomechanical properties – such as the tissue modulus – is related to the spatial variations in the densities of proteins (e.g. collagen content) in the vocal fold lamina propria. If this is the case, the anisotropy of the vocal ligament will also be spatially varying. How such anisotropy in biomechanical properties and the spatial variation in anisotropy affect the fundamental frequency and vibration characteristics has never been investigated.

In this study, the biomechanical properties of the vocal ligament were investigated with mechanical testing and digital image correlation analysis during mechanical testing, establishing the spatial variation in tissue properties. Subsequently, the vibration characteristics of the vocal fold were studied by a computational model which allows us to account for both variation in material properties and cross-section geometry with spatial location, as well as the influence of tissue anisotropy.

2. Experiments

2.1 Experimental Methods

The specimen under consideration was a vocal ligament carefully dissected from an excised 60-year-old male larynx. The experimental protocol was approved by the Institutional Review Board of UT Southwestern Medical Center. The specimen is depicted in Fig. 1(a). The in situ vocal fold length (the distance from the vocal process to the anterior commissure) was defined as L₀. The vocal ligament specimen was assumed to possess circular cross sections. A coordinate system was inscribed such that the z-axis coincides with the anterior-posterior direction, the y-axis points in the medial-lateral direction, and the x-axis points into inferior-superior direction, Fig. 1(b). The origin of the coordinate was inscribed as z = 0 at the vocal process. Its local diameters in the undeformed configuration D(z) were measured from calibrated digital images taken before the load was applied. The digital image area was calibrated by determining a pixel/mm ratio from the dimensions of an object of known dimension. Local cross-sectional areas A(z) = [D(z) ²]π / 4 and a mean cross-sectional area A̅ were calculated.

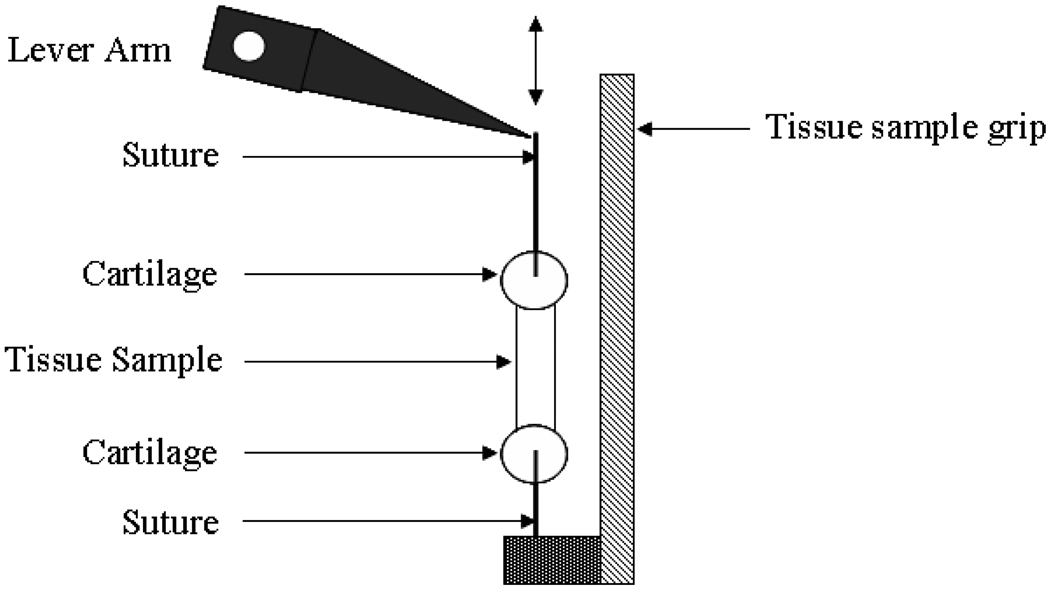
For applying tensile deformation, sutures were attached through a section of the arytenoid cartilage and a section of the thyroid cartilage naturally attached to the vocal ligament during dissection. The arytenoid cartilage section was then connected to the moving actuator of a servo-controlled lever system,ⁱ while the thyroid cartilage section was connected to the support by sutures. Figure 2 depicts the experimental apparatus. The servo-controlled lever system was under displacement feedback control, and was connected to a function generator and an oscilloscope to monitor the displacement input. The tensile force response of the specimen was detected by the lever system, digitized at 1000 samples/s and output for further analysis. The specimen was kept in air during the experiment such that optical distortions related to a glass container with physiological solution are avoided. However, the tissue was hydrated periodically throughout the dissection, the test preparation, and the actual experiment with phosphate buffered saline (PBS) to avoid changes in the mechanical properties due to dehydration. The applied displacement and loading rate were applied to the ligament to mimic physiologically relevant conditions. It has been documented that during speech and singing the vocal folds can elongate up to 40% at a loading rate of 1–10 Hz (Hollien, 1960; Ohala et al., 1973; Sundberg, 1979; Titze et al., 1997). The lever system was set to apply a displacement of 1.0 mm at a rate of 70 mm/sec, and subsequently kept the displacement constant. The overall elongation of the ligament was measured optically from digital images of the undeformed and the deformed specimen as the change in distance between the vocal process (z = 0) and the anterior commissure (z = L₀). When conducting stretching experiments of the tissue it is not possible to control the set-up such that the initial conditions are of exactly zero slack/tautness of the suture. By using optical measurements instead of machine described displacements to determine specimen deformation uncertainties in the measured magnitude of deformation are avoided. The force was recorded until a relaxed state was reached after 30 seconds of hold time. The force measured in the relaxed state can then be used to calculate the (long term) equilibrium response of the tissue.

Figure 2.

The experimental apparatus.

A 2D digital image correlation system was used to analyze the deformation state of the tissue specimen as such a system is sufficient for the determination of the axial deformation of the specimen. A speckle pattern on the tissue specimen was created by applying an enamel based black spray paint, Fig. 1(a). During the tensile test, images of the specimen were taken with a CCD camera,ⁱⁱ with a CCD pixel size of 6.7 × 6.7 µm for image acquisition. In particular, the image at the initial configuration (ΔL =0 mm) and the deformed configuration after full relaxation were considered. These images were analyzed by a digital image correlation softwareⁱⁱⁱ. From the pair of images of the specimen in the undeformed and the deformed configurations, the distribution of displacements u_z(z) was obtained. Differentiation of the displacement field provided the strain distribution, ε_z(z) = d [u_z(z)] / dz. Consequently, the local equilibrium modulus of elasticity E(z) may be calculated as:

$$E(z)=\frac{{\sigma }_z(z)}{{\epsilon }_z(z)}=\frac{P}{A(z){\epsilon }_z(z)}$$ (2)

2.1 Experimental Results

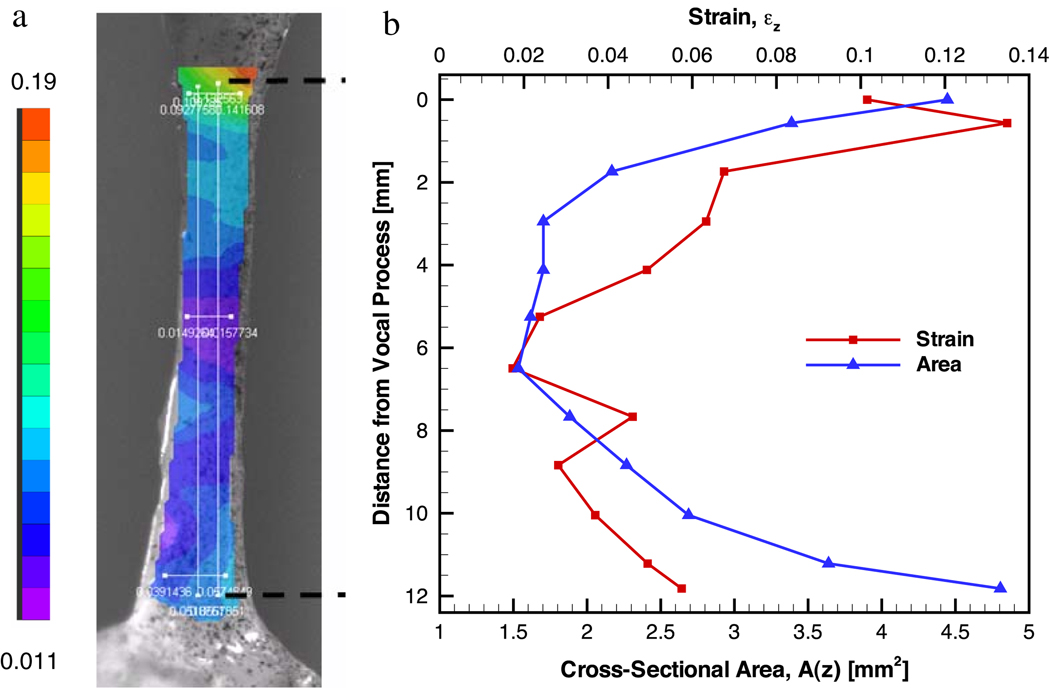
The vocal ligament specimen considered had an initial length of L₀ = 12 mm. In the undeformed state, the cross-sectional area was found to depend on the z-coordinate as A(z) = 0.0826z² − 0.9339z + 4.0106 (mm²) with R² = 0.9405. The average cross-sectional area for the undeformed state was determined to be A̅ = 2.65 mm². The variation of A(z) with spatial location is depicted in Fig. 3(b).

Figure 3.

(a) Ligament specimen with longitudinal strain distribution obtained from digital image correlation; (b) The spatial distributions of longitudinal strain and cross sectional area along the vocal ligament specimen.

From the image obtained for the deformed state, the elongation of the ligament between the vocal process (z = 0) to the anterior commissure (z = L₀) was 0.6 mm. The tensile force in the fully relaxed state was found to be 0.0193 N. As shown in Fig. 3(a) the spatial strain distribution resulting from the digital image correlation is depicted. Strain values for constant z locations were determined and averaged. The averaged strains are given in Fig. 3(b) in dependence of the distance from the vocal process. The longitudinal strain distribution was found to be highly heterogeneous. It revealed that the lowest strain value of the ligament specimen was found in the area of smallest cross-section, while larger values of strain were found closer to the cartilage attachments on both ends of the specimen, around the macula flavae.

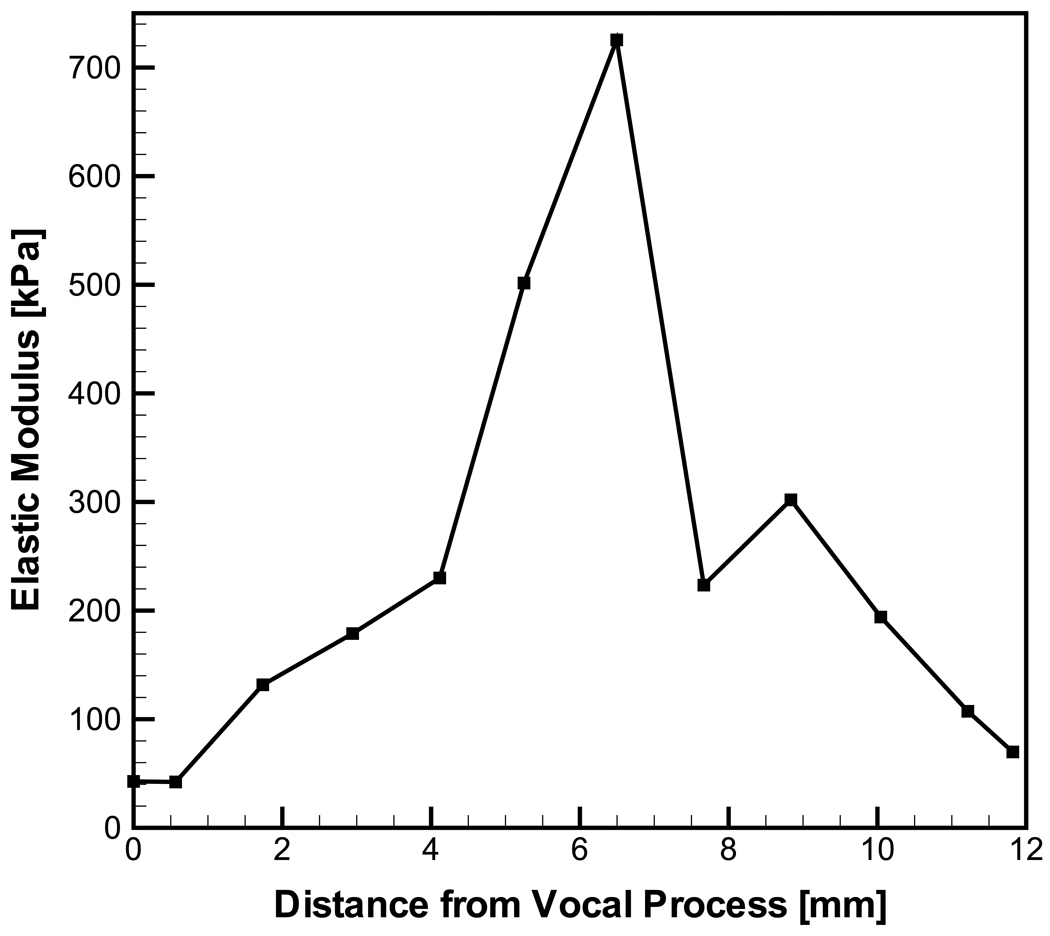
Figure 4 clearly shows that the local elastic modulus varies greatly with location along the vocal ligament. The elastic modulus of the smallest cross-section (around the midpoint region) was approximately 10 times greater than those at the anterior and posterior regions of the specimen.

Figure 4.

The longitudinal elastic modulus in dependence of spatial location in the vocal ligament specimen.

3. Analysis

3.1 Model Definition and Analysis Method

Computational models of the tissue specimen were created and analyzed with the finite element method. The finite element method was employed predominantly to determine the natural frequencies of the specimen. When dealing with beam problems where rotatory inertia and transverse shear deformation (Timoshenko, 1922) are present together with spatial property variations, numerical methods are commonly required for solutions of vibration characteristics (Zhou and Cheung, 2001; Suits, 2001) while closed form solutions have been provided for standard beam problems (Huang, 1961). In order to allow for both a stress analysis of the specimen and an eigenfrequency analysis accounting for bending modes, three-dimensional models were considered. The first model (Fig. 5a) considered the actual specimen cross-section measurements following from Fig. 3(b). The specimen was of circular cross-section geometry with its outline equal to that of the tissue specimen and revolved about the z-axis. The second model was of constant circular cross-section shape, cross-sectional area A̅, and with length L₀. The constant cross-section model was created in order to elicit the separate effects of the spatially varying cross section geometry and the spatially varying elastic properties. In the models we assumed that the cartilages (arytenoid and thyroid cartilages) were much stiffer than the ligament. It has also been documented that the cartilages do not undergo vibration (Zemlin, 1997). Thus, the cartilages did not enter the computation and their presence was reflected only in the displacement boundary conditions.

Figure 5.

(a) Model with varying (actual) cross-section, A = A(z); (b) constant cross-section model, A = const.

To simulate the tensile test, the nodes representing the interface between the thyroid cartilage and the ligament were fixed in the x, y, and z-directions (u_x = u_y = u_z = 0) and an applied displacement (u_z = U₀ = ΔL = 0.6 mm) was prescribed at the nodes representing the interface between the ligament and the vocal process. From the computation, the reaction force was computed and the overall force-displacement response was obtained. In the computation of the eigenmodes and eigenfrequencies boundary conditions were applied so that the cartilage-ligament interface at z = 0 and z = L₀ were fixed (u_x = u_y = u_z = 0). Therefore, only the ligament and portions of the anterior and posterior macula flavae contributed in the vibration analysis. Also, all nodes were constrained to motion in the yz plane (u_x = 0) in order to constrain bending into one direction only.

From an initial macroscopic viewpoint we consider the tissue as a linear elastic, isotropic solid. Then, two material parameters are needed to fully define the three-dimensional tissue response, i.e., the Young’s modulus E, and Poisson’s ratio ν. The Young’s modulus is obtained from the experiments, while a reasonable value the Poisson’s ratio is assumed as the present experiments did not allow for its measurement. Hooke’s law in three dimensions relates stress and strain as

$${\epsilon }_{\mathit{\text{ij}}}=S_{\mathit{\text{ijkl}}}{\sigma }_{\mathit{\text{ij}}}$$ (3)

where the isotropic compliance tensor S_ijkl depends on E and ν following the definition in Appendix 1. For the current experiments, we consider that the modulus can potentially depend on the spatial location in the ligament as E = E(z) as following from Eq. (2). Nevertheless, no spatial variation of the Poisson’s ratio is considered for the isotropic material model.

Once the anisotropic microstructure of the vocal fold lamina propria is considered, microstrucural anisotropy needs to be reflected in the constitutive model. Considering a transversely isotropic microstructure, four elastic constants, the moduli E_x = E_y, E_z, and the Poisson’s ratios ν_zx, and ν_xy, define the biomechanical response, with the xy plane as the plane of isotropy. The tensor Ŝ_ijkl for the transverse isotropic case is also given in Appendix 1. A consistent set of constants E_x = E_y, E_z, ν_zx, and ν_xy can be obtained from a micromechanical model that considers the tissue to consist of two phases, fibrous proteins (collagen and elastin) and ground substances (interstitial proteins), given by subscripts fp and gs, respectively. Then, the elastic constants of the transverse isotropic model can be related to the elastic modulus of the fibrous proteins E_fp, elastic modulus of the ground substances E_gs, Poisson’s ratio of the fibrous proteins ν_fp, Poisson’s ratio of the ground substances ν_gs, and the volume fractions of fibrous proteins V_fp and ground substance V_g = _s1−_fV _p. An upper-bound micromechanical model provides a reasonable first-order approximation for the elastic constants of transversely isotropic two-phase solids (Clyne and Withers, 1993; Daniel and Ishai, 2006):

$$E_z=V_{\mathit{\text{fp}}}{E}_{\mathit{\text{fp}}}+V_{\mathit{\text{gs}}}{E}_{\mathit{\text{gs}}},E_x=E_y=\frac{E_{\mathit{\text{fp}}}{E}_{\mathit{\text{gs}}}}{V_{\mathit{\text{fp}}}{E}_{\mathit{\text{gs}}}+V_{\mathit{\text{gs}}}{E}_{\mathit{\text{fp}}}}$$ (4a),(4b)

$$G_{\mathit{\text{xx}}}=V_{\mathit{\text{fp}}}{G}_{\mathit{\text{fp}}}+V_{\mathit{\text{gs}}}{G}_{\mathit{\text{gs}}},G_{\mathit{\text{xz}}}=\frac{G_{\mathit{\text{fp}}}{G}_{\mathit{\text{gs}}}}{V_{\mathit{\text{fp}}}{G}_{\mathit{\text{gs}}}+V_{\mathit{\text{gs}}}{G}_{\mathit{\text{fp}}}}$$ (4c),(4d)

$${\nu }_{\mathit{\text{zx}}}=V_{\mathit{\text{fp}}}{\nu }_{\mathit{\text{fp}}}+V_{\mathit{\text{gs}}}{\nu }_{\mathit{\text{gs}}},{\nu }_{\mathit{\text{xy}}}=1-\frac{E_x}{3K_T}-{\nu }_{\mathit{\text{xz}}},{\nu }_{\mathit{\text{xz}}}={\nu }_{\mathit{\text{zx}}}\left(\frac{E_x}{E_z}\right)$$ (4e),(4f),(4g)

where K_T = (K_fpK_gs) / (V_fpK_gs + V_gsK_fp) is the bulk modulus of the tissue. The shear modulus (G) and the bulk modulus (K) for both constituent phases are calculated by the standard relationships of elasticity, i.e., G = E / [2(1 + ν)] and K = E / [3(1 − ν)]. Considering staining intensities, the study (Chan et al., 2007) has considered that local variations in the collagen and elastin concentrations would exist. Staining intensities were, however, not translatable into actual volume fraction measurements. Therefore, values for E _fp and E _gs were established with V _fp varying such that the spatial variation of the longitudinal elastic modulus E_z matched the experimental results in Fig. 4. Consequently, not only E_z but all other elastic constants vary spatially.

Computations were conducted using a commercially available finite element software package^iv. Tetrahedron-shaped quadratic elements with 10 nodes and modified formulation (C3D10M) were used. Spatial variations of the elastic modulus were implemented into the computational model via a user defined field subroutine (USDFLD). This subroutine defined the elastic modulus as a function of the z coordinate.

3.2 Model Results

3.2.1 Isotropic Tissue Response

The first part of the analysis considered an isotropic tissue response only. Thereby, the measured longitudinal modulus is assumed to be present in all spatial directions. A Poisson’s ratio of ν =0.4 was assumed in the calculations such that the tissue retains some compressibility. This choice is made as Hooke’s law requires ν < 0.5, and as experimental findings on deformation of soft human tissue at high rates (Saraf et al., 2006) which indicate that the commonly assumed incompressible response of soft tissue may not hold at high rates of deformation which also occur during vocal fold vibration. In order to assess the influence of the spatial distribution of the elastic modulus on the ligament’s biomechanical response it is useful to determine what equivalent tissue modulus such that the force-elongation response for the case with spatial varying modulus is identical to that of a case where the modulus is constant. The force-elongation response for the model with spatially varying cross section and modulus following Fig. 3(b) was obtained. At an applied displacement of U₀ = 0.6 mm a reaction force of 0.02 N was computed, well approximating the experimental value of 0.0193 N. Subsequently, the model was analyzed assuming a homogeneous modulus. A range of modulus values were considered. The effective modulus E̅ was obtained from the computation where the force-elongation response was identical to that of the model with a spatially varying modulus. The effective modulus was found to be E̅ =195 kPa.

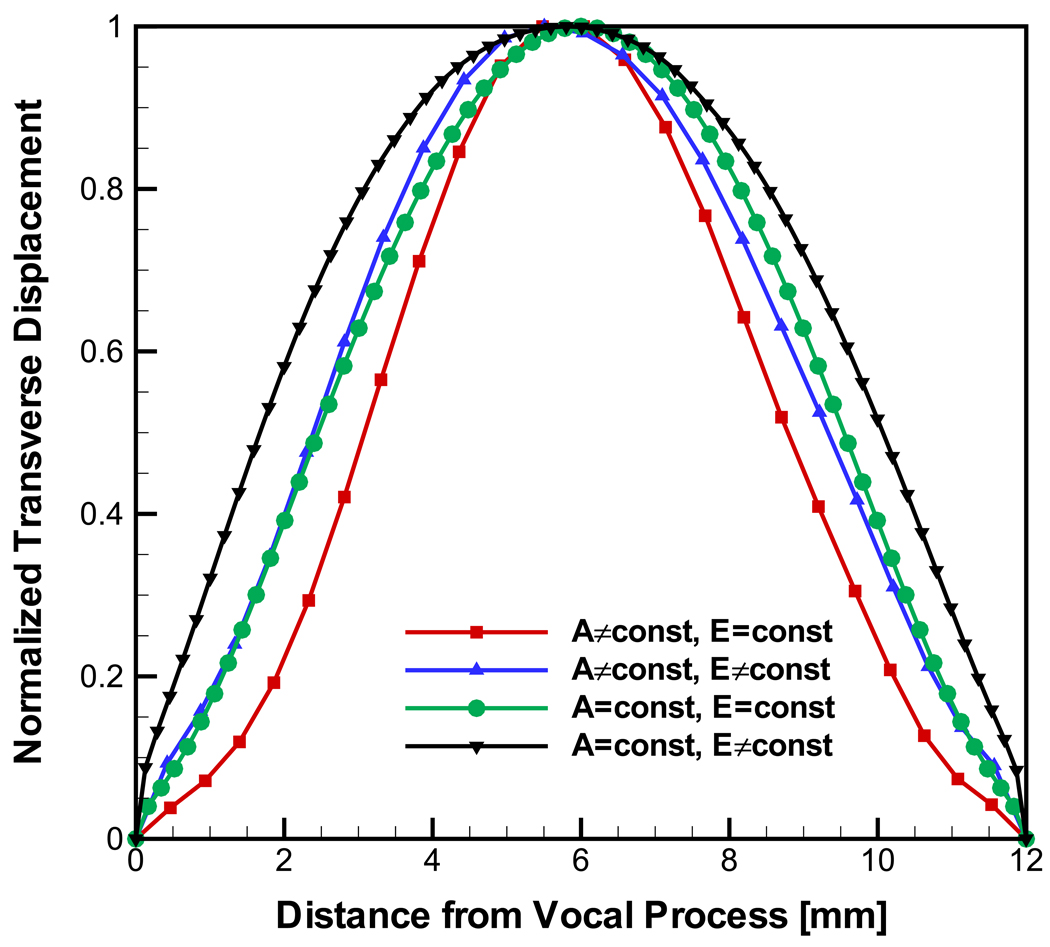
To see how the spatial variations in cross-section geometry and elastic modulus effected the eigenfrequency and the eigenmodes, the model was analyzed further. Table 1 compares the predicted fundamental frequency (frequency of the first mode of vibration, F₀) for four combinations of cross-section and modulus distribution. It was found that a gradient in the elastic modulus had no effect on F₀ for the case of A = const but decreased F₀ for the varying cross-section model (Fig. 5). When considering the spatially varying cross-section higher values of F₀ are predicted independent of whether a constant or spatially varying modulus was considered.

Table 1.

Predicted eigenfrequencies for models with isotropic elasticity.

Model		Mode 1 Frequency [Hz]
Area = constant	E = constant	141
	E ≠ constant	141
Area ≠ constant	E = constant	219
	E ≠ constant	191

Figure 6 shows the corresponding eigenmodes as normalized displacements in the transverse direction, u_y. In the model with a uniform modulus and spatial varying cross-section, the deflection was most strongly concentrated towards the center of the ligament. This short effective length of vibration reflected the highest predicted value of F₀ for this case. Once the spatially varying modulus was considered, the mode pattern broadened and the effective length increased, leading to a reduced F₀. In the case of the model with constant cross-section, the modulus distribution was found to have the same effect, but the missing spatial variation in the cross-section led to even broader mode patterns. The effective lengths of vibration again correspond to lower values of F₀ for the case of the constant cross-section model relative to the cases considering the actual ligament geometry.

Figure 6.

Predicted eigenmodes for models considering isotropic tissue modulus.

The present model assumes a Poisson’s ratio of 0.4. A sensitivity study on the effect of the Poisson’s ratio on the predicted fundamental frequencies was conducted. It was found that a Poisson’s ratio of 0.3 reduced the fundamental frequency by less than 3% while an increase of the Poisson’s ratio to close to 0.5 increased the predicted fundamental frequency by 5%.

3.2.2 Transversely Isotropic Tissue Response

The effects of tissue anisotropy were explored for both the spatially varying cross-section model and the constant cross-section model. As the longitudinal elastic modulus varies spatially, it was assumed that such a variation would emerge from a spatial variation of the underlying fraction of fibrous proteins. The volume fraction of the fibrous proteins was assumed to be the highest in the center of the ligament, while decreasing in the anterior and posterior directions. The volume fraction was assumed to be the highest in the center of the ligament because the longitudinal elastic modulus was determined from the DIC results to be the highest in the center. The elastic moduli for the fibrous proteins and for ground substances were chosen such that the longitudinal modulus matched the experimental data (Fig. 4). It is important to realize that the definition of a volume fraction and moduli values here are abstract, with no physical interpretation or correlation with histological data. They were used simply to create a set of consistent elastic constants.

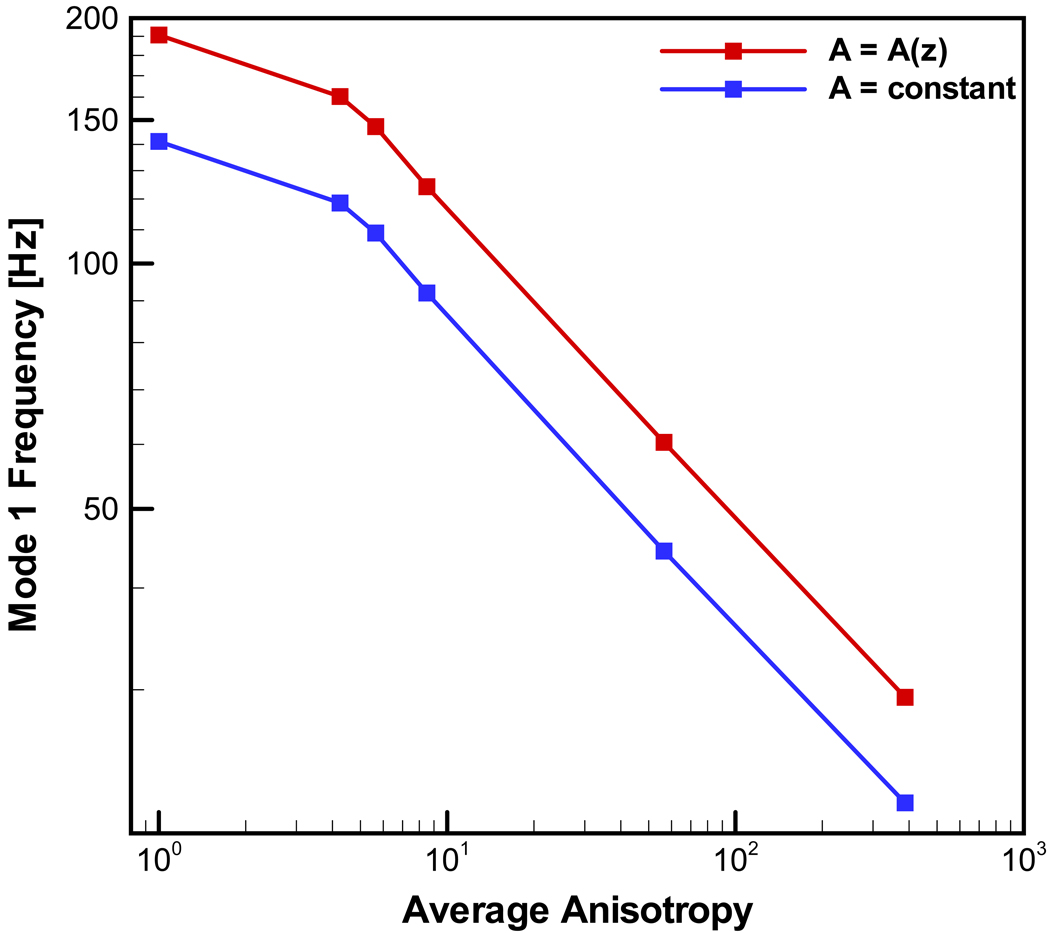
When creating these transversely isotropic models, it was found that the degree of anisotropy (i.e. the modulus ratio E_z / E_y) had a great influence on the predicted eigenfrequencies. Figure 7 shows the fundamental frequency in dependence of the modulus ratio based on computations with six different degrees of anisotropy in the transversely isotropic elastic description of the tissue. All models considered a spatially varying longitudinal elastic modulus. Consequently, the degree of anisotropy also varies within each model in dependence of the distance from the vocal process. These levels of anisotropy were achieved by using six different (assumed) pairs of E _fp and E _gs. However, the transverse modulus, E_x = E_y, also depended upon the values chosen for E _fp and E _gs, and the volume fraction. As the difference between E _fp and E _gs increased, so does the anisotropy (E_z / E_y). Simultaneously, the ratio between the longitudinal modulus E_z and shear modulus G_xz also increases. The six cases considered in the computations are characterized as:

1. E_z / E_x = 1.0, E_z / G_xz = 3.0, isotropic;

2. E_z / E_x = 1.0 to 7.5, E_z / G_xz = 3.0 to 21.9, avg(E_z / E_x) = 4.2;

3. E_z / E_x = 1.3 to 10.0, E_z / G_xz = 3.9 to 30.2, avg(E_z / E_x) = 5.7 ;

4. E_z / E_x = 2.0 to 15.0, E_z / G_xz = 7.1 to 48.0, avg(E_z / E_x) = 8.5 ;

5. E_z / E_x = 13.0 to 100.0, E_z / E_xz = 38.5 to 302.1 avg(E_z / E_x) = 56.5 ;

6. E_z / E_x = 50.0 to 725.0, E_z / G_xz = 166.7 to 2416.7, avg(E_z / E_x) = 387.5.

Figure 7.

The dependence of fundamental frequency on the degree of anisotropy (average value of modulus ratio E_z / E_x) for six levels of anisotropy, all considering spatial variation of the modulus and the cross-section area.

The average anisotropy was defined as the mean value of maximum and minimum anisotropy. As the degree of anisotropy – assessed the ratio E_z / E_x increases, so does the ratio between the longitudinal modulus and the longitudinal-transverse shear modulus E_z / G_xz.

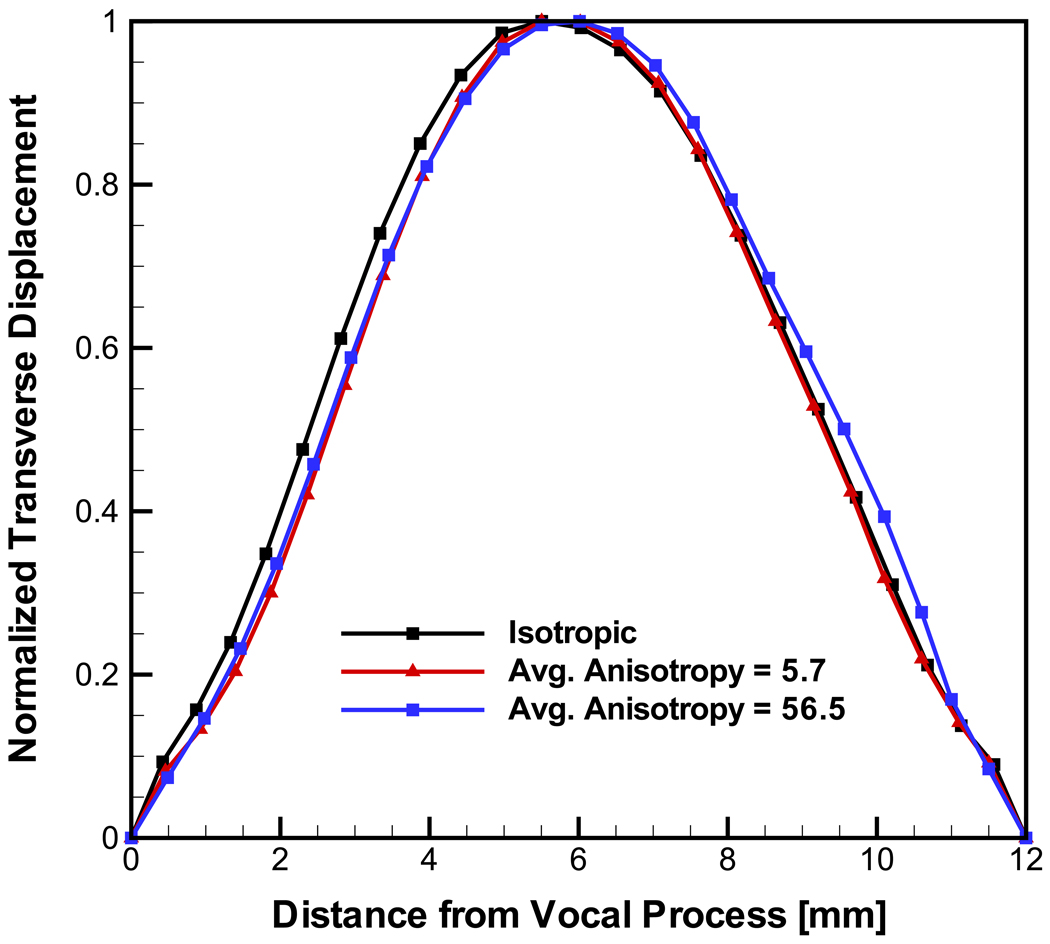
Figure 7 demonstrates that the predicted fundamental frequencies strongly depend on the degree anisotropy. Again the fundamental frequencies for the case of spatially varying cross section are predicted to be higher than those for the constant cross-section model. The predicted fundamental frequencies for the transversely isotropic models excluding the isotropic case and low degree of anisotropy could be described as F₀ = C (E_z / E_x)^m, with m = −0.38 independent of the model cross-section geometry and C a constant depending on the cross-section geometry. The eigenmodes were compared to those depicted in Fig. 6 for the isotropic material model. It was found that the degree of anisotropy did not change the shape of the deflection. Figure 8 depicts these results.

Figure 8.

Predicted eigenmodes for models considering transversely isotropic material model. Results for the spatially varying cross section model.

4. Discussion

The results of a biomechanical stress-stretch experiment on a vocal ligament specimen evaluated with the digital image correlation method revealed that the local deformation of the vocal ligament specimen may vary greatly with spatial location, illustrating the importance of optical measurements. Assuming a constant elastic modulus, the present results on the measured strains were counterintuitive. Considering the hourglass-type specimen shape and the initial assumption of constant elastic properties one would predict that the region of smallest cross section would undergo the highest strain. However, the strain distribution determined showed the lowest strain at location of smallest cross section. For the specimen tested, the tensile elastic modulus in the specimen’s longitudinal direction was much greater (approximately 10 times) in the mid-membranous vocal fold region than in the anterior and posterior (macula flavae) regions. DIC is an effective method but it may have some limitations. If the experiment was conducted in a physiological fluid (e.g. Krebs-Ringer solution) in a glass environmental chamber, as mechanical testing of tissue would normally, there may be optical distortions interfering with the DIC results. Eliminating any potential optical distortion would be crucial for determining the true deformation field.

The heterogeneous elastic modulus observed along the vocal ligament could be due to local variations in the content of structural proteins in the extracellular matrix (ECM). Previous studies have speculated that there may be local variations in the collagen and elastin concentrations (Chan et al., 2007). This would affect the fiber volume fraction used in the transverse isotropy relations. It is well known in the field of mechanobiology that mechanical forces influence gene expression in cells. Numerous studies have shown that fibroblasts upregulate the production of matrix proteins to strengthen the ECM when exposed to higher forces (Leung et al., 1976; Yang et al., 2004; Hsieh et al., 2000). Gray (2000) suggested that the variation in collagen content between the different layers of the vocal fold lamina propria could be related to the magnitude of force experienced at each layer. As the mid-membranous vocal fold region of the ligament has the smallest cross section, it may experience higher stresses, leading to a higher density of fibrous proteins and hence higher elastic modulus.

Also, it was possible that there were age-related effects since the ligament specimen was obtained from a 60-year-old male. Matrix proteins experience increased cross-linking as they age, reducing the elasticity of elastin (Niewoehner et al., 1975) and increasing the stiffness of collagen (Schneider and Kohn, 1982). It has also been observed that the histoarchitectural arrangement of collagen fibers of geriatric vocal folds are less organized (Gray et al., 2000) and curved irregularly (Ishii et al., 1996). Such age-related changes do indeed affect the biomechanical properties of vocal fold tissue. Zhang et al. (2006) have determined the age dependence of the biomechanical properties of male vocal fold tissue, and found that most age-related changes occur below age 60, and that properties are much less age dependent above that age. The situation found in the specimen of concern to the present study thus may be representative of the age group above 60 years for which biomechanical changes in the tissue can contribute to alterations in communication (Torre and Barlow, 2009).

The fundamental frequencies of the varying cross-section models were predicted to be higher than those predicted for the constant cross-section models. Also, the spatial gradient in modulus decreased the fundamental frequency for the varying cross-section case. Consequently, the nonlinear variation in geometry and the heterogeneous modulus must be accounted for in models of vocal fold mechanics and vibration. For the case of isotropic tissue mechanical properties, the change in eigenfrequency is attributed to an emerging of an effective vibration length. If the cross-section geometry is reduced in the mid-membranous vocal fold region then deflection will predominantly occur towards this domain, thus effectively shortening the length of the ligament. An increased modulus in the mid-membranous vocal fold region counters this effect and increases the effective length. The degree of anisotropy also showed a great impact on the predicted eigenfrequencies but altered the eigenmodes little. The findings of the specific problem addressed here bears similar outcomes as a study on the vibration and sound characteristics of musical instruments (Suits, 2001) where homogeneous elastic solids were considered.

This finding is attributed to the changes in rotatory inertia along the ligament and to the increase in the contribution from transverse shear deformation as the ratio of E_z / G_xz increases with increasing anisotropy. A beam theory accounting for rotatory inertia and transverse shear deformation (Timoshenko, 1922) predicts that the local influence of rotatory inertia scales as r² = I / (AL²), where I = D⁴π / 64, and that shear deformation scales with the non-dimensional parameter s² = [(EI) / (κL²AG)], where the Timoshenko shear coefficient κ is a non-dimensional coefficient depending on cross-section geometry and Poisson’s ratio. In the case of the present problem and a circular cross section, one can write r² = D² / (16L²) and s² = [(E_z / G_xz)(D² / 16κL²)]. As the diameter and the degree of anisotropy vary within the ligament the contribution of rotatory inertia and transverse shear deformation will vary along the distance from the vocal process. Close to the cartilages the diameter is large but the anisotropy is small while towards the mid-membranous vocal fold region the diameter is small but the anisotropy is large. Rotatory inertia is large towards the cartilages and reduced in the mid-membranous section, thus increasing the flexibility of the tissue and lowering its fundamental frequency. Furthermore, as [max(D)]² / [min(D)]² = 5.06 / 1.9 = 2.6 the contribution of transverse shear deformations are dominated by the ratio E_z / G_xz and increase the flexibility of the tissue and lowering its fundamental frequency except for small values of anisotropy. Such arguments also explain why the results for F₀ for the isotropic case deviates from the power law found for higher anisotropies as depicted in Fig. 7. For a low degree of anisotropy the vibration response is dominated by the spatial dependence of the cross-section geometry, while above a critical level of anisotropy, here (E_z / E_x) ≥ 10, the spatial dependence of the anisotropy dominates the response.

5. Conclusion

Uniaxial tensile deformation testing was performed on an excised vocal ligament with a spatially varying cross-section. Using digital image correlation, the spatial distribution of tensile strain (i.e., deformation field) was obtained and was found to be heterogeneous, with the smallest deformation observed at the mid-membranous vocal fold region. This heterogeneous displacement field was used to calculate the elastic modulus locally, which was found to vary greatly depending on the spatial location along the vocal ligament. The mid-point region was estimated to be 10 times stiffer than the anterior and the posterior regions (i.e., the macula flavae). These results were implemented into isotropic finite element models to observe their effect on the fundamental frequency. Results showed that the nonlinear variation in geometry of the vocal ligament impacted the frequency more than the spatially varying elastic modulus but interactions between the two effects exist. Additionally, finite element models with transversely isotropic material descriptions were created to study the fundamental frequency, with a micromechanical model assuming locally varying volume fraction of fibrous proteins to account for the spatially varying elastic modulus. It was found that the degree of anisotropy (expressed as a modulus ratio) had a substantial impact on the fundamental frequency. The transverse shear deformation was determined to be the critical parameter in regulating the frequency for transversely isotropic models. The present results suggest that the Euler-Bernoulli beam theory for the vibration analysis of vocal folds should be augmented or substituted with Timoshenko’s beam theory. Such a theory would especially be needed if overtones are to be predicted (Suits, 2001). Clearly, as enhanced constitutive descriptions of the vocal tissue become relevant, the theories describing the function of the tissue need to expand accordingly. While the present study focuses on rather small magnitudes of deformation, it will also be necessary to investigate how spatial property changes interact with the nonlinear deformation characteristics of the vocal fold tissue at large deformations. It would be premature to derive definite clinical implications based on the results of the present study. Nevertheless, our results indicate that phonation can be influenced by the spatially varying geometry, the spatially varying elastic properties, and the degree of elastic anisotropy of the vocal fold ligament. It is likely that the relative size of the contribution of each of these influences differs among different subjects due to anatomical and biomechanical variability in the vocal fold lamina propria. Such differences could contribute to dictate how fundamental frequency control is achieved distinctly among different subjects.

Appendix

The compliance tensor for an isotropic material:

$$S_{\mathit{\text{ijkl}}}=\left[\begin{array}{cccccc}\frac{1}{E}\hfill & \frac{-\nu }{E}\hfill & \frac{-\nu }{E}\hfill & 0\hfill & 0\hfill & 0\hfill \\ \frac{-\nu }{E}\hfill & \frac{1}{E}\hfill & \frac{-\nu }{E}\hfill & 0\hfill & 0\hfill & 0\hfill \\ \frac{-\nu }{E}\hfill & \frac{-\nu }{E}\hfill & \frac{1}{E}\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & \frac{1}{G}\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & \frac{1}{G}\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & \frac{1}{G}\hfill \end{array}\right]$$

The compliance tensor for a transversely isotropy material with the xy plane as the plane of isotropy.

$${\widehat{S}}_{\mathit{\text{ijkl}}}=\left[\begin{array}{cccccc}\frac{1}{E_x}\hfill & \frac{-{\nu }_{\mathit{\text{xy}}}}{E_x}\hfill & \frac{-{\nu }_{\mathit{\text{zx}}}}{E_z}\hfill & 0\hfill & 0\hfill & 0\hfill \\ \frac{-{\nu }_{\mathit{\text{xy}}}}{E_x}\hfill & \frac{1}{E_x}\hfill & \frac{-{\nu }_{\mathit{\text{zx}}}}{E_z}\hfill & 0\hfill & 0\hfill & 0\hfill \\ \frac{-{\nu }_{\mathit{\text{xz}}}}{E_x}\hfill & \frac{-{\nu }_{\mathit{\text{xz}}}}{E_x}\hfill & \frac{1}{E_z}\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & \frac{1}{G_{\mathit{\text{xz}}}}\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & \frac{1}{G_{\mathit{\text{xz}}}}\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & \frac{1}{G_{\mathit{\text{xx}}}}\hfill \end{array}\right]$$

Additionally, the tensor must be symmetric, imposing that $\frac{{\nu }_{\mathit{\text{xz}}}}{E_x}=\frac{{\nu }_{\mathit{\text{zx}}}}{E_z}$ , thus reducing the number of elastic constants needed to only four (E_x = E_y, E_z, ν _zx, and ν _xy).