Orientation of Tie-Lines in the Phase Diagram of DOPC:DPPC:Cholesterol Model Biomembranes

Abstract

We report the direction of tie-lines of coexisting phases in a ternary diagram of DOPC:DPPC:Cholesterol lipid bilayers, which has been a system of interest in the discussion of biological rafts. For coexisting Ld and Lo phases we find that the orientation angle α of the tie-lines increases as the cholesterol concentration increases and it also increases as temperature increases from T=15 °C to T=30 °C. Results at lower cholesterol concentrations support the existence of a different 2-phase coexistence region of Ld and So phases and the existence of a 3-phase region separating the two 2-phase regions. Our method uses the X-ray lamellar D-spacings observed in oriented bilayers as a function of varying hydration. Although this method does not obtain the ends of the tie-lines, it gives precise values (±1°) of their angles α in the ternary phase diagram.

1. Introduction

While it has been intuitively obvious to many biophysicists that the presence of many different lipids in biomembranes should lead to lateral heterogeneity of lipids and proteins (a speculation of one of the authors goes back thirty years¹), “the notion that specific lipids could serve to organize membranes into discrete domains with different properties had received only sporadic attention over the years”² until the last decade which saw an explosion of interest and the establishment of the raft paradigm. Like many paradigms, ‘raft’ may mean different things to different researchers. Nevertheless, lateral heterogeneity is clearly an important focus for biomembrane research.

Lateral lipid heterogeneity is caused by differences in the effective interaction free energies between the different lipids^3–8. Such free energies necessarily involve an entropic component, and therefore cannot be obtained by simple molecular mechanics energy calculations. They can be obtained in principle from atomic level molecular dynamics (MD) simulations⁹, but there is generally insufficient computer time to achieve the equilibrium lateral distribution of lipids unless the initial distribution is fortuitously chosen very close to the correct distribution. Sufficient time is available in coarse grained (CG) simulations^10–13 and infinite time is available in analytic theories^7–8, but in both cases effective interactions must be estimated. One way to obtain effective interactions is to tune them to agree with experimental phase diagrams^{3–5,7–8,14}, and that is another reason why accurate equilibrium phase diagrams could be valuable even if biological rafts consist of smaller, more transient entities that may not be in thermodynamic equilibrium. However, even when the regions of large scale phase coexistence are obtained using fluorescence spectroscopy, the effective interactions are not known until the tie-lines that give the compositions of coexisting phases are determined.

Tie-line determination has been fraught with uncertainty and is a focus of current study^15–19. It would make a considerable difference in the quantitative values of the effective interactions if the cholesterol concentration were only modestly different in the coexisting phases as occurs in some published work²⁰, or if the cholesterol were largely excluded from the fluid ordered Lo phase, as is sometimes qualitatively described in the popular raft literature². Comparing analytic theories^7–8 to phase diagrams with tie-lines could provide an estimate of the effective interaction free energies which could then be used in CG simulations^4–6,21 to provide approximations to the lateral distributions of molecules. These lateral distributions could then be chosen for the initial states of atomic level simulations which can then be tested directly against experimental data. If such a long term multi-faceted program is successful, we will better understand lipid lateral heterogeneity.

The role of this paper within this long term program is to add a probe-free X-ray method to existing spectroscopic methods^{16–20,22–23} and to use it to determine the angles that the tie-lines make relative to the horizontal in ternary phase diagrams of DOPC:DPPC:Chol. However, we do not advocate using our method to locate the ends of the tie-lines and it is clear that our method, which relies on observation of two lamellar D-spacings, does not always succeed even when there is 2-phase coexistence²⁴. Nevertheless, we suggest that our method is more precise than previous methods at obtaining the orientations of the tie-lines in at least one phase diagram of interest.

2. Materials and Methods

DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine), DPPC (1,2-dipalmitoyl-sn-glycero-3-phosphocholine) and cholesterol(Chol) were purchased in lyophilized form from Avanti Polar Lipids (Alabaster, AL) and used as received. Fresh stock solutions were prepared by dissolving individual components in chloroform. Appropriate amounts of these stock solutions were then mixed for each desired DOPC:DPPC:Chol mole percentage to make duplicate aliquots of the components and the chloroform was evaporated. Table 1 lists the composition of the samples studied in the present work; uncertainties in mole percentages were estimated to be 0.04% mostly due to weighing uncertainties. (We note that dry phospholipids typically have one-two tightly bound water molecules so all apparent cholesterol concentrations reported in this paper should be increased by multiplying them by approximately 1.02–1.04 and this makes at most a negligible difference of 0.1–0.2° in our reported angles of the tie-lines). Chloroform: trifluoroethanol in volume ratio 2:1, which is desirable for forming oriented bilayers of these mixtures with small mosaic spread, was then added to the dry mixture and vortexed. An aliquot containing about 4mg of the components, was plated onto the surface (1.5 × 3 cm) of a polished silicon wafer using the rock-and–roll procedure²⁵ to prepare a sample of oriented lipid bilayers consisting of ~ 2000 bilayers. After drying for one day in a glove box with a solvent-rich atmosphere and for another day in a fume hood, the sample on the wafer was then trimmed to a 0.5 × 3 cm strip and was stored at 2 °C in a dessicator prior to X-ray measurements.

Table 1.

Compositions of samples and their phases at T=15 °C.

Sample name	Compositions (mole %)			Phases
	DOPC	DPPC	Cholesterol
M25	30	45	25	Lo-Ld
L30	40	30	30	Lo-Ld
L21.5	44.6	33.9	21.5	Lo-Ld
L21	44.8	34.2	21	Lo-Ld
L20	45	35	20	Lo-Ld
L17	40	43	17	Lo-Ld
L15	40	45	15	Lo-Ld
L12.5	40	47.5	12.5	2 or 3
L10	40	50	10	Lo-Ld-So
L8	42	50	8	Lo-Ld-So
L5	45	50	5	Ld-So
L0	50	50	0	Ld-So
R35	25	40	35	Lo-Ld
R30	15	55	30	Lo-Ld
R29	15.2	55.8	29	Lo-Ld
R20	20	60	20	Lo-Ld
R12.5	27.5	60	12.5	2 or 3
R10	25	65	10	Lo-Ld-So
R6	30	64	6	Lo-Ld-So
R5	30	65	5	Lo-Ld-So
R4.5	30	65.5	4.5	Ld-So
R4	30	66	4	Ld-So
R0	30	70	0	Ld-So
S37.5	32.5	30	37.5	1

X-ray data were taken using a Rigaku (Woodlands, TX) RUH3R microfocus rotating Cu anode (λ=1.54 Å) at 40kV × 100mA power, equipped with Xenocs (Sassenage, France) FOX2D focusing collimation optics with beam width 1 mm. Lamellar intensity data were collected with a Rigaku Mercury CCD two-dimensional detector with 1024× 1024 pixel array (0.068 mm/pixel) while rotating the sample angle θ between −3° and 7° at 10°/s for 120–180s to include Bragg angles for all orders of diffraction²⁶. The sample to detector distance S (= 103.5 mm) was calibrated using a silver behenate sample on a Si wafer with the same geometry as the lipid samples.

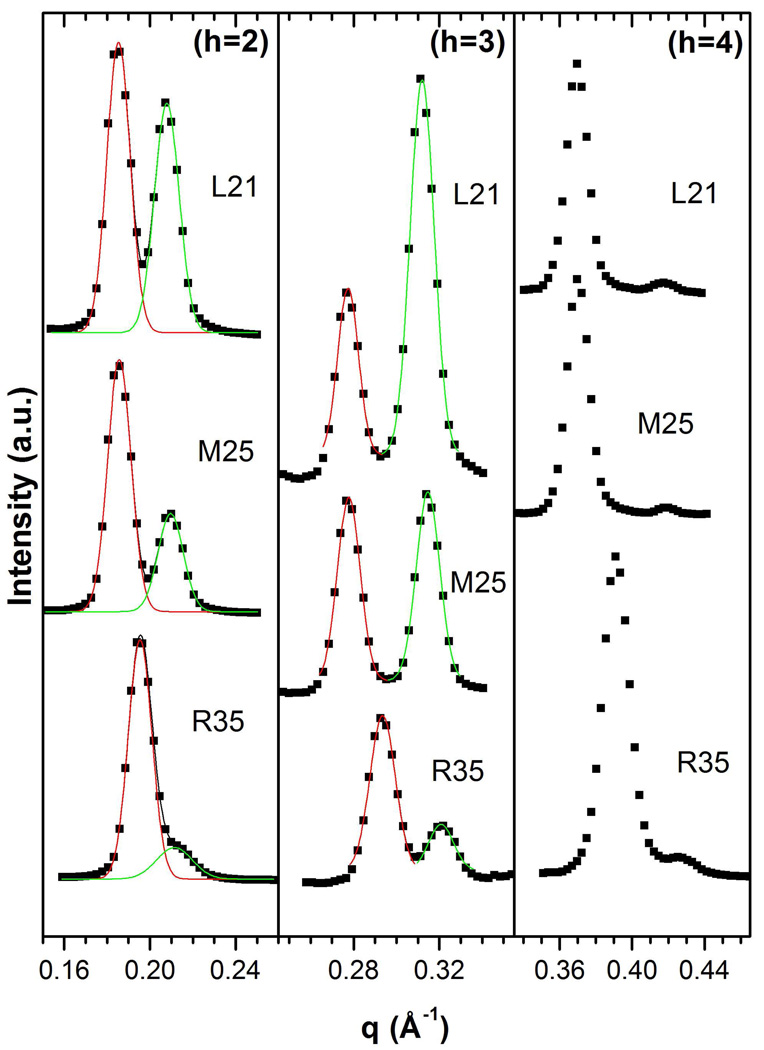
The D-spacings of the lamellar X-ray diffraction data such as those in Fig. 1 were usually obtained simply from the peak positions of well separated peaks. For samples where the difference between D-spacings was small, such as the second order peaks of the R35 sample in Fig. 1, the OriginLab (Northampton, MA) peak fitting module was employed to separate the overlapping peaks and obtain the D-spacings as shown in Fig. 1. Typically, orders h=2 and h=3 were used (the h=1 peak was distorted by beam-stop absorption and the h=4 order of the Ld phase was usually very weak due to fluctuation degradation²⁷.)

Figure 1.

Lamellar peak data (squares) versus q for orders h=2–4 for three samples, L21, M25 and R35. The green and red lines are Gaussian fits and uncertainties in their peak positions correspond to 0.2 Å uncertainties in D-spacings.

Dried, oriented multilayer samples (~10µm thick) were mounted onto a Peltier element on a rotation stage inside a hydration chamber²⁶. The level of hydration was varied by changing the Peltier current and a series of lamellar repeat D-spacings were determined as a function of increasing hydration level. After setting a new Peltier current the sample was deemed to be equilibrated when there was no further shift in the D-spacings. Equilibration typically took about one hour, but as much as 24 h near 3-phase regions. Radiation damage was minimized by moving the sample laterally in the beam after multiple exposures. Data were obtained at T=15±0.1°C unless noted otherwise.

3. Results

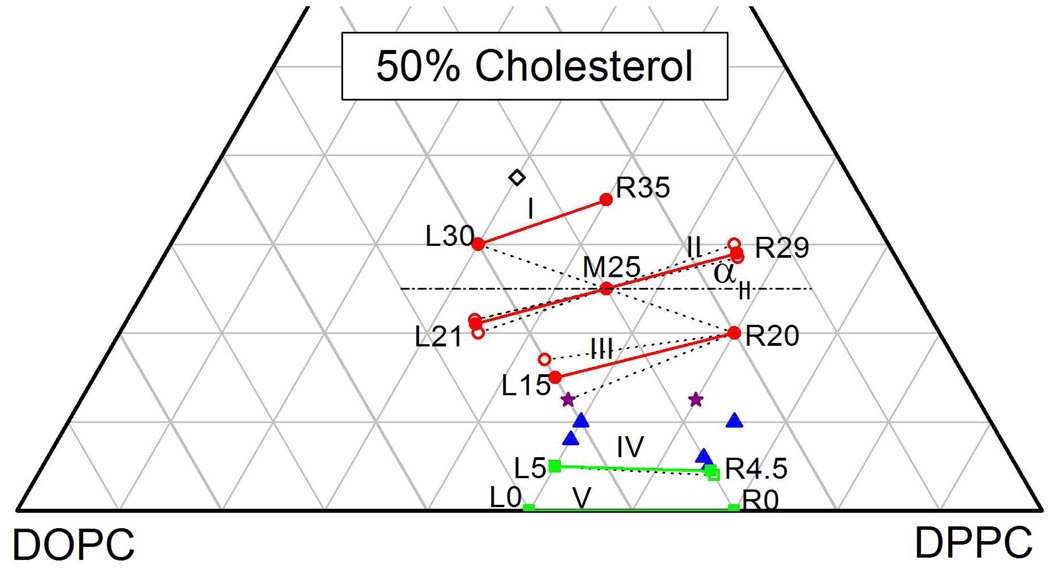
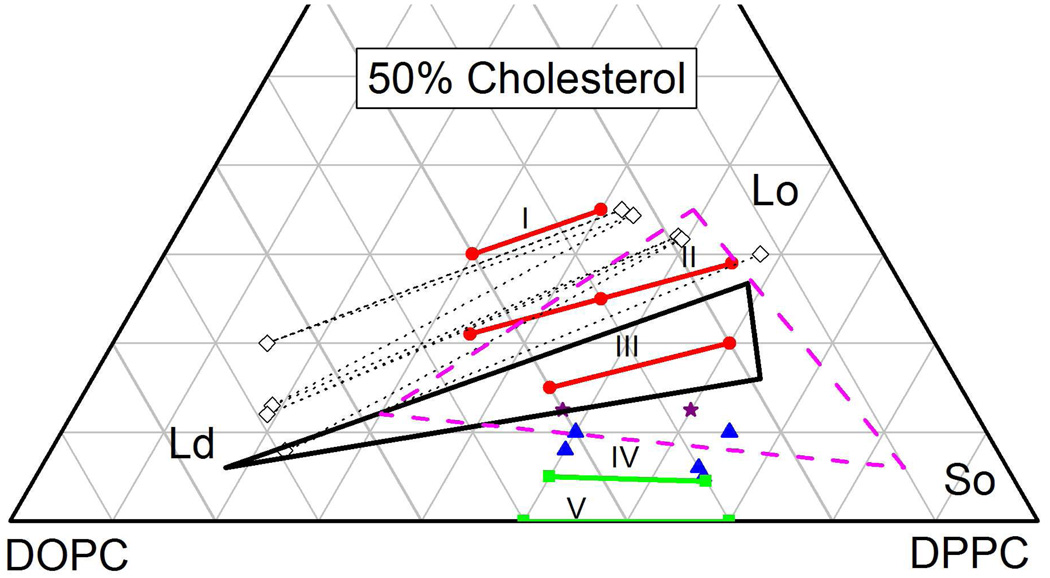
Figure 2 shows a DOPC:DPPC:Chol ternary composition diagram on which are located the compositions of some of the samples we have studied. We give a short name for each composition using L for samples to the left, R for samples to the right, and M for a middle sample, followed by a number that gives the mole percentage of cholesterol. Table 1 lists the short names of all samples studied and it gives their full DOPC:DPPC:Chol compositions.

Figure 2.

A truncated ternary DOPC:DPPC:Chol Gibbs composition triangle showing compositions of studied samples with some of their short names. Table 1 lists all numerical compositions by name. Circles (red) indicate compositions with Ld-Lo coexistence, squares (green) indicate Ld-So coexistence, triangles (blue) indicate Ld-Lo-So coexistence, stars (purple) could be either in 2-phase or in 3-phase coexistence, and the open (black) diamond is in a single phase. The solid lines labeled with Roman numerals show the orientations of our best determined tie-lines at T=15°C and the dashed lines show orientations that were determined not to be tie-lines. The ends of the tie-lines were not determined in this study, so the tie-lines shown are partial fragments of the tie-lines that must extend further in both directions.

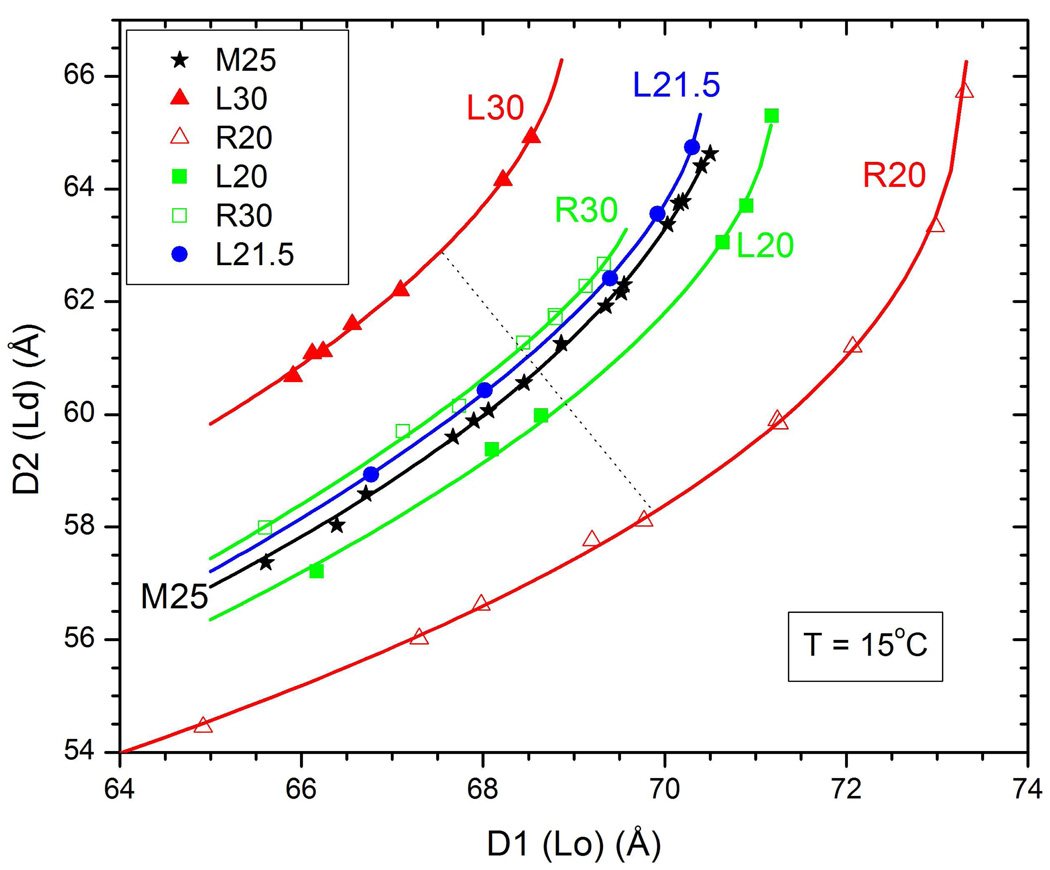
Figure 3 shows the two lamellar D-spacings that were obtained at many different hydration levels. Comparison of the relative intensities of the peaks for the M25 composition with the L21 composition in Fig. 1 shows that the Lo phase has the larger D1 spacing and the Ld phase has the smaller D2 spacing. As expected, both D-spacings increase with increasing hydration. The smooth curves in Fig. 3 are fits to the function

$${\mathrm{D}}_2={\mathrm{D}}_{2\text{max}}-\mathrm{c}{({\mathrm{D}}_{1\text{max}}-{\mathrm{D}}_1)}^{\mathrm{p}},$$ (1)

which is merely a convenient fitting function that has no special theoretical significance. Values of p were typically between 0.5 and 0.7 and values of D_1max and D_2max were similar to D-spacings obtained from fully hydrated, isotropic multilamellar vesicles (MLV).

Figure 3.

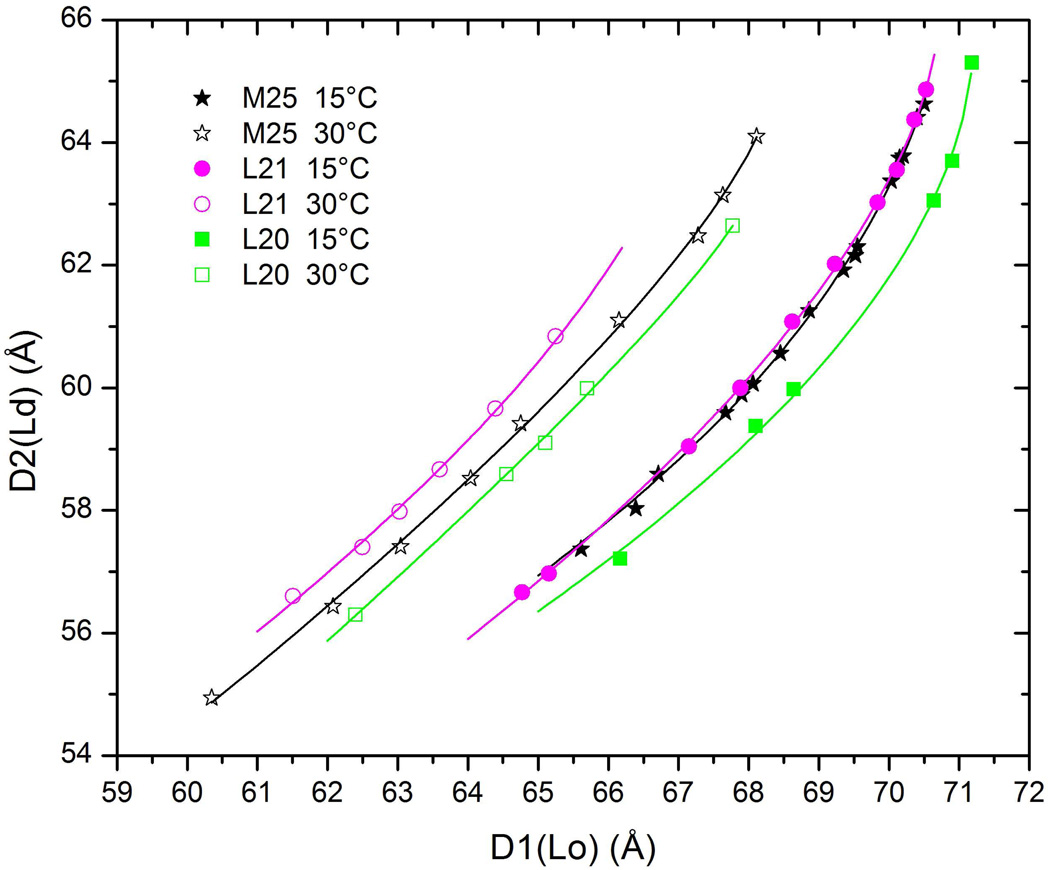
D2 is the repeat spacing of the Ld phase and D1 is the repeat spacing of the Lo phase for many different equilibrated hydration levels for six samples with short names indicated in the legend. Lines are fits of Eq. 1 to the data. Deviations of individual D values from these lines are consistent with the uncertainties obtained from fitting the data in Fig. 1. The different L and R samples are equidistant from the M25 sample in the composition triangle in Fig. 2. For quantitative error analysis average differences between hydration curves along several lines like the dotted line were used.

If two samples are on the same tie-line, then the intrinsic properties of the two phases must be the same for the two samples even though the amounts of the two phases will necessarily be different for the two samples. Our method uses the hydration curves for the lamellar D-spacings as the assay for intrinsic properties. Figure 3 clearly shows that the compositions L30-M25-R20 in Fig. 2 cannot be on a tie-line because the hydration curves do not overlay. By this assay the compositions L20-M25-R30 are closer to being on a tie-line and the result that the L20 curve in Fig. 3 is below the M25 curve while the L21.5 curve is above the M25 curve suggests that the true tie-line through M25 has a cholesterol concentration of the L composition between that of L21.5 and that of L20. Figure 4 indicates that the compositions L21-M25-R29 in Fig. 2 are on a line which is even closer to being on a tie-line. This line, named tie-line II in Fig. 2, makes an angle α=15.2 ° relative to the horizontal.

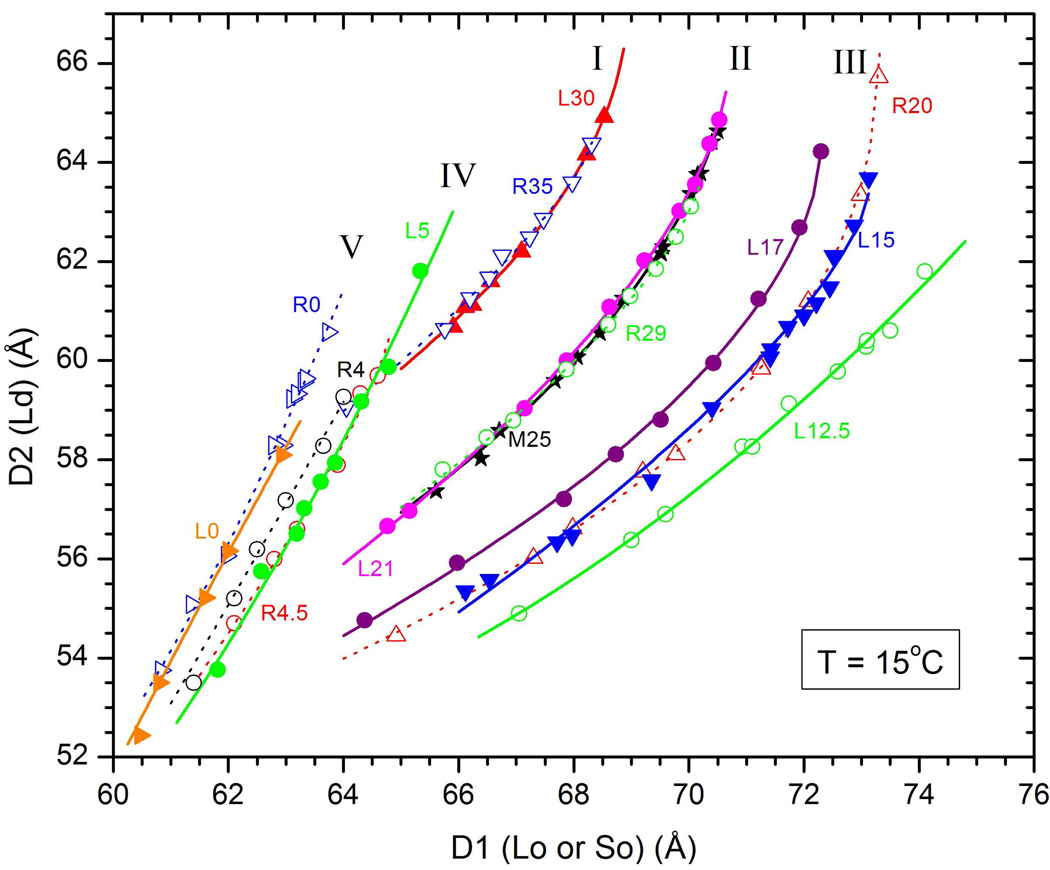
Figure 4.

Double D-spacing data that locate tie-lines: I (L30-R35 with α_I=19.2°), II (L21-M25-R29 with α_II=15.2°), III (L15-R20 with α_III=14.1°), IV (L5-R4.5 with α_IV=−2°) and V (L0-R0 with α_V=0). Solid lines are fits to the L data (solid symbols) and dotted lines are fits to the R data (open symbols).

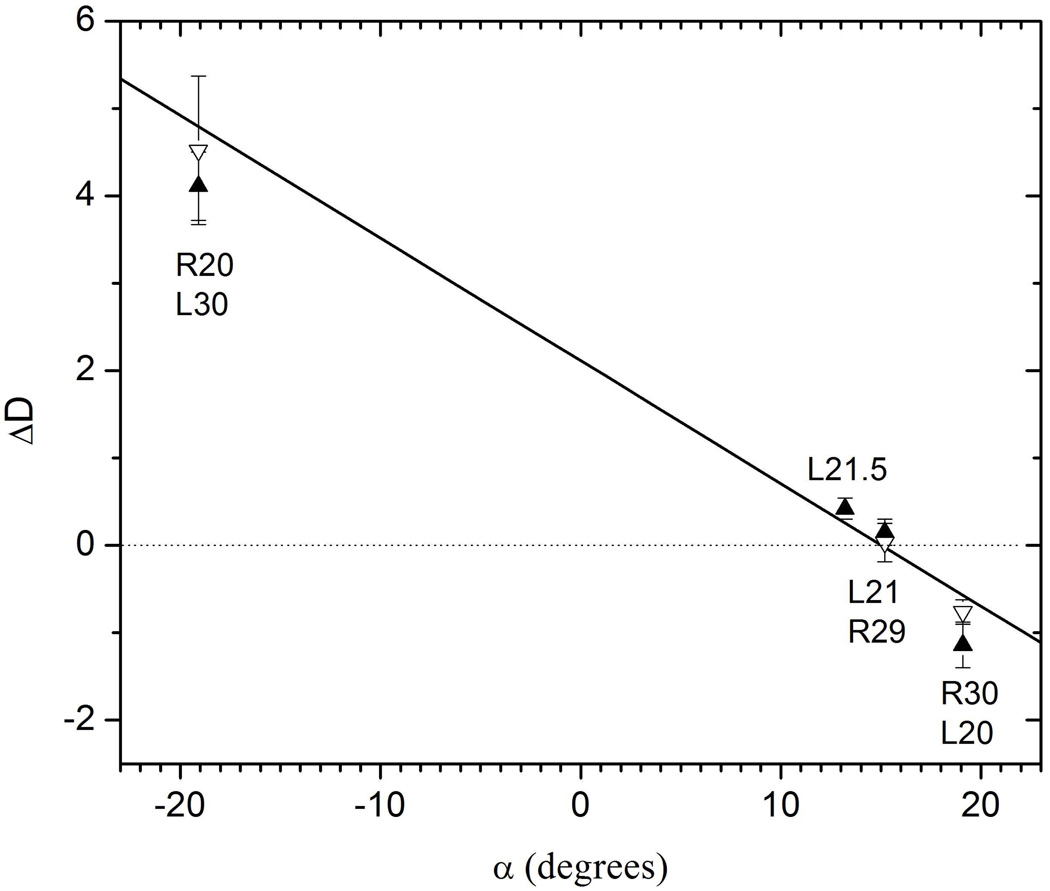
We have also quantified the differences ΔD between the M25 curve in Fig. 3 and the L and R curves in Figs. 3 and 4. We defined ΔD to be the average distance to the M25 hydration curve measured along the perpendicular to the M25 hydration curve (see dotted line in Fig. 3). A linear fit to the results in Fig. 5 suggests that the tie-line through M25 has an angle α_II=15.0±0.5°, which is indistinguishable from line II in Fig. 2.

Figure 5.

Differences ΔD between curves of the double D-spacing data in Figs. 3 and 4 relative to the M25 data as a function of α which is the angle of the lines passing through M25 in Fig. 2. Solid symbols are for the L compositions and the open symbols are for the R compositions. The linear fit to all data is shown by the solid line.

Figure 4 also shows that the compositions L30 and R35 yield another tie-line, named I in Fig. 2, to comparable accuracy as tie-line II through M25. Compositions L15 and R20 in Fig. 4 yield tie-line III in Fig. 2. As a function of increasing cholesterol α, relative to the horizontal, increases from α_III=14.1° to α_II=15.2° to α_I=19.2°.

Hydration curves for low concentrations of cholesterol are also shown in Fig. 4. The angle of the tie-line for 0% cholesterol α_V is, of course, exactly zero. Tie-line IV through the L5-R4.5 compositions in Fig. 2 has a slightly negative angle α_IV = − 2°. Importantly, the hydration curve for tie-lines IV and V shift in a regular way with cholesterol concentration. Also, the tie-lines I, II and III shift regularly, but there is clearly a considerable difference between the I–III set of hydration curves in Fig. 4 and the IV–V set. This indicates that at least one of the coexisting phases is different. Comparison of the intensities of the diffraction peaks for the L5 and R4.5 or the L0 and R0 compositions shows that the smaller D-spacing is the Ld phase and the larger D-spacing is the different phase which is often just called a solid (So) phase.

The two samples indicated as 2-phase or 3-phase in Fig. 2 (purple stars) initially showed three D-spacings but they also had diffraction peaks that did not index well. After equilibrating for nearly 24 h these samples showed only two D-spacings.

Figure 6 shows the effect on the double D plot of raising the temperature from T=15°C to 30°C. Clearly, at 30 °C the L21 sample is no longer on the tie-line through M25. However, interpolation between the hydration curves of the L21 and the L20 samples indicates that the tie-line through M25 at T=30 °C has rotated from α_III=15.2° at T=15 °C to an angle α_II~17.1° which is midway between the angle of 15.2° of line L21-M25 and the angle 19.1° of line L20-M25. However, this rotation was not linear as a function of temperature; no discernable rotation was observed between T=15 °C and T=20 °C and the rotation between T=20 °C and T=25 °C was smaller than the rotation between T=25 °C and T=30 °C.

Figure 6.

Temperature dependence of the double D-spacing data which show that α_II rotates from 15.2° at 15 °C to 17.1° at 30 °C. Data not shown indicate that dα_II/dT increases with increasing T.

4. Discussion

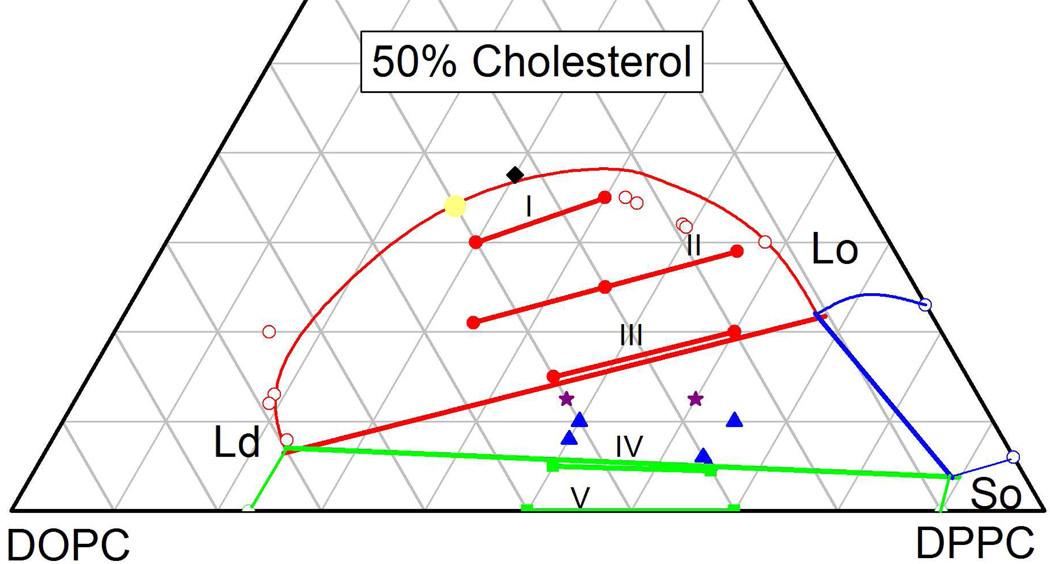
Figure 7 first compares our results with the NMR results of Veatch et al. (VSKG)¹⁸. The angle α_I=19.1° of our tie-line I is in excellent agreement with the earlier results at the higher cholesterol concentrations. As can be seen in Fig. 7, the VSKG orientations are subject to much more uncertainty than our uncertainty of 1°. Even within the uncertainties, however, as cholesterol concentration is decreased, our α_II=15.2° is somewhat smaller than the previously determined tie-lines. The greatest discrepancy is that our tie-line III is in the middle of their three-phase region and this raises a methodological issue that we address next.

Figure 7.

NMR tie-lines of VSKG¹⁸ are shown by dotted straight lines and open diamonds show endpoints at the 2-phase Ld-Lo boundary. The Ld-Lo-So 3-phase region is shown as a solid black triangle¹⁸ and the dashed magenta triangle is the 3-phase region from DCJ¹⁹. As in Fig. 2, the orientation (not the endpoints) of our tie-lines are labeled I–V. The red circles and the green squares are in 2-phase regions, the blue triangles are in a 3-phase region and the purple stars could be either in 2-phase or 3-phase regions. All results are for T=15 °C except for T=18 °C for the 3-phase triangle of DCJ¹⁹.

As has been discussed before²⁴ observation of N different D-spacings in a well equilibrated sample suffices to conclude that there are N phases present. However, even if there are N phases present in the individual bilayers, it is not necessary that there be N different D-spacings. Aside from the accidental degeneracy that two or more phases may have the same D-spacing, more importantly, frustration in obtaining regular stacking, especially of small domains, may result in a smaller number of D-spacings than the number of phases. In particular, one might also have only one D-spacing even when there are two phases present, as was reported for 1:1:1 DOPC:bBSM:Chol²⁸. Indeed, based on previous unsuccessful attempts to observe two D-spacings for DPPC:Chol mixtures²⁹ we decided not to pursue that side of the ternary phase diagram in this study. We might also add that we had difficulty observing two D-spacings in POPC:ESM:Chol mixtures (ESM is egg sphingomyelin), although we did observe double D-spacings in DOPC:ESM:Chol.

Therefore, our result that the two compositions on our tie-line III only exhibited two D-spacings did not, by itself, imply that those samples had only Ld-Lo phase coexistence. If the So phase had been present, it could have been silent to our assay by not exhibiting a separate D-spacing. However, we performed a simple test that ruled out this possibility. Each sample with an overall composition within a 3-phase Ld-Lo-So region is, of course, a mixture of three phases, each of which must have a composition given by one of the corners of the 3-phase triangle. Therefore, the individual phases for any sample with overall composition within a 3-phase region must have exactly the same properties, including the D-spacings. This is different from the case of samples with overall composition in a 2-phase region where the end points of two different tie-lines may have different compositions and therefore different hydration curves. Even if one of the phases in a 3-phase region is silent, the other two phases are then required to have the same hydration curves for any composition in the 3-phase region that also has the same silent phase. Fig. 4 shows that this was not the case for tie-line III. Instead, the hydration curves shifted systematically with small changes in the cholesterol concentration, proving that tie-line III was a binary phase tie-line between Ld and Lo.

Although Davis et al. (DCJ) ¹⁹ did not report the orientations of tie-lines, Figure 7 emphasizes an incompatibility in their 3-phase triangle with both our and the VSKG tie-lines¹⁹. The Ld-Lo side of the 3-phase region is also the limiting tie-line for the Ld-Lo 2-phase region, and the DCJ orientation of this line is considerably greater than, and cuts through, the others in Fig. 7. Another significant difference between the two reported results is that the angle of the Ld-So side of the triangle is negative in DCJ¹⁹ and positive in VSKG. (Although generous uncertainties were quoted by VSKG¹⁸, within those uncertainties the VSKG angles are all positive.) Therefore, on the bottom of the 3-phase triangle, our negative angle for tie-line IV (α_IV = −2°) agrees better with DCJ than with VSKG. It is clear from the compositions of the samples that had three D-spacings (blue triangles in Fig. 7) that our 3-phase triangle is shifted to lower cholesterol concentrations from either NMR result. There is a difference in samples in that the NMR uses deuterated DPPC and that is known to reduce the main transition temperatures, but there does not appear to be a large enough temperature dependence to account for all the differences with our results. In any case, there are large differences between the 3-phase triangles determined by NMR^18–20 studies which used the same deuterated lipids.

We were hopeful that our method could obtain, not only the orientations of the tie-lines, but also their end points. If all the lipid is in either the Lo or the Ld phase, then extrapolating the integrated intensities under the diffraction peaks to zero as a function of composition along the tie-lines straightforwardly locates the end points where that phase is no longer present. Our attempts to do this gave clearly unphysical results. There is a qualitative trend in the relative intensities of the different phases along a tie-line, which is one of the ways we identified which D-spacing corresponded to which phase. (The other way is that the higher orders of the Ld phase become more diffuse and less intense with increased hydration.) However, due to the stacking frustration²⁴ mentioned three paragraphs earlier, a non-zero fraction of the bilayers are silent regarding lamellar repeat diffraction, and that fraction is not necessarily the same for the different phases and/or for the different compositions along a tie-line. It was therefore not possible to perform a quantitative extrapolation to determine the ends of the tie-lines. Our original intention was to use wide angle X-ray scattering (WAXS) which, like NMR, is sensitive only to the internal structure of individual bilayers rather than to the stacking superstructure required by low angle X-ray scattering employed in this paper. Unfortunately, there was not enough contrast in the WAXS data to determine tie-lines unequivocally.

A caveat should be added here. One might question whether the same phases are present in properly stacked bilayers that exhibit D-spacings as in the more amorphous parts of the sample where the bilayers are not properly stacked. In other words, does the interaction between bilayers affect the phases and their properties? (This would also be a concern for NMR studies on MLV systems.) However, interbilayer interactions are weak compared to the intrabilayer interactions that determine the phases provided there is sufficient water between the bilayers in the stacks. This is why we carried our hydration curves to high hydration levels where the interbilayer water layer is large compared to the thermally effective range of the interbilayer interactions when considered on a per molecule basis. Another way to think about this is that the interbilayer interactions are too weak to stack the large scale bilayers in the entire sample in an orderly way during any reasonable equilibration time that is long enough for lateral diffusion to bring about phase separation within individual bilayers. We did anneal some of our samples, and this changed the relative intensities of the peaks corresponding to the different D-spacings, while keeping the same D values.

A possible source of artifactual non-equilibrium that could be hypothesized is that the in-plane composition of domains formed in the initially dry samples persists rather than equilibrating as the samples are slowly hydrated, and this would have meant we were obtaining the phase behavior of dry samples. Our data in Fig. 6 shows that this could not have been the case. The M25 and L21 samples have overlaying hydration curves at 15°C and would therefore have had to have overlaying hydration curves at 25°C if they did not undergo in-plane equilibration, but our data clearly negate this hypothesis. We also found that when one sample was heated into a single phase region, it had only one D-spacing, and then when it was cooled again, its hydration curve was identical to its original hydration curve. Finally, one can estimate from coefficients of lateral diffusion that mixing on length scales of 0.5 mm should occur within the equilibration time allowed for our experiments; larger scale in-plane heterogeneity was eliminated by the hydration curves being the same for different locations on the sample and our beam width of 1 mm.

Let us now suggest a phase diagram in Fig. 8 that is based on our data and other data in the literature. The endpoints of the 2-phase region of DOPC:DPPC were obtained many years ago³⁰. Our observation of three D-spacings in some samples (Table I) and the qualitative difference in the hydration curves for tie-lines IV and V compared to tie-lines I–III in Fig. 4 are consistent with the usual conclusion that there is a three-phase coexistence region. Our tie-line IV and our observation of three phases in R5 suggests that the orientation of the Ld-So side of the 3-phase triangle be drawn as shown. We also suggest that the orientation of the Ld-Lo side of the 3-phase triangle is close to that of our tie-line III. As mentioned above, our samples indicated by stars in Fig. 8 could have been either in a 2-phase or a 3-phase region, so our data would allow the Ld-Lo side to be lowered considerably in Chol concentration compared to what is shown. However, keeping the same orientation would require that it intersect at the Ld vertex of the 3-phase triangle far from the endpoints reported by VSKG¹⁸. If we keep that same Ld vertex and were to rotate the Ld-Lo side of the 3-phase triangle, its angle would decrease much more compared to tie-line III than the decrease in angle from tie-line II to tie-line III. Furthermore, three D-spacings have been reported for unoriented MLV samples of DOPC:DPPC:Chol 44:44:12 at T=22 °C³¹; this is consistent with our placement of the Ld-Lo side shown in Fig. 8. It may also be noted that our angle of ~15° agrees quite well with the angle of ~13° shown for the Ld-Lo 3-phase boundary of DOPC/DSPC/Chol¹⁷. Although we have drawn the Ld-Lo coexistence curve at its DOPC end to conform to the VSKG data, we allow it to move away from many of the compositions between Lo ends of the I and II tie-lines because we would not have been able to see two D-spacings in our samples if they had been at the boundary of the 2-phase region. Earlier NMR work (VPGK²⁰) showed the 2-phase region extending to 5% DOPC, even further than the 10% DOPC in our Fig. 8. These considerations locate the Lo vertex of the 3-phase triangle. We also indicate a possible location for a consulate (critical) point, by qualitatively taking into account that the angles of the tie-lines increase with increasing cholesterol concentration; our choice is about halfway between those inferred from VSKG¹⁸ and VPGK²⁰.

Figure 8.

Suggested phase diagram at T=15 °C. The Ld-So 2-phase region is enclosed by three straight green lines and contains our IV and V tie-line fragments; the two open green circles at zero Chol show the coexistence compositions of Mitsui³⁰. The Ld-Lo 2-phase region is enclosed by one straight and one curved line and it contains our I, II and III tie-line fragments; the open red circles show the coexistence compositions of VSKG¹⁸. The Lo-So 2-phase region is enclosed by two straight and one curved blue lines; the open blue circles at zero DOPC show the coexistence compositions of Vist and Davis³⁴. The yellow point suggests the location of an upper consulate (critical) point and we found only one D-spacing for the composition of the black diamond.

It might seem that we cannot say much about the So vertex of the 3-phase triangle because we have no data in that region. However, rigorous thermodynamics in the form of Schreinemakers’ rule^32–33 pins that point down fairly closely. The rule can be illustrated using Fig. 8. At the Ld vertex a smooth extension of the Lo-Ld coexistence curve would enter the Ld-So 2-phase region and an extension of the So-Ld coexistence curve would enter the Ld-Lo 2-phase region. Another allowed possibility is at the Lo vertex where extensions of both the Ld-Lo and the So-Lo coexistence curves would enter the 3-phase triangle. It is not allowed that one of the extensions enters a 2-phase region and the other enters the 3-phase triangle, and it is not allowed thermodynamically that both extensions enter a one phase region. Given the open green circle on the DPPC-DOPC axis, the blue circle on the DPPC-Chol axis, the Lo vertex and the So-Ld side of the 3-phase triangle, the So vertex is constrained to greater than 86% and less than 93% DPPC. This, in turn, constrains the 2-phase coexistence lines incident on the Lo vertex. As drawn in Fig. 8, the extension of the Ld-Lo coexistence line enters the 3-phase triangle, so the extension of the So-Lo line must also. This does not allow drawing a straight line from the open circle at DPPC:Chol 77:23 and we have therefore drawn it curved. (Schreinemakers’ rule is often violated in the lipid ternary phase diagram literature, for example, see vertices B and C in Fig. 9a of DCJ¹⁹ and the Lo vertex of Fig. 3a of VSKG¹⁸.)

The precision of our technique allows us to obtain quantitative data for two features that could be important for discriminating theories. One is that the orientation of the tie-line at a given composition is likely to change with temperature. We found that the angle of tie-line II increases, though not uniformly, from ~15° at T=15 °C to ~17° at T=30°C. Rotation of a tie-line with temperature was first shown by VPGK²⁰, although their reported rotation was rather larger than ours, about 10° between T=20°C and T=30°C, and the angle of their tie-line closest to our tie-line II was only about 5° at T=20 °C. Compared to the earlier NMR data, VSKG¹⁸ also had a similar rate of increase with T although the angle for the tie-line closest to our tie-line II was larger at about 20° at T=20 °C.

The other feature is that the orientations of tie-lines change with composition within 2-phase regions. We have found for DOPC:DPPC:Chol at T=15 °C that the angle increases with increasing cholesterol concentration in the Ld-Lo 2-phase region. This agrees well qualitatively with the theoretical phase diagram shown in Fig. 2 of Putzel and Schick⁷. The theory of Idema et al.³⁵ has this behavior in their Fig. 3, which, however, does not have a 3-phase region. A recent theoretical phase diagram of Radhakrishnan³⁶ has strongly varying tilt angle in the opposite direction, but that paper focused on higher temperatures at which there is no 3-phase region. Importantly, the same condensed complex theory but with different parameters has tie-lines with quite different angles⁸ which illustrates the point that obtaining theoretical phase diagrams that agree with tie-line data should help to reduce the number of unconstrained theoretical parameters.