Abstract
To demonstrate the relationship between lingual myoarchitecture and mechanics during swallowing, we performed a finite-element (FE) simulation of lingual deformation employing mesh aligned with the vector coordinates of myofiber tracts obtained by diffusion tensor imaging with tractography in humans. Material properties of individual elements were depicted in terms of Hill's three-component phenomenological model, assuming that the FE mesh was composed of anisotropic muscle and isotropic connective tissue. Moreover, the mechanical model accounted for elastic constraints by passive and active elements from the superior and inferior directions and the effect of out-of-plane muscles and connective tissue. Passive bolus effects were negligible. Myofiber tract activation was simulated over 500 ms in 1-ms steps following lingual tip association with the hard palate and incorporated specifically the accommodative and propulsive phases of the swallow. Examining the displacement field, active and passive muscle stress, elemental stretch, and strain rate relative to changes of global shape, we demonstrate that lingual reconfiguration during these swallow phases is characterized by (in sequence) the following: 1) lingual tip elevation and shortening in the anterior-posterior direction; 2) inferior displacement related to hyoglossus contraction at its inferior-most position; and 3) dominant clockwise rotation related to regional contraction of the genioglossus and contraction of the hyoglossus following anterior displacement. These simulations demonstrate that lingual deformation during the indicated phases of swallowing requires temporally patterned activation of intrinsic and extrinsic muscles and delineate a method to ascertain the mechanics of normal and pathological swallowing.
Keywords: multiscale model, diffusion tensor imaging tractography, Hill's three-element model, muscle mechanics
the tongue is an intricately configured muscular organ, which is responsible for the manipulation and transport of food in the oral cavity during swallowing, as well as the variations in shape and stiffness occurring during human speech. The tongue's exquisite mechanical virtuosity is closely linked with the complexity of its myoarchitecture (11, 17) and the resulting patterns of regional muscle activation and relaxation (4, 5, 26–28, 35). Lingual myoarchitecture consists of a large array of variably aligned and extensively interwoven intrinsic and extrinsic muscles. The intrinsic musculature consists of a core region of orthogonally aligned fibers, contained within a sheathlike bundle of longitudinally oriented fibers. The intrinsic fibers are delicately merged with extrinsic muscles that modify shape and position from the superior (palatoglossus), posterior, (styloglossus), and inferior directions (genioglossus and hyoglossus). Accordingly, the relationship between tissue structure and mechanical function is fundamental for the quantitative understanding of normal and abnormal physiology. While previous modeling has provided methods to examine these relationships (46), further development of such methodology has been hindered by difficulties representing the tissue's myoarchitecture at a spatial scale consistent with practical mechanical simulations.
To delineate lingual myoarchitecture, we employed magnetic resonance imaging methods, which derive myocyte alignment in muscular tissue as a function of the directional specificity of water diffusion (1, 37). Myoarchitecture may thus be displayed at the scale of a multicellular array (i.e., mesoscale) reflecting the net three-dimensional (3D) orientation of similarly aligned myofiber populations. Our laboratory has recently demonstrated multidirectional anisotropy of water diffusion in the setting of excised lingual skeletal muscle with diffusion spectrum imaging (DSI) (10), validated these findings in relation to 3D microscopy (8), and applied these concepts toward the visualization of myofiber orientation in humans employing diffusion tensor methods (7). To display orientational coherence of myofiber populations over adjacent voxels, our laboratory employed diffusion-based tractography (12). Multivoxel myofiber tracts constructed in this manner approximate the alignment of local strain rate vectors during swallowing (4) and thus provide a suitable template to define the directionality of local contractility. The ability to relate the deformation of mesoscale myofiber tracts to physiological tissue deformation should improve our understanding of multiscale mechanical relationships existing among the structurally complex regions of the tongue, as well as in other muscular tissues.
During normal swallowing, the tongue undergoes a prescribed sequence of deformations, which contain, translate, and propel the bolus retrograde into the pharynx. Employing phase-contrast (PC) MRI, a method that derives local strain rate by determining differences among the local velocity vectors, we previously observed that these swallow phases consist of a coordinated series of compressions (both active and passive) and expansions (5). Most prominent among these events was the early reconfiguration of the tongue displacing the bolus into the posterior oral cavity, a complex action involving active compression in the distribution of the genioglossus, vertically aligned compressive strain in the distribution of the verticalis, and passive compression related to the contraction of the laterally inserted styloglossus. Lingual deformation during the latter portion of the propulsive phase was characterized by large and oblique configured compressive strain in the midportion of the tongue, combined with vertically and transversely aligned contractions in the lingual core. To correlate these mechanical events with the underlying myoarchitecture, we merged the outputs of diffusion tensor imaging (DTI) tractography and strain-rate tractography to create a novel metric, fiber-aligned strain rate (FASR) (4). This method associates the orientation of the principal diffusion vectors and the principal strain rate vectors for each voxel, resulting in a measure of the elongation or shortening of the underlying fiber. By depicting time-sensitive FASR data, it is possible to demonstrate mechanical compression along the line of a set of aligned muscle fibers and, therefore, to infer local contractility.
We present herein the initial formulation of a finite-element (FE) model simulating lingual deformation during the accommodative and propulsive phases of human swallowing based on the shortening of mesoscale myofiber tracts defined by DTI tractography. Such a model is distinct from previous models, since it is derived from measurable human anatomic data and incorporates concepts of nonlinear skeletal muscle activation and neuromuscular control. The proposed model is intended to provide a mathematical description of lingual mechanics that links anatomically accurate lingual myofiber alignment obtained by DTI tractography with local and global mechanics.
METHODS
General methods employed in the development of a lingual FE model.
The development of a FE model (FEM) of lingual mechanics provides a method to characterize tissue deformation and force generation based on the multiscale attributes of skeletal muscle's instantaneous material properties and geometry. At the molecular scale, strain-dependent transitions between molecular contractile states define the instantaneous capacity for muscle to generate active force and stiffness. These molecular transitions can best be described by conservation laws expressed as field equations in vector form. The solution of these partial differential equations provides a probability density function, from which the active component of the stress and muscle stiffness originating in actomyosin bonds can be calculated. This instantaneous muscle stiffness directly contributes to local constitutive relationships and thus the balance of forces. Instantaneous material attributes of the muscular tissue, derived from local actomyosin (molecular) interactions and the material characteristics of the connective tissue and muscle, can then be prescribed in FE integration points, also termed Gaussian points. Tissue scale myoarchitecture, obtained experimentally from diffusion-weighted MRI images, can be represented as a set of FEs aligned with the principal direction of the myofiber tracts. This anatomically aligned mesh thus provides a structural pattern upon which it becomes possible to carry out calculations of lingual deformation and force generation. Using this comprehensive methodology, the configuration at a given time can be obtained from the displacement field, which is incrementally calculated in an iterative scheme by the equilibrium of internal (muscle contraction, connective tissue elasticity) and external (boundary actions and loading) forces. Macroscopic stresses then can be obtained from active stresses acting in the direction of muscle fibers and the components of elastic tensor representing connective tissue resistance to deformation.
Physiological assumptions underlying lingual skeletal muscle activation.
Recent approaches simulating skeletal muscle contractility include cross-bridge (33, 34) and phenomenological models (16, 22). Cross-bridge models are believed to be more accurate than phenomenological models, because they incorporate knowledge of the underlying muscle biochemistry, but they are difficult to implement in FE code and require extensive computational resources. In contrast, phenomenological models are computationally effective, easier to implement, and more appropriate as a first approximation of the movement and deformation of complex muscular organs, such as the tongue. In the present study, we used an intermediate approach between the truly multiscale approach and purely phenomenological single-scale approach: we employed Hill's three-component phenomenological model (23) and its computational application (19, 20, 38, 40, 41) to simulate the mechanical performance of discrete tractlike structures derived from the orientational intervoxel coherence of magnetic resonance diffusivity. For this analysis, the individual tract was assumed to constitute an array of homogeneously aligned myofibers, whose resolution may be defined by the constraints of the imaging methodology, i.e., signal-to-noise ratio.
From an anatomic perspective, each muscle cell is regarded as a cylindrical, elongated cell, surrounded by a thin layer of connective tissue called the endomysium, which is then wrapped by a thin layer of connective tissue termed the perimysium to form the muscle bundle. These aligned muscle bundles comprise the myofiber tract obtained by DTI tractography employing the current approach. Because the myofibers in tissue contract in coordinated manner to provide the desired tongue movement, these actions are guided by specified muscle activation and relaxation. The muscle activation involves the mobilization of calcium from the cell's sarcoplasmic reticulum, conformational change of thin-filament regulatory proteins related to the allosteric binding of calcium to troponin C, and cross-bridge attachment and cycling. Force generation and muscle stiffness may thus be considered to be functions of the number of attached cross bridges (i.e., elastic links between myosin and actin filaments) that is modulated by the level of the activation.
Lingual muscle is defined as a material body that moves and deforms under external and internal mechanical action. Figure 1 shows a schematic representation of a skeletal muscle discretized into arbitrary 3D FEs. The muscle deforms as a function of internal excitation and external loading, involving large displacements and nonlinear constitutive relationships. Omitting inertial forces, muscle motion can be described as an incremental FE process. The FE mesh is composed of a large number of FEs, in which each element incorporates muscle fiberlike material and a connective tissuelike material. The connective tissue material is mostly composed of collagen and elastin, and it is assumed to be isotropic and not subject to activation. The connective tissue, therefore, functions as an elastic element, which is either part of the passive elasticity associated with the muscle fiber or the thin intermuscle connective tissue layer. Muscle fibers are assumed to be orthotropic, with active contractile component acting in the muscle's principal direction. These fibers are submerged in an elastic 3D matrix, which preserves element stiffness in all three principal directions and accounts for element volume changes. To simulate lingual mechanical function, we applied different activation functions to specified groups of FEs.
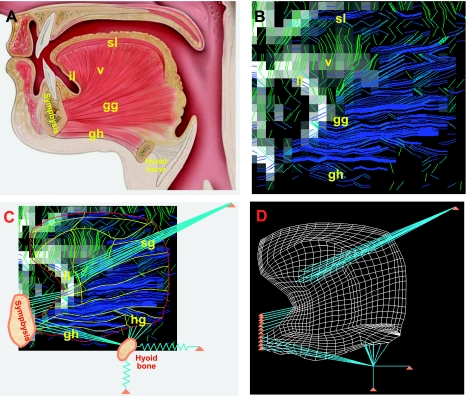
Fig. 1.
Development of finite element (FE) mesh from images of human lingual myofiber tracts obtained by diffusion tensor MRI with tractography. A: anatomy of the muscles present in the midsagittal plane of the tongue, shown in schematic view displaying several principal muscle groups and their bony attachments. Distinguished muscle groups include genioglossus (gg), verticalis (v), geniohyoid (gh), superior longitudinalis (sl), and inferior longitudinalis (il), with connections shown to the symphysis and the hyoid bones. B: diffusion tensor imaging (DTI) tractography images of myofiber tracts noted in A. For these imaging experiments, diffusion-weighted gradients were applied in 90 directions, employing single-shot echo-planar spatial encoding with repetition time = 3,000 ms, echo time = 80 ms, field of view 192 mm × 192 mm, slice thickness 3 mm, and b-value of 500 s/mm2, followed by the streamline construction of multivoxel myofiber tracts along the maximum diffusion vector per voxel. C: DTI tractography myofiber tracts displayed along with the points of insertion into midsagittal and non-midsagittal structures: geniohyoid (gh), hyoglossus (hg), styloglossus (sg), and inferior longitudinalis (il). D: FE mesh whose elemental alignment is derived from the principal diffusion direction per voxel obtained through DTI, including midsagittal and out-of-plane muscles, as well as boundary conditions such as attachments to the symphysis and hyoid bones. Note specifically that the hyoid bone is attached to fixed structures via elastic (connective tissue) structures.
General FE formulation for deforming lingual muscle.
Muscle has the capacity to generate active force and modulate stiffness by transforming chemical energy into mechanical work. This mechanochemical transduction occurs at a molecular scale, where myosin molecules interact with actin filaments. The collective action of myosin molecules, interacting with actin filaments via the actomyosin enzymatic cycle, generates active force and controls muscle stiffness. At supramolecular scales, the constitutive properties of muscle are thus defined by the number of molecular interconnections between the myosin and actin filaments. To account for these effects, the instantaneous material characteristics are prescribed on FE integration points, so-called Gaussian points (Fig. 2). The governing equilibrium equation of a FE structure in deformed configuration at a load step (n) and iteration (i) is formulated as:
where n+1Fext(i−1), n+1Fint(i−1), and n+1Factive(i−1) are vectors of external physiological loads, internal (structural) nodal forces, and integrated active molecular forces lumped into FE nodal forces, respectively; n+1Kel(i−1) and n+1Kmol(i−1) are stiffness matrices of the passive components of constitutive FE and of cumulative stiffness of actomyosin bonds, respectively; δU(i) is the increments of nodal displacements at iteration (i); and the left-upper index n + 1 indicates that the equilibrium equations correspond to the end of the load step. Note that the discrete interaction of actin and myosin molecules is represented at the macroscopic scale as a continuum. The continuum representation of muscle active stress in the FE formulation is denoted as nodal FE forces n+1Factive(i−1) and of muscle stiffness as nodal FE stiffness, n+1Kmol(i−1). Here, the contribution of variable stiffness of actomyosin bonds, n+1Kmol(i−1), and of the passive component representing connective tissue, n+1Kel(i−1), define the material resistance to deformation across spatial scales. Details about calculation of the FE stiffness matrices have been previously published (19, 20) (see appendix). We cite here the expression for the element nodal internal and active forces with the stresses within the muscle, whose evaluation is the key step in a standard FE formulation:
where n+1 BLT(i−1) is the geometric linear strain-displacement matrix (superscript T means transpose), n+1 σ(i−1) is the stress tensor within the muscle, and n+1 V(i−1) is the volume of a FE; details are given in Appendix. Note that the index (i − 1) indicates the last known muscle configuration during the equilibrium iterations within the step. This dynamic equilibrium of forces in Eq. 1, taken together with other boundary conditions and constraints, uniquely predicts the mechanical response of muscle tissues (19). After assembling the element balance equations (Eq. 1), the FE equilibrium equations for the entire midsagittal plane of tongue are solved, securing the equilibrium of Fext, Fint, and Factive within the prescribed tolerance at the end of each time step, n + 1 (2, 18). The displacement vector U(i) is updated during iterations by the current increment δU(i), until δU(i) ≈ 0 at the convergence. Active force generation and n+1Kmol(i − 1) are directly dependent on the rate of muscle deformation in the principal direction of muscle fibers (19). Thus the solution of the above equation includes the effects of strain-dependent modulation at various different length scales (24, 33, 34). While models based on cross-bridge kinetics require a comprehensive knowledge of kinetics rate constants, elasticity of actin and myosin filaments, and intersarcomere inhomogeneities, the absence of such data for lingual musculature supports the use of much simpler phenomenological models, such as Hill's model (14, 23), as a first approximation model of tongue movements relying on contractile mechanics.
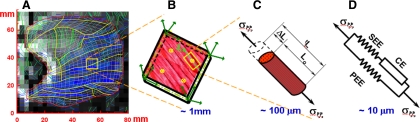
Fig. 2.
Multiscale model of tongue contraction, displayed in the manner in which lingual mechanical function is characterized across relevant spatial scales. A: DTI tractography image of the midsagittal plane of the tongue discretized into FEs. Actual tongue dimensions are denoted along horizontal and vertical axis in millimeters. B: diagram depicting the muscle fibers contained within a characteristic three-dimensional (3D) FE, including denoted integration points and the principal direction muscle fibers, ξ. C: elongation of an individual muscle fiber at the indicated spatial scale under stress is denoted by σξξ. L, length; ΔL, change in length; tL, length at current time t; Lo, slack (relaxed) length. D: Hill's three-element model, displayed as the contractile element (CE) connected to series elastic elements (SEE) and parallel elastic elements (PEE).
The constitutive properties of a muscle fiber and Hill's three-element model.
We show in Fig. 2 an arbitrary FE that represents a small portion of a muscle fiber whose principal direction is defined by the unit vector ξo. The fiber stress vector σξξ is aligned with the fiber direction and depends on the elongation ΔLξ or stretch λξ = 1 + ΔLξ/Loξ of the fiber in the same direction. The elongation ΔLξ is equivalent to the displacement Uξ. The stress-stretch dependence σξξ − λξ represents the active part of the constitutive law for the indicated muscle fiber. This law includes active and passive parts of the muscle fiber, with contractile and nonlinear elastic components, respectively [i.e., contractile element (CE) and series elastic element (SEE) are connected in series]. In addition, the elasticity of connective tissues and elasticity of the noncontractile part of muscle cell cytoskeleton is represented by element parallel elastic element (PEE), connected in parallel with CE and SEE, denoted as σE.
The active part of the constitutive law is based on mechanical measurements of muscle contractility (CE). The elastic element (SEE) takes into account the nonlinear elasticity of tendons and extensibility of actin and myosin filaments. This representation is in accordance with Hill's three-element model (Figs. 2 and 3). Because σξξ − λξ relation is applied in direction of muscle contractility, for simplicity, the vector notation is replaced by a scalar notation representing the magnitude of displacement, stress, stretch, rate of deformation, tension, and shortening velocity, all acting in the fiber direction ξ.
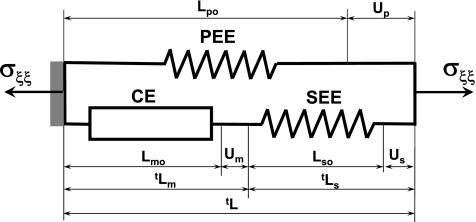
Fig. 3.
Hill's functional model of skeletal muscle. Muscle mechanical function will be represented in terms of the Hill's phenomenological model. By this model, active muscle is composed of three elements: CE, SEE, and PEE. CE represents contractile (sarcomeric) part of muscle, which generates active force and increases overall muscle stiffness. In the relaxed state, this element generates zero tension and zero stiffness. The SEE includes the elasticity of actin and myosin filaments and tendons, and the PEE includes the elasticity of the surrounding connective tissue and the elasticity of the noncontractile part of the muscle cell's cytoskeleton. The lengths of CE, SEE, and PEE in the relaxed state are denoted as Lmo, Lso, and Lpo, respectively. The relaxed muscle length is equal to Lpo = Lmo + Lso. The lengths of the Hill's model components during contraction are tLm = Lmo + tUm, tLs = Lso + tUs and tLp = Lpo + tUp, where tUm, tUs, and tUp are displacements, i.e., change of length from undeformed configuration of CE, SEE, and PEE, respectively.
The CE element is defined by Hill's equation in dimensionless form (14)
| (3) |
where σm is muscle tension, and ν is velocity of the muscle's contraction in the fiber direction ξ, νo = (bσmo/a) is the maximum muscle velocity, and c = (σmo/a) is normalized tension. Thus Hill's equation includes three independent constants: σmo, a, and b, where σmo is the maximum tension developed in the muscle under isometric conditions, and a and b are model parameters (23). The constitutive property of the CE defines the amount of tension, σm, that muscle can generate at a prescribed rate of shortening (Eq. 3). The isometric tension σmo is a function of the muscle length L and is structurally described by Gordon's tension-length relationship (13), where σmo is modulated by the overlap of actin and myosin filaments between which the cycling cross bridges generate active force (see Fig. 4B). For practical purposes, the maximum isometric force and muscle length can be normalized as fLm = σmo/σmo,max and λmξ = Lm/Lmo, where σmo,max is maximum isometric tension at the reference (optimal) muscle length Lmo. The dimensionless Gordon's tension-stretch relationship, fLm(λmξ) is a convenient way to define the relationship between the isometric force and local muscle length, specified as a muscle stretch, λmξ. In further derivations, the subscript ξ is omitted in the equations, which include the muscle stretch in the muscle fiber direction.
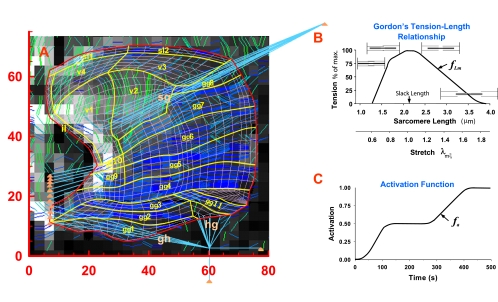
Fig. 4.
The FEs mesh and assigned mechanical characteristics in the Gaussian points for each FE. A: the mesh overlaid on the original DTI image slice. The thick yellow lines indicate muscle fiber groups for which mechanical characteristic are assigned. The specific muscle groups and subgroups employed in the current simulations are identified. B: Gordon's tension-length relationship indicates the fraction of the active muscle tension at arbitrary length, tL, in relation to the tension at a slack (relaxed) length, Lo. Muscle length can be prescribed as a sarcomere length at a micrometer scale that, after normalization by the slack length, can be represented as stretch, λmξ, at the macroscopic scale. C: activation function denotes fraction of the isometric force at time t to the maximum active force that can be generated at the same length, tL. The tabular values of the activation functions associated with the FE groups denoted in A are shown in Table 1. fLm, maximum isometric force and muscle length; fa, activation function.
Hill's equation was developed principally from quick-release experiments in tetanized muscle under steady-state conditions and, as such, cannot solely explain unsteady muscle shortening and fast transients. In addition, this model does not account per se for changes in muscle stiffness due to variation of the number-bound cross bridges in activated muscle and for the behavior of unstimulated muscle, including the effect of the elasticity of tendons and other noncontractile tissues on whole muscle mechanics. The effect of the such elasticity is taken in account in Hill's three-element model via the PEE and SEE components (Fig. 3), while the variable muscle stiffness can be achieved only by multiscale models, which include models based on cross-bridge kinetics. For simplicity, variable cross-bridge stiffness function is not included in this study. The tension-stretch relationship for the SEE (σs) is nonlinear and can be described by:
| (4) |
where σs* is tension at a reference stretch λ* in the direction of the muscle fiber, while α and β are material constants (6).
Stress and strain in Hill's three-element model.
The total stress σ is expressed as the contribution of active muscle forces and the contribution of (passive) elasticity of collagenous connective tissue, cell membrane, and muscle noncontractile cytoskeleton in parallel to muscle cells:
| (5) |
where ϕ is the fraction of muscle fibers (i.e., the fraction of active muscle, represented by the CE and the SEE) in the total muscle volume, σm is active stress generated in muscle, and σE is stress in PEE. Therefore, the quantity 1 − ϕ is the fraction of passive muscle and connective tissue represented by the PEE. Note that the total stress (Eq. 5) refers to the local coordinate system (Fig. 2), where the principal axis is in the muscle fiber direction, ξ. Serial topology also requires that 1) the stresses in CE, σm, is equal to the stress in SEE, σs, at any instant of time, i.e., σm = σs; and 2) a precise accounting of length changes and corresponding stretches or strains (Fig. 3).
To calculate the stretches within the three components of Hill's model in terms of displacements at the material point inside a FE, let us define ratio of the unloaded and relaxed length of the serial elastic element, Lso, to the length of the CE, Lmo, as k = Lso/Lmo. The quantitative relationship of CE and SEE elements and corresponding displacements, Um and Us, respectively, to the total length change at any instant of time (Fig. 3) is defined as:
| (6) |
where Lpo is the initial length, and Up is the current elongation of PEE. The initial length and current elongation of the whole three-element system are Lpo and Up, respectively. Because these lengths and displacements are internal model variables, and constitutive relations for the muscle should be defined in terms of strains or (in this case more convenient) stretches, it is necessary to rearrange Eq. 6 in terms of such stretches:
| (7) |
where λm = (1 + Um/Lmo), λs = (1 + Us/Lso), and λp = (1 + Up/Lpo). In the undeformed configuration, the (initial) stretches are equal to unity, i.e., oλm = oλs = oλp = 1. Despite its phenomenological nature, this model is useful in calculating the mechanical behavior of skeletal muscle under physiological loading conditions. For specified boundary conditions and prescribed load as a function of time (either stress or displacements on the boundaries, and the level of muscle activation), the dynamic system response can be quantitatively determined and various physiological tasks mechanistically evaluated.
Incremental formulation of the constitutive equations.
The total stress in the direction of a muscle fiber includes active muscle stress vectors σm and passive muscle stress vectors σξE (scalar notation in direction, ξ), while, in other principal directions, the stress tensor includes only the remaining components of σE. The muscle constitutive equation, defined by Hill's three-element model, includes in the CE the Hill's tension-velocity curve (Eq. 3), which relates active muscle tension to shortening velocity, ν/νo, or to corresponding rates of deformation in the muscle fiber direction. Thus, in accordance with Hill's equation (Eq. 3), the active stress in 3D muscle structures is defined here in terms of the ratio of current strain rates to maximum shortening rates of the CE, λ̇m/λ̇mo, in fiber direction ξ.
We present below a transformation of the above expressions of Hill's model (Eq. 3) to an incremental-iterative FE computational scheme. First, we approximate the ratio ν/νo in Eq. 3 by the ratio of the stretch increments in time step: ν/νo = λ̇m/λ̇mo ≅ Δλm/Δλmo and express the active stress at the end of each time step as:
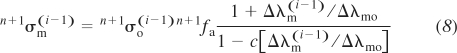 |
where n+1fa is the activation function of the muscle at the end of a current time step n + 1 (Fig. 4C), and n+1σo(i − 1) = σofLm[n+1λm(i − 1)] is the maximum isometric tension in muscle fiber at n+1λm(i − 1). The factor fLm is obtained from Gordon's curve (Fig. 4B) for the stretch at previous iteration, i − 1. Because n+1λ̇m is not known a priori, an iterative procedure, described below, is used. The increment in stretch of the CE Δλm(i − 1) = 1 + ΔUm(i − 1)/Lmo is obtained from the increment in displacements ΔUm(i − 1) within time step n + 1 at previous iteration i − 1, while the value for Δλmo is calculated from the maximum rate of muscle isotonic shortening at zero load, as Δλo = Δλ̇oΔt, where Δt is time step. Note that λ̇o = −νo, where the maximum isotonic shortening velocity, νo, is expressed as the velocity per unit muscle length (14). The change of sign is related to the Hill's equation (Eq. 3) that traditionally takes the shortening velocity as a positive, which is opposite to the usual definition of the strain rates where shortening has a negative sign. The Hill's force-velocity curves are well established and have been measured in a large number of muscle types. Therefore values of νo are readily available. The activation function is a function of time and is regulated by the rate of firing of myelinated nerve fibers. This function is defined here as a scaling factor of isometric active stress with respect to the stress at tetanized state, and varies between 0 and 1, i.e., 0 ≤ fa ≤ 1. The passive state corresponds to fa = 0, while the fully tetanized state corresponds to fa = 1.
The serial topology of the serial elastic component and the CE requires the quantification of how the overall strain is sheared between SEE and CEE. These strains are obtained for arbitrary boundary conditions and prescribed temporal level of activation from a set of several nonlinear algebraic equations related to force equilibrium, the compatibility of strains, and the constitutive relations for CE and SEE. Namely, the force equilibrium of the elements in series requires that the active stress in CE, σm is equal to the stress in SEE, σs, at any instant of time, i.e., n+1σm = n+1σs. The stress in CE in the current time step is defined by Eq. 8 in terms of the strain increment Δλm, while the stress in SEE is defined by nonlinear tension-stretch relationship (Eq. 4), which, in terms of the strain increments Δλs, is:
where nσs is the stress in the previous time step nσs = β[eα(nλs − 1) − 1]. The relationship between the strain increments Δλm and Δλs is derived in incremental form by substituting n+1λm = nλm + Δλm and n+1λs = nλs + Δλs into Eq. 7:
| (10) |
Substituting the expressions for the stresses σm(Δλm) and σs(Δλs) (Eqs. 8 and 9) into the equilibrium equation n+1σm(i − 1) = n+1σs(i − 1) and further substituting Δλm as a function of Δλs (Eq. 10) provides the nonlinear algebraic equation solely in terms of Δλs (with omitting iteration counter a):
| (11) |
The algebraic expressions for coefficients a1–a5 in terms of the known quantities are provided in the appendix. Note that the total sarcomere increment in stretch Δλp is calculated from displacements, which follow from the FE solution of the global equilibrium. Hence, this nonlinear equation has only one unknown quantity, the stretch increment Δλs; this increment is calculated by Newton's iterative method at each integration point.
The stress in the PEE is calculated as follows
where CE is the elastic constitutive matrix, and n+1e(i−1) is the strain at a material point of muscle. The strain n+1e is calculated from displacements, and the surrounding connective tissue is assumed to be linear elastic isotropic medium. Finally, the total stress is expressed at the time step n + 1 as
where ϕ is the fraction of the muscle fibers (active part) in the total muscle volume. We note that the stress n+1σs has only one nonzero component in the direction of the fiber. Finally, the internal (passive) and muscle-active FE nodal forces n+1Fint(i − 1) and n+1Factive(i − 1) are calculated from the stresses n+1σE(i − 1) and n+1σs(i − 1) = n+1σm(i − 1), respectively.
However, since the calculated total stress (Eq. 5) may not be in equilibrium with overall global stresses for the prescribed global equilibrium (Eq. 1), iterative calculations of global equilibrium are conducted until this global debalance is smaller than the prescribed tolerance at convergence. In an incremental FE analysis, we have that the stresses and stretches at the start of the time step are known. Also, the total sarcomere stretch n+1λp at the end of time step can be calculated from the displacements n+1U. Hence, all coefficients a1, a2,..., a5 are known, and the only unknown quantity is the stretch increment Δλs of the serial elastic element. Once the convergence is achieved, the calculations for the new time step are performed. The results of the FE modeling provide the distribution of displacements, stretches, and stresses within the muscle structure at each time step. The above theoretical concepts are implemented in FE package PAK-S (19), and this package along with a companion visualization program, MUSCULO, is used for the simulations of the lingual functional movement during swallowing.
Deriving human lingual myoarchitecture with DTI tractography.
DTI tractography derives the orientation of local fiber populations in tissue by measuring anisotropic proton diffusion within tissue (1, 25, 37, 44, 45). In brief, diffusion represents the random translational motion of water molecules in biological tissue and is principally modulated by the presence and location of macromolecular barriers to water displacement. Thus the preferential motion in the direction of myofibers provides the basis for deducing 3D fiber alignment. The diffusion tensor depicts net proton diffusion in a volume of tissue with a symmetric second rank tensor and can be interpreted as an ellipsoid whose axes are constructed along its three orthogonal eigenvectors with each axis proportional to its eigenvalues. The application of gradients, configured as evenly spaced directions on the surface of a model sphere, results in a system of linear equations that overconstrains the components of the diffusion tensor and may be solved using multiple linear regression. Diffusion-weighted gradients were applied in 90 unique directions, employing single shot echo-planar spatial encoding and the following imaging parameters: repetition time = 3,000 ms, echo time = 80 ms, field of view 192 mm × 192 mm, 3-mm slice thickness, and a b-value of 500 s/mm2. These parameters allowed complete acquisitions of the DTI tractography image set in ∼5 min. Maximum diffusion is a vector defined as the largest eigenvector of the diffusion tensor. Multivoxel myofiber tracts were generated along the maximum diffusion vector per voxel, employing streamline construction, a method for constructing connections along the vector directions in a vector field (7, 12). The specific method operates by applying the constraint that a certain angular threshold must be met to establish intervoxel connectivity and thus constitute the myofiber tract. In the present work, if the angular difference between a given streamline and the maximum diffusion vector of an adjacent voxel is less than ±35°, intervoxel myofiber tract continuity was established.
Derivation of FE mesh from DTI tractography.
From a tractographic image derived from DTI, a two-dimensional (2D) mesh was generated to approximate lingual anatomy (Fig. 1). Specifically, myofiber tracts resolved in 3D were projected onto the plane representing the midline of the tongue. Elements were determined according to actual myofiber projections. While this approach to FE mesh generation requires the use of novel MRI methodology and thus may not be generally available, its advantages include the anatomic accuracy of the 3D architectural elements, enhanced physiological relevance, and potential use in the study of human mechanopathology. The resolution of the myofiber tracts was approximately one voxel in width, and the 3D elements were generated with the element principal direction aligned with the myofiber tract elements. Pixel coordinates were translated to absolute coordinates in millimeters. Given knowledge of image resolution and voxel size (3 mm) in the original DTI image, the final mean size of the tongues was ∼6.5 cm in each dimension. In addition to the FE mesh derived from DTI tractography of the myofiber tracts, the model includes additional extrinsic muscles and boundary constraints tethered by the elastic elements, such as attachments to the symphysis and hyoid bones (Fig. 1, C and D).
Model assumptions.
The FE mesh is composed of two materials, a muscle fiberlike material and a connective tissuelike material. Muscle fibers are assumed to be orthotropic, which includes an active contractile component, according to the Hill's model (described above) acting in the direction of the underlying fiber. The connective tissue material is composed principally of collagen and elastin, and it is assumed to be isotropic and not subject to activation, functioning as an elastic 3D structure that permits axial and lateral deformation of the FEs. This elasticity of connective tissue is a part of passive elasticity of muscle fiber. Taken together, the muscle unidirectional elements, aligned with muscle fibers, are overlaid on elastic 3D elements. Here the elastic matrix preserves the element stiffness in all three principal directions and accounts for the element volume changes. The change of volume in muscle cells during contraction is negligible; thus we assume the Poisson ratio to be slightly smaller than 0.5. The net contribution of contractile component of the muscle element is defined by the fraction of (active) muscle fibers in the total muscle volume ϕ, represented by the CE and SEE, while the quantity 1 − ϕ represents the fraction of connective tissue volume represented by the PEE in principal muscle fiber direction. Since our model incorporates some connective tissue outside of the Hill's model, consistent with tongue anatomy, we set the fraction ϕ of active muscle in the muscle elements to be 0.7. In other principal directions, ϕ is equal to zero, i.e., only passive elasticity is taken into account. The thickness of the interfiber elastic elements comprising the noncontractile and isotropic components (i.e., collagenous tissue) was based on its anatomy (3) and designated in the current model as a fraction of muscle passive elasticity, 1 − ϕ. In addition, the ratio of connective tissue to skeletal muscle, including both of the above components, can be varied to simulate clinical conditions defined by different degrees of fibrous tissue infiltration and internal stiffness. In practice, this variation in stiffness was introduced by varying the elastic modulus of the connective tissue, while Poisson's ratio, which governs the compressibility of the bulk material (collagenous tissue and muscle), was kept approximately constant.
For the elements comprised of connective tissuelike material, we assigned a Young's modulus of 0.25 MPa and a Poisson ratio of 0.499. The modulus of collagenous tissues is typically small (0.1–0.5 MPa) for strains smaller than slack length (λ < 1) and progressively increases during stretching above the muscle slack length (λ > 1). At larger stretches, the elastic modulus could reach 1 GPa. The elastic modulus of elastin, the other major component of connective tissue, is ∼0.6 MPa (6). In this study, we implemented the elasticity of connective tissue and the elasticity of other compliant cytoskeletal structures in two ways: first, as passive FE element elasticity acting in all three dimensions, which corresponds, in part, to serial elastic component of the Hill three element model; and second, in terms of serial elastic component of the Hill's model acting exclusively in direction of muscle fibers (Fig. 2). The passive 3D FE element elasticity is assumed to be linear elastic, with Young's modulus of 0.25 MPa and Poisson ratio of 0.499, reflecting the near incompressibility of the tongue muscles. This modulus corresponds to the modulus of relaxed rabbit psoas muscle at 20°C at strains <20% (i.e., λ < 1.2). The series elastic nonlinear elements are represented in terms of the constants α and β for which we assigned values of 9.4 and 0.11 MPa, respectively. We assigned the ratio of the SEE length to CE length, k, to be 0.3. The maximum shortening strain rate λ̇mo of the CE was taken to be 2 s−1, and the normalized tension c = 3.15. The maximum tetanized isometric stress To was 220 kPa.
To account for the interval of lingual reconfiguration occurring during bolus transfer, several physiological conditions were assumed, namely, first, the anterior-inferior segment of the tongue is rigidly associated with the genioid process through the genioglossus; second, the anterior-superior segment of the tongue is rigidly associated with the hard palate throughout the indicated sequence; and third, the tongue is elastically constrained from the superior-lateral (via the styloglossus) and the inferior and anterior (via the hyoglossus) directions (Fig. 1). Transverse myofibers and the associated transverse mechanical events are not considered.
Although the physical attributes of the swallowed bolus are expected to passively affect tissue displacement immediately adjacent to the bolus, as well as to modulate the active properties associated with skeletal muscle activation in various regions of the tongue during the swallow, for simplicity, these factors were not considered.
Application of activation functions to FE mesh of tongue musculature.
The activation and subsequent movement of the tongue were simulated over 500 ms in steps of 1 ms. Lingual reconfiguration during swallowing was simulated from the point of lingual tip contact with the hard palate through the phases of the swallow generated, attributed to accommodation of propulsion, although in the absence of a bolus. Activation functions applied to individual elements or group of elements were provided as input to the simulation package (Fig. 4A). It should be noted that the activation functions defined by the current FEM cannot be measured directly due to a large number of tongue muscles and the complexity of their interactions. As a result of these limitations, we employed an inverse approach in which we extracted the best set of activation functions to predict a known history of lingual tissue deformations. Specifically, such activation functions can be obtained from an iterative fitting of model perditions to history of displacement obtained from prior DTI imaging. We defined these activation functions over different areas of the tongue so that they qualitatively reproduced the intended deformations. The specific outcome measures of the simulations were represented in terms of local displacements, stresses, stretches, and strain rates.
RESULTS
We present FE simulations of lingual shape changes occurring following lingual tip contact with the hard palate during human swallowing, which is based on the deformation of FEs aligned with the principal orientation of the myofiber tracts defined by DTI tractography. These simulations provide an explicit representation of the relationship between mesoscale myoarchitecture and mechanical function at both the local (individual element) and global (aggregate of elements comprising the tissue) scales. Such elemental simulations represent the underlying material and activation properties defined at each relevant spatial scale, i.e., contractile proteins, individual myocytes, and aligned myocytes. We specifically present the following mechanical features: 1) the displacement field representing the local movements associated with lingual shape change; 2) active muscle stress representing local force as a function of prescribed history of activation of multiple muscle groups and subgroups; 3) passive stress representing the resistance to deformation resulting from the presence of connective tissues surrounding lingual myocytes and the internal resistance within the muscle cells themselves; 4) elemental stretch as a metric of local deformation; and 5) local strain rate function. Information regarding the physiological patterns of global deformation are derived from prior videofluoroscopy (29) and MRI experiments employing the aforementioned assumptions regarding relevant molecular and cellular scale mechanics (4, 5, 9). For each sequence of images, lingual mechanical function was acquired at intervals of 10 ms over a total period of 500 ms during the course of the indicated swallows, and selected images within such sequences are displayed. In each instance, global deformation was referenced to the initial tongue shape (obtained before the swallowing-related deformation) depicted as a gray mesh.
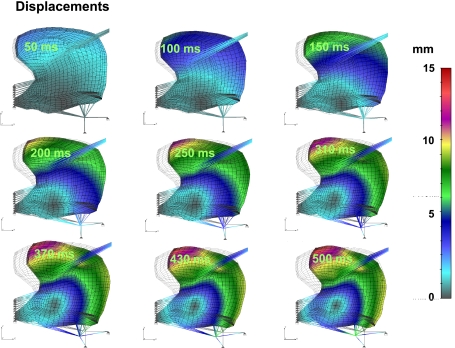
Figure 5 depicts the relationship between the local displacement fields relative to gross lingual deformation. The magnitude of local displacement is represented by a color code, displayed in terms of millimeters of displacement. The impression of vectorial movement is constituted by the difference between the initial mesh (gray lines) and the deformed mesh (black lines). The intent of this representation is to display the relationship between the direction and magnitude of nodal displacement and net tissue deformation. The indicated displacements are a function of the sequence of activation functions defined in Table 1 for both the intrinsic and extrinsic motor functions in relation to the set of aligned elements defined by MRI experiments. These results demonstrate the following effects: 1) the initial phase of swallowing deformation (beginning at 0 ms and linearly increasing to 150 ms) is the elevation of the lingual tip and shortening in the anterior-posterior orientation; 2) between ∼150 and 250 ms, we observe inferior displacement, principally related to contraction of the hyoglossus at its inferior-most position; and 3) between ∼250 and 500 ms, clockwise rotation, principally related to regional contraction of the genioglossus and contraction of the hyoglossus following anterior displacement. It should be noted that the majority of this rotation is about the point of genioglossus insertion at the genioid process.
Fig. 5.
Simulated displacement field relative to tissue deformation during swallowing. For Figs. 5–9, the deformed mesh (black lines) is superimposed on the original mesh (gray lines in background) for perspective to the initial configuration of the tongue. Elemental displacement is defined as a vector of the difference between current position of a material position (at time t) and the position of the same point in initial configuration (at t = 0). The color code represents magnitude of the displacement vector in millimeters. Shown is prototypical lingual deformation during swallowing, initiating with lingual tip contact with the hard palate and extending through the accommodative and propulsive phases. These results demonstrate the significance of the upward deformation of the lingual tip and anterior-posterior shortening, followed by inferior displacement (principally related to hyoglossus contraction) and clockwise rotation (principally related to superior-inferior sequential contractions of the genioglossus regions).
Table 1.
The activation functions are described as linear functions of time between the values denoted in the table for each group of finite elements
| Muscle Groups | 0 ms | 150 ms | 250 ms | 500 ms |
|---|---|---|---|---|
| hg | 0.000 | 0.500 | 0.500 | 1.000 |
| sg | 0.000 | 0.500 | 0.500 | 0.500 |
| gh | 0.000 | 0.000 | 0.000 | 1.000 |
| sl1 and sl2 | 0.000 | 1.000 | 1.000 | 1.000 |
| gg8 and v3 | 0.000 | 0.000 | 1.000 | 1.000 |
| v2 | 0.000 | 0.000 | 0.600 | 0.600 |
| gg11 | 0.000 | 0.000 | 0.300 | 0.150 |
| gg1–4 | 0.000 | 0.000 | 0.300 | 0.000 |
| gg5 and gg9 | 0.000 | 0.000 | 0.114 | 0.400 |
| gg7 | 0.000 | 0.000 | 0.229 | 0.800 |
| gg6 | 0.000 | 0.000 | 0.086 | 0.300 |
The groups of finite elements are denoted in Fig. 4A. hg, Hyoglossus; sg, styloglossus; gh, geniohyoid; sl, superior longitudinalis; gg, genioglossus; v, verticalis.
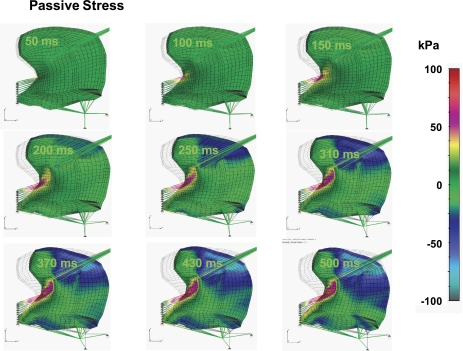
Acknowledging the complex nature of lingual mechanical stress (denoted as force per unit area) due to the presence of both active and passive components, we elected to represent these elements separately. We demonstrate in Fig. 6 the active stress component present in the tongue during the indicated phases of swallowing. The color code displayed represents the magnitude of active stress (in kPa), while the direction of the stress (denoted as ξ in Fig. 3) is prescribed parallel to the longer side of each FE denoted as a thin gray lines within the FEs. The specific sequence of images denotes the sequence of stress events during the swallow based on the presumed sequence of activations previously defined in Table 1. While stress is distributed throughout the tissue as a function of motor actions, we observe that largest stress is present during lingual rotation and is associated with a superior-to-inferior sequence of regional genioglossus contractions. Given the hydrostatic nature of lingual tissue, the aforementioned contractions necessarily generate deformation of the surrounding myocytes and connective tissue. The resistance to that deformation may be depicted in terms of passive stress (Fig. 7) displayed in terms of a color code representing passive stress in the direction of elements possessing the largest magnitude and, therefore, the elements most relevant to global deformation. These results were displayed in terms of kilopascals, with red signifying expansive stress and gray signifying compressive stress. Although not shown in the current 2D simulation, it should be anticipated that both active and passive stress elements also occur in the transverse direction. Future 3D simulations will necessarily incorporate these data. The principal observation drawn from these simulations is that passive stress tends to be closely associated with active stress, with principal passive components primarily observed in the apparent distribution of the superior genioglossus.
Fig. 6.
Simulated active muscle stress during swallowing. Active stress is defined in Eq. 8 and denoted as σm. The color code represents the magnitude of active muscle tension (kPa) in the direction of muscle fibers ξ. The dominant patters of active stress (largest magnitude) is associated with lingual rotation about the genioid process and is associated with sequential regional contraction of the regions of the genioglossus.
Fig. 7.
Simulated passive stress field during swallowing. Passive stress is defined by Eq. 12 and represents the stress in the parallel elastic element, σξξE, in direction of muscle fiber ξ. The color code represents the magnitude of σξξE in kilopascals. σE is the passive stress tensor, and σξξE is the most relevant component of this tensor. These results demonstrate that, within the current two-dimensional framework, passive stress tends to align with active stress in the apparent distribution of the superior regions of the genioglossus. The passive stress in both the longitudinal and the transverse directions considers only the passive elasticity and does not account for the increase of stiffness during contraction caused by bound cross bridges.
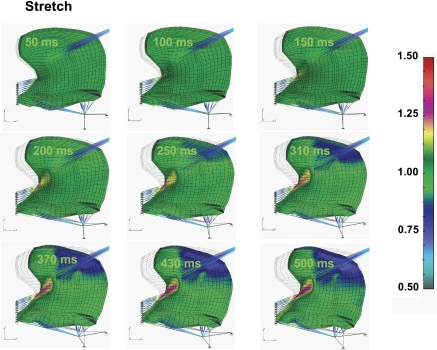
We demonstrate in Fig. 8 local stretch in the direction of myofiber tract orientation. This simplified representation of the strain tensor is used based on the fact that this data form 1) represents the maximum deformation for the majority of elements during swallowing; 2) allows iterative calculation of the relationship between internal deformation and the contractile and serial components in the Hill three-element model; and 3) provides a means to calculate the strain rates (previously defined experimentally) (4, 5) as a differential of the stretches between two sequential time steps over duration of the time step. The current results were displayed in terms of stretch functions that are conventionally used for nonlinear systems (36). The component of stretch in muscle-fiber direction showed regions of compression (gray), where the active stress is the strongest, and the regions of extension (red), where lingual muscles are relaxed. This pattern is similar to the passive stress distribution observed in Fig. 7, but relative magnitudes are skewed due to the presence of material and geometric nonlinearities. Despite some differences, the orientations of maximum and minimum stretches coincided with the orientations of maximum and minimum passive stresses.
Fig. 8.
Simulated local stretch during swallowing. Local stretch is defined as λp = tLp/Lop = (1 + tUp)/Lop. Because, as the length of parallel elastic component is equal to the muscle length (Fig. 3), i.e., tLp = tL, the local parallel elastic stretch λp is equal to macroscopic stretch in Gaussian point of a FE, λ (Eq. A1). The color code represents the magnitude of the muscle stretch in direction of muscle fibers ξ. Stretch in the direction of indicated muscle fibers may be displayed as regions of compression (gray) or extension (red). The pattern of stretch displayed is similar to that exhibited by passive stress (Fig. 7), although relative magnitudes are skewed due to material and geometric nonlinearities.
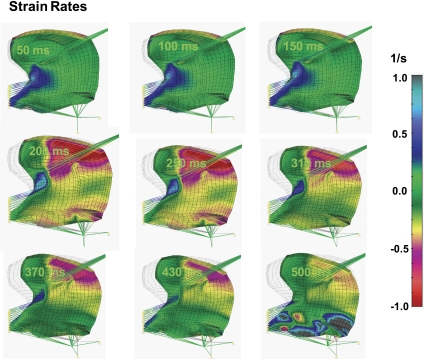
Figure 9 depicts the computed mechanical attributes of the deforming tongue in terms of local strain rate to compare with experimental results previously obtained employing lingual pressure-gated PC MRI combined with DTI tractography to represent local fiber shortening (4, 5). This association specifically links the aligned strain rates ascertained through FE representations in the midsagittal plane with those obtained experimentally. The aforementioned experimental approach associates the orientation of the principal diffusion vectors and the principal strain rate vectors for each voxel, resulting in a measure of the elongation or shortening of the underlying fiber. Moreover, FASR may be displayed as a multivoxel myofiber tract by associating such vectors between locations, thus providing a mesoscale representation of local mechanical function referenced to specific fiber populations. By this method, the strain rate tensor is transformed onto the reference plane with ξ-axis parallel to the diffusion vector. Both the experimental (4, 5) and simulated results emphasize the complex array of compressive and expansive strain rates occurring in the midsagittal plane during water bolus swallowing, specifically displaying the early-stage (0–150 ms) compressions in the region of the longitudinalis and the verticalis, and the prominent latter stage (300–400 ms) compressions occurring in the region of the genioglossus, along with expansion occurring in the regions of the geniohyoid and the verticalis. These mechanical events were largely replicated in the current simulation of aligned strain rates, although we acknowledge a difference of the explicit timing of events due to the fact that the simulation did not account for the passive deforming effect of the bolus and the pressure-detecting bulb, and for the tongue stiffening by contraction of transversely aligned muscles.
Fig. 9.
Simulated local strain rate during swallowing. Local strain rate is computed to serve as a comparison with prior experimental work deriving aligned strain rate from lingual pressure-gated phase-contrast MRI and DTI tractography (4, 5). In the current simulation, local strain rate is calculated as a difference between consecutive images of the local stretches divided by time intervals between times when these images were obtained. The images of local stretches were collected at 1-ms intervals, and then the strain rates were collected at specified times denoted in the left corners of the presented images. The color code represents the magnitude of the strain rate in direction of muscle fibers ξ. Strain rate is displayed as regions of contraction rates (red) or elongation rates (gray).
DISCUSSION
To comprehend the mechanics of lingual function during the human swallow, it is necessary to synthesize data obtained from multiple experimental approaches spanning multiple spatial scales. Accordingly, we have developed a theoretical framework, embodying concepts of multiscale mechanics and the results of the MRI methods depicting lingual myoarchitecture (7) to relate the physiological attributes of individual myocytes, coupled myocytes and myocyte regions during swallowing. Myocyte alignment was obtained experimentally from diffusion-weighted MRIs and then represented as a FE mesh capable of deformation, with the instantaneous material attributes of the tissue prescribed in FE Gaussian points.
While prior muscle models have been based largely on curve fitting from macroscopic experimental data (16, 22), the current simulation employs the phenomenological Hill's three-element model (6, 23) to simulate skeletal muscle contractility. This model specifically employs established values for muscle material and activation characteristics (19, 20). We anticipate however, that the use of a more realistic sliding filament model (33, 34) will provide instantaneous constitutive properties distinguishable from those obtained via the generally used Mooney-Rivlin model (31, 39, 48) or the Hill model. It should be noted that such constitutive properties are not readily achievable via the Mooney-Rivlin model, since the derivation of material constants depends on the history of muscle activation and deformation. One could alternatively use a material model based on structurally relevant parameters and rate constants, such as derived from myofilament cross-bridge kinetics. However, since these latter models are complex and computationally intense, we employed the simpler Hill's three-element model as a proof of concept for multiscale simulation, recognizing that future work will need to reconsider these results based on the underlying cross-bridge kinetics and the regulation of myosin binding. The current multiscale simulation, while somewhat limited by its underlying assumptions, is nonetheless a useful first step for understanding the complex mechanics associated with normal and pathological lingual mechanics. Previous research has proposed methods by which anatomic data may be translated into FE representations from which deformation may be modeled in the case of the human tongue (15, 30, 46) and analogous hydrostatic organs in nonhuman species (21, 32, 42, 43, 47). These efforts substantially support the role of a complex myoarchitecture in contributing to lingual deformation, yet do not fully account for the presence of highly dynamic synergies across spatial scales. On the other hand, Yekutieli et al. (49) described a dynamic control model for the octopus arm in which orthogonally aligned muscles generate motion through variations of internal stiffening. Our results extend these concepts and additionally account for the multiscale factors that contribute to the directionality and force generation exhibited by the constituting myofibers of the human tongue.
Our initial model assumptions included the following considerations. 1) The FE mesh is composed of muscle fiberlike material and a connective tissuelike material. The connective tissue material is mostly composed of collagen and elastin and is assumed to be isotropic and unsusceptible to activation. Such material functions as a thin elastic element, which permits sliding between the muscular elements or comprise a component of the passive elasticity contained in muscle fiber. Muscle fibers are assumed to be anisotropic and include an active contractile component according to the Hill's model overlaid on elastic 3D elements, which preserve elemental stiffness in the three principal directions, accounting for muscle and connective tissue passive elasticity and changes of volume. 2) Boundary conditions consist of the following: first, the anterior-inferior segment of the tongue is rigidly associated with the genioid process through the genioglossus; second, the anterior-superior segment of the tongue is rigidly associated with the hard palate; and third, the tongue is elastically constrained from the superior-lateral (via the styloglossus) and the inferior-lateral (via the hyoglossus) directions. The activation and subsequent movement of the tongue are simulated stepwise, employing linear submaximal activation and material attributes derived from the muscle's multiscale properties. As a first approximation, our model does not consider modulation of lingual muscle mechanical characteristics caused by transverse fiber expansion or compression, passive deformation in the adjacent tissue imposed by the bolus, or active accommodative changes in response to the bolus, and any out-of-plane deformations.
The simulations shown in Figs. 5–9 illustrate the relationship between myoarchitecture and mechanics of the tongue during the indicated phases of swallowing at the local (individual element) and global (aggregate of elements comprising the tissue) scales. Examining the local displacement field (Fig. 5) in relation to global shape changes, we demonstrate that lingual reconfiguration during the indicated phases of swallowing includes an initial phase (0–150 ms), consisting of tip elevation and shortening in the anterior-posterior direction, a second phase (150–250 ms), consisting of inferior displacement due to hyoglossus contraction at its inferior-most position, and a highly dominant third phase (250–500 ms), consisting of clockwise rotation attributable to a sequence of regional contractions of the genioglossus and contraction of the hyoglossus following displacement to its maximally anterior position. The dominance of the third lingual phase is affirmed by the fact that active stress is maximal during lingual rotation and is associated with a superior-to-inferior sequence of regional genioglossus contractions (Fig. 6). Recognizing the hydrostatic nature of lingual tissue and the resultant fact that lingual stress necessarily embodies both active and passive components, we demonstrate that the maximum resistance to deformation, i.e., passive stress, generally aligns with active stress in the apparent distribution of the superior regions of the genioglossus. We did not consider however the active and passive stress components in the transverse direction in this initial 2D simulation. Lastly, representing local stretch as a measure of determination in the direction of the indicated myofiber tracts, the pattern of local stretch distribution coincided approximately with the pattern of passive stress (Fig. 8). Overall, these results demonstrated that the proposed methodology is capable of delineating complex mechanical relationships in the tongue by incorporating realistic anatomic attributes and patterns of multiscale activation. This may be important in building a quantitative understanding of pathological lingual mechanics, since systematic variation of the model parameters or modes of activation can quantitatively predict physiological outcomes and test mechanistic hypotheses.
Recognizing that complete validation of a model of this degree of complexity will require multiple iterative steps relating experimental and simulated results at varying spatial scales, the fundamental components of this model have been substantiated through the following. 1) Our laboratory has performed microscopic validation of DSI/DTI tractography through the multiscale analysis of lingual myoarchitecture, employing multislice two-photon microscopy in an excised mouse tongue (8). In these experiments, we ascertained 3D fiber direction at microscopic scales with microscopy and then correlated these values with mesoscale determinations of fiber direction obtained via DSI. The orientation distribution of fibers obtained by diffusion-based imaging reflects the principal directions and permeabilities of the constituting cell membranes and fluid compartments, whereas the orientational distribution obtained from microscopy reflects the morphology and mean alignment of individual muscle fibers. 2) The material and contractile properties of the individual tongue muscles were obtained from the literature as the best available representation of overall muscle contractility (6). Specific differences of contractility among the distinguished muscle groups were considered to be insignificant. The activation functions of individual muscle groups and subgroups were obtained by inverse adjustment to mimic observed tongue contour movement. Owing to the fact that these activation functions may be nonunique to the prescribed contours, this problem can be addressed by direct measurement of the activation of muscle groups and subgroups or specifically constrain the inverse determinations of activation functions with the observed strain rates. 3) Our laboratory has demonstrated the similarity of simulated FASR with that obtained through direct measurement through gated PC MRI (4, 5), although recognizing quantitative differences likely caused by the absence of transverse mechanical effects and the passive influence of the swallowed bolus.
Given the early stage of the current model, we acknowledge several additional limitations. 1) The connective tissue filling the interstitial spaces between muscles is composed mostly of collagen and elastin and is assumed to consist of an isotropic, linear elastic material with a Poisson ratio of ∼0.5. This material characteristic is prescribed in each of the Gaussian points in the 3D FE element. In the direction coaligned with muscle fibers, this attribute corresponds to the parallel component of Hill's component. However, it is conceivable that the material attributes of lingual connective tissue are, in fact, nonlinear and orthotropic and will thus require further experimental validation. 2) Instantaneous muscle stiffness is generally proportional to active muscle stress, except for fast transients. Excess muscle stiffness during activation can be assumed to be proportional to the increased number of cross bridges and active muscle stress and, as such, can be included the current Hill's model. However, this should be regarded only as a first approximation, since it is correct only for slow or steady-state muscle shortening or lengthening. 3) To explain full functionality of the tongue during swallowing and other relevant physiological tasks, it is necessary to expand our analysis to account for the 3D structure of the tongue and model fully the attachments of the tongue to surrounding structures. 4) The activation functions employed for specific lingual regions were obtained through knowledge of multiscale skeletal mechanics and local deformation patterns during swallowing, along with the application of inverse activation functions intended to follow approximately the variations of lingual contour.
We recognize, however, that multiple sets of model parameters may equally well fit the experimental data. To achieve a unique and robust set of model parameters, it is necessary to refine and update the model parameters incrementally with microscopic mechanical and physiological data specific to the mammalian tongue. Similarly, the volumetric distribution of muscle and connective tissue may need to be reconsidered by more extensive sampling of normal and pathological human lingual tissue. Specific consideration may be given to the mechanics underlying pathological fibrogenesis, in which changes in the density of myofilament cross-linkages may affect the elasticity of the connective tissue. Despite these limitations, the current model provides, for the first time, a FE representation of the tongue, embodying actual human anatomic representations, and is rooted in multiscale mechanical conceptualizations. Moreover, these results affirm the paramount role of muscular synergy in producing changes of lingual shape and force generation. Specific to muscular hydrostats, synergistic contractions of orthogonally aligned fibers contribute to volume-conserving tissue deformation. The tongue appears to be a unique form of muscular hydrostat in that it displays actuation that is both untethered (intrinsic muscles) and tethered by mechanical relationships with the extrinsic musculature and adjacent bony structures. While we have previously suggested that the extrinsically attached muscles of the tongue promote gross deformations, while intrinsic muscles apply more subtle mechanical adjustments to those deformations (11), the current work suggests that the interactions between the various lingual muscles may be considerably more complex and embody bidirectional signaling across all relevant spatial scales.
The high level of structural redundancy exhibited by the tongue precludes a definition of lingual mechanics based solely on conventional analyses of lingual deformation or assays of force generation. Our approach is based on the postulate that lingual mechanics may best be conceived as a set of discretely coupled mechanical units, whose function is predicted by its underlying myoarchitecture, optimally conceived at the mesoscale. By referencing tissue deformation to such intermediate scale structures, we provide a mechanism by which the tongue's remarkable degree of microscopic complexity can be practically translated into physiological changes of shape and the ability to perform versatile physiological tasks. We contend moreover that the study of lingual mechanics is best performed within a multiscale theoretical framework, relating the physiological attributes of individual and coupled myocytes, patterns of activation and relaxation at relevant length scales, to the structure-function relationship of the integrated system during swallowing. This process is intended to yield a mathematical depiction of tongue mechanics that links the strain-dependent underlying binding and regulation of contractile proteins within muscle cells, the alignment of the muscle cells in tongue tissue, correct anatomic dimensions based on lingual imaging, and biomechanical data.
GRANTS
This work was supported in part by National Institutes of Health Grants R01 AR048776 (S. M. Mijailovich); R01 DC005604 (R. J. Gilbert); National Administration Grant NNJ06HE06A (M. Kojic) and Ministry of Science and Technological Development of Serbia Grant 10-144028 (M. Kojic).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
ACKNOWLEDGMENTS
We thank Teresa T. Wang, Terry A. Gaige, Thomas Benner, and Ruopeng Wang for assistance in the magnetic resonance imaging and data acquisition for the tongue images employed in this work.
APPENDIX
We provide the equation derivations below for calculations of tissue stretch, FE forces, and the tangent constitutive matrix. The equation derivations are derived from our laboratory's prior work (2, 18, 19).
Calculation of tissue stretch.
The calculation of the displacements and stretch for the current configuration of muscle within the incremental-iterative FE scheme is described by Eq. 1. The stress and tangent constitutive matrix are functions of this stretch. Let n+1x(i−1) specify the position vector of a material point at the last known configuration for the time step n and iteration i within the step. We denote the displacements as n+1u(i−1). The stretch n+1λ(i−1) in the fiber direction can be calculated as
where n+1ξ0i(i − 1) and n+1ξ0j(i − 1) are components of the unit vector n+1ξ0(i − 1), and n+10Dij are components of the inverse left Cauchy-Green deformation tensor n+10D(i−1). This tensor can be calculated from the inverse deformation gradient tensor n+10X(i−1) as:
Here, the indexes 0 and n + 1 denote the differentiation ∂n+1x/∂0x, where 0x corresponds to the initial (unstretched) configuration.
In turn, the inverse deformation gradient tensor n+10X(i−1) can be calculated using the displacements n+1u(i−1) (here written in terms of components with subscripts i and j, where δij = 1, if i = j, and δij = 0 for i ≠ j):
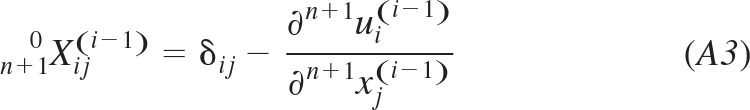 |
To calculate the derivatives, we must use interpolation of the displacements (again separated into components):
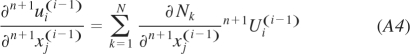 |
Here Nk are the interpolation functions and n+1Ui(i − 1) are the components of the nodal displacements.
In summary, for the current configuration, we calculate the unit vector n+1ξ0(i − 1) and find the stretch in the fiber direction n+1λ(i−1) from Eq. A1. Then we evaluate the stress n+1σs(i − 1) from the muscle material model (Eq. 9), as well as the coefficient n+1Cs(i − 1) necessary for the tangent constitutive matrix n+1C(i−1) (see Eq. A7 below):
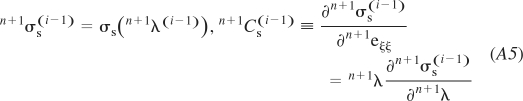 |
Here, we have used the relation ∂(●)/∂eξξ = λ∂(●)/∂λ, where eξξ = ln(L/Lo) is the fiber strain.
In the section below, we present details for calculation of the FE nodal forces and the constitutive coefficient n+1Cs(i−1) for Hill's model.
Calculation of FE forces.
The internal (structural) forces and active forces in Eq. 1 are calculated from corresponding stresses using a standard FE element procedure (2, 18, 19) as:
where n+1σE and n+1σm are passive (elastic, structural) and muscle (active) stresses, respectively, at current time step, n + 1, and at previous iteration, i − 1. The external forces, n+1Fext(i − 1), in Eq. 1 include external body forces, as well as those arising from boundary conditions, which can be force or displacements; the element formulation of these forces can be found elsewhere (2, 18, 19). The stiffness matrix, which depends on the constitutive material law, can be expressed as
where n+1BLT represents the linear strain-displacement matrix, which contains derivatives of interpolation functions that approximate the displacement field within the element; n+1C(i−1) is the tangent constitutive matrix of stress-strain relations within the FE; and V is the element's volume. The calculation of the tangent constitutive matrix [n+1C(i−1)] is described below. Our material model includes both the history of deformation and muscle activation so that, at any instant, the constitutive law can be derived, depending on local conditions. Note that a geometrically nonlinear matrix KNL, which takes into account effects of geometry change, can be also included into Eq. 1 to improve the convergence rate in the iterative solution scheme, but it does not affect the solution.
Tangent constitutive matrix.
The tangent constitutive matrix n+1C of the muscle and connective tissue considered as a continuum, can be calculated by using the expression (we further omit iteration counter for simplicity):
This constitutive matrix corresponds to the global coordinate system. However, we only can determine the derivatives ∂n+1σs/∂n+1e in the local coordinate system ξ, η, ζ, where ξ is the fiber direction at the integration point, while η and ζ are the axes orthogonal to ξ. This is because we have here the dependence n+1σs(n+1λp) defined by Eqs. 9 and 11 along the local axis ξ. Therefore, we form the local constitutive matrix n+1C̄ in which the terms are:
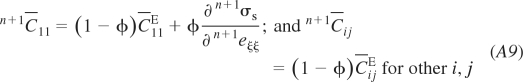 |
where C̄ijE are elastic matrix terms of the surrounding connective tissue. Finally, the matrix n+1C̄ is transformed to the global coordinate system and used in Eq. 1.
We further present a procedure for determining the derivative ∂n+1σs/∂n+1eξξ ≡ n+1Cs. We express n+1Cs as (see Eq. A5)
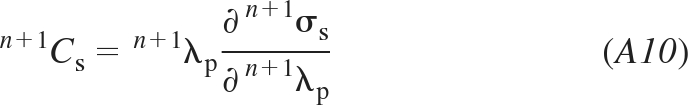 |
where
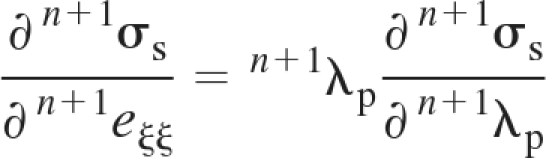 |
From Eq. 9 it follows
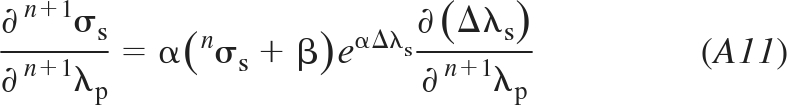 |
To calculate x ≡ ∂(Δλs)/∂n+1λp, we differentiate the nonlinear Eq. 11 with respect to n+1λp and obtain
| (A12) |
From this equation it follows that
| (A13) |
where
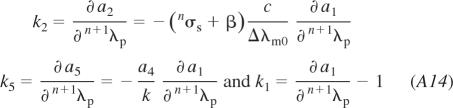 |
Hence, we find ∂(Δλs)/∂n+1λp from Eq. A13, substitute into Eq. A11 to obtain ∂n+1σs/∂n+1λp, and further substitute into Eq. A10 to determine n+1Cs. Note that we could use the derivatives ∂n+1σs/∂n+1eξξ to obtain n+1Cm = n+1Cs, since n+1σm = n+1σs.
Finally, the algebraic formulae for the coefficients of Eqs. 10 and 11 and Eqs. A12A13–A14 are:
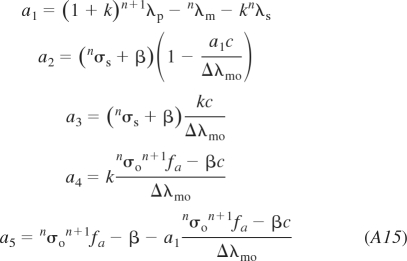 |
REFERENCES
- 1. Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys J 66: 259–267, 1994 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Bathe KJ. Finite Element Procedures. Englewood Cliffs, NJ: Prentice-Hall, 1996 [Google Scholar]
- 3. Doran GA. Review of the evolution and phylogeny of the mammalian tongue. Acta Anat (Basel) 91: 118–129, 1975 [DOI] [PubMed] [Google Scholar]
- 4. Felton SM, Gaige TA, Benner T, Wang R, Wedeen VJ, Reese TG, Gilbert RJ. Association of mesoscale myofiber architecture with local strain rate during the propulsive phase of human swallowing. J Biomech 41: 1782–1789, 2008 [DOI] [PubMed] [Google Scholar]
- 5. Felton SM, Gaige TA, Reese TG, Wedeen VJ, Gilbert RJ. Mechanical basis for lingual deformation during the propulsive phase of swallowing as determined by phase-contrast magnetic resonance imaging. J Appl Physiol 103: 255–265, 2007 [DOI] [PubMed] [Google Scholar]
- 6. Fung YC. Biomechanics: Mechanical Properties of Living Tissues. New York: Springer-Verlag, 1993 [Google Scholar]
- 7. Gaige TA, Benner T, Wang R, Wedeen VJ, Gilbert RJ. Three dimensional myoarchitecture of the human tongue determined in vivo by diffusion tensor imaging with tractography. J Magn Reson Imaging 26: 654–661, 2007 [DOI] [PubMed] [Google Scholar]
- 8. Gaige TA, Kwon HS, Benner T, Wang R, Dai G, Wedeen VJ, So PT, Gilbert RJ. Deriving mesoscale myoarchitecture of the mouse tongue with multiphoton microscopy and diffusion spectrum magnetic resonance imaging. J Biomed Opt 13: 064005, 2008 [Google Scholar]
- 9. Gilbert RJ, Daftary S, Campbell TA, Weisskoff RM. Patterns of lingual tissue deformation associated with bolus containment and propulsion during deglutition as determined by echo-planar MRI. J Magn Reson Imaging 8: 554–560, 1998 [DOI] [PubMed] [Google Scholar]
- 10. Gilbert RJ, Magnusson LH, Napadow VJ, Benner T, Wang R, Wedeen VJ. Mapping complex myoarchitecture in the bovine tongue with diffusion-spectrum magnetic resonance imaging. Biophys J 91: 1014–1022, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Gilbert RJ, Napadow VJ, Gaige TA, Wedeen VJ. Anatomical basis of lingual hydrostatic deformation. J Exp Biol 210: 4069–4082, 2007 [DOI] [PubMed] [Google Scholar]
- 12. Gilbert RJ, Wedeen VJ, Magnusson LH, Benner T, Wang R, Dai G, Napadow VJ, Roche KK. Diffusion spectrum magnetic resonance imaging with tractography depicts the 3D muscular architecture of the bovine tongue. Anat Rec 288: 1173–1182, 2006 [DOI] [PubMed] [Google Scholar]
- 13. Gordon AM, Huxley AF, Julian FJ. The variation in isometric tension with sarcomere length in vertebrate muscle fibres. J Physiol 184: 170–192, 1966 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Hill AV. The heat of shortening and the dynamic constants of muscle. Proc R Soc B 126: 136–195, 1938 [Google Scholar]
- 15. Kakita Y, Fujimura O, Honda K. Computation of mapping from muscular contraction patterns in vowel space. In: Phonetic Linguistics: Essays in Honor or Peter Ladefoged, edited by Fromkin VA. San Diego, CA: Academic, 1985, p. 133–144 [Google Scholar]
- 16. Kerckhoffs RC, Neal ML, Gu Q, Bassingthwaighte JB, Omens JH, McCulloch AD. Coupling of a 3D finite element model of cardiac ventricular mechanics to lumped systems models of the systemic and pulmonic circulation. Ann Biomed Eng 35: 1–18, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Kier WM, Smith KK. Tongues, tentacles and trunks: the biomechanics and movement of muscular hydrostats. Zool J Linn Soc 83: 307–324 1985 [Google Scholar]
- 18. Kojic M, Bathe KJ. Inelastic Analysis of Solids and Structures. Berlin, Germany: Springer-Verlag, 2005 [Google Scholar]
- 19. Kojic M, Filipovic N, Stojanovic B, Kojic N. Computer Modeling in Bioengineering. Chichester, UK: Wiley, 2008 [Google Scholar]
- 20. Kojic M, Mijailovic S, Zdravkovic N. Modelling of muscle behaviour by the finite element method using Hill's three-element model. Int J Numer Methods Eng 43: 941–953, 1998 [Google Scholar]
- 21. Kristan WB, Jr, Eisenhart FJ, Johnson LA, French KA. Development of neuronal circuits and behaviors in the medicinal leech. Brain Res Bull 53: 561–570, 2000 [DOI] [PubMed] [Google Scholar]
- 22. Loeffler L, 3rd, Sagawa K. A one-dimensional viscoelastic model of cat heart muscle studied by small length perturbations during isometric contraction. Circ Res 36: 498–512, 1975 [DOI] [PubMed] [Google Scholar]
- 23. McMahon TA. Muscles, Reflexes, Locomotion. Princeton, NJ: Princeton University Press, 1984 [Google Scholar]
- 24. Mijailovich SM, Fredberg JJ, Butler JP. On the theory of muscle contraction: filament extensibility and the development of isometric force and stiffness. Biophys J 71: 1475–1484, 1996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Napadow VJ, Chen Q, Mai V, So PT, Gilbert RJ. Quantitative analysis of three-dimensional-resolved fiber architecture in heterogeneous skeletal muscle tissue using nmr and optical imaging methods. Biophys J 80: 2968–2975, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Napadow VJ, Chen Q, Wedeen VJ, Gilbert RJ. Biomechanical basis for lingual muscular deformation during swallowing. Am J Physiol Gastrointest Liver Physiol 277: G695–G701, 1999 [DOI] [PubMed] [Google Scholar]
- 27. Napadow VJ, Chen Q, Wedeen VJ, Gilbert RJ. Intramural mechanics of the human tongue in association with physiological deformations. J Biomech 32: 1–12, 1999 [DOI] [PubMed] [Google Scholar]
- 28. Nishikawa KC, Kier WM, Smith KK. Morphology and mechanics of tongue movement in the African pig-nosed frog Hemisus marmoratum: a muscular hydrostatic model. J Exp Biol 202: 771–780, 1999 [DOI] [PubMed] [Google Scholar]
- 29. Paydarfar D, Gilbert RJ, Poppel CS, Nassab PF. Respiratory phase resetting and airflow changes induced by swallowing in humans. J Physiol 483: 273–288, 1995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Sanguineti V, Laboissiere R, Payan Y. A control model of human tongue movements in speech. Biol Cybern 77: 11–22, 1997 [DOI] [PubMed] [Google Scholar]
- 31. Sarma PA, Pidaparti RM, Moulik PN, Meiss RA. Non-linear material models for tracheal smooth muscle tissue. Biomed Mater Eng 13: 235–245, 2003 [PubMed] [Google Scholar]
- 32. Skierczynski BA, Wilson RJ, Kristan WB, Jr, Skalak R. A model of the hydrostatic skeleton of the leech. J Theor Biol 181: 329–342, 1996 [DOI] [PubMed] [Google Scholar]
- 33. Smith DA, Mijailovich SM. Toward a unified theory of muscle contraction. II. Predictions with the mean-field approximation. Ann Biomed Eng 36: 1353–1371, 2008 [DOI] [PubMed] [Google Scholar]
- 34. Smith DA, Mijailovich SM. Toward a unified theory of muscle contraction. II. Predictions with the mean-field approximation. Ann Biomed Eng 36: 2149, 2008 [DOI] [PubMed] [Google Scholar]
- 35. Smith KK. Morphology and function of the tongue and hyoid apparatus in Varanus (Varanidae, Lacertilia). J Morphol 187: 261–287, 1986 [DOI] [PubMed] [Google Scholar]
- 36. Sokolnikoff IS. Mathematical Theory of Elasticity. New York: McGraw-Hill, 1986 [Google Scholar]
- 37. Stejskal EO. Use of spin echoes in a pulsed magnetic field gradient to study anisotropic, restricted diffusion and flow. J Chem Phys 43: 3597–3603, 1965 [Google Scholar]
- 38. Stojanovic B, Kojic M, Rosic M, Tsui CP, Tang CY. An extension of Hill's three-component model to include different fiber types in finite element modeling of muscle. Int J Num Meth Eng 71: 801–817, 2007 [Google Scholar]
- 39. Suki B, Ito S, Majumdar A. Multiscale network modeling of the dynamic nonlinear properties of airway smooth muscle tissue. J Biomech 39: S399, 2006 [DOI] [PubMed] [Google Scholar]
- 40. Tang CY, Tsui CP, Stojanovic B, Kojic M. Finite element modeling of skeletal muscles coupled with fatigue. Int J Mech Sciences 49: 1179–1191, 2007 [Google Scholar]
- 41. Tang W, Zhang L, Linninger AA, Tranter RS, Brezinsky K. Solving kinetic inversion problems via a physical bounded Gauss-Newton (PGN) method. Ind Eng Chem Res 44: 3626–3637, 2005 [Google Scholar]
- 42. Van Leeuwen JL, Kier WM. Functional design of tentacles in squid: linking sarcomere ultrastructure to gross morphological dynamics. Philos Trans R Soc Lond B Biol Sci 352: 551–571, 1997 [Google Scholar]
- 43. Wadepuhl M, Beyn WJ. Computer simulation of the hydrostatic skeleton. The physical equivalent, mathematics and application to worm-like forms. J Theor Biol 136: 379–402, 1989 [DOI] [PubMed] [Google Scholar]
- 44. Wedeen VJ, Reese TG, Napadow VJ, Gilbert RJ. Demonstration of primary and secondary muscle fiber architecture of the bovine tongue by diffusion tensor magnetic resonance imaging. Biophys J 80: 1024–1028, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Wedeen VJ, Reese TG, Tuch DS, Wiegell MR, Dou JG, Weisskoff RM, Chessler D. Mapping fiber orientation spectra in cerebral white matter with Fourier-transform diffusion MRI. In: 8th Annual Meeting of the ISMRM, Denver, Colorado Berkeley, CA: ISMRM, 2000 [Google Scholar]
- 46. Wilhelms-Tricarico R. Physiological modeling of speech production: methods for modeling soft-tissue articulators. J Acoust Soc Am 97: 3085–3098, 1995 [DOI] [PubMed] [Google Scholar]
- 47. Wilson JF, Mahajan U, Wainwright SA, Croner LJ. A continuum model of elephant trunks. J Biomech Eng 113: 79–84, 1991 [DOI] [PubMed] [Google Scholar]
- 48. Yang C, Tang D, Haber I, Geva T, del Nido PJ. In vivo MRI-based 3D FSI RV/LV models for human right ventricle and patch design for potential computer-aided surgery optimization. Comput Struct 85: 988–997, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Yekutieli Y, Sagiv-Zohar R, Aharonov R, Engel Y, Hochner B, Flash T. Dynamic model of the octopus arm. I. Biomechanics of the octopus reaching movement. J Neurophysiol 94: 1443–1458, 2005 [DOI] [PubMed] [Google Scholar]