Free energy surfaces for the interaction of D-glucose with planar aromatic groups in aqueous solution

Abstract

Multidimensional potentials of mean force for the interactions in aqueous solution of both anomers of D-glucopyranose with two planar aromatic molecules, indole and para-methyl-phenol, have been calculated using molecular dynamics simulations with umbrella sampling and were subsequently used to estimate binding free energies. Indole and para-methyl-phenol serve as models for the side chains of the amino acids tryptophan and tyrosine, respectively. In all cases, a weak affinity between the glucose molecules and the flat aromatic surfaces was found. The global minimum for these interactions was found to be for the case when the pseudoplanar face of β-D -glucopyranose is stacked against the planar surfaces of the aromatic residues. The calculated binding free energies are in good agreement with both experiment and previous simulations. The multidimensional free energy maps suggest a mechanism that could lend kinetic stability to the complexes formed by sugars bound to sugar-binding proteins.

INTRODUCTION

Many proteins, such as sugar-binding proteins,^{1, 2} or enzymes with carbohydrate substrates, such as lysozyme³ or cellulases,⁴ have been designed by evolution to bind sugars, but the affinity of sugar molecules for such proteins is relatively weak. Lectins, which are the most common class of sugar-binding proteins, bind monosaccharides with binding constants around10³M⁻¹,^{5, 6} which corresponds to binding free energies on the order of 10k_BT at physiological temperatures. For oligosaccharides the typical binding constants are higher, up to10⁶–10⁷M⁻¹.⁷ This is still fairly low and constitutes a challenge to both biochemists and nature itself in the design of carbohydrate-recognizing proteins.⁵

The binding sites in sugar-binding proteins often feature the flat side chains of the aromatic amino acids phenylalanine (Phe), tyrosine (Tyr), or particularly, tryptophan (Trp).⁸ The extended active sites of cellulases, for example, contain several such residues spaced so as to interact with several sugar rings in cellulose.⁸ In complexes of these proteins with their substrates, the carbohydrate rings are in many cases known from X-ray diffraction studies⁹ to stack their hydrophobic, aliphatic protons against the flat hydrophobic faces of these aromatic side chains. This binding motif for carbohydrate binding sites is sufficiently widespread as to suggest a special affinity between sugar rings and these aromatic side chains.^{10, 11}

There are relatively few studies investigating carbohydrate-aromatic interactions in isolation. Fernández-Alonzo et al.¹² used NMR to demonstrate that monosaccharides (methyl β-galactoside) and aromatic rings (benzene) do indeed form complexes in solution and used ab initio calculations to quantify the interaction energies to around 12 kJ∕mol (in vacuum). The same strategy was employed by Vandenbussche et al.,¹⁰ who also used NMR in conjunction with ab initio and molecular mechanics modeling to study the same carbohydrate-aromatic complex. They further used titration to estimate the binding affinity to be very low, below1M⁻¹. They also found a significant hydrophobic component in their results, since the affinity disappeared in other polar solvents than water.

Preliminary MD simulation studies of D-glucose interacting with a model peptide in solution have indeed found a highly specific and localized interaction site for D-glucose molecules adjacent to the planar face of tryptophan, with an estimated interaction energy of about −2.5kJ∕mol, equal to k_BT at room temperature.¹³ Moreover, a recent experimental study of the thermal denaturation of synthetic peptides containing a tryptophan residue and a covalently bound saccharide, positioned so as to be able to stack against each other in the folded state, also estimated this interaction energy to be of the same magnitude, −3.35 kJ∕mol.¹⁴ This shows the importance of X-H⋯π interactions for carbohydrate recognition, but also, not surprisingly, that these interactions alone are not sufficient to account for the affinities of real binding sites, which are an order of magnitude larger. Clearly, some cooperativity at the binding site is present, usually attributed to hydrogen bonding,^{5, 10, 14} which helps desolvate and stabilize the sugar at the binding site. There is also some cooperativity present between binding sites, in that the binding affinities for oligosaccharides to multivalent sugar-binding proteins are greater that the sum of the individual affinities. This effect has been coined the cluster glycoside effect.⁷

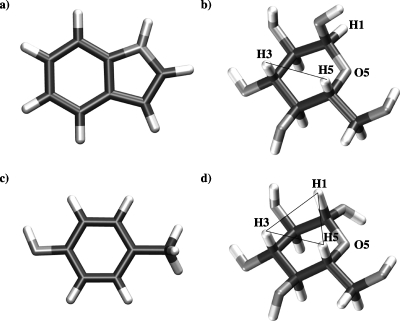
Given that sugar-aromatic interactions seem to play a crucial role for carbohydrate recognition, as indicated by the widespread occurrence of this stacking motif in sugar-binding proteins, it would be of use to have a more complete description of the energetics of the interactions of sugar molecules with such planar functional groups. In this paper, we report the calculation of the potentials of mean force (pmf) for the interactions of both anomers of D-glucopyranose with two planar aromatic molecules, indole and para-methyl-phenol, which serve as models for the side chains of Trp and Tyr, respectively. Figure 1 illustrates the geometries of these molecules. The approach employed used symmetry considerations to identify the relevant degrees of freedom of the bound complex and molecular dynamics (MD) simulations with umbrella sampling to construct multidimensional pmfs, which are three dimensional descriptions of the Gibbs free energy as a function of both separation distance and relative orientations of the two molecules.

Figure 1.

The molecules modeled in the present study: (a) indole, (c) para-methyl-phenol, (b) α-D -glucopyranose, and (d) β-D -glucopyranose. Both glucose molecules are shown with their primary alcohol groups in the gt conformation (Ref. ¹⁶).

METHODS

The goal of the present study was to calculate the binding free energy of two species, AandB, forming a complex AB in solution. A possible way to proceed is to consider the equilibrium constant, K_b, of the binding reactionA+B⇆AB. It can be expressed asK_b=[AB]∕[A][B], where[A], [B], and [AB] are the equilibrium concentrations of A andB, and the bound complexAB, respectively. From this, the binding free energy ΔG^∘ is calculated fromΔG^∘=−k_BT ln(C^∘K_b), where k_B is Boltzmann's constant, Tis the temperature, and C^∘ is a standard concentration, usually 1M, which corresponds to1∕1.661 nm⁻³.

From a classical statistical mechanical point of view, ΔG^∘can be expressed as

$$\Delta G^{\circ }=-RT\left(\frac{C^{\circ }}{8{\pi }^2}\frac{Z_{AB+S}{Z}_S}{Z_{A+S}{Z}_{B+S}}\right)+P^{\circ }\Delta V,$$ (1)

where R is the universal gas constant, Z_Xare configuration integrals overA, B, and S (solvent) degrees of freedom. If the volume change ΔV upon binding is small, the pressure-volume term in Eq. 1 is negligible. Following Gilson et al.,¹⁵ ΔG^∘ can be written in a form which is more convenient for computer simulations,

$$\Delta G=-k_{B}T\text{\hspace{0.17em}ln}\left(\frac{C^{\circ }}{8{\pi }^2}{\int }_{V_B}drd\xi e^{-W\left(r,\xi \right)∕k_{B}T}\right),$$ (2)

where W(r,ξ) is the potential of mean force, or work function, which represents the work needed to bring molecule A from a point far away in the solution to(r,ξ). Note that W by construction includes all relevant contributions to the configuration integrals, including solvent effects. The integral is taken overV_B, which is the volume associated with the bound state complexAB. In Eq. 2, W is assumed to be a function only of the six coordinates that describes the position and orientation of molecule A relative to moleculeB. This approximation rests on the assumption that the molecules’ internal degrees of freedom do not change significantly upon binding, and thus do not contribute to the binding free energy. The validity of this assumption may be questioned, especially for larger molecules like proteins which may undergo quite profound conformational changes upon ligand binding∕unbinding. For monosaccharides, which are relatively small molecules, the main concern would be rotations of the primary alcohol.¹⁶ If such changes in the conformational space for this particular degree of freedom do not significantly contribute to the total free energy, the assumption seems justified.

Even with the given approximations, the configurational integral must be evaluated over six degrees of freedom, which for most biomolecular systems poses a significant challenge in terms of simulation times needed for satisfactory convergence. Usually, one proceeds from this point by making some approximations regarding the relative motion of A andB. In an isotropic, infinitely dilute system, Ais assumed to rotate freely in the reference frame ofB, and the integration over the Euler angles can be carried out directly.¹⁷ For the case of spherical symmetry, the simplest possible case, the work function is a function of only one variable, the distancer. The free energy then becomes¹⁸

$$\Delta G=-k_B\text{\hspace{0.17em}ln}\left(4\pi C^{\circ }{\int }_0^{r_C}dr{e}^{-W\left(r\right)∕k_{B}T}\right),$$ (3)

where r_c is some cut off radius that distinguishes the bound state from the free state. The value selected for r_c is somewhat arbitrary, but a common choice is to select it to be where W flattens out, showing no significant structure that could be attributed to a bound state.

Other approaches include the adoption of a model for the coordinates of the bound state, usually a harmonic or quasiharmonic approximation,^{17, 19} or combinations of restrained MD and thermodynamic decoupling methods.²⁰ The selected approximations must, of course, be justified by existing symmetries of the system under study. Assuming spherical symmetry will for most biomolecular systems greatly overestimate the available phase space volume of the bound state, but leads on the other hand to fairly straightforward calculations. Assuming that A rotates completely freely also seems like a very crude approximation in most cases. It should however be possible to identify which degrees of freedom are the most relevant, for a particular type of problem, and eliminate the rest.

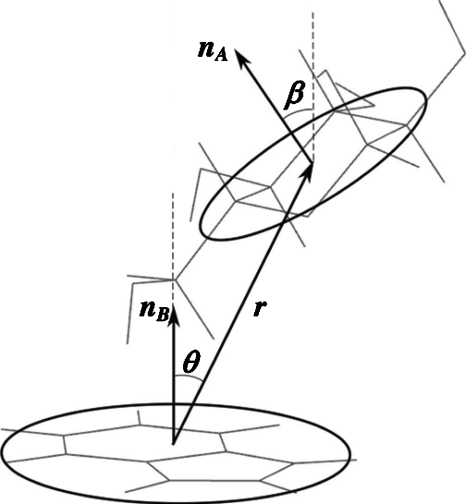
In the present case, a monosaccharide A interacts with a flat aromatic moleculeB, at close distances presumably being restricted to a stacked arrangement. Clearly, this problem does not exhibit spherical symmetry, nor does A rotate freely with respect to B at very close distances. Considering the system to be composed of two flat, circular disks as in Fig. 2, from symmetry considerations, three coordinates are sufficient to describe their relative positions and orientations. Using spherical coordinates for their relative position, one coordinate is the center of mass (COM) distance, r=|r_A−r_B|, while θ is the angle that |r_A−r_B| makes with the normal ${\stackrel{̑}{n}}_B$ to moleculeB. The second angle, ϕ, is not needed, and can be integrated over directly. For their orientation, only one Euler angle β is needed, which is the angle the normal to the plane of moleculeA, ${\stackrel{̑}{n}}_A$, makes with${\stackrel{̑}{n}}_B$. The remaining two Euler angles, usually denoted α andγ, do not need to be considered, and can be integrated out. This leads to a work function which is a function of three variables, W=W(r,θ,β), and the free energy of binding becomes

$$\Delta G=-k_{B}T\text{\hspace{0.17em}ln}\left(\pi C^{\circ }\int drd\theta d\beta r^2\text{\hspace{0.17em}sin}\theta \text{\hspace{0.17em}sin}\beta e^{-W\left(r,\theta ,\beta \right)∕k_{B}T}\right),$$ (4)

where r runs from 0 tor_c, and the angles from 0 to2π.

Figure 2.

Definition of the reaction coordinates.

The work function W(r,θ,β) can be obtained from MD simulations via the probability distributionρ(r,θ,β), which is the probability of finding the system in the state described by the three coordinates, as

$$W\left(r,\theta ,\beta \right)=-k_{B}T\text{\hspace{0.17em}ln}\left[\rho \left(r,\theta ,\beta \right)\right].$$ (5)

This probability distribution can be calculated from a sufficiently long simulation simply by counting states. Such an approach would converge very slowly, however, and it is usually better to instead use some sort of biased simulation. In the present work, umbrella sampling along the COM separation was employed, using a harmonic umbrella potential²¹ of the form

$$U\left(r\right)=k{\left(r-r_i\right)}^2,$$ (6)

with r=|r_A−r_B| as before, and i ranging from 1 to the total number of simulationsN. Each of the trajectories from the N simulations were decomposed into N_θ×N_β probability distributions, where N_θ and N_β are the number of grid points in θ and β space, respectively. All probability distributions belonging to the same θ-β-pair were combined into a single, unbiased, probability distribution using WHAM,²² and the corresponding free energy profile was calculated using Eq. 5. Although the system is contoured along one coordinate, the COM distance, the procedure leads to an approximation of the three dimensional work functionW(r,θ,β). Finally, the free energy of binding, ΔG˚, can be calculated by numerical integration of Eq. 4.

Molecular dynamics simulations

The MD simulations in this work were performed with the GROMACS 4.0 simulation software,²³ using the CHARMM22 (Ref. ²⁴) and CSFF (Ref. ²⁵) force fields, as implemented in GROMACS,²⁶ for the solutes, and the CHARMM implementation of the TIP3P potential for the water.²⁷ The integration was done using a leap-frog algorithm with a 2 fs time step. All bonds involving hydrogen atoms were constrained to their equilibrium values using P-LINCS,²⁸ and water molecules were kept completely rigid using SETTLE.²⁹ Nonbonded electrostatic interactions were treated with PME (Ref. ³⁰) using a cut off of 1.0 nm for the real space part, and Lennard-Jones interactions were shifted to zero between 1.0 and 1.2 nm. The simulations were run at a constant temperature of 298 K, using velocity rescaling,³¹ and constant pressure using a Parrinello–Rahman barostat with reference pressure of 1 atm.³²

As described above, the system was made subject to a biasing harmonic potential along a coordinate defined by the center-of-mass separation between the two solutes, r [see Eq. 6]. The force constant k was set to 836.8 kJ∕mol (Ref. ²¹) and r_i ranged from 0.4 to 1.2 nm in 0.05 nm increments. Each sampling window was simulated for 5 ns, with the exception for simulations at the very shortest distances (0.4–0.5 nm), which were run for a total of 25 ns to enhance the sampling. Since r is a one dimensional reaction coordinate in three dimensional space, a Jacobian correction of 2k_BT ln(r) was added to the pmfs³³ to make them level off to a constant value at large distances.

Starting coordinates for the solutes were generated using CHARMM (Ref. ³⁴) and subsequently placed into a cubic simulation box with side lengths 2.6 nm, which was filled with TIP3P water. The system was then subjected to energy minimization followed by a short 100 ps equilibration run in which all solute atoms were harmonically constrained, to allow for the water to equilibrate around the solutes, and for pressure and temperature to settle.

RESULTS AND DISCUSSION

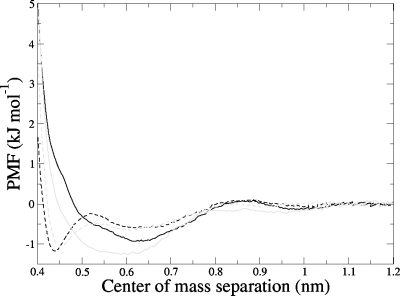
Figure 3 displays the radially averaged pmfs for each of the four cases studied; that is, for both of the anomers of D-glucopyranose (αandβ) paired with the flat aromatic molecules indole and para-methyl-phenol, which are models for the side chains of the amino acids tryptophan and tyrosine, respectively. These functions are averaged over all possible relative orientations of the two molecules (that is, all values of β andθ) at each separation distance. As can be seen, all four pmf functions suggest a weak affinity of both glucose anomers for the flat aromatic surfaces. The calculated well depths are only between 0.9 and 1.5 kJ∕mol, or around one-halfk_BT. The statistical errors, however, which were calculated using a bootstrap procedure described in Hub and de Groot,³⁵ are reassuringly small, of the order of ±9.6%. For each glucose anomer, there is little difference in the interaction with these two flat surfaces. However, the pmfs show a striking difference in the nature of the interaction for the two different anomers. The β-D -glucopyranose anomer, on both indole and para-methyl-phenol, gives a narrow first minimum, centered around approximately 0.45 nm, which is essentially the contact distance for a stacked conformation, with a second, much broader minimum around 0.6–0.7 nm. The α-D -glucopyranose anomer, however, exhibits only a very broad minimum around 0.6 nm, on both aromatic residues. This distance is clearly too large to be associated with direct stacking interactions, but is rather, as will be seen below, the separation for a conformation in which the glucose molecules are significantly tilted with respect to the planar residue. This difference in interaction geometry is consistent with the results of recent simulations of glucose interacting with a tryptophan residue in a model peptide,¹³ where more optimal stacking was exhibited by the β-anomer, with its hydrophobic H1-H3-H5 triad face [see Fig. 1d].

Figure 3.

Potentials of mean force as function of center-of-mass separation for α-D -glucopyranose-indole (solid black), β-D -glucopyranose-indole (dashed black), α-D -glucopyranose-para-methyl-phenol (solid gray), and β-D -glucopyranose-para-methyl-phenol (dashed gray).

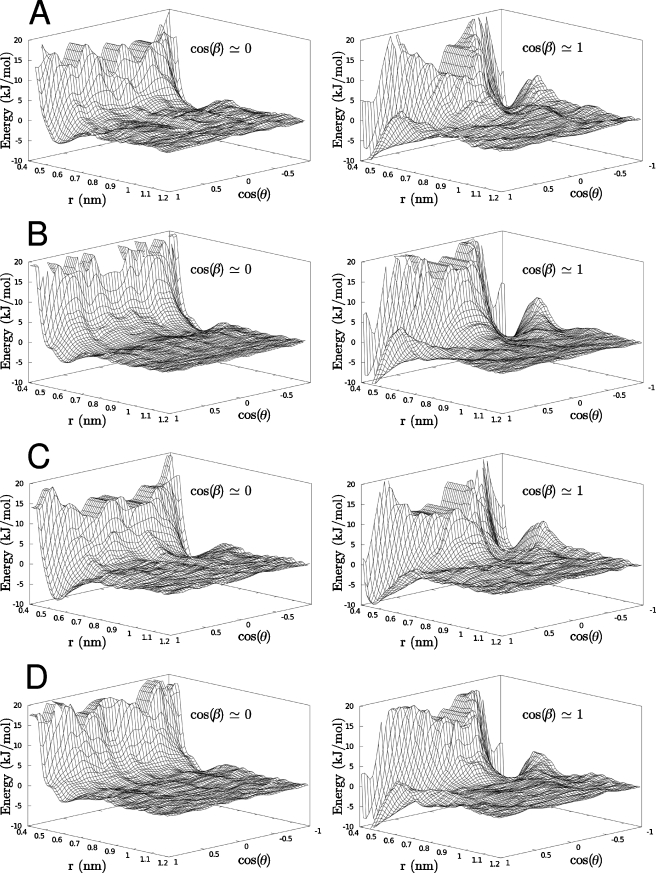
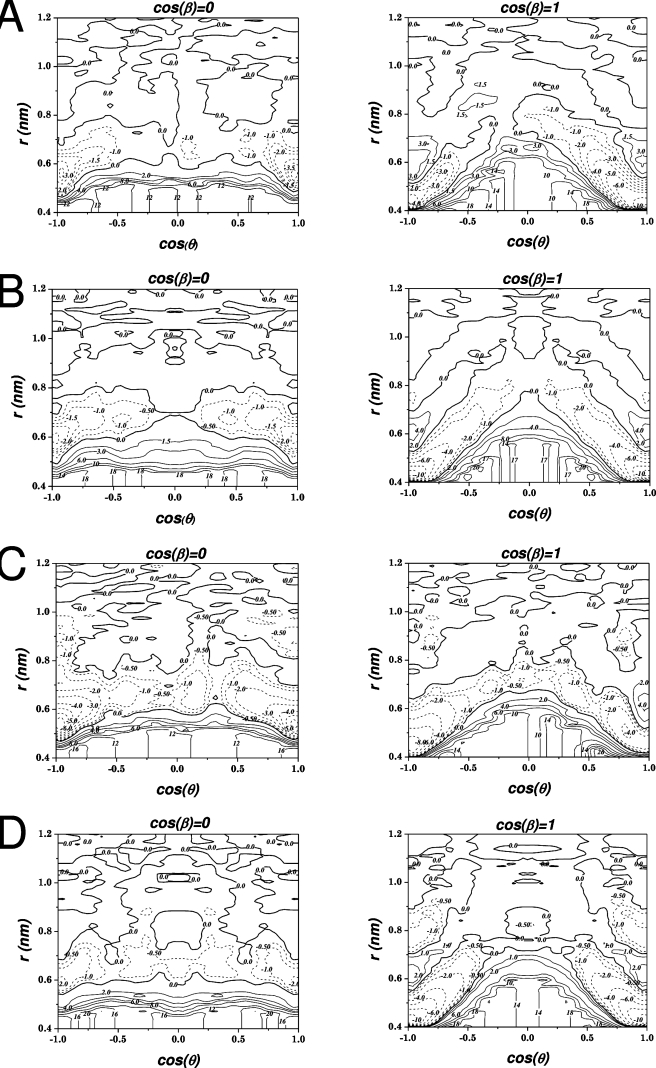
By decomposition of the one dimensional work function into three explicit reaction coordinates as described in the previous section, three dimensional free energy surfaces were calculated as a function of the COM separation between each molecular pair and the two angles θ and β describing their relative orientation. Representations of these free energies are displayed in Figs. 45, where the free energy is plotted as a function of two variables r and the cosine of the angle θ for two different values of the angleβ, cos(β)≅1, for which the two solutes are more or less planar, and cos(β)≅0, for which the glucose molecule is tilted 90° with respect to the aromatic molecule. The free energy surfaces for all four systems look similar. For cos(β)≅1 there are two deep wells located at r≅0.45 nm and cos(θ)≅±1. It is easy to see that this corresponds to a situation where the glucose is stacked on top of the aromatic molecule in an almost completely flat arrangement, and that the two minima originate from the two different faces of the glucose. For β-D -glucopyranose, the depths of the two minima are the same, which is reasonable since the two faces differ by only one axial aliphatic proton (see Fig. 1). The depths of these minima, which are also the global minima, are about −10 kJ∕mol, relative to the separated state. For α-D -glucopyranose, the minimum at cos(θ)≅−1 is only about half as deep as the minimum at cos(θ)≅+1, around −5 kJ∕mol. That there is a difference is not unexpected, since α-D -glucopyranose has its anomeric hydroxyl group in an axial position, i.e., more or less perpendicular to the mean plane of the molecule (Fig. 2). This difference means that the anomeric group in one of the arrangements is pointing directly toward the aromatic molecule, and in the other, it is pointing away, allowing it to hydrogen bond to solvent. That these stacked arrangements correspond to free energy minima could broadly be understood as arising from hydrophobic association freeing structured water molecules from these weakly hydrated faces.

Figure 4.

Free energy surfaces for glucose-aromatic systems: α-D -glucopyranose-indole (a), β-D -glucopyranose-indole (b), α-D -glucopyranose-para-methyl-phenol (c), and β-D -glucopyranose-para-methyl-phenol (d). Energies are given as a function of separation r and cos(θ), for two values of cos(θ); cos(β)≅0 (left) for which the glucose is tilted with respect to the aromatic molecule, and cos(β)≅1 (right) which corresponds to a planar arrangement (see Fig. 2 and text).

Figure 5.

Free energy surfaces for glucose-aromatic systems: α-D -glucopyranose-indole (a), β-D -glucopyranose-indole (b), α-D -glucopyranose-para-methyl-phenol (c), and β-D -glucopyranose-para-methyl-phenol (d). Energy contours are in kJ∕mol.

For cos(β)≅0 there are also two minima at cos(θ)≅±1, which corresponds to an arrangement where the glucose is still more or less on top of the aromatic residue, but tilted 90° with respect to its normal. These minima are located further out than in the stacked arrangement, atr≅0.6 nm. Furthermore, they are much shallower than the one for cos(β)≅1, only −3 to −5 kJ∕mol, with the more negative value for the α-D -glucopyranose. A qualitative interpretation for the shallow minimum corresponding to perpendicular approach is more difficult to visualize than in the hydrophobic stacking case.

It should be noted that the lowest energy state, in all cases, is the stacked, flat geometry, which has an energy considerably lower than the fully separated state. This result is also apparent in the one dimensional pmfs shown in Fig. 3, but only in those for β-D -glucopyranose. For α-D -glucopyranose, the global minimum in the pmf instead coincides with the minimum associated with a tilted arrangement. Of course, the one dimensional pmf is an average over many relevant degrees of freedom and may therefore not convey all important features of the total free energy landscape.

The contour plots in Fig. 5 illustrate that while the lowest energy geometry for the glucose molecules relative to either aromatic partner is to be stacked against its face withθ≅0°, pulling these two molecules directly apart would require surmounting a significant barrier as a vacuum was initially created between the two surfaces until they had separated enough to allow water molecules to fill the space between them. For this reason, it can be seen that the lowest energy pathway for separation involves displacing the two molecules off-center, following a diagonal path of decreasing cos(θ) and increasing r on the contour plots until cos(θ) is almost 0 and r is approximately 0.9 nm, after which the molecules can separately more freely, particularly in the case of the β-D -glucopyranose anomer. In the restricted environment of a sugar-binding site in a protein, where the sugar molecule presumably is stabilized by hydrogen bonds to polar residues and caged by steric interactions, this lateral displacement may not be possible, forcing the sugar ligand to directly surmount such a barrier to escape, perhaps giving the protein-ligand complex greater kinetic stability than might be expected from the magnitude of the association energy alone. It is possible that such displacement could be facilitated by conformational changes in the protein, particularly if triggered by some signal at the site where the sugar ligand is to be given up. If so, such an arrangement would be more functional than a high absolute binding free energy, which would work against giving up the sugar when required.

As seen from Figs. 345, little significant difference can be found in the binding of the glucose molecules to the faces of the two different aromatic molecules, indicating that they are principally serving as flat hydrophobic surfaces rather than as specific asymmetric sites. Thus, hydrogen bonding between the sugar and the N–H or O–H functional groups of the aromatic systems did not serve to anchor the sugar in a particular arrangement on the surface, somewhat justifying the assumption of treating these molecules as symmetric disks, and ignoring the degrees of freedom describing the anisotropic placement of these groups. Inspection of the calculated trajectories found that no persistent hydrogen bonding took place between the two solute molecules in any of the calculations at any distance. This is in agreement with Laughrey et al.,¹⁴ who concluded that hydrogen bonding contributed to the total interaction energy with, at most, 0.4 kJ∕mol.¹⁴ In the simulations, the rotameric conformational distribution of the exocyclic hydroxymethyl group for most separations was an approximately 60:40 partitioning between gg andgt,¹⁶ respectively, as it would be for free glucose both in simulations²⁵ and from NMR experiments.³⁶ However, for a COM distance of around 0.4 nm, this primary alcohol conformational equilibrium shifted to 40:60, perhaps as a result of steric crowding when this exocyclic group is pointing axially down toward the aromatic surface. This shift also shows that hydrogen bonding between the molecules is of little importance, since this group would presumably have to be in this conformation to have any chance of making even a strained hydrogen bond to the aromatic hydroxyl, in the case of the para-methyl-phenol. Presumably even a strained hydrogen bond to the N–H group of the indole in a stacked arrangement would be topologically unlikely.

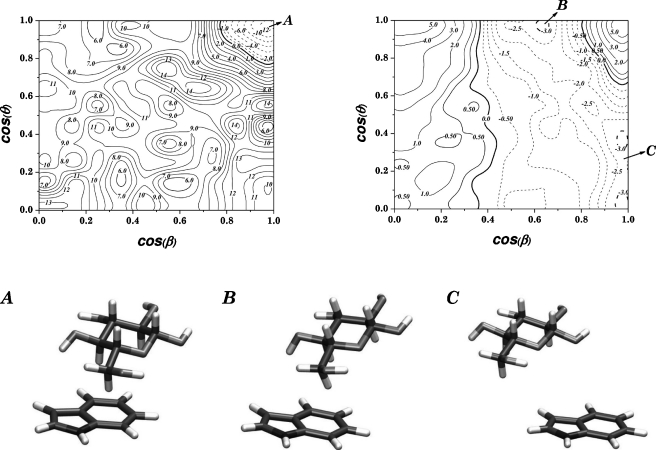
Figure 6 illustrates the variation of the potential of mean force with θ and β at two different values of the COM separationr_c, 0.42 nm, corresponding to near van der Waals contact, and 0.62 nm, for β-D -glucopyranose interacting with indole. As can be seen, for the short COM separation the free energy landscape is complex. This is reasonable since the motion (rotation∕tilting) of the sugar molecule is restricted by steric interactions, and only one position is energetically preferred, with both |cos(θ)| and |cos(β)| being approximately 1 (see the left contour plot in Fig. 6). This particular position represents parallel stacking of the sugar against the aromatic surface (relative orientation “A” in Fig. 6). The barrier for motion away from this orientation is more than 25 kJ∕mol before other local minima can be reached, which are both more shallow and higher in energy. On the other hand, at larger COM distances the rotation of the sugar molecule is less restricted and it takes less energy to tilt the sugar against the aromatic ring plane and the energy landscape becomes flatter. This effect can be seen in the contour plot shown on the right in Fig. 6, which shows that there is no preferred parallel stacking, but rather tilting of the sugar molecule (relative orientations “B” and “C” in Fig. 6), with practically no energy barrier (compared tok_BT) for moving between different values ofθ.

Figure 6.

Contour plots of the θ-β free energy landscape for β-D -glucopyranose interacting with indole, for two different values ofr_c, 0.42 and 0.62 nm, along with illustrations of the relative orientations represented by three specific points, indicated on the plots by the corresponding letters. All energy contours are in kJ∕mol.

Finally, estimates of the standard free energy of binding ΔG^∘ were calculated using the methods described above, both by assuming spherical symmetry and integrating the one dimensional pmfs over the bound region [Eq. 3], and by integrating the three dimensional free energy according to Eq. 4. The results are shown in Table 1, for different choices of the cut off radius r_c for the bound region, along with the corresponding one dimensional pmf well depth for comparison. The data in Table 1 show that there is a strong dependence of ΔG^∘ on the selected cutoff distancer_c, around a factor of 2 between the shortest and the longest cut offs. Considering the somewhat arbitrary nature of the choice ofr_c, it is difficult to make any precise statements regarding the absolute values ofΔG^∘. Unfortunately, this is a characteristic of systems that are very weakly bound. Since the free energy landscape is relatively flat everywhere, even regions where the work function W is close to zero will give rise to non-negligible contributions toΔG^∘. For more strongly bound systems, contributions from regions of large negative W will dominate, and ΔG^∘ will not depend so strongly upon the choice ofr_c. However, it seems that it is at least possible to say that α-D -glucopyranose prefers para-methyl-phenol over indole, while β-D -glucopyranose prefers indole over para-methyl-phenol. This is somewhat consistent with Laughrey et al.,¹⁴ who see an increased affinity of glucose for a tryptophan compared to a phenol. Furthermore, by changing the equatorial hydroxyl group at C4 to axial, thereby transforming the glucose to a galactose, the affinity for Trp decreases.

Table 1.

Standard free energies of binding, calculated using different values for the cutoff for the bound region, r_c. The first value is calculated using Eq. 4 and the approximation described in the previous section. The second value is calculated using Eq. 3 assuming spherical symmetry. ΔWare the well depths of the one dimensional pmfs in Fig. 3. All values are given in kJ∕mol.

	rc=0.85 nm	rc=0.9 nm	rc=0.95 nm	ΔW
α-glucose-indole	−0.8∕−1.6	−1.3∕−1.9	−1.8∕−2.2	−0.9
β-glucose-indole	−1.1∕−1.6	−1.5∕−1.9	−1.8∕−2.2	−1.2
α-glucose– p -methyl-phenol	−1.7∕−1.8	−2.1∕−2.1	−2.4∕−2.4	−1.4
β-glucose– p -methyl-phenol	−0.6∕−1.6	−1.1∕−1.9	−1.5∕−2.3	−1.0

Finally, it should be noted that in the present model, rotations aboutϕ, α, and γ were neglected, essentially treating both the aromatic and sugar molecules as symmetric disks. Of course, this constitutes an approximation, especially since the glucose molecule is not symmetric with respect to rotations around its normal, and, strictly speaking, not even flat. There are certainly conformations that are more favorable than others even along these coordinates, and how that would affect the calculated ΔG^∘ is not investigated in this work. With present available resources, such approximations were necessary since convergence of the data would become a critical issue if an attempt was made to decompose the pmf into all six internal coordinates. Each additional coordinate would require an estimated increase in the simulation lengths by approximately an order of magnitude.

CONCLUSIONS

Surveys of the reported crystal structures for proteins that bind glucose reveal that nearly all of the sugar-binding sites in such proteins contain amino acids with aromatic side chains, such as Phe, Tyr, and Trp. These residues are believed to promote sugar-binding and selectivity by allowing the nearly flat face of the sugar molecule to interact in a stacked arrangement with the aromatic side chain. Recent experimental studies¹⁴ as well as MD simulations¹³ give a magnitude of the binding energy between glucose and such aromatic residues of aboutk_BT.

The present calculation found an energetically small but significant binding affinity for glucose molecules for the hydrophobic faces of both indole and para-methyl-phenol. These affinities apparently arise from hydrophobic association, with virtually no contribution from hydrogen bonding, and are not strongly dependent on the structural features of the aromatic groups, apart from their extended flat surfaces. Absolute binding free energies were estimated to be 0.6–2.4 kJ∕mol, i.e., less thank_BT, and were found to depend strongly on the cutoff radius used to define the bound state. However, no large differences between the different solutes were found. These values correlate well with previous experimental^{10, 14} and MD (Ref. ¹³) simulation values, but are considerably lower than most ab initio results.¹² These numbers constitute extremely weak affinities, and it is clear that some other element is needed to reach the binding free energies of real sugar-binding sites, which typically are an order of magnitude greater. Hydrogen bonds between the polar groups that line sugar molecule and polar protein residues are probably needed to help desolvate the sugar, but do not contribute significantly to the total binding free energy, since hydrogen bonds to water are likely to be of the same magnitude from an energetic point of view. It is worth noting, however, that in many sugar-binding proteins, at least one of the hydrogen bonding side chains in the binding site is often a charged acid group, with much stronger potential hydrogen bonding interaction energies.^{1, 37}

On the other hand, the multidimensional free energy maps presented here show that while the sugar-aromatic complex could be easily disrupted in aqueous solution by the molecules simply sliding sideways as they move apart, if forced to move straight out in a perpendicular fashion from a stacked arrangement, more significant kinetic barriers oppose the separation. Such sideways motions might be restricted in the binding sites of proteins, e.g., due to hydrogen bonds that could help stabilize the bound complex, thereby giving protein-sugar ligand interactions significant kinetic stability without requiring strong thermodynamic complexation.