Use of likelihood ratios for comparisons of binary diagnostic tests: Underlying ROC curves

Abstract

Purpose: When comparing binary test results from two diagnostic systems, superiority in both “sensitivity” and “specificity” also implies differences in all conventional summary indices and locally in the underlying receiver operating characteristics (ROC) curves. However, when one of the two binary tests has higher sensitivity and lower specificity (or vice versa), comparisons of their performance levels are nontrivial and the use of different summary indices may lead to contradictory conclusions. A frequently used approach that is free of subjectivity associated with summary indices is based on the comparison of the underlying ROC curves that requires the collection of rating data using multicategory scales, whether natural or experimentally imposed. However, data for reliable estimation of ROC curves are frequently unavailable. The purpose of this article is to develop an approach of using “diagnostic likelihood ratios,” namely, likelihood ratios of “positive” or “negative” responses, to make simple inferences regarding the underlying ROC curves and associated areas in the absence of reliable rating data or regarding the relative binary characteristics, when these are of primary interest.

Methods: For inferences related to underlying curves, the authors exploit the assumption of concavity of the true underlying ROC curve to describe conditions under which these curves have to be different and under which the curves have different areas. For scenarios when the binary characteristics are of primary interest, the authors use characteristics of “chance performance” to demonstrate that the derived conditions provide strong evidence of superiority of one binary test as compared to another. By relating these derived conditions to hypotheses about the true likelihood ratios of two binary diagnostic tests being compared, the authors enable a straightforward statistical procedure for the corresponding inferences.

Results: The authors derived simple algebraic and graphical methods for describing the conditions for superiority of one of two diagnostic tests with respect to their binary characteristics, the underlying ROC curves, or the areas under the curves. The graphical regions are useful for identifying potential differences between two systems, which then have to be tested statistically. The simple statistical tests can be performed with well known methods for comparison of diagnostic likelihood ratios. The developed approach offers a solution for some of the more difficult to analyze scenarios, where diagnostic tests do not demonstrate concordant differences in terms of both sensitivity and specificity. In addition, the resulting inferences do not contradict the conclusions that can be obtained using conventional and reasonably defined summary indices.

Conclusions: When binary diagnostic tests are of primary interest, the proposed approach offers an objective and powerful method for comparing two binary diagnostic tests. The significant advantage of this method is that it enables objective analyses when one test has higher sensitivity but lower specificity, while ensuring agreement with study conclusions based on other reasonable and widely acceptable summary indices. For truly multicategory diagnostic tests, the proposed method can help in concluding inferiority of one of the diagnostic tests based on binary data, thereby potentially saving the need for conducting a more expensive multicategory ROC study.

INTRODUCTION

Performance assessments of diagnostic tests using receiver operating characteristics (ROC) approaches constitute an important area of investigation in many fields. Conceptual and statistical components of the conventional ROC analysis have been described in a number of books.^{1, 2, 3, 4, 5, 6} This general area remains of interest and there continues to be development of an ensemble of statistical tools facilitating assessments of diagnostic tests, in general, and in diagnostic imaging applications, in particular.

Diagnostic tests for the detection of a specific condition (“abnormality”) being investigated (Dfor actually present or “abnormal” and $\overline{D}$ for actually absent or “normal”) can be implemented using different rating scales, such as pseudocontinuous, categorical, or binary. The simplest, and often more clinically relevant, form of a diagnostic test is a binary test, which provides results indicating the presence (“+”) or absence (“−”) of the abnormality. The binary form of a test is frequently achieved by dichotomizing a multicategory scale. This dichotomization can be implicit or explicit depending on whether multicategory test results are actually observable or latent.

Since specific dichotomization could affect the performance of the resulting binary test, an important question when comparing two tests is whether they actually originated from different dichotomizations of the same, or different, underlying multicategory diagnostic tests. The ROC curve [“sensitivity” as a function of “1–specificity” or ROC(f)] of a given multicategory diagnostic test describes the performance characteristics of all binary diagnostic tests resulting from dichotomizations of a multicategory scale with different thresholds.²

$$f=1-\text{specificity}=P\left(+|\overline{D}\right),$$$$t=\text{sensitivity}=P\left(+|D\right).$$ 1

Comparisons of ROC curves help address the underlying issue whether or not different binary diagnostic tests result from the same or different multicategory tests.⁷ However, in some instances, multicategory data may be unavailable or may not be as reliable as binary data. For example, in imaging studies, the experimental collection of multicategory results for well-defined diagnostic tasks that are primarily binary in nature from a perception point of view (e.g., presence or absence of pneumothorax on a chest x ray or microcalcifications on mammograms) could lead to imprecise and possibly incorrect conclusions.⁸ Moreover, in tests where the observer’s interpretation is considered an integral part of the diagnostic system itself, the practical usefulness of the portions of ROC curves derived by the conventional rating approach could be questioned. Indeed, although the points on the rating-based ROC curve provide estimates of sensitivity for every possible value of specificity, the question remains whether all of these operating points can be actually achieved in practice.

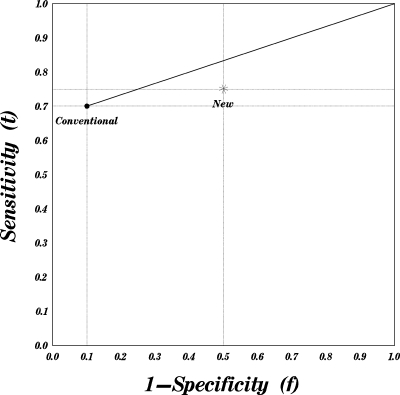
However, in some instances, even without actual ROC-type rating data, it is still possible to determine the relationship between ROC curves underlying two binary diagnostic tests. Indeed, without any assumptions about the ROC curve itself, one can state that a binary diagnostic test with both better sensitivity (denoted here ast) and “specificity” (denoted here as1−f) corresponds to at least a locally higher ROC curve. Thus, a result of comparisons of the underlying ROC curves and related indices can be inferred when both sensitivity and specificity associated with one binary test can be shown to be statistically simultaneously better than sensitivity and specificity associated with another binary test. Statistical analysis is important since performance characteristics computed from a sample of the targeted population can appear to be better for an actually inferior test just by chance (i.e., due to “lucky” sampling). Unfortunately, it is quite common to obtain data sets that do not demonstrate a simultaneous superiority in both estimated characteristics. In these cases statistical tests for simultaneous superiority in both measures are automatically insignificant. The superiority in both characteristics is frequently more difficult to demonstrate during developmental phases and initial testing of newly proposed diagnostic technologies. For example, during developmental efforts of systems for screening purposes (whether imaging based or not), the initial phase∕stage of assessments often aims to increase sensitivity of a binary test regardless of any possible increases in false positive rates (i.e., a decrease in specificity). This often results in scenarios where the new test initially has both statistically and apparently higher sensitivity but lower specificity (e.g., Fig. 1).

Figure 1.

True operating characteristics of a conventional and a new diagnostic test. The conventional test has a better negative diagnostic likelihood ratio and better specificity. The points on the bold line connecting the operating characteristics of the conventional test to the trivial corner (1,1) demonstrate characteristics achievable by augmenting the conventional test by a random guess.

In cases when the interest lies in the binary characteristics rather than in underlying ROC curves, the comparison of two binary diagnostic tests, one of which has higher sensitivity but lower specificity, may present several issues. In such instances, informative inferences are still possible with scalar indices, such as “accuracy,” “Youden’s index,” “odds ratio,” or “expected utility.”⁴ These approaches frequently incorporate explicitly subjective or sample-dependent information, such as prevalence in approaches based on accuracy and both prevalence and utility function in approaches based on expected utility. In general, all approaches that are based on summarizing two characteristics (e.g., sensitivity and specificity) by a single index impose a specific type of equivalence between different diagnostic tests, which leads to the possibility of contradicting conclusions when different approaches are used. For example, due to differences in the general shape of isolines for the odds ratio (hyperbolae) and for Youden’s index (a line with a slope of 1), a test with a better odds ratio can have a lower Youden’s index and vice versa.

The background for generating inferences about ROC curves based on binary data was described almost half a century ago.¹⁷ One of the approaches mentioned in Ref. 17 is also applicable for two binary diagnostic tests, one of which has truly higher sensitivity but lower specificity. However, statistical analysis for this approach was never considered. We demonstrate that the comparison of diagnostic likelihood ratios (i.e., likelihood ratios of “positive” or “negative” responses) enables straightforward statistical inferences regarding underlying ROC curves. Furthermore, using considerations similar to Refs. ^{15, 17}, one can develop an approach for approximate inferences about the area under the underlying ROC curve (AUC). This approach is also applicable in instances when of one of two diagnostic tests being compared has higher estimated sensitivity but lower specificity and may be useful whether the interest lies in the underlying ROC curves, the areas under the curves, or in binary characteristics at naturally adopted thresholds. For scenarios in which the binary characteristics are of primary interest, we discuss the objectivity of the resulting inferences in that a binary test superior in likelihood ratios is also superior according to the conventional intrinsic indices, such as Youden’s index and odds ratio. Finally, we discuss the constraints on prevalence levels and utility structure without which the nonintrinsic indices, such as accuracy and expected utility, could potentially lead to paradoxical study conclusions.

In Sec. 2A we discuss the implications associated with expected concavity (or equivalently up-convexity) of ROC curves and outline the justification as to why the violation of true concavity is often unreasonable to expect. We also provide in this section background information on diagnostic likelihood ratios. In Sec. 2B we describe inferences that can be made based on likelihood ratios of two binary diagnostic tests and relationships to other indices. Section 3 offers a discussion of the proposed methodology and the Appendix0 provides a detailed basis for generating inferences in regard to AUCs of underlying ROC curves.

MATERIALS AND METHODS

Background

Concavity of ROC curves and implications regarding the properties of a diagnostic test

The solution proposed in this paper exploits the assumption of concavity of the underlying ROC curve. The assumption of concavity of “practically reasonable” ROC curves has been promoted by many authors^{10, 11} as an important, useful, and frequently necessary property. Several investigators also considered a variety of ROC inferences resulting from the exploitation of the assumption of concavity (or equivalently up-convexity).^{11, 15} The implications of concavity have also been used to make the graphical comparison of operating characteristics of diagnostic tests.^{12, 17}

Concavity of ROC curves is “natural” to assume in a large number of practical applications, including observer performance studies, because violation of this property implies that a diagnostic system could locally perform worse than a purely guessing system. This follows from the fact that a straight line connecting two experimentally ascertained operating points (determined by 1–specificity or “ f ” and sensitivity or “ t ”) for two binary tests represents the performance of a system that randomly chooses between the decisions of the two tests.¹² For the straight line connecting the operating point of a binary test to the trivial points (0,0) or (1,1), there is an even more intuitively appealing interpretation.⁷ Namely, any point on a straight line connecting an operating point (f₁,t₁) of a given diagnostic test with the trivial operating point (1,1) describes an operating characteristic of a test that relabels as positive a random fraction of those subjects which had been originally called negative.^{7, 17} Indeed, if the probability of relabeling a negative subject as positive is p regardless of its true status (e.g., by flipping a coin), the operating characteristics of such an augmented test (f^p,t^p) can be represented as

$$t^p=P\left(+|D\right)+\left[1-P\left(+|D\right)\right]\times p=t_1+\left(1-t_1\right)\times p=t_1\times \left(1-p\right)+1\times p,$$$$f^p=P\left(+|\overline{D}\right)+\left[1-P\left(+|\overline{D}\right)\right]\times p=f_1+\left(1-f_1\right)\times p=f_1\times \left(1-p\right)+1\times p.$$ 2

This important consideration provides a useful interpretation for comparisons of two binary diagnostic tests when the true operating point of one test resides below the straight line connecting the true operating point of the other test to the trivial corners in the ROC space as shown in Fig. 1. Specifically, treating points depicted on Fig. 1 as representing the true operating characteristics of a test, one can claim that the “conventional” diagnostic test is better because by random augmentation, it is possible to construct a diagnostic test that is better than the “new” test with respect to both sensitivity and specificity (hence a better test regardless of prevalence and∕or utilities). The algebraic relationships and statistical inferences for these comparisons can be obtained from the straightforward relationship of the straight lines passing through the trivial points to the isolines of diagnostic likelihood ratios.¹³

Diagnostic likelihood ratios

As an alternative to using a pair of operating characteristics (f,t) [i.e., (1–specificity, sensitivity)], a binary diagnostic test can also be uniquely characterized by a pair of “diagnostic likelihood ratios,” or briefly DLR,⁵ (sometimes also termed simply “likelihood ratios” if the binary nature of the test is implied⁴), which can be expressed as follows:

$$\{\begin{array}{c}{\text{DLR}}^{+}=\frac{P\left(+|D\right)}{P\left(+|\overline{D}\right)}=\frac{t}{f}\\ {\text{DLR}}^{-}=\frac{P\left(-|D\right)}{P\left(-|\overline{D}\right)}=\frac{1-t}{1-f}\end{array}\phantom{\}}.$$ (3)

The use of diagnostic likelihood ratios has additional practical significance, since superiority in positive (greater is better) or negative (smaller is better) diagnostic likelihood ratios is equivalent to dominance in positive and negative predictive values, correspondingly.¹³ It is worth noting, however, that the superiority in terms of diagnostic likelihood ratios is more general than the superiority in terms of sensitivity-specificity pairs. Indeed, a binary diagnostic test superior with respect to both sensitivity and specificity is superior with respect to likelihood ratios. However, it is possible that a binary test is superior in terms of likelihood ratios but actually has lower sensitivity, or alternatively lower specificity, but not simultaneously both. Hence, DLR superiority does not have as strong an implication as the dominance of sensitivity and specificity and for certain utility and prevalence structures, a binary diagnostic test with lower likelihood ratios could have a higher expected utility.^{13, 14} At the same time, in light of the interpretation of DLR isolines as performance curves of a random augmentation (Sec. 2A1), the claim of the adequacy of a binary diagnostic test with inferior likelihood ratios is rather questionable. For the subsequent discussion, it is also important to note that isolines of the diagnostic likelihood ratios are the straight lines passing through the trivial points (0,0) (for DLR⁺) and (1,1) (for DLR⁻).

Diagnostic likelihood ratios and the ROC curve

Given a single point representing the true operating characteristics of a binary diagnostic test in the ROC space and assuming that the binary test had been obtained by a specific dichotomization of a multicategory rating scale of the original (but unobserved) test results, one could attempt to describe the general location of the actual entire performance curve. Since a ROC curve is, by definition, monotonically nondecreasing, the operating characteristics of a given point limits the location of possible ROC curves to a region with better sensitivity or specificity, but not both simultaneously. However, this range is typically too wide for many practical applications.

Using the assumption of the concavity of the ROC curve, we can narrow the range where possible ROC curves could reside. Indeed, a concave ROC curve cannot lie below the straight line connecting any of its two points or, in other words,

$$f∊\left(f_1,f_2\right)\text{ROC}\left(f\right)\ge \text{ROC}\left(f_1\right)\times \frac{f_2-f}{f_2-f_1}+\text{ROC}\left(f_2\right)\times \frac{f-f_1}{f_2-f_1}.$$

As a result, a concave ROC curve cannot lie within the triangle obtained by connecting an operating point (f₁,ROC(f₁)) on the curve and the trivial points (0,0) and (1,1), i.e.,

$$f∊\left(0,f_1\right)\text{ROC}\left(f\right)\ge \text{ROC}\left(f_1\right)\times \frac{f}{f_1},$$$$f∊\left(f_1,1\right)\text{ROC}\left(f\right)\ge \text{ROC}\left(f_1\right)\times \frac{1-f}{1-f_1}+\frac{f-f_1}{1-f_1}.$$ 4

In addition, a concave ROC curve cannot lie above the straight line complimenting the extensions of these lines beyond a binary operating point, i.e.,

$$f∊\left(0,f_1\right)\text{ROC}\left(f\right)\le \text{ROC}\left(f_1\right)\times \frac{1-f}{1-f_1}+\frac{f-f_1}{1-f_1},$$$$f∊\left(f_1,1\right)\text{ROC}\left(f\right)\le \text{ROC}\left(f_1\right)\times \frac{f}{f_1}.$$ 5

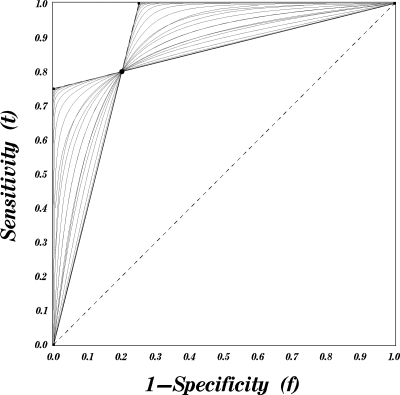
Had it been otherwise, the ROC curve could no longer be concave around(f₁,ROC(f₁)). These lines are illustrated in Fig. 2.

Figure 2.

Concave ROC curves passing through a given point.

As noted in Sec. 2A, straight lines passing through a given operating point and the trivial corners represent the isolines of the positive and negative DLRs. Thus, a concave ROC curve passing though any given point always resides between two DLR isolines passing though this very point (Fig. 2). In other words, the true likelihood ratios of a given binary diagnostic test determine the upper and lower bounds for the family of all concave ROC curves that could characterize underlying multicategory results.

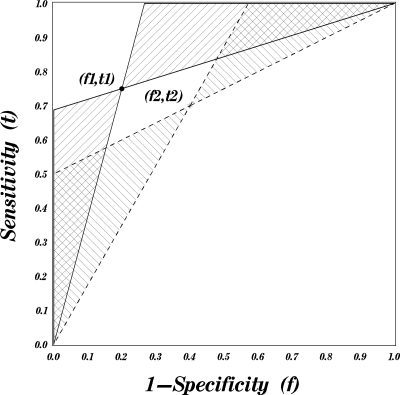
Thus, if the true characteristics of a test are inferior with respect to both diagnostic likelihood ratios, it has at least a locally inferior ROC curve (in the range including both points), as shown, for example, in Fig. 3.

Figure 3.

Possible locations (regions) for concave ROC curves passing through two given points. The regions marked with a 45° pattern correspond to curves passing through the point (f₁,t₁) and those marked with a 135° pattern correspond to curves passing through the point(f₂,t₂).

Similar regions can be constructed using estimated characteristics of the binary diagnostic test. However, the fact that the estimated characteristics of one of the diagnostic tests are beyond the region of the ROC curve of the other merely demonstrates the possibility that one can statistically reject a hypothesis of equality of the ROC curves. Formal statistical inferences can then be made using straightforward asymptotic techniques either directly in regards to likelihood ratios^{5, 16} or indirectly in regards to predictive values.¹⁸

Diagnostic likelihood ratios and the overall discriminative ability

There is frequently an interest in comparing overall discriminative ability of two diagnostic tests, i.e., in the ability to distinguish a normal from an abnormal subject. The discriminative ability of a multicategory test is numerically equivalent to the area under its ROC curve.^{4, 5} Hence, the discriminative ability of a reasonable diagnostic test is always smaller than the area under the highest concave ROC curve passing though a known (given) binary point. On the other hand, since a reasonable diagnostic test could discriminate subsets or patients better than chance, its discriminative ability is better than the area under the lowest concave ROC curve passing though a known binary point. Indeed, as discussed previously, the straight lines connecting a given binary point to (0,0) and (1,1) describe the “chance performance” in the subsets of subjects labeled by the binary test as positive and negative, correspondingly.

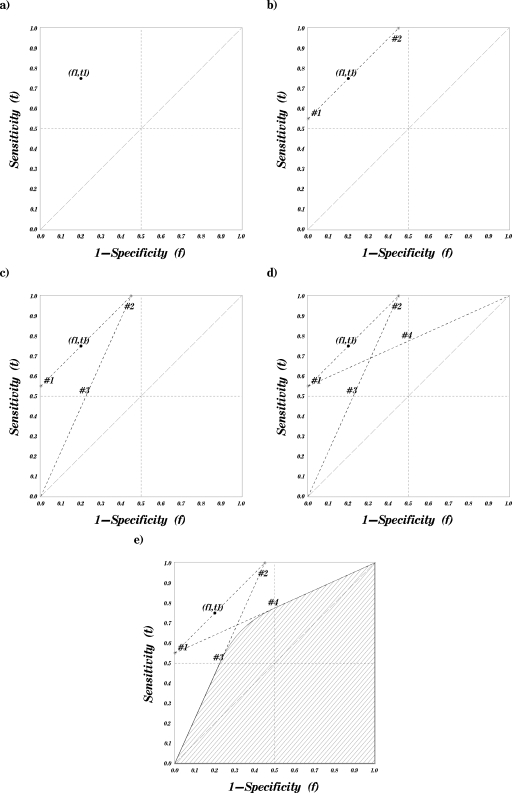
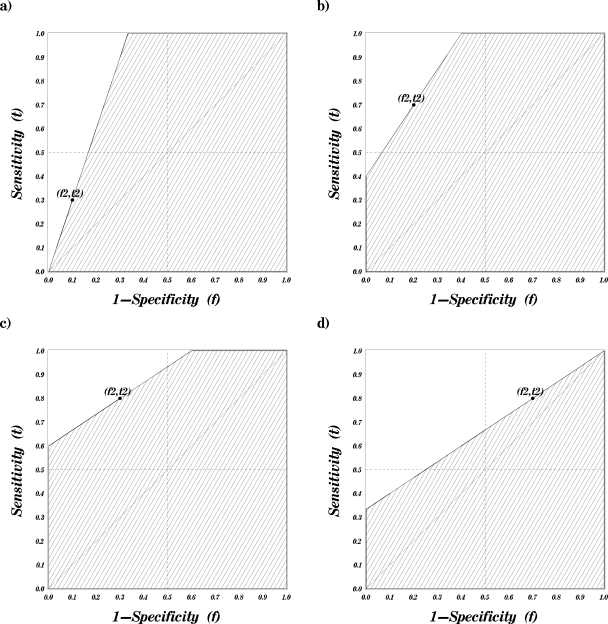
Thus, by comparing the minimum possible AUC for one point with the maximum AUC for the other point, it is possible to derive both algebraic and graphical rules for the location of the point, which ensures inferiority of the area under the latent ROC curve. The graphical approach for constructing the region in which a given point dominates in terms of possible associated AUC has three steps that are illustrated in Fig. 4. These are

• (1)Draw a straight line though the given point (f₁,t₁) parallel to the “guessing line” (diagonal line with slope of 1) [the isoline of the Youden’s index (or area under the lowest concave ROC curve)]. Note the points of intersection of this line with the borders of the ROC space: Points 1 and 2 [Fig. 4b].
• (2)
  Connect the trivial corner (1,1) to point 1 and the trivial corner (0,0) to point 2 with straight lines [Figs. 4c, 4d]. These lines represent the upper bound of the dominated region in the lower left quadrant [f<0.5,t≤0.5]and the upper right quadrant [0.5≤f,0.5≤t]of the ROC unit square (The isolines of the diagnostic likelihood ratios of a specific magnitude (see Eq. 6)]. Note the points of intersection of the first line with the vertical midline (f=0.5) (point 4) and of the second line with the horizontal middle line (t=0.5) (point 3).

  • (3)
    Complete the upper boundary of the dominant region in the upper left quadrant of the ROC unit square (i.e.,f<0.5<t) with a section of a hyperbola connecting points 3 and 4 [Fig. 4e].

Figure 4.

A step by step construction of an AUC dominance region.

Algebraic expressions and justification for this representation are provided in the Appendix0.

The set of points that must have smaller latent AUCs than that of a given point (i.e., AUC dominance region) can be approximated by the region below two straight lines passing though the trivial corners of the ROC space in Fig. 4. As discussed in Sec. 2A, these are isolines of specific positive and negative DLRs; hence, any point that falls below both lines has worse DLRs than the slopes of the corresponding lines. Using this relationship (algebraic details are given in the Appendix0), the AUC dominance region of a point (f₁,t₁) can be approximated using diagnostic likelihood ratios as follows:

$$\{\begin{array}{c}{\text{DLR}}_{\left(f,t\right)}^{+}<\frac{1}{1-t_1+f_1}\\ {\text{DLR}}_{\left(f,t\right)}^{-}>1-t_1+f_1\end{array}\phantom{\}}.$$ (6)

Alternatively, if one of two diagnostic system being compared is known to have lower specificity, one can test inferiority of the latent AUCs exactly by verifying that both DLR⁻ is sufficiently poor (higher) and the specificity is lower than 0.5, i.e.,

$$\{\begin{array}{c}{f}_1>0.5\\ {\text{DLR}}_{\left(f,t\right)}^{-}>1-t_1+f_1\end{array}\phantom{\}}.$$ (7)

The substantial advantage of expressing regions of AUC inferiority in the form of Eq. 6, 7, as well as relating local differences in ROC curves to the diagnostic likelihood ratios (end of Sec. 2B), is the ability to perform straightforward nonparametric inferences. Asymptotic inferences about DLRs can be made using a closed-form approximation for the variance of their logarithms.⁵ Similarly, the variance and covariance of estimated log(DLR) and log(1−t+f) can be readily computed and used to test the relationships in Eq. 6, 7.

Diagnostic likelihood ratios and performance of a binary test

As previously discussed, inferiority with respect to both diagnostic likelihood ratios beyond certain limits [e.g., Eq. 6] implies both inferiority with respect to the area under the underlying ROC curves and at least a local inferiority of the ROC curves themselves. Inferiority with respect to both diagnostic likelihood ratios also has a direct implication in regards to relative performance levels of two binary diagnostic tests. Indeed, if, as in Fig. 1, the conventional test actually has better diagnostic likelihood ratios than the new test, it also means that it is possible to augment the “conventional” test with a random guess (see Sec. 2A), in a manner that results in either a better sensitivity at the same specificity as of the new test or a better specificity at the same sensitivity as of the new test. This would make any statement of superiority of the new test according to any of the performance indices rather questionable.

Naturally, the inferiority with respect to both diagnostic likelihood ratios also implies inferiority with respect to many conventional summary indices. For example, if a test is inferior with respect to both diagnostic likelihood ratios it is also inferior with respect to

• (1)Youden’s index,⁹ since a test with smaller Youden’s index corresponds to a point below the unislope line [Fig. 4b] and a region of DLR inferiority is completely below this line.
• (2)Odds ratio, since its isolines⁴ are ROC-like concave curves and there is no concave ROC curve that can pass through both a point and its corresponding region of DLR inferiority.
• (3)Positive and negative predictive values (in the same population), since the isolines for predictive values are the same as for diagnostic likelihood ratios.¹³

Interpretation of DLR isolines as performance curves of a given binary diagnostic test augmented with a guessing process highlights an important problem with the use of an accuracy index and the need for caution when defining the utility function for the expected utility index. The problem stems from the fact that even when performance is assessed for the same sample of subjects, accuracy and expected utility may be greater for a binary test which is inferior with respect to likelihood ratios (hence, offers less sensitivity and specificity that the other test augmented by “guess”). Indeed, the isolines for the accuracy and expected utility are straight lines with slopes that depend on prevalence (and a utility function in case of expected utility) and by varying these parameters, the slope can be made arbitrarily close to 0. Hence, if a binary diagnostic test is inferior with respect to both likelihood ratios but has higher sensitivity, it is possible to find values of prevalence (and utility structure) that result in higher accuracy (expected utility). Thus, even for the same sample, a reasonable use of these nonintrinsic performance measures should be limited to comparisons of tests which are unlikely to have a uniform ordering in both diagnostic likelihood ratios simultaneously.

DISCUSSION

One of the more challenging problems in comparing binary diagnostic tests arises when one test has higher sensitivity but lower specificity than the other. We described several objective solutions based on diagnostic likelihood ratios. In scenarios where comparisons of binary characteristics are of interest, the proposed use of the diagnostic likelihood ratios offers an objective comparison, which holds regardless of the prevalence or utility structure. This approach is also applicable to instances where estimated sensitivity and specificity levels of diagnostic tests do not differ consistently. For scenarios where the underlying ROC curve or the overall discriminative ability are of interest, the methods presented here can help determine the inferiority of one of the tests based on the binary data without conducting a more complicated multicategory ROC study.

The proposed methodology permits one to resolve problems that are typically addressed by expensive effort-intensive ROC studies. However, the proposed approach cannot and is not intended to replace ROC studies in general. For example, this methodology does not permit assessment of potential improvements in sensitivity for some diagnostic tests with lower specificity but a smaller (better) negative diagnostic likelihood ratio. Furthermore, even in cases when inferences with diagnostic likelihood ratios are possible, when reliable multicategorical data for constructing and comparing ROC curves are available, traditional methods often provide for more powerful and complete inferences than the approach described here. However, this conjecture rests on the underlying assumption of the reliability of the rating-based ROC curve and the practical ability of a system to actually operate at any given point (i.e., with any desired level of specificity). For example, the system’s ability to operate at a point with any given specificity level is not always possible if a system has intrinsically a limited ability to distinguish among a fraction of the subjects (e.g., due to finite image resolution or contrast sensitivity). In this case, regardless of the decision threshold, it is unclear whether the system is able to achieve a specificity level which is lower than the proportion of subjects originally perceived as completely negative (e.g., all cases that were given a rating of “0”).

Relative to other procedures for comparing performance of a binary task, it is useful to highlight the general statistical properties of the procedures when comparing DLRs and∕or sensitivity-specificity characteristics of diagnostic tests∕systems. Without any loss of generality, we discuss the relative properties using the example of two diagnostic systems with known specificity levels. For diagnostic systems that truly differ in sensitivity alone (actual specificity levels being the same), the statistical test for equality of sensitivity will naturally be more powerful than the test for equality of negative diagnostic likelihood ratios(DLR⁻). However, as differences in true specificity levels increase (while keeping the difference in sensitivity levels the same), the statistical power of the test based on DLR⁻ gradually increases and the test eventually becomes more powerful than a simple comparison of sensitivity levels. This is easy to visualize, for example, in systems with approximately the same sensitivity. In addition, if a more “specific” system is also more “sensitive,” a comparison of binary characteristics or the underlying (but unobserved) ROC curves using sensitivity-specificity pairs has to rely on a subjective combination of both characteristics, while it is possible to draw objective conclusions through a comparison of diagnostic likelihood ratios.

APPENDIX: AUC DOMINANCE REGION

By definition, a concave curve cannot lie above any of its tangent lines. As a result, the maximum-area concave curve passing through a given point coincides with a certain straight line passing through this point. By maximizing the area under such a straight-line ROC curve passing though a point(f₂,t₂), the maximum area under a concave ROC curve passing through it can be shown to be equal to¹⁵

$$A_{\left(f_2,t_2\right)}^{\text{max}}=\{\begin{array}{ll}1-\frac{f_2}{2t_2}\hfill & f_2<t_2\le 0.5\hfill \\ 1-2f_2\left(1-t_2\right)\hfill & f_2<0.5<t_2\hfill \\ 1-\frac{\left(1-t_2\right)}{2\left(1-f_2\right)}\hfill & 0.5\le f_2<t_2\hfill \end{array}\phantom{\}}.$$ (A1)

The parameters of the maximum-area straight-line ROC passing through a specific point depend on the coordinate of that point. Different possibilities are demonstrated in Fig. 5.

Figure 5.

The concave ROC curves passing though a point (f₂,t₂) that have maximum possible areas under them.

Regardless of the coordinates of the point(f₁,t₁), the lowest possible concave ROC curve passing though the point consists of the two line segments connecting the point to the trivial extremes (corners). Hence, the minimum area under a concave ROC curve passing through (f₁,t₁) has the form

$$A_{\left(f_1,t_1\right)}^{\text{min}}=\frac{t_1+1-f_1}{2}$$ (A2)

or it is equal to half the corresponding Youden’s index.¹⁴

Both minimum and maximum areas under the concave ROC curves passing through a given point have explicit formulation in terms of sensitivity and specificity. Therefore, one can derive an explicit formulation for the regions of AUC dominance. Specifically, for a given point(f₁,t₁), one can explicitly construct the region of points (f,t) such that any concave ROC curve passing through this point (f₁,t₁) has a higher AUC than any other concave ROC curve passing through any point within that region. This region can be defined as

$$\left\{\left(f,t\right):A_{\left(f,t\right)}^{\text{max}}<A_{\left(f_1,t_1\right)}^{\text{min}}\right\}=\{\begin{array}{ll}t<\frac{1}{1-t_1+f_1}\times f\hfill & f<t\le 0.5\hfill \\ t<1-\frac{1-t_1+f_1}{4}\times \frac{1}{f}\hfill & f<0.5<t\hfill \\ t<\left(1-t_1+f_1\right)\times f+\left(t_1-f_1\right)\hfill & 0.5\le f<t\hfill \end{array}\phantom{\}}.$$ (A3)

Since the maximum area for a point (f₂,t₂) varies depending on the quadrant the point belongs to, in order to demonstrate Eq. A3 we consider points within each of these quadrants.

First, let (f₂,t₂) be in the lowest left quadrant in the ROC space (i.e., f₂<0.5, t₂≤0.5). Then

$$A_{\left(f_2,t_2\right)}^{\text{max}}=1-\frac{f_2}{2t_2}$$

and

$$A_{\left(f_2,t_2\right)}^{\text{max}}<A_{\left(f_1,t_1\right)}^{\text{min}}\iff 1-\frac{f_2}{2t_2}<\frac{t_1+1-f_1}{2}\iff t_2<\frac{1}{1-t_1+f_1}\times f_2.$$

Second, when (f₂,t₂) is in the upper left quadrant (i.e.,f₂<0.5<t₂), then

$$A_{\left(f_2,t_2\right)}^{\text{max}}=1-2f_2\left(1-t_2\right)$$

and

$$A_{\left(f_2,t_2\right)}^{\text{max}}<A_{\left(f_1,t_1\right)}^{\text{min}}\iff 1-2f_2\left(1-t_2\right)<\frac{t_1+1-f_1}{2}\iff t_2<1-\frac{1-t_1+f_1}{4}\times \frac{1}{f_2}.$$

Last, if (f₂,t₂) is in the upper right triangle (i.e., 0.5≤f₂<t₂), then

$$A_{\left(f_2,t_2\right)}^{\text{max}}=1-\frac{\left(1-t_2\right)}{2\left(1-f_2\right)}$$

and

$$A_{\left(f_2,t_2\right)}^{\text{max}}<A_{\left(f_1,t_1\right)}^{\text{min}}\iff 1-\frac{\left(1-t_2\right)}{2\left(1-f_2\right)}<\frac{t_1+1-f_1}{2}\iff t_2<\left(1-t_1+f_1\right)\times f_2+\left(t_1-f_1\right).$$

The shape of the domain can be confirmed by geometric considerations. Indeed, the minimum-area concave ROC curve passing through (f₁,t₁) is composed from the two lines connecting (f₁,t₁) to the trivial corners (0,0) and (1,1). The isoline for the area under such a triangle is a straight line with a unit slope [e.g., Fig. 4b]. The isoline for the maximum-area ROC curve passing through (f₂,t₂) in the lower left, i.e., f<t≤0.5, or the upper right, i.e., 0.5≤f<t, quadrants of ROC square is a straight line passing through (0,0) or (1,1) correspondingly [e.g., Figs. 5a, 5d]. Hence, the border of the domain in the lower left or upper right quadrants is a straight line connecting trivial corners (0,0) and (1,1) to the point where the unislope line passing through (f₁,t₁) intersects the upper boundary of the ROC square (space) [Fig. 4d]. The coordinates of these intersections are (1−t₁+f₁,1) and(0,t₁−f₁). A section of a hyperbola (the isoline of maximum AUC forf≤0.5<t) completes the boundary of the domain in the upper left quadrant of the ROC space as shown in Fig. 4e.