Picosecond absorption relaxation measured with nanosecond laser photoacoustics

Abstract

Picosecond absorption relaxation—central to many disciplines—is typically measured by ultrafast (femtosecond or picosecond) pump-probe techniques, which however are restricted to optically thin and weakly scattering materials or require artificial sample preparation. Here, we developed a reflection-mode relaxation photoacoustic microscope based on a nanosecond laser and measured picosecond absorption relaxation times. The relaxation times of oxygenated and deoxygenated hemoglobin molecules, both possessing extremely low fluorescence quantum yields, were measured at 576 nm. The added advantages in dispersion susceptibility, laser-wavelength availability, reflection sensing, and expense foster the study of natural—including strongly scattering and nonfluorescent—materials.

Picosecond absorption relaxation is central to many optical phenomena in physics, chemistry, biology, and medicine—such as absorption saturation,^{1, 2, 3} photosynthesis,⁴ and photolysis.^{5, 6, 7} Typically, relaxation times are studied via an ultrafast (femtosecond or picosecond) pump-probe technique by measuring either fluorescence in a reflection configuration or absorption in a transmission configuration.^{8, 9} In the reflection-based approach, the molecules are excited by a laser pulse through the transition|0⟩→|i⟩. A probe pulse with a variable delay time τ relative to the pump pulse monitors the time evolution of the population densityN_i(t).⁸ When applied to molecules with low fluorescence quantum yield, this approach is noisy. In the transmission-based approach, the relaxation time is extracted by measuring pump-induced changes in probe-beam transmittivityΔT=T(I_p)−T(0), where T(I_p) and T(0) are the probe beam transmittivities with and without a pump of intensityI_p.⁹ In both approaches, the time resolution is limited by the pulse width of both the pump and the probe pulses. Hence, not only is an expensive picosecond or femtosecond laser required, but also the detection is susceptible to pulse broadening in dispersive media. Alternatively, intensity correlation of nanosecond laser pulses can be used.^{10, 11} Working in transmission mode, this technique is not suitable for optically thick media. All of the current techniques are limited to optically thin and weakly scattering materials or require artificial sample preparation.

Photoacoustic microscopy and photoacoustic computed tomography, usually based on nanosecond laser excitation, are effective functional and molecular imaging tools in vivo. In the photoacoustic phenomenon, light is absorbed by a material and converted to heat. The subsequent thermoelastic expansion generates a detectable acoustic wave.¹² Photoacoustic sensing presents an exquisite sensitivity due to its inherent background-free nature. Its relative sensitivity to absorption reaches the theoretical limit of 100%, by far the highest among all optical imaging modalities. Most quantitative photoacoustic studies have assumed a linear dependence between the photoacoustic signal and the local optical fluence, which holds only at laser intensities much less than the saturation intensity. Recently, optical-resolution photoacoustic microscopy (OR-PAM) (Ref. ¹³) was developed to achieve higher resolution by reducing the laser beam diameter, which increased the light intensity. As intensity increases, mechanisms such as saturation of the optical absorption or multiphoton∕multistep absorption can occur, resulting in a nonlinear dependence of the photoacoustic signal on the excitation pulse fluence.^{14, 15} Saturation of the optical absorption in pulsed photoacoustic spectroscopy was previously observed in gases^{16, 17} and solutions.¹⁸ However, it has never been used to extract picosecond relaxation times.

Here, we developed a reflection-mode relaxation photoacoustic microscope (rPAM) based on a nanosecond laser and measured picosecond relaxation times. Even nonfluorescent chromophores can be studied because photoacoustic signals detect nonradiative relaxation.¹² The relaxation times of oxygenated and deoxygenated hemoglobin molecules, both possessing extremely low fluorescence quantum yields, were measured at 576 nm using rPAM.

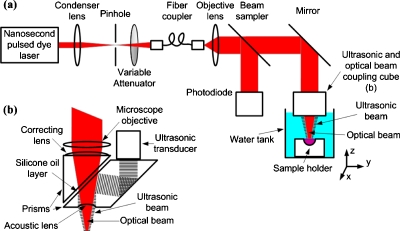
We measured the photoacoustic signal as a function of the incident laser fluence, using a custom-built OR-PAM system¹³ shown in Fig. 1. The light source is a nanosecond pulsed dye laser, pumped by a Nd:YLF laser (INNOSLAB IS811-E, Edgwave). The 4 ns laser pulses are spatially filtered by a 50 μm diameter pinhole (P50C, Thorlabs) and coupled into a single-mode fiber (460HP, Thorlabs). The fiber output is imaged by a microscope objective lens (0.1 N.A, Leica) to a focal spot with a diameter of 3.9 μm (1∕e²value, as measured by a scanning knife edge). A fraction of the fiber output light is reflected by a beam sampler (BSF05-A, Thorlabs) and detected by a photodiode (S1226–18BK, Hamamatsu). A variable attenuator (NDC-100C-4M, Thorlabs) set the pulse energy to values between 0 and 250 nJ. The ultrasonic signal is collected by a concave lens (6 mm in diameter, 4 mm in radius of curvature) and detected by a 50-MHz broadband ultrasonic transducer (V214BB, Panametrics). The optical objective lens and the ultrasonic transducer are coaxially and confocally aligned. The entire optical and acoustic block is mounted on three one-dimensional motorized stages (PLS-85, Micos) to allow positioning in the depth direction and raster scanning of the surface. For in vitro measurements, the sample holder is sealed with a plastic membrane and immersed in a water tank to provide acoustic coupling between the sample and the ultrasound transducer.

Figure 1.

System diagrams. (a) Schematic of the optical-resolution photoacoustic microscopy (OR-PAM) system (b) Ultrasonic and optical beam coupling cube.

In an absorbing medium, the photoacoustic signal generated due to single photon absorption at frequency ν is proportional to the local pressure rise, as follows:¹⁹

$$q\left(\nu \right)\propto \Gamma {\eta }_{th}{\mu }_{a}F,$$ (1)

where Γ is the Grueneisen parameter (dimensionless), η_this the percentage of absorbed energy that is converted to heat, μ_ais the optical absorption coefficient(cm⁻¹), and F is the local optical fluence(J∕cm²). The small signal absorption coefficient can be written as the absorption cross section of the absorber, σ_A, multiplied by the number of absorbers per unit volume, N₀, as follows:

$${\mu }_a\left(0\right)={\sigma }_A{N}_0.$$ (2)

The absorption coefficient, μ_a, commonly saturates withincreasing intensity in the form²⁰

$${\mu }_a\left(I\right)={\sigma }_A\frac{N_0}{1+I∕I_{sat}}.$$ (3)

Under the assumption of a three-level system with no bottlenecking, the saturation intensity that reduces the small signal absorption coefficient to half of its value is given by²⁰

$$I_{sat}=\frac{h\nu }{{\sigma }_A{\tau }_{eff}},$$ (4)

where h is Plank’s constant, νis the laser frequency, and τ_eff is the absorption relaxation time. From Eqs. 3, 4, we obtain

$$q\left(\nu \right)\propto \Gamma {\eta }_{th}{\sigma }_A\frac{N_0}{1+\frac{F}{{\tau }_{laser}{I}_{sat}}}F,$$ (5)

where τ_laser is the incident laser pulse duration. Therefore, the absorption relaxation time, τ_eff, can be extracted by measuring the intensity saturation of the absorber at a specific wavelength.

To demonstrate our technique, we measured the photoacoustic signal from two known dyes as a function of the incident laser intensity. As sample dyes, a 10⁻⁴ M concentration of Saturable Absorber 580 (#05800, Exciton) in ethylene glycol and 10⁻⁴ M of DQOCI (#05920, Exciton) in ethanol were used. The low dye concentration introduced a relatively small absorption coefficient, and therefore, resulted in a small temperature rise, T=(μ_aF)∕(ρC_v)≈0.4 K, where ρ (∼1 g∕cm³)is the mass density, and C_v (∼4 J g⁻¹ K⁻¹) is the heat capacity at constant volume.¹⁹ Moreover, we repeated the following experiment using a lower dye concentration (2.5×10⁻⁵ M) and found no difference in the measured absorption relaxation time (within experimental error). Hence, temperature-dependent nonlinearity of the Grueneisen parameter was ignored. We ensured the same beam diameter on the sample surface for all measurements by maintaining a constant delay time between the detected photoacoustic signal and the laser pulse. Figure 2 presents the photoacoustic amplitudes (maximum absolute value of the Hilbert-transform of the raw photoacoustic signal) generated from Saturable Absorber 580 dye [Fig. 2a] and DQOCI dye [Fig. 2b] as a function of the incident laser fluence. The tangent of the saturation curve at the origin passes through the first measured points, showing a linear dependency of the photoacoustic signals on the laser fluence at low intensities. First, we extracted the incident beam diameter for the selected constant delay time by fitting Eq. 5 to the saturated photoacoustic signal of Saturable Absorber 580 with the known absorption relaxation time of 35 ps and the known absorption cross section (see Table 1). The Grueneisen parameter and η_th are considered to be constant at all intensities and do not influence the saturation intensity. Therefore, these coefficients can be normalized. Then, we used the extracted beam diameter to fit Eq. 5 to the saturated photoacoustic signal of DQOCI for the absorption relaxation time. The absorption relaxation time of DQOCI measured from five repetitions was 18±2 ps at 592 nm. We reversed the procedure by using DQOCI as the calibration source for the beam diameter. The relaxation time of DQOCI was taken to be 19.5 ps (the average of two previous pump-probe measurements, see Table 1) and the calculated absorption relaxation time of Saturable Absorber 580 was 37±2 ps at 576 nm. These two measurements are within 10% of previously reported absorption relaxation times.^{1, 2}

Figure 2.

Average photoacoustic amplitude as a function of the incident laser fluence. (a) Saturable Absorber 580 dye, (b) DQOCI dye, (c) oxygenated lysed bovine blood, and (d) deoxygenated lysed bovine blood. Error bars represent the standard deviations of 1800 measurements.

Table 1.

Absorption relaxation times and saturation intensities of different absorbers.

Name	λ (nm)	ε (M−1 cm−1)	σ (cm2)	τ (ps)	Isat (W∕m2)	Fsata (mJ∕cm2)	Reference
Saturable Absorber 580 in Ethylene glycol	576	69 500b	2.66×10−16	37±2 c	3.5×1011	140	This work
	615			35			Ref. 2
DQOCI in ethanol	592	135 000d	5.16×10−16	18±2 c	3.7×1011	148	This work
	613			15±0.5			Ref. 1
	585			24±1			Ref. 1
Oxygenated bovine hemoglobin	576	15 190e	5.81×10−17	22±5 f	2.7×1012	1080	This work
Deoxygenated bovine hemoglobin	576	10 010e	3.83×10−17	2.3±1.8 f	3.9×1013	15 600	This work

^aSaturation fluence (F_sat) was calculated from the saturation intensity (I_sat) using the measured 4 ns laser pulse duration.

^bSee Ref. 2.

^cThe standard error was calculated from five experiments.

^dU. Brackmann, Lambdachrome^® Laser Dyes (Lambda Physik, Goettingen, 2000).

^eW. G. Zijlistra, A. Buursma, and O. W. van Assendelft, Visible and Near Infrared Absorption Spectra of Human and Animal Hemoglobin: Determination and Application (VSP, Zeist, 2000).

^fThe standard error was calculated from three experiments.

We then applied this technique to measure unknown relaxation times of two absorbers with low quantum yield. We extracted the absorption relaxation times of oxyhemoglobin (HbO₂) and deoxyhemoglobin (HbR) in vitro at 576 nm, the local absorption peak of(HbO₂). Oxygenated hemoglobin was prepared by mixing oxygen with lysed bovine blood (905–250, Quadfive) for 2 h at8 °C. Deoxygenated hemoglobin was prepared by mixing carbon dioxide with lysed bovine blood for 4 h at37 °C. After calibrating the incident beam diameter using Saturable Absorber 580, we measured the average photoacoustic amplitudes generated from bovine HbO₂ [Fig. 2c] and HbR [Fig. 2d] as a function of the incident laser fluence.

The absorption relaxation times of bovine HbO₂ and HbR at Q-band 576 nm measured 22±5 ps and2.3±1.8 ps, respectively. Such a pronounced difference between the relaxation times is consistent with previous measurements in the Soret band.⁵

Table 1 summarizes the measured absorption relaxation times of different absorbers. The measured molecular extinction coefficient ε (in M⁻¹⋅cm⁻¹) is converted to the absorption cross-section (in cm²) by the Beer–Lambert law,²¹$\sigma =\epsilon \text{\hspace{0.17em}ln}\left(10\right)\raisebox{1ex}{$1000$}\!\left/ \!\raisebox{-1ex}{$N_a$}\right.,$ where N_a is the Avogadro number.

In conclusion, we have extracted picosecond relaxation times using a nanosecond laser on the basis of optical absorption saturation in reflection-mode photoacoustic sensing. rPAM offers many advantages over conventional measurement methods of relaxation times and provides practical applications in photoacoustic microscopy. First, unlike the fluorescence-based reflection approach, rPAM is unaffected by background fluorescence and Raman scattering. Second, it can measure molecules with low or even zero fluorescence quantum yield. Third, unlike the absorption-based transmission approach, rPAM permits relaxation time measurements in optically thick media, particularly living biological tissue. Lastly, unlike the femtosecond or picosecond techniques, the nanosecond rPAM is less susceptible to pulse broadening, is less costly, and can use a wide variety of wavelengths.