Modeling Diauxic Glycolytic Oscillations in Yeast

Abstract

Glycolytic oscillations in a stirred suspension of starved yeast cells is an excellent model system for studying the dynamics of metabolic switching in living systems. In an open-flow system the oscillations can be maintained indefinitely at a constant operating point where they can be characterized quantitatively by experimental quenching and bifurcation analysis. In this article, we use these methods to show that the dynamics of oscillations in a closed system is a simple transient version of the open-system dynamics. Thus, easy-setup closed-system experiments are also useful for investigations of central metabolism dynamics of yeast cells. We have previously proposed a model for the open system comprised of the primary fermentative reactions in yeast that quantitatively describes the oscillatory dynamics. However, this model fails to describe the transient behavior of metabolic switching in a closed-system experiment by feeding the yeast suspension with a glucose pulse—notably the initial NADH spike and final NADH rise. Another object of this study is to gain insight into the secondary low-flux metabolic pathways by feeding starved yeast cells with various metabolites. Experimental and computational results strongly suggest that regulation of acetaldehyde explains the observed behavior. We have extended the original model with regulation of pyruvate decarboxylase, a reversible alcohol dehydrogenase, and drainage of pyruvate. Using the method of time rescaling in the extended model, the description of the transient closed-system experiments is significantly improved.

Introduction

The short periodic metabolic oscillations observed in a continuous-flow stirred-tank reactor (CSTR) with a suspension of starved yeast cells is an example of a system where observations from the known biochemical network and from rate parameters determined in vitro can be successfully modeled (1). In this article, we aim to extend the scope of this model to include the transient behavior observed in the analogous closed system originally investigated by Duysens and Chance (2,3). Fig. 1 compares typical closed-system behavior (a) with that observed after a straightforward adjustment of the open-system model by removing the flow of nutrients and setting the initial concentration of extracellular glucose to 24 mM (b), as in the experiment.

Figure 1.

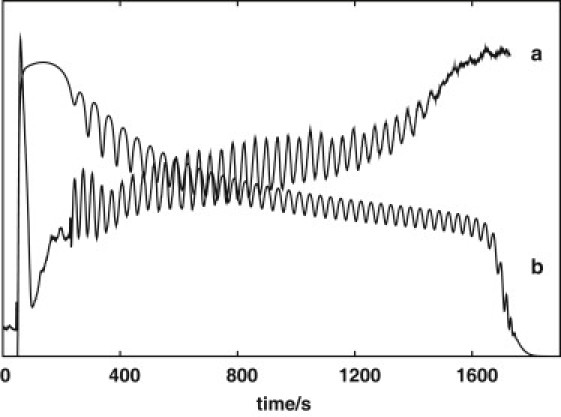
(a) Fluorescence of NAD(P)H in a stirred suspension of yeast cells with respect to time (s). As fluorescence signals are recorded in an arbitrary unit, it is not shown. The first steep rise of fluorescence signal is caused by the addition of glucose at 50 s and the second sharp change by the addition of cyanide at 230 s, yielding initial concentrations of 24 mM and 5 mM, respectively. (b) Concentration of NAD(P)H in a closed system obtained from the model in a previous study (1) by removing the flow and setting the initial concentration of extracellular glucose to 24 mM.

Note that the oscillations are faithfully reproduced, but that the adjusted model incorrectly describes the slow drift of the average behavior during the oscillations, as well as the behavior just after addition of glucose and when glucose is depleted. This model includes the primary reactions of the glycolytic pathway (Fig. 2, black and blue arrows). Here, we call it Model-0 and use it as the basis for the following discussion. (For definitions of the terms used in Fig. 2, see the Supporting Material.)

Figure 2.

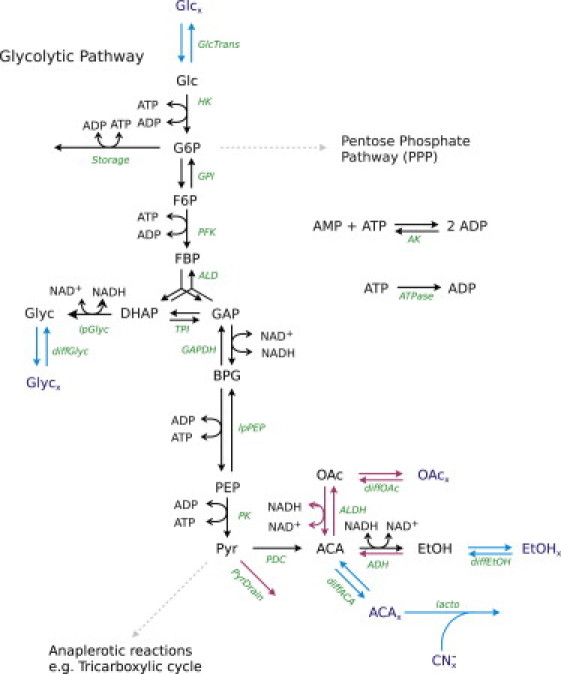
Network structure of the main catabolic pathways of glucose-fed yeast cells. The primary reactions include membrane transport and glycolytic and fermentative reactions, as well as extracellular reactions. The black and blue reactions constitute the reactions included in Model-0. The reactions in red constitute the additional reactions included in Model-1. Dashed gray arrows indicate normally important catabolic reactions that we assume to be inactive under the experimental conditions and which therefore are excluded in the models. Enzymatic names corresponding to the model in sections S8 and S9 in the Supporting Material are shown in green. Subscript x denotes extracellular species.

Although the different cells oscillate independently, they have been shown (1,4) to be strongly coupled by exchange of acetaldehyde (ACA) such that the average oscillations can be faithfully modeled as a single Hopf oscillator embedded in the extracellular medium, and this is maintained in the closed models described here. The operating point for the oscillator is at or close to the Hopf bifurcation point. For the open system, this has been confirmed by experimental and model investigations of amplitude dependence on distance from the bifurcation point, by quenching experiments, and by studies focusing on the dependence of oscillations on cell density.

In the open system, a constant influx of nutrients and fresh yeast cells eliminates any drift of cellular state and any buildup of waste products. The truly constant operating point enables small-amplitude sinusoidal oscillations to be maintained indefinitely. In the closed system, slow changes of the operating point must be taken into consideration.

The primary fermentative reactions determine the dynamic behavior at high glucose concentrations (see Fig. 2). In addition to the glycolytic pathway, they include the adenylate kinase reaction and unspecified ATP consumption. At low glucose concentrations, secondary reactions (e.g., Fig. 2, gray arrows) may take over, explaining the insufficiency of Model-0 at these conditions.

Under anaerobic conditions, and with glucose as the only source of nutrition, starved yeast cells are prohibited from increasing biomass. Flux through the mitochondrial tricarboxylic acid cycle is not assumed to occur. However, for replenishment of important precursor compounds, e.g., α-ketoglutarate, there may be a small carbon flux into the tricarboxylic acid cycle. The pentose phosphate pathway (PPP) is the main provider of NADPH and three precursor metabolites, but as biosynthesis is prohibited, we assume that flux through the PPP is negligible. This is supported by Teusink's report of a low nonoscillatory NADPH level (7). However, other NAD(P)H-producing secondary reactions may be of importance in closed-system experiments at low glycolytic flux.

In this study, we compare closed-system with open-system experiments to investigate what dynamic properties are to be preserved in the development of an extended model that can reproduce transient oscillations.

Methods

Cell preparation and NAD(P)H measurement

Yeast cells (Saccharomyces cerevisiae X2180) were grown aerobically at 30°C in closed-batch culture in a rotary shaker to the point of glucose depletion, as described previously (5). The cells were washed twice in 0.1 M potassium phosphate-buffered saline (PBS) and resuspended in PBS to the desired cell density. The cells were starved for at least 1 h and then kept at ∼0°C until the start of experiments. Experiments were carried out in a thermostated (25°C) cuvette using 2 ml cell suspension with a dry weight of 12.8 mg/ml (except for the density experiments (see Fig. 4)). NAD(P)H fluorescence was achieved by excitation with the 365-nm mercury line and measured as the emission of light in the interval 420−660 nm with a photomultiplier (arbitrary units), as described previously (3,6). Closed-system experiments giving rise to oscillations were induced by a pulse addition of 24 mM glucose followed by a 5-mM pulse of KCN after the initial spike in NADH. All other additions of chemicals are described in the relevant figure legends.

Figure 4.

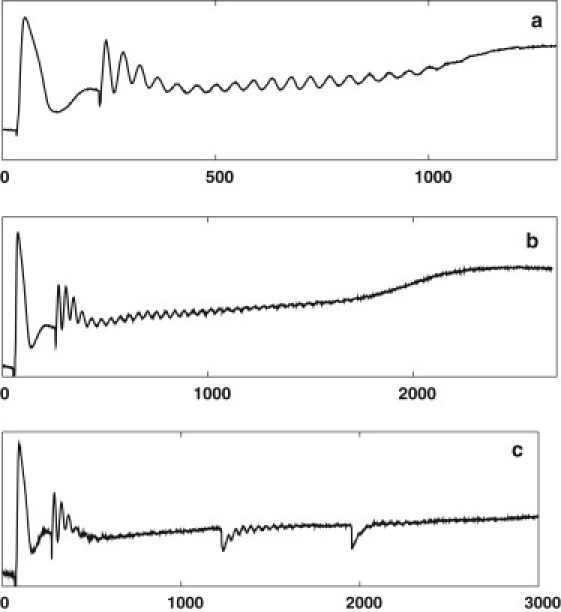
Closed-system experiments at different yeast dry weights of 11 (a), 6 (b), and 4 mg/ml (c). In a, oscillations continue until the glucose is used up. (b and c) At lower weights oscillations are either marginally possible and die out before the glucose is used up (b) or die out quickly (c), but damped oscillations can be induced by perturbations with acetaldehyde at t = 1400 and t = 2100, as expected for a Hopf oscillator below the bifurcation point. In all three experiments, the initial glucose concentration was 25 mM.

Simulations

Models were simulated on a standard PC using the CVODE solver for stiff ODE systems (SUNDIALS) with a relative tolerance of 10⁻¹⁰ and absolute tolerance of 10⁻¹⁸.

Theory

Kinetic information for most of the glycolytic enzymes can be obtained from in vitro experiments. It is in general safe to use the K_m values from such investigations for in vivo modeling, but the maximal rates are best fitted directly to in vivo measurements, as the relation of maximal rates to the total amounts of enzyme, e.g., determined by measuring expression levels, is weak. In a previous study (1) (see Direct method therein), this was done by fitting maximal rates to measured average metabolite concentrations and oscillatory amplitudes and phases. The oscillatory period was then fitted to the experimental value by dividing all maximal rates by a factor (a in Eq. 1) to fit the oscillatory period to the measured value. Provided the rate of the enzyme reactions has the general form v = V × g(c,p), where the maximal rate V has been factored out explicitly, we have

$$\frac{d{c}_i}{d\left(at\right)}=\sum _j{N}_{i,j}\frac{V_j}{a}{g}_j(\mathbf{c},\mathbf{p}),$$ (1)

where N_i,j is the stoichiometric matrix. This is equivalent to a time rescaling and will not affect the average metabolite concentrations.

A change in any parameter of a single flux will in general lead to a change of the period and amplitude of the oscillations. Thus, introducing new models actually calls for a new full-parameter optimization, but to repeat the procedure from our previous study (1) would be prohibitively expensive for a closed system, which does not have a true steady state. A way to overcome this difficulty will be treated in a separate article. As the extended model during glucose flux discussed here is close to Model-0, and since we lack detailed structural information on the kinetics of the added reactions, we have chosen to fit the model manually, guided by sensitivity analysis of Model-0 (8).

Results

Comparison of open- and closed-system experiments

In a previous study (6), it was demonstrated that for the open system, the properties of the observed small-amplitude oscillations corresponded exactly to the oscillations of the two-dimensional normal form of a Hopf oscillator with normal-form parameter values depending on the operating point. For parameter values above the bifurcation point, the normal form describes the observed limit cycle. The study demonstrated that it was possible to shift the state of the oscillator to the unstable steady state at the center of the limit cycle by adding a metabolite (e.g., ACA) at a characteristic phase of the oscillation. By this switch of state, the oscillations are quenched momentarily, after which there is a slow increase in amplitude during the return to the limit cycle. The characteristic concentration shift for a perfect quenching is called the quenching amplitude. For the closed system, this property is demonstrated by quenching with ACA at an angle of −100° (Fig. 3). Fig. S1 in the Supporting Material shows a numerical quenching perturbation with ACA at the same phase as in the experiment using Model-0.

Figure 3.

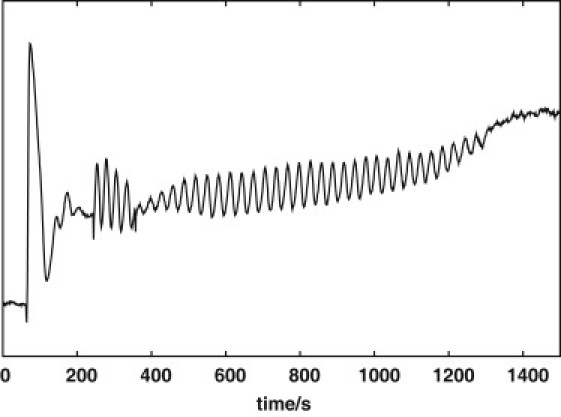
Experimental quenching of oscillations by addition of ACA at 380 s. All other conditions are as in Fig. 1a.

In a previous study (4), we measured the amplitude of the oscillations as a function of cell density to show that cell density may serve as a bifurcation parameter. The bifurcation point for the open system was found at a cell density of 6.3 (mg dry weight). For a cell density above the bifurcation value, the system displayed small-amplitude oscillations, and for a density below the bifurcation value, the system behaved as a damped oscillator. Fig. 4 shows exactly the same behavior for the closed system at all densities above (Fig. 4 a), at (Fig. 4 b), and under (Fig. 4 c) the open-system bifurcation point. During glucose consumption in a closed system, the parameters of the equivalent Hopf oscillator (as well as the distance from the current bifurcation point) are changing slowly with time, but the behavior of the system at an intermediate timescale approximates the behavior of the current equivalent Hopf oscillator. This is valid also if the system passes with a small but finite rate through the bifurcation point (transient bifurcation).

We conclude that the dynamic behavior of the closed system in the oscillatory subdomain (i.e., from start to end of oscillations) is very similar to that of the open system except for small changes in amplitude and level of the NAD(P)H signal.

Probing secondary metabolism

To investigate what pathways involving NAD(P)H are active when glucose is not present, we conducted a series of experiments on starved yeast cells without addition of glucose.

Oxidative phosphorylation

For each experiment, we observed a fairly rapid increase in fluorescence at some indeterminate time after the start of the experiment. A representative example is shown in Fig. 5 (a). The jump in NAD(P)H is attributed to depletion of O₂ in the suspension, as confirmed using O₂ electrodes, and is due to an indeterminate amount of O₂ that is mixed in during preparation of the suspension (see Materials section). When O₂ is added into the suspension (by bubbling) (Fig. 5, d), the fluorescence signal rapidly decreases to the previous level, but as O₂ is again depleted, another jump ensues. Qualitatively, a doubling of the bubbling period is roughly equal to a doubling of the time required to return to base level (Fig. 5, d and e). O₂ jumps can be ascribed to functional oxidative phosphorylation, and can be eliminated almost completely by addition of cyanide (Fig. 5, g), i.e., superoxide formation and consequent NAD(P)H consumption is small in comparison. It is well known that addition of cyanide (CN⁻) inhibits enzyme cytochrome c oxidase, blocking the reoxidation of NADH to NAD⁺. However, the NAD(P)H response to addition of CN⁻ (Fig. 5, f) is very pronounced and is likely caused by other unknown reactions involving CN⁻ and NAD(P)H.

Figure 5.

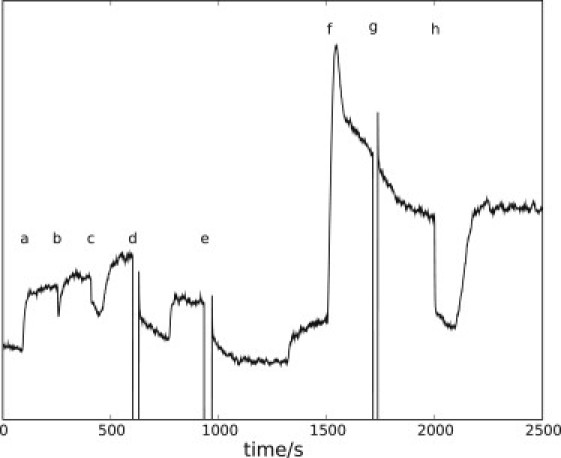
ACA, O₂, and KCN responses of starved yeast cells. A representative trace of NAD(P)H fluorescence from starved yeast cells treated with ACA, O₂, and KCN is shown. The labels indicate the depletion of O₂ in suspension (a) (see text); addition of 30 μl 0.005 M ACA (b); addition of 15 μl 0.05 M ACA (c); bubbling O₂ through suspension for 10 s (d); bubbling O₂ through suspension for 20 s (e); addition of 100 μl 0.1 M KCN (f); bubbling O₂ through suspension for 10 s (g); and addition of 15 μl 0.05 M ACA (h). Note that huge changes in fluorescence are possible without addition of glucose.

Acetaldehyde addition

Addition of ACA to starved yeast cells results in a rapid decrease in fluorescence, independent of cyanide addition (Fig. 5, b, c, and h). This supports the idea that ACA is rapidly converted into ethanol (EtOH) by the NADH-consuming alcohol dehydrogenase (ADH). However, addition of the same amount of ACA to the cells at low and high fluorescence (Fig. 5, c and h, respectively) leads to dissimilar NAD(P)H decreases. This effect may be due to some ACA being converted to acetate by aldehyde dehydrogenase (ALDH) or to other reactions of minor activity in low-NADH conditions.

Ethanol, acetate, and cyanide responses

To evaluate the effects of EtOH, acetate (OAc), and KCN on NAD(P)H production, we fed starved yeast cells with EtOH and OAc in pulses with an amount of substance similar to that of the glucose pulse (Fig. 6). The oxygen jumps at Fig. 6, a and I, are not of equal size, which may be due to unequal oxygen amounts in the suspensions or slightly different cellular makeups. In fact, slight differences in cellular properties can be seen as an experimental variation from batch to batch and also during aging of cells. For instance, oscillation periods and shape vary a little (in Figs. 1 and 3, the periods are 38 and 40 s, respectively), and KCN addition to suspensions from different cell batches sometimes yields different responses (compare Fig. 5, f, and Fig. 6, II, as well as Fig. S6), indicating the dependence of cellular makeup on the harvesting point (5).

Figure 6.

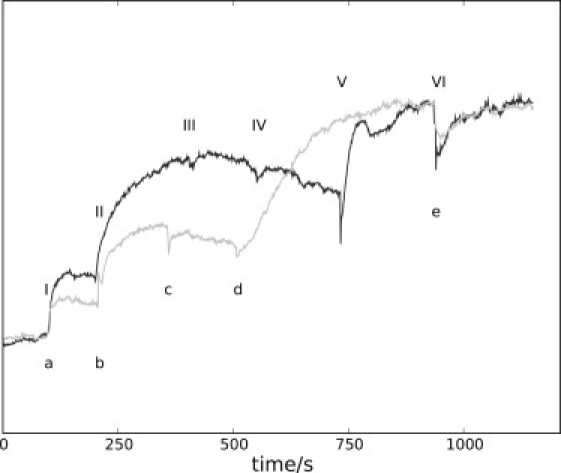
EtOH and KCN responses of starved yeast cells. Gray trace: O₂ depletion (a); addition of 50 μl 1 M EtOH (b); addition of 50 μl 1 M EtOH (c); addition of 100 μl 0.1 M KCN (d); and addition of 50 μl 1 M EtOH (e). Black trace: O₂ depletion (I); addition of 50 μl 0.1 M KCN (II); addition of 50 μl 0.1 M KCN (III); addition of 50 μl 0.1 M KCN (IV); addition of 100 μl 1 M EtOH (V); and addition of 100 μl 1 M EtOH (VI).

The KCN response is much stronger than the O₂ jump (Fig. 6, I and II). If the NAD(P)H level remains high, subsequent additions of KCN (Fig. 6, III and IV) do not give further increases in fluorescence, indicating that the effects of the given CN⁻ amount are mostly due either to inhibitions or to a saturation of reactions. CN⁻ is known to react with α-keto-acids (e.g., Pyr (9) and ACA (10)) to form cyanohydrins. However, these levels are low in starved cells. But even with no O₂, Pyr, or ACA present (Fig. 6, II), CN⁻ strongly increases fluorescence, suggesting other impacts on metabolism as well. At this point, addition of an EtOH pulse (Fig. 6, V) produces an immediate drop followed by an increase in the concentration of NAD(P)H, as expected. Paradoxically, the concentration of NADH will not increase further after another EtOH pulse (Fig. 6, VI). An explanation for this could be that the primary EtOH metabolizing pathways are clogged due to the large amount of added EtOH and the lack of oxygen. The immediate drop observed reveals secondary, NADH-consuming effects of EtOH.

Adding EtOH before KCN produces similar responses. The first addition increases fluorescence (Fig. 6, b), but a subsequent addition (Fig. 6, c) leads to small decreases in the NAD(P)H trace. The increase in NAD(P)H is stronger when KCN is added after, rather than before, an EtOH pulse (Fig. 6, d vs. II), indicating that CN⁻ indeed reacts with ACA.

Acetate (OAc) diffuses poorly into cells at a pH equal to that of the extracellular medium, and additions of OAc only led to small impacts on the NAD(P)H level. However, OAc is able to quench glycolytic oscillations if added in the right phase and amount (Fig. S2). Using glycerol as a carbon source did not have any effect on fluorescence, indicating that reactions leading from DHAP to glycerol are almost irreversible under normal conditions.

Our observations show that (disregarding experimental variation) starved cells are in a metabolic state capable of responding quickly to redox changes in the surroundings, although no high-energy carbon source is present.

Modeling

The aim of this study is to modify Model-0 to improve its description of cell behavior 1), before glucose, 2), at glucose addition, and 3), at glucose depletion. In accordance with the findings reported above, we modify Model-0 without sacrificing the overall satisfactory description of the amplitude and period of oscillations during glucose consumption (see also section S2 in in the Supporting Material). Specifically, the extended model should conform to the following criteria:

• 1.It must retain the oscillatory dynamics seen in the open system and retain a good correlation between experimentally measured concentrations and simulated concentrations.
• 2.It must display the significant features of the closed-system experiments, i.e., the initial spike and the final rise in NAD(P)H.
• 3.Beside new structural models, only the V_j values of the system should be changed, as these are subject to the greatest uncertainty in vivo.

Stoichiometry

Network stoichiometry induces dynamic constraints on the concentration changes arising from conservation of mass. [NADH] + [NAD], for example, must be conserved on the timescale of oscillations. From the reaction network constituting Model-0 (see Fig. 2), it can be seen that NADH is produced only at the GAPDH reaction, whereas NADH is consumed in both the glycerol- and ethanol-producing reactions. Due to stoichiometry, NADH eventually becomes depleted in simulations (Fig. 1, b). As the opposite is seen in experiments, additional production of NADH must take place. Figs. 5 and 6 also show that restoration of NAD(P)H levels occurs readily even without a glucose pulse.

A complete list of reactions involving NADH/NAD can be found at www.yeastgenome.org. A likely candidate for an NADH-producing reaction is the conversion of ACA to OAc catalyzed by ALDH. However, OAc production is known to be much lower than EtOH production. Other possibilities for NAD(P)H adjustment may be glutathione and amino acid conversions acting as redox buffers.

A puzzling fact from experiments is that the biggest overall increase in NAD(P)H is seen around glucose depletion. Intuitively, one would guess that the final fermentative reaction between ACA and EtOH (NADH-consuming) would imply a huge decrease upon glucose depletion, as ΔG′ is very low for this reaction. In the closed system, the accumulated reservoir of extracellular ACA must thus be depleted in reactions giving rise to a total increase in the NAD(P)H level. This indeed gives rise to a very precise regulation of ACA, e.g., deflection of carbon from ADH or inactivation of ADH during glucose depletion. In Model-0, all carbon from 1,3-BPG is eventually converted into ACA, as the PDC-catalyzed reaction is more or less irreversible (due to the expel of CO₂). ADH inactivation during glucose depletion is unlikely for two reasons: 1), addition of EtOH to starved cells gives rise to a steep NAD(P)H increase (Fig. 6, a), so an uninhibited and reversible ADH reaction is needed; and 2), ACA is toxic.

A deflection of carbon from ACA therefore seems the more probable mechanism. Regulation of ACA production at low high-energy carbon levels can also partly explain the first spike of NAD(P)H seen upon glucose addition, because of the delay in ADH activation.

Extended model

We made four structural changes to the enzymatic model (see sections S8 and S9 in the Supporting Material for the complete Model-1, including notes about changes compared to Model-0):

• 1.To implement carbon deflection, we used a hypothetical Pyr outflow (Michaelis-Menten kinetics) with a very small velocity (in simulations, the flux is >25 times smaller than the PDC flux).
• 2.Using a nonessential activation model (11), we regulated the PDC reaction such that the activity becomes low at low G6P levels.
• 3.We used kinetic data from Ganzhom et al. (12) to change the ADH reaction from an irreversible Michaelis-Menten type to a reversible ordered Bi Bi mechanism (13).
• 4.Crude models of the ACA-to-OAc conversion (ALDH) and OAc diffusion were inserted in agreement with our experimental observations. However, due to limited kinetic information we reduced the reaction velocity to near insignificance.

From the 24 reactions and 18 metabolites (of which four are present both intra- and extracellularly and two are conserved) of Model-0, the extended model now has 27 reactions and 19 metabolites. As noted above, changing Model-0 this way yielded simulations in which the amplitude and period of oscillations, as well as time for glucose consumption, were significantly different from the experimental data, necessitating parameter changes. As described below, we lowered the V_max of the glucose transporter to slow down the glycolytic flux. Due to its low sensitivity in the system, this had to be changed drastically. To tune the amplitude of oscillations, we modified the maximal velocities of HK, PFK, ATPase, and glycogen buildup reactions manually, building upon a previous analysis of the amplitude and frequency dependencies of enzymes in the open-flow model (8). Finally, the rate constant for the unspecific ACA + CN⁻ reaction was increased, in agreement with Richard et al. (10). The period of oscillations was then fitted to experimental values by rescaling all maximal velocities as explained above. A simulation profile of the resulting model, called Model-1, is shown in Fig. 7.

Figure 7.

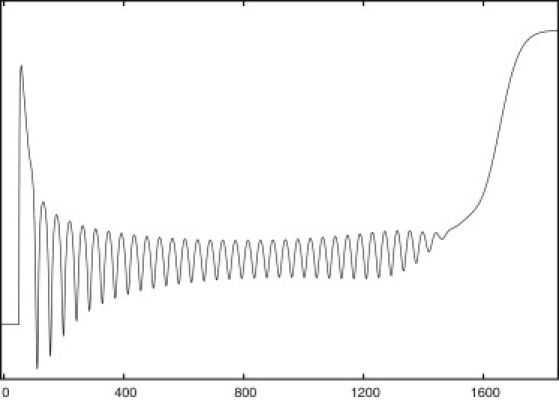
Simulation of Model-1 upon 24 mM glucose pulse addition.

Simulations

Fig. 7 shows that the model now produces both an initial spike in NADH and a general increase in NADH at glucose depletion that are consistent with experimental findings. In addition, the oscillatory subdomain satisfactorily describes Hopf oscillations with a slowly declining amplitude, as seen in closed-system experiments. In Fig. 7, note that the amplitude changes a little along the oscillatory subdomain. This property is frequently seen in experiments. In the model, we can easily decrease or increase this property primarily by fine-tuning the maximal velocities of the glucose transporter, the storage reaction, or PDC.

The initial spike in Fig. 7 displays features similar to those of the spike seen in Fig. 1—a steep increase preceding a slower decrease. However, the spikes do not seem as pronounced as in experiments. Also, unlike in experiments, the oscillations begin right after the spike, but this may be due to the model simulating only a single cell. In experiments, synchronized oscillations take place only after extracellular substances (primarily ACA) begin to oscillate.

It is significant that the model only begins stable oscillations after addition of CN⁻—consistent with experiments. With no CN⁻, only damped oscillations are seen (see Fig. S4). Although CN⁻ apparently has a number of unknown influences on yeast cells, the modeled cyanohydrin reaction is sufficient to describe the lowering of extracellular ACA (in simulations from ∼0.11 mM to 0.05 mM, without and with CN⁻, respectively) into the oscillatory domain.

In simulations, there are three main reasons for the final rise in NAD(P)H seen at glucose depletion in closed-system experiments: 1), a slower flux through glycolysis causing a slower decline of metabolites as glucose depletes; 2), a Pyr outflow that causes a breakage of the tight stoichiometric link between GAPDH and ADH (it is thus essential that the outflow happens before the regulated PDC reaction); and 3), a reversible ADH reaction to produce NADH when ACA is drained from the system. ACA emerges as a central entity in the metabolic regulation of starved yeast cells. As predicted, simulations show that a smooth final NADH increase is only possible if ACA is regulated such that it is virtually depleted in the entire closed system.

Discussion

In this study, we have modeled the central metabolism of starved yeast cells at a nonstationary operating point and during metabolic switching. We have demonstrated experimentally that the dynamics of the oscillations in open-flow experiments and in the oscillatory domain of transient experiments are very similar. This behavior can be reproduced very well by Model-0, allowing for extensive reuse of Model-0 in developing Model-1, which is capable of reproducing transient oscillations in closed-system experiments.

In Model-1, we have fixed some of the discrepancies of Model-0 by adding reactions that are of minor importance when glucose concentration is high but determine the dynamic behavior at low glucose concentrations. Discrepancies still present in Model-1 are 1), the oscillations in Model-1 start immediately after the addition of glucose, whereas in the experiments they are delayed until the addition of KCN; and 2), the intermediate metabolite levels are somewhat too low (see section S2 in the Supporting Material). A thorough search in parameter space may find more optimal parameter combinations where these discrepancies are alleviated. Typically, however, optimizing a model against some properties weakens the description of other properties (as seen here). We cannot exclude the possibility that the model is structurally insufficient. Another general limitation in the described models is that we implicitly assume that all yeast cells oscillate in synchrony. In most cases, this is a very good approximation, but the validity could be investigated by modeling the dynamics of a partially synchronized population of nonidentical yeast cells. This will be treated in a separate article.

Comparison of open and closed experiments

The sensitive dependence of yeast oscillations on the harvesting time has been reported by Richard et al. (5). Despite the cellular heterogeneity of freshly prepared yeast cells obtained by aerobic growth, the basic oscillatory dynamics is to a large extent reproducible from batch to batch, which indicates that the oscillatory dynamics is a robust property arising even though the variations between individual cells and cell cultures are significant. The main difference between the closed system during glucose consumption and the similar open system is that the operating point of the pseudo-steady state in the first system changes with the almost linear decrease of external glucose concentration and increase in waste products (EtOH, OAc, glycerol, and cyanohydrin), whereas it is constant in the CSTR. In CSTR experiments, we observe that the amplitude of oscillations depends on the distance of the operating point from the bifurcation point. Thus, we expect that the oscillations in the closed system should go through an inverse Hopf bifurcation and that the amplitude of the limit cycle should decrease and abruptly become zero at the bifurcation point. Due to critical slowing down when the system passes the bifurcation point at a finite speed, a gradual decrease of the amplitude is expected. This is to some degree observed in the experiments, although more complicated amplitude changes, such as a decrease followed by an increase, are sometimes observed before the oscillations disappear. As observed, Model-1 is capable of reproducing both kinds of behavior. From the results of the open system, it is also expected that the frequency should remain almost constant during glucose consumption, which is in fact observed. The quenching behavior of the closed system is almost identical to that of the open system, demonstrating that the dynamics of the oscillatory subsystem can be largely considered as uncoupled from the comparatively slow concentration changes of glucose and EtOH.

Contrary to properties of the central oscillatory dynamics, some of the observed properties, for example, the O₂ jump, NAD(P)H spike, amplitude, and level of oscillations, etc., may differ somewhat from batch to batch, particularly at low glucose concentration, where relatively large differences are sometimes observed for responses due to KCN, EtOH, and other metabolites.

CN⁻, ACA, and the NADH link

Cyanide addition is not needed for producing the spike or final rise in NAD(P)H in closed-system experiments, but it is usually essential to produce glycolytic oscillations. The classical interpretation of the necessity for CN⁻ addition is that it ensures the inhibition of oxidative phosphorylation taking place in the mitochondrial membrane (see Fig. 5). If oxidative phosphorylation is active, the reoxidation of NADH disrupts the NAD/NADH feedback necessary to produce oscillations. Fig. 5 indicates that the yeast cells possess other means of restoring the redox status apart from oxidative phosphorylation. These probably include the glutathione system and amino acid conversions, many of which require NAD/NADH as a cofactor. Redox restoration could also stem from a small release of glucose from glycogenic sources.

CN⁻ has other influences on yeast metabolism that make it a much better inducer of oscillations than, e.g., azide. Most important is its reactions with ACA and Pyr, giving rise to cyanohydrins. The kinetic constant for the ACA + CN⁻ reaction was measured by Richard et al. (10) as on the order of 1.5 (Ms)⁻¹ at 25°C. (However, this value is probably much too high or is a typographical error, as this would consume all ACA and prevent cell oscillations. Our preliminary experimental results correspond to a value of 0.1 (Mmin)⁻¹.) Increasing the amounts of CN⁻ also decreased the amount of excreted EtOH, supporting a relatively high reaction rate (10). Our studies suggest that CN⁻ has even further impacts on metabolism (see, e.g., Fig. 6).

It is well established that ACA is of major importance to glycolytic oscillations. It serves as a synchronizing factor (14–16) due to its diffusive properties and pronounced effects on the redox status of the cell. In this study, we suggest that regulation of ACA production also determines much of the very reproducible closed-system dynamics of starved yeast cells at the transients in the beginning and end of a glucose pulse. We propose a diversion of carbon flux at the pyruvate node brought about through G6P regulation of PDC activity (PDC activation could also be achieved by other high-energy derivatives of glucose) combined with a pyruvate drain creating the excess NADH needed for reduction of ACA. Glucose activation of PDC can explain both the initial NADH spike and the final NADH increase due to a delay and decrease, respectively, in the activation of ADH. Many genes and enzyme activities are regulated by glucose (17,18) and it has been shown experimentally, that PDC activity increases upon glucose addition (19). In addition, using membrane-inlet mass spectrometry it has been found that the CO₂ production from yeast cells in a transient experiment decreases rapidly during the last ∼100 s. of transient oscillations, i.e., well before glucose depletion (Fig. 4 a in Poulsen et al. (20)).

However, part of the NAD(P)H dynamics could also stem from fluxes through the PPP, but as noted in the introduction, PPP flux is found to be negligible, suggesting the need for a closer investigation of the carbon flows across the biochemical pathways.

The drain of pyruvate we have left unspecified, but it may represent the well-known conversions of pyruvate and/or ACA into acetoin, 2-acetolactate, and acetoin derivatives, which are natural byproducts of fermentation and known to impart flavor in alcoholic beverages. Preliminary results using GC-MS show that higher-order alcohols increase in the extracellular medium during anaerobic fermentation. In addition, due to the exponential growth phase before starvation, pyruvate transaminations into alanine cannot be ruled out. The drainage highlights 1), the need for further investigations into the carbon sinks of the system; and 2), the importance of NADH regulation in minimizing fusel alcohols produced by fermentation.

Conclusions

The study presented here demonstrates that closed-system glycolytic oscillations can be described as the transient dynamics of a Hopf oscillator in a slowly changing environment. The similarity between the experimentally observed dynamic properties of the oscillations in open and closed systems during glucose consumption demonstrates that quenching experiments on transient oscillations can replace the more laborious experiments in a CSTR. We also show that Model-0 is a good starting point for extending the modeling of CSTR oscillations into the domain of transient oscillations. Our modeling results indicate that some regulation of ACA production is needed to explain the observed behavior, most likely a regulation of PDC. We demonstrate that a drainage of pyruvate is needed to model the observed smooth transition from the oscillatory regime to a nonoscillatory, slowly rising level of NAD(P)H when glucose is depleted. Quantitative modeling of realistic biological systems is hampered by the structural complexity of the biochemical network involved and the wide range of characteristic timescales for the dynamics. This study indicates that for this system, significant reduction in complexity can be obtained by considering this system as a Hopf oscillator driven through the bifurcation point by the slowly decreasing glucose concentration (transient bifurcation).